Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-18T22:05:45.117Z Has data issue: false hasContentIssue false
  • English
  • Français

Solitary waves in power-law deformable conduits with laminar or turbulent fluid flow

Published online by Cambridge University Press:  10 January 2020

Aaron G. Stubblefield Open the ORCID record for Aaron G. Stubblefield [Opens in a new window] ,
Marc Spiegelman  and
Timothy T. Creyts
Aaron G. Stubblefield*
Affiliation:
Lamont-Doherty Earth Observatory, Columbia University, Palisades, NY 10964, USA
Marc Spiegelman
Affiliation:
Lamont-Doherty Earth Observatory, Columbia University, Palisades, NY 10964, USA Department of Applied Physics and Applied Math, Columbia University, NY 10027, USA
Timothy T. Creyts
Affiliation:
Lamont-Doherty Earth Observatory, Columbia University, Palisades, NY 10964, USA
*
†Email address for correspondence: aaron@ldeo.columbia.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

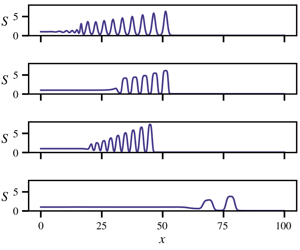
Fluid flow through pipe-like conduits embedded in viscously deformable material occurs in many natural systems, including magma transport in the Earth’s mantle and channelized water flow beneath glaciers. Here, we present and explore a model of fluid flow in viscously deformable conduits that unifies previously published models of magmatic and glacial systems. Previous results for magmatic systems have demonstrated the existence of solitary wave solutions for the case of laminar flow in Newtonian conduits. Here we extend these models to allow turbulent fluid flow in power-law materials consistent with models used in subglacial hydrology. The generalized model encompasses both laminar and turbulent fluid flow, and the solid matrix may deform according to any power-law rheology. A quasilinear approximation of the governing equations is introduced, along with an initial condition that develops into a perfect step shock. This initial condition is used in numerical solution of the full nonlinear system where a dispersive wave train forms at shock time. We show that solitary wave solutions exist for all parameters. Rheology-dependent flattening of the wave peaks is investigated. In the limit of a perfectly plastic matrix, the solitary waves approach square waves asymptotically. Motivated by subglacial hydrology models, we study the effect of discharge-dependent melting on evolution of the solitary waves. We find that melting focuses at the wave peaks, causing the waves to grow and accelerate over time.

JFM classification

Geophysical and Geological Flows: Magma and lava flow Geophysical and Geological Flows: Ice sheets Waves/Free-surface Flows: Solitary waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 886 , 10 March 2020 , A10
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adhikari, S., Ivins, E. R. & Larour, E. 2017 Mass transport waves amplified by intense Greenland melt and detected in solid Earth deformation. Geophys. Res. Lett. 44 (10), 4965–4975.CrossRefGoogle Scholar
Alnæs, M. S., Blechta, J., Hake, J., Johansson, A., Kehlet, B., Logg, A., Richardson, C., Ring, J., Rognes, M. E. & Wells, G. N. 2015 The FEniCS Project Version 1.5. Arch. Numer. Softw. 3 (100), 9–23.Google Scholar
Barcilon, V. & Lovera, O. M. 1989 Solitary waves in magma dynamics. J. Fluid Mech. 204, 121–133.CrossRefGoogle Scholar
Barcilon, V. & Richter, F. M. 1986 Nonlinear waves in compacting media. J. Fluid Mech. 164, 429–448.CrossRefGoogle Scholar
Bell, R. E., Ferraccioli, F., Creyts, T. T., Braaten, D., Corr, H., Das, I., Damaske, D., Frearson, N., Jordan, T., Rose, K. et al. 2011 Widespread persistent thickening of the east antarctic ice sheet by freezing from the base. Science 331 (6024), 1592–1595.CrossRefGoogle Scholar
Bell, R. E., Tinto, K., Das, I., Wolovick, M., Chu, W., Creyts, T. T., Frearson, N., Abdi, A. & Paden, J. D. 2014 Deformation, warming and softening of Greenland’s ice by refreezing meltwater. Nat. Geosci. 7 (7), 497–502.CrossRefGoogle Scholar
Chandler, D. M., Wadham, J. L., Lis, G. P., Cowton, T., Sole, A., Bartholomew, I., Telling, J., Nienow, P., Bagshaw, E. B., Mair, D. et al. 2013 Evolution of the subglacial drainage system beneath the greenland ice sheet revealed by tracers. Nat. Geosci. 6 (3), 083101, 195–198.CrossRefGoogle Scholar
Clarke, G. K. C. 2003 Hydraulics of subglacial outburst floods – new insights from the Spring–Hutter formulation (Clarke, 2003).pdf. J. Glaciol. 49 (165), 299–313.CrossRefGoogle Scholar
Connolly, J. A. D. & Podladchikov, Y. Y. 1998 Compaction-driven fluid flow in viscoelastic rock. Geodinamica Acta 11 (2–3), 55–84.CrossRefGoogle Scholar
Creyts, T. T. & Clarke, G. K. C. 2010 Hydraulics of subglacial supercooling: theory and simulations for clear water flows. J. Geophys. Res. 115 (3), 1–21.CrossRefGoogle Scholar
Creyts, T. T. & Schoof, C. G. 2009 Drainage through subglacial water sheets. J. Geophys. Res. 114 (4), 1–18.CrossRefGoogle Scholar
Cuffey, K. M. & Paterson, W. S. B. 2010 The Physics of Glaciers. Academic Press.Google Scholar
Dallaston, M. C. & Hewitt, I. J. 2014 Free-boundary models of a meltwater conduit. Phys. Fluids 26 (8), 1–21.CrossRefGoogle Scholar
Evatt, G. W. 2015 Röthlisberger channels with finite ice depth and open channel flow. Ann. Glaciol. 56 (70), 45–50.CrossRefGoogle Scholar
Fowler, A. C. 1982 Waves on glaciers. J. Fluid Mech. 120 (6), 283–321.CrossRefGoogle Scholar
Fowler, A. C. 1999 Breaking the seal at Grímsvötn, Iceland. J. Glaciol. 45 (151), 24–29.CrossRefGoogle Scholar
Glen, J. W. 1958 The flow law of ice: a discussion of the assumptions made in glacier theory, their experimental foundations and consequences. I.A.H.S. Publ. 47, 171–183.Google Scholar
Grimshaw, R. H. J., Helfrich, K. R. & Whitehead, J. A. 1992 Conduit solitary waves in a visco-elastic medium. Geophys. Astrophys. Fluid Dyn. 65 (1–4), 127–147.CrossRefGoogle Scholar
Helfrich, K. R. & Whitehead, J. A. 1990 Solitary waves on conduits of buoyant fluid in a more viscous fluid. Geophys. Astrophys. Fluid Dyn. 51 (1–4), 35–52.CrossRefGoogle Scholar
Hewitt, I. J. 2011 Modelling distributed and channelized subglacial drainage: the spacing of channels. J. Glaciol. 57 (202), 302–314.CrossRefGoogle Scholar
Hewitt, I. J. 2013 Seasonal changes in ice sheet motion due to melt water lubrication. Earth Planet. Sci. Lett. 371–372, 16–25.CrossRefGoogle Scholar
Hewitt, I. J. & Fowler, A. C. 2008 Seasonal waves on glaciers. Hydrol. Process. 22, 3919–3930.CrossRefGoogle Scholar
Hewitt, I. J., Schoof, C. & Werder, M. A. 2012 Flotation and free surface flow in a model for subglacial drainage. Part 2. Channel flow. J. Fluid Mech. 702, 157–187.CrossRefGoogle Scholar
Kalousová, K., Souček, O., Tobie, G., Choblet, G. & Čadek, O. 2014 Ice melting and downward transport of meltwater by two-phase flow in Europa’s ice shell. J. Geophys. Res. E 119 (3), 532–549.CrossRefGoogle Scholar
Keller, T., May, D. A. & Kaus, B. J. P. 2013 Numerical modelling of magma dynamics coupled to tectonic deformation of lithosphere and crust. Geophys. J. Intl 195 (3), 1406–1442.CrossRefGoogle Scholar
Logg, A., Mardal, K.-A. & Wells, G.(Eds) 2012 Automated Solution of Differential Equations by the Finite Element Method, vol. 84. Springer.CrossRefGoogle Scholar
Lowman, N. K. & Hoefer, M. A. 2013a Dispersive hydrodynamics in viscous fluid conduits. Phys. Rev. E 88 (2), 1–11.Google Scholar
Lowman, N. K. & Hoefer, M. A. 2013b Dispersive shock waves in viscously deformable media. J. Fluid Mech. 718, 524–557.CrossRefGoogle Scholar
Lowman, N. K., Hoefer, M. A. & El, G. A. 2014 Interactions of large amplitude solitary waves in viscous fluid conduits. J. Fluid Mech. 750, 372–384.CrossRefGoogle Scholar
Maiden, M. D. & Hoefer, M. A. 2016 Modulations of viscous fluid conduit periodic waves. Proc. R. Soc. Lond. A 472 (2196), 20160533.CrossRefGoogle Scholar
Maiden, M. D., Lowman, N. K., Anderson, D. V., Schubert, M. E. & Hoefer, M. A. 2016 Observation of dispersive shock waves, solitons, and their interactions in viscous fluid conduits. Phys. Rev. Lett. 116 (17), 174501.CrossRefGoogle ScholarPubMed
Meyer, C., Hewitt, I. & Neufeld, J. 2017 Turbulent flow through channels in a viscously deforming matrix. In APS Meeting Abstracts. American Physical Society.Google Scholar
Meyer, C. R., Fernandes, M. C., Creyts, T. T. & Rice, J. R. 2016 Effects of ice deformation on Röthlisberger channels and implications for transitions in subglacial hydrology. J. Glaciol. 62 (234), 750–762.CrossRefGoogle Scholar
Nye, J. F. 1953 The flow law of ice from measurements in glacier tunnels, laboratory experiments and the Jungfraufirn Borehole experiment. Proc. R. Soc. Lond. A 219 (1139), 477–489.Google Scholar
Nye, J. F. 1976 Water flow in glaciers: jokulhaups, tunnels, and veins. J. Glaciol. 76 (17), 181–207.CrossRefGoogle Scholar
Olson, P. & Christensen, U. 1986 Solitary wave propagation in a fluid conduit within a viscous matrix. J. Geophys. Res. 91 (B6), 6367–6374.CrossRefGoogle Scholar
Röthlisberger, H. 1972 Water pressure in intra- and subglacial channels. J. Glaciol. 11 (62), 177–203.CrossRefGoogle Scholar
Schoof, C., Hewitt, I. J. & Werder, M. A. 2012 Flotation and free surface flow in a model for subglacial drainage. Part 1. Distributed drainage. J. Fluid Mech. 702, 126–156.CrossRefGoogle Scholar
Scott, D. R. & Stevenson, D. J. 1984 Magma solitons. Geophys. Res. Lett. 11 (11), 1161–1164.CrossRefGoogle Scholar
Scott, D. R., Stevenson, D. J. & Whitehead, J. A. 1986 Observations of solitary waves in a viscously deformable pipe. Nature 319, 759–761.CrossRefGoogle Scholar
Siegfried, M. R., Fricker, H. A., Carter, S. P. & Tulaczyk, S. 2016 Episodic ice velocity fluctuations triggered by a subglacial flood in West Antarctica. Geophys. Res. Lett. 43 (6), 2640–2648.CrossRefGoogle Scholar
Simpson, G. & Spiegelman, M. 2011 Solitary wave benchmarks in magma dynamics. J. Sci. Comput. 49 (3), 268–290.CrossRefGoogle Scholar
Simpson, G. & Weinstein, M. I. 2008 Asymptotic stability of ascending solitary magma waves. SIAM J. Math. Anal. 40 (4), 1337–1391.CrossRefGoogle Scholar
Simpson, G., Weinstein, M. I. & Rosenau, P. S. 2008 On a Hamiltonian PDE arising in magma dynamics. Discrete Continuous Dyn. Syst. Ser. B 10 (4), 903–924.CrossRefGoogle Scholar
Spencer, J. R. & Nimmo, F. 2013 Enceladus: an active ice world in the Saturn system. Annu. Rev. Earth Planet. Sci. 41 (1), 693–717.CrossRefGoogle Scholar
Spiegelman, M. 1993a Flow in deformable porous media. Part 1. Simple analysis. J. Fluid Mech. 247, 17–37.CrossRefGoogle Scholar
Spiegelman, M. 1993b Flow in deformable porous media. Part 2. Numerical analysis – the relationship between shock waves and solitary waves. J. Fluid Mech. 247, 39–63.CrossRefGoogle Scholar
Spohn, T. & Schubert, G. 2003 Oceans in the icy Galilean satellites of Jupiter. Icarus 161 (2), 456–467.CrossRefGoogle Scholar
Yarushina, V. M., Podladchikov, Y. Y. & Connolly, J. A. D. 2015 (de) compaction of porous viscoelastoplastic media: solitary porosity waves. J. Geophys. Res. 120 (7), 4843–4862.CrossRefGoogle Scholar