Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-18T21:51:18.646Z Has data issue: false hasContentIssue false
  • English
  • Français

Impact of centrifugal buoyancy on strato-rotational instability

Published online by Cambridge University Press:  11 March 2020

Juan M. Lopez Open the ORCID record for Juan M. Lopez [Opens in a new window]  and
Francisco Marques
Juan M. Lopez*
Affiliation:
School of Mathematical and Statistical Sciences, Arizona State University, Tempe, AZ85287, USA
Francisco Marques
Affiliation:
Departament de Física Aplicada, Univ. Politècnica de Catalunya, Barcelona08034, Spain
*
†Email address for correspondence: juan.m.lopez@asu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

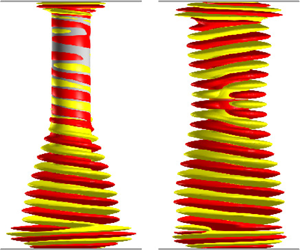
In a recent experiment on the flow between two concentric cylinders with the inner cylinder rotating and the fluid being stably stratified, Flór et al. (Phys. Fluids, vol. 30, 2018, 084103) found helical wave structures confined to the inner cylinder in an annulus with small inner-to-outer radius ratio (very large gap) in regimes where the Froude number (ratio of cylinder rotation frequency to buoyancy frequency) is less than one. These helical waves were reported to originate at the corners where the inner cylinder meets the top and bottom boundaries, and were found to be asymmetric with the lower helical wave being more intense. These observations are in marked contrast with other stratified Taylor–Couette experiments that employed much larger inner-to-outer radius ratios and much larger annulus height-to-gap ratios. Here, we present direct numerical simulations of the Navier–Stokes equations, with a Boussinesq approximation that accounts for centrifugal buoyancy effects which are normally neglected. Fixing the stratification and increasing the rotation rate of the inner cylinder (quantified by a Reynolds number), we find a sequence of bifurcations, each one introducing a new frequency, from the steady base state to a three-torus state. The instabilities are generated at the corners where the inner cylinder meets the endwalls, and the first instability is localized at the lower corner as a consequence of centrifugal buoyancy effects. We have also conducted simulations without centrifugal buoyancy and find that centrifugal buoyancy plays a crucial role in breaking the up–down reflection symmetry of the problem, capturing the most salient features of the experimental observations.

JFM classification

Geophysical and Geological Flows: Stratified flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 890 , 10 May 2020 , A9
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abshagen, J., Lopez, J. M., Marques, F. & Pfister, G. 2005a Mode competition of rotating waves in reflection-symmetric Taylor–Couette flow. J. Fluid Mech. 540, 269–299.CrossRefGoogle Scholar
Abshagen, J., Lopez, J. M., Marques, F. & Pfister, G. 2005b Symmetry breaking via global bifurcations of modulated rotating waves in hydrodynamics. Phys. Rev. Lett. 94, 074501.CrossRefGoogle Scholar
Abshagen, J., Lopez, J. M., Marques, F. & Pfister, G. 2008 Bursting dynamics due to a homoclinic cascade in Taylor–Couette flow. J. Fluid Mech. 613, 357–384.CrossRefGoogle Scholar
Ahlers, G. & Cannell, D. S. 1983 Vortex-front propagation in rotating Couette–Taylor flow. Phys. Rev. Lett. 50, 1583–1586.CrossRefGoogle Scholar
Avila, M. 2012 Stability and angular-momentum transport of fluid flows between corotating cylinders. Phys. Rev. Lett. 108, 124501.CrossRefGoogle ScholarPubMed
Avila, M., Grimes, M., Lopez, J. M. & Marques, F. 2008 Global endwall effects on centrifugally stable flows. Phys. Fluids 20, 104104.CrossRefGoogle Scholar
Barcilon, V. & Pedlosky, J. 1967 On the steady motions produced by a stable stratification in a rapidly rotating fluid. J. Fluid Mech. 29, 673–690.CrossRefGoogle Scholar
Benjamin, T. B. 1978a Bifurcation phenomena in steady flows of a viscous fluid. I. Theory. Proc. R. Soc. Lond. A 359, 1–26.Google Scholar
Benjamin, T. B. 1978b Bifurcation phenomena in steady flows of a viscous fluid. II. Experiments. Proc. R. Soc. Lond. A 359, 27–43.Google Scholar
Benjamin, T. B. & Mullin, T. 1981 Anomalous modes in the Taylor experiment. Proc. R. Soc. Lond. A 377, 221–249.Google Scholar
Boubnov, B. M., Gledzer, E. B. & Hopfinger, E. J. 1995 Stratified circular Couette flow: instability and flow regimes. J. Fluid Mech. 292, 333–358.CrossRefGoogle Scholar
Boubnov, B. M., Gledzer, E. B., Hopfinger, E. J. & Orlandi, P. 1996 Layer formation and transitions in stratified circular Couette flow. Dyn. Atmos. Oceans 23, 139–153.CrossRefGoogle Scholar
Caton, F., Janiaud, B. & Hopfinger, E. J. 2000 Stability and bifurcations in stratified Taylor–Couette flow. J. Fluid Mech. 419, 93–124.CrossRefGoogle Scholar
Cliffe, K. A., Kobine, J. J. & Mullin, T. 1992 The role of anomalous modes in Taylor–Couette flow. Proc. R. Soc. Lond. A 439, 341–357.Google Scholar
Curbelo, J., Lopez, J. M., Mancho, A. M. & Marques, F. 2014 Confined rotating convection with large Prandtl number: centrifugal effects on wall modes. Phys. Rev. E 89, 013019.Google ScholarPubMed
Czarny, O., Serre, E., Bontoux, P. & Lueptow, R. M. 2002 Interaction between Ekman pumping and the centrifugal instability in Taylor–Couette flow. Phys. Fluids 15, 467–477.CrossRefGoogle Scholar
Flór, J. B., Hirschberg, L., Oostenrijk, B. H. & van Heijst, G. J. F. 2018 Onset of centrifugal instability at a rotating cylinder in a stratified fluid. Phys. Fluids 30, 084103.CrossRefGoogle Scholar
Gellert, M. & Rüdiger, G. 2009 Stratorotational instability in Taylor–Couette flow heated from above. J. Fluid Mech. 623, 375–385.CrossRefGoogle Scholar
Hart, J. E. 1979 Finite amplitude baroclinic instability. Annu. Rev. Fluid Mech. 11, 147–172.CrossRefGoogle Scholar
Hua, B. L., Le Gentil, S. & Orlandi, P. 1997 First transitions in circular Couette flow with axial stratification. Phys. Fluids 9, 365–375.CrossRefGoogle Scholar
Ibanez, R., Swinney, H. L. & Rodenborn, B. 2016 Observations of the stratorotational instability in rotating concentric cylinders. Phys. Rev. Fluids 1, 053601.CrossRefGoogle Scholar
Le Bars, M. & Le Gal, P. 2007 Experimental analysis of the stratorotational instability in a cylindrical Couette flow. Phys. Rev. Lett. 99, 064502.CrossRefGoogle Scholar
Le Dizès, S. & Riedinger, X. 2010 The strato-rotational instability of Taylor–Couette and Keplerian flows. J. Fluid Mech. 660, 147–161.CrossRefGoogle Scholar
Leclereq, C., Nguyen, F. & Kerswell, R. R. 2016 Connections between centrifugal, stratorotational, and radiative instabilities in viscous Taylor–Couette flow. Phys. Rev. E 94, 043103.Google Scholar
Lopez, J. M. 2016 Subcritical instability of finite circular Couette flow with stationary inner cylinder. J. Fluid Mech. 793, 589–611.CrossRefGoogle Scholar
Lopez, J. M. & Marques, F. 2014 Three-dimensional instabilities in a discretely heated annular flow: onset of spatio-temporal complexity via defect dynamics. Phys. Fluids 26, 064102.CrossRefGoogle Scholar
Lopez, J. M., Marques, F. & Avila, M. 2013 The Boussinesq approximation in rapidly rotating flows. J. Fluid Mech. 737, 56–77.CrossRefGoogle Scholar
Lopez, J. M., Marques, F. & Shen, J. 2000 Endwall effects in a periodically forced centrifugally unstable flow. Fluid Dyn. Res. 27, 91–108.CrossRefGoogle Scholar
Lorenzen, A., Pfister, G. & Mullin, T. 1983 End effects on the transition to time-dependent motion in the Taylor experiment. Phys. Fluids 26, 10–13.CrossRefGoogle Scholar
Marques, F. & Lopez, J. M. 2006 Onset of three-dimensional unsteady states in small aspect-ratio Taylor–Couette flow. J. Fluid Mech. 561, 255–277.CrossRefGoogle Scholar
Marques, F., Mercader, I., Batiste, O. & Lopez, J. M. 2007 Centrifugal effects in rotating convection: axisymmetric states and three-dimensional instabilities. J. Fluid Mech. 580, 303–318.CrossRefGoogle Scholar
Molemaker, M. J., McWilliams, J. C. & Yavneh, I. 2001 Instability and equilibration of centrifugally stable stratified Taylor–Couette flow. Phys. Rev. Lett. 86, 5270–5273.CrossRefGoogle ScholarPubMed
Park, J. & Billant, P. 2013 The stably stratified Taylor–Couette flow is always unstable except for solid-body rotation. J. Fluid Mech. 725, 262–280.CrossRefGoogle Scholar
Park, J., Billant, P., Baik, J.-J. & Seo, J. M. 2018 Competition between the centrifugal and strato-rotational instabilities in the stratified Taylor–Couette flow. J. Fluid Mech. 840, 5–24.CrossRefGoogle Scholar
Plougonven, R. & Zhang, F. 2014 Internal gravity waves from atmospheric jets and fronts. Rev. Geophys. 52, 33–76.CrossRefGoogle Scholar
Riedinger, X., Le Dizès, S. & Meunier, P. 2011 Radiative instability of the flow around a rotating cylinder in a stratified fluid. J. Fluid Mech. 672, 130–146.CrossRefGoogle Scholar
Rubio, A., Lopez, J. M. & Marques, F. 2010 Onset of Küppers–Lortz-like dynamics in finite rotating thermal convection. J. Fluid Mech. 644, 337–357.CrossRefGoogle Scholar
Rüdiger, G., Seelig, T., Schultz, M., Gellert, M., Egbers, C. & Harlander, U. 2017 The stratorotational instability of Taylor–Couette flows with moderate Reynolds numbers. Geophys. Astrophys. Fluid Dyn. 111, 429–447.CrossRefGoogle Scholar
Seelig, T., Harlander, U. & Gellert, M. 2018 Experimental investigation of stratorotational instability using a thermally stratified system: instability, waves and associated momentum flux. Geophys. Astrophys. Fluid Dyn. 112, 239–264.CrossRefGoogle Scholar
Shalybkov, D. & Rüdiger, G. 2005 Stability of density-stratified viscous Taylor–Couette flows. Astron. Astrophys. 438, 411–417.CrossRefGoogle Scholar
Taylor, G. I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. A 223, 289–343.Google Scholar
Yavneh, I., McWilliams, J. C. & Molemaker, M. J. 2001 Non-axisymmetric instability of centrifugally stable stratified Taylor–Couette flow. J. Fluid Mech. 448, 1–21.CrossRefGoogle Scholar

Lopez and Marques supplementary movie 1

Animations of the two rotating waves found neglecting centrifugal buoyancy: the centrosymmetric rotating wave at Re=6150 and the reflection symmetric rotating wave at Re=6250.

Download Lopez and Marques supplementary movie 1(Video)
Video 364.7 KB

Lopez and Marques supplementary movie 2

Animation of the rotating wave accounting for centrifugal buoyancy, at Re=6100.

Download Lopez and Marques supplementary movie 2(Video)
Video 176.2 KB

Lopez and Marques supplementary movie 3

Animation of the modulated rotating wave accounting for centrifugal buoyancy, at Re=6500, shown both in the inertial (laboratory) and the rotating frames of reference.
Download Lopez and Marques supplementary movie 3(Video)
Video 7 MB

Lopez and Marques supplementary movie 4

Animation of the 3-frequency modulated rotating wave accounting for centrifugal buoyancy, at Re=6510, shown both in the inertial (laboratory) and the rotating frames of reference.
Download Lopez and Marques supplementary movie 4(Video)
Video 6 MB