Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-26T13:02:17.041Z Has data issue: false hasContentIssue false
  • English
  • Français

Evolution of enstrophy in shock/homogeneous turbulence interaction

Published online by Cambridge University Press:  08 August 2012

Krishnendu Sinha
Krishnendu Sinha*
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Bombay, Mumbai 400076, India
*
†Email address for correspondence: krish@aero.iitb.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

Interaction of turbulent fluctuations with a shock wave plays an important role in many high-speed flow applications. This paper studies the amplification of enstrophy, defined as mean-square fluctuating vorticity, in homogeneous isotropic turbulence passing through a normal shock. Linearized Navier–Stokes equations written in a frame of reference attached to the unsteady shock wave are used to derive transport equations for the vorticity components. These are combined to obtain an equation that describes the evolution of enstrophy across a time-averaged shock wave. A budget of the enstrophy equation computed using results from linear interaction analysis and data from direct numerical simulations identifies the dominant physical mechanisms in the flow. Production due to mean flow compression and baroclinic torques are found to be the major contributors to the enstrophy amplification. Closure approximations are proposed for the unclosed correlations in the production and baroclinic source terms. The resulting model equation is integrated to obtain the enstrophy jump across a shock for a range of upstream Mach numbers. The model predictions are compared with linear theory results for varying levels of vortical and entropic fluctuations in the upstream flow. The enstrophy model is then cast in the form of 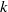– equations and used to compute the interaction of homogeneous isotropic turbulence with normal shocks. The results are compared with available data from direct numerical simulations. The equations are further used to propose a model for the amplification of turbulent viscosity across a shock, which is then applied to a canonical shock–boundary layer interaction. It is shown that the current model is a significant improvement over existing models, both for homogeneous isotropic turbulence and in the case of complex high-speed flows with shock waves.

JFM classification

Turbulent Flows: Compressible turbulence Aerodynamics: High-speed flow Turbulent Flows: Turbulence modelling
Type
Papers
Information
Journal of Fluid Mechanics , Volume 707 , 25 September 2012 , pp. 74 - 110
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Berndt, S. B. 1966 The vorticity jump across a flow discontinuity. J. Fluid Mech. 26 (3), 433–436.CrossRefGoogle Scholar
2. Bowersox, R. D. 2009 Extension of equilibrium turbulent heat flux models to high-speed shear flows. J. Fluid Mech. 633, 61–70.CrossRefGoogle Scholar
3. Guarini, S. E., Moser, R. D., Shariff, K. & Wray, A. 2000 Direct numerical simulation of a supersonic turbulent boundary layer at Mach 2.5. J. Fluid Mech. 414, 1–33.CrossRefGoogle Scholar
4. Hayes, W. D. 1957 The vorticity jump across a gasdynamic discontinuity. J. Fluid Mech. 3, 595–600.Google Scholar
5. Huang, P. G., Coleman, G. N. & Bradshaw, P. 1995 Compressible turbulent channel flows: DNS results and modelling. J. Fluid Mech. 305, 185–218.CrossRefGoogle Scholar
6. Jamme, S., Cazalbou, J.-B., Torres, F. & Chassaing, P. 2002 Direct numerical simulation of the interaction between a shock wave and various types of isotropic turbulence. Flow Turbul. Combust. 68, 227–268.CrossRefGoogle Scholar
7. Kevlahan, N. K.-R. 1997 The vorticity jump across a shock in a non-uniform flow. J. Fluid Mech. 341, 371–384.CrossRefGoogle Scholar
8. Kovasznay, L. S. G. 1953 Turbulence in supersonic flow. J. Aeronaut. Sci. 20 (10), 657–674.CrossRefGoogle Scholar
9. Larsson, J. & Lele, S. K. 2009 Direct numerical simulation of canonical shock/turbulence interaction. Phys. Fluids 21, 126101.CrossRefGoogle Scholar
10. Lee, S., Lele, S. K. & Moin, P. 1993 Direct numerical simulation of isotropic turbulence interacting with a weak shock wave. J. Fluid Mech. 251, 533–562.CrossRefGoogle Scholar
11. MacCormack, R. W. & Candler, G. V. 1989 The solution of the Navier–Stokes equations using Gauss–Seidel line relaxation. Comput. Fluids 17 (1), 135–150.CrossRefGoogle Scholar
12. Mahesh, K., Lele, S. K. & Moin, P. 1997 The influence of entropy fluctuations on the interation of turbulence with a shock wave. J. Fluid Mech. 334, 353–379.CrossRefGoogle Scholar
13. Pasha, A. A. & Sinha, K. 2008 Shock-unsteadiness model applied to oblique shock-wave/ turbulent boundary layer interaction. Intl J. Comput. Fluid Dyn. 22 (8), 569–582.CrossRefGoogle Scholar
14. Pasha, A. A. & Sinha, K. 2012 Simulation of hypersonic shock/turbulent boundary-layer interactions using shock-unsteadiness model. J. Propul. Power 28 (1), 46–60.CrossRefGoogle Scholar
15. Pirozzoli, S., Grasso, F. & Gatski, T. 2004 Direct numerical simulation and analysis of a spatially evolving supersonic turbulent boundary layer at . Phys. Fluids 16 (3), 530–545.CrossRefGoogle Scholar
16. Roy, C. J. & Blottner, F. G. 2006 Review and assessment of turbulence models for hypersonic flows. Prog. Aerosp. Sci. 42 (7–8), 469–530.CrossRefGoogle Scholar
17. Settles, G. S. & Dodson, L. J. 1994 Supersonic and hypersonic shock/boundary layer interaction database. AIAA J. 32 (7), 1377–1383.CrossRefGoogle Scholar
18. Sinha, K., Mahesh, K. & Candler, G. V. 2003 Modeling shock unsteadiness in shock/turbulence interaction. Phys. Fluids 15 (8), 2290–2297.CrossRefGoogle Scholar
19. Sinha, K., Mahesh, K. & Candler, G. V. 2005 Modeling the effect of shock unsteadiness in shock/turbulent boundary layer interactions. AIAA J. 43 (3), 586–594.CrossRefGoogle Scholar
20. Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence, p. 66. MIT.CrossRefGoogle Scholar
21. Thivet, F., Knight, D. D., Zheltovodov, A. A. & Maksimov, A. I. 2001 Insights in turbulence modeling for crossing-shock-wave/boundary-layer interactions. AIAA J. 39 (6), 985–995.CrossRefGoogle Scholar
22. Veera, V. K. & Sinha, K. 2009 Modelling the effect of upstream temperature fluctuations on shock/homogeneous turbulence interaction. Phys. Fluids 21, 025101.CrossRefGoogle Scholar
23. Wilcox, D. C. 1998 Turbulence Modelling for CFD, 2nd edn. p. 236. DCW Industries.Google Scholar
24. Wilcox, D. C. 2008 Formulation of the turbulence model revisited. AIAA J. 46 (11), 2823–2838.CrossRefGoogle Scholar