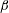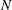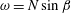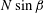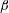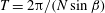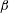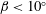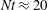1 Introduction
Topographic internal gravity waves are a major driver of turbulent mixing in the ocean that, in turn, is a key control on ocean stratification and the meridional overturning circulation. Internal waves and associated turbulence have been the subject of observational studies at several locations, e.g. continental slopes (Thorpe, Hall & White Reference Thorpe, Hall and White1990; Moum et al. Reference Moum, Caldwell, Nash and Gunderson2002; Nash et al. Reference Nash, Kunze, Toole and Schmitt2004), oceanic ridges (Aucan et al. Reference Aucan, Merrifield, Luther and Flament2006; Legg & Klymak Reference Legg and Klymak2008; Alford et al. Reference Alford, Peacock, MacKinnon, Nash, Buijsman, Centurioni, Chao, Chang, Farmer and Fringer2015) and deep rough topographies (Polzin et al. Reference Polzin, Toole, Ledwell and Schmitt1997; Ledwell et al. Reference Ledwell, Montgomery, Polzin, Laurent, Schmitt and Toole2000). The near-bottom flow created by internal waves at topography involves periodic modulation of stratification and shear. The flow may break down to turbulence (see e.g. Lamb Reference Lamb2014; Sarkar & Scotti Reference Sarkar and Scotti2017; and the references therein) through different scenarios that involve shear instability and/or convective instability. Thorpe (Reference Thorpe2018) highlights a difference between these scenarios: energy transfer to turbulent scales is primarily governed by the gradient Richardson number in shear instability and by wave steepness in convective instability. Turbulence from convective instability in a fluid that has otherwise stable stratification, especially when the statically unstable patch is near a wall, has received less attention than shear instability and is the focus of this paper.
Convective overturns have been identified in the context of breaking lee waves in observations (Alford, Klymak & Carter Reference Alford, Klymak and Carter2014) and two-dimensional simulations (Legg & Klymak Reference Legg and Klymak2008; Buijsman, Legg & Klymak Reference Buijsman, Legg and Klymak2012) of tidal flow over oceanic ridges. Turbulence at specific phases, notably from down- to upslope flow, has been traced to convective overturns in three-dimensional simulations of oscillating flow past steep model obstacles, e.g. a linear slope at critical angle (Gayen & Sarkar Reference Gayen and Sarkar2011a ), a triangular obstacle (Rapaka, Gayen & Sarkar Reference Rapaka, Gayen and Sarkar2013; Jalali, Rapaka & Sarkar Reference Jalali, Rapaka and Sarkar2014), a multiscale obstacle patterned after a transect of a ridge at Luzon Strait (Jalali & Sarkar Reference Jalali and Sarkar2017), and in the internal-wave-driven bottom boundary layer of lakes (Becherer & Umlauf Reference Becherer and Umlauf2011; Lorke, Umlauf & Mohrholz Reference Lorke, Umlauf and Mohrholz2015). Details of the breakdown of convective instability to turbulence in near-bottom internal waves have been examined using direct numerical simulation (DNS): generation of waves at a critical slope (Gayen, Sarkar & Taylor Reference Gayen, Sarkar and Taylor2010), reflection at critical and near-critical slopes (Chalamalla et al. Reference Chalamalla, Gayen, Scotti and Sarkar2013) and breaking of a solitary wave on a sloping bottom (Venayagamoorthy & Fringer Reference Venayagamoorthy and Fringer2007; Arthur & Fringer Reference Arthur and Fringer2014). Laboratory experiments (Lim, Ivey & Jones Reference Lim, Ivey and Jones2010) and observations (Bluteau, Jones & Ivey Reference Bluteau, Jones and Ivey2011) of internal waves at slopes also note convective instability in addition to shear instability.
Stratified flows have not only kinetic energy but also potential energy, of which only a fraction, the available potential energy (APE) first discussed by Lorenz (Reference Lorenz1955), can be released to flow and mixing. A positive definite expression of APE for arbitrary stratification (Holliday & McIntyre Reference Holliday and McIntyre1981) was used by Winters et al. (Reference Winters, Lombard, Riley and D’Asaro1995) to study different aspects of the potential energy field and energy transfer in a stratified fluid. Since then, the definition of APE, its approximations and its interpretation in different model problems have evolved in the literature (e.g. Roullet & Klein Reference Roullet and Klein2009; Winters & Barkan Reference Winters and Barkan2013; Scotti & White Reference Scotti and White2014).
We follow the approach of Scotti & White (Reference Scotti and White2014), who discuss the Lorenz energy cycle (LEC) approximations of APE, which is accurate to its quadratic limit, and introduce an evolution equation for the mean (MAPE) and turbulent (TAPE) components of available potential energy. This framework was used by Scotti (Reference Scotti2015) to distinguish energy pathways of shear-driven flow from those of convective instability. Unlike the present model problem of convective instability on a slope, Scotti (Reference Scotti2015) considered a statically unstable patch that was far from boundaries and was non-sloping.
Overturns in potential density profiles have been used as both a diagnostic (in field observations) and a prognostic (in ocean models) of dissipation rates and mixing using Thorpe sorting. The accuracy of Thorpe-sorted dissipation rates in internal-wave-driven turbulence is the subject of discussion (e.g. Mater et al. Reference Mater, Venayagamoorthy, Laurent and Moum2015; Jalali, Challamala & Sarkar Reference Jalali, Chalamalla and Sarkar2017) and it is possible that Thorpe sorting overestimates dissipation in convectively driven turbulence (Scotti Reference Scotti2015; Jalali et al. Reference Jalali, Chalamalla and Sarkar2017).
The mixing efficiency, fraction (
![]() $\unicode[STIX]{x1D6E4}$
) of the total energy loss rate that is used for the mixing of density, has received much attention in the literature on stratified turbulence because it quantifies the inevitable modification by small-scale processes of the large-scale stratification in the ocean. Although
$\unicode[STIX]{x1D6E4}$
) of the total energy loss rate that is used for the mixing of density, has received much attention in the literature on stratified turbulence because it quantifies the inevitable modification by small-scale processes of the large-scale stratification in the ocean. Although
![]() $\unicode[STIX]{x1D6E4}$
is typically assumed to be 0.2 in mixing parametrizations and in estimates derived from ocean observations, its measurements exhibit considerable variability. In particular, convective instability can drive mixing with
$\unicode[STIX]{x1D6E4}$
is typically assumed to be 0.2 in mixing parametrizations and in estimates derived from ocean observations, its measurements exhibit considerable variability. In particular, convective instability can drive mixing with
![]() $\unicode[STIX]{x1D6E4}$
that exceeds 50 % as shown in laboratory experiments (Dalziel et al.
Reference Dalziel, Patterson, Caulfield and Coomaraswamy2008; Wykes & Dalziel Reference Wykes and Dalziel2014), DNS and large-eddy simulations (LES) (Chalamalla & Sarkar Reference Chalamalla and Sarkar2015) conducted at high Rayleigh numbers, and DNS of an idealized Southern Ocean model (Sohail, Gayen & Hogg Reference Sohail, Gayen and Hogg2018). In shear-driven turbulence,
$\unicode[STIX]{x1D6E4}$
that exceeds 50 % as shown in laboratory experiments (Dalziel et al.
Reference Dalziel, Patterson, Caulfield and Coomaraswamy2008; Wykes & Dalziel Reference Wykes and Dalziel2014), DNS and large-eddy simulations (LES) (Chalamalla & Sarkar Reference Chalamalla and Sarkar2015) conducted at high Rayleigh numbers, and DNS of an idealized Southern Ocean model (Sohail, Gayen & Hogg Reference Sohail, Gayen and Hogg2018). In shear-driven turbulence,
![]() $\unicode[STIX]{x1D6E4}$
is likely to be dependent on the gradient Richardson number (
$\unicode[STIX]{x1D6E4}$
is likely to be dependent on the gradient Richardson number (
![]() $Ri_{g}$
) and buoyancy Reynolds number (
$Ri_{g}$
) and buoyancy Reynolds number (
![]() $Re_{b}$
) (Mashayek & Peltier Reference Mashayek and Peltier2013; Mater & Venayagamoorthy Reference Mater and Venayagamoorthy2014; Salehipour & Peltier Reference Salehipour and Peltier2015; Venayagamoorthy & Koseff Reference Venayagamoorthy and Koseff2016).
$Re_{b}$
) (Mashayek & Peltier Reference Mashayek and Peltier2013; Mater & Venayagamoorthy Reference Mater and Venayagamoorthy2014; Salehipour & Peltier Reference Salehipour and Peltier2015; Venayagamoorthy & Koseff Reference Venayagamoorthy and Koseff2016).
Central questions that are fundamental to internal-wave-driven near-bottom turbulence and also have implications for the diagnostic and prognostic ability of convective overturns with regards to turbulence are as follows: What is the rate at which the APE of a convective overturn is lost and how is this energy loss partitioned among kinetic energy dissipation and APE dissipation? What is the net amount of initial energy that is dissipated by turbulence? What are the salient characteristics of the turbulence that arises from a convective overturn on a slope? How do the answers to the previous three questions depend on slope steepness?

Figure 1. Schematic of the problem. Flow is induced by a convective instability introduced over a slope inclined at angle
![]() $\unicode[STIX]{x1D6FD}$
with the horizontal. The instability is imposed at
$\unicode[STIX]{x1D6FD}$
with the horizontal. The instability is imposed at
![]() $t=0$
through a density perturbation of amplitude
$t=0$
through a density perturbation of amplitude
![]() $\unicode[STIX]{x1D70C}_{p}$
and wavelength
$\unicode[STIX]{x1D70C}_{p}$
and wavelength
![]() $2\unicode[STIX]{x03C0}/m$
in
$2\unicode[STIX]{x03C0}/m$
in
![]() $z_{s}$
.
$z_{s}$
.
We address the aforementioned questions using simulations of a model problem, formulated in § 2, that is designed to study the behaviour of a near-bottom convective overturn in isolation, as an idealization motivated by recent observations of large isolated convective overturns in energetic regions (Aucan et al. Reference Aucan, Merrifield, Luther and Flament2006; Alford et al. Reference Alford, MacKinnon, Nash, Simmons, Pickering, Klymak, Pinkel, Sun, Rainville and Musgrave2011; Bluteau et al. Reference Bluteau, Jones and Ivey2011). In particular, an initial density disturbance with finite APE (but with zero initial mean kinetic energy and turbulence) is introduced in a stratified fluid over a slope (figure 1), and its evolution is followed for different values of the disturbance amplitude and slope angle. Then § 3 gives a summary of the diagnostics used for quantifying turbulence and energy pathways in the model problem. In § 4, we discuss the temporal variability of the mean flow and introduce linear theory to help explain the observed temporal oscillation. We delve into the nonlinear aspects of the flow that develops on a moderately sloped bottom in § 5. In § 6, the transfers among the four major energy reservoirs, namely mean and turbulent kinetic energy and available potential energy are discussed. Steeper slopes are discussed in § 7. The results are summarized and conclusions are drawn in § 8.
2 Formulation
2.1 Governing equations
The Navier–Stokes equations govern the velocity
![]() $\boldsymbol{u}=(u,v,w)$
and the density
$\boldsymbol{u}=(u,v,w)$
and the density
![]() $\unicode[STIX]{x1D70C}$
. The density is given by
$\unicode[STIX]{x1D70C}$
. The density is given by
![]() $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{b}(z)+\unicode[STIX]{x1D70C}^{\ast }(\boldsymbol{x},\boldsymbol{t})$
where
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{b}(z)+\unicode[STIX]{x1D70C}^{\ast }(\boldsymbol{x},\boldsymbol{t})$
where
![]() $\unicode[STIX]{x1D70C}^{\ast }(\boldsymbol{x},\boldsymbol{t})$
is the density departure from the vertically varying background,
$\unicode[STIX]{x1D70C}^{\ast }(\boldsymbol{x},\boldsymbol{t})$
is the density departure from the vertically varying background,
![]() $\unicode[STIX]{x1D70C}_{b}(z)$
. The Boussinesq approximation is made, i.e. density is taken to be a constant (
$\unicode[STIX]{x1D70C}_{b}(z)$
. The Boussinesq approximation is made, i.e. density is taken to be a constant (
![]() $\unicode[STIX]{x1D70C}_{0}$
, taken here as the value of
$\unicode[STIX]{x1D70C}_{0}$
, taken here as the value of
![]() $\unicode[STIX]{x1D70C}_{b}$
at the top right corner of the domain) in the inertial terms of the momentum equation. The LES approach is employed and the following dimensional governing equations for
$\unicode[STIX]{x1D70C}_{b}$
at the top right corner of the domain) in the inertial terms of the momentum equation. The LES approach is employed and the following dimensional governing equations for
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() $\unicode[STIX]{x1D70C}^{\ast }$
(now interpreted as LES fields) are numerically solved:
$\unicode[STIX]{x1D70C}^{\ast }$
(now interpreted as LES fields) are numerically solved:
Here,
![]() $p^{\ast }$
denotes deviation from background hydrostatic pressure and
$p^{\ast }$
denotes deviation from background hydrostatic pressure and
![]() $g$
is the acceleration due to gravity. The important fluid properties are molecular viscosity,
$g$
is the acceleration due to gravity. The important fluid properties are molecular viscosity,
![]() $\unicode[STIX]{x1D708}$
, and thermal diffusivity,
$\unicode[STIX]{x1D708}$
, and thermal diffusivity,
![]() $\unicode[STIX]{x1D705}$
. The stable background stratification leads to a natural inverse time scale, the buoyancy frequency (
$\unicode[STIX]{x1D705}$
. The stable background stratification leads to a natural inverse time scale, the buoyancy frequency (
![]() $N$
), defined by
$N$
), defined by
![]() $N^{2}=-(g/\unicode[STIX]{x1D70C}_{0})\,\text{d}\unicode[STIX]{x1D70C}_{b}/\text{d}z$
.
$N^{2}=-(g/\unicode[STIX]{x1D70C}_{0})\,\text{d}\unicode[STIX]{x1D70C}_{b}/\text{d}z$
.
The subgrid-scale (SGS) stress tensor,
![]() $\unicode[STIX]{x1D749}$
, is calculated from the dynamic mixed model (Zang, Street & Koseff Reference Zang, Street and Koseff1993; Vreman, Geurts & Kuerten Reference Vreman, Geurts and Kuerten1997) and the SGS density flux vector,
$\unicode[STIX]{x1D749}$
, is calculated from the dynamic mixed model (Zang, Street & Koseff Reference Zang, Street and Koseff1993; Vreman, Geurts & Kuerten Reference Vreman, Geurts and Kuerten1997) and the SGS density flux vector,
![]() $\unicode[STIX]{x1D733}$
, is computed from the dynamic eddy diffusivity model (Armenio & Sarkar Reference Armenio and Sarkar2002):
$\unicode[STIX]{x1D733}$
, is computed from the dynamic eddy diffusivity model (Armenio & Sarkar Reference Armenio and Sarkar2002):
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D749}_{ij}=-2\unicode[STIX]{x1D708}_{sgs}\overline{S_{ij}}+\widehat{\overline{u}_{i}\overline{u}_{j}}-\widehat{\overline{u}_{i}}\widehat{\overline{u}_{j}},\quad \unicode[STIX]{x1D708}_{sgs}=C_{u}\overline{\unicode[STIX]{x1D6E5}}^{2}|\overline{S}|,\\ \displaystyle \unicode[STIX]{x1D733}_{j}=-\unicode[STIX]{x1D705}_{sgs}\frac{\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D70C}^{\ast }}}{\unicode[STIX]{x2202}x_{j}},\quad \unicode[STIX]{x1D705}_{sgs}=C_{\unicode[STIX]{x1D70C}}\overline{\unicode[STIX]{x1D6E5}}^{2}|\overline{S}|.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D749}_{ij}=-2\unicode[STIX]{x1D708}_{sgs}\overline{S_{ij}}+\widehat{\overline{u}_{i}\overline{u}_{j}}-\widehat{\overline{u}_{i}}\widehat{\overline{u}_{j}},\quad \unicode[STIX]{x1D708}_{sgs}=C_{u}\overline{\unicode[STIX]{x1D6E5}}^{2}|\overline{S}|,\\ \displaystyle \unicode[STIX]{x1D733}_{j}=-\unicode[STIX]{x1D705}_{sgs}\frac{\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D70C}^{\ast }}}{\unicode[STIX]{x2202}x_{j}},\quad \unicode[STIX]{x1D705}_{sgs}=C_{\unicode[STIX]{x1D70C}}\overline{\unicode[STIX]{x1D6E5}}^{2}|\overline{S}|.\end{array}\right\}\end{eqnarray}$$
For clarity, filtered variables are denoted explicitly in (2.4) by
![]() $\overline{(\cdot )}$
, and
$\overline{(\cdot )}$
, and
![]() $\overline{\unicode[STIX]{x1D6E5}}=(\unicode[STIX]{x0394}x\unicode[STIX]{x0394}y\unicode[STIX]{x0394}z)^{1/3}$
denotes the size of the grid filter. The coefficients
$\overline{\unicode[STIX]{x1D6E5}}=(\unicode[STIX]{x0394}x\unicode[STIX]{x0394}y\unicode[STIX]{x0394}z)^{1/3}$
denotes the size of the grid filter. The coefficients
![]() $C_{u}$
and
$C_{u}$
and
![]() $C_{\unicode[STIX]{x1D70C}}$
represent the plane-averaged Smagorinsky coefficients, which are computed dynamically using the approach described by Germano et al. (Reference Germano, Piomelli, Moin and Cabot1991) with the help of an additional test filter, represented as
$C_{\unicode[STIX]{x1D70C}}$
represent the plane-averaged Smagorinsky coefficients, which are computed dynamically using the approach described by Germano et al. (Reference Germano, Piomelli, Moin and Cabot1991) with the help of an additional test filter, represented as
![]() $\widehat{(\cdot )}$
. The strain-rate tensor
$\widehat{(\cdot )}$
. The strain-rate tensor
![]() $S_{ij}$
is computed as
$S_{ij}$
is computed as
![]() $(\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j}+\unicode[STIX]{x2202}u_{j}/\unicode[STIX]{x2202}x_{i})/2$
and
$(\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j}+\unicode[STIX]{x2202}u_{j}/\unicode[STIX]{x2202}x_{i})/2$
and
![]() $|S|=\sqrt{2S_{ij}S_{ij}}$
.
$|S|=\sqrt{2S_{ij}S_{ij}}$
.
The coordinate axis is rotated in the
![]() $x$
–
$x$
–
![]() $z$
plane by the slope angle
$z$
plane by the slope angle
![]() $\unicode[STIX]{x1D6FD}$
for ease of numerical simulation. The governing equations in this rotated coordinate system (
$\unicode[STIX]{x1D6FD}$
for ease of numerical simulation. The governing equations in this rotated coordinate system (
![]() $x_{s},y_{s},z_{s}$
) are as follows:
$x_{s},y_{s},z_{s}$
) are as follows:
where
![]() $\boldsymbol{u}_{s}$
is the velocity field in the rotated coordinates with components
$\boldsymbol{u}_{s}$
is the velocity field in the rotated coordinates with components
![]() $u_{s}$
,
$u_{s}$
,
![]() $v_{s}$
and
$v_{s}$
and
![]() $w_{s}$
along the
$w_{s}$
along the
![]() $x_{s}$
,
$x_{s}$
,
![]() $y_{s}$
and
$y_{s}$
and
![]() $z_{s}$
directions, respectively.
$z_{s}$
directions, respectively.
2.2 Numerical method
Equations (2.6) and (2.7) are advanced in time with the low-storage, third-order Runge–Kutta–Wray (RKW3) method for (convective) terms and the second-order Crank–Nicolson method for the viscous and diffusive terms.
The time interval,
![]() $\unicode[STIX]{x0394}t_{n}$
, is determined at each time point by ensuring that the Courant–Friedrichs–Lewy number
$\unicode[STIX]{x0394}t_{n}$
, is determined at each time point by ensuring that the Courant–Friedrichs–Lewy number
![]() $\text{CFL}\leqslant 1.0$
. Spatial derivatives are computed with a mixed method: Fourier collocation in the periodic (
$\text{CFL}\leqslant 1.0$
. Spatial derivatives are computed with a mixed method: Fourier collocation in the periodic (
![]() $x_{s},y_{s}$
) directions and central second-order in the
$x_{s},y_{s}$
) directions and central second-order in the
![]() $z_{s}$
direction. A sponge layer with Rayleigh damping is applied to minimize spurious reflection of internal gravity waves. In the sponge layer,
$z_{s}$
direction. A sponge layer with Rayleigh damping is applied to minimize spurious reflection of internal gravity waves. In the sponge layer,
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() $\unicode[STIX]{x1D70C}^{\ast }$
are damped to their zero background values by imposing damping functions
$\unicode[STIX]{x1D70C}^{\ast }$
are damped to their zero background values by imposing damping functions
![]() $-\unicode[STIX]{x1D70E}_{u}(z_{s})[u_{s},v_{s},w_{s}]$
and
$-\unicode[STIX]{x1D70E}_{u}(z_{s})[u_{s},v_{s},w_{s}]$
and
![]() $-\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70C}}(z_{s})[\unicode[STIX]{x1D70C}^{\ast }]$
on the right-hand side of their respective transport equations. Owing to
$-\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70C}}(z_{s})[\unicode[STIX]{x1D70C}^{\ast }]$
on the right-hand side of their respective transport equations. Owing to
![]() $x_{s}$
–
$x_{s}$
–
![]() $y_{s}$
periodicity, the Poisson equation for the pressure correction reduces to the solution of a tridiagonal system of equations for each Fourier mode.
$y_{s}$
periodicity, the Poisson equation for the pressure correction reduces to the solution of a tridiagonal system of equations for each Fourier mode.
At the bottom boundary
![]() $(z_{s}=0)$
, no slip (
$(z_{s}=0)$
, no slip (
![]() $\boldsymbol{u}=0$
) is imposed on the velocity and
$\boldsymbol{u}=0$
) is imposed on the velocity and
![]() $\unicode[STIX]{x1D70C}$
obeys the zero normal-flux boundary condition (BC). Since,
$\unicode[STIX]{x1D70C}$
obeys the zero normal-flux boundary condition (BC). Since,
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}z_{s}=0$
at
$\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}z_{s}=0$
at
![]() $z_{s}=0$
requires
$z_{s}=0$
requires
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}^{\ast }/\unicode[STIX]{x2202}z_{s}=-\cos \unicode[STIX]{x1D6FD}\,\text{d}\unicode[STIX]{x1D70C}_{b}/\text{d}z$
as the BC for
$\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}^{\ast }/\unicode[STIX]{x2202}z_{s}=-\cos \unicode[STIX]{x1D6FD}\,\text{d}\unicode[STIX]{x1D70C}_{b}/\text{d}z$
as the BC for
![]() $\unicode[STIX]{x1D70C}^{\ast }$
.
$\unicode[STIX]{x1D70C}^{\ast }$
.
2.3 Problem set-up
The model problem is illustrated in figure 1. The background at time
![]() $t=0$
has zero velocity and is unstable owing to a finite-height disturbance: a single wavelength of a mode,
$t=0$
has zero velocity and is unstable owing to a finite-height disturbance: a single wavelength of a mode,
![]() $\unicode[STIX]{x1D70C}^{\ast }=-\unicode[STIX]{x1D70C}_{p}\sin (mz_{s})$
, with specified wavenumber
$\unicode[STIX]{x1D70C}^{\ast }=-\unicode[STIX]{x1D70C}_{p}\sin (mz_{s})$
, with specified wavenumber
![]() $m$
. The problem choice is motivated by overturns that have been observed adjacent to bottom bathymetry in the ocean and implicated as a key mechanism for turbulence in the deep ocean. This simple model enables the study of the dynamics of near-bottom convective instability in isolation. The
$m$
. The problem choice is motivated by overturns that have been observed adjacent to bottom bathymetry in the ocean and implicated as a key mechanism for turbulence in the deep ocean. This simple model enables the study of the dynamics of near-bottom convective instability in isolation. The
![]() $\unicode[STIX]{x1D70C}^{\ast }$
perturbation at
$\unicode[STIX]{x1D70C}^{\ast }$
perturbation at
![]() $t=0$
is of the form
$t=0$
is of the form
![]() $\unicode[STIX]{x1D70C}^{\ast }=-\unicode[STIX]{x1D70C}_{p}\sin (mz_{s})$
and spans a single wavelength, extending from the bottom to
$\unicode[STIX]{x1D70C}^{\ast }=-\unicode[STIX]{x1D70C}_{p}\sin (mz_{s})$
and spans a single wavelength, extending from the bottom to
![]() $z_{s}=\unicode[STIX]{x1D706}=2\unicode[STIX]{x03C0}/m$
.
$z_{s}=\unicode[STIX]{x1D706}=2\unicode[STIX]{x03C0}/m$
.
A non-dimensional measure of the initial density perturbation is
![]() $R_{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}_{b}$
, where
$R_{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}_{b}$
, where
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}_{b}$
is the variation of background density over a distance of
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}_{b}$
is the variation of background density over a distance of
![]() $z_{s}=1/m$
. For a linearly stratified background,
$z_{s}=1/m$
. For a linearly stratified background,
where the perturbation buoyancy frequency is given by
![]() $N_{p}^{2}=gm\unicode[STIX]{x1D70C}_{p}\cos \unicode[STIX]{x1D6FD}/(\unicode[STIX]{x1D70C}_{0})$
. As
$N_{p}^{2}=gm\unicode[STIX]{x1D70C}_{p}\cos \unicode[STIX]{x1D6FD}/(\unicode[STIX]{x1D70C}_{0})$
. As
![]() $R_{\unicode[STIX]{x1D70C}}$
(equivalently,
$R_{\unicode[STIX]{x1D70C}}$
(equivalently,
![]() $N_{p}/N$
) increases, the distortion of the initial stable background density also increases and so does the resulting flow.
$N_{p}/N$
) increases, the distortion of the initial stable background density also increases and so does the resulting flow.
It is possible to analytically relate the height,
![]() $h_{0}$
, of the statically unstable zone with
$h_{0}$
, of the statically unstable zone with
![]() $\text{d}\unicode[STIX]{x1D70C}/\text{d}z>0$
to the prescribed density perturbation. The density at
$\text{d}\unicode[STIX]{x1D70C}/\text{d}z>0$
to the prescribed density perturbation. The density at
![]() $t=0$
is given by
$t=0$
is given by
where
![]() $\text{d}\unicode[STIX]{x1D70C}_{b}/\text{d}z$
is a constant. It follows that the initial density gradient in the vertical is
$\text{d}\unicode[STIX]{x1D70C}_{b}/\text{d}z$
is a constant. It follows that the initial density gradient in the vertical is
Thus, the region with
![]() $\text{d}\unicode[STIX]{x1D70C}/\text{d}z>0$
in the perturbed density profile satisfies
$\text{d}\unicode[STIX]{x1D70C}/\text{d}z>0$
in the perturbed density profile satisfies
whose solution leads to the following expression for the statically unstable region:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{2\unicode[STIX]{x03C0}}{m}-\frac{1}{m}\cos ^{-1}\left(\frac{-N^{2}\unicode[STIX]{x1D70C}_{0}}{g\unicode[STIX]{x1D70C}_{p}m\cos \unicode[STIX]{x1D6FD}}\right)>z_{s}>\frac{1}{m}\cos ^{-1}\left(\frac{-N^{2}\unicode[STIX]{x1D70C}_{0}}{g\unicode[STIX]{x1D70C}_{p}m\cos \unicode[STIX]{x1D6FD}}\right),\\ \displaystyle \frac{2\unicode[STIX]{x03C0}}{m}-\frac{1}{m}\cos ^{-1}\left(\frac{-1}{R_{\unicode[STIX]{x1D70C}}}\right)>z_{s}>\frac{1}{m}\cos ^{-1}\left(\frac{-1}{R_{\unicode[STIX]{x1D70C}}}\right).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{2\unicode[STIX]{x03C0}}{m}-\frac{1}{m}\cos ^{-1}\left(\frac{-N^{2}\unicode[STIX]{x1D70C}_{0}}{g\unicode[STIX]{x1D70C}_{p}m\cos \unicode[STIX]{x1D6FD}}\right)>z_{s}>\frac{1}{m}\cos ^{-1}\left(\frac{-N^{2}\unicode[STIX]{x1D70C}_{0}}{g\unicode[STIX]{x1D70C}_{p}m\cos \unicode[STIX]{x1D6FD}}\right),\\ \displaystyle \frac{2\unicode[STIX]{x03C0}}{m}-\frac{1}{m}\cos ^{-1}\left(\frac{-1}{R_{\unicode[STIX]{x1D70C}}}\right)>z_{s}>\frac{1}{m}\cos ^{-1}\left(\frac{-1}{R_{\unicode[STIX]{x1D70C}}}\right).\end{array}\right\}\end{eqnarray}$$
From (2.13), we obtain the overturn height in the
![]() $x_{s}$
–
$x_{s}$
–
![]() $z_{s}$
frame of reference (
$z_{s}$
frame of reference (
![]() $h_{0}^{\prime }$
) as
$h_{0}^{\prime }$
) as
and, therefore, the non-dimensional, vertical height of the statically unstable region,
![]() $h_{0}=h_{0}^{\prime }\cos \unicode[STIX]{x1D6FD}$
, is given by
$h_{0}=h_{0}^{\prime }\cos \unicode[STIX]{x1D6FD}$
, is given by
For a constant
![]() $\unicode[STIX]{x1D70C}_{p}$
, the variation in
$\unicode[STIX]{x1D70C}_{p}$
, the variation in
![]() $h_{0}$
with
$h_{0}$
with
![]() $\unicode[STIX]{x1D6FD}$
is negligible up to
$\unicode[STIX]{x1D6FD}$
is negligible up to
![]() $\unicode[STIX]{x1D6FD}=5^{\circ }$
. However
$\unicode[STIX]{x1D6FD}=5^{\circ }$
. However
![]() $h_{0}$
reduces appreciably as the steepness increases beyond
$h_{0}$
reduces appreciably as the steepness increases beyond
![]() $5^{\circ }$
. Above
$5^{\circ }$
. Above
![]() $z_{s}=\unicode[STIX]{x1D706}$
, the density attains its background value and hence the turbulence generation in this zone is expected to be minimal.
$z_{s}=\unicode[STIX]{x1D706}$
, the density attains its background value and hence the turbulence generation in this zone is expected to be minimal.
Two series of simulations are performed. The first series A (table 1) contains six cases that combine two values of
![]() $\unicode[STIX]{x1D70C}_{p}$
and three values of
$\unicode[STIX]{x1D70C}_{p}$
and three values of
![]() $\unicode[STIX]{x1D6FD}$
, and is designed to obtain an overall view of the flow that results from the convective overturn and the pathways taken by the potential energy associated with the initial density profile. The streamwise domain length (
$\unicode[STIX]{x1D6FD}$
, and is designed to obtain an overall view of the flow that results from the convective overturn and the pathways taken by the potential energy associated with the initial density profile. The streamwise domain length (
![]() $L_{xs}$
) in the non-sloping cases (ANG0) is twice that in the sloping cases, and is found to be sufficiently large to accommodate the initial overturn that occurs before the onset of turbulence. In the second series B (table 2), a wide range of angles is examined with
$L_{xs}$
) in the non-sloping cases (ANG0) is twice that in the sloping cases, and is found to be sufficiently large to accommodate the initial overturn that occurs before the onset of turbulence. In the second series B (table 2), a wide range of angles is examined with
![]() $\unicode[STIX]{x1D6FD}$
up to 45
$\unicode[STIX]{x1D6FD}$
up to 45
![]() $^{\circ }$
. The Rayleigh number,
$^{\circ }$
. The Rayleigh number,
![]() $Ra=g\unicode[STIX]{x1D70C}_{p}h_{0}^{3}/(\unicode[STIX]{x1D70C}_{0}\unicode[STIX]{x1D708}\unicode[STIX]{x1D705})$
, is
$Ra=g\unicode[STIX]{x1D70C}_{p}h_{0}^{3}/(\unicode[STIX]{x1D70C}_{0}\unicode[STIX]{x1D708}\unicode[STIX]{x1D705})$
, is
![]() $O(10^{13})$
, sufficiently large for full-blown turbulence. The height
$O(10^{13})$
, sufficiently large for full-blown turbulence. The height
![]() $h_{0}$
(as given in (2.15)) of the convective zone reduces from
$h_{0}$
(as given in (2.15)) of the convective zone reduces from
![]() $0.41\unicode[STIX]{x1D706}$
in ANG0-2 to
$0.41\unicode[STIX]{x1D706}$
in ANG0-2 to
![]() $0.26\unicode[STIX]{x1D706}$
in ANG45 at
$0.26\unicode[STIX]{x1D706}$
in ANG45 at
![]() $t=0$
, and up to
$t=0$
, and up to
![]() $150$
grid points are deployed across this zone for excellent resolution of the energy-containing scales of the turbulence that ensues.
$150$
grid points are deployed across this zone for excellent resolution of the energy-containing scales of the turbulence that ensues.
Table 1. Key parameters of series A. There are six LES cases, denoted by ANG
![]() $\unicode[STIX]{x1D6FD}$
-
$\unicode[STIX]{x1D6FD}$
-
![]() $\unicode[STIX]{x1D70C}^{\ast }$
, with
$\unicode[STIX]{x1D70C}^{\ast }$
, with
![]() $\unicode[STIX]{x1D6FD}=\{0^{\circ },2.5^{\circ },5^{\circ }\}$
and
$\unicode[STIX]{x1D6FD}=\{0^{\circ },2.5^{\circ },5^{\circ }\}$
and
![]() $\unicode[STIX]{x1D70C}^{\ast }=\{0.01,0.02\}~\text{kg}~\text{m}^{-3}$
. The spanwise domain length
$\unicode[STIX]{x1D70C}^{\ast }=\{0.01,0.02\}~\text{kg}~\text{m}^{-3}$
. The spanwise domain length
![]() $L_{ys}$
is 10 m with
$L_{ys}$
is 10 m with
![]() $N_{y}=64$
points. Grid spacing is uniform in the streamwise and spanwise directions, with
$N_{y}=64$
points. Grid spacing is uniform in the streamwise and spanwise directions, with
![]() $\unicode[STIX]{x0394}x_{s}=0.23~\text{m}$
and
$\unicode[STIX]{x0394}x_{s}=0.23~\text{m}$
and
![]() $\unicode[STIX]{x0394}y_{s}=0.156~\text{m}$
, respectively. The slope-normal size is
$\unicode[STIX]{x0394}y_{s}=0.156~\text{m}$
, respectively. The slope-normal size is
![]() $L_{zs}=150~\text{m}$
and there are
$L_{zs}=150~\text{m}$
and there are
![]() $N_{z}=641$
variably spaced points with
$N_{z}=641$
variably spaced points with
![]() $\unicode[STIX]{x0394}z_{min}=0.0037~\text{m}$
. The density disturbance has a wavelength (
$\unicode[STIX]{x0394}z_{min}=0.0037~\text{m}$
. The density disturbance has a wavelength (
![]() $2\unicode[STIX]{x03C0}/m$
) of 130 m. Here,
$2\unicode[STIX]{x03C0}/m$
) of 130 m. Here,
![]() $Ra$
is given by
$Ra$
is given by
![]() $g\unicode[STIX]{x1D70C}_{p}h_{0}^{3}/(\unicode[STIX]{x1D70C}_{0}\unicode[STIX]{x1D708}\unicode[STIX]{x1D705})$
, where
$g\unicode[STIX]{x1D70C}_{p}h_{0}^{3}/(\unicode[STIX]{x1D70C}_{0}\unicode[STIX]{x1D708}\unicode[STIX]{x1D705})$
, where
![]() $h_{0}$
is computed from (2.15).
$h_{0}$
is computed from (2.15).

Table 2. Series B has slope angle (
![]() $\unicode[STIX]{x1D6FD}$
) that is steeper than in series A. The
$\unicode[STIX]{x1D6FD}$
) that is steeper than in series A. The
![]() $\unicode[STIX]{x1D6FD}$
value varies between 10
$\unicode[STIX]{x1D6FD}$
value varies between 10
![]() $^{\circ }$
and 45
$^{\circ }$
and 45
![]() $^{\circ }$
while the initial disturbance of density amplitude
$^{\circ }$
while the initial disturbance of density amplitude
![]() $\unicode[STIX]{x1D70C}_{p}=0.02~\text{kg}~\text{m}^{-3}$
, wavenumber
$\unicode[STIX]{x1D70C}_{p}=0.02~\text{kg}~\text{m}^{-3}$
, wavenumber
![]() $m=2\unicode[STIX]{x03C0}/130~\text{m}^{-1}$
;
$m=2\unicode[STIX]{x03C0}/130~\text{m}^{-1}$
;
![]() $Ra$
decreases with increasing
$Ra$
decreases with increasing
![]() $\unicode[STIX]{x1D6FD}$
due to reducing size of overturns. The domain with slope-parallel dimensions of
$\unicode[STIX]{x1D6FD}$
due to reducing size of overturns. The domain with slope-parallel dimensions of
![]() $L_{xs}=30~\text{m}$
and
$L_{xs}=30~\text{m}$
and
![]() $L_{ys}=10~\text{m}$
has a grid with
$L_{ys}=10~\text{m}$
has a grid with
![]() $N_{x}=128$
and
$N_{x}=128$
and
![]() $N_{y}=64$
points, and
$N_{y}=64$
points, and
![]() $\unicode[STIX]{x0394}x_{s}=0.23~\text{m}$
and
$\unicode[STIX]{x0394}x_{s}=0.23~\text{m}$
and
![]() $\unicode[STIX]{x0394}y_{s}=0.156~\text{m}$
. Here,
$\unicode[STIX]{x0394}y_{s}=0.156~\text{m}$
. Here,
![]() $Ra$
is given by
$Ra$
is given by
![]() $g\unicode[STIX]{x1D70C}_{p}h_{0}^{3}/(\unicode[STIX]{x1D70C}_{0}\unicode[STIX]{x1D708}\unicode[STIX]{x1D705})$
, where
$g\unicode[STIX]{x1D70C}_{p}h_{0}^{3}/(\unicode[STIX]{x1D70C}_{0}\unicode[STIX]{x1D708}\unicode[STIX]{x1D705})$
, where
![]() $h_{0}$
is computed from (2.15).
$h_{0}$
is computed from (2.15).

3 Preliminaries for the analysis of turbulent flow energetics
The Reynolds-averaged equations for kinetic and potential energy provide a convenient framework to characterize energy pathways in stratified turbulent flow. The Reynolds average,
![]() $\langle \unicode[STIX]{x1D719}\rangle (z_{s},t)$
, of an arbitrary variable
$\langle \unicode[STIX]{x1D719}\rangle (z_{s},t)$
, of an arbitrary variable
![]() $\unicode[STIX]{x1D719}$
is computed as a slope-parallel (
$\unicode[STIX]{x1D719}$
is computed as a slope-parallel (
![]() $x_{s}$
–
$x_{s}$
–
![]() $y_{s}$
) planar average and
$y_{s}$
) planar average and
![]() $\unicode[STIX]{x1D719}^{\prime }=\unicode[STIX]{x1D719}-\langle \unicode[STIX]{x1D719}\rangle$
denotes the fluctuation. The four major reservoirs of energy are: mean kinetic energy (MKE), turbulent kinetic energy (TKE), mean available potential energy (MAPE) and mean turbulent potential energy (TAPE). The equations governing the temporal evolution of these reservoirs are similar to those in Scotti & White (Reference Scotti and White2014) and are given below.
$\unicode[STIX]{x1D719}^{\prime }=\unicode[STIX]{x1D719}-\langle \unicode[STIX]{x1D719}\rangle$
denotes the fluctuation. The four major reservoirs of energy are: mean kinetic energy (MKE), turbulent kinetic energy (TKE), mean available potential energy (MAPE) and mean turbulent potential energy (TAPE). The equations governing the temporal evolution of these reservoirs are similar to those in Scotti & White (Reference Scotti and White2014) and are given below.
3.1 Kinetic energy
Kinetic energy has a contribution from the mean, MKE (represented as
![]() $E_{KE}^{M}$
), evaluated as
$E_{KE}^{M}$
), evaluated as
![]() $\langle u_{i}\rangle \langle u_{i}\rangle /2$
, and a contribution from turbulence, TKE (represented as
$\langle u_{i}\rangle \langle u_{i}\rangle /2$
, and a contribution from turbulence, TKE (represented as
![]() $E_{KE}^{T}$
), evaluated as
$E_{KE}^{T}$
), evaluated as
![]() $\langle u_{i}^{\prime }u_{i}^{\prime }\rangle /2$
. The MKE equation is given by
$\langle u_{i}^{\prime }u_{i}^{\prime }\rangle /2$
. The MKE equation is given by
where
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \text{mean buoyancy flux }(B^{M}):\quad -\frac{g}{\unicode[STIX]{x1D70C}_{0}}\langle \unicode[STIX]{x1D70C}^{\ast }\rangle \langle w\rangle ,\\ \displaystyle \text{production }(P):\quad -\langle u_{i}^{\prime }u_{j}^{\prime }\rangle \langle S_{ij}\rangle -\langle \unicode[STIX]{x1D70F}_{ij}\rangle \langle S_{ij}\rangle ,\\ \displaystyle \text{transport of MKE }(T_{j}^{M}):\quad \frac{1}{\unicode[STIX]{x1D70C}_{0}}\langle p^{\ast }\rangle \langle u_{j}\rangle -2\unicode[STIX]{x1D708}\langle S_{ij}\rangle \langle u_{i}\rangle +\langle u_{i}^{\prime }u_{j}^{\prime }\rangle \langle u_{i}\rangle +\langle \unicode[STIX]{x1D70F}_{ij}\rangle \langle u_{i}\rangle ,\\ \displaystyle \text{mean flow dissipation }(\unicode[STIX]{x1D716}^{M}):\quad 2\unicode[STIX]{x1D708}\langle S_{ij}\rangle \langle S_{ij}\rangle .\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \text{mean buoyancy flux }(B^{M}):\quad -\frac{g}{\unicode[STIX]{x1D70C}_{0}}\langle \unicode[STIX]{x1D70C}^{\ast }\rangle \langle w\rangle ,\\ \displaystyle \text{production }(P):\quad -\langle u_{i}^{\prime }u_{j}^{\prime }\rangle \langle S_{ij}\rangle -\langle \unicode[STIX]{x1D70F}_{ij}\rangle \langle S_{ij}\rangle ,\\ \displaystyle \text{transport of MKE }(T_{j}^{M}):\quad \frac{1}{\unicode[STIX]{x1D70C}_{0}}\langle p^{\ast }\rangle \langle u_{j}\rangle -2\unicode[STIX]{x1D708}\langle S_{ij}\rangle \langle u_{i}\rangle +\langle u_{i}^{\prime }u_{j}^{\prime }\rangle \langle u_{i}\rangle +\langle \unicode[STIX]{x1D70F}_{ij}\rangle \langle u_{i}\rangle ,\\ \displaystyle \text{mean flow dissipation }(\unicode[STIX]{x1D716}^{M}):\quad 2\unicode[STIX]{x1D708}\langle S_{ij}\rangle \langle S_{ij}\rangle .\end{array}\right\}\end{eqnarray}$$
The corresponding temporal evolution of TKE is given by
where
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \text{turbulent buoyancy flux }(B^{T}):\quad \frac{-g}{\unicode[STIX]{x1D70C}_{0}}\langle \unicode[STIX]{x1D70C}^{\ast \prime }w^{\prime }\rangle ,\\ \displaystyle \text{transport of TKE }(T_{j}^{T}):\quad \frac{1}{\unicode[STIX]{x1D70C}_{0}}\langle {p^{\ast }}^{\prime }u_{j}^{\prime }\rangle -2\unicode[STIX]{x1D708}\langle u_{i}^{\prime }S_{ij}^{\prime }\rangle +\frac{1}{2}\langle u_{i}^{\prime }u_{i}^{\prime }u_{j}^{\prime }\rangle +\langle \unicode[STIX]{x1D70F}_{ij}^{\prime }u_{i}^{\prime }\rangle ,\\ \displaystyle \text{turbulent dissipation }(\unicode[STIX]{x1D716}^{T}):\quad 2\unicode[STIX]{x1D708}\langle S_{ij}^{\prime }S_{ij}^{\prime }\rangle -\langle \unicode[STIX]{x1D70F}_{ij}S_{ij}\rangle .\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \text{turbulent buoyancy flux }(B^{T}):\quad \frac{-g}{\unicode[STIX]{x1D70C}_{0}}\langle \unicode[STIX]{x1D70C}^{\ast \prime }w^{\prime }\rangle ,\\ \displaystyle \text{transport of TKE }(T_{j}^{T}):\quad \frac{1}{\unicode[STIX]{x1D70C}_{0}}\langle {p^{\ast }}^{\prime }u_{j}^{\prime }\rangle -2\unicode[STIX]{x1D708}\langle u_{i}^{\prime }S_{ij}^{\prime }\rangle +\frac{1}{2}\langle u_{i}^{\prime }u_{i}^{\prime }u_{j}^{\prime }\rangle +\langle \unicode[STIX]{x1D70F}_{ij}^{\prime }u_{i}^{\prime }\rangle ,\\ \displaystyle \text{turbulent dissipation }(\unicode[STIX]{x1D716}^{T}):\quad 2\unicode[STIX]{x1D708}\langle S_{ij}^{\prime }S_{ij}^{\prime }\rangle -\langle \unicode[STIX]{x1D70F}_{ij}S_{ij}\rangle .\end{array}\right\}\end{eqnarray}$$
3.2 Potential energy
To evaluate the potential energy, one must define a reference state (equilibrium depth)
![]() $z_{r}(\unicode[STIX]{x1D70C})$
for each fluid parcel of density
$z_{r}(\unicode[STIX]{x1D70C})$
for each fluid parcel of density
![]() $\unicode[STIX]{x1D70C}$
. A widely accepted definition of APE (Holliday & McIntyre Reference Holliday and McIntyre1981; Roullet & Klein Reference Roullet and Klein2009) of a fluid parcel with
$\unicode[STIX]{x1D70C}$
. A widely accepted definition of APE (Holliday & McIntyre Reference Holliday and McIntyre1981; Roullet & Klein Reference Roullet and Klein2009) of a fluid parcel with
![]() $\unicode[STIX]{x1D70C}(x,y,z,t)$
is as follows:
$\unicode[STIX]{x1D70C}(x,y,z,t)$
is as follows:
where
![]() $\unicode[STIX]{x1D70C}_{r}(z)$
is the density profile of the background state,
$\unicode[STIX]{x1D70C}_{r}(z)$
is the density profile of the background state,
![]() $z_{r}(\unicode[STIX]{x1D70C})$
being its inverse mapping. It is to be noted here that
$z_{r}(\unicode[STIX]{x1D70C})$
being its inverse mapping. It is to be noted here that
![]() $E_{APE}$
is defined per unit mass. For a linearly stratified fluid, equation (3.5) can be simplified by its quadratic approximation (Kang & Fringer Reference Kang and Fringer2010) as
$E_{APE}$
is defined per unit mass. For a linearly stratified fluid, equation (3.5) can be simplified by its quadratic approximation (Kang & Fringer Reference Kang and Fringer2010) as
where
![]() $N_{r}$
is the buoyancy frequency of the background state. In this study,
$N_{r}$
is the buoyancy frequency of the background state. In this study,
![]() $N_{r}$
is a constant, denoted for simplicity as
$N_{r}$
is a constant, denoted for simplicity as
![]() $N$
, and APE is computed with respect to the linearly varying background density. Scotti & White (Reference Scotti and White2014) showed that the contribution of the mean and fluctuating density to the average of APE (defined by (3.6)) can be approximated in the LEC limit as follows:
$N$
, and APE is computed with respect to the linearly varying background density. Scotti & White (Reference Scotti and White2014) showed that the contribution of the mean and fluctuating density to the average of APE (defined by (3.6)) can be approximated in the LEC limit as follows:
The transport equation for MAPE is
where
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \text{scalar production }(P_{\unicode[STIX]{x1D70C}}):\quad \frac{-g^{2}}{\unicode[STIX]{x1D70C}_{0}^{2}N^{2}}\left\{\langle u_{j}^{\prime }\unicode[STIX]{x1D70C}^{\ast \prime }\rangle \frac{\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D70C}^{\ast }\rangle }{\unicode[STIX]{x2202}x_{j}}+\langle \unicode[STIX]{x1D70C}^{\ast \prime }w^{\prime }\rangle \frac{\text{d}\unicode[STIX]{x1D70C}_{b}}{\text{d}z}+\langle \unicode[STIX]{x1D6F9}_{j}\rangle \frac{\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D70C}^{\ast }\rangle }{\unicode[STIX]{x2202}x_{j}}\right\},\\ \displaystyle \begin{array}{@{}lll@{}} & & \displaystyle \text{transport of mean APE }(T_{\unicode[STIX]{x1D70C}}^{M}):\qquad \\ & & \displaystyle \qquad \frac{g^{2}}{\unicode[STIX]{x1D70C}_{0}^{2}N^{2}}\left\{\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{j}}\left(-\langle \unicode[STIX]{x1D70C}^{\ast }\rangle \langle \unicode[STIX]{x1D70C}^{\ast \prime }u_{j}^{\prime }\rangle +\unicode[STIX]{x1D705}\langle \unicode[STIX]{x1D70C}^{\ast }\rangle \frac{\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D70C}^{\ast }\rangle }{\unicode[STIX]{x2202}x_{j}}-\langle \unicode[STIX]{x1D70C}^{\ast }\rangle \langle \unicode[STIX]{x1D6F9}_{j}\rangle \right)\right\},\end{array}\\ \displaystyle \text{mean APE dissipation }(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D70C}}^{M}):\quad \frac{g^{2}}{\unicode[STIX]{x1D70C}_{0}^{2}N^{2}}\left\{\unicode[STIX]{x1D705}\left(\frac{\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D70C}^{\ast }\rangle }{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D70C}^{\ast }\rangle }{\unicode[STIX]{x2202}x_{j}}\right)\right\}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \text{scalar production }(P_{\unicode[STIX]{x1D70C}}):\quad \frac{-g^{2}}{\unicode[STIX]{x1D70C}_{0}^{2}N^{2}}\left\{\langle u_{j}^{\prime }\unicode[STIX]{x1D70C}^{\ast \prime }\rangle \frac{\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D70C}^{\ast }\rangle }{\unicode[STIX]{x2202}x_{j}}+\langle \unicode[STIX]{x1D70C}^{\ast \prime }w^{\prime }\rangle \frac{\text{d}\unicode[STIX]{x1D70C}_{b}}{\text{d}z}+\langle \unicode[STIX]{x1D6F9}_{j}\rangle \frac{\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D70C}^{\ast }\rangle }{\unicode[STIX]{x2202}x_{j}}\right\},\\ \displaystyle \begin{array}{@{}lll@{}} & & \displaystyle \text{transport of mean APE }(T_{\unicode[STIX]{x1D70C}}^{M}):\qquad \\ & & \displaystyle \qquad \frac{g^{2}}{\unicode[STIX]{x1D70C}_{0}^{2}N^{2}}\left\{\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{j}}\left(-\langle \unicode[STIX]{x1D70C}^{\ast }\rangle \langle \unicode[STIX]{x1D70C}^{\ast \prime }u_{j}^{\prime }\rangle +\unicode[STIX]{x1D705}\langle \unicode[STIX]{x1D70C}^{\ast }\rangle \frac{\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D70C}^{\ast }\rangle }{\unicode[STIX]{x2202}x_{j}}-\langle \unicode[STIX]{x1D70C}^{\ast }\rangle \langle \unicode[STIX]{x1D6F9}_{j}\rangle \right)\right\},\end{array}\\ \displaystyle \text{mean APE dissipation }(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D70C}}^{M}):\quad \frac{g^{2}}{\unicode[STIX]{x1D70C}_{0}^{2}N^{2}}\left\{\unicode[STIX]{x1D705}\left(\frac{\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D70C}^{\ast }\rangle }{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D70C}^{\ast }\rangle }{\unicode[STIX]{x2202}x_{j}}\right)\right\}.\end{array}\right\}\end{eqnarray}$$
A similar equation can be derived for the time evolution of TAPE:
where
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \text{transport of turbulent APE }(T_{\unicode[STIX]{x1D70C}}^{T}):\quad \frac{g^{2}}{2\unicode[STIX]{x1D70C}_{0}^{2}N^{2}}\left\{\unicode[STIX]{x1D705}\frac{\unicode[STIX]{x2202}^{2}\langle \unicode[STIX]{x1D70C}^{\ast \prime 2}\rangle }{\unicode[STIX]{x2202}x_{j}^{2}}-\frac{\unicode[STIX]{x2202}\langle u_{j}^{\prime }\unicode[STIX]{x1D70C}^{\ast \prime 2}\rangle }{\unicode[STIX]{x2202}x_{j}}-2\frac{\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D6F9}_{j}^{\prime }\unicode[STIX]{x1D70C}^{\ast \prime }\rangle }{\unicode[STIX]{x2202}x_{j}}\right\},\\ \displaystyle \text{turbulent APE dissipation }(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D70C}}^{T}):\quad \frac{g^{2}}{\unicode[STIX]{x1D70C}_{0}^{2}N^{2}}\left(\unicode[STIX]{x1D705}\left\langle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}^{\ast \prime }}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}^{\ast \prime }}{\unicode[STIX]{x2202}x_{j}}\right\rangle -\left\langle \unicode[STIX]{x1D6F9}_{j}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}^{\ast }}{\unicode[STIX]{x2202}x_{j}}\right\rangle \right).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \text{transport of turbulent APE }(T_{\unicode[STIX]{x1D70C}}^{T}):\quad \frac{g^{2}}{2\unicode[STIX]{x1D70C}_{0}^{2}N^{2}}\left\{\unicode[STIX]{x1D705}\frac{\unicode[STIX]{x2202}^{2}\langle \unicode[STIX]{x1D70C}^{\ast \prime 2}\rangle }{\unicode[STIX]{x2202}x_{j}^{2}}-\frac{\unicode[STIX]{x2202}\langle u_{j}^{\prime }\unicode[STIX]{x1D70C}^{\ast \prime 2}\rangle }{\unicode[STIX]{x2202}x_{j}}-2\frac{\unicode[STIX]{x2202}\langle \unicode[STIX]{x1D6F9}_{j}^{\prime }\unicode[STIX]{x1D70C}^{\ast \prime }\rangle }{\unicode[STIX]{x2202}x_{j}}\right\},\\ \displaystyle \text{turbulent APE dissipation }(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D70C}}^{T}):\quad \frac{g^{2}}{\unicode[STIX]{x1D70C}_{0}^{2}N^{2}}\left(\unicode[STIX]{x1D705}\left\langle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}^{\ast \prime }}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}^{\ast \prime }}{\unicode[STIX]{x2202}x_{j}}\right\rangle -\left\langle \unicode[STIX]{x1D6F9}_{j}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}^{\ast }}{\unicode[STIX]{x2202}x_{j}}\right\rangle \right).\end{array}\right\}\end{eqnarray}$$
Initially, all the energy resides in the MAPE reservoir, with none in the other three reservoirs. It is thus natural to normalize all energy variables with the MAPE at
![]() $t=0$
, denoted hereafter as
$t=0$
, denoted hereafter as
![]() $E_{0}$
. The energy variables, e.g.
$E_{0}$
. The energy variables, e.g.
![]() $E_{APE}^{T}(z_{s},t)$
, are Reynolds averages obtained by a planar (
$E_{APE}^{T}(z_{s},t)$
, are Reynolds averages obtained by a planar (
![]() $x_{s},y_{s}$
) average and, for studying the bulk energetics, it is convenient to perform a further average in the slope-normal direction, e.g.
$x_{s},y_{s}$
) average and, for studying the bulk energetics, it is convenient to perform a further average in the slope-normal direction, e.g.
![]() $\langle E_{APE}^{T}\rangle _{z_{s}}$
, to obtain energy variables that depend only on time. In the upcoming results section, we will discuss two important bulk quantities: (1) the cumulative energy loss
$\langle E_{APE}^{T}\rangle _{z_{s}}$
, to obtain energy variables that depend only on time. In the upcoming results section, we will discuss two important bulk quantities: (1) the cumulative energy loss
![]() $E_{loss}$
, and (2) the cumulative mixing efficiency
$E_{loss}$
, and (2) the cumulative mixing efficiency
![]() $\unicode[STIX]{x1D6E4}$
. Their definitions are as follows:
$\unicode[STIX]{x1D6E4}$
. Their definitions are as follows:
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6E4}(t)=\frac{\displaystyle \int _{0}^{t}\langle \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D70C}}^{T}+\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D70C}}^{M}\rangle _{z_{s}}\,\text{d}t}{\displaystyle \int _{0}^{t}\langle \unicode[STIX]{x1D716}^{T}+\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D70C}}^{T}+\unicode[STIX]{x1D716}^{M}+\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D70C}}^{M}\rangle _{z_{s}}\,\text{d}t}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6E4}(t)=\frac{\displaystyle \int _{0}^{t}\langle \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D70C}}^{T}+\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D70C}}^{M}\rangle _{z_{s}}\,\text{d}t}{\displaystyle \int _{0}^{t}\langle \unicode[STIX]{x1D716}^{T}+\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D70C}}^{T}+\unicode[STIX]{x1D716}^{M}+\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D70C}}^{M}\rangle _{z_{s}}\,\text{d}t}. & \displaystyle\end{eqnarray}$$
The mixing efficiency (
![]() $\unicode[STIX]{x1D6E4}$
) defined by (3.13) measures the fraction of irreversible energy loss that goes towards scalar mixing. It does not involve quantities like the buoyancy flux that can be negative, and varies between 0 and 1 as an efficiency should. In a high-
$\unicode[STIX]{x1D6E4}$
) defined by (3.13) measures the fraction of irreversible energy loss that goes towards scalar mixing. It does not involve quantities like the buoyancy flux that can be negative, and varies between 0 and 1 as an efficiency should. In a high-
![]() $Re$
turbulent flow, the mean dissipation terms
$Re$
turbulent flow, the mean dissipation terms
![]() $\unicode[STIX]{x1D716}^{M}$
and
$\unicode[STIX]{x1D716}^{M}$
and
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D70C}}^{M}$
are expected to be much smaller than their turbulent counterparts, as will be evident from the results of § 6, and the definition of
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D70C}}^{M}$
are expected to be much smaller than their turbulent counterparts, as will be evident from the results of § 6, and the definition of
![]() $\unicode[STIX]{x1D6E4}(t)$
reduces to an efficiency based on turbulent losses alone (e.g. Peltier & Caulfield Reference Peltier and Caulfield2003; Basak & Sarkar Reference Basak and Sarkar2006). The mixing efficiency is sometimes taken to be equivalent to the flux Richardson number (
$\unicode[STIX]{x1D6E4}(t)$
reduces to an efficiency based on turbulent losses alone (e.g. Peltier & Caulfield Reference Peltier and Caulfield2003; Basak & Sarkar Reference Basak and Sarkar2006). The mixing efficiency is sometimes taken to be equivalent to the flux Richardson number (
![]() $Ri_{f}=B/P$
or
$Ri_{f}=B/P$
or
![]() $Ri_{f}=B/(B+\unicode[STIX]{x1D716}^{T})$
and their intuitive time-integrated extensions). As discussed by Venayagamoorthy & Koseff (Reference Venayagamoorthy and Koseff2016), the mixing efficiency defined by
$Ri_{f}=B/(B+\unicode[STIX]{x1D716}^{T})$
and their intuitive time-integrated extensions). As discussed by Venayagamoorthy & Koseff (Reference Venayagamoorthy and Koseff2016), the mixing efficiency defined by
![]() $\unicode[STIX]{x1D6E4}(t)$
(the mean quantities can be neglected for high
$\unicode[STIX]{x1D6E4}(t)$
(the mean quantities can be neglected for high
![]() $Re$
) that uses irreversible fluxes is a better measure of mixing in stratified shear flows than
$Re$
) that uses irreversible fluxes is a better measure of mixing in stratified shear flows than
![]() $Ri_{f}$
based on
$Ri_{f}$
based on
![]() $B$
when
$B$
when
![]() $Ri_{g}>0.25$
.
$Ri_{g}>0.25$
.

Figure 2. Temporal evolution of
![]() $\langle u\rangle$
and
$\langle u\rangle$
and
![]() $\langle \unicode[STIX]{x1D70C}^{\ast }\rangle$
in case ANG2.5-1 at
$\langle \unicode[STIX]{x1D70C}^{\ast }\rangle$
in case ANG2.5-1 at
![]() $z_{s}/L_{zs}=0.096$
(a) and
$z_{s}/L_{zs}=0.096$
(a) and
![]() $z_{s}/L_{zs}=0.21$
(b). The theoretical result for
$z_{s}/L_{zs}=0.21$
(b). The theoretical result for
![]() $\langle u\rangle$
, equation (4.8), is plotted as a solid orange line and compares well with the simulation results for
$\langle u\rangle$
, equation (4.8), is plotted as a solid orange line and compares well with the simulation results for
![]() $\langle u\rangle$
.
$\langle u\rangle$
.
4 Temporal variability of the mean flow
The presence of the slope leads to a qualitative difference in the evolution of the initially unstable patch. A mean flow develops along the slope and oscillates in time, contrary to the non-sloping case where the mean flow is zero. Figure 2 shows
![]() $u$
and
$u$
and
![]() $\unicode[STIX]{x1D70C}^{\ast }$
at two different vertical heights in case ANG2.5-1. It can be seen that
$\unicode[STIX]{x1D70C}^{\ast }$
at two different vertical heights in case ANG2.5-1. It can be seen that
![]() $\langle u\rangle$
and
$\langle u\rangle$
and
![]() $\langle \unicode[STIX]{x1D70C}^{\ast }\rangle$
oscillate with the frequency
$\langle \unicode[STIX]{x1D70C}^{\ast }\rangle$
oscillate with the frequency
![]() $N\sin \unicode[STIX]{x1D6FD}$
, and the velocity lags density by a phase of
$N\sin \unicode[STIX]{x1D6FD}$
, and the velocity lags density by a phase of
![]() $\unicode[STIX]{x03C0}/2$
. Linear theory will be used to explain these features of the oscillation.
$\unicode[STIX]{x03C0}/2$
. Linear theory will be used to explain these features of the oscillation.
The governing equations are linearized about a base state,
![]() $\boldsymbol{u}=\unicode[STIX]{x1D70C}^{\ast }=p^{\ast }=0$
, diffusive effects are neglected and normal-mode perturbations of the form
$\boldsymbol{u}=\unicode[STIX]{x1D70C}^{\ast }=p^{\ast }=0$
, diffusive effects are neglected and normal-mode perturbations of the form
![]() $A_{p}(z)\exp$
$A_{p}(z)\exp$
![]() $\{\text{i}(kx+ly)\}\exp \{st\}$
are introduced for each flow variable. The modal amplitudes satisfy the following system:
$\{\text{i}(kx+ly)\}\exp \{st\}$
are introduced for each flow variable. The modal amplitudes satisfy the following system:
The boundary condition at
![]() $z_{s}=0$
is
$z_{s}=0$
is
![]() $u_{p}=v_{p}=w_{p}=0$
and
$u_{p}=v_{p}=w_{p}=0$
and
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}z_{s}=0$
. It is straightforward to simplify (4.1)–(4.5) to obtain the following eigenvalue relation:
$\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}z_{s}=0$
. It is straightforward to simplify (4.1)–(4.5) to obtain the following eigenvalue relation:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \quad \left[\left(\sin ^{2}\unicode[STIX]{x1D6FD}+\frac{s^{2}}{N^{2}}\right)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}z_{s}^{2}}-2\text{i}k\cos \unicode[STIX]{x1D6FD}\sin \unicode[STIX]{x1D6FD}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}z_{s}}\right]\unicode[STIX]{x1D70C}_{p}=\left[\frac{s^{2}}{N^{2}}(k^{2}+l^{2})+l^{2}+k^{2}\cos ^{2}\unicode[STIX]{x1D6FD}\right]\unicode[STIX]{x1D70C}_{p}\nonumber\\ \displaystyle & & \displaystyle \Rightarrow \,\left(\sin ^{2}\unicode[STIX]{x1D6FD}+\frac{s^{2}}{N^{2}}\right)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}_{p}}{\unicode[STIX]{x2202}z_{s}^{2}}-\text{i}k\sin (2\unicode[STIX]{x1D6FD})\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}_{p}}{\unicode[STIX]{x2202}z_{s}}-\left(\frac{s^{2}}{N^{2}}(k^{2}+l^{2})+l^{2}+k^{2}\cos ^{2}\unicode[STIX]{x1D6FD}\right)\unicode[STIX]{x1D70C}_{p}=0.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \quad \left[\left(\sin ^{2}\unicode[STIX]{x1D6FD}+\frac{s^{2}}{N^{2}}\right)\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}z_{s}^{2}}-2\text{i}k\cos \unicode[STIX]{x1D6FD}\sin \unicode[STIX]{x1D6FD}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}z_{s}}\right]\unicode[STIX]{x1D70C}_{p}=\left[\frac{s^{2}}{N^{2}}(k^{2}+l^{2})+l^{2}+k^{2}\cos ^{2}\unicode[STIX]{x1D6FD}\right]\unicode[STIX]{x1D70C}_{p}\nonumber\\ \displaystyle & & \displaystyle \Rightarrow \,\left(\sin ^{2}\unicode[STIX]{x1D6FD}+\frac{s^{2}}{N^{2}}\right)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}_{p}}{\unicode[STIX]{x2202}z_{s}^{2}}-\text{i}k\sin (2\unicode[STIX]{x1D6FD})\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}_{p}}{\unicode[STIX]{x2202}z_{s}}-\left(\frac{s^{2}}{N^{2}}(k^{2}+l^{2})+l^{2}+k^{2}\cos ^{2}\unicode[STIX]{x1D6FD}\right)\unicode[STIX]{x1D70C}_{p}=0.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
It is evident that if
![]() $k=l=0$
, a perturbation of background density in the
$k=l=0$
, a perturbation of background density in the
![]() $z_{s}$
direction leads to a non-trivial steady harmonic response (since
$z_{s}$
direction leads to a non-trivial steady harmonic response (since
![]() $s$
is purely imaginary) with frequency
$s$
is purely imaginary) with frequency
![]() $\unicode[STIX]{x1D714}$
and time period
$\unicode[STIX]{x1D714}$
and time period
![]() $T$
given as
$T$
given as
Substitution of
![]() $k=0$
in (4.2) leads to
$k=0$
in (4.2) leads to
![]() $u_{p}=\text{i}(g/\unicode[STIX]{x1D70C}_{0}N)\unicode[STIX]{x1D70C}_{p}$
for the
$u_{p}=\text{i}(g/\unicode[STIX]{x1D70C}_{0}N)\unicode[STIX]{x1D70C}_{p}$
for the
![]() $k=l=0$
mode, implying a temporal phase difference of
$k=l=0$
mode, implying a temporal phase difference of
![]() $\unicode[STIX]{x03C0}/2$
between the mean (
$\unicode[STIX]{x03C0}/2$
between the mean (
![]() $k=l=0$
) density and velocity fields. Finally, the solution for the mean flow after neglecting diffusion and dissipation becomes
$k=l=0$
) density and velocity fields. Finally, the solution for the mean flow after neglecting diffusion and dissipation becomes
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \langle \unicode[STIX]{x1D70C}^{\ast }\rangle =\unicode[STIX]{x1D70C}_{0}^{\ast }(z_{s})\cos (\unicode[STIX]{x1D714}t),\\ \displaystyle \langle u_{s}\rangle =-\frac{g\unicode[STIX]{x1D70C}_{0}^{\ast }(z_{s})}{\unicode[STIX]{x1D70C}_{0}N}\sin (\unicode[STIX]{x1D714}t)=\frac{b_{0}(z_{s})}{N}\sin (\unicode[STIX]{x1D714}t),\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \langle \unicode[STIX]{x1D70C}^{\ast }\rangle =\unicode[STIX]{x1D70C}_{0}^{\ast }(z_{s})\cos (\unicode[STIX]{x1D714}t),\\ \displaystyle \langle u_{s}\rangle =-\frac{g\unicode[STIX]{x1D70C}_{0}^{\ast }(z_{s})}{\unicode[STIX]{x1D70C}_{0}N}\sin (\unicode[STIX]{x1D714}t)=\frac{b_{0}(z_{s})}{N}\sin (\unicode[STIX]{x1D714}t),\end{array}\right\}\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70C}_{0}^{\ast }(z_{s})$
is the initial density departure from the background and
$\unicode[STIX]{x1D70C}_{0}^{\ast }(z_{s})$
is the initial density departure from the background and
![]() $b_{0}(z_{s})$
is the corresponding buoyancy. The maximum value attained by
$b_{0}(z_{s})$
is the corresponding buoyancy. The maximum value attained by
![]() $u_{s}$
is
$u_{s}$
is
![]() $b_{0}/N$
, much larger than the magnitude of steady diffusion-driven upslope flow that arises at a sloping boundary in a stratified fluid (Phillips Reference Phillips1970; Phillips, Shyu & Salmun Reference Phillips, Shyu and Salmun1986; Peacock, Stocker & Aristoff Reference Peacock, Stocker and Aristoff2004).
$b_{0}/N$
, much larger than the magnitude of steady diffusion-driven upslope flow that arises at a sloping boundary in a stratified fluid (Phillips Reference Phillips1970; Phillips, Shyu & Salmun Reference Phillips, Shyu and Salmun1986; Peacock, Stocker & Aristoff Reference Peacock, Stocker and Aristoff2004).
Equation (4.8) can be interpreted as an oscillatory exchange of energy between the MAPE and MKE reservoirs. The APE of the initial density anomaly leads to a slope-parallel oscillatory current whose speed has amplitude
![]() $b_{0}/N$
. The analytical result, equation (4.8), agrees well with the mean velocity in the simulation as shown for case ANG2.5-1. All the sloping cases simulated here exhibit a mean flow that oscillates with
$b_{0}/N$
. The analytical result, equation (4.8), agrees well with the mean velocity in the simulation as shown for case ANG2.5-1. All the sloping cases simulated here exhibit a mean flow that oscillates with
![]() $\unicode[STIX]{x1D714}=N\sin \unicode[STIX]{x1D6FD}$
and a phase difference of
$\unicode[STIX]{x1D714}=N\sin \unicode[STIX]{x1D6FD}$
and a phase difference of
![]() $\unicode[STIX]{x03C0}/2$
between the mean velocity and density. The focus of this paper is on near-bottom density perturbations with large value of aspect ratio of horizontal to vertical scale. Therefore, we defer the study of initial density anomalies with finite
$\unicode[STIX]{x03C0}/2$
between the mean velocity and density. The focus of this paper is on near-bottom density perturbations with large value of aspect ratio of horizontal to vertical scale. Therefore, we defer the study of initial density anomalies with finite
![]() $k$
and
$k$
and
![]() $l$
to future work, and move on to the vertical variability of the nonlinearly evolving flow that develops in the limit of infinitely large aspect ratio.
$l$
to future work, and move on to the vertical variability of the nonlinearly evolving flow that develops in the limit of infinitely large aspect ratio.

Figure 3. Vertical profiles of mean density (dash-dotted blue line) and streamwise velocity (solid red line) for ANG0-2 case: (a)
![]() $Nt=0$
, (b)
$Nt=0$
, (b)
![]() $Nt=15$
, (c)
$Nt=15$
, (c)
![]() $Nt=18$
and (d)
$Nt=18$
and (d)
![]() $Nt=36$
. Initial background density is shown by the dashed blue line.
$Nt=36$
. Initial background density is shown by the dashed blue line.

Figure 4. Vertical profiles of mean density (dash-dotted blue line) and mean streamwise velocity (solid red line) in case ANG5-2 at eight time instants (circles on the velocity time series of the header). The variables are made non-dimensional with
![]() $\unicode[STIX]{x1D70C}_{p}$
and
$\unicode[STIX]{x1D70C}_{p}$
and
![]() $u_{p}=g\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{0}N$
, respectively. First row: (a)
$u_{p}=g\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{0}N$
, respectively. First row: (a)
![]() $t=0$
, (b)
$t=0$
, (b)
![]() $t=T/4$
(
$t=T/4$
(
![]() $Nt=18$
), (c)
$Nt=18$
), (c)
![]() $t=T/2$
(
$t=T/2$
(
![]() $Nt=36$
) and (d)
$Nt=36$
) and (d)
![]() $t=T$
(
$t=T$
(
![]() $Nt=72$
). Second row: (e)
$Nt=72$
). Second row: (e)
![]() $t=3T$
, (f)
$t=3T$
, (f)
![]() $t=3T+T/4$
, (g)
$t=3T+T/4$
, (g)
![]() $t=3T+T/2$
and (h)
$t=3T+T/2$
and (h)
![]() $t=4T$
. Background
$t=4T$
. Background
![]() $\unicode[STIX]{x1D70C}_{b}$
is in dashed blue.
$\unicode[STIX]{x1D70C}_{b}$
is in dashed blue.
5 Vertical variability of the mean flow
Profiles of mean velocity and density for the non-sloping case ANG0-2 are shown in figure 3(a–d). Starting from an unstable density profile in figure 3(a), a mixed layer starts to develop after a short delay of
![]() $Nt\approx 10$
, has appreciable thickness by
$Nt\approx 10$
, has appreciable thickness by
![]() $Nt=15$
and is close to its final thickness by
$Nt=15$
and is close to its final thickness by
![]() $Nt=18$
(figure 3
c). Figure 3(d) indicates that the mixed layer thickness
$Nt=18$
(figure 3
c). Figure 3(d) indicates that the mixed layer thickness
![]() $h_{m}(t)$
approaches
$h_{m}(t)$
approaches
![]() $1.9h_{0}$
at
$1.9h_{0}$
at
![]() $Nt=36$
, which is past the end of the turbulent mixing phase. The mean velocity which is prominent at
$Nt=36$
, which is past the end of the turbulent mixing phase. The mean velocity which is prominent at
![]() $Nt=18$
reduces considerably around this time and eventually decays to 0.
$Nt=18$
reduces considerably around this time and eventually decays to 0.
In the sloping cases, the evolution is qualitatively different. The oscillatory mean flow discussed in § 4 modulates the density so that mixing is superimposed on an oscillatory mean stratification. Case ANG5-2 is used as an example to discuss features of the vertical variability that are found to be common to all the sloping cases simulated for this study. Eight different time points are selected in the evolution of ANG5-2 and the slope-normal profiles of
![]() $\langle u\rangle$
and
$\langle u\rangle$
and
![]() $\langle \unicode[STIX]{x1D70C}^{\ast }\rangle$
at those times are plotted in figure 4. The velocity, hereafter denoted as
$\langle \unicode[STIX]{x1D70C}^{\ast }\rangle$
at those times are plotted in figure 4. The velocity, hereafter denoted as
![]() $\langle u\rangle _{max}$
, chosen for the header is at
$\langle u\rangle _{max}$
, chosen for the header is at
![]() $z=0.21L_{zs}$
, the vertical location at which the velocity variation is maximum.
$z=0.21L_{zs}$
, the vertical location at which the velocity variation is maximum.
Figure 4(a–d) show four quarter phases of the first oscillatory cycle marked on the header as A, B, C and D, respectively. The values of
![]() $Nt$
for the non-sloping case profiles shown earlier in figure 3(a,c,d) were selected to be the same as for figure 4(a–c) in the sloping case so as to directly demonstrate the remarkable influence that even a moderate slope exerts on the flow evolution. The APE is maximum at time A (figure 4
a) and is completely transferred to MKE at time B (figure 4
b) when the density profile coincides with the initial background. At this point,
$Nt$
for the non-sloping case profiles shown earlier in figure 3(a,c,d) were selected to be the same as for figure 4(a–c) in the sloping case so as to directly demonstrate the remarkable influence that even a moderate slope exerts on the flow evolution. The APE is maximum at time A (figure 4
a) and is completely transferred to MKE at time B (figure 4
b) when the density profile coincides with the initial background. At this point,
![]() $\langle u\rangle$
achieves its maximum amplitude, giving rise to upslope and downslope currents centred at
$\langle u\rangle$
achieves its maximum amplitude, giving rise to upslope and downslope currents centred at
![]() $z_{s}/L_{zs}=0.21$
and
$z_{s}/L_{zs}=0.21$
and
![]() $z_{s}/L_{zs}=0.66$
, respectively. These currents disturb the equilibrium density configuration and eventually strengthen the stratification in the central zone at C (figure 4
c) so that
$z_{s}/L_{zs}=0.66$
, respectively. These currents disturb the equilibrium density configuration and eventually strengthen the stratification in the central zone at C (figure 4
c) so that
![]() $N^{2}$
exceeds its initial background value. At
$N^{2}$
exceeds its initial background value. At
![]() $t=3T/4$
(not shown),
$t=3T/4$
(not shown),
![]() $\langle u\rangle$
reaches a local maximum in amplitude and is oppositely directed to that at
$\langle u\rangle$
reaches a local maximum in amplitude and is oppositely directed to that at
![]() $t=T/4$
. As the flow approaches
$t=T/4$
. As the flow approaches
![]() $t=T$
, the density cannot recover to its initial unstable configuration. A large convective overturning event (LCOE) with turbulence is initiated and it results in the
$t=T$
, the density cannot recover to its initial unstable configuration. A large convective overturning event (LCOE) with turbulence is initiated and it results in the
![]() $\langle \unicode[STIX]{x1D70C}^{\ast }\rangle$
profile (figure 4
d) that has much weaker density variation than in the initial anomaly.
$\langle \unicode[STIX]{x1D70C}^{\ast }\rangle$
profile (figure 4
d) that has much weaker density variation than in the initial anomaly.
Examination of the fourth cycle (points E, F, G and H shown in the bottom row of figure 4) leads to the following observations. First, at E (figure 4 e), the initial unstable density profile is absent. Second, the velocity currents are weaker at F (figure 4 f) compared to those at the same phase (B) in the first cycle. These two observations are related to the mixing that has taken place over three cycles.

Figure 5. LCOE in case ANG5-2 shown by contours of
![]() $\unicode[STIX]{x1D70C}_{b}+\unicode[STIX]{x1D70C}^{\ast }$
(a–c) and
$\unicode[STIX]{x1D70C}_{b}+\unicode[STIX]{x1D70C}^{\ast }$
(a–c) and
![]() $u$
(d–f). Left, centre and right columns at times D
$u$
(d–f). Left, centre and right columns at times D
![]() $-$
, D (
$-$
, D (
![]() $t=T$
) and D
$t=T$
) and D
![]() $+$
in the header of figure 4.
$+$
in the header of figure 4.
Between points B and C, energy is transferred from MKE back to MAPE, with some energy lost to dissipation and mixing. At C, the central region (
![]() $z_{s}/L_{zs}=0.33$
to 0.66) is stable but there is a region of instability adjacent to the bottom. While the flow proceeds from D
$z_{s}/L_{zs}=0.33$
to 0.66) is stable but there is a region of instability adjacent to the bottom. While the flow proceeds from D
![]() $-$
toward its initial state (D), the differential advection of the fluid brings heavier fluid over lighter fluid to cause convective instability. To study the events leading to scalar mixing in the LCOE, we investigate the velocity and density contours in a vertical
$-$
toward its initial state (D), the differential advection of the fluid brings heavier fluid over lighter fluid to cause convective instability. To study the events leading to scalar mixing in the LCOE, we investigate the velocity and density contours in a vertical
![]() $x$
–
$x$
–
![]() $z$
plane as the flow approaches and passes through time
$z$
plane as the flow approaches and passes through time
![]() $t=T$
. At
$t=T$
. At
![]() $Nt=61.76$
(time D
$Nt=61.76$
(time D
![]() $-$
), the opposing slope-parallel velocity jets are significant (figure 5
d) and the stratification is close to the background state. Small-scale variability in the density (figure 5
a) is insignificant at this time. These jets subsequently decay at
$-$
), the opposing slope-parallel velocity jets are significant (figure 5
d) and the stratification is close to the background state. Small-scale variability in the density (figure 5
a) is insignificant at this time. These jets subsequently decay at
![]() $t=T$
(figure 5
e). During the quarter cycle preceding
$t=T$
(figure 5
e). During the quarter cycle preceding
![]() $t=T$
, the jets act to displace lighter fluid below denser fluid instigating an overturn (figure 5
b). The overturn leads to turbulent mixing as is qualitatively clear from the small scales and weak density contrast in the central region of figure 5(c). The upper and lower oppositely directed jets remerge in the next cycle (figure 5
f).
$t=T$
, the jets act to displace lighter fluid below denser fluid instigating an overturn (figure 5
b). The overturn leads to turbulent mixing as is qualitatively clear from the small scales and weak density contrast in the central region of figure 5(c). The upper and lower oppositely directed jets remerge in the next cycle (figure 5
f).

Figure 6. Time evolution of TKE, MKE, TAPE and MAPE averaged over
![]() $z_{s}$
: (a) non-sloping case ANG0-2, and (b) sloping case ANG2.5-2. The corresponding values of time-integrated dissipation terms are shown in panels (c) and (d).
$z_{s}$
: (a) non-sloping case ANG0-2, and (b) sloping case ANG2.5-2. The corresponding values of time-integrated dissipation terms are shown in panels (c) and (d).

Figure 7. Temporal evolution of vertically averaged terms in the energy budget equations for case ANG5-2: (a) TKE budget, and (b) TAPE budget.

Figure 8. Temporal evolution of vertically averaged terms in the mean energy budget equations for case ANG5-2: (a) MKE budget, and (b) MAPE budget.
6 Energetics
The problem is initialized with zero velocity, an unstable mean density and no density fluctuations. Thus, at
![]() $t=0$
the energy resides exclusively in the MAPE reservoir. Figure 6 illustrates the effect of finite slope on the evolution of the energy reservoirs and the time-integrated dissipation terms. In the non-sloping case ANG0-2 (figure 6
a), the initial APE decays and asymptotes to an approximately constant value by
$t=0$
the energy resides exclusively in the MAPE reservoir. Figure 6 illustrates the effect of finite slope on the evolution of the energy reservoirs and the time-integrated dissipation terms. In the non-sloping case ANG0-2 (figure 6
a), the initial APE decays and asymptotes to an approximately constant value by
![]() $Nt\approx 30$
. The transfer to MKE is negligible. Both TKE and TAPE increase initially, peak at
$Nt\approx 30$
. The transfer to MKE is negligible. Both TKE and TAPE increase initially, peak at
![]() $Nt\approx 15$
, and then decay. Visualizations (not shown) indicate that it is a single LCOE whose breakdown is responsible for energy transfer from MAPE to TKE and TAPE, which then gets dissipated. The loss in net energy (
$Nt\approx 15$
, and then decay. Visualizations (not shown) indicate that it is a single LCOE whose breakdown is responsible for energy transfer from MAPE to TKE and TAPE, which then gets dissipated. The loss in net energy (
![]() $E_{loss}$
in figure 6
c) increases rapidly after TAPE and TKE peak. Approximately three-quarters of the initial energy is dissipated in case ANG0-2. The energy loss is calculated in two ways: directly as
$E_{loss}$
in figure 6
c) increases rapidly after TAPE and TKE peak. Approximately three-quarters of the initial energy is dissipated in case ANG0-2. The energy loss is calculated in two ways: directly as
![]() $E_{loss}$
defined by (3.12), and as the time-integrated dissipation,
$E_{loss}$
defined by (3.12), and as the time-integrated dissipation,
Figure 6(c) shows that the numerics satisfy the requirement that
![]() $E_{loss}(t)$
be equal to
$E_{loss}(t)$
be equal to
![]() $E_{dissip}(t)$
.
$E_{dissip}(t)$
.
In contrast to the case with zero bottom slope, case ANG2.5-2 has significant MKE. The evolution of MAPE and MKE (figure 6
b) corresponds to a damped harmonic oscillator with frequency
![]() $2N\sin \unicode[STIX]{x1D6FD}$
. During the oscillation, there is energy transfer to TKE and TAPE as well as dissipation. In this case, the bottom has a shallow slope so that the time period
$2N\sin \unicode[STIX]{x1D6FD}$
. During the oscillation, there is energy transfer to TKE and TAPE as well as dissipation. In this case, the bottom has a shallow slope so that the time period
![]() $T=2\unicode[STIX]{x03C0}/(N\sin \unicode[STIX]{x1D6FD})$
is large (
$T=2\unicode[STIX]{x03C0}/(N\sin \unicode[STIX]{x1D6FD})$
is large (
![]() $NT=144$
) in terms of the buoyancy time scale. There is substantial dissipation during the first cycle with
$NT=144$
) in terms of the buoyancy time scale. There is substantial dissipation during the first cycle with
![]() $E_{loss}\approx 60\,\%$
at
$E_{loss}\approx 60\,\%$
at
![]() $t=T$
(figure 6
d). The loss is entirely due to turbulence (primarily
$t=T$
(figure 6
d). The loss is entirely due to turbulence (primarily
![]() $\unicode[STIX]{x1D700}^{T}$
) with negligible contribution from mean dissipation and, furthermore, occurs at specific intervals during the oscillation. The underlying turbulence mechanism remains the same as in the non-sloping ANG0-2 case, i.e. convective instability, but the oscillatory nature of the flow causes convectively unstable overturns at multiple phases of the cycle instead of the LCOE of ANG0-2. The largest burst of turbulence occurs at the end of each cycle as the near-bottom flow reverses from downslope to upslope.
$\unicode[STIX]{x1D700}^{T}$
) with negligible contribution from mean dissipation and, furthermore, occurs at specific intervals during the oscillation. The underlying turbulence mechanism remains the same as in the non-sloping ANG0-2 case, i.e. convective instability, but the oscillatory nature of the flow causes convectively unstable overturns at multiple phases of the cycle instead of the LCOE of ANG0-2. The largest burst of turbulence occurs at the end of each cycle as the near-bottom flow reverses from downslope to upslope.
To better understand the energy transfer between potential and kinetic energy, on the one hand, and between mean and turbulence fields, on the other, the four budget equations ((3.1), (3.3), (3.8) and (3.10)) are quantified in case ANG5-2. Figure 7(a,b) show the evolution of terms in the
![]() $z_{s}$
-averaged TKE and TAPE equations, respectively. During the first cycle, there are three episodes of turbulent dissipation with a minor peak when
$z_{s}$
-averaged TKE and TAPE equations, respectively. During the first cycle, there are three episodes of turbulent dissipation with a minor peak when
![]() $\langle u_{max}\rangle$
peaks followed by two prominent peaks at
$\langle u_{max}\rangle$
peaks followed by two prominent peaks at
![]() $t=T/2$
and
$t=T/2$
and
![]() $t=T$
, respectively, just after the flow passes through
$t=T$
, respectively, just after the flow passes through
![]() $\langle u_{max}\rangle =0$
. During the second episode at
$\langle u_{max}\rangle =0$
. During the second episode at
![]() $Nt\approx 36$
, the buoyancy flux is positive (a source of TKE), and is balanced by the tendency (TKE rate of change) and dissipation terms. This is the signature of a turbulence burst that is driven by convective instability (between
$Nt\approx 36$
, the buoyancy flux is positive (a source of TKE), and is balanced by the tendency (TKE rate of change) and dissipation terms. This is the signature of a turbulence burst that is driven by convective instability (between
![]() $z_{s}=0$
and
$z_{s}=0$
and
![]() $z_{s}=0.2L_{zs}$
in figure 4
c) due to differential advection at the boundary. The third episode is at the end of a full cycle (
$z_{s}=0.2L_{zs}$
in figure 4
c) due to differential advection at the boundary. The third episode is at the end of a full cycle (
![]() $Nt\approx 72$
) when the flow tries to recover to its initial density profile (but cannot because of static instability); this episode features convectively driven turbulence and has the largest burst of TKE. In addition, there is a period of negative production since shear acts on turbulence driven by buoyancy, and the flux-gradient relationship of shear-driven turbulence does not apply (Gayen & Sarkar Reference Gayen and Sarkar2011b
).
$Nt\approx 72$
) when the flow tries to recover to its initial density profile (but cannot because of static instability); this episode features convectively driven turbulence and has the largest burst of TKE. In addition, there is a period of negative production since shear acts on turbulence driven by buoyancy, and the flux-gradient relationship of shear-driven turbulence does not apply (Gayen & Sarkar Reference Gayen and Sarkar2011b
).
The zero-velocity phases are also associated with TAPE events (figure 7
b). The scalar production,
![]() $P_{\unicode[STIX]{x1D70C}}$
, defined in (3.9) is the source of TAPE and is balanced by the tendency and dissipation terms. Thus, the scalar production transfers energy from MAPE to TAPE during these turbulence events.
$P_{\unicode[STIX]{x1D70C}}$
, defined in (3.9) is the source of TAPE and is balanced by the tendency and dissipation terms. Thus, the scalar production transfers energy from MAPE to TAPE during these turbulence events.

Figure 9. Schematic of energy pathways in flow over a slope.
A map of energy transfers in the problem is rendered in figure 9. In all cases, the pathways of MAPE to TKE and MAPE to TAPE are active and responsible for dissipation in the system. The energy loss is dominated by dissipation of turbulent KE and APE; the direct dissipation of mean components is negligible. In the absence of slope, there is negligible MKE at all times. However, in the sloping cases, there is a significant mean buoyancy flux that facilitates an oscillatory MKE–MAPE exchange (figure 8). The mean flow also introduces a non-zero production (
![]() $P$
) that additionally modulates TKE.
$P$
) that additionally modulates TKE.

Figure 10. Energetics for steeper slopes: (a) ANG10 and (b) ANG30.
7 Flow over steeper slopes
Although oceanic slopes typically range from 0
![]() $^{\circ }$
to 5
$^{\circ }$
to 5
![]() $^{\circ }$
, steeper slopes of 10–20
$^{\circ }$
, steeper slopes of 10–20
![]() $^{\circ }$
are also present at straits (Alford et al.
Reference Alford, Peacock, MacKinnon, Nash, Buijsman, Centurioni, Chao, Chang, Farmer and Fringer2015), ridges (Merrifield, Holloway & Johnston Reference Merrifield, Holloway and Johnston2001) and continental slopes (Cuny et al.
Reference Cuny, Rhines, Schott and Lazier2005). Features with length scales less than 10 km in canyons and bumps can have a slope that is even larger than 20
$^{\circ }$
are also present at straits (Alford et al.
Reference Alford, Peacock, MacKinnon, Nash, Buijsman, Centurioni, Chao, Chang, Farmer and Fringer2015), ridges (Merrifield, Holloway & Johnston Reference Merrifield, Holloway and Johnston2001) and continental slopes (Cuny et al.
Reference Cuny, Rhines, Schott and Lazier2005). Features with length scales less than 10 km in canyons and bumps can have a slope that is even larger than 20
![]() $^{\circ }$
. Steep bathymetry exerts an influence on internal-wave-driven turbulence and on the spatial scale of eddies and fronts, which can directly affect abyssal circulation and deep-ocean convection. We are thus motivated to extend the scope of previous sections to include steeper slopes.
$^{\circ }$
. Steep bathymetry exerts an influence on internal-wave-driven turbulence and on the spatial scale of eddies and fronts, which can directly affect abyssal circulation and deep-ocean convection. We are thus motivated to extend the scope of previous sections to include steeper slopes.
The frequency (
![]() $N\sin \unicode[STIX]{x1D6FD}$
) of the oscillatory flow increases with slope angle and decreases the time scale intrinsic to the flow sloshing. Meanwhile, the overturn height,
$N\sin \unicode[STIX]{x1D6FD}$
) of the oscillatory flow increases with slope angle and decreases the time scale intrinsic to the flow sloshing. Meanwhile, the overturn height,
![]() $h_{0}$
, reduces with increasing slope angle since the slope-normal extent of the perturbation is fixed. Consequently, turbulence and associated energy loss change as a function of
$h_{0}$
, reduces with increasing slope angle since the slope-normal extent of the perturbation is fixed. Consequently, turbulence and associated energy loss change as a function of
![]() $\unicode[STIX]{x1D6FD}$
. Figure 10 compares the energy evolution between ANG10 and ANG30. The total energy residing in the mean field (shown in solid brown) is seen to decay with time. There is an initial phase (up to
$\unicode[STIX]{x1D6FD}$
. Figure 10 compares the energy evolution between ANG10 and ANG30. The total energy residing in the mean field (shown in solid brown) is seen to decay with time. There is an initial phase (up to
![]() $Nt\approx 75$
in figure 10
a) where the mean energy variation exhibits steps since the energy decay occurs as discrete events with bursts of turbulence. As discussed in § 6, convective instability is the dominant progenitor of turbulence in these bursts. This initial energy loss will be hereafter referred to as convective-instability-dominated loss (CDL). After
$Nt\approx 75$
in figure 10
a) where the mean energy variation exhibits steps since the energy decay occurs as discrete events with bursts of turbulence. As discussed in § 6, convective instability is the dominant progenitor of turbulence in these bursts. This initial energy loss will be hereafter referred to as convective-instability-dominated loss (CDL). After
![]() $Nt\approx 75$
, ANG10 exhibits a phase with energy loss at an approximately constant rate which will be referred to as quasi-steady loss (QSL). The role of convective instability in turbulence generation diminishes with increasing slope angle (due to smaller
$Nt\approx 75$
, ANG10 exhibits a phase with energy loss at an approximately constant rate which will be referred to as quasi-steady loss (QSL). The role of convective instability in turbulence generation diminishes with increasing slope angle (due to smaller
![]() $h_{0}$
), contributing to reduction of CDL. It should be noted that, for a fixed
$h_{0}$
), contributing to reduction of CDL. It should be noted that, for a fixed
![]() $\unicode[STIX]{x1D70C}_{p}$
, there exists a critical slope beyond which convective instability is absent. In our cases, for
$\unicode[STIX]{x1D70C}_{p}$
, there exists a critical slope beyond which convective instability is absent. In our cases, for
![]() $\unicode[STIX]{x1D70C}_{p}=0.02~\text{kg}~\text{m}^{-3}$
, we can estimate this critical slope to be
$\unicode[STIX]{x1D70C}_{p}=0.02~\text{kg}~\text{m}^{-3}$
, we can estimate this critical slope to be
![]() $\unicode[STIX]{x1D6FD}_{critical}=75^{\circ }$
from (2.15). All sloping cases considered here have
$\unicode[STIX]{x1D6FD}_{critical}=75^{\circ }$
from (2.15). All sloping cases considered here have
![]() $\unicode[STIX]{x1D6FD}<\unicode[STIX]{x1D6FD}_{critical}$
, and exhibit CDL followed by QSL, with the discrete steps during CDL becoming less prominent at large
$\unicode[STIX]{x1D6FD}<\unicode[STIX]{x1D6FD}_{critical}$
, and exhibit CDL followed by QSL, with the discrete steps during CDL becoming less prominent at large
![]() $\unicode[STIX]{x1D6FD}$
.
$\unicode[STIX]{x1D6FD}$
.
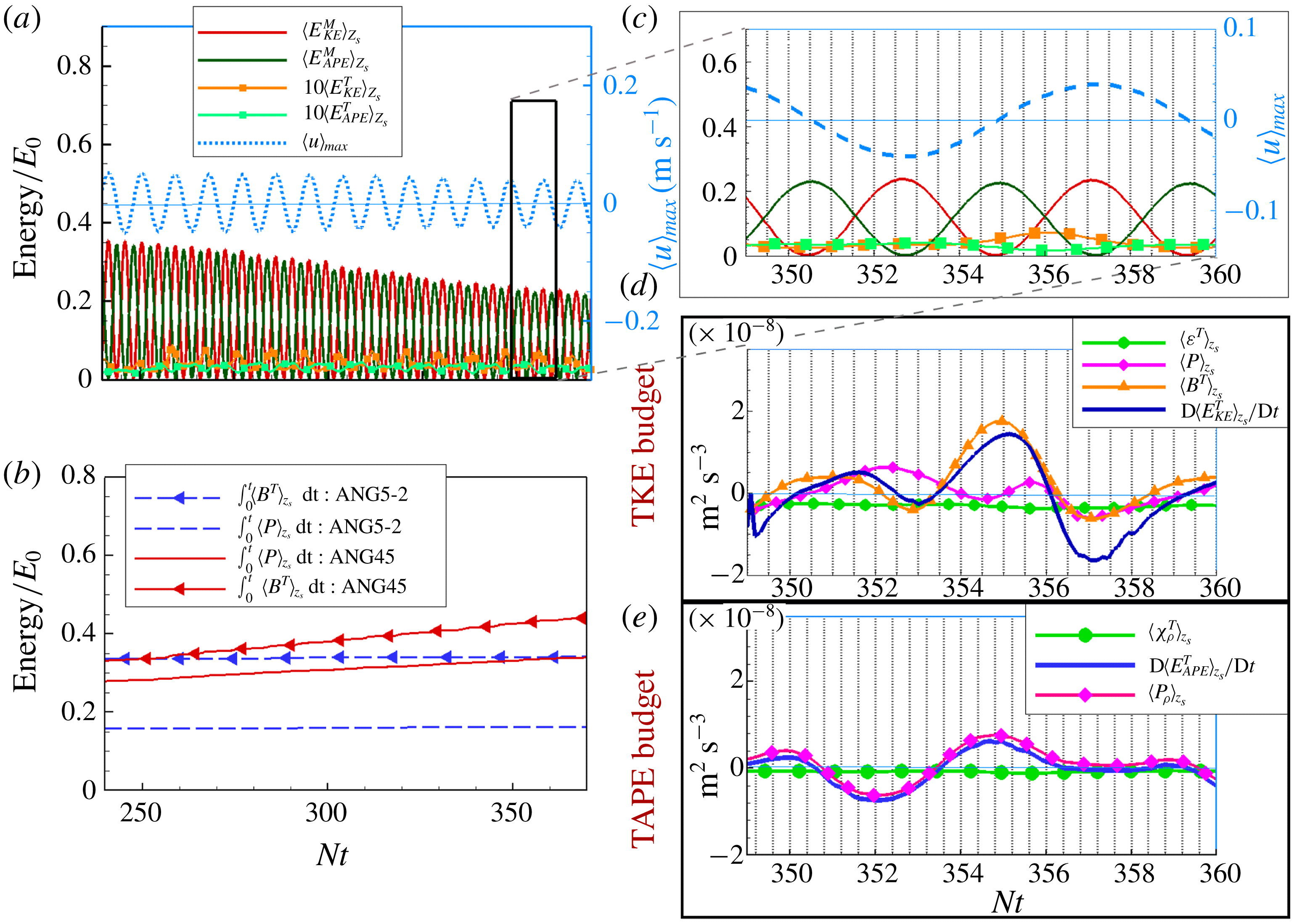
Figure 11. (a) Energetics in the QSL phase of case ANG45. A temporal window between
![]() $Nt=350$
and 360 denoted by the black rectangular box is enlarged in panel (c). The evolution of terms in the TKE and TAPE equations for this time window is displayed in panels (d) and (e), respectively. (b) Comparison of integrated shear production and buoyancy flux in ANG5-2 and ANG45 cases, depicting the importance of shear production in the case with a steeper slope of
$Nt=350$
and 360 denoted by the black rectangular box is enlarged in panel (c). The evolution of terms in the TKE and TAPE equations for this time window is displayed in panels (d) and (e), respectively. (b) Comparison of integrated shear production and buoyancy flux in ANG5-2 and ANG45 cases, depicting the importance of shear production in the case with a steeper slope of
![]() $45^{\circ }$
.
$45^{\circ }$
.
Details of the QSL phase are described for case ANG45. Figure 11(a) shows the evolution of the energy reservoirs, and the column to the right shows a smaller time window (
![]() $Nt=350\text{ to }365$
) with panel (c) showing the energy-reservoir evolution and panels (d) and (e) showing the corresponding TKE and TAPE budget terms. Except dissipation, which is dominated by small-scale fluctuations, all terms exhibit a harmonic oscillation. TKE generation is due to
$Nt=350\text{ to }365$
) with panel (c) showing the energy-reservoir evolution and panels (d) and (e) showing the corresponding TKE and TAPE budget terms. Except dissipation, which is dominated by small-scale fluctuations, all terms exhibit a harmonic oscillation. TKE generation is due to
![]() $B^{T}$
(attributed to buoyancy) and
$B^{T}$
(attributed to buoyancy) and
![]() $P$
(attributed to shear). Meanwhile,
$P$
(attributed to shear). Meanwhile,
![]() $P_{\unicode[STIX]{x1D70C}}$
drives TAPE generation. The scalar and turbulent dissipation remain approximately constant throughout the QSL phase, accounting for the constant rate of energy loss.
$P_{\unicode[STIX]{x1D70C}}$
drives TAPE generation. The scalar and turbulent dissipation remain approximately constant throughout the QSL phase, accounting for the constant rate of energy loss.
Turbulence generation during the QSL phase increases with increasing
![]() $\unicode[STIX]{x1D6FD}$
as illustrated by comparing the time-integrated turbulent buoyancy flux and production between ANG45 and ANG5-2 in figure 11(b). The slope of their variation in ANG45 (solid red lines) is larger than in ANG5 (dashed blue lines). The cumulative energy loss is larger at
$\unicode[STIX]{x1D6FD}$
as illustrated by comparing the time-integrated turbulent buoyancy flux and production between ANG45 and ANG5-2 in figure 11(b). The slope of their variation in ANG45 (solid red lines) is larger than in ANG5 (dashed blue lines). The cumulative energy loss is larger at
![]() $\unicode[STIX]{x1D6FD}=45^{\circ }$
compared to
$\unicode[STIX]{x1D6FD}=45^{\circ }$
compared to
![]() $5^{\circ }$
. It is also worth noting from figure 11(b) that the contribution of buoyancy flux to TKE generation exceeds that of production for both ANG5-2 and ANG45. The difference between cumulative buoyancy flux and production decreases with increasing
$5^{\circ }$
. It is also worth noting from figure 11(b) that the contribution of buoyancy flux to TKE generation exceeds that of production for both ANG5-2 and ANG45. The difference between cumulative buoyancy flux and production decreases with increasing
![]() $\unicode[STIX]{x1D6FD}$
.
$\unicode[STIX]{x1D6FD}$
.

Figure 12. (a) Temporal variation of the cumulative energy loss. (b) The effect of the bottom slope on the energy loss rate in the QSL phase. The squares represent cases with
![]() $\unicode[STIX]{x1D70C}_{p}=0.02$
and the diamonds represent cases with
$\unicode[STIX]{x1D70C}_{p}=0.02$
and the diamonds represent cases with
![]() $\unicode[STIX]{x1D70C}_{p}=0.01$
listed in tables 1 and 2).
$\unicode[STIX]{x1D70C}_{p}=0.01$
listed in tables 1 and 2).
The slope angle and the strength of the initial density anomaly,
![]() $R_{\unicode[STIX]{x1D70C}}$
, determine the energy loss (figure 12
a) in the system. The energy loss in the case with
$R_{\unicode[STIX]{x1D70C}}$
, determine the energy loss (figure 12
a) in the system. The energy loss in the case with
![]() $\unicode[STIX]{x1D6FD}=0^{\circ }$
is accomplished relatively faster and is complete by
$\unicode[STIX]{x1D6FD}=0^{\circ }$
is accomplished relatively faster and is complete by
![]() $Nt=30$
when almost three-quarters of the initial energy is lost. Our sloping cases exhibit a CDL phase followed by a QSL phase. There are discrete overturn events during CDL for all cases. The energy loss per event reduces with increasing
$Nt=30$
when almost three-quarters of the initial energy is lost. Our sloping cases exhibit a CDL phase followed by a QSL phase. There are discrete overturn events during CDL for all cases. The energy loss per event reduces with increasing
![]() $\unicode[STIX]{x1D6FD}$
since the overturn height decreases but the number (proportional to
$\unicode[STIX]{x1D6FD}$
since the overturn height decreases but the number (proportional to
![]() $\unicode[STIX]{x1D714}=N\sin \unicode[STIX]{x1D6FD}$
) of such events increases. Therefore, the ordering of energy loss with angle depends on the chosen time. At
$\unicode[STIX]{x1D714}=N\sin \unicode[STIX]{x1D6FD}$
) of such events increases. Therefore, the ordering of energy loss with angle depends on the chosen time. At
![]() $Nt=350$
,
$Nt=350$
,
![]() $E_{loss}/E_{0}$
varies between 0.6 and 0.8 with ANG45 having the largest dissipation. The influence of
$E_{loss}/E_{0}$
varies between 0.6 and 0.8 with ANG45 having the largest dissipation. The influence of
![]() $R_{\unicode[STIX]{x1D70C}}$
is more straightforward. The cases with smaller
$R_{\unicode[STIX]{x1D70C}}$
is more straightforward. The cases with smaller
![]() $R_{\unicode[STIX]{x1D70C}}$
have smaller dissipation with
$R_{\unicode[STIX]{x1D70C}}$
have smaller dissipation with
![]() $E_{loss}/E_{0}\approx 0.3$
at long time.
$E_{loss}/E_{0}\approx 0.3$
at long time.
The energy loss rate in the QSL phase is obtained by performing linear regression on the
![]() $E_{loss}$
time-series data beyond
$E_{loss}$
time-series data beyond
![]() $Nt=300$
. The
$Nt=300$
. The
![]() ${\dot{E}}$
value in the QSL phase increases linearly with
${\dot{E}}$
value in the QSL phase increases linearly with
![]() $\sin \unicode[STIX]{x1D6FD}$
(figure 12
b). There is also a mild influence of
$\sin \unicode[STIX]{x1D6FD}$
(figure 12
b). There is also a mild influence of
![]() $R_{\unicode[STIX]{x1D70C}}$
: ANG2.5-2 and ANG5-2 (square symbols) have slightly larger loss rates than ANG2.5-1 and ANG5-1 (diamond symbols), respectively. The linear variation of
$R_{\unicode[STIX]{x1D70C}}$
: ANG2.5-2 and ANG5-2 (square symbols) have slightly larger loss rates than ANG2.5-1 and ANG5-1 (diamond symbols), respectively. The linear variation of
![]() ${\dot{E}}$
with
${\dot{E}}$
with
![]() $\sin \unicode[STIX]{x1D6FD}$
provides a simple model for the energy loss rate. It can be understood as follows. Both shear production and buoyancy flux increase with initial APE and it is reasonable to characterize
$\sin \unicode[STIX]{x1D6FD}$
provides a simple model for the energy loss rate. It can be understood as follows. Both shear production and buoyancy flux increase with initial APE and it is reasonable to characterize
![]() ${\dot{E}}$
during the QSL phase with an energy scale that is proportional to
${\dot{E}}$
during the QSL phase with an energy scale that is proportional to
![]() $E_{0}$
. A natural inverse time scale is the oscillation frequency
$E_{0}$
. A natural inverse time scale is the oscillation frequency
![]() $N\sin \unicode[STIX]{x1D6FD}$
. It follows that
$N\sin \unicode[STIX]{x1D6FD}$
. It follows that
![]() ${\dot{E}}\propto E_{0}N\sin \unicode[STIX]{x1D6FD}$
.
${\dot{E}}\propto E_{0}N\sin \unicode[STIX]{x1D6FD}$
.
The cumulative mixing efficiency (
![]() $\unicode[STIX]{x1D6E4}$
defined by (3.13)) is plotted in figure 13. In the non-sloping case ANG0-2,
$\unicode[STIX]{x1D6E4}$
defined by (3.13)) is plotted in figure 13. In the non-sloping case ANG0-2,
![]() $\unicode[STIX]{x1D6E4}$
increases rapidly to its peak value of almost 0.8 before decreasing to approximately 0.3. This result is in agreement with a previous laboratory experiment of an unstable density interface immersed in a stable background (Wykes & Dalziel Reference Wykes and Dalziel2014), where
$\unicode[STIX]{x1D6E4}$
increases rapidly to its peak value of almost 0.8 before decreasing to approximately 0.3. This result is in agreement with a previous laboratory experiment of an unstable density interface immersed in a stable background (Wykes & Dalziel Reference Wykes and Dalziel2014), where
![]() $\unicode[STIX]{x1D6E4}$
was found to reach values that exceeded 0.75. Results from other numerical studies of oscillating flows with convective and shear-driven turbulence, e.g. an oscillating stratified boundary layer on a slope (Chalamalla & Sarkar Reference Chalamalla and Sarkar2015) and internal wave breaking at a pycnocline owing to parametric subharmonic instability (Gayen & Sarkar Reference Gayen and Sarkar2014) have reported similar findings of
$\unicode[STIX]{x1D6E4}$
was found to reach values that exceeded 0.75. Results from other numerical studies of oscillating flows with convective and shear-driven turbulence, e.g. an oscillating stratified boundary layer on a slope (Chalamalla & Sarkar Reference Chalamalla and Sarkar2015) and internal wave breaking at a pycnocline owing to parametric subharmonic instability (Gayen & Sarkar Reference Gayen and Sarkar2014) have reported similar findings of
![]() $\unicode[STIX]{x1D6E4}>0.2$
, with the asymptotic values of
$\unicode[STIX]{x1D6E4}>0.2$
, with the asymptotic values of
![]() $\unicode[STIX]{x1D6E4}$
reaching 0.3–0.4 in most cases. The long-time
$\unicode[STIX]{x1D6E4}$
reaching 0.3–0.4 in most cases. The long-time
![]() $\unicode[STIX]{x1D6E4}$
(figure 13
b) lies between 0.24 and 0.27, independent of the slope angle, when
$\unicode[STIX]{x1D6E4}$
(figure 13
b) lies between 0.24 and 0.27, independent of the slope angle, when
![]() $\unicode[STIX]{x1D6FD}\neq 0$
. The long-time
$\unicode[STIX]{x1D6FD}\neq 0$
. The long-time
![]() $\unicode[STIX]{x1D6E4}$
of 0.3 for the ANG0-2 case is somewhat higher. Based on the present simulations, the conventional assumption of
$\unicode[STIX]{x1D6E4}$
of 0.3 for the ANG0-2 case is somewhat higher. Based on the present simulations, the conventional assumption of
![]() $\unicode[STIX]{x1D6E4}=0.2$
in parametrizations of ocean mixing may induce a bias when applied to situations with convectively driven mixing, e.g. internal waves at rough bathymetry.
$\unicode[STIX]{x1D6E4}=0.2$
in parametrizations of ocean mixing may induce a bias when applied to situations with convectively driven mixing, e.g. internal waves at rough bathymetry.
8 Summary and conclusions
The evolution of a finite-height buoyancy disturbance in a stratified fluid over a flat bottom is studied for different values of density perturbation amplitude (
![]() $R_{\unicode[STIX]{x1D70C}}$
defined by (2.9)) and bottom slope angle (
$R_{\unicode[STIX]{x1D70C}}$
defined by (2.9)) and bottom slope angle (
![]() $\unicode[STIX]{x1D6FD}$
). Motivated by previous observations of near-bottom convective overturns and associated turbulence in the ocean, we conduct LES of this idealized problem with a focus on energy transfers and mixing.
$\unicode[STIX]{x1D6FD}$
). Motivated by previous observations of near-bottom convective overturns and associated turbulence in the ocean, we conduct LES of this idealized problem with a focus on energy transfers and mixing.
A slope, i.e.
![]() $\unicode[STIX]{x1D6FD}\neq 0$
, introduces a qualitative change: a flow that oscillates with frequency
$\unicode[STIX]{x1D6FD}\neq 0$
, introduces a qualitative change: a flow that oscillates with frequency
![]() $\unicode[STIX]{x1D714}=N\sin \unicode[STIX]{x1D6FD}$
. Linear theory explains this finding by showing that the density (
$\unicode[STIX]{x1D714}=N\sin \unicode[STIX]{x1D6FD}$
. Linear theory explains this finding by showing that the density (
![]() $\unicode[STIX]{x1D70C}$
) and slope-parallel velocity (
$\unicode[STIX]{x1D70C}$
) and slope-parallel velocity (
![]() $u_{s}$
) oscillate at
$u_{s}$
) oscillate at
![]() $\unicode[STIX]{x1D714}=N\sin \unicode[STIX]{x1D6FD}$
with a phase difference of
$\unicode[STIX]{x1D714}=N\sin \unicode[STIX]{x1D6FD}$
with a phase difference of
![]() $\unicode[STIX]{x03C0}/2$
, and the amplitude of
$\unicode[STIX]{x03C0}/2$
, and the amplitude of
![]() $u_{s}(z_{s})$
is
$u_{s}(z_{s})$
is
![]() $b_{0}(z_{s})/N$
, where
$b_{0}(z_{s})/N$
, where
![]() $b_{0}$
is the initial buoyancy disturbance. When the initial buoyancy amplitude is small (
$b_{0}$
is the initial buoyancy disturbance. When the initial buoyancy amplitude is small (
![]() $R_{\unicode[STIX]{x1D70C}}\ll 1$
), the density configuration is always statically stable, LES is not necessary, and linear theory is a good approximation to the numerical results except for a slow viscous decay. When
$R_{\unicode[STIX]{x1D70C}}\ll 1$
), the density configuration is always statically stable, LES is not necessary, and linear theory is a good approximation to the numerical results except for a slow viscous decay. When
![]() $R_{\unicode[STIX]{x1D70C}}$
is sufficiently large, as in the simulations discussed here, the initial density profile is statically unstable and, owing to turbulence, there is significant energy loss. Nevertheless, the frequency
$R_{\unicode[STIX]{x1D70C}}$
is sufficiently large, as in the simulations discussed here, the initial density profile is statically unstable and, owing to turbulence, there is significant energy loss. Nevertheless, the frequency
![]() $N\sin \unicode[STIX]{x1D6FD}$
is evident over the entire time history in all simulated cases, and the initial amplitude of the velocity is as predicted by linear theory.
$N\sin \unicode[STIX]{x1D6FD}$
is evident over the entire time history in all simulated cases, and the initial amplitude of the velocity is as predicted by linear theory.
Of the four reservoirs (MAPE, TAPE, MKE and TKE), only MAPE has energy at
![]() $Nt=0$
. The simulations of series A (table 1) with
$Nt=0$
. The simulations of series A (table 1) with
![]() $\unicode[STIX]{x1D6FD}$
between 0
$\unicode[STIX]{x1D6FD}$
between 0
![]() $^{\circ }$
and 5
$^{\circ }$
and 5
![]() $^{\circ }$
provide an overall view of the energy transfers among the reservoirs. In the non-sloping case, the mean flow is negligible and so is MKE. MAPE is continually transferred to TKE and TAPE during the breakdown of a single LCOE. However, when
$^{\circ }$
provide an overall view of the energy transfers among the reservoirs. In the non-sloping case, the mean flow is negligible and so is MKE. MAPE is continually transferred to TKE and TAPE during the breakdown of a single LCOE. However, when
![]() $\unicode[STIX]{x1D6FD}\neq 0$
, the mean buoyancy flux mediates a harmonic exchange of energy between the MAPE and MKE reservoirs with frequency
$\unicode[STIX]{x1D6FD}\neq 0$
, the mean buoyancy flux mediates a harmonic exchange of energy between the MAPE and MKE reservoirs with frequency
![]() $2N\sin \unicode[STIX]{x1D6FD}$
. TKE generation peaks at specific phases: at zero velocity when differential advection tends to bring heavy fluid over light fluid, leading to a local maximum of positive buoyancy flux (
$2N\sin \unicode[STIX]{x1D6FD}$
. TKE generation peaks at specific phases: at zero velocity when differential advection tends to bring heavy fluid over light fluid, leading to a local maximum of positive buoyancy flux (
![]() $B^{T}$
); and at maximum speed when there is a local maximum of shear production (
$B^{T}$
); and at maximum speed when there is a local maximum of shear production (
![]() $P$
). TAPE production peaks at the zero-velocity phase. Both TKE dissipation and TAPE dissipation peak shortly after the corresponding peaks in production. For moderate
$P$
). TAPE production peaks at the zero-velocity phase. Both TKE dissipation and TAPE dissipation peak shortly after the corresponding peaks in production. For moderate
![]() $\unicode[STIX]{x1D6FD}$
, most of the TKE generation is due to the cumulative effect of episodes of positive
$\unicode[STIX]{x1D6FD}$
, most of the TKE generation is due to the cumulative effect of episodes of positive
![]() $B^{T}$
. With increasing
$B^{T}$
. With increasing
![]() $\unicode[STIX]{x1D6FD}$
, the importance of
$\unicode[STIX]{x1D6FD}$
, the importance of
![]() $P$
increases since the characteristic velocity
$P$
increases since the characteristic velocity
![]() $(b_{0}\sin \unicode[STIX]{x1D6FD})/N$
increases. Nevertheless, until
$(b_{0}\sin \unicode[STIX]{x1D6FD})/N$
increases. Nevertheless, until
![]() $\unicode[STIX]{x1D6FD}=45^{\circ }$
(the maximum slope in the present simulations), cumulative
$\unicode[STIX]{x1D6FD}=45^{\circ }$
(the maximum slope in the present simulations), cumulative
![]() $B^{T}$
remains larger than
$B^{T}$
remains larger than
![]() $P$
.
$P$
.
Dissipative dynamics of a convectively unstable patch are qualitatively changed by the presence of a slope. In the zero-slope case, there is an explosive breakdown to turbulence so that, by
![]() $Nt=20$
, a substantial portion of
$Nt=20$
, a substantial portion of
![]() $E_{loss}$
is accomplished, in contrast to sloping cases where, even for
$E_{loss}$
is accomplished, in contrast to sloping cases where, even for
![]() $\unicode[STIX]{x1D6FD}$
as small as 2.5
$\unicode[STIX]{x1D6FD}$
as small as 2.5
![]() $^{\circ }$
, less than 10 % of the net loss occurs by
$^{\circ }$
, less than 10 % of the net loss occurs by
![]() $Nt=20$
. The oscillatory along-slope current (frequency
$Nt=20$
. The oscillatory along-slope current (frequency
![]() $\unicode[STIX]{x1D714}=N\sin \unicode[STIX]{x1D6FD}$
) tends to move the density away from its statically unstable state at a rate that increases with slope steepness. Thorpe sorting assumes total conversion of APE of the initially unstable density patch to turbulence as the convective instability progresses whereas, at a slope, only a fraction of the initial APE is converted to turbulence by the initial overturning event as a consequence of the oscillatory mean flow. This aspect may contribute to the bias that Thorpe sorting exhibits towards overestimating turbulent dissipation that was found in both observations (Mater et al.
Reference Mater, Venayagamoorthy, Laurent and Moum2015) and simulations (Jalali et al.
Reference Jalali, Chalamalla and Sarkar2017) of near-bottom turbulence driven by internal waves at the steep topography of the Luzon Strait.
$\unicode[STIX]{x1D714}=N\sin \unicode[STIX]{x1D6FD}$
) tends to move the density away from its statically unstable state at a rate that increases with slope steepness. Thorpe sorting assumes total conversion of APE of the initially unstable density patch to turbulence as the convective instability progresses whereas, at a slope, only a fraction of the initial APE is converted to turbulence by the initial overturning event as a consequence of the oscillatory mean flow. This aspect may contribute to the bias that Thorpe sorting exhibits towards overestimating turbulent dissipation that was found in both observations (Mater et al.
Reference Mater, Venayagamoorthy, Laurent and Moum2015) and simulations (Jalali et al.
Reference Jalali, Chalamalla and Sarkar2017) of near-bottom turbulence driven by internal waves at the steep topography of the Luzon Strait.
When
![]() $\unicode[STIX]{x1D6FD}\neq 0$
, the energy loss occurs in two stages: an initial convective-instability-dominated loss (CDL) phase where the dissipation occurs mainly as discrete events when velocity is zero and the density is statically unstable, and a later quasi-steady loss (QSL) phase with an approximately constant energy decay rate attributed to both shear and convective instability. The decay rate (
$\unicode[STIX]{x1D6FD}\neq 0$
, the energy loss occurs in two stages: an initial convective-instability-dominated loss (CDL) phase where the dissipation occurs mainly as discrete events when velocity is zero and the density is statically unstable, and a later quasi-steady loss (QSL) phase with an approximately constant energy decay rate attributed to both shear and convective instability. The decay rate (
![]() ${\dot{E}}$
) during QSL is found to be approximately proportional to
${\dot{E}}$
) during QSL is found to be approximately proportional to
![]() $E_{0}N\sin \unicode[STIX]{x1D6FD}$
. When the slope angle is moderate, say less that 5
$E_{0}N\sin \unicode[STIX]{x1D6FD}$
. When the slope angle is moderate, say less that 5
![]() $^{\circ }$
, most of the energy is dissipated in the CDL phase. For steeper slopes, the duration and amount of energy lost in the later QSL phase increase with increasing
$^{\circ }$
, most of the energy is dissipated in the CDL phase. For steeper slopes, the duration and amount of energy lost in the later QSL phase increase with increasing
![]() $\unicode[STIX]{x1D6FD}$
, e.g. at
$\unicode[STIX]{x1D6FD}$
, e.g. at
![]() $\unicode[STIX]{x1D6FD}=45^{\circ }$
more than half of the net
$\unicode[STIX]{x1D6FD}=45^{\circ }$
more than half of the net
![]() $E_{loss}$
occurs during the QSL phase. Since the QSL phase is sustained over a long time, the net energy loss can be substantial for steep slopes although, initially,
$E_{loss}$
occurs during the QSL phase. Since the QSL phase is sustained over a long time, the net energy loss can be substantial for steep slopes although, initially,
![]() $E_{loss}$
is much smaller than in the zero-slope case.
$E_{loss}$
is much smaller than in the zero-slope case.
The cumulative mixing efficiency (
![]() $\unicode[STIX]{x1D6E4}$
defined by (3.13) and plotted in figure 13) varies rapidly during the CDL phase in all cases. At early time (
$\unicode[STIX]{x1D6E4}$
defined by (3.13) and plotted in figure 13) varies rapidly during the CDL phase in all cases. At early time (
![]() $Nt<15$
),
$Nt<15$
),
![]() $\unicode[STIX]{x1D6E4}$
exceeds 0.5. Eventually,
$\unicode[STIX]{x1D6E4}$
exceeds 0.5. Eventually,
![]() $\unicode[STIX]{x1D6E4}$
reaches a value around 0.24–0.27 in the QSL phase for the cases with sloping bottom, independent of
$\unicode[STIX]{x1D6E4}$
reaches a value around 0.24–0.27 in the QSL phase for the cases with sloping bottom, independent of
![]() $\unicode[STIX]{x1D6FD}$
. The value of
$\unicode[STIX]{x1D6FD}$
. The value of
![]() $\unicode[STIX]{x1D6E4}$
in the non-sloping bottom case, ANG0-2, asymptotes to approximately 0.3, which is somewhat higher than in the other cases. Our simulations suggest that, in the presence of boundaries, the mixing efficiency is smaller than the
$\unicode[STIX]{x1D6E4}$
in the non-sloping bottom case, ANG0-2, asymptotes to approximately 0.3, which is somewhat higher than in the other cases. Our simulations suggest that, in the presence of boundaries, the mixing efficiency is smaller than the
![]() $\unicode[STIX]{x1D6E4}=0.5$
–0.75 values seen in previous studies of an unstable patch in an unbounded fluid.
$\unicode[STIX]{x1D6E4}=0.5$
–0.75 values seen in previous studies of an unstable patch in an unbounded fluid.
Acknowledgement
We are pleased to acknowledge financial support from NSF grant OCE-1459774.