Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-19T20:46:19.369Z Has data issue: false hasContentIssue false
  • English
  • Français

Electrokinetically enhanced cross-stream particle migration in viscoelastic flows

Published online by Cambridge University Press:  08 July 2020

Akash Choudhary ,
Di Li ,
T. Renganathan ,
Xiangchun Xuan  and
S. Pushpavanam Open the ORCID record for S. Pushpavanam [Opens in a new window]
Akash Choudhary
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology Madras, TN 600036, India
Di Li
Affiliation:
Department of Mechanical Engineering, Clemson University, SC 29634-0921, USA
T. Renganathan
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology Madras, TN 600036, India
Xiangchun Xuan*
Affiliation:
Department of Mechanical Engineering, Clemson University, SC 29634-0921, USA
S. Pushpavanam*
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology Madras, TN 600036, India
*
†Email addresses for correspondence: xcxuan@clemson.edu, spush@iitm.ac.in
†Email addresses for correspondence: xcxuan@clemson.edu, spush@iitm.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

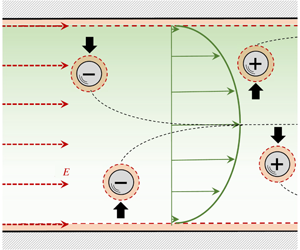
Advancements in understanding the lateral migration of particles have helped in enhanced focusing in microfluidic devices. In this work, we investigate the effects of electrokinetics on particle migration in a viscoelastic flow, where the electric field is applied parallel to the flow. Through experiments and use of perturbation theory in conjunction with the reciprocal theorem, we show that the interaction of electrokinetic and rheological effects can result in an enhancement in migration by an order of magnitude. The theoretical analysis, in agreement with the experiments, demonstrates that the particles can be focused at different equilibrium positions based on their intrinsic electrical properties.

JFM classification

Micro-/Nano-fluid dynamics: Microfluidics Non-Newtonian Flows: Viscoelasticity
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 898 , 10 September 2020 , A20
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, J. L. 1989 Colloid transport by interfacial forces. Annu. Rev. Fluid Mech. 21 (1), 61–99.CrossRefGoogle Scholar
Becker, L. E., McKinley, G. H. & Stone, H. A. 1996 Sedimentation of a sphere near a plane wall: weak non-Newtonian and inertial effects. J. Non-Newtonian Fluid Mech. 63 (2–3), 201–233.CrossRefGoogle Scholar
Bird, R. B., Armstrong, R. C. & Hassager, O. 1987 Dynamics of Polymeric Liquids, Vol. 1: Fluid Mechanics. Wiley.Google Scholar
Brenner, H. 1961 The slow motion of a sphere through a viscous fluid towards a plane surface. Chem. Engng Sci. 16 (3–4), 242–251.CrossRefGoogle Scholar
Brenner, H. 1962 Effect of finite boundaries on the Stokes resistance of an arbitrary particle. J. Fluid Mech. 12 (1), 35–48.CrossRefGoogle Scholar
Caswell, B. & Schwarz, W. H. 1962 The creeping motion of a non-Newtonian fluid past a sphere. J. Fluid Mech. 13 (3), 417–426.CrossRefGoogle Scholar
Chen, B., Le, W., Wang, Y., Li, Z., Wang, D., Ren, L., Lin, L., Cui, S., Hu, J. J., Hu, Y. et al. 2016 Targeting negative surface charges of cancer cells by multifunctional nanoprobes. Theranostics 6 (11), 1887–1898.CrossRefGoogle ScholarPubMed
Choudhary, A., Renganathan, T. & Pushpavanam, S. 2019 Inertial migration of an electrophoretic rigid sphere in a two-dimensional Poiseuille flow. J. Fluid Mech. 874, 856–890.CrossRefGoogle Scholar
Datt, C., Natale, G., Hatzikiriakos, S. G. & Elfring, G. J. 2017 An active particle in a complex fluid. J. Fluid Mech. 823, 675–688.CrossRefGoogle Scholar
D’Avino, G., Greco, F. & Maffettone, P. L. 2017 Particle migration due to viscoelasticity of the suspending liquid and its relevance in microfluidic devices. Annu. Rev. Fluid Mech. 49, 341–360.CrossRefGoogle Scholar
Di Carlo, D. 2009 Inertial microfluidics. Lab on a Chip 9 (21), 3038–3046.CrossRefGoogle ScholarPubMed
Faxén, H. 1922 The resistance to the movement of a rigid sphere in a zippered liquid enclosed between two parallel plane w. Ann. Phys. 373 (10), 89–119.CrossRefGoogle Scholar
Gauthier, F., Goldsmith, H. L. & Mason, S. G. 1971 Particle motions in non-Newtonian media. II. Poiseuille flow. Trans. Soc. Rheol. 15 (2), 297–330.CrossRefGoogle Scholar
Ghosh, U., Chaudhury, K. & Chakraborty, S. 2016 Electroosmosis over non-uniformly charged surfaces: modified Smoluchowski slip velocity for second-order fluids. J. Fluid Mech. 809, 664–690.CrossRefGoogle Scholar
Giesekus, H. 1963 Die simultane translations-und rotationsbewegung einer kugel in einer elastoviskosen flüssigkeit. Rheol. Acta 3 (1), 59–71.CrossRefGoogle Scholar
Guazzelli, E. & Morris, J. F. 2011 A Physical Introduction to Suspension Dynamics, vol. 45. Cambridge University Press.CrossRefGoogle Scholar
Happel, J. & Brenner, H. 2012 Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media, vol. 1. Springer Science and Business Media.Google Scholar
Ho, B. P. & Leal, L. G. 1974 Inertial migration of rigid spheres in two-dimensional unidirectional flows. J. Fluid Mech. 65 (2), 365–400.CrossRefGoogle Scholar
Ho, B. P. & Leal, L. G. 1976 Migration of rigid spheres in a two-dimensional unidirectional shear flow of a second-order fluid. J. Fluid Mech. 76 (4), 783–799.CrossRefGoogle Scholar
Karnis, A. & Mason, S. G. 1966 Particle motions in sheared suspensions. XIX. Viscoelastic media. Trans. Soc. Rheol. 10 (2), 571–592.CrossRefGoogle Scholar
Keh, H.-J. & Anderson, J. L. 1985 Boundary effects on electrophoretic motion of colloidal spheres. J. Fluid Mech. 153, 417–439.CrossRefGoogle Scholar
Kim, B. & Kim, J. M. 2016 Elasto-inertial particle focusing under the viscoelastic flow of dna solution in a square channel. Biomicrofluidics 10 (2), 024111.CrossRefGoogle ScholarPubMed
Kim, J. Y., Ahn, S. W., Lee, S. S. & Kim, J. M. 2012 Lateral migration and focusing of colloidal particles and dna molecules under viscoelastic flow. Lab on a Chip 12 (16), 2807–2814.Google ScholarPubMed
Kim, S. & Karrila, S. J. 2013 Microhydrodynamics: Principles and Selected Applications. Courier Corporation.Google Scholar
Koch, D. L. & Subramanian, G. 2006 The stress in a dilute suspension of spheres suspended in a second-order fluid subject to a linear velocity field. J. Non-Newtonian Fluid Mech. 138 (2–3), 87–97.CrossRefGoogle Scholar
Lamb, H. 1975 Hydrodynamics, 6th edn. Cambridge University Press.Google Scholar
Le, W., Chen, B., Cui, Z., Liu, Z. & Shi, D. 2019 Detection of cancer cells based on glycolytic-regulated surface electrical charges. Biophys. Rep. 5 (1), 10–18.CrossRefGoogle Scholar
Leal, L. G. 1975 The slow motion of slender rod-like particles in a second-order fluid. J. Fluid Mech. 69 (2), 305–337.CrossRefGoogle Scholar
Leshansky, A. M., Bransky, A., Korin, N. & Dinnar, U. 2007 Tunable nonlinear viscoelastic focusing in a microfluidic device. Phys. Rev. Lett. 98 (23), 234501.CrossRefGoogle Scholar
Li, D. & Xuan, X. 2018 Electrophoretic slip-tuned particle migration in microchannel viscoelastic fluid flows. Phys. Rev. Fluids 3 (7), 074202.CrossRefGoogle Scholar
Liang, L., Qian, S. & Xuan, X. 2010 Three-dimensional electrokinetic particle focusing in a rectangular microchannel. J. Colloid Interface Sci. 350 (1), 377–379.CrossRefGoogle Scholar
Lu, X., Liu, C., Hu, G. & Xuan, X. 2017 Particle manipulations in non-Newtonian microfluidics: a review. J. Colloid Interface Sci. 500, 182–201.CrossRefGoogle ScholarPubMed
Lu, X. & Xuan, X. 2015 Elasto-inertial pinched flow fractionation for continuous shape-based particle separation. Analyt. Chem. 87 (22), 11523–11530.CrossRefGoogle ScholarPubMed
Nam, J., Tan, J. K. S., Khoo, B. L., Namgung, B., Leo, H. L., Lim, C. T. & Kim, S. 2015 Hybrid capillary-inserted microfluidic device for sheathless particle focusing and separation in viscoelastic flow. Biomicrofluidics 9 (6), 064117.CrossRefGoogle ScholarPubMed
Rodd, L. E., Scott, T. P., Boger, D. V., Cooper-White, J. J. & McKinley, G. H. 2005 The inertio-elastic planar entry flow of low-viscosity elastic fluids in micro-fabricated geometries. J. Non-Newtonian Fluid Mech. 129 (1), 1–22.CrossRefGoogle Scholar
Rossi, M., Marin, A., Cevheri, N., Kähler, C. J. & Yoda, M. 2019 Particle distribution and velocity in electrokinetically induced banding. Microfluid Nanofluid 23 (5), 67.CrossRefGoogle Scholar
Smoluchowski, M. 1903 Contribution à la théorie de l’endosmose électrique et de quelques phénomènes corrélatifs. Bull. Akad. Sci. Cracovie. 8, 182–200.Google Scholar
Stoecklein, D. & Di Carlo, D. 2018 Nonlinear microfluidics. Analyt. Chem. 91 (1), 296–314.CrossRefGoogle ScholarPubMed
Sze, A., Erickson, D., Ren, L. & Li, D. 2003 Zeta-potential measurement using the Smoluchowski equation and the slope of the current–time relationship in electroosmotic flow. J. Colloid Interface Sci. 261 (2), 402–410.CrossRefGoogle ScholarPubMed
Tian, F., Feng, Q., Chen, Q., Liu, C., Li, T. & Sun, J. 2019 Manipulation of bio-micro/nanoparticles in non-Newtonian microflows. Microfluid Nanofluid 23 (5), 68.CrossRefGoogle Scholar
Warkiani, M. E., Tay, A. K. P., Guan, G. & Han, J. 2015 Membrane-less microfiltration using inertial microfluidics. Sci. Rep. 5, 11018.CrossRefGoogle ScholarPubMed
Yang, S., Kim, J. Y., Lee, S. J., Lee, S. S. & Kim, J. M. 2011 Sheathless elasto-inertial particle focusing and continuous separation in a straight rectangular microchannel. Lab on a Chip 11 (2), 266–273.CrossRefGoogle Scholar
Yariv, E. 2006 ‘Force-free’ electrophoresis? Phys. Fluids 18 (3), 031702.CrossRefGoogle Scholar
Yuan, D., Zhao, Q., Yan, S., Tang, S.-Y., Alici, G., Zhang, J. & Li, W. 2018 Recent progress of particle migration in viscoelastic fluids. Lab on a Chip 18 (4), 551–567.CrossRefGoogle ScholarPubMed
Zhang, J., Yan, S., Alici, G., Nguyen, N.-T., Di Carlo, D. & Li, W. 2014 Real-time control of inertial focusing in microfluidics using dielectrophoresis (dep). RSC Adv. 4 (107), 62076–62085.CrossRefGoogle Scholar
Zhang, J., Yan, S., Yuan, D., Alici, G., Nguyen, N.-T., Warkiani, M. E. & Li, W. 2016 Fundamentals and applications of inertial microfluidics: a review. Lab on a Chip 16 (1), 10–34.CrossRefGoogle ScholarPubMed

Choudhary et al. supplementary movie 1

The movie shows the particles entering the channel, with no potential difference applied at the channel ends. The figure corresponds to fig.1 (a). Other parameters are described in the caption of Fig.1 of the main text.

Download Choudhary et al. supplementary movie 1(Video)
Video 7 MB

Choudhary et al. supplementary movie 2

The movie shows the particles exiting the channel, with no potential difference applied at the channel ends. The figure corresponds to fig.1 (a). Other parameters are described in the caption of Fig.1 of the main text.

Download Choudhary et al. supplementary movie 2(Video)
Video 7 MB

Choudhary et al. supplementary movie 3

The movie shows the particles entering the channel, with +600V potential difference applied at the channel ends. The figure corresponds to fig.1 (c). Other parameters are described in the caption of Fig.1 of the main text.

Download Choudhary et al. supplementary movie 3(Video)
Video 7 MB

Choudhary et al. supplementary movie 4

The movie shows the particles exiting the channel, with +600V potential difference applied at the channel ends. The figure corresponds to fig.1 (c). Other parameters are described in the caption of Fig.1 of the main text.

Download Choudhary et al. supplementary movie 4(Video)
Video 7 MB

Choudhary et al. supplementary movie 5

The movie shows the particles entering the channel, with -600V potential difference applied at the channel ends. The figure corresponds to fig.1 (b). Other parameters are described in the caption of Fig.1 of the main text.

Download Choudhary et al. supplementary movie 5(Video)
Video 7 MB

Choudhary et al. supplementary movie 6

The movie shows the particles exiting the channel, with -600V potential difference applied at the channel ends. The figure corresponds to fig.1 (b). Other parameters are described in the caption of Fig.1 of the main text.

Download Choudhary et al. supplementary movie 6(Video)
Video 7 MB
Supplementary material: PDF

Choudhary et al. supplementary material

Supplementary data

Download Choudhary et al. supplementary material(PDF)
PDF 315.1 KB
Supplementary material: PDF

Choudhary et al. supplementary material

Migration code

Download Choudhary et al. supplementary material(PDF)
PDF 99.3 KB