Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-22T02:19:18.290Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of stratified turbulence decaying from a high buoyancy Reynolds number

Published online by Cambridge University Press:  01 December 2015

A. Maffioli  and
P. A. Davidson
A. Maffioli*
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
P. A. Davidson
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
*
†Email address for correspondence: maffioli@mech.kth.se
Get access Rights & Permissions [Opens in a new window]

Abstract

We present direct numerical simulations (DNS) of unforced stratified turbulence with the objective of testing the strongly stratified turbulence theory. According to this theory the characteristic vertical scale of the turbulence is given by 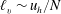$\ell _{v}\sim u_{h}/N$, where 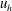$u_{h}$ is the horizontal velocity scale and 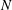$N$ the Brunt–Väisälä frequency. Combined with the hypothesis of the energy dissipation rate scaling as 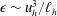${\it\epsilon}\sim u_{h}^{3}/\ell _{h}$, this theory predicts inertial range scalings for the horizontal spectrum of horizontal kinetic energy and of potential energy, according to 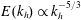$E(k_{h})\propto k_{h}^{-5/3}$. We begin by presenting a scaling analysis of the horizontal vorticity equation from which we recover the result regarding the vertical scale, 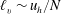$\ell _{v}\sim u_{h}/N$, highlighting in the process the important dynamical role of large-scale vertical shear of horizontal velocity. We then present the results from decaying DNS, which show a good agreement with aspects of the theory. In particular, the vertical Froude number is found to reach a constant plateau in time, of the form 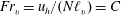$Fr_{v}=u_{h}/(N\ell _{v})=C$ with 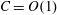$C=O(1)$ in all the runs. The derivation of the dissipation scaling 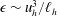${\it\epsilon}\sim u_{h}^{3}/\ell _{h}$ at low Reynolds number in the context of decaying stratified turbulence highlights that the same scaling holds at high 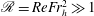$\mathscr{R}=ReFr_{h}^{2}\gg 1$ as well as at low 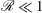$\mathscr{R}\ll 1$, which is known (see Brethouwer et al., J. Fluid Mech., vol. 585, 2007, pp. 343–368) but not sufficiently emphasized in recent literature. We find evidence in our DNS of the dissipation scaling holding at 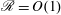$\mathscr{R}=O(1)$, which we interpret as being in the viscous regime. We also find 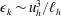${\it\epsilon}_{k}\sim u_{h}^{3}/\ell _{h}$ and 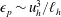${\it\epsilon}_{p}\sim u_{h}^{3}/\ell _{h}$ (with 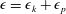${\it\epsilon}={\it\epsilon}_{k}+{\it\epsilon}_{p}$), in our high-resolution run at earlier times corresponding to 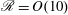$\mathscr{R}=O(10)$, which is in the transition between the strongly stratified and the viscous regimes. The horizontal spectrum of horizontal kinetic energy collapses in time using the scaling 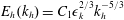$E_{h}(k_{h})=C_{1}{\it\epsilon}_{k}^{2/3}k_{h}^{-5/3}$ and the horizontal potential energy spectrum is well described by 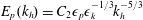$E_{p}(k_{h})=C_{2}{\it\epsilon}_{p}{\it\epsilon}_{k}^{-1/3}k_{h}^{-5/3}$. The presence of an inertial range in the horizontal direction is confirmed by the constancy of the energy flux spectrum over narrow ranges of 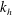$k_{h}$. However, the vertical energy spectrum is found to differ significantly from the expected 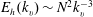$E_{h}(k_{v})\sim N^{2}k_{v}^{-3}$ scaling, showing that 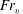$Fr_{v}$ is not of order unity on a scale-by-scale basis, thus providing motivation for further investigation of the vertical structure of stratified turbulence.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Turbulent Flows: Stratified turbulence Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 786 , 10 January 2016 , pp. 210 - 233
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Almalkie, S. & de Bruyn Kops, S. M. 2012 Kinetic energy dynamics in forced, homogeneous, and axisymmetric stably stratified turbulence. J. Turbul. 13 (29), 1–32.Google Scholar
Augier, P., Billant, P. & Chomaz, J.-M. 2015 Stratified turbulence forced with columnar dipoles: numerical study. J. Fluid Mech. 769, 403–443.CrossRefGoogle Scholar
Augier, P., Chomaz, J.-M. & Billant, P. 2012 Spectral analysis of the transition to turbulence from a dipole in stratified fluid. J. Fluid Mech. 713, 86–108.CrossRefGoogle Scholar
Bartello, P. & Tobias, S. M. 2013 Sensitivity of stratified turbulence to the buoyancy Reynolds number. J. Fluid Mech. 725, 1–22.CrossRefGoogle Scholar
Billant, P. & Chomaz, J.-M. 2001 Self-similarity of strongly stratified inviscid flows. Phys. Fluids 13 (6), 1645–1651.CrossRefGoogle Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J.-M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.CrossRefGoogle Scholar
de Bruyn Kops, S. M. & Riley, J. J. 1998 Direct numerical simulation of laboratory experiments in isotropic turbulence. Phys. Fluids 10 (9), 2125–2127.CrossRefGoogle Scholar
Davidson, P. A. 2004 Turbulence. An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Davidson, P. A. 2013 Turbulence in Rotating, Stratified and Electrically Conducting Fluids. Cambridge University Press.CrossRefGoogle Scholar
Dewan, E. M. & Good, R. E. 1986 Saturation and the ‘universal’ spectrum for vertical profiles of horizontal scalar winds in the atmosphere. J. Geophys. Res. 91 (D2), 2742–2748.CrossRefGoogle Scholar
Eswaran, V. & Pope, S. B. 1988 An examination of forcing in direct numerical simulations of turbulence. Comput. Fluids 16 (3), 257–278.CrossRefGoogle Scholar
Fincham, A. M., Maxworthy, T. & Spedding, G. R. 1996 Energy dissipation and vortex structure in freely decaying stratified grid turbulence. Dyn. Atmos. Oceans 23, 155–169.CrossRefGoogle Scholar
Godoy-Diana, R., Chomaz, J.-M. & Billant, P. 2004 Vertical length scale selection for pancake vortices in strongly stratified viscous fluids. J. Fluid Mech. 504, 229–238.CrossRefGoogle Scholar
Hebert, D. A. & de Bruyn Kops, S. M. 2006 Predicting turbulence in flows with strong stable stratification. Phys. Fluids 18, 066602.CrossRefGoogle Scholar
Laval, J.-P., McWilliams, J. C. & Dubrulle, B. 2003 Forced stratified turbulence: successive transitions with Reynolds number. Phys. Rev. E 68, 036308.Google ScholarPubMed
Lindborg, E. 2006 The energy cascade in a strongly stratified fluid. J. Fluid Mech. 550, 207–242.CrossRefGoogle Scholar
Lindborg, E. & Brethouwer, G. 2007 Stratified turbulence forced in rotational and divergent modes. J. Fluid Mech. 586, 83–108.CrossRefGoogle Scholar
Maffioli, A., Davidson, P. A., Dalziel, S. B. & Swaminathan, N. 2014 The evolution of a stratified turbulent cloud. J. Fluid Mech. 739, 229–253.CrossRefGoogle Scholar
Praud, O., Fincham, A. M. & Sommeria, J. 2005 Decaying grid turbulence in a strongly stratified fluid. J. Fluid Mech. 522, 1–33.CrossRefGoogle Scholar
Riley, J. J. & de Bruyn Kops, S. M. 2003 Dynamics of turbulence strongly influenced by buoyancy. Phys. Fluids 15 (7), 2047–2059.CrossRefGoogle Scholar
Riley, J. J. & Lelong, M.-P. 2000 Fluid motions in the presence of strong stable stratification. Annu. Rev. Fluid Mech. 32, 613–657.CrossRefGoogle Scholar
Riley, J. J. & Lindborg, E. 2008 Stratified turbulence: a possible interpretation of some geophysical turbulence measurements. J. Atmos. Sci. 65, 2416–2424.CrossRefGoogle Scholar
Riley, J. J. & Lindborg, E. 2013 Recent progress in stratified turbulence. In Ten Chapters in Turbulence (ed. Davidson, P. A., Kaneda, Y. & Sreenivasan, K. R.). Cambridge University Press.Google Scholar
Rogallo, R. S.1981 Numerical experiments in homogeneous turbulence. NASA Technical Memorandum 81315. NASA Ames Research Center.Google Scholar
Smith, L. M. & Waleffe, F. 2002 Generation of slow large scales in forced rotating stratified turbulence. J. Fluid Mech. 451, 145–168.CrossRefGoogle Scholar
Smyth, W. D. & Moum, J. N. 2000 Length scales of turbulence in stably stratified mixing layers. Phys. Fluids 12 (6), 1327–1342.CrossRefGoogle Scholar
Waite, M. L. 2011 Stratified turbulence at the buoyancy scale. Phys. Fluids 23 (6), 066602.CrossRefGoogle Scholar
Waite, M. L. & Bartello, P. 2004 Stratified turbulence dominated by vortical motion. J. Fluid Mech. 517, 281–308.CrossRefGoogle Scholar
Yeung, P. K. & Zhou, Y. 1997 Universality of the Kolmogorov constant in numerical simulations of turbulence. Phys. Rev. E 56 (2), 1746–1752.Google Scholar