Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-19T00:42:11.777Z Has data issue: false hasContentIssue false
  • English
  • Français

Aerodynamic-force production mechanisms in hovering mosquitoes

Published online by Cambridge University Press:  08 July 2020

Long-Gui Liu ,
Gang Du  and
Mao Sun Open the ORCID record for Mao Sun [Opens in a new window]
Long-Gui Liu
Affiliation:
Institute of Fluid Mechanics, Beihang University, Beijing, China
Gang Du
Affiliation:
Institute of Fluid Mechanics, Beihang University, Beijing, China
Mao Sun*
Affiliation:
Institute of Fluid Mechanics, Beihang University, Beijing, China
*
†Email address for correspondence: m.sun@buaa.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

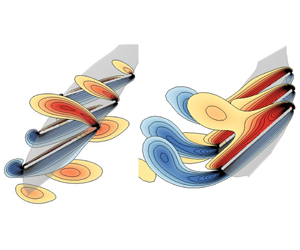
For many insects in hovering flight, the stroke amplitude is relatively large (above $120^{\circ }$) and the lift is mainly produced by the leading-edge vortex (LEV) attaching to the wing (the delayed-stall mechanism). Mosquitoes have a very small stroke amplitude (${\approx}45^{\circ }$) and the LEV does not have enough time to form before a stroke ends; thus, the delayed-stall mechanism can not be used. In the present study, we show that their lift is produced by different aerodynamic mechanisms from those of insects with a large stroke amplitude: in a downstroke and upstroke, two large lift peaks and a relatively small one are generated. The first large lift peak (at the beginning of the stroke) mainly comes from the added-mass force caused by the large acceleration of the wing. The second large lift peak (in the mid-portion of the stroke) is produced by the ‘fast-pitching-up rotation’ mechanism: the wing fast pitches up while moving forward, generating a large-magnitude, opposite-sign vorticity at the trailing edge of the wing and near the leading edge of the wing; the rapid generation of opposite-sign vorticity at different locations of the wing results in a large time rate of change in the first moment of vorticity, hence a large aerodynamic force. The third lift peak, which is near the end of the stroke and is small, is a result of the fast-pitching-up rotation of a rapidly decelerating wing. Note that although the added-mass force contributes positive lift in the beginning part of the stroke when the wing is in acceleration, it gives negative lift in the next part of the stroke when the wing is in deceleration; i.e. the added-mass force has no effect on the time-average lift, but it greatly changes the time distribution of the lift.

JFM classification

Biological Fluid Dynamics: Swimming/flying Vortex Flows: Vortex dynamics Wakes/Jets: Separated flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 898 , 10 September 2020 , A19
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aono, H., Liang, F. Y. & Liu, H. 2008 Near- and far-field aerodynamics in insect hovering flight: an integrated computational study. J. Expl Biol. 211, 239–257.CrossRefGoogle Scholar
Bomphrey, R. J., Nakata, T., Phillips, N. & Walker, S. M. 2017 Smart wing rotation and trailing-edge vortices enable high frequency mosquito flight. Nature 544, 92–95.CrossRefGoogle ScholarPubMed
Bomphrey, R. J., Srygley, R. B., Taylor, G. K. & Thomas, A. L. R. 2002 Visualizing the flow around insect wings. Phys. Fluids 14, S4.CrossRefGoogle Scholar
Cheng, X. & Sun, M. 2018 Very small insects use novel wing flapping and drag principle to generate the weight-supporting vertical force. J. Fluid Mech. 855, 646–670.CrossRefGoogle Scholar
Dickerson, A. K., Shankles, P. G., Berry, B. E. & Hu, D. L. 2015 Fog and dense gas disrupt mosquito flight due to increased aerodynamic drag on halteres. J. Fluids Struct. 55, 451–462.CrossRefGoogle Scholar
Dickerson, A. K., Shankles, P. G., Madhavan, N. M. & Hu, D. L. 2012 Mosquitoes survive raindrop collisions by virtue of their low mass. Proc. Natl Acad. Sci. USA 109, 9822–9827.CrossRefGoogle ScholarPubMed
Dickinson, M. H., Lehmann, F. O. & Sane, S. P. 1999 Wing rotation and the aerodynamic basis of insect flight. Science 284 (5422), 1954–1960.CrossRefGoogle ScholarPubMed
Du, G. & Sun, M. 2008 Effects of unsteady deformation of flapping wing on its aerodynamic forces. Appl. Maths Mech. 29, 731–743.CrossRefGoogle Scholar
Du, G. & Sun, M. 2010 Effects of wing deformation on aerodynamic forces in hovering hoverflies. J. Expl Biol. 213, 2273–2283.CrossRefGoogle ScholarPubMed
Eldredge, J. D. & Jones, A. R. 2019 Leading-edge vortices: mechanics and modeling. Annu. Rev. Fluid Mech. 51 (1), 75–104.CrossRefGoogle Scholar
Ellington, C. P. 1984a The aerodynamics of hovering insect flight. I. The quasi-steady analysis. Phil. Trans. R. Soc. B 305 (1122), 1–15.Google Scholar
Ellington, C. P. 1984b The aerodynamics of hovering insect flight. III. Kinematics. Phil. Trans. R. Soc. B 305 (1122), 41–78.Google Scholar
Ellington, C. P. 1984c The aerodynamics of hovering insect flight. IV. Aerodynamic mechanisms. Phil. Trans. R. Soc. B 305 (1122), 79–113.Google Scholar
Ellington, C. P. 1984d The aerodynamics of hovering insect flight. VI. Lift and power requirements. Phil. Trans. R. Soc. B 305 (1122), 145–181.Google Scholar
Ellington, C. P., Van Den Berg, C., Willmott, A. P. & Thomas, A. L. R. 1996 Leading-edge vortices in insect flight. Nature 384 (19), 626–630.CrossRefGoogle Scholar
Fry, S. N., Sayaman, R. & Dickinson, M. H. 2005 The aerodynamics of hovering flight in Drosophila. J. Expl Biol. 208 (12), 2303–2318.CrossRefGoogle ScholarPubMed
Garmann, D. J. & Visbal, M. R. 2014 Dynamics of revolving wings for various aspect ratios. J. Fluid Mech. 748, 932–956.CrossRefGoogle Scholar
Hamdani, H. & Sun, M. 2000 Aerodynamic forces and flow structures of an airfoil in some unsteady motions at small Reynolds number. Acta Mechanica 145, 173–187.CrossRefGoogle Scholar
Han, J.-S., Chang, J. W. & Han, J.-H. 2016 The advance ratio effect on the lift augmentations of an insect-like flapping wing in forward flight. J. Fluid Mech. 808, 485–510.CrossRefGoogle Scholar
Harbig, R. R., Sheridan, J. & Thompson, M. C. 2013 Reynolds number and aspect ratio effects on the leading-edge vortex for rotating insect wing planforms. J. Fluid Mech. 717, 166–192.CrossRefGoogle Scholar
Hilgenstock, A. 1988 A fast method for the elliptic generation of three dimensional grids with full boundary control. In Numerical Grid Generation in Computational Fluid Mechanics, Swansea, UK (ed. Sengupta, S., Hauster, J., Eiseman, P. R. & Thompson, J. F.), pp. 137–146. Pineridge Press.Google Scholar
Howe, M. S. 1989 On unsteady surface forces, and sound produced by the normal chopping of a rectilinear vortex. J. Fluid Mech. 206, 131–153.CrossRefGoogle Scholar
Howe, M. S. 1995 On the force and moment on a body in an incompressible fluid, with application to rigid bodies and bubbles at high and low Reynolds numbers. Q. J. Mech. Appl. Maths 48, 401–426.CrossRefGoogle Scholar
Jardin, T., Farcy, A. & David, L. 2012 Three-dimensional effects in hovering flapping flight. J. Fluid Mech. 702, 102–125.CrossRefGoogle Scholar
Kim, D. & Gharib, M. 2010 Experimental study of three-dimensional vortex structures in translating and rotating plates. Exp. Fluids 49, 329–339.CrossRefGoogle Scholar
Lan, S. L. & Sun, M. 2001 Aerodynamic properties of a wing performing unsteady rotational motions at low Reynolds number. Acta Mechanica 149, 135–147.CrossRefGoogle Scholar
Liang, B. & Sun, M. 2013 Aerodynamic interactions between wing and body of a model insect in forward flight and maneuvers. J. Bionic Engng 10, 19–27.CrossRefGoogle Scholar
Lee, J., Choi, H. & Kim, H. 2015 A scaling law for the lift of hovering insects. J. Fluid Mech. 782, 479–490.CrossRefGoogle Scholar
Lee, Y. J., Lua, K. B. & Lim, T. T. 2016 Aspect ratio effects on revolving wings with Rossby number consideration. Bioinspir. Biomim. 11 (5), 056013.CrossRefGoogle ScholarPubMed
Lighthill, M. J. 1973 On the Weis–Fogh mechanism of lift generation. J. Fluid Mech. 60, 1–17.CrossRefGoogle Scholar
Liu, G., Dong, H. & Li, C. 2016 Vortex dynamics and new lift enhancement mechanism of wing–body interaction in insect forward flight. J. Fluid Mech. 795, 634–651.CrossRefGoogle Scholar
Liu, H., Ellington, C. P., Kawachi, K., van den Berg, C. & Willmott, A. P. 1998 A computational fluid dynamic study of Hawkmoth hovering. J. Expl Biol. 201, 461–477.Google ScholarPubMed
Liu, L. G. & Sun, M. 2018 The added mass forces in insect flapping wings. J. Theor. Biol. 437, 45–50.CrossRefGoogle ScholarPubMed
Liu, Y. P. & Sun, M. 2008 Wing kinematics measurement and aerodynamics of hovering droneflies. J. Expl Biol. 211 (13), 2014–2025.CrossRefGoogle ScholarPubMed
Meng, X. G. & Sun, M. 2015 Aerodynamics and vortical structures in hovering fruitflies. Phys. Fluids 27, 031901.CrossRefGoogle Scholar
Meng, X. G. & Sun, M. 2016 Wing and body kinematics of forward flight in drone-flies. Bioinspir. Biomim. 11, 1–19.CrossRefGoogle ScholarPubMed
Mou, X. L., Liu, Y. P. & Sun, M. 2011 Wing motion measurement and aerodynamics of hovering true hoverflies. J. Expl Biol. 214, 2832–2844.CrossRefGoogle ScholarPubMed
Newman, J. N. 1977 Marine hydrodynamics. In The Motion of an Ideal Fluid, pp. 135–140. MIT Press.Google Scholar
Rogers, S. E., Kwak, D. & Kiris, C. 1991 Steady and unsteady solutions of the incompressible Navier–Stokes equations. AIAA J. 29 (4), 603–610.CrossRefGoogle Scholar
Sahin, I., Crane, J. W. & Waston, K. P. 1993 Added mass coefficients for submerged bodies by a low-order panel method. Trans. ASME J. Fluids Engng 115, 452–457.CrossRefGoogle Scholar
Sane, S. P. 2003 The aerodynamics of insect flight. J. Expl Biol. 206 (23), 4191–4208.CrossRefGoogle ScholarPubMed
Sun, M. & Du, G. 2003 Lift and power requirements of hovering insect flight. Acta Mechanica Sin. 19, 458–469.Google Scholar
Sun, M. & Tang, J. 2002 Unsteady aerodynamic force generation by a model fruit fly wing in flapping motion. J. Expl Biol. 205 (1), 55–70.Google ScholarPubMed
Sun, M. & Yu, X. 2006 Aerodynamic force generation in hovering flight in a tiny insect. AIAA J. 44 (7), 1532–1540.CrossRefGoogle Scholar
Walker, S. M., Thomas, A. L. R. & Taylor, G. K. 2010 Deformable wing kinematics in free-flying hoverflies. J. R. Soc. Interface 7 (42), 131–142.CrossRefGoogle ScholarPubMed
Wang, Z. J., Birch, J. M. & Dickinson, M. H. 2004 Unsteady forces and flows in low Reynolds number hovering flight: two-dimensional computations versus robotic wing experiments. J. Expl Biol. 207, 449–460.CrossRefGoogle Scholar
Weis-Fogh, T. 1973 Quick estimates of flight fitness in hovering animals, including novel mechanisms for lift production. J. Expl Biol. 59, 169–203.Google Scholar
Werner, N. H., Chung, H., Wang, J., Liu, G., Cimbala, J. M., Dong, H. & Cheng, B. 2019 Radial planetary vorticity tilting in the leading-edge vortex of revolving wings Radial planetary vorticity tilting in the leading-edge vortex of revolving wings. Phys. Fluids 31, 041902.CrossRefGoogle Scholar
Wu, J. C. 1981 Theory for aerodynamic force and moment in viscous flows. AIAA J. 19 (4), 432–441.CrossRefGoogle Scholar
Yu, X. & Sun, M. 2009 A computational study of the wing-wing and wing-body interactions of a model insect. Acta Mechanica Sin. 25, 421–431.CrossRefGoogle Scholar
Zhu, H. J. & Sun, M. 2017 Unsteady aerodynamic force mechanisms of a hoverfly hovering with a short stroke-amplitude. Phys. Fluids 29, 081901.CrossRefGoogle Scholar

Liu et al. supplementary movie 1

Hover flight of M1. The left part of the movie shows the flight captured by the top-view camera; the middle and right parts of the movie show the flight captured by the two horizontal-view cameras, respectively. Playback speed is 10fps, approximately 0.2% of the actual speed of the movie.

Download Liu et al. supplementary movie 1(Video)
Video 4 MB

Liu et al. supplementary movie 2

Hover flight of M5. The left part of the movie shows the flight captured by the top-view camera; the middle and right parts of the movie show the flight captured by the two horizontal-view cameras, respectively. Playback speed is 10fps, approximately 0.2% of the actual speed of the movie.

Download Liu et al. supplementary movie 2(Video)
Video 2.7 MB