Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bouchard, Michel
Marty, Julien
Deck, Sébastien
and
Costes, Michel
2022.
ZDES accounting for transition of the OA209 airfoil in poststall conditions.
Bader, Shujaut H.
Yin, Zifei
and
Durbin, Paul A.
2022.
A Hybrid Model for Turbulence and Transition, with a Locally Varying Coefficient.
Flow, Turbulence and Combustion,
Vol. 108,
Issue. 4,
p.
935.
Yin, Zifei
and
Durbin, Paul A.
2022.
Detached Eddy Simulation of Transition in Turbomachinery: Linear Compressor Cascade.
Journal of Turbomachinery,
Vol. 144,
Issue. 3,
Bader, Shujaut H.
Yin, Zifei
and
Durbin, Paul A.
2022.
Large Eddy Simulation of passive scalar transport in transitional boundary layer and development toward improving models.
Computers & Fluids,
Vol. 241,
Issue. ,
p.
105485.
Pang, Kaiwen
Huang, Xianbei
Liu, Zhuqing
Li, Yaojun
and
Yang, Wei
2022.
A Hybrid Model Based on the Bifurcation Approach for Internal Turbulent Flow with Rotation and Streamline Curvature Effects.
Journal of Marine Science and Engineering,
Vol. 10,
Issue. 12,
p.
2022.
Liu, Haochen
Yin, Zifei
Le, Jialing
and
Liu, Hong
2023.
On the subgrid dissipation concept for large eddy simulation of turbulent combustion.
Combustion and Flame,
Vol. 258,
Issue. ,
p.
113099.
Möller, Felix
Tucker, Paul G.
Wang, Zhong-Nan
and
Morsbach, Christian
2023.
Critical Assessment of a Transitional Delayed Detached-Eddy Simulation Model for the Prediction of the Linear Compressor Cascade V103.
Qu, Lipeng
Bader, Shujaut H.
and
Yin, Zifei
2023.
Assessment of the shear stress transport dynamic ℓ2−ω delayed detached eddy simulation in Bachalo–Johnson flow with shock-induced separation.
Physics of Fluids,
Vol. 35,
Issue. 5,
Qiao, Lei
Shen, Jian
Li, Yi
Huang, Jiangtao
Zhang, Jiao
Xu, Jiakuan
and
Bai, Junqiang
2023.
Improved hybrid model for transitional separated flows over a rough compressor blade.
Aerospace Science and Technology,
Vol. 140,
Issue. ,
p.
108434.
Liu, Haochen
Yin, Zifei
Xu, Chao
Le, Jialing
and
Liu, Hong
2024.
Large eddy simulation of lean blow-off in swirl-stabilized flame with the subgrid dissipation concept.
Combustion and Flame,
Vol. 267,
Issue. ,
p.
113596.
Möller, Felix M.
Tucker, Paul G.
Wang, Zhong-Nan
and
Morsbach, Christian
2024.
Transitional Delayed Detached-Eddy Simulation for a Compressor Cascade: A Critical Assessment.
Journal of Propulsion and Power,
Vol. 40,
Issue. 4,
p.
533.
Liu, Haochen
Yin, Zifei
and
Liu, Hong
2024.
Adaptive detached eddy simulation of turbulent combustion with the subgrid dissipation concept.
Physics of Fluids,
Vol. 36,
Issue. 5,
Liu, Haochen
Zhang, Xinlei
Yin, Zifei
and
He, Guowei
2024.
An Explicit Algebraic Stress-Based Delayed Detached Eddy Simulation Model for Turbulent Flows.
AIAA Journal,
p.
1.
2025.
Coarse Graining Turbulence.
p.
261.
Israel, Daniel M.
2025.
Coarse Graining Turbulence.
p.
263.
Wu, Haocheng
Xiang, Yang
Li, Gaohua
and
Yin, Zifei
2025.
Interaction of freestream turbulence and surface roughness in separation-induced transition.
Physical Review Fluids,
Vol. 10,
Issue. 1,
Zhou, Ziyu
Xiao, Maochao
Li, Dian
and
Zhang, Yufei
2025.
Enhanced delayed detached-eddy simulation with anisotropic minimum dissipation subgrid length scale.
Physics of Fluids,
Vol. 37,
Issue. 2,
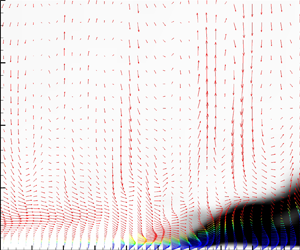
 $\ell ^2$–
$\ell ^2$– $\omega$ adaptive detached eddy simulation model (Yin & Durbin, Intl J. Heat Fluid Flow, vol. 62, 2016, pp. 499–509) does so. It dynamically adjusts a model constant, based on local mesh resolution and instantaneous flow features. In a laminar flow, the adaptive procedure returns zero subgrid viscosity, and large-scale low-frequency perturbations are resolved on the grid. However, rather than fully simulating transition, the hybrid model switches on at transition; small-scale turbulence is not resolved. It is found that the correct transitional behaviour is captured because the adaptive formulation responds to the initiation of small-scale components in the field of velocity gradient. The current work addresses flat-plate transition under the influence of free-stream turbulence and pressure gradient, encompassing bypass and separation-induced transition. First, the transition prediction mechanism of the adaptive model is explained. Then, the ability to predict transition statistically is evaluated, along with sensitivity studies of boundary conditions and mesh resolution.
$\omega$ adaptive detached eddy simulation model (Yin & Durbin, Intl J. Heat Fluid Flow, vol. 62, 2016, pp. 499–509) does so. It dynamically adjusts a model constant, based on local mesh resolution and instantaneous flow features. In a laminar flow, the adaptive procedure returns zero subgrid viscosity, and large-scale low-frequency perturbations are resolved on the grid. However, rather than fully simulating transition, the hybrid model switches on at transition; small-scale turbulence is not resolved. It is found that the correct transitional behaviour is captured because the adaptive formulation responds to the initiation of small-scale components in the field of velocity gradient. The current work addresses flat-plate transition under the influence of free-stream turbulence and pressure gradient, encompassing bypass and separation-induced transition. First, the transition prediction mechanism of the adaptive model is explained. Then, the ability to predict transition statistically is evaluated, along with sensitivity studies of boundary conditions and mesh resolution.


