Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-18T06:06:04.624Z Has data issue: false hasContentIssue false
  • English
  • Français

Unsteady motion past a sphere translating steadily in wormlike micellar solutions: a numerical analysis

Published online by Cambridge University Press:  18 February 2021

Chandi Sasmal Open the ORCID record for Chandi Sasmal [Opens in a new window]
Chandi Sasmal*
Affiliation:
Soft Matter Engineering and Microfluidics Lab, Department of Chemical Engineering, Indian Institute of Technology Ropar, Rupnagar140001, India
*
†Email address for correspondence: csasmal@iitrpr.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

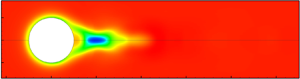
This study numerically investigates the flow characteristics past a solid and smooth sphere translating steadily along the axis of a cylindrical tube filled with wormlike micellar solutions in the creeping flow regime. The two-species Vasquez–Cook–McKinley and single-species Giesekus constitutive models are used to characterize the rheological behaviour of the micellar solutions. Once the Weissenberg number exceeds a critical value, an unsteady motion downstream of the sphere is observed in the case of the two-species model. We provide evidence that this unsteady motion downstream of the sphere is caused by the sudden rupture of long and stretched micelles in this region, resulting from an increase in the extensional flow strength. The corresponding single-species Giesekus model for the wormlike micellar solution, with no breakage and reformation, predicts a steady flow field under otherwise identical conditions. Therefore, it further provides evidence presented herein for the onset of this unsteady motion. Furthermore, we find that the onset of this unsteady motion downstream of the sphere is delayed as the ratio of sphere to tube diameter decreases. A similar kind of unsteady motion has also been observed in several earlier experiments for the problem of a sphere sedimenting in a tube filled with wormlike micellar solutions. We find a remarkable qualitative similarity in the flow characteristics between the present numerical results for a steadily translating sphere and prior experimental results for a falling sphere.

JFM classification

Non-Newtonian Flows: Polymers Non-Newtonian Flows: Rheology
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 912 , 10 April 2021 , A52
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Arigo, M.T. & McKinley, G.H. 1998 An experimental investigation of negative wakes behind spheres settling in a shear-thinning viscoelastic fluid. Rheol. Acta 37, 307–327.CrossRefGoogle Scholar
Arigo, M.T., Rajagopalan, D., Shapley, N. & McKinley, G.H. 1995 The sedimentation of a sphere through an elastic fluid. Part 1. Steady motion. J. Non-Newtonian Fluid Mech. 60 (2–3), 225–257.CrossRefGoogle Scholar
Bisgaard, C. 1983 Velocity fields around spheres and bubbles investigated by laser-Doppler anemometry. J. Non-Newtonian Fluid Mech. 12 (3), 283–302.CrossRefGoogle Scholar
Bush, M.B. 1994 On the stagnation flow behind a sphere in a shear-thinning viscoelastic liquid. J. Non-Newtonian Fluid Mech. 55 (3), 229–247.CrossRefGoogle Scholar
Cates, M.E. 1987 Reptation of living polymers: dynamics of entangled polymers in the presence of reversible chain-scission reactions. Macromolecules 20, 2289–2296.CrossRefGoogle Scholar
Chen, S. & Rothstein, J.P. 2004 Flow of a wormlike micelle solution past a falling sphere. J. Non-Newtonian Fluid Mech. 116, 205–234.CrossRefGoogle Scholar
Chhabra, R.P. 2006 Bubbles, Drops, and Particles in Non-Newtonian Fluids. CRC Press.CrossRefGoogle Scholar
Giesekus, H. 1982 A simple constitutive equation for polymer fluids based on the concept of deformation-dependent tensorial mobility. J. Non-Newtonian Fluid Mech. 11, 69–109.CrossRefGoogle Scholar
Harlen, O.G. 2002 The negative wake behind a sphere sedimenting through a viscoelastic fluid. J. Non-Newtonian Fluid Mech. 108, 411–430.CrossRefGoogle Scholar
Jayaraman, A. & Belmonte, A. 2003 Oscillations of a solid sphere falling through a wormlike micellar fluid. Phy. Rev. E 67, 065301.CrossRefGoogle ScholarPubMed
Kalb, A., Villasmil U., L.A. & Cromer, M. 2017 Role of chain scission in cross-slot flow of wormlike micellar solutions. Phys. Rev. Fluids 2, 071301.CrossRefGoogle Scholar
Kalb, A., Villasmil U., L.A. & Cromer, M. 2018 Elastic instability and secondary flow in cross-slot flow of wormlike micellar solutions. J. Non-Newtonian Fluid Mech. 262, 79–91.CrossRefGoogle Scholar
Khan, M.B. & Sasmal, C. 2020 Effect of chain scission on flow characteristics of wormlike micellar solutions past a confined microfluidic cylinder: a numerical analysis. Soft Matt. 16, 5261–5272.CrossRefGoogle Scholar
Kumar, N., Majumdar, S., Sood, A., Govindarajan, R., Ramaswamy, S. & Sood, A.K. 2012 Oscillatory settling in wormlike-micelle solutions: bursts and a long time scale. Soft Matt. 8, 4310–4313.CrossRefGoogle Scholar
McKinley, G.H. 2002 Steady and transient motion of spherical particles in viscoelastic liquids. In Transport Processes in Bubble, Drops, and Particles (ed. D. De Kee & R.P. Chhabra), pp. 338–375. CRC Press.Google Scholar
Michaelides, E. 2006 Particles, Bubbles & Drops: Their Motion, Heat and Mass transfer. World Scientific.CrossRefGoogle Scholar
Mohammadigoushki, H. & Muller, S.J. 2016 Sedimentation of a sphere in wormlike micellar fluids. J. Rheol. 60, 587–601.CrossRefGoogle Scholar
Mohammadigoushki, H. & Muller, S.J. 2018 Creeping flow of a wormlike micelle solution past a falling sphere: role of boundary conditions. J. Non-Newtonian Fluid Mech. 257, 44–49.CrossRefGoogle Scholar
Mohammadigoushki, H., Dalili, A., Zhou, L. & Cook, P. 2019 Transient evolution of flow profiles in a shear banding wormlike micellar solution: experimental results and a comparison with the VCM model. Soft Matt. 15, 5483–5494.CrossRefGoogle Scholar
Moroi, Y. 1992 Micelles: Theoretical and Applied Aspects. Springer Science & Business Media.CrossRefGoogle Scholar
OpenFOAM 2020 Openfoam user guide. Available at: https://www.openfoam.com/documentation/user-guide/.Google Scholar
Pimenta, F. & Alves, M.A. 2016 rheoTool. Available at: https://github.com/fppimenta/rheoTool.Google Scholar
Pipe, C.J., Kim, N.J., Vasquez, P.A., Cook, L.P. & McKinley, G.H. 2010 Wormlike micellar solutions: II. Comparison between experimental data and scission model predictions. J. Rheol. 54, 881–913.CrossRefGoogle Scholar
Rothstein, J.P. 2003 Transient extensional rheology of wormlike micelle solutions. J. Rheol. 47, 1227–1247.CrossRefGoogle Scholar
Rothstein, J.P. 2008 Strong flows of viscoelastic wormlike micelle solutions. Rheol. Rev. 2008, 1–46.Google Scholar
Sasmal, C. 2020 Flow of wormlike micellar solutions through a long micropore with step expansion and contraction. Phys. Fluids 32, 013103.CrossRefGoogle Scholar
Vasquez, P.A., McKinley, G.H. & Cook, L.P. 2007 A network scission model for wormlike micellar solutions: I. Model formulation and viscometric flow predictions. J. Non-Newtonian Fluid Mech. 144, 122–139.CrossRefGoogle Scholar
Wang, Z., Wang, S., Xu, L., Dou, Y. & Su, X. 2020 Extremely slow settling behavior of particles in dilute wormlike micellar fluid with broad spectrum of relaxation times. J. Dispersion Sci. Technol. 41, 639–647.CrossRefGoogle Scholar
Weller, H.G., Tabor, G., Jasak, H. & Fureby, C. 1998 A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 12, 620–631.CrossRefGoogle Scholar
Wu, S. & Mohammadigoushki, H. 2018 Sphere sedimentation in wormlike micelles: effect of micellar relaxation spectrum and gradients in micellar extensions. J. Rheol. 62, 1061–1069.CrossRefGoogle Scholar
Zhang, Y. & Muller, S.J. 2018 Unsteady sedimentation of a sphere in wormlike micellar fluids. Phys. Rev. Fluids 3, 043301.CrossRefGoogle Scholar
Zhou, L., McKinley, G.H. & Cook, L.P. 2014 Wormlike micellar solutions: III. VCM model predictions in steady and transient shearing flows. J. Non-Newtonian Fluid Mech. 211, 70–83.CrossRefGoogle Scholar