Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-19T11:56:26.124Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasi-geostrophy against the wall

Published online by Cambridge University Press:  28 April 2020

A. Venaille Open the ORCID record for A. Venaille [Opens in a new window]
A. Venaille*
Affiliation:
Univ Lyon, Ens de Lyon, Univ Claude Bernard, CNRS, Laboratoire de Physique, F-69342 Lyon, France
*
†Email address for correspondence: antoine.venaille@ens-lyon.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

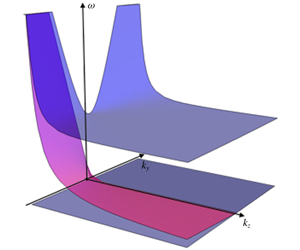
Coasts are obstructions to the classical derivation of continuously stratified quasi-geostrophic equations, due to possible resonances between slow internal coastally trapped Kelvin waves and anticyclones. Deremble et al. (Ocean Model., vol. 119, 2017, pp. 1–12) proposed a coupled model between a quasi-geostrophic interior and boundary-layer Kelvin-wave dynamics. We revisit the derivation of this model, paying particular attention to conservation laws. We find that quasi-geostrophic energy is conserved, despite the existence of Kelvin-wave shocks in the boundary layer. The effect of those shocks is to change the global distribution of potential vorticity, and, consequently, the interior flow structure. In that respect, we show that there is an active control of the boundary region on the interior flow.

JFM classification

Geophysical and Geological Flows: Quasi-geostrophic flows Geophysical and Geological Flows: Waves in rotating fluids Geophysical and Geological Flows: Shallow water flows
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 894 , 10 July 2020 , R1
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bühler, O. 2000 On the vorticity transport due to dissipating or breaking waves in shallow-water flow. J. Fluid Mech. 407, 235–263.CrossRefGoogle Scholar
Deremble, B., Johnson, E. R. & Dewar, W. K. 2017 A coupled model of interior balanced and boundary flow. Ocean Model. 119, 1–12.CrossRefGoogle Scholar
Dewar, W. K., Berloff, P. & Hogg, A. M. 2011 Submesoscale generation by boundaries. J. Mar. Res. 69 (4–5), 501–522.CrossRefGoogle Scholar
Dewar, W. K. & Hogg, A. M. 2010 Topographic inviscid dissipation of balanced flow. Ocean Model. 32 (1–2), 1–13.CrossRefGoogle Scholar
Hogg, A. M., Dewar, W. K., Berloff, P. & Ward, M. L. 2011 Kelvin wave hydraulic control induced by interactions between vortices and topography. J. Fluid Mech. 687, 194–208.CrossRefGoogle Scholar
McWilliams, J. C. 1977 A note on a consistent quasigeostrophic model in a multiply connected domain. Dyn. Atmos. Oceans 1 (5), 427–441.CrossRefGoogle Scholar
Nguyen Van Yen, N., Waidmann, M., Klein, R., Farge, M. & Schneider, K. 2018 Energy dissipation caused by boundary layer instability at vanishing viscosity. J. Fluid Mech. 849, 676–717.CrossRefGoogle Scholar
Peregrine, D. H. 1998 Surf zone currents. Theor. Comput. Fluid Dyn. 10 (1–4), 295–309.CrossRefGoogle Scholar
Pratt, L. J. & Whitehead, J. A. 2007 Rotating Hydraulics: Nonlinear Topographic Effects in the Ocean and Atmosphere, vol. 36. Springer Science and Business Media.CrossRefGoogle Scholar
Rostami, M. & Zeitlin, V. 2019 Eastward-moving convection-enhanced modons in shallow water in the equatorial tangent plane. Phys. Fluids 31 (2), 021701.CrossRefGoogle Scholar
Roullet, G. & Klein, P. 2010 Cyclone–anticyclone asymmetry in geophysical turbulence. Phys. Rev. Lett. 104 (21), 218501.CrossRefGoogle ScholarPubMed
Roullet, G. & McWilliams, J. C. 2014 2D turbulence with complicated boundaries. In AGU Fall Meeting Abstracts. Wiley.Google Scholar
Vallis, G. K. 2017 Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Zeitlin, V. 2018 Geophysical Fluid Dynamics: Understanding (Almost) Everything with Rotating Shallow Water Models. Oxford University Press.CrossRefGoogle Scholar