Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-17T21:29:40.476Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of a perturbed solid-body rotation flow in a finite-length straight rotating pipe

Published online by Cambridge University Press:  16 May 2018

Chunjuan Feng Open the ORCID record for Chunjuan Feng [Opens in a new window] ,
Feng Liu ,
Zvi Rusak Open the ORCID record for Zvi Rusak [Opens in a new window]  and
Shixiao Wang Open the ORCID record for Shixiao Wang [Opens in a new window]
Chunjuan Feng
Affiliation:
School of Aeronautics, Northwestern Polytechnical University, Xian, 710072, PR China
Feng Liu
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California, Irvine, CA 92697-3975, USA
Zvi Rusak
Affiliation:
Department of Mechanical, Aerospace and Nuclear Engineering, Rensselaer Polytechnic Institute, Troy, NY 12180-3590, USA
Shixiao Wang*
Affiliation:
University of Auckland, 38 Princes Street, Auckland, 1142, New Zealand
*
†Email address for correspondence: wang@math.auckland.ac.nz
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations are used to study the three-dimensional, incompressible and viscous flow dynamics of a base solid-body rotation flow with a uniform axial velocity entering a rotating, finite-length, straight circular pipe. Steady in time profiles of the axial, radial and circumferential velocities are prescribed along the pipe inlet. The convective boundary conditions for each velocity flux component is set at the pipe outlet. The simulation results describe the neutral stability line in response to either axisymmetric or three-dimensional perturbations in a diagram of Reynolds number ( 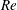$Re$ , based on inlet axial velocity and pipe radius) versus the incoming flow swirl ratio ( 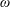$\unicode[STIX]{x1D714}$ ). This line is in good agreement with the neutral stability line recently predicted by the linear stability theory of Wang et al. (J. Fluid Mech., vol. 797, 2016, pp. 284–321). The computed time history of the velocity components at a certain point in the flow is used to describe three-dimensional phase portraits of the flow global dynamics and its long-term behaviour. They show three types of flow evolution scenarios. First, the Wang & Rusak (Phys. Fluids, vol. 8 (4), 1996, pp. 1007–1016) axisymmetric instability mechanism and evolution to a stable axisymmetric breakdown state is recovered at certain operational conditions in terms of 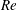$Re$ and 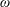$\unicode[STIX]{x1D714}$ . 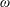However, at other operational conditions with same $\unicode[STIX]{x1D714}$ but with a higher 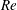$Re$ , a second scenario is found. The axisymmetric breakdown state continues to evolve and a spiral instability mode appears on it and grows to a rotating spiral breakdown state. Moreover, at higher levels of 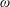$\unicode[STIX]{x1D714}$ a third scenario is found where there exists a dominant three-dimensional spiral type of instability mode that agrees with the linear stability theory of Wang et al. (J. Fluid Mech., vol. 797, 2016, pp. 284–321). The growth of this mode leads directly to a spiral type of flow roll-up and nonlinearly saturates on a rotating spiral type of vortex breakdown. The Reynolds–Orr equation is used to reveal the mechanism that drives all the instabilities as well as the nonlinear global flow evolution. At high swirl ratios, the confined kinetic energy in the swirling flow can be triggered to be released through various physical agents, such as the asymmetric inlet–outlet conditions, that eliminate axial homogeneity along the pipe and induce flow instabilities and evolution to breakdown states. It is also shown that local instability analysis or its extension using the assumption of a weakly non-parallel flow to conduct convective instability–absolute instability analyses is definitely not related to any of the instability modes found in the present study. Moreover, a stability study based on the strongly non-parallel flow character, including axial inhomogeneity due to a finite-domain boundary conditions, must be conducted to reveal instabilities in such flows.

JFM classification

Vortex Flows: Vortex breakdown Vortex Flows: Vortex dynamics Vortex Flows: Vortex instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 846 , 10 July 2018 , pp. 1114 - 1152
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ash, R. L. & Khorrami, M. R. 1995 Vortex stability. In Fluid Vortices (ed. Green, S. I.), chap. 8, pp. 317–372. Kluwer.CrossRefGoogle Scholar
Batchelor, G. K. 1964 Axial flow in trailing line vortices. J. Fluid Mech. 20, 645–658.Google Scholar
Benjamin, T. B. 1962 Theory of the vortex breakdown phenomenon. J. Fluid Mech. 14, 593–629.Google Scholar
Brucker, Ch. & Althaus, W. 1995 Study of vortex breakdown by particle tracking velocimetry (PTV). Part 3: time-dependent structure and development of breakdown modes. Exp. Fluids 18, 174–186.Google Scholar
Cary, A. W., Darmofal, D. L. & Powell, K. G.1997 Onset of the spiral mode of vortex breakdown. AIAA Paper 97-0439.Google Scholar
Chomaz, J. M., Huerre, P. & Redekopp, L. G. 1988 Bifurcations to local and global modes in spatially-developing flows. Phys. Rev. Lett. 60, 25–28.Google Scholar
Delbende, I., Chomaz, J.-M. & Huerre, P. 1998 Absolute/convective instabilities in the Batchelor vortex: a numerical study of the linear impulse response. J. Fluid Mech. 355, 229–254.Google Scholar
Dennis, D. J. C., Seraudie, C. & Poole, R. J. 2014 Controlling vortex breakdown in swirling pipe flows: experiments and simulations. Phys. Fluids 26 (5), 053602.Google Scholar
Faler, J. H. & Leibovich, S. 1977 Disrupted states of vortex flow and vortex breakdown. Phys. Fluids 20, 1385–1400.Google Scholar
Gallaire, F., Ruith, M., Meiburg, E., Chomaz, J.-M. & Huerre, P. 2006 Spiral vortex breakdown as a global mode. J. Fluid Mech. 549, 71–80.CrossRefGoogle Scholar
Garg, A. K. & Leibovich, S. 1979 Spectral characteristics of vortex breakdown flow field. Phys. Fluids 22, 2053–2064.Google Scholar
Gong, R.2017 Stability analysis of swirling flow in a finite-length pipe. PhD thesis, Auckland University, Auckland, New Zealand.Google Scholar
Grabowski, W. J. & Berger, S. A. 1976 Solutions of the Navier–Stokes equations for vortex breakdown. J. Fluid Mech. 75, 525–544.Google Scholar
Hall, M. G. 1972 Vortex breakdown. Annu. Rev. Fluid Mech. 4, 195–217.Google Scholar
Howard, L. N. & Gupta, A. S. 1962 On the hydrodynamics and hydromagnetic stability of swirling flows. J. Fluid Mech. 14, 463–476.Google Scholar
Huerre, P. & Monkewitz, P. 1985 Absolute and convective instabilities in free shear layers. J. Fluid Mech. 159, 151–168.CrossRefGoogle Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.Google Scholar
Jones, M. C., Hourigan, K. & Thomson, M. C. 2015 A study of the geometry and parameter dependence of vortex breakdown. Phys. Fluids 27, 044102.Google Scholar
Kelvin, L. 1880 Vibrations of a columnar vortex. Phil. Mag. 10, 155–168.Google Scholar
Keller, J. J., Egli, W. & Exley, W. 1985 Force- and loss-free transitions between flow states. Z. Angew. Math. Phys. 36, 854–889.Google Scholar
Liang, H. & Maxworthy, T. 2005 An experimental investigation of swirling jets. J. Fluid Mech. 525, 115–159.CrossRefGoogle Scholar
Leibovich, S. 1984 Vortex stability and breakdown: survey and extension. AIAA J. 22, 1192–1206.CrossRefGoogle Scholar
Leibovich, S. & Kribus, A. 1990 Large amplitude wavetrains and solitary waves in vortices. J. Fluid Mech. 216, 459–504.Google Scholar
Leibovich, S. & Stewartson, K. 1983 A sufficient condition for the instability of columnar vortices. J. Fluid Mech. 126, 335–356.Google Scholar
Lessen, M., Singh, M. J. & Paillet, F. 1974 The stability of a trailing line vortex. Part 1. Inviscid theory. J. Fluid Mech. 63 (4), 753–763.Google Scholar
Lessen, M. & Paillet, F. 1974 The stability of a trailing line vortex. Part 2. Viscous theory. J. Fluid Mech. 65 (4), 769–779.Google Scholar
Malkiel, E., Cohen, J., Rusak, Z. & Wang, S. 1996 Axisymmetric vortex breakdown in a pipe: theoretical and experimental studies. In Proceedings of the 36th Israel Annual Conference on Aerospace Sciences (February), pp. 24–34.Google Scholar
Mattner, T. W., Joubert, P. N. & Chong, M. S. 2002 Vortical flow. Part 1. Flow through a constant diameter pipe. J. Fluid Mech. 463, 259–291.Google Scholar
Meliga, P. & Gallaire, F. 2011 Global instability of helical vortex breakdown. In 6th AIAA Theoretical Fluid Mechanics Conference, Honolulu, Hawaii, USA. AIAA 2011-3604.Google Scholar
Olendraru, C., Sellier, A. & Huerre, P. 1999 Inviscid instability of the Batchelor vortex: absolute-convective transition and spatial branches. Phys. Fluids 11, 1805–1820.Google Scholar
Randall, J. D. & Leibovich, S. 1973 The critical state: a trapped wave model of vortex breakdown. J. Fluid Mech. 53, 48–493.Google Scholar
Rayleigh, Lord 1916 On the dynamics of revolving fluids. Proc. R. Soc. Lond. A 93, 148–154.Google Scholar
Ruith, M. R., Chen, P., Meiburg, E. & Maxworthy, T. 2003 Three-dimensional vortex breakdown in swirling jets and wakes: direct numerical simulation. J. Fluid Mech. 486, 331–378.CrossRefGoogle Scholar
Rusak, Z., Wang, S. & Whiting, C. H. 1998 The evolution of a perturbed vortex in a pipe to axisymmetric vortex breakdown. J. Fluid Mech. 366, 211–237.Google Scholar
Rusak, Z., Wang, S., Xu, L. & Taylor, S. 2012 On the global nonlinear stability of near-critical swirling flows in a long finite-length pipe and the path to vortex breakdown. J. Fluid Mech. 712, 295–326.Google Scholar
Rusak, Z. & Wang, S. 2014 Wall-separation and vortex-breakdown zones in a solid-body rotation flow in a rotating finite-length straight circular pipe. J. Fluid Mech. 759, 321–359.Google Scholar
Salvetti, M. V., Orlandi, P. & Verzicco, R. 1996 Numerical simulations of transitional axisymmetric coaxial jets. AIAA J. 34 (4), 736–743.Google Scholar
Sarpkaya, T. 1971 On stationary and traveling vortex breakdowns. J. Fluid Mech. 45, 545–559.Google Scholar
Sarpkaya, T. 1974 Effect of adverse pressure-gradient on vortex breakdown. AIAA J. 12 (5), 602–607.Google Scholar
Serrin, L. J. 1959 Mathematical Principles of Classic Fluid Mechanics, vol. III.1. Springer.Google Scholar
Spall, R. E. & Gatski, T. B. 1991 A computational study of the topology of vortex breakdown. Proc. R. Soc. Lond. A 435, 321–337.Google Scholar
Spall, R. E. 1996 Transition from spiral-to bubble-type vortex breakdown. Phys. Fluids 8 (5), 1330–1332.Google Scholar
Synge, L. 1933 The stability of heterogeneous liquids. Trans. R. Soc. Can. 27, 1–18.Google Scholar
Tromp, J. C. & Beran, P. S. 1997 The role of nonunique axisymmetric solutions in 3-D vortex breakdown. Phys. Fluids 9, 992–1002.Google Scholar
Umeh, C., Rusak, Z., Gutmark, E., Villalva, R. & Cha, D. J. 2010 Experimental and computational study of nonreacting vortex breakdown in a swirl-stabilized combustor. AIAA J. 48 (11), 2576–2585.Google Scholar
Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flows in cylindrical coordinates. J. Comput. Phys. 123, 402–414.Google Scholar
Wang, S. & Rusak, Z. 1996 On the stability of an axisymmetric rotating flow in a pipe. Phys. Fluids 8 (4), 1007–1016.Google Scholar
Wang, S. & Rusak, Z. 1997 The dynamics of a swirling flow in a pipe and transition to axisymmetric vortex breakdown. J. Fluid Mech. 340, 177–223.Google Scholar
Wang, S. & Rusak, Z. 2011 Energy transfer mechanism of the instability of an axisymmetric swirling flow in a finite-length pipe. J. Fluid Mech. 679, 505–543.Google Scholar
Wang, S., Rusak, Z., Gong, R. & Liu, F. 2016 On the three-dimensional stability of a solid-body-rotation flow in a finite-length rotating pipe. J. Fluid Mech. 797, 284–321.Google Scholar