Article contents
The asymptotic downstream flow of plane turbulent wall jets without external stream
Published online by Cambridge University Press: 17 August 2015
Abstract
The plane turbulent wall-jet flow without externally imposed stream is considered. It is assumed that the wall jet does not emerge from a second wall perpendicular to the velocity vector of the initial wall jet. The (kinematic) momentum flux 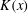 $K(x)$ of the wall jet decreases downstream owing to the shear stress at the wall. This investigation is based on the hypothesis that the total friction force on the wall is smaller than the total inflow momentum flux. In other words, the turbulent wall jet tends to a turbulent ‘half-free jet’ with a non-zero momentum flux
$K(x)$ of the wall jet decreases downstream owing to the shear stress at the wall. This investigation is based on the hypothesis that the total friction force on the wall is smaller than the total inflow momentum flux. In other words, the turbulent wall jet tends to a turbulent ‘half-free jet’ with a non-zero momentum flux 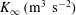 $K_{\infty }\;(\text{m}^{3}~\text{s}^{-2})$ far downstream. The fact that the turbulent half-free jet is the asymptotic form of a turbulent wall jet is the basis for a singular perturbation method by which the wall-jet flow is determined. It turns out that the ratio between the wall distance
$K_{\infty }\;(\text{m}^{3}~\text{s}^{-2})$ far downstream. The fact that the turbulent half-free jet is the asymptotic form of a turbulent wall jet is the basis for a singular perturbation method by which the wall-jet flow is determined. It turns out that the ratio between the wall distance 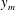 $y_{m}$ of the maximum velocity and the wall distance
$y_{m}$ of the maximum velocity and the wall distance 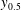 $y_{0.5}$ of half the maximum velocity decreases downstream to zero. Dimensional analysis leads immediately to a universal function of the dimensionless momentum flux
$y_{0.5}$ of half the maximum velocity decreases downstream to zero. Dimensional analysis leads immediately to a universal function of the dimensionless momentum flux 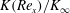 $K(\mathit{Re}_{x})/K_{\infty }$ that depends asymptotically only on the local Reynolds number
$K(\mathit{Re}_{x})/K_{\infty }$ that depends asymptotically only on the local Reynolds number 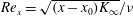 $\mathit{Re}_{x}=\sqrt{(x-x_{0})K_{\infty }}/{\it\nu}$, where
$\mathit{Re}_{x}=\sqrt{(x-x_{0})K_{\infty }}/{\it\nu}$, where 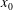 $x_{0}$ denotes the coordinate of the virtual origin. When the values
$x_{0}$ denotes the coordinate of the virtual origin. When the values 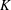 $K$ and
$K$ and  ${\it\nu}$ at the position
${\it\nu}$ at the position 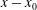 $x-x_{0}$ are known, the asymptotic momentum flux
$x-x_{0}$ are known, the asymptotic momentum flux 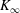 $K_{\infty }$ can be determined. Experimental data on all turbulent plane wall jets (except those emerging from a second plane wall) collapse to a single universal curve. Comparisons between available experimental data and the analysis make the hypothesis
$K_{\infty }$ can be determined. Experimental data on all turbulent plane wall jets (except those emerging from a second plane wall) collapse to a single universal curve. Comparisons between available experimental data and the analysis make the hypothesis 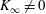 $K_{\infty }\neq 0$ plausible. A convincing verification, however, will be possible in the future, preferably by direct numerical simulations.
$K_{\infty }\neq 0$ plausible. A convincing verification, however, will be possible in the future, preferably by direct numerical simulations.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 16
- Cited by



