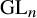1 Introduction
Let F be a finite extension of the field
![]() $\mathbf {Q}_p$
of p-adic numbers, and let G be a connected reductive group defined over F. Scholze [Reference Scholze and WeinsteinSW20, §23] introduced a tower of moduli spaces of mixed-characteristic shtukas
$\mathbf {Q}_p$
of p-adic numbers, and let G be a connected reductive group defined over F. Scholze [Reference Scholze and WeinsteinSW20, §23] introduced a tower of moduli spaces of mixed-characteristic shtukas
depending on a
![]() $\sigma $
-conjugacy class of
$\sigma $
-conjugacy class of
![]() $b\in G(\breve F)$
(where
$b\in G(\breve F)$
(where
![]() $\breve F$
is the completion of the maximal unramified extension of F) and on a conjugacy class of cocharacters
$\breve F$
is the completion of the maximal unramified extension of F) and on a conjugacy class of cocharacters
![]() $\mu \colon \mathbf {G}_{\mathrm {m}}\to G$
defined over
$\mu \colon \mathbf {G}_{\mathrm {m}}\to G$
defined over
![]() $\overline {F}$
. Here, K ranges over open compact subgroups of
$\overline {F}$
. Here, K ranges over open compact subgroups of
![]() $G(F)$
. Each
$G(F)$
. Each
![]() $\operatorname {\mathrm {Sht}}_{G,b,\mu ,K}$
is a locally spatial diamond defined over
$\operatorname {\mathrm {Sht}}_{G,b,\mu ,K}$
is a locally spatial diamond defined over
![]() $\operatorname {\mathrm {Spd}} \breve {E}$
, where E is the field of definition of the conjugacy class of
$\operatorname {\mathrm {Spd}} \breve {E}$
, where E is the field of definition of the conjugacy class of
![]() $\mu $
.
$\mu $
.
When
![]() $\mu $
is minuscule,
$\mu $
is minuscule,
![]() $\operatorname {\mathrm {Sht}}_{G,b,\mu ,K}$
is the diamond associated to a rigid-analytic variety
$\operatorname {\mathrm {Sht}}_{G,b,\mu ,K}$
is the diamond associated to a rigid-analytic variety
![]() $\mathcal {M}_{G,b,\mu ,K}$
[Reference Scholze and WeinsteinSW20, §24]. The latter is a local Shimura variety, whose general existence was conjectured in [Reference Rapoport and ViehmannRV14]. The theory of Rapoport–Zink spaces [Reference Rapoport and ZinkRZ96] provides instances of
$\mathcal {M}_{G,b,\mu ,K}$
[Reference Scholze and WeinsteinSW20, §24]. The latter is a local Shimura variety, whose general existence was conjectured in [Reference Rapoport and ViehmannRV14]. The theory of Rapoport–Zink spaces [Reference Rapoport and ZinkRZ96] provides instances of
![]() $\mathcal {M}_{G,b,\mu ,K}$
admitting a moduli interpretation, as the generic fiber of a deformation space of p-divisible groups.
$\mathcal {M}_{G,b,\mu ,K}$
admitting a moduli interpretation, as the generic fiber of a deformation space of p-divisible groups.
The Kottwitz conjecture [Reference RapoportRap95, Conjecture 5.1], [Reference Rapoport and ViehmannRV14, Conjecture 7.3] relates the cohomology of
![]() $\mathcal {M}_{G,b,\mu ,K}$
to the local Langlands correspondence in the case that b lies in the unique basic class in
$\mathcal {M}_{G,b,\mu ,K}$
to the local Langlands correspondence in the case that b lies in the unique basic class in
![]() $B(G,\mu )$
. There is a natural generalization of this conjecture for
$B(G,\mu )$
. There is a natural generalization of this conjecture for
![]() $\operatorname {\mathrm {Sht}}_{G,b,\mu ,K}$
, as we now explain.
$\operatorname {\mathrm {Sht}}_{G,b,\mu ,K}$
, as we now explain.
Let
![]() $G_b$
the inner form of G associated to b. The tower
$G_b$
the inner form of G associated to b. The tower
![]() $\operatorname {\mathrm {Sht}}_{G,b,\mu ,K}$
admits commuting actions of
$\operatorname {\mathrm {Sht}}_{G,b,\mu ,K}$
admits commuting actions of
![]() $G_b(F)$
and
$G_b(F)$
and
![]() $G(F)$
. The action of
$G(F)$
. The action of
![]() $G_b(F)$
preserves each
$G_b(F)$
preserves each
![]() $\operatorname {\mathrm {Sht}}_{G,b,\mu ,K}$
, whereas the action of
$\operatorname {\mathrm {Sht}}_{G,b,\mu ,K}$
, whereas the action of
![]() $g\in G(F)$
sends
$g\in G(F)$
sends
![]() $\operatorname {\mathrm {Sht}}_{G,b,\mu ,K}$
to
$\operatorname {\mathrm {Sht}}_{G,b,\mu ,K}$
to
![]() $\operatorname {\mathrm {Sht}}_{G,b,\mu ,gKg^{-1}}$
. There is furthermore a (not necessarily effective) Weil descent datum on this tower from
$\operatorname {\mathrm {Sht}}_{G,b,\mu ,gKg^{-1}}$
. There is furthermore a (not necessarily effective) Weil descent datum on this tower from
![]() $\breve {E}$
down to E.
$\breve {E}$
down to E.
Let
![]() $\ell $
be a prime distinct from p. The geometric Satake equivalence produces an object
$\ell $
be a prime distinct from p. The geometric Satake equivalence produces an object
![]() $\mathcal {S}_{\mu }$
in the derived category of étale
$\mathcal {S}_{\mu }$
in the derived category of étale
![]() $\mathbf {Z}_{\ell }$
-sheaves on
$\mathbf {Z}_{\ell }$
-sheaves on
![]() $\operatorname {\mathrm {Sht}}_{G,b,\mu ,K}$
; this is compatible with the actions of
$\operatorname {\mathrm {Sht}}_{G,b,\mu ,K}$
; this is compatible with the actions of
![]() $G(F)$
and
$G(F)$
and
![]() $G_b(F)$
on the tower. Let C be the completion of an algebraic closure of
$G_b(F)$
on the tower. Let C be the completion of an algebraic closure of
![]() $\breve {E}$
. For a smooth representation
$\breve {E}$
. For a smooth representation
![]() $\rho $
of
$\rho $
of
![]() $G_b(F)$
with coefficients in
$G_b(F)$
with coefficients in
![]() $\overline {\mathbf {Q}}_{\ell }$
, we define:
$\overline {\mathbf {Q}}_{\ell }$
, we define:
Then
![]() $R\Gamma (G,b,\mu )[\rho ]$
lies in the derived category of smooth representations of
$R\Gamma (G,b,\mu )[\rho ]$
lies in the derived category of smooth representations of
![]() $G(F)\times W_E$
with coefficients in
$G(F)\times W_E$
with coefficients in
![]() $\overline {\mathbf {Q}}_{\ell }$
, where
$\overline {\mathbf {Q}}_{\ell }$
, where
![]() $W_E$
is the Weil group. Informally, this is the
$W_E$
is the Weil group. Informally, this is the
![]() $\rho $
-isotypic component of the cohomology of the tower
$\rho $
-isotypic component of the cohomology of the tower
![]() $\operatorname {\mathrm {Sht}}_{G,b,\mu }$
.
$\operatorname {\mathrm {Sht}}_{G,b,\mu }$
.
A recent result of Fargues–Scholze [Reference Fargues and ScholzeFS21, Corollary I.7.3] states that, if
![]() $\rho $
is finite length and admissible, then
$\rho $
is finite length and admissible, then
![]() $R\Gamma (G,b,\mu )[\rho ]$
is a complex of finite length admissible representations of
$R\Gamma (G,b,\mu )[\rho ]$
is a complex of finite length admissible representations of
![]() $G(F)$
admitting a continuous action of
$G(F)$
admitting a continuous action of
![]() $W_E$
.
$W_E$
.
Let
![]() $\operatorname {\mathrm {Groth}}(G_b(F))$
be the Grothendieck group of the category of finite length admissible representations of
$\operatorname {\mathrm {Groth}}(G_b(F))$
be the Grothendieck group of the category of finite length admissible representations of
![]() $G(F)$
with
$G(F)$
with
![]() $\overline {\mathbf {Q}}_{\ell }$
coefficients. Also, let
$\overline {\mathbf {Q}}_{\ell }$
coefficients. Also, let
![]() $\operatorname {\mathrm {Groth}}(G(F)\times W_E)$
be the Grothendieck group of the category of finite length admissible representations of
$\operatorname {\mathrm {Groth}}(G(F)\times W_E)$
be the Grothendieck group of the category of finite length admissible representations of
![]() $G(F)$
with
$G(F)$
with
![]() $\overline {\mathbf {Q}}_{\ell }$
coefficients, which come equipped with a continuous action of
$\overline {\mathbf {Q}}_{\ell }$
coefficients, which come equipped with a continuous action of
![]() $W_E$
commuting with the
$W_E$
commuting with the
![]() $G(F)$
-action. Following [Reference ShinShi11], we define a map
$G(F)$
-action. Following [Reference ShinShi11], we define a map
(for ‘Mantovan’, referencing [Reference MantovanMan04]) sending
![]() $\rho $
to the Euler characteristic of
$\rho $
to the Euler characteristic of
![]() $R\Gamma (G,b,\mu )[\rho ]$
.
$R\Gamma (G,b,\mu )[\rho ]$
.
The Kottwitz conjecture (appropriately generalized) describes
![]() $\operatorname {\mathrm {Mant}}_{b,\mu }(\rho )$
in terms of the local Langlands correspondence when
$\operatorname {\mathrm {Mant}}_{b,\mu }(\rho )$
in terms of the local Langlands correspondence when
![]() $\rho $
lies in a supercuspidal L-packet. The complex dual groups of G and
$\rho $
lies in a supercuspidal L-packet. The complex dual groups of G and
![]() $G_b$
are canonically identified, and we write
$G_b$
are canonically identified, and we write
![]() $\widehat {G}$
for either. Let
$\widehat {G}$
for either. Let
![]() $^LG=\widehat G \rtimes W_F$
be the L-group. The basic form of the local Langlands conjecture predicts that the set of isomorphism classes of essentially square-integrable representations of
$^LG=\widehat G \rtimes W_F$
be the L-group. The basic form of the local Langlands conjecture predicts that the set of isomorphism classes of essentially square-integrable representations of
![]() $G(F)$
(resp.,
$G(F)$
(resp.,
![]() $G_b(F)$
) is partitioned into L-packets
$G_b(F)$
) is partitioned into L-packets
![]() $\Pi _{\phi }(G)$
(resp.,
$\Pi _{\phi }(G)$
(resp.,
![]() $\Pi _{\phi }(G_b)$
) and that each such packet is indexed by a discrete Langlands parameter
$\Pi _{\phi }(G_b)$
) and that each such packet is indexed by a discrete Langlands parameter
![]() $\phi : W_F \times \mathrm {SL}_2(\mathbf {C}) \to {^LG}$
. When
$\phi : W_F \times \mathrm {SL}_2(\mathbf {C}) \to {^LG}$
. When
![]() $\phi $
is discrete and trivial on
$\phi $
is discrete and trivial on
![]() $\mathrm {SL}_2(\mathbf {C})$
, we say
$\mathrm {SL}_2(\mathbf {C})$
, we say
![]() $\phi $
is supercuspidal; in this case, it is expected that the packets
$\phi $
is supercuspidal; in this case, it is expected that the packets
![]() $\Pi _{\phi }(G)$
and
$\Pi _{\phi }(G)$
and
![]() $\Pi _{\phi }(G_b)$
consist entirely of supercuspidal representations.
$\Pi _{\phi }(G_b)$
consist entirely of supercuspidal representations.
Our generalized Kottwitz conjecture is conditional on the refined local Langlands correspondence for supercuspidal L-parameters in the formulation of [Reference KalethaKal16a, Conjecture G]. In particular, it relies crucially on the endoscopic character identities satisfied by L-packets. These are reviewed in Appendix A. Note that we do not assume any compatibility between the validity of [Reference KalethaKal16a, Conjecture G] and the construction of [Reference Fargues and ScholzeFS21], i.e., we do not require that the construction of [Reference Fargues and ScholzeFS21] satisfy any portion of [Reference KalethaKal16a, Conjecture G].
We take this opportunity to give a brief summary of the status of [Reference KalethaKal16a, Conjecture G]. In short, the full conjecture is known for regular supercuspidal parameters [Reference KalethaKal19a, Definition 5.2.3] provided G splits over a tame extension of F, F has characteristic zero and p is sufficiently large (at least
![]() $(e+2)n$
, where e is the ramification index of
$(e+2)n$
, where e is the ramification index of
![]() $F/\mathbf {Q}_p$
and n is the smallest size of a faithful algebraic representation of G). The proof is contained in [Reference KalethaKal19a, §5.3] and [Reference Fintzen, Kaletha and SpiceFKS19, §4.4]. However, various parts of that conjecture are known under less restrictive assumptions. To describe this, we remind the reader that [Reference KalethaKal16a, Conjecture G] consists of the following assertions:
$F/\mathbf {Q}_p$
and n is the smallest size of a faithful algebraic representation of G). The proof is contained in [Reference KalethaKal19a, §5.3] and [Reference Fintzen, Kaletha and SpiceFKS19, §4.4]. However, various parts of that conjecture are known under less restrictive assumptions. To describe this, we remind the reader that [Reference KalethaKal16a, Conjecture G] consists of the following assertions:
-
1. The existence of a finite set
 $\Pi _{\phi }$
of representations of rigid inner forms of G for each tempered L-parameter
$\Pi _{\phi }$
of representations of rigid inner forms of G for each tempered L-parameter
 $\phi $
.
$\phi $
. -
2. The existence and uniqueness of a generic constituent of
 $\Pi _{\phi }$
for a fixed Whittaker datum.
$\Pi _{\phi }$
for a fixed Whittaker datum. -
3. A bijection between
 $\Pi _{\phi }$
and the set
$\Pi _{\phi }$
and the set
 $\mathrm {Irr}(\pi _0(S_{\phi }^+))$
of irreducible representations of the refined centralizer component group associated to
$\mathrm {Irr}(\pi _0(S_{\phi }^+))$
of irreducible representations of the refined centralizer component group associated to
 $\phi $
.
$\phi $
. -
4. The character identities of ordinary endoscopy, as recalled in Appendix A.
At the moment, a set
![]() $\Pi _{\phi }$
has been constructed in [Reference KalethaKal19b, §§4.1,4.2] for every supercuspidal parameter
$\Pi _{\phi }$
has been constructed in [Reference KalethaKal19b, §§4.1,4.2] for every supercuspidal parameter
![]() $\phi $
provided G splits over a tame extension of F and p does not divide the order of the Weyl group of G (this assumption on p implies that any supercuspidal parameter maps wild inertia into a torus of
$\phi $
provided G splits over a tame extension of F and p does not divide the order of the Weyl group of G (this assumption on p implies that any supercuspidal parameter maps wild inertia into a torus of
![]() $\widehat G$
; under weaker assumptions on p, this is not automatically true, but for parameters
$\widehat G$
; under weaker assumptions on p, this is not automatically true, but for parameters
![]() $\phi $
that do have this property, the construction of [Reference KalethaKal19b] works under weaker assumptions on p). A bijection between
$\phi $
that do have this property, the construction of [Reference KalethaKal19b] works under weaker assumptions on p). A bijection between
![]() $\Pi _{\phi }$
and
$\Pi _{\phi }$
and
![]() $\mathrm {Irr}(\pi _0(S_{\phi }^+))$
has been constructed in [Reference KalethaKal19b, §§4.3-4.5] for any supercuspidal parameter
$\mathrm {Irr}(\pi _0(S_{\phi }^+))$
has been constructed in [Reference KalethaKal19b, §§4.3-4.5] for any supercuspidal parameter
![]() $\phi $
. Assuming F has characteristic zero and
$\phi $
. Assuming F has characteristic zero and
![]() $p \geq (e+2)n$
, the existence and uniqueness of a generic constituent in
$p \geq (e+2)n$
, the existence and uniqueness of a generic constituent in
![]() $\Pi _{\phi }(G)$
, as well as the character identities of ordinary endoscopy, are proved in [Reference Fintzen, Kaletha and SpiceFKS19, §4.4] for all regular supercuspidal parameters
$\Pi _{\phi }(G)$
, as well as the character identities of ordinary endoscopy, are proved in [Reference Fintzen, Kaletha and SpiceFKS19, §4.4] for all regular supercuspidal parameters
![]() $\phi $
. They are also proved for nonregular supercuspidal parameters
$\phi $
. They are also proved for nonregular supercuspidal parameters
![]() $\phi $
but only for certain endoscopic elements.
$\phi $
but only for certain endoscopic elements.
Returning to the subject of this paper, let
![]() $S_{\phi }=\mathrm {Cent}(\phi ,\widehat {G})$
. For any
$S_{\phi }=\mathrm {Cent}(\phi ,\widehat {G})$
. For any
![]() $\pi \in \Pi _{\phi }(G)$
and
$\pi \in \Pi _{\phi }(G)$
and
![]() $\rho \in \Pi _{\phi }(G_b)$
, the refined form of the local Langlands conjecture implies the existence of an algebraic representation
$\rho \in \Pi _{\phi }(G_b)$
, the refined form of the local Langlands conjecture implies the existence of an algebraic representation
![]() $\delta _{\pi ,\rho }$
of
$\delta _{\pi ,\rho }$
of
![]() $S_{\phi }$
, which can be thought of as measuring the relative position of
$S_{\phi }$
, which can be thought of as measuring the relative position of
![]() $\pi $
and
$\pi $
and
![]() $\rho $
. (The representation
$\rho $
. (The representation
![]() $\delta _{\pi ,\rho }$
also depends on b, but we suppress this from the notation.) The conjugacy class of
$\delta _{\pi ,\rho }$
also depends on b, but we suppress this from the notation.) The conjugacy class of
![]() $\mu $
determines by duality a conjugacy class of weights of
$\mu $
determines by duality a conjugacy class of weights of
![]() $\widehat G$
; we denote by
$\widehat G$
; we denote by
![]() $r_{\mu }$
the irreducible representation of
$r_{\mu }$
the irreducible representation of
![]() $\widehat G$
of highest weight
$\widehat G$
of highest weight
![]() $\mu $
. There is a natural extension of
$\mu $
. There is a natural extension of
![]() $r_{\mu }$
to
$r_{\mu }$
to
![]() $^LG_E$
, the L-group of the base change of G to E [Reference KottwitzKot84a, Lemma 2.1.2]. Write
$^LG_E$
, the L-group of the base change of G to E [Reference KottwitzKot84a, Lemma 2.1.2]. Write
![]() $r_{\mu } \circ \phi _E$
for the representation of
$r_{\mu } \circ \phi _E$
for the representation of
![]() $S_{\phi } \times W_E$
, given by
$S_{\phi } \times W_E$
, given by
Conjecture 1.0.1. Let
![]() $\phi : W_F \to {^LG}$
be a supercuspidal Langlands parameter. Given
$\phi : W_F \to {^LG}$
be a supercuspidal Langlands parameter. Given
![]() $\rho \in \Pi _{\phi }(G_b)$
, we have the following equality in
$\rho \in \Pi _{\phi }(G_b)$
, we have the following equality in
![]() $\operatorname {\mathrm {Groth}}(G(F)\times W_E)$
:
$\operatorname {\mathrm {Groth}}(G(F)\times W_E)$
:
 $$ \begin{align} \operatorname{\mathrm{Mant}}_{b,\mu}(\rho) = \sum_{\pi \in \Pi_{\phi}(G)} \pi \boxtimes \mathrm{Hom}_{S_{\phi}}(\delta_{\pi,\rho},r_{\mu} \circ \phi_E). \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Mant}}_{b,\mu}(\rho) = \sum_{\pi \in \Pi_{\phi}(G)} \pi \boxtimes \mathrm{Hom}_{S_{\phi}}(\delta_{\pi,\rho},r_{\mu} \circ \phi_E). \end{align} $$
This conjecture is more general than the formulation of Kottwitz’s conjecture in [Reference RapoportRap95] and [Reference Rapoport and ViehmannRV14], in that two conditions are removed. The first is that we are allowing the cocharacter
![]() $\mu $
to be nonminuscule—this is what requires passage from the local Shimura varieties
$\mu $
to be nonminuscule—this is what requires passage from the local Shimura varieties
![]() $\mathcal {M}_{G,b,\mu }$
to the local shtuka spaces
$\mathcal {M}_{G,b,\mu }$
to the local shtuka spaces
![]() $\operatorname {\mathrm {Sht}}_{G,b,\mu }$
. The second is that we do not require G to be a B-inner form of its quasi-split inner form
$\operatorname {\mathrm {Sht}}_{G,b,\mu }$
. The second is that we do not require G to be a B-inner form of its quasi-split inner form
![]() $G^*$
. This condition, reviewed in §2.2, has the effect of making the definition of
$G^*$
. This condition, reviewed in §2.2, has the effect of making the definition of
![]() $\delta _{\pi ,\rho }$
straightforward. To remove it, we use the formulation of the refined local Langlands correspondence [Reference KalethaKal16a, Conjecture G] based on the cohomology sets
$\delta _{\pi ,\rho }$
straightforward. To remove it, we use the formulation of the refined local Langlands correspondence [Reference KalethaKal16a, Conjecture G] based on the cohomology sets
![]() $H^1(u \to W,Z \to G)$
of [Reference KalethaKal16b]. The definition of
$H^1(u \to W,Z \to G)$
of [Reference KalethaKal16b]. The definition of
![]() $\delta _{\pi ,\rho }$
in this setting is a bit more involved and is given in §2.3; see Definition 2.3.2.
$\delta _{\pi ,\rho }$
in this setting is a bit more involved and is given in §2.3; see Definition 2.3.2.
We now present our main theorem.
Theorem 1.0.2. Assume the refined local Langlands correspondence [Reference KalethaKal16a, Conjecture G]. Let
![]() $\phi \colon W_F \times \mathrm {SL}_2 \to {^LG}$
be a discrete Langlands parameter with coefficients in
$\phi \colon W_F \times \mathrm {SL}_2 \to {^LG}$
be a discrete Langlands parameter with coefficients in
![]() $\overline {\mathbf {Q}}_{\ell }$
, and let
$\overline {\mathbf {Q}}_{\ell }$
, and let
![]() $\rho \in \Pi _{\phi }(G_b)$
be a member of its L-packet. After ignoring the action of
$\rho \in \Pi _{\phi }(G_b)$
be a member of its L-packet. After ignoring the action of
![]() $W_E$
, we have an equality in
$W_E$
, we have an equality in
![]() $\operatorname {\mathrm {Groth}}(G(F))$
:
$\operatorname {\mathrm {Groth}}(G(F))$
:
 $$\begin{align*}\operatorname{\mathrm{Mant}}_{b,\mu}(\rho)=\sum_{\pi\in\Pi_{\phi}(G)} \left[\dim \operatorname{\mathrm{Hom}}_{S_{\phi}}(\delta_{\pi,\rho},r_{\mu})\right]\pi + \mathrm{err}, \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Mant}}_{b,\mu}(\rho)=\sum_{\pi\in\Pi_{\phi}(G)} \left[\dim \operatorname{\mathrm{Hom}}_{S_{\phi}}(\delta_{\pi,\rho},r_{\mu})\right]\pi + \mathrm{err}, \end{align*}$$
where
![]() $\mathrm {err} \in \operatorname {\mathrm {Groth}}(G(F))$
is a virtual representation whose character vanishes on the locus of elliptic elements of
$\mathrm {err} \in \operatorname {\mathrm {Groth}}(G(F))$
is a virtual representation whose character vanishes on the locus of elliptic elements of
![]() $G(F)$
.
$G(F)$
.
If the packet
![]() $\Pi _{\phi }(G)$
consists entirely of supercuspidal representations and the semisimple L-parameter
$\Pi _{\phi }(G)$
consists entirely of supercuspidal representations and the semisimple L-parameter
![]() $\varphi _{\rho }$
associated with
$\varphi _{\rho }$
associated with
![]() $\rho $
as in [Reference Fargues and ScholzeFS21, §I.9.6] is supercuspidal, then in fact
$\rho $
as in [Reference Fargues and ScholzeFS21, §I.9.6] is supercuspidal, then in fact
![]() $\mathrm {err}=0$
.
$\mathrm {err}=0$
.
Of course we expect that
![]() $\varphi _{\rho }=\phi ^{\mathrm {ss}}$
so that, if
$\varphi _{\rho }=\phi ^{\mathrm {ss}}$
so that, if
![]() $\phi $
is supercuspidal, the error term should vanish. In that case, we obtain Conjecture 1.0.1 modulo ignoring the action of
$\phi $
is supercuspidal, the error term should vanish. In that case, we obtain Conjecture 1.0.1 modulo ignoring the action of
![]() $W_E$
. For a discrete but nonsupercuspidal parameter
$W_E$
. For a discrete but nonsupercuspidal parameter
![]() $\phi $
, the error term in Theorem 1.0.2 is often provably nonzero; cf. [Reference ImaiIma] for some examples. However, for applications to the local Langlands correspondence, it is crucial to have Theorem 1.0.2 in this extra generality.
$\phi $
, the error term in Theorem 1.0.2 is often provably nonzero; cf. [Reference ImaiIma] for some examples. However, for applications to the local Langlands correspondence, it is crucial to have Theorem 1.0.2 in this extra generality.
The shtukas appearing in our work have only one ‘leg’. Scholze defines moduli spaces of mixed-characteristic shtukas
![]() $\operatorname {\mathrm {Sht}}_{G,b,\left \{ \mu _i \right \}}$
with arbitrarily many legs, fibered over a product
$\operatorname {\mathrm {Sht}}_{G,b,\left \{ \mu _i \right \}}$
with arbitrarily many legs, fibered over a product
![]() $\prod _{i=1}^r \operatorname {\mathrm {Spd}} \breve {E}_i$
. It is straightforward to extend Conjecture 1.0.1 and Theorem 1.0.2 to this setting as well. In fact, Theorem 1.0.2 in this extended level of generality follows immediately from the results already proved in this paper, by allowing the legs to coalesce and using the fact that cohomology of shtuka spaces forms a local system over
$\prod _{i=1}^r \operatorname {\mathrm {Spd}} \breve {E}_i$
. It is straightforward to extend Conjecture 1.0.1 and Theorem 1.0.2 to this setting as well. In fact, Theorem 1.0.2 in this extended level of generality follows immediately from the results already proved in this paper, by allowing the legs to coalesce and using the fact that cohomology of shtuka spaces forms a local system over
![]() $(\mathrm {Div}^1)^I$
. We leave the details to the interested reader.
$(\mathrm {Div}^1)^I$
. We leave the details to the interested reader.
Theorem 1.0.2 has an application to the local Langlands correspondence.
Theorem 1.0.3. Let G be any inner form of
![]() $\mathrm {GL}_n/F$
, and let
$\mathrm {GL}_n/F$
, and let
![]() $\pi $
be an irreducible smooth representation of
$\pi $
be an irreducible smooth representation of
![]() $G(F)$
. Then the L-parameter
$G(F)$
. Then the L-parameter
![]() $\varphi _{\pi }$
associated with
$\varphi _{\pi }$
associated with
![]() $\pi $
by the construction of Fargues–Scholze [Reference Fargues and ScholzeFS21, §I.9] agrees with the usual semisimplified L-parameter attached to
$\pi $
by the construction of Fargues–Scholze [Reference Fargues and ScholzeFS21, §I.9] agrees with the usual semisimplified L-parameter attached to
![]() $\pi $
.
$\pi $
.
1.1 Remarks on the proof and relation with prior work
Ultimately, Theorem 1.0.2 is proved by an application of a Lefschetz–Verdier trace formula. Let us illustrate the idea in the Lubin–Tate case: Say
![]() $F=\mathbf {Q}_p$
,
$F=\mathbf {Q}_p$
,
![]() $G=\operatorname {\mathrm {GL}}_n$
,
$G=\operatorname {\mathrm {GL}}_n$
,
![]() $\mu =(1,0,\dots ,0)$
, and b is basic of slope
$\mu =(1,0,\dots ,0)$
, and b is basic of slope
![]() $1/n$
. Let
$1/n$
. Let
![]() $H_0$
be the p-divisible group over
$H_0$
be the p-divisible group over
![]() $\overline {\mathbf {F}}_p$
with isocrystal b so that
$\overline {\mathbf {F}}_p$
with isocrystal b so that
![]() $H_0$
has dimension
$H_0$
has dimension
![]() $1$
and height n. In this case,
$1$
and height n. In this case,
![]() $G_b(F)=\operatorname {\mathrm {Aut}}^0 H_0=D^{\times }$
, where
$G_b(F)=\operatorname {\mathrm {Aut}}^0 H_0=D^{\times }$
, where
![]() $D/\mathbf {Q}_p$
is the division algebra of invariant
$D/\mathbf {Q}_p$
is the division algebra of invariant
![]() $1/n$
. The spaces
$1/n$
. The spaces
![]() $\mathcal {M}_K=\mathcal {M}_{G,b,\mu ,K}$
are known as the Lubin–Tate tower; we consider these as rigid-analytic spaces over C, where
$\mathcal {M}_K=\mathcal {M}_{G,b,\mu ,K}$
are known as the Lubin–Tate tower; we consider these as rigid-analytic spaces over C, where
![]() $C/\mathbf {Q}_p$
is a complete algebraically closed field.
$C/\mathbf {Q}_p$
is a complete algebraically closed field.
Atop the tower sits the infinite-level Lubin–Tate space
![]() $\mathcal {M}=\varprojlim _K\mathcal {M}_K$
as described in [Reference Scholze and WeinsteinSW13]. This is a perfectoid space admitting an action of
$\mathcal {M}=\varprojlim _K\mathcal {M}_K$
as described in [Reference Scholze and WeinsteinSW13]. This is a perfectoid space admitting an action of
![]() $G(\mathbf {Q}_p)\times G_b(\mathbf {Q}_p)$
. The C-points of
$G(\mathbf {Q}_p)\times G_b(\mathbf {Q}_p)$
. The C-points of
![]() $\mathcal {M}$
classify equivalence classes of triples
$\mathcal {M}$
classify equivalence classes of triples
![]() $(H,\alpha ,\iota )$
, where
$(H,\alpha ,\iota )$
, where
![]() $H/\mathcal {O}_{C}$
is a p-divisible group,
$H/\mathcal {O}_{C}$
is a p-divisible group,
![]() $\alpha \colon \mathbf {Q}_p^n\to VH$
is a trivialization of the rational Tate module and
$\alpha \colon \mathbf {Q}_p^n\to VH$
is a trivialization of the rational Tate module and
![]() $\iota \colon H_0\otimes _{\overline {\mathbf {F}}_p} \mathcal {O}_C/p\to H\otimes _{\mathcal {O}_{C}} \mathcal {O}_C/p$
is an isomorphism in the isogeny category. (Equivalence between two such triples is a quasi-isogeny between p-divisible groups which makes both diagrams commute.) Then
$\iota \colon H_0\otimes _{\overline {\mathbf {F}}_p} \mathcal {O}_C/p\to H\otimes _{\mathcal {O}_{C}} \mathcal {O}_C/p$
is an isomorphism in the isogeny category. (Equivalence between two such triples is a quasi-isogeny between p-divisible groups which makes both diagrams commute.) Then
![]() $\mathcal {M}$
admits an action of
$\mathcal {M}$
admits an action of
![]() $G(\mathbf {Q}_p)\times G_b(\mathbf {Q}_p)$
via composition with
$G(\mathbf {Q}_p)\times G_b(\mathbf {Q}_p)$
via composition with
![]() $\alpha $
and
$\alpha $
and
![]() $\iota $
, respectively.
$\iota $
, respectively.
The Hodge–Tate period map exhibits
![]() $\mathcal {M}$
as a pro-étale
$\mathcal {M}$
as a pro-étale
![]() $D^{\times }$
-torsor over Drinfeld’s upper half-space
$D^{\times }$
-torsor over Drinfeld’s upper half-space
![]() $\Omega ^{n-1}$
(the complement in
$\Omega ^{n-1}$
(the complement in
![]() $\mathbf {P}^{n-1}$
of all
$\mathbf {P}^{n-1}$
of all
![]() $\mathbf {Q}_p$
-rational hyperplanes). This map
$\mathbf {Q}_p$
-rational hyperplanes). This map
![]() $\mathcal {M}\to \Omega ^{n-1}$
is equivariant for the action of
$\mathcal {M}\to \Omega ^{n-1}$
is equivariant for the action of
![]() $G(\mathbf {Q}_p)$
.
$G(\mathbf {Q}_p)$
.
Now suppose
![]() $g\in G(\mathbf {Q}_p)$
is a regular elliptic element (that is, an element with irreducible characteristic polynomial). Then g has exactly n fixed points on
$g\in G(\mathbf {Q}_p)$
is a regular elliptic element (that is, an element with irreducible characteristic polynomial). Then g has exactly n fixed points on
![]() $\Omega ^{n-1}$
. For each such fixed point
$\Omega ^{n-1}$
. For each such fixed point
![]() $x\in (\Omega ^{n-1})^g$
, the element g acts on the fiber
$x\in (\Omega ^{n-1})^g$
, the element g acts on the fiber
![]() $\mathcal {M}_x$
. Because
$\mathcal {M}_x$
. Because
![]() $\mathcal {M}\to \Omega ^{n-1}$
is a
$\mathcal {M}\to \Omega ^{n-1}$
is a
![]() $G_b(F)$
-torsor, there must exist
$G_b(F)$
-torsor, there must exist
![]() $g'\in G_b(\mathbf {Q}_p)$
such that
$g'\in G_b(\mathbf {Q}_p)$
such that
![]() $(g,g')$
fixes a point in the fiber
$(g,g')$
fixes a point in the fiber
![]() $\mathcal {M}_x$
.
$\mathcal {M}_x$
.
Key observation. The elements
![]() $g\in G(\mathbf {Q}_p)$
and
$g\in G(\mathbf {Q}_p)$
and
![]() $g'\in G_b(\mathbf {Q}_p)$
are related, meaning they become conjugate over
$g'\in G_b(\mathbf {Q}_p)$
are related, meaning they become conjugate over
![]() $\overline {\mathbf {Q}}_p$
.
$\overline {\mathbf {Q}}_p$
.
We sketch the proof of this claim. Suppose y corresponds to the triple
![]() $(H,\alpha ,\iota )$
. This means there exists an automorphism
$(H,\alpha ,\iota )$
. This means there exists an automorphism
![]() $\gamma $
of H (in the isogeny category) which corresponds to g on the Tate module and
$\gamma $
of H (in the isogeny category) which corresponds to g on the Tate module and
![]() $g'$
on the special fiber, respectively. We verify now that g and
$g'$
on the special fiber, respectively. We verify now that g and
![]() $g'$
are related. Let
$g'$
are related. Let
![]() $B_{\operatorname {\mathrm {cris}}}=B_{\operatorname {\mathrm {cris}}}(C)$
be the crystalline period ring. There are isomorphisms
$B_{\operatorname {\mathrm {cris}}}=B_{\operatorname {\mathrm {cris}}}(C)$
be the crystalline period ring. There are isomorphisms
where the first map is induced from
![]() $\alpha $
, and the second map comes from the comparison isomorphism between étale and crystalline cohomology of H (using
$\alpha $
, and the second map comes from the comparison isomorphism between étale and crystalline cohomology of H (using
![]() $\iota $
to identify the latter with
$\iota $
to identify the latter with
![]() $M(H_0)$
). The composite map carries the action of g onto that of
$M(H_0)$
). The composite map carries the action of g onto that of
![]() $g'$
, which is to say that g and
$g'$
, which is to say that g and
![]() $g'$
become conjugate over
$g'$
become conjugate over
![]() $B_{\operatorname {\mathrm {cris}}}$
. This implies that g and
$B_{\operatorname {\mathrm {cris}}}$
. This implies that g and
![]() $g'$
are related.
$g'$
are related.
Suppose that
![]() $\rho $
is an admissible representation of
$\rho $
is an admissible representation of
![]() $D^{\times }$
with coefficients in
$D^{\times }$
with coefficients in
![]() $\overline {\mathbf {Q}}_{\ell }$
. There is a corresponding
$\overline {\mathbf {Q}}_{\ell }$
. There is a corresponding
![]() $\overline {\mathbf {Q}}_{\ell }$
-local system
$\overline {\mathbf {Q}}_{\ell }$
-local system
![]() $\mathcal {L}_{\rho }$
on
$\mathcal {L}_{\rho }$
on
![]() $\Omega ^{n-1}_{C,\mathrm {\acute {e}t}}$
.
$\Omega ^{n-1}_{C,\mathrm {\acute {e}t}}$
.
Let
![]() $g\in G(F)$
be elliptic. A naïve form of the Lefschetz trace formula would predict that:
$g\in G(F)$
be elliptic. A naïve form of the Lefschetz trace formula would predict that:
 $$\begin{align*}\operatorname{\mathrm{tr}}\left(g\vert R\Gamma_c(\Omega^{n-1},\mathcal{L}_{\rho})\right) = \sum_{x\in (\Omega^{n-1})^g} \operatorname{\mathrm{tr}}(g\vert \mathcal{L}_{\rho,x}). \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{tr}}\left(g\vert R\Gamma_c(\Omega^{n-1},\mathcal{L}_{\rho})\right) = \sum_{x\in (\Omega^{n-1})^g} \operatorname{\mathrm{tr}}(g\vert \mathcal{L}_{\rho,x}). \end{align*}$$
For each fixed point x, the key observation above gives
![]() $\operatorname {\mathrm {tr}}(g\vert \mathcal {L}_{\rho ,x})=\operatorname {\mathrm {tr}} \rho (g')$
, where g and
$\operatorname {\mathrm {tr}}(g\vert \mathcal {L}_{\rho ,x})=\operatorname {\mathrm {tr}} \rho (g')$
, where g and
![]() $g'$
are related. By the Jacquet–Langlands correspondence, there exists a discrete series representation
$g'$
are related. By the Jacquet–Langlands correspondence, there exists a discrete series representation
![]() $\pi $
of
$\pi $
of
![]() $G(\mathbf {Q}_p)$
satisfying
$G(\mathbf {Q}_p)$
satisfying
![]() $\operatorname {\mathrm {tr}} \pi (g)=(-1)^{n-1}\operatorname {\mathrm {tr}} \rho (g')$
(here
$\operatorname {\mathrm {tr}} \pi (g)=(-1)^{n-1}\operatorname {\mathrm {tr}} \rho (g')$
(here
![]() $\operatorname {\mathrm {tr}} \pi (g)$
is interpreted as a Harish–Chandra character). Thus, the Euler characteristic of
$\operatorname {\mathrm {tr}} \pi (g)$
is interpreted as a Harish–Chandra character). Thus, the Euler characteristic of
![]() $R\Gamma _c(\Omega ^{n-1},\mathcal {L}_{\rho })$
equals
$R\Gamma _c(\Omega ^{n-1},\mathcal {L}_{\rho })$
equals
![]() $(-1)^{n-1}n\pi $
up to a virtual representation with trace zero on the elliptic locus.
$(-1)^{n-1}n\pi $
up to a virtual representation with trace zero on the elliptic locus.
In this situation,
![]() $\mathcal {S}_{\mu } = \mathbf {Z}_{\ell }[n-1]$
(up to a Tate twist), and we find that
$\mathcal {S}_{\mu } = \mathbf {Z}_{\ell }[n-1]$
(up to a Tate twist), and we find that
![]() $R\Gamma (G,b,\mu )[\rho ]$
is the shift by
$R\Gamma (G,b,\mu )[\rho ]$
is the shift by
![]() $n-1$
of the dual of
$n-1$
of the dual of
![]() $R\Gamma _c(\Omega ^{n-1},\mathcal {L}_{\rho ^{\vee }})$
. Therefore, in
$R\Gamma _c(\Omega ^{n-1},\mathcal {L}_{\rho ^{\vee }})$
. Therefore, in
![]() $\operatorname {\mathrm {Groth}}(\operatorname {\mathrm {GL}}_n(\mathbf {Q}_p))$
, we have
$\operatorname {\mathrm {Groth}}(\operatorname {\mathrm {GL}}_n(\mathbf {Q}_p))$
, we have
where the character of err vanishes on the locus of elliptic elements. This is in accord with Theorem 1.0.2.
This argument goes back at least to the 1990s, as discussed in [Reference HarrisHar15, Chap. 9] and as far as we know first appears in [Reference FaltingsFal94]. The present article is our attempt to push this argument as far as it will go. If a suitable Lefschetz formula is valid, then the equality in Theorem 1.0.2 can be reduced to an endoscopic character identity relating representations of
![]() $G(F)$
and
$G(F)$
and
![]() $G_b(F)$
(Theorem 3.2.9), which we prove in §3.
$G_b(F)$
(Theorem 3.2.9), which we prove in §3.
Therefore, the difficulty in Theorem 1.0.2 lies in proving the validity of the Lefschetz formula. Prior work of Strauch and Mieda proved Theorem 1.0.2 in the case of the Lubin–Tate tower [Reference StrauchStr05], [Reference StrauchStr08], [Reference MiedaMie12], [Reference MiedaMie14a] and also in the case of a basic Rapoport–Zink space for GSp(4) [Reference MiedaMie].
In applying a Lefschetz formula to a nonproper rigid space, care must be taken to treat the boundary. For instance, if X is the affinoid unit disc
![]() $\left \{ \left \lvert T \right \rvert \leq 1 \right \}$
in the adic space
$\left \{ \left \lvert T \right \rvert \leq 1 \right \}$
in the adic space
![]() $\mathbf {A}^1$
, then the automorphism
$\mathbf {A}^1$
, then the automorphism
![]() $T\mapsto T+1$
has Euler characteristic 1 on X, despite having no fixed points. The culprit is that this automorphism fixes the single boundary point in
$T\mapsto T+1$
has Euler characteristic 1 on X, despite having no fixed points. The culprit is that this automorphism fixes the single boundary point in
![]() $\overline {X}\backslash X$
. Mieda [Reference MiedaMie14b] proves a Lefschetz formula for an operator on a rigid space under an assumption that the operator has no topological fixed points on a compactification. Now, in all of the above cases,
$\overline {X}\backslash X$
. Mieda [Reference MiedaMie14b] proves a Lefschetz formula for an operator on a rigid space under an assumption that the operator has no topological fixed points on a compactification. Now, in all of the above cases,
![]() $\mathcal {M}_{G,b,\mu ,K}$
admits a cellular decomposition. This means (approximately) that
$\mathcal {M}_{G,b,\mu ,K}$
admits a cellular decomposition. This means (approximately) that
![]() $\mathcal {M}_{G,b,\mu ,K}$
contains a compact open subset, whose translates by Hecke operators cover all of
$\mathcal {M}_{G,b,\mu ,K}$
contains a compact open subset, whose translates by Hecke operators cover all of
![]() $\mathcal {M}_{G,b,\mu ,K}$
. This is enough to establish the ‘topological fixed point’ hypothesis necessary to apply Mieda’s Lefschetz formula. Shen [Reference ShenShe14] constructs a cellular decomposition for a basic Rapoport–Zink space attached to the group
$\mathcal {M}_{G,b,\mu ,K}$
. This is enough to establish the ‘topological fixed point’ hypothesis necessary to apply Mieda’s Lefschetz formula. Shen [Reference ShenShe14] constructs a cellular decomposition for a basic Rapoport–Zink space attached to the group
![]() $U(1,n-1)$
, which paves the way for a similar proof of Theorem 1.0.2 in this case as well. For general
$U(1,n-1)$
, which paves the way for a similar proof of Theorem 1.0.2 in this case as well. For general
![]() $(G,b,\mu )$
, however, the
$(G,b,\mu )$
, however, the
![]() $\mathcal {M}_{G,b,\mu ,K}$
do not admit a cellular decomposition, and so there is probably no hope of applying the methods of [Reference MiedaMie14b].
$\mathcal {M}_{G,b,\mu ,K}$
do not admit a cellular decomposition, and so there is probably no hope of applying the methods of [Reference MiedaMie14b].
We had no idea how to proceed until we learned of the shift of perspective offered by Fargues’ program on the geometrization of local Langlands [Reference FarguesFar], followed by the work [Reference Fargues and ScholzeFS21]. At the center of that program is the stack
![]() $\operatorname {\mathrm {Bun}}_G$
of G-bundles on the Fargues–Fontaine curve. This is a geometrization of the Kottwitz set
$\operatorname {\mathrm {Bun}}_G$
of G-bundles on the Fargues–Fontaine curve. This is a geometrization of the Kottwitz set
![]() $B(G)$
: There is a bijection
$B(G)$
: There is a bijection
![]() $b\mapsto \mathcal {E}^b$
between
$b\mapsto \mathcal {E}^b$
between
![]() $B(G)$
and points of the underlying topological space of
$B(G)$
and points of the underlying topological space of
![]() $\operatorname {\mathrm {Bun}}_G$
. For basic b, there is an open substack
$\operatorname {\mathrm {Bun}}_G$
. For basic b, there is an open substack
![]() $\operatorname {\mathrm {Bun}}_G^b\subset \operatorname {\mathrm {Bun}}_G$
classifing G-bundles which are everywhere isomorphic to
$\operatorname {\mathrm {Bun}}_G^b\subset \operatorname {\mathrm {Bun}}_G$
classifing G-bundles which are everywhere isomorphic to
![]() $\mathcal {E}^b$
; in this situation,
$\mathcal {E}^b$
; in this situation,
![]() $\operatorname {\mathrm {Aut}} \mathcal {E}^b=G_b(F)$
, and so we have an isomorphism
$\operatorname {\mathrm {Aut}} \mathcal {E}^b=G_b(F)$
, and so we have an isomorphism
![]() $\operatorname {\mathrm {Bun}}_G^b\cong [\ast /G_b(F)]$
.
$\operatorname {\mathrm {Bun}}_G^b\cong [\ast /G_b(F)]$
.
Let
![]() $\mu $
be a cocharacter of G. As in geometric Langlands, there is a stack
$\mu $
be a cocharacter of G. As in geometric Langlands, there is a stack
![]() $\operatorname {\mathrm {Hecke}}_{G,\leq \mu }$
lying over the product
$\operatorname {\mathrm {Hecke}}_{G,\leq \mu }$
lying over the product
![]() $\operatorname {\mathrm {Bun}}_G\times \operatorname {\mathrm {Bun}}_G$
, which parametrizes
$\operatorname {\mathrm {Bun}}_G\times \operatorname {\mathrm {Bun}}_G$
, which parametrizes
![]() $\mu $
-bounded modifications of G-bundles at one point of the curve. For each
$\mu $
-bounded modifications of G-bundles at one point of the curve. For each
![]() $\mu $
, one uses
$\mu $
, one uses
![]() $\operatorname {\mathrm {Hecke}}_{G,\leq \mu }$
to define a Hecke operator
$\operatorname {\mathrm {Hecke}}_{G,\leq \mu }$
to define a Hecke operator
![]() $T_{\mu }$
on a suitable derived category
$T_{\mu }$
on a suitable derived category
![]() $D(\operatorname {\mathrm {Bun}}_G,\mathbf {Z}_{\ell })$
of étale
$D(\operatorname {\mathrm {Bun}}_G,\mathbf {Z}_{\ell })$
of étale
![]() $\mathbf {Z}_{\ell }$
-sheaves on
$\mathbf {Z}_{\ell }$
-sheaves on
![]() $\operatorname {\mathrm {Bun}}_G$
. If
$\operatorname {\mathrm {Bun}}_G$
. If
![]() $b\in B(G,\mu )$
, then the moduli space of local shtukas
$b\in B(G,\mu )$
, then the moduli space of local shtukas
![]() $\operatorname {\mathrm {Sht}}_{G,b,\mu }$
appears as the fiber of
$\operatorname {\mathrm {Sht}}_{G,b,\mu }$
appears as the fiber of
![]() $\operatorname {\mathrm {Hecke}}_{G,\leq \mu }$
over the point
$\operatorname {\mathrm {Hecke}}_{G,\leq \mu }$
over the point
![]() $(\mathcal {E}^b,\mathcal {E}^1)$
of
$(\mathcal {E}^b,\mathcal {E}^1)$
of
![]() $\operatorname {\mathrm {Bun}}_G\times \operatorname {\mathrm {Bun}}_G$
. Consequently, there is an expression for
$\operatorname {\mathrm {Bun}}_G\times \operatorname {\mathrm {Bun}}_G$
. Consequently, there is an expression for
![]() $R\Gamma (G,b,\mu )[\rho ]$
in terms of the Hecke operators
$R\Gamma (G,b,\mu )[\rho ]$
in terms of the Hecke operators
![]() $T_{\mu }$
; see Proposition 6.4.5.
$T_{\mu }$
; see Proposition 6.4.5.
Heavy use is made in [Reference Fargues and ScholzeFS21] of the notion of universal local acyclity (ULA) as a property of objects
![]() $A\in D(X,\mathbf {Z}_{\ell })$
for Artin v-stacks X. When
$A\in D(X,\mathbf {Z}_{\ell })$
for Artin v-stacks X. When
![]() $X=[*/G_b(F)]$
, a ULA object is an admissible complex of representations of
$X=[*/G_b(F)]$
, a ULA object is an admissible complex of representations of
![]() $G_b(F)$
. It is proved in [Reference Fargues and ScholzeFS21] that the Hecke operators
$G_b(F)$
. It is proved in [Reference Fargues and ScholzeFS21] that the Hecke operators
![]() $T_{\mu }$
preserve ULA objects; the admissibility of
$T_{\mu }$
preserve ULA objects; the admissibility of
![]() $R\Gamma (G,b,\mu )[\rho ]$
is deduced from this.
$R\Gamma (G,b,\mu )[\rho ]$
is deduced from this.
We learned from [Reference Lu and ZhengLZ22] that the ULA condition is precisely the right hypothesis necessary to prove a Lefschetz–Verdier trace formula applicable to the cohomology of A. This explains the counterexample above:
![]() $j_!\mathbf {Z}_{\ell }$
fails to be ULA, where j is the inclusion of the affinoid disc X into its compactification
$j_!\mathbf {Z}_{\ell }$
fails to be ULA, where j is the inclusion of the affinoid disc X into its compactification
![]() $\overline {X}$
. In fact, [Reference Lu and ZhengLZ22] is written in the context of schemes, but their formalism applies equally well in the context of rigid-analytic spaces and diamonds. Indeed, some interesting new phenomena occur in the diamond context. For instance, if H is a locally profinite group acting continuously on a proper diamond X and
$\overline {X}$
. In fact, [Reference Lu and ZhengLZ22] is written in the context of schemes, but their formalism applies equally well in the context of rigid-analytic spaces and diamonds. Indeed, some interesting new phenomena occur in the diamond context. For instance, if H is a locally profinite group acting continuously on a proper diamond X and
![]() $A\in D(X,\mathbf {Z}_{\ell })$
is a ULA object which is H-equivariant, then
$A\in D(X,\mathbf {Z}_{\ell })$
is a ULA object which is H-equivariant, then
![]() $R\Gamma (X,A)$
is an admissible H-module. One gets a formula for the trace distribution of H acting on
$R\Gamma (X,A)$
is an admissible H-module. One gets a formula for the trace distribution of H acting on
![]() $R\Gamma (X,A)$
in terms of local terms living on the fixed-point locus in
$R\Gamma (X,A)$
in terms of local terms living on the fixed-point locus in
![]() $H\times X$
. We explain the Lefschetz–Verdier trace formula for diamonds in §4.
$H\times X$
. We explain the Lefschetz–Verdier trace formula for diamonds in §4.
In §5, we study the Lefschetz–Verdier trace formula as it pertains to the mixed-characteristic affine Grassmannian
![]() $\operatorname {\mathrm {Gr}}_{G,\leq \mu }$
. The object
$\operatorname {\mathrm {Gr}}_{G,\leq \mu }$
. The object
![]() $\mathcal {S}_{\mu }$
is ULA on
$\mathcal {S}_{\mu }$
is ULA on
![]() $\operatorname {\mathrm {Gr}}_{G,\leq \mu }$
and
$\operatorname {\mathrm {Gr}}_{G,\leq \mu }$
and
![]() $G(F)$
-equivariant, so it makes sense to ask for its local term
$G(F)$
-equivariant, so it makes sense to ask for its local term
![]() $\operatorname {\mathrm {loc}}_g(x,A)$
at a fixed point x of a regular element
$\operatorname {\mathrm {loc}}_g(x,A)$
at a fixed point x of a regular element
![]() $g\in G(F)$
. (Such fixed points are all isolated.) We found quickly that that result we needed for Theorem 1.0.2 would follow if we knew that
$g\in G(F)$
. (Such fixed points are all isolated.) We found quickly that that result we needed for Theorem 1.0.2 would follow if we knew that
![]() $\operatorname {\mathrm {loc}}_g(x,A)$
agreed with the naïve local term
$\operatorname {\mathrm {loc}}_g(x,A)$
agreed with the naïve local term
![]() $\operatorname {\mathrm {tr}}(g\vert A_x)$
. We asked Varshavsky, who devised a method for proving this agreement in the scheme setting. We show how to deduce the required statement for
$\operatorname {\mathrm {tr}}(g\vert A_x)$
. We asked Varshavsky, who devised a method for proving this agreement in the scheme setting. We show how to deduce the required statement for
![]() $\operatorname {\mathrm {Gr}}_{G,\leq \mu }$
, using the Witt vector affine Grassmannian as a bridge between diamonds and schemes. (We thank the referee for pointing out that an earlier argument we had here was incorrect.)
$\operatorname {\mathrm {Gr}}_{G,\leq \mu }$
, using the Witt vector affine Grassmannian as a bridge between diamonds and schemes. (We thank the referee for pointing out that an earlier argument we had here was incorrect.)
Finally, in §6, we prove Theorem 1.0.2 by applying our trace formula to the Hecke stack
![]() $\operatorname {\mathrm {Hecke}}_{G,b,\leq \mu }$
. An important step is to show that fixed points of elliptic elements
$\operatorname {\mathrm {Hecke}}_{G,b,\leq \mu }$
. An important step is to show that fixed points of elliptic elements
![]() $g\in G(F)$
acting on
$g\in G(F)$
acting on
![]() $\operatorname {\mathrm {Gr}}_{G,\leq \mu }$
are admissible, as we observed above in the Lubin–Tate case.
$\operatorname {\mathrm {Gr}}_{G,\leq \mu }$
are admissible, as we observed above in the Lubin–Tate case.
2 Review of the objects appearing in Kottwitz’s conjecture
2.1 Basic notions
Let
![]() $\breve {F}$
be the completion of the maximal unramified extension of F, and let
$\breve {F}$
be the completion of the maximal unramified extension of F, and let
![]() $\sigma \in \operatorname {\mathrm {Aut}} \breve {F}$
be the Frobenius automorphism. Let G be a connected reductive group defined over F. Fix a quasi-split group
$\sigma \in \operatorname {\mathrm {Aut}} \breve {F}$
be the Frobenius automorphism. Let G be a connected reductive group defined over F. Fix a quasi-split group
![]() $G^*$
and a
$G^*$
and a
![]() $G^*(\overline {F})$
-conjugacy class
$G^*(\overline {F})$
-conjugacy class
![]() $\Psi $
of inner twists
$\Psi $
of inner twists
![]() $G^*\to G$
; thus, elements
$G^*\to G$
; thus, elements
![]() $\psi \in \Psi $
are isomorphisms
$\psi \in \Psi $
are isomorphisms
![]() $G^*_{\overline {F}} \to G_{\overline {F}}$
such that for each
$G^*_{\overline {F}} \to G_{\overline {F}}$
such that for each
![]() $\tau \in \Gamma $
the automorphism
$\tau \in \Gamma $
the automorphism
![]() $\psi ^{-1}\circ \tau (\psi )$
of
$\psi ^{-1}\circ \tau (\psi )$
of
![]() $G^*_{\overline {F}}$
is inner. Given an element
$G^*_{\overline {F}}$
is inner. Given an element
![]() $b\in G(\breve {F})$
, there is an associated inner form
$b\in G(\breve {F})$
, there is an associated inner form
![]() $G_b$
of a Levi subgroup of
$G_b$
of a Levi subgroup of
![]() $G^*$
as described in [Reference KottwitzKot97, §3.3,§3.4]. Its group of F-points is given by
$G^*$
as described in [Reference KottwitzKot97, §3.3,§3.4]. Its group of F-points is given by
Up to isomorphism, the group
![]() $G_b$
depends only on the
$G_b$
depends only on the
![]() $\sigma $
-conjugacy class
$\sigma $
-conjugacy class
![]() $[b]$
. It will be convenient to choose b to be decent [Reference Rapoport and ZinkRZ96, Definition 1.8]. Then there exists a finite unramified extension
$[b]$
. It will be convenient to choose b to be decent [Reference Rapoport and ZinkRZ96, Definition 1.8]. Then there exists a finite unramified extension
![]() $F'/F$
such that
$F'/F$
such that
![]() $b \in G(F')$
. This allows us to replace
$b \in G(F')$
. This allows us to replace
![]() $\breve F$
by
$\breve F$
by
![]() $F'$
in the above formula. The slope morphism
$F'$
in the above formula. The slope morphism
![]() $\nu : \mathbf {D} \to G_{\breve F}$
of b [Reference KottwitzKot85, §4] is also defined over
$\nu : \mathbf {D} \to G_{\breve F}$
of b [Reference KottwitzKot85, §4] is also defined over
![]() $F'$
. The centralizer
$F'$
. The centralizer
![]() $G_{F',\nu }$
of
$G_{F',\nu }$
of
![]() $\nu $
in
$\nu $
in
![]() $G_{F'}$
is a Levi subgroup of
$G_{F'}$
is a Levi subgroup of
![]() $G_{F'}$
. The
$G_{F'}$
. The
![]() $G(F')$
-conjugacy class of
$G(F')$
-conjugacy class of
![]() $\nu $
is defined over F and then so is the
$\nu $
is defined over F and then so is the
![]() $G(F')$
-conjugacy class of
$G(F')$
-conjugacy class of
![]() $G_{F',\nu }$
. There is a Levi subgroup
$G_{F',\nu }$
. There is a Levi subgroup
![]() $M^*$
of
$M^*$
of
![]() $G^*$
defined over F and
$G^*$
defined over F and
![]() $\psi \in \Psi $
that restricts to an inner twist
$\psi \in \Psi $
that restricts to an inner twist
![]() $\psi : M^* \to G_b$
; see [Reference KottwitzKot97, §4.3].
$\psi : M^* \to G_b$
; see [Reference KottwitzKot97, §4.3].
From now on, assume that b is basic. This is equivalent to
![]() $M^*=G^*$
so that
$M^*=G^*$
so that
![]() $G_b$
is in fact an inner form of
$G_b$
is in fact an inner form of
![]() $G^*$
and of G. Furthermore,
$G^*$
and of G. Furthermore,
![]() $\Psi $
is an equivalence class of inner twists
$\Psi $
is an equivalence class of inner twists
![]() $G^* \to G$
as well as
$G^* \to G$
as well as
![]() $G^* \to G_b$
. This identifies the dual groups of
$G^* \to G_b$
. This identifies the dual groups of
![]() $G^*$
, G and
$G^*$
, G and
![]() $G_b$
, and we write
$G_b$
, and we write
![]() $\widehat G$
for either of them.
$\widehat G$
for either of them.
Let
![]() $\phi : W_F \times \mathrm {SL}_2(\mathbf {C}) \to {^LG}$
be a discrete Langlands parameter, and let
$\phi : W_F \times \mathrm {SL}_2(\mathbf {C}) \to {^LG}$
be a discrete Langlands parameter, and let
![]() $S_{\phi }=\mathrm {Cent}(\phi ,\widehat G)$
. For
$S_{\phi }=\mathrm {Cent}(\phi ,\widehat G)$
. For
![]() $\lambda \in X^*(Z(\widehat {G})^{\Gamma })$
, write
$\lambda \in X^*(Z(\widehat {G})^{\Gamma })$
, write
![]() $\mathrm {Rep}(S_{\phi },\lambda )$
for the set of isomorphism classes of algebraic representations of the algebraic group
$\mathrm {Rep}(S_{\phi },\lambda )$
for the set of isomorphism classes of algebraic representations of the algebraic group
![]() $S_{\phi }$
whose restriction to
$S_{\phi }$
whose restriction to
![]() $Z(\widehat {G})^{\Gamma }$
is
$Z(\widehat {G})^{\Gamma }$
is
![]() $\lambda $
-isotypic, and write
$\lambda $
-isotypic, and write
![]() $\mathrm {Irr}(S_{\phi },\lambda )$
for the subset of irreducible such representations. The class of b corresponds to a character
$\mathrm {Irr}(S_{\phi },\lambda )$
for the subset of irreducible such representations. The class of b corresponds to a character
![]() $\lambda _b : Z(\widehat G)^{\Gamma } \to \mathbf {C}^{\times }$
via the isomorphism
$\lambda _b : Z(\widehat G)^{\Gamma } \to \mathbf {C}^{\times }$
via the isomorphism
![]() $B(G)_{\mathrm {bas}} \to X^*(Z(\widehat G)^{\Gamma })$
of [Reference KottwitzKot85, Proposition 5.6]. Assuming the validity of the refined local Langlands conjecture [Reference KalethaKal16a, Conjecture G], we will construct in the following two subsections for any
$B(G)_{\mathrm {bas}} \to X^*(Z(\widehat G)^{\Gamma })$
of [Reference KottwitzKot85, Proposition 5.6]. Assuming the validity of the refined local Langlands conjecture [Reference KalethaKal16a, Conjecture G], we will construct in the following two subsections for any
![]() $\pi \in \Pi _{\phi }(G)$
and
$\pi \in \Pi _{\phi }(G)$
and
![]() $\rho \in \Pi _{\phi }(G_b)$
an element
$\rho \in \Pi _{\phi }(G_b)$
an element
![]() $\delta _{\pi ,\rho } \in \mathrm {Rep}(S_{\phi },\lambda _b)$
that measures the relative position of
$\delta _{\pi ,\rho } \in \mathrm {Rep}(S_{\phi },\lambda _b)$
that measures the relative position of
![]() $\pi $
and
$\pi $
and
![]() $\rho $
.
$\rho $
.
2.2 Construction of
 $\delta _{\pi ,\rho }$
in a special case
$\delta _{\pi ,\rho }$
in a special case
The statements of the Kottwitz conjecture given in [Reference RapoportRap95, Conjecture 5.1] and [Reference Rapoport and ViehmannRV14, Conjecture 7.3] make the assumption that G is a B-inner form of
![]() $G^*$
. In that case, the construction of
$G^*$
. In that case, the construction of
![]() $\delta _{\pi ,\rho }$
is straightforward, and we shall now recall it.
$\delta _{\pi ,\rho }$
is straightforward, and we shall now recall it.
The assumption on G means that some
![]() $\psi \in \Psi $
can be equipped with a decent basic
$\psi \in \Psi $
can be equipped with a decent basic
![]() $b^* \in G^*(F^{\mathrm {nr}})$
such that
$b^* \in G^*(F^{\mathrm {nr}})$
such that
![]() $\psi $
is an isomorphism
$\psi $
is an isomorphism
![]() $G^*_{F^{\mathrm {nr}}} \to G_{F^{\mathrm {nr}}}$
satisfying
$G^*_{F^{\mathrm {nr}}} \to G_{F^{\mathrm {nr}}}$
satisfying
![]() $\psi ^{-1}\sigma (\psi )=\mathrm {Ad}(b^*)$
. In other words,
$\psi ^{-1}\sigma (\psi )=\mathrm {Ad}(b^*)$
. In other words,
![]() $\psi $
becomes an isomorphism over F from the group
$\psi $
becomes an isomorphism over F from the group
![]() $G^*_{b^*}$
to G. Under this assumption and after choosing a Whittaker datum
$G^*_{b^*}$
to G. Under this assumption and after choosing a Whittaker datum
![]() $\mathfrak {w}$
for
$\mathfrak {w}$
for
![]() $G^*$
, the isocrystal formulation of the refined local Langlands correspondence [Reference KalethaKal16a, Conjecture F], which is implied by the rigid formulation [Reference KalethaKal16a, Conjecture G] according to [Reference KalethaKal18], predicts the existence of bijections
$G^*$
, the isocrystal formulation of the refined local Langlands correspondence [Reference KalethaKal16a, Conjecture F], which is implied by the rigid formulation [Reference KalethaKal16a, Conjecture G] according to [Reference KalethaKal18], predicts the existence of bijections
 $$ \begin{align*} \Pi_{\phi}(G) &\cong \operatorname{\mathrm{Irr}}(S_{\phi},\lambda_{b*})\\ \Pi_{\phi}(G_b) &\cong \operatorname{\mathrm{Irr}}(S_{\phi},\lambda_{b^*}+\lambda_b), \end{align*} $$
$$ \begin{align*} \Pi_{\phi}(G) &\cong \operatorname{\mathrm{Irr}}(S_{\phi},\lambda_{b*})\\ \Pi_{\phi}(G_b) &\cong \operatorname{\mathrm{Irr}}(S_{\phi},\lambda_{b^*}+\lambda_b), \end{align*} $$
where we have used the isomorphisms
![]() $B(G)_{\operatorname {\mathrm {bas}}}\cong X^*(Z(\widehat {G})^{\Gamma }) \cong B(G^*)_{\mathrm {bas}}$
of [Reference KottwitzKot85, Proposition 5.6] to obtain from
$B(G)_{\operatorname {\mathrm {bas}}}\cong X^*(Z(\widehat {G})^{\Gamma }) \cong B(G^*)_{\mathrm {bas}}$
of [Reference KottwitzKot85, Proposition 5.6] to obtain from
![]() $[b] \in B(G)_{\mathrm {bas}}$
and
$[b] \in B(G)_{\mathrm {bas}}$
and
![]() $[b^*] \in B(G^*)_{\mathrm {bas}}$
characters
$[b^*] \in B(G^*)_{\mathrm {bas}}$
characters
![]() $\lambda _{b}$
and
$\lambda _{b}$
and
![]() $\lambda _{b^*}$
of
$\lambda _{b^*}$
of
![]() $Z(\widehat G)^{\Gamma }$
.
$Z(\widehat G)^{\Gamma }$
.
These bijections are uniquely characterized by the endoscopic character identities which are part of [Reference KalethaKal16a, Conjecture F]. Write
![]() $\pi \mapsto \tau _{b^*,\mathfrak {w},\pi }$
,
$\pi \mapsto \tau _{b^*,\mathfrak {w},\pi }$
,
![]() $\rho \mapsto \tau _{b^*,\mathfrak {w},\rho }$
for these bijections, and define
$\rho \mapsto \tau _{b^*,\mathfrak {w},\rho }$
for these bijections, and define
While these bijections depend on the choice of Whittaker datum
![]() $\mathfrak {w}$
and the choice of
$\mathfrak {w}$
and the choice of
![]() $b^*$
, we will argue in Subsection 2.3 that for any pair
$b^*$
, we will argue in Subsection 2.3 that for any pair
![]() $\pi $
and
$\pi $
and
![]() $\rho $
the representation
$\rho $
the representation
![]() $\delta _{\pi ,\rho }$
is independent of these choices. Of course, it does depend on b, but this we take as part of the given data.
$\delta _{\pi ,\rho }$
is independent of these choices. Of course, it does depend on b, but this we take as part of the given data.
2.3 Construction of
 $\delta _{\pi ,\rho }$
in the general case
$\delta _{\pi ,\rho }$
in the general case
We now drop the assumption that G is a B-inner form of
![]() $G^*$
. Because of this, we no longer have the isocrystal formulation of the refined local Langlands correspondence. However, we do have the formulation based on rigid inner twists [Reference KalethaKal16a, Conjecture G]. What this means with regards to the Kottwitz conjecture is that neither
$G^*$
. Because of this, we no longer have the isocrystal formulation of the refined local Langlands correspondence. However, we do have the formulation based on rigid inner twists [Reference KalethaKal16a, Conjecture G]. What this means with regards to the Kottwitz conjecture is that neither
![]() $\pi $
nor
$\pi $
nor
![]() $\rho $
correspond to representations of
$\rho $
correspond to representations of
![]() $S_{\phi }$
. Rather, they correspond to representations
$S_{\phi }$
. Rather, they correspond to representations
![]() $\tau _{\pi }$
and
$\tau _{\pi }$
and
![]() $\tau _{\rho }$
of a different group
$\tau _{\rho }$
of a different group
![]() $\pi _0(S_{\phi }^+)$
. Nonetheless, it will turn out that
$\pi _0(S_{\phi }^+)$
. Nonetheless, it will turn out that
![]() $\check \tau _{\pi } \otimes \tau _{\rho }$
provides in a natural way a representation
$\check \tau _{\pi } \otimes \tau _{\rho }$
provides in a natural way a representation
![]() $\delta _{\pi ,\rho }$
of
$\delta _{\pi ,\rho }$
of
![]() $S_{\phi }$
.
$S_{\phi }$
.
In order to make this precise, we will need the material of [Reference KalethaKal16b] and [Reference KalethaKal18], some of which is summarized in [Reference KalethaKal16a]. First, we will need the cohomology set
![]() $H^1(u \to W,Z \to G^*)$
defined in [Reference KalethaKal16b, §3] for any finite central subgroup
$H^1(u \to W,Z \to G^*)$
defined in [Reference KalethaKal16b, §3] for any finite central subgroup
![]() $Z \subset G^*$
defined over F. As in [Reference KalethaKal18, §3.2], it will be convenient to package these sets for varying Z into the single set
$Z \subset G^*$
defined over F. As in [Reference KalethaKal18, §3.2], it will be convenient to package these sets for varying Z into the single set
The transition maps on the right are injective, so the colimit can be seen as an increasing union.
Next, we will need the reinterpretation, given in [Reference KottwitzKot], of
![]() $B(G)$
as the set of cohomology classes of algebraic 1-cocycles of a certain Galois gerbe
$B(G)$
as the set of cohomology classes of algebraic 1-cocycles of a certain Galois gerbe
![]() $1 \to \mathbf {D}(\bar F) \to \mathcal {E} \to \Gamma \to 1$
. This reinterpretation is also reviewed in [Reference KalethaKal18, §3.1]. For this, we recall that inflation along
$1 \to \mathbf {D}(\bar F) \to \mathcal {E} \to \Gamma \to 1$
. This reinterpretation is also reviewed in [Reference KalethaKal18, §3.1]. For this, we recall that inflation along
![]() $W_F \to \mathbf {Z}$
induces an isomorphism between
$W_F \to \mathbf {Z}$
induces an isomorphism between
![]() $B(G)=H^1(\langle \sigma \rangle ,G(L))$
and
$B(G)=H^1(\langle \sigma \rangle ,G(L))$
and
![]() $H^1(W_F,G(\bar L))$
, where we have written
$H^1(W_F,G(\bar L))$
, where we have written
![]() $L=\breve F$
to ease typesetting. In [Reference KottwitzKot97, App B], Kottwitz constructs a continuous homomorphism
$L=\breve F$
to ease typesetting. In [Reference KottwitzKot97, App B], Kottwitz constructs a continuous homomorphism
![]() $W_F \to \mathcal {E}$
whose composition with the natural projection
$W_F \to \mathcal {E}$
whose composition with the natural projection
![]() $\mathcal {E} \to \Gamma $
is the natural map
$\mathcal {E} \to \Gamma $
is the natural map
![]() $W_F \to \Gamma $
. He proves in [Reference KottwitzKot97, §8 and App B] that pulling back along this homomorphism and pushing along the inclusion
$W_F \to \Gamma $
. He proves in [Reference KottwitzKot97, §8 and App B] that pulling back along this homomorphism and pushing along the inclusion
![]() $G(\bar F) \to G(\bar L)$
gives an isomorphism
$G(\bar F) \to G(\bar L)$
gives an isomorphism
![]() $H^1_{\mathrm {alg}}(\mathcal {E},G(\bar F)) \to B(G)$
and, in particular,
$H^1_{\mathrm {alg}}(\mathcal {E},G(\bar F)) \to B(G)$
and, in particular,
![]() $H^1_{\mathrm {bas}}(\mathcal {E},G(\bar F)) \to B_{\mathrm {bas}}(G)$
. While the section
$H^1_{\mathrm {bas}}(\mathcal {E},G(\bar F)) \to B_{\mathrm {bas}}(G)$
. While the section
![]() $W_F \to \mathcal {E}$
is not completely canonical, the induced isomorphism on cohomology is independent of the choice of section. Strictly speaking, Kottwitz gives the proof only in the case of tori, but the general case is immediate from that.
$W_F \to \mathcal {E}$
is not completely canonical, the induced isomorphism on cohomology is independent of the choice of section. Strictly speaking, Kottwitz gives the proof only in the case of tori, but the general case is immediate from that.
Finally, we will need the comparison map
of [Reference KalethaKal18, §3.3].
After this short review, we turn to the construction of
![]() $\delta _{\pi ,\rho } \in \operatorname {\mathrm {Rep}}(S_{\phi },\lambda _b)$
. For this, it is not enough to work with the cohomology class of b, because
$\delta _{\pi ,\rho } \in \operatorname {\mathrm {Rep}}(S_{\phi },\lambda _b)$
. For this, it is not enough to work with the cohomology class of b, because
![]() $\delta _{\pi ,\rho }$
is an invariant of the equivalence class of the triple
$\delta _{\pi ,\rho }$
is an invariant of the equivalence class of the triple
![]() $(b,\pi ,\rho )$
, and changing b within its cohomology class must be accompanied with a corresponding change in
$(b,\pi ,\rho )$
, and changing b within its cohomology class must be accompanied with a corresponding change in
![]() $\rho $
. Therefore, we must work with cocycles.
$\rho $
. Therefore, we must work with cocycles.
To that end, fix the section
![]() $W_F \to \mathcal {E}$
. If
$W_F \to \mathcal {E}$
. If
![]() $z_b \in Z^1_{\mathrm {bas}}(\mathcal {E},G(\bar F))$
denotes a representative of the element of
$z_b \in Z^1_{\mathrm {bas}}(\mathcal {E},G(\bar F))$
denotes a representative of the element of
![]() $H^1_{\mathrm {bas}}(\mathcal {E},G(\bar F))$
corresponding to the class of b, there exists
$H^1_{\mathrm {bas}}(\mathcal {E},G(\bar F))$
corresponding to the class of b, there exists
![]() $g \in G(\bar L)$
, unique up to right multiplication by elements of
$g \in G(\bar L)$
, unique up to right multiplication by elements of
![]() $G_b(F)$
such that
$G_b(F)$
such that
where
![]() $|w|$
is the image of w under
$|w|$
is the image of w under
![]() $W_F \to \mathbf {Z}$
. Note that the image of g in
$W_F \to \mathbf {Z}$
. Note that the image of g in
![]() $G_{\mathrm {ad}}(\bar L)$
lies in
$G_{\mathrm {ad}}(\bar L)$
lies in
![]() $G_{\mathrm {ad}}(\bar F)$
and that
$G_{\mathrm {ad}}(\bar F)$
and that
![]() $\mathrm {Ad}(g)$
induces an F-isomorphism
$\mathrm {Ad}(g)$
induces an F-isomorphism
![]() $G_{z_b} \to G_b$
. Therefore,
$G_{z_b} \to G_b$
. Therefore,
![]() $\rho \circ \mathrm {Ad}(g)$
is an irreducible representation of
$\rho \circ \mathrm {Ad}(g)$
is an irreducible representation of
![]() $G_{z_b}(F)$
whose isomorphism class does not depend on the choice of g.
$G_{z_b}(F)$
whose isomorphism class does not depend on the choice of g.
Choose any inner twist
![]() $\psi \in \Psi $
and let
$\psi \in \Psi $
and let
![]() $\bar z_{\sigma } := \psi ^{-1}\sigma (\psi ) \in G^*_{\mathrm {ad}}(\overline {F})$
. Then
$\bar z_{\sigma } := \psi ^{-1}\sigma (\psi ) \in G^*_{\mathrm {ad}}(\overline {F})$
. Then
![]() $\bar z \in Z^1(F,G^*_{\mathrm {ad}})$
and the surjectivity of the natural map
$\bar z \in Z^1(F,G^*_{\mathrm {ad}})$
and the surjectivity of the natural map
![]() $H^1(u \to W,Z(G^*) \to G^*) \to H^1(F,G^*_{\mathrm {ad}})$
asserted in [Reference KalethaKal16b, Corollary 3.8] allows us to choose
$H^1(u \to W,Z(G^*) \to G^*) \to H^1(F,G^*_{\mathrm {ad}})$
asserted in [Reference KalethaKal16b, Corollary 3.8] allows us to choose
![]() $z \in Z^1(u \to W,Z(G^*) \to G^*)$
lifting
$z \in Z^1(u \to W,Z(G^*) \to G^*)$
lifting
![]() $\bar z$
. Then
$\bar z$
. Then
![]() $(\psi ,z) : G^* \to G$
is a rigid inner twist, and
$(\psi ,z) : G^* \to G$
is a rigid inner twist, and
![]() $(\psi ,\psi ^{-1}(z)\cdot z_b) : G^* \to G_{z_b}$
is also a rigid inner twist.
$(\psi ,\psi ^{-1}(z)\cdot z_b) : G^* \to G_{z_b}$
is also a rigid inner twist.
The L-packets
![]() $\Pi _{\phi }(G)$
and
$\Pi _{\phi }(G)$
and
![]() $\Pi _{\phi }(G_{z_b})$
are now parameterized by representations of a certain cover
$\Pi _{\phi }(G_{z_b})$
are now parameterized by representations of a certain cover
![]() $S_{\phi }^+$
of
$S_{\phi }^+$
of
![]() $S_{\phi }$
. While [Reference KalethaKal16a, Conjecture G] is formulated in terms of a finite cover depending on an auxiliary choice of a finite central subgroup
$S_{\phi }$
. While [Reference KalethaKal16a, Conjecture G] is formulated in terms of a finite cover depending on an auxiliary choice of a finite central subgroup
![]() $Z \subset G^*$
, we will adopt here the point of view of [Reference KalethaKal18] and work with a canonical infinite cover, namely the preimage of
$Z \subset G^*$
, we will adopt here the point of view of [Reference KalethaKal18] and work with a canonical infinite cover, namely the preimage of
![]() $S_{\phi }$
in the universal cover of
$S_{\phi }$
in the universal cover of
![]() $\widehat G$
. Following [Reference KalethaKal18, §3.3], we can present this universal cover as follows. Let
$\widehat G$
. Following [Reference KalethaKal18, §3.3], we can present this universal cover as follows. Let
![]() $Z_n \subset Z(G)$
be the subgroup of those elements whose image in
$Z_n \subset Z(G)$
be the subgroup of those elements whose image in
![]() $Z(G)/Z(G_{\mathrm {der}})$
is n-torsion, and let
$Z(G)/Z(G_{\mathrm {der}})$
is n-torsion, and let
![]() $G_n=G/Z_n$
. Then
$G_n=G/Z_n$
. Then
![]() $G_n$
has adjoint derived subgroup and connected center. More precisely,
$G_n$
has adjoint derived subgroup and connected center. More precisely,
![]() $G_n=G_{\mathrm {ad}} \times C_n$
, where
$G_n=G_{\mathrm {ad}} \times C_n$
, where
![]() $C_n=C_1/C_1[n]$
and
$C_n=C_1/C_1[n]$
and
![]() $C_1=Z(G)/Z(G_{\mathrm {der}})$
. It is convenient to identify
$C_1=Z(G)/Z(G_{\mathrm {der}})$
. It is convenient to identify
![]() $C_n=C_1$
as algebraic tori and take the
$C_n=C_1$
as algebraic tori and take the
![]() $m/n$
-power map
$m/n$
-power map
![]() $C_1 \to C_1$
as the transition map
$C_1 \to C_1$
as the transition map
![]() $C_n \to C_m$
for
$C_n \to C_m$
for
![]() $n|m$
. The isogeny
$n|m$
. The isogeny
![]() $G \to G_n$
dualizes to
$G \to G_n$
dualizes to
![]() $\widehat G_n \to \widehat G$
, and we have
$\widehat G_n \to \widehat G$
, and we have
![]() $\widehat G_n = \widehat G_{\mathrm {sc}} \times \widehat C_1$
. Note that
$\widehat G_n = \widehat G_{\mathrm {sc}} \times \widehat C_1$
. Note that
![]() $\widehat C_1=Z(\widehat G)^{\circ }$
. The transition map
$\widehat C_1=Z(\widehat G)^{\circ }$
. The transition map
![]() $\widehat G_m \to \widehat G_n$
is then the identity on
$\widehat G_m \to \widehat G_n$
is then the identity on
![]() $\widehat G_{\mathrm {sc}}$
, and the
$\widehat G_{\mathrm {sc}}$
, and the
![]() $m/n$
-power map on
$m/n$
-power map on
![]() $\widehat C_1$
. Set
$\widehat C_1$
. Set
![]() $\widehat {\bar G} = \varprojlim \widehat G_n = \widehat G_{\mathrm {sc}} \times \widehat C_{\infty }$
, where
$\widehat {\bar G} = \varprojlim \widehat G_n = \widehat G_{\mathrm {sc}} \times \widehat C_{\infty }$
, where
![]() $\widehat C_{\infty } = \varprojlim \widehat C_n$
. Then
$\widehat C_{\infty } = \varprojlim \widehat C_n$
. Then
![]() $\widehat {\bar G}$
is the universal cover of
$\widehat {\bar G}$
is the universal cover of
![]() $\widehat G$
. Elements of
$\widehat G$
. Elements of
![]() $\widehat {\bar G}$
can be written as
$\widehat {\bar G}$
can be written as
![]() $(a,(b_n)_n)$
, where
$(a,(b_n)_n)$
, where
![]() $a \in \widehat G_{\mathrm {sc}}$
and
$a \in \widehat G_{\mathrm {sc}}$
and
![]() $(b_n)_n$
is a sequence of elements
$(b_n)_n$
is a sequence of elements
![]() $b_n \in \widehat C_1$
satisfying
$b_n \in \widehat C_1$
satisfying
![]() $b_n=(b_m)^{\frac {m}{n}}$
for
$b_n=(b_m)^{\frac {m}{n}}$
for
![]() $n|m$
. In this presentation, the natural map
$n|m$
. In this presentation, the natural map
![]() $\widehat {\bar G} \to \widehat G$
sends
$\widehat {\bar G} \to \widehat G$
sends
![]() $(a,(b_n))$
to
$(a,(b_n))$
to
![]() $a_{\mathrm {der}} \cdot b_1$
, where
$a_{\mathrm {der}} \cdot b_1$
, where
![]() $a_{\mathrm {der}} \in \widehat G_{\mathrm {der}}$
is the image of
$a_{\mathrm {der}} \in \widehat G_{\mathrm {der}}$
is the image of
![]() $a \in \widehat G_{\mathrm {sc}}$
under the natural map
$a \in \widehat G_{\mathrm {sc}}$
under the natural map
![]() $\widehat G_{\mathrm {sc}} \to \widehat G_{\mathrm {der}}$
.
$\widehat G_{\mathrm {sc}} \to \widehat G_{\mathrm {der}}$
.
Definition 2.3.1. Let
![]() $Z(\widehat {\bar G})^+ \subset S_{\phi }^+ \subset \widehat {\bar G}$
be the preimages of
$Z(\widehat {\bar G})^+ \subset S_{\phi }^+ \subset \widehat {\bar G}$
be the preimages of
![]() $Z(\widehat G)^{\Gamma } \subset S_{\phi } \subset \widehat G$
under
$Z(\widehat G)^{\Gamma } \subset S_{\phi } \subset \widehat G$
under
![]() $\widehat {\bar G}\to \widehat G$
.
$\widehat {\bar G}\to \widehat G$
.
Given a character
![]() $\lambda : \pi _0(Z(\widehat {\bar G})^+) \to \mathbf {C}^{\times }$
(which we will always assume trivial on the kernel of
$\lambda : \pi _0(Z(\widehat {\bar G})^+) \to \mathbf {C}^{\times }$
(which we will always assume trivial on the kernel of
![]() $Z(\widehat {\bar G})^+ \to \widehat G_n$
for some n), let
$Z(\widehat {\bar G})^+ \to \widehat G_n$
for some n), let
![]() $\operatorname {\mathrm {Rep}}(\pi _0(S_{\phi }^+),\lambda )$
denote the set of isomorphism classes of representations of
$\operatorname {\mathrm {Rep}}(\pi _0(S_{\phi }^+),\lambda )$
denote the set of isomorphism classes of representations of
![]() $\pi _0(S_{\phi }^+)$
whose pullback to
$\pi _0(S_{\phi }^+)$
whose pullback to
![]() $\pi _0(Z(\widehat {\bar G})^+)$
is
$\pi _0(Z(\widehat {\bar G})^+)$
is
![]() $\lambda $
-isotypic, and let
$\lambda $
-isotypic, and let
![]() $\operatorname {\mathrm {Irr}}(\pi _0(S_{\phi }^+),\lambda )$
be the (finite) subset of irreducible representations. Let
$\operatorname {\mathrm {Irr}}(\pi _0(S_{\phi }^+),\lambda )$
be the (finite) subset of irreducible representations. Let
![]() $\lambda _z$
be the character corresponding to the class of z under the Tate–Nakayama isomorphism
$\lambda _z$
be the character corresponding to the class of z under the Tate–Nakayama isomorphism
of [Reference KalethaKal16b, Corollary 5.4], and let
![]() $\lambda _{z_b}$
be the character corresponding to the class of
$\lambda _{z_b}$
be the character corresponding to the class of
![]() $z_b$
in
$z_b$
in
![]() $H^1(u \to W,Z(G) \to G)$
. Then according to [Reference KalethaKal16a, Conjecture G], upon fixing a Whittaker datum
$H^1(u \to W,Z(G) \to G)$
. Then according to [Reference KalethaKal16a, Conjecture G], upon fixing a Whittaker datum
![]() $\mathfrak {w}$
for
$\mathfrak {w}$
for
![]() $G^*$
, there are bijections
$G^*$
, there are bijections
 $$ \begin{align*} \Pi_{\phi}(G) &\cong \operatorname{\mathrm{Irr}}(\pi_0(S_{\phi}^+),\lambda_{z})\\ \Pi_{\phi}(G_{z_b}) &\cong \operatorname{\mathrm{Irr}}(\pi_0(S_{\phi}^+),\lambda_{z}+\lambda_{z_b}) \end{align*} $$
$$ \begin{align*} \Pi_{\phi}(G) &\cong \operatorname{\mathrm{Irr}}(\pi_0(S_{\phi}^+),\lambda_{z})\\ \Pi_{\phi}(G_{z_b}) &\cong \operatorname{\mathrm{Irr}}(\pi_0(S_{\phi}^+),\lambda_{z}+\lambda_{z_b}) \end{align*} $$
again uniquely determined by the endoscopic character identities. We write
![]() $\pi \mapsto \tau _{z,\mathfrak {w},\pi }$
,
$\pi \mapsto \tau _{z,\mathfrak {w},\pi }$
,
![]() $\rho \mapsto \tau _{z,\mathfrak {w},\rho }$
for these bijections and
$\rho \mapsto \tau _{z,\mathfrak {w},\rho }$
for these bijections and
![]() $\tau \mapsto \pi _{z,\mathfrak {w},\tau }$
,
$\tau \mapsto \pi _{z,\mathfrak {w},\tau }$
,
![]() $\tau \mapsto \rho _{z,\mathfrak {w},\tau }$
for their inverses. We form the representation
$\tau \mapsto \rho _{z,\mathfrak {w},\tau }$
for their inverses. We form the representation
![]() $\check \tau _{z,\mathfrak {w},\pi } \otimes \tau _{z,\mathfrak {w},\rho } \in \operatorname {\mathrm {Rep}}(\pi _0(S_{\phi }^+),\lambda _{z_b})$
, where we are identifying
$\check \tau _{z,\mathfrak {w},\pi } \otimes \tau _{z,\mathfrak {w},\rho } \in \operatorname {\mathrm {Rep}}(\pi _0(S_{\phi }^+),\lambda _{z_b})$
, where we are identifying
![]() $\rho $
with the representation
$\rho $
with the representation
![]() $\rho \circ \mathrm {Ad}(g)$
of
$\rho \circ \mathrm {Ad}(g)$
of
![]() $G_{z_b}(F)$
.
$G_{z_b}(F)$
.
Recall the map [Reference KalethaKal18, (4.7)]
Here,
![]() $a_{\mathrm {der}} \in \widehat G_{\mathrm {der}}$
is the image of
$a_{\mathrm {der}} \in \widehat G_{\mathrm {der}}$
is the image of
![]() $a \in \widehat G_{\mathrm {sc}}$
under the natural map
$a \in \widehat G_{\mathrm {sc}}$
under the natural map
![]() $\widehat G_{\mathrm {sc}} \to \widehat G_{\mathrm {der}}$
and
$\widehat G_{\mathrm {sc}} \to \widehat G_{\mathrm {der}}$
and
![]() $E/F$
is a sufficiently large finite Galois extension. This map is independent of the choice of
$E/F$
is a sufficiently large finite Galois extension. This map is independent of the choice of
![]() $E/F$
. According to [Reference KalethaKal18, Lemma 4.1], pulling back along this map defines a natural bijection
$E/F$
. According to [Reference KalethaKal18, Lemma 4.1], pulling back along this map defines a natural bijection
![]() $\operatorname {\mathrm {Irr}}(\pi _0(S_{\phi }^+),\lambda _{z_b}) \cong \operatorname {\mathrm {Irr}}(S_{\phi },\lambda _b)$
. Note that since
$\operatorname {\mathrm {Irr}}(\pi _0(S_{\phi }^+),\lambda _{z_b}) \cong \operatorname {\mathrm {Irr}}(S_{\phi },\lambda _b)$
. Note that since
![]() $\phi $
is discrete the group
$\phi $
is discrete the group
![]() $S_{\phi }^{\natural }$
defined in loc. cit. is equal to
$S_{\phi }^{\natural }$
defined in loc. cit. is equal to
![]() $S_{\phi }$
. The lemma remains valid, with the same proof, if we remove the requirement of the representations being irreducible, and we obtain the bijection
$S_{\phi }$
. The lemma remains valid, with the same proof, if we remove the requirement of the representations being irreducible, and we obtain the bijection
![]() $\operatorname {\mathrm {Rep}}(\pi _0(S_{\phi }^+),\lambda _{z_b}) \to \operatorname {\mathrm {Rep}}(S_{\phi },\lambda _b)$
.
$\operatorname {\mathrm {Rep}}(\pi _0(S_{\phi }^+),\lambda _{z_b}) \to \operatorname {\mathrm {Rep}}(S_{\phi },\lambda _b)$
.
Definition 2.3.2. Let
![]() $\delta _{\pi ,\rho }$
be the image of
$\delta _{\pi ,\rho }$
be the image of
![]() $\check \tau _{z,\mathfrak {w},\pi } \otimes \tau _{z,\mathfrak {w},\rho }$
under the bijection
$\check \tau _{z,\mathfrak {w},\pi } \otimes \tau _{z,\mathfrak {w},\rho }$
under the bijection
![]() $\operatorname {\mathrm {Rep}}(\pi _0(S_{\phi }^+),\lambda _{z_b}) \to \operatorname {\mathrm {Rep}}(S_{\phi },\lambda _b)$
.
$\operatorname {\mathrm {Rep}}(\pi _0(S_{\phi }^+),\lambda _{z_b}) \to \operatorname {\mathrm {Rep}}(S_{\phi },\lambda _b)$
.
In the situation when G is a B-inner form of
![]() $G^*$
, this definition of
$G^*$
, this definition of
![]() $\delta _{\pi ,\rho }$
agrees with the one of Subsection 2.2, because then we can obtain z from
$\delta _{\pi ,\rho }$
agrees with the one of Subsection 2.2, because then we can obtain z from
![]() $b^*$
just like we obtained
$b^*$
just like we obtained
![]() $z_b$
from b, and then
$z_b$
from b, and then
![]() $\tau _{z,\mathfrak {w},\pi }$
and
$\tau _{z,\mathfrak {w},\pi }$
and
![]() $\tau _{b^*,\mathfrak {w},\pi }$
are related via equation (2.3.2) and so are
$\tau _{b^*,\mathfrak {w},\pi }$
are related via equation (2.3.2) and so are
![]() $\tau _{z,\mathfrak {w},\rho }$
and
$\tau _{z,\mathfrak {w},\rho }$
and
![]() $\tau _{b^*,\mathfrak {w},\rho }$
; see [Reference KalethaKal18, §4.2].
$\tau _{b^*,\mathfrak {w},\rho }$
; see [Reference KalethaKal18, §4.2].
Lemma 2.3.3. Assume [Reference KalethaKal16a, Conjecture G]. The representation
![]() $\delta _{\pi ,\rho }$
is independent of the choices of Whittaker datum
$\delta _{\pi ,\rho }$
is independent of the choices of Whittaker datum
![]() $\mathfrak {w}$
and of a rigidifying 1-cocycle
$\mathfrak {w}$
and of a rigidifying 1-cocycle
![]() $z \in Z^1(u \to W,Z(G^*) \to G^*)$
.
$z \in Z^1(u \to W,Z(G^*) \to G^*)$
.
Proof. Both of these statements follow from [Reference KalethaKal16a, Conjecture G]. For the independence of Whittaker datum, one can prove that the validity of this conjecture implies that if
![]() $\mathfrak {w}$
is replaced by another choice
$\mathfrak {w}$
is replaced by another choice
![]() $\mathfrak {w'}$
, then there is an explicitly constructed character
$\mathfrak {w'}$
, then there is an explicitly constructed character
![]() $(\mathfrak {w},\mathfrak {w'})$
of
$(\mathfrak {w},\mathfrak {w'})$
of
![]() $\pi _0(S_{\phi }/Z(\widehat G)^{\Gamma })$
whose inflation to
$\pi _0(S_{\phi }/Z(\widehat G)^{\Gamma })$
whose inflation to
![]() $\pi _0(S_{\phi }^+)$
satisfies
$\pi _0(S_{\phi }^+)$
satisfies
![]() $\tau _{z,\mathfrak {w},\sigma }=\tau _{z,\mathfrak {w'},\sigma } \otimes (\mathfrak {w},\mathfrak {w'})$
for any
$\tau _{z,\mathfrak {w},\sigma }=\tau _{z,\mathfrak {w'},\sigma } \otimes (\mathfrak {w},\mathfrak {w'})$
for any
![]() $\sigma \in \Pi _{\phi }(G) \cup \Pi _{\phi }(G_b)$
. See §4 and in particular Theorem 4.3 of [Reference KalethaKal13], the proof of which is valid for a general G that satisfies [Reference KalethaKal16a, Conjecture G], bearing in mind that the transfer factor we use here is related to the one used there by
$\sigma \in \Pi _{\phi }(G) \cup \Pi _{\phi }(G_b)$
. See §4 and in particular Theorem 4.3 of [Reference KalethaKal13], the proof of which is valid for a general G that satisfies [Reference KalethaKal16a, Conjecture G], bearing in mind that the transfer factor we use here is related to the one used there by
![]() $s \mapsto s^{-1}$
. The independence of z follows from the same type of argument but now using [Reference KalethaKal18, Lemma 6.2].
$s \mapsto s^{-1}$
. The independence of z follows from the same type of argument but now using [Reference KalethaKal18, Lemma 6.2].
2.4 Spaces of local shtukas and their cohomology
We recall here some material from [Reference Scholze and WeinsteinSW20] and [Reference FarguesFar] regarding the Fargues–Fontaine curve and moduli spaces of local shtukas.
Let k be the residue field of F. For a perfectoid space S over k, we have the Fargues–Fontaine curve
![]() $X_S$
[Reference Fargues and FontaineFF18], an adic space over F. For
$X_S$
[Reference Fargues and FontaineFF18], an adic space over F. For
![]() $S=\operatorname {\mathrm {Spa}}(R,R^+)$
affinoid with pseudouniformiser
$S=\operatorname {\mathrm {Spa}}(R,R^+)$
affinoid with pseudouniformiser
![]() $\varpi $
, the adic space
$\varpi $
, the adic space
![]() $X_S$
is defined as follows:
$X_S$
is defined as follows:
 $$ \begin{align*} Y_S &= (\operatorname{\mathrm{Spa}} W_{\mathcal{O}_F}(R^+))\backslash\left\{ p[\varpi]=0 \right\} \\ X_S &= Y_S/\operatorname{\mathrm{Frob}}^{\mathbf{Z}}. \end{align*} $$
$$ \begin{align*} Y_S &= (\operatorname{\mathrm{Spa}} W_{\mathcal{O}_F}(R^+))\backslash\left\{ p[\varpi]=0 \right\} \\ X_S &= Y_S/\operatorname{\mathrm{Frob}}^{\mathbf{Z}}. \end{align*} $$
Here,
![]() $\operatorname {\mathrm {Frob}}$
is the qth power Frobenius on S.
$\operatorname {\mathrm {Frob}}$
is the qth power Frobenius on S.
For an affinoid perfectoid space S lying over the residue field of F, the following sets are in bijection:
-
1. S-points of
 $\operatorname {\mathrm {Spd}} F$
,
$\operatorname {\mathrm {Spd}} F$
, -
2. Untilts
 $S^{\sharp }$
of S over F,
$S^{\sharp }$
of S over F, -
3. Cartier divisors of
 $Y_S$
of degree 1.
$Y_S$
of degree 1.
Given an untilt
![]() $S^{\sharp }$
, we let
$S^{\sharp }$
, we let
![]() $D_{S^{\sharp }}\subset Y_S$
be the corresponding divisor. If
$D_{S^{\sharp }}\subset Y_S$
be the corresponding divisor. If
![]() $S^{\sharp }=\operatorname {\mathrm {Spa}}(R^{\sharp },R^{\sharp +})$
is affinoid, then the completion of
$S^{\sharp }=\operatorname {\mathrm {Spa}}(R^{\sharp },R^{\sharp +})$
is affinoid, then the completion of
![]() $Y_S$
along
$Y_S$
along
![]() $D_{S^{\sharp }}$
is
$D_{S^{\sharp }}$
is
![]() $\operatorname {\mathrm {Spf}} B_{\operatorname {\mathrm {dR}}}^+(R^{\sharp })$
, where
$\operatorname {\mathrm {Spf}} B_{\operatorname {\mathrm {dR}}}^+(R^{\sharp })$
, where
![]() $B_{\operatorname {\mathrm {dR}}}^+(R^{\sharp })$
is the de Rham period ring attached to the perfectoid algebra
$B_{\operatorname {\mathrm {dR}}}^+(R^{\sharp })$
is the de Rham period ring attached to the perfectoid algebra
![]() $R^{\sharp }$
. The untilt
$R^{\sharp }$
. The untilt
![]() $S^{\sharp }$
determines a Cartier divisor on
$S^{\sharp }$
determines a Cartier divisor on
![]() $X_S$
, which we still refer to as
$X_S$
, which we still refer to as
![]() $D_{S^{\sharp }}$
.
$D_{S^{\sharp }}$
.
There is a functor
![]() $b \mapsto \mathcal {E}^b$
from the category of isocrystals with G-structure to the category of G-bundles on
$b \mapsto \mathcal {E}^b$
from the category of isocrystals with G-structure to the category of G-bundles on
![]() $X_S$
(for any S). When S is a geometric point this functor induces a bijection between the sets of isomorphism classes [Reference FarguesFar20].
$X_S$
(for any S). When S is a geometric point this functor induces a bijection between the sets of isomorphism classes [Reference FarguesFar20].
We now recall Scholze’s definition of the local shtuka space. It is a set-valued functor on the pro-étale site of perfectoid spaces over
![]() $\mathbf {F}_p$
and is equipped with a morphism to
$\mathbf {F}_p$
and is equipped with a morphism to
![]() $\operatorname {\mathrm {Spd}} C$
. Thus, it can be described equivalently as a set-valued functor on the pro-étale site of perfectoid spaces over C.
$\operatorname {\mathrm {Spd}} C$
. Thus, it can be described equivalently as a set-valued functor on the pro-étale site of perfectoid spaces over C.
Definition 2.4.1. The local shtuka space
![]() $\operatorname {\mathrm {Sht}}_{G,b,\mu }$
inputs a perfectoid C-algebra
$\operatorname {\mathrm {Sht}}_{G,b,\mu }$
inputs a perfectoid C-algebra
![]() $(R,R^+)$
and outputs the set of isomorphisms
$(R,R^+)$
and outputs the set of isomorphisms
of G-torsors that are meromorphic along
![]() $D_R$
and bounded by
$D_R$
and bounded by
![]() $\mu $
pointwise on
$\mu $
pointwise on
![]() $\operatorname {\mathrm {Spa}} R$
.
$\operatorname {\mathrm {Spa}} R$
.
Let us briefly recall the condition of being pointwise bounded by
![]() $\mu $
. If
$\mu $
. If
![]() $\operatorname {\mathrm {Spa}}(C,O_C) \to \operatorname {\mathrm {Spa}} R$
is a geometric point, we obtain via pullback
$\operatorname {\mathrm {Spa}}(C,O_C) \to \operatorname {\mathrm {Spa}} R$
is a geometric point, we obtain via pullback
![]() $\gamma : \mathcal {E}^1|_{X_{C^{\flat }} \smallsetminus \{x_C\}} \to \mathcal {E}^b|_{X_{C^{\flat }} \smallsetminus \{x_C\}}$
, where we have written
$\gamma : \mathcal {E}^1|_{X_{C^{\flat }} \smallsetminus \{x_C\}} \to \mathcal {E}^b|_{X_{C^{\flat }} \smallsetminus \{x_C\}}$
, where we have written
![]() $x_C$
in place of
$x_C$
in place of
![]() $D_C$
to emphasize that this a point on
$D_C$
to emphasize that this a point on
![]() $X_{C^{\flat }}$
. The completed local ring of
$X_{C^{\flat }}$
. The completed local ring of
![]() $X_{C^{\flat }}$
at
$X_{C^{\flat }}$
at
![]() $x_C$
is Fointaine’s ring
$x_C$
is Fointaine’s ring
![]() $B_{\operatorname {\mathrm {dR}}}^+(C)$
. A trivialization of both bundles
$B_{\operatorname {\mathrm {dR}}}^+(C)$
. A trivialization of both bundles
![]() $\mathcal {E}^1$
and
$\mathcal {E}^1$
and
![]() $\mathcal {E}^b$
on a formal neighborhood of
$\mathcal {E}^b$
on a formal neighborhood of
![]() $x_C$
, together with
$x_C$
, together with
![]() $\gamma $
, leads to an element of
$\gamma $
, leads to an element of
![]() $G(B_{\operatorname {\mathrm {dR}}}(C))$
, well-defined up to left and right multiplication by elements of
$G(B_{\operatorname {\mathrm {dR}}}(C))$
, well-defined up to left and right multiplication by elements of
![]() $G(B_{\operatorname {\mathrm {dR}}}^+(C))$
. The corresponding element of the double coset space
$G(B_{\operatorname {\mathrm {dR}}}^+(C))$
. The corresponding element of the double coset space
![]() $G(B_{\operatorname {\mathrm {dR}}}^+(C)) \setminus G(B_{\operatorname {\mathrm {dR}}}(C)) / G(B_{\operatorname {\mathrm {dR}}}^+(C))$
is indexed by a conjugacy class of cocharacters of
$G(B_{\operatorname {\mathrm {dR}}}^+(C)) \setminus G(B_{\operatorname {\mathrm {dR}}}(C)) / G(B_{\operatorname {\mathrm {dR}}}^+(C))$
is indexed by a conjugacy class of cocharacters of
![]() $G/C$
according to the Cartan decomposition, and we demand that this conjugacy class is dominated by
$G/C$
according to the Cartan decomposition, and we demand that this conjugacy class is dominated by
![]() $\mu $
in the usual order (given by the simple roots of the universal Borel pair).
$\mu $
in the usual order (given by the simple roots of the universal Borel pair).
The space
![]() $\operatorname {\mathrm {Sht}}_{G,b,\mu }$
is a locally spatial diamond [Reference Scholze and WeinsteinSW20, §23]. Since the automorphism groups of
$\operatorname {\mathrm {Sht}}_{G,b,\mu }$
is a locally spatial diamond [Reference Scholze and WeinsteinSW20, §23]. Since the automorphism groups of
![]() $\mathcal {E}^1$
and
$\mathcal {E}^1$
and
![]() $\mathcal {E}^b$
are the constant group diamonds
$\mathcal {E}^b$
are the constant group diamonds
![]() $\underline {G(\mathbf {Q}_p)}$
and
$\underline {G(\mathbf {Q}_p)}$
and
![]() $\underline {G_b(\mathbf {Q}_p)}$
, respectively, the space
$\underline {G_b(\mathbf {Q}_p)}$
, respectively, the space
![]() $\operatorname {\mathrm {Sht}}_{G,b,\mu }$
is equipped with commuting actions of
$\operatorname {\mathrm {Sht}}_{G,b,\mu }$
is equipped with commuting actions of
![]() $G(\mathbf {Q}_p)$
and
$G(\mathbf {Q}_p)$
and
![]() $G_b(\mathbf {Q}_p)$
, acting by pre- and postcomposition on
$G_b(\mathbf {Q}_p)$
, acting by pre- and postcomposition on
![]() $\gamma $
.
$\gamma $
.
Remark 2.4.2. According to [Reference Scholze and WeinsteinSW20, Corollary 23.2.2], the above definition recovers the moduli space of local shtukas with one leg and infinite level structure. We have dropped the subscript
![]() $\infty $
used in [Reference Scholze and WeinsteinSW20] to denote the infinite level structure.
$\infty $
used in [Reference Scholze and WeinsteinSW20] to denote the infinite level structure.
We will use the cohomology theory developed in [Reference ScholzeSch17]. For any compact open subgroup
![]() $K \subset G(F)$
, the quotient
$K \subset G(F)$
, the quotient
![]() $\operatorname {\mathrm {Sht}}_{G,b,\mu ,K}=\operatorname {\mathrm {Sht}}_{G,b,\mu }/K$
is again a locally spatial diamond [Reference Scholze and WeinsteinSW20, §23]. For each
$\operatorname {\mathrm {Sht}}_{G,b,\mu ,K}=\operatorname {\mathrm {Sht}}_{G,b,\mu }/K$
is again a locally spatial diamond [Reference Scholze and WeinsteinSW20, §23]. For each
![]() $n=1,2,\dots $
, let
$n=1,2,\dots $
, let
![]() $V_{\mu ,n}\in \operatorname {\mathrm {Rep}}(\widehat {G},\mathbf {Z}/\ell ^n\mathbf {Z})$
be the Weyl module associated to
$V_{\mu ,n}\in \operatorname {\mathrm {Rep}}(\widehat {G},\mathbf {Z}/\ell ^n\mathbf {Z})$
be the Weyl module associated to
![]() $\mu $
. By the geometric Satake equivalence (Theorem 5.1.1), there is a corresponding object
$\mu $
. By the geometric Satake equivalence (Theorem 5.1.1), there is a corresponding object
![]() $\mathcal {S}_{\mu ,n}$
of
$\mathcal {S}_{\mu ,n}$
of
![]() $D_{\mathrm {\acute {e}t}}(\operatorname {\mathrm {Gr}}_{G,b,\leq \mu },\mathbf {Z}/\ell ^n\mathbf {Z}[\sqrt {q}])$
. Define
$D_{\mathrm {\acute {e}t}}(\operatorname {\mathrm {Gr}}_{G,b,\leq \mu },\mathbf {Z}/\ell ^n\mathbf {Z}[\sqrt {q}])$
. Define
where
![]() $U\subset \operatorname {\mathrm {Sht}}_{G,b,\mu }/K$
runs over quasicompact open subsets and where we have put
$U\subset \operatorname {\mathrm {Sht}}_{G,b,\mu }/K$
runs over quasicompact open subsets and where we have put
Then
![]() $R\Gamma _c(\operatorname {\mathrm {Sht}}_{G,b,\mu }/K,\mathcal {S}_{\mu })$
is a complex of
$R\Gamma _c(\operatorname {\mathrm {Sht}}_{G,b,\mu }/K,\mathcal {S}_{\mu })$
is a complex of
![]() $\mathbf {Z}_{\ell }[\sqrt {q}]$
-modules carrying an action of
$\mathbf {Z}_{\ell }[\sqrt {q}]$
-modules carrying an action of
![]() $G_b(F)\times W_E$
.
$G_b(F)\times W_E$
.
Definition 2.4.3. Let
![]() $\rho $
be a finite-length admissible representation of
$\rho $
be a finite-length admissible representation of
![]() $G_b(F)$
with coefficients in
$G_b(F)$
with coefficients in
![]() $\overline {\mathbf {Q}_{\ell }}$
. Then we define
$\overline {\mathbf {Q}_{\ell }}$
. Then we define
where K runs over the set of open compact subgroups of
![]() $G(F)$
.
$G(F)$
.
By Proposition 6.4.5 below, this defines a finite-length
![]() $W_E$
-equivariant object in the derived category of smooth representations of
$W_E$
-equivariant object in the derived category of smooth representations of
![]() $G(F)$
with coefficients in
$G(F)$
with coefficients in
![]() $\overline {\mathbf {Q}_{\ell }}$
, and we write
$\overline {\mathbf {Q}_{\ell }}$
, and we write
![]() $\operatorname {\mathrm {Mant}}_{b,\mu }(\rho )$
for the image of
$\operatorname {\mathrm {Mant}}_{b,\mu }(\rho )$
for the image of
![]() $R\Gamma (G,b,\mu )[\rho ]$
in
$R\Gamma (G,b,\mu )[\rho ]$
in
![]() $\operatorname {\mathrm {Groth}}(G(F) \times W_E)$
.
$\operatorname {\mathrm {Groth}}(G(F) \times W_E)$
.
Remark 2.4.4. We now discuss the relationship between our definition of
![]() $\operatorname {\mathrm {Mant}}_{b,\mu }(\rho )$
and the virtual representation
$\operatorname {\mathrm {Mant}}_{b,\mu }(\rho )$
and the virtual representation
![]() $H^*(G,b,\mu )[\rho ]$
defined in [Reference Rapoport and ViehmannRV14].
$H^*(G,b,\mu )[\rho ]$
defined in [Reference Rapoport and ViehmannRV14].
When
![]() $\mu $
is minuscule,
$\mu $
is minuscule,
![]() $\operatorname {\mathrm {Sht}}_{G,b,\mu ,K}$
is the diamond
$\operatorname {\mathrm {Sht}}_{G,b,\mu ,K}$
is the diamond
![]() $\mathcal {M}_{G,b, \mu ,K}^{\diamond }$
associated to the local Shimura variety
$\mathcal {M}_{G,b, \mu ,K}^{\diamond }$
associated to the local Shimura variety
![]() $\mathcal {M}_{G,b,\mu ,K}$
[Reference Scholze and WeinsteinSW20, §24.1]. The latter is a rigid-analytic variety of dimension
$\mathcal {M}_{G,b,\mu ,K}$
[Reference Scholze and WeinsteinSW20, §24.1]. The latter is a rigid-analytic variety of dimension
![]() $d=\left < \mu ,2\rho _G \right>$
, where
$d=\left < \mu ,2\rho _G \right>$
, where
![]() $2\rho _G$
is the sum of the positive roots. Moreover, in that case,
$2\rho _G$
is the sum of the positive roots. Moreover, in that case,
![]() $\mathcal {S}_{\mu }=\mathbf {Z}_{\ell }[\sqrt {q}][d](\tfrac {d}{2})$
is a shift and twist of the constant sheaf. In [Reference Rapoport and ViehmannRV14],
$\mathcal {S}_{\mu }=\mathbf {Z}_{\ell }[\sqrt {q}][d](\tfrac {d}{2})$
is a shift and twist of the constant sheaf. In [Reference Rapoport and ViehmannRV14],
![]() $H^*(G,b,\mu )[\rho ]$
is defined as the alternating sum
$H^*(G,b,\mu )[\rho ]$
is defined as the alternating sum
 $$\begin{align*}\sum_{i,j\in\mathbf{Z}} (-1)^{i+j} H^{i,j}(G,b,\mu)[\rho](-d),\end{align*}$$
$$\begin{align*}\sum_{i,j\in\mathbf{Z}} (-1)^{i+j} H^{i,j}(G,b,\mu)[\rho](-d),\end{align*}$$
where
Note that
![]() $H^{i,j}(G,b,\mu )[\rho ]$
vanishes for all but finitely many
$H^{i,j}(G,b,\mu )[\rho ]$
vanishes for all but finitely many
![]() $(i,j)$
, and each
$(i,j)$
, and each
![]() $H^{i,j}(G,b,\mu )[\rho ]$
is an admissible representation of
$H^{i,j}(G,b,\mu )[\rho ]$
is an admissible representation of
![]() $G_b(F)$
by the analysis in [Reference Fargues and ScholzeFS21]. On the other hand, unwinding definitions, we see that there is a spectral sequence
$G_b(F)$
by the analysis in [Reference Fargues and ScholzeFS21]. On the other hand, unwinding definitions, we see that there is a spectral sequence
![]() $H^{i,j-d}(G,b,\mu )[\rho ](-\tfrac {d}{2}) \implies H^{i+j}\left ( R\Gamma (G,b,\mu )[\rho ] \right )$
.
$H^{i,j-d}(G,b,\mu )[\rho ](-\tfrac {d}{2}) \implies H^{i+j}\left ( R\Gamma (G,b,\mu )[\rho ] \right )$
.
Putting these observations together, we get the equality
Note that in our formulation, the Tate twist appearing in [Reference Rapoport and ViehmannRV14, Conjecture 7.3] has been absorbed into the normalization of
![]() $\operatorname {\mathrm {Mant}}_{b,\mu }$
.
$\operatorname {\mathrm {Mant}}_{b,\mu }$
.
3 Transfer of conjugation-invariant functions from
 $G(F)$
to
$G(F)$
to
 $G_b(F)$
$G_b(F)$
Throughout,
![]() $F/\mathbf {Q}_p$
is a finite extension, and
$F/\mathbf {Q}_p$
is a finite extension, and
![]() $G/F$
is a connected reductive group.
$G/F$
is a connected reductive group.
3.1 The space of strongly regular conjugacy classes in
 $G(F)$
$G(F)$
The following definitions are important for our work.
-
•
 $G_{\operatorname {\mathrm {rs}}}\subset G$
is the open subvariety of regular semisimple elements, meaning those whose connected centralizer is a maximal torus.
$G_{\operatorname {\mathrm {rs}}}\subset G$
is the open subvariety of regular semisimple elements, meaning those whose connected centralizer is a maximal torus. -
•
 $G_{\operatorname {\mathrm {sr}}}\subset G$
is the open subvariety of strongly regular semisimple elements, meaning those regular semisimple elements whose centralizer is connected, i.e., a maximal torus.
$G_{\operatorname {\mathrm {sr}}}\subset G$
is the open subvariety of strongly regular semisimple elements, meaning those regular semisimple elements whose centralizer is connected, i.e., a maximal torus. -
•
 $G(F)_{\operatorname {\mathrm {ell}}}\subset G(F)$
is the open subset of strongly regular elliptic elements, meaning those strongly regular semisimple elements in
$G(F)_{\operatorname {\mathrm {ell}}}\subset G(F)$
is the open subset of strongly regular elliptic elements, meaning those strongly regular semisimple elements in
 $G(F)$
whose centralizer is an elliptic maximal torus.
$G(F)$
whose centralizer is an elliptic maximal torus.
We put
![]() $G(F)_{\operatorname {\mathrm {sr}}}=G_{\operatorname {\mathrm {sr}}}(F)$
and
$G(F)_{\operatorname {\mathrm {sr}}}=G_{\operatorname {\mathrm {sr}}}(F)$
and
![]() $G(F)_{\operatorname {\mathrm {rs}}}=G_{\operatorname {\mathrm {rs}}}(F)$
. Note that
$G(F)_{\operatorname {\mathrm {rs}}}=G_{\operatorname {\mathrm {rs}}}(F)$
. Note that
![]() $G(F)_{\operatorname {\mathrm {ell}}}\subset G(F)_{\operatorname {\mathrm {sr}}}\subset G(F)_{\operatorname {\mathrm {rs}}}$
. The inclusion
$G(F)_{\operatorname {\mathrm {ell}}}\subset G(F)_{\operatorname {\mathrm {sr}}}\subset G(F)_{\operatorname {\mathrm {rs}}}$
. The inclusion
![]() $G(F)_{\operatorname {\mathrm {sr}}}\subset G(F)_{\operatorname {\mathrm {rs}}}$
is dense.
$G(F)_{\operatorname {\mathrm {sr}}}\subset G(F)_{\operatorname {\mathrm {rs}}}$
is dense.
If g is regular semisimple, then it is necessarily contained in a unique maximal torus T, namely the neutral component
![]() $\operatorname {\mathrm {Cent}}(g,G)^{\circ }$
, but this is not necessarily all of
$\operatorname {\mathrm {Cent}}(g,G)^{\circ }$
, but this is not necessarily all of
![]() $\operatorname {\mathrm {Cent}}(g,G)$
. If
$\operatorname {\mathrm {Cent}}(g,G)$
. If
![]() $G_{\mathrm {der}}$
is simply connected, then
$G_{\mathrm {der}}$
is simply connected, then
![]() $\operatorname {\mathrm {Cent}}(g,G)$
is connected; thus, in such a group, regular semisimple and strongly regular semisimple mean the same thing.
$\operatorname {\mathrm {Cent}}(g,G)$
is connected; thus, in such a group, regular semisimple and strongly regular semisimple mean the same thing.
Observe that if g is regular semisimple, then
![]() $\alpha (g)\neq 1$
for all roots
$\alpha (g)\neq 1$
for all roots
![]() $\alpha $
relative to the action of T. Indeed, if
$\alpha $
relative to the action of T. Indeed, if
![]() $\alpha (g)=1$
, then the root subgroup of
$\alpha (g)=1$
, then the root subgroup of
![]() $\alpha $
would commute with g, and then it would have dimension strictly greater than
$\alpha $
would commute with g, and then it would have dimension strictly greater than
![]() $\dim T$
.
$\dim T$
.
All of the sets
![]() $G(F)_{\operatorname {\mathrm {sr}}}$
,
$G(F)_{\operatorname {\mathrm {sr}}}$
,
![]() $G(F)_{\operatorname {\mathrm {rs}}}$
,
$G(F)_{\operatorname {\mathrm {rs}}}$
,
![]() $G(F)_{\operatorname {\mathrm {ell}}}$
are conjugacy-invariant, so we may for instance consider the quotient
$G(F)_{\operatorname {\mathrm {ell}}}$
are conjugacy-invariant, so we may for instance consider the quotient
![]() , considered as a topological space.
, considered as a topological space.
Lemma 3.1.1.
![]() is locally profinite, in fact equal to the disjoint union of the locally profinite sets
is locally profinite, in fact equal to the disjoint union of the locally profinite sets
![]() $T(F)_{\operatorname {\mathrm {rs}}}/N(T,G)(F)$
, where T runs over the set of
$T(F)_{\operatorname {\mathrm {rs}}}/N(T,G)(F)$
, where T runs over the set of
![]() $G(F)$
-conjugacy classes of F-rational maximal tori in G, and
$G(F)$
-conjugacy classes of F-rational maximal tori in G, and
![]() $N(T,G)$
is the normalizer of T in G. The same is true with ‘rs’ replaced by ‘sr’.
$N(T,G)$
is the normalizer of T in G. The same is true with ‘rs’ replaced by ‘sr’.
Proof. Let
![]() $T\subset G$
be a F-rational maximal torus. The set
$T\subset G$
be a F-rational maximal torus. The set
![]() $H^1(F,N(T,G))$
classifies conjugacy classes of F-rational tori, as follows: Given a F-rational torus
$H^1(F,N(T,G))$
classifies conjugacy classes of F-rational tori, as follows: Given a F-rational torus
![]() $T'$
, we must have
$T'$
, we must have
![]() $T'=xTx^{-1}$
for some
$T'=xTx^{-1}$
for some
![]() $x\in G(\overline {F})$
. Then for all
$x\in G(\overline {F})$
. Then for all
![]() $\sigma \in \operatorname {\mathrm {Gal}}(\overline {F}/F)$
,
$\sigma \in \operatorname {\mathrm {Gal}}(\overline {F}/F)$
,
![]() $x^{-1} x^{\sigma }$
normalizes T. We associate to
$x^{-1} x^{\sigma }$
normalizes T. We associate to
![]() $T'$
the class of
$T'$
the class of
![]() $\sigma \mapsto x^{-1}x^{\sigma }$
in
$\sigma \mapsto x^{-1}x^{\sigma }$
in
![]() $H^1(F,N(T,G))$
, and it is a simple matter to see that this defines a bijection as claimed. (In fact
$H^1(F,N(T,G))$
, and it is a simple matter to see that this defines a bijection as claimed. (In fact
![]() $H^1(F,N(T,G))$
is finite.)
$H^1(F,N(T,G))$
is finite.)
There is a map
![]() , sending the conjugacy class of
, sending the conjugacy class of
![]() $g\in G(F)_{\operatorname {\mathrm {rs}}}$
to the conjugacy class of the unique F-rational torus containing it, namely
$g\in G(F)_{\operatorname {\mathrm {rs}}}$
to the conjugacy class of the unique F-rational torus containing it, namely
![]() $\operatorname {\mathrm {Cent}}(g,G)^{\circ }$
. We claim that this map is locally constant.
$\operatorname {\mathrm {Cent}}(g,G)^{\circ }$
. We claim that this map is locally constant.
To prove the claim, we consider
a morphism of p-adic analytic varieties. We would like to show that
![]() $\varphi $
is open. To do this, we will compute its differential at the point
$\varphi $
is open. To do this, we will compute its differential at the point
![]() $(g,t)$
by means of a change of variable. Consider the map
$(g,t)$
by means of a change of variable. Consider the map
Explicitly, for
![]() $(z,w) \in G(F) \times T(F)$
, we have
$(z,w) \in G(F) \times T(F)$
, we have
![]() $\psi (z,w)=gt^{-1}ztwz^{-1}g^{-1}$
.
$\psi (z,w)=gt^{-1}ztwz^{-1}g^{-1}$
.
Let
![]() $\mathfrak {g}=\operatorname {\mathrm {Lie}} G$
,
$\mathfrak {g}=\operatorname {\mathrm {Lie}} G$
,
![]() $\mathfrak {t}=\operatorname {\mathrm {Lie}} T$
. The derivative
$\mathfrak {t}=\operatorname {\mathrm {Lie}} T$
. The derivative
![]() $d\psi (1,1) : \mathfrak {g} \times \mathfrak {t} \to \mathfrak {g}$
is given by the formula
$d\psi (1,1) : \mathfrak {g} \times \mathfrak {t} \to \mathfrak {g}$
is given by the formula
We would like to check that
![]() $d\psi (1,1)$
is surjective. We may decompose
$d\psi (1,1)$
is surjective. We may decompose
![]() $\mathfrak {g}=\mathfrak {t} \oplus \mathfrak {t}^{\perp }$
, where
$\mathfrak {g}=\mathfrak {t} \oplus \mathfrak {t}^{\perp }$
, where
![]() $\mathfrak {t}^{\perp }$
is the descent to F of the direct sum of all root subspaces of
$\mathfrak {t}^{\perp }$
is the descent to F of the direct sum of all root subspaces of
![]() $\mathfrak {g}_{\overline {F}}$
for the action of T.
$\mathfrak {g}_{\overline {F}}$
for the action of T.
The element t is regular, hence
![]() $\alpha (t)\neq 1$
for all roots of
$\alpha (t)\neq 1$
for all roots of
![]() $\mathfrak {g}$
for the action of T. Therefore,
$\mathfrak {g}$
for the action of T. Therefore,
![]() $\mathrm {Ad}(t^{-1})-\mathrm {id} : \mathfrak {g}/\mathfrak {t} \to \mathfrak {t}^{\perp }$
is an isomorphism. It follows that
$\mathrm {Ad}(t^{-1})-\mathrm {id} : \mathfrak {g}/\mathfrak {t} \to \mathfrak {t}^{\perp }$
is an isomorphism. It follows that
![]() $d\psi $
is surjective. The derivative of
$d\psi $
is surjective. The derivative of
![]() $\varphi $
at
$\varphi $
at
![]() $(g,t)$
is
$(g,t)$
is
All terms
![]() $dL$
are isomorphisms, so
$dL$
are isomorphisms, so
![]() $d\varphi (g,t)$
is also surjective. Thus,
$d\varphi (g,t)$
is also surjective. Thus,
![]() $\varphi $
is a submersion in the sense of Bourbaki VAR §5.9.1; hence, it is open by loc. cit. §5.9.4.
$\varphi $
is a submersion in the sense of Bourbaki VAR §5.9.1; hence, it is open by loc. cit. §5.9.4.
Therefore, if
![]() $g\in T(F)_{\operatorname {\mathrm {rs}}}$
and
$g\in T(F)_{\operatorname {\mathrm {rs}}}$
and
![]() $g'$
is sufficiently close to g in
$g'$
is sufficiently close to g in
![]() $G(F)$
, then
$G(F)$
, then
![]() $g'$
is conjugate in
$g'$
is conjugate in
![]() $G(F)$
to an element of
$G(F)$
to an element of
![]() $T(F)$
, which proves the claim about the local constancy of
$T(F)$
, which proves the claim about the local constancy of
![]() .
.
The fiber of this map over
![]() $T'$
is
$T'$
is
![]() $T'(F)_{\operatorname {\mathrm {rs}}}$
modulo the action of the finite group
$T'(F)_{\operatorname {\mathrm {rs}}}$
modulo the action of the finite group
![]() $N(T',G)(F)/T'(F)$
. Since
$N(T',G)(F)/T'(F)$
. Since
![]() $T'(F)_{\operatorname {\mathrm {rs}}}$
is locally profinite so is its quotient by the action of a finite group.
$T'(F)_{\operatorname {\mathrm {rs}}}$
is locally profinite so is its quotient by the action of a finite group.
3.2 Hecke transfer maps
Suppose that
![]() $b\in G(\breve {F})$
is basic. The goal of this section is to define a family of explicit maps, which input a conjugation-invariant function on
$b\in G(\breve {F})$
is basic. The goal of this section is to define a family of explicit maps, which input a conjugation-invariant function on
![]() $G(F)_{\operatorname {\mathrm {sr}}}$
and output a conjugation-invariant function on
$G(F)_{\operatorname {\mathrm {sr}}}$
and output a conjugation-invariant function on
![]() $G_b(F)_{\operatorname {\mathrm {sr}}}$
. We shall call them Hecke transfer maps as a way of foreshadowing their relation to the Hecke operators defined on the stack
$G_b(F)_{\operatorname {\mathrm {sr}}}$
. We shall call them Hecke transfer maps as a way of foreshadowing their relation to the Hecke operators defined on the stack
![]() $\operatorname {\mathrm {Bun}}_G$
.
$\operatorname {\mathrm {Bun}}_G$
.
Given a sufficiently strong version of the local Langlands conjectures, we will show that the Hecke transfer maps act predictably on the trace characters attached to irreducible admissible representations.
We begin by recalling the concept of related elements and the definition of their invariant in the isocrystal setting from [Reference KalethaKal14].
Lemma 3.2.1. Suppose
![]() $g\in G(F)$
and
$g\in G(F)$
and
![]() $g'\in G_b(F)$
are strongly regular elements which are conjugate over an algebraic closure of
$g'\in G_b(F)$
are strongly regular elements which are conjugate over an algebraic closure of
![]() $\breve {F}$
. Then they are conjugate over
$\breve {F}$
. Then they are conjugate over
![]() $\breve F$
.
$\breve F$
.
Proof. Let K be an algebraic closure of
![]() $\breve {F}$
. Say
$\breve {F}$
. Say
![]() $g'=zgz^{-1}$
with
$g'=zgz^{-1}$
with
![]() $z\in G(K)$
. Let
$z\in G(K)$
. Let
![]() $T=\operatorname {\mathrm {Cent}}(g,G)$
; then for all
$T=\operatorname {\mathrm {Cent}}(g,G)$
; then for all
![]() $\tau $
in the inertia group
$\tau $
in the inertia group
![]() $ \operatorname {\mathrm {Gal}}(\overline {F}/F^{\operatorname {\mathrm {nr}}})$
,
$ \operatorname {\mathrm {Gal}}(\overline {F}/F^{\operatorname {\mathrm {nr}}})$
,
![]() $z^{-\tau }z$
commutes with g and therefore lies in
$z^{-\tau }z$
commutes with g and therefore lies in
![]() $T(K)$
. Then
$T(K)$
. Then
![]() $\tau \mapsto z^{-\tau } z$
is a cocycle in
$\tau \mapsto z^{-\tau } z$
is a cocycle in
![]() $H^1(\breve {F},T)$
. Since T is a connected algebraic group,
$H^1(\breve {F},T)$
. Since T is a connected algebraic group,
![]() $H^1(\breve {F},T)=0$
[Reference SteinbergSte65, Theorem 1.9]. If
$H^1(\breve {F},T)=0$
[Reference SteinbergSte65, Theorem 1.9]. If
![]() $x\in T(K)$
splits the cocycle, then
$x\in T(K)$
splits the cocycle, then
![]() $y=zx^{-1}\in G(\breve {F})$
, and
$y=zx^{-1}\in G(\breve {F})$
, and
![]() $g'=ygy^{-1}$
so that g and
$g'=ygy^{-1}$
so that g and
![]() $g'$
are related.
$g'$
are related.
It is customary to call elements
![]() $g,g'$
as in the above lemma stably conjugate, or related. Suppose we have strongly regular elements
$g,g'$
as in the above lemma stably conjugate, or related. Suppose we have strongly regular elements
![]() $g\in G(F)_{\operatorname {\mathrm {sr}}}$
and
$g\in G(F)_{\operatorname {\mathrm {sr}}}$
and
![]() $g'\in G_b(F)_{\operatorname {\mathrm {sr}}}$
which are related. Let
$g'\in G_b(F)_{\operatorname {\mathrm {sr}}}$
which are related. Let
![]() $T=\operatorname {\mathrm {Cent}}(g,G)$
, and suppose
$T=\operatorname {\mathrm {Cent}}(g,G)$
, and suppose
![]() $y\in G(\breve {F})$
with
$y\in G(\breve {F})$
with
![]() $g'=ygy^{-1}$
. The rationality of g means that
$g'=ygy^{-1}$
. The rationality of g means that
![]() $g^{\sigma }=g$
, whereas the rationality of
$g^{\sigma }=g$
, whereas the rationality of
![]() $g'$
in
$g'$
in
![]() $G_b$
means that
$G_b$
means that
![]() $(g')^{\sigma } = b^{-1}g' b$
. Combining these statements shows that
$(g')^{\sigma } = b^{-1}g' b$
. Combining these statements shows that
![]() $b_0:=y^{-1}by^{\sigma }$
commutes with g and therefore lies in
$b_0:=y^{-1}by^{\sigma }$
commutes with g and therefore lies in
![]() $T(\breve {F})$
.
$T(\breve {F})$
.
Definition 3.2.2. For strongly regular related elements
![]() $g\in G(F)_{\operatorname {\mathrm {sr}}}$
and
$g\in G(F)_{\operatorname {\mathrm {sr}}}$
and
![]() $g'\in G_b(F)_{\operatorname {\mathrm {sr}}}$
, the invariant
$g'\in G_b(F)_{\operatorname {\mathrm {sr}}}$
, the invariant
![]() $\operatorname {\mathrm {inv}}[b](g,g')$
is the class of
$\operatorname {\mathrm {inv}}[b](g,g')$
is the class of
![]() $y^{-1}by^{\sigma }$
in
$y^{-1}by^{\sigma }$
in
![]() $B(T)$
, where
$B(T)$
, where
![]() $y\in G(\breve {F})$
satisfies
$y\in G(\breve {F})$
satisfies
![]() $g'=ygy^{-1}$
.
$g'=ygy^{-1}$
.
Fact 3.2.3. The invariant
![]() $\operatorname {\mathrm {inv}}[b](g,g')\in B(T)$
only depends on b, g and
$\operatorname {\mathrm {inv}}[b](g,g')\in B(T)$
only depends on b, g and
![]() $g'$
and not on the element y which conjugates g into
$g'$
and not on the element y which conjugates g into
![]() $g'$
. It depends on the rational conjugacy classes of g and
$g'$
. It depends on the rational conjugacy classes of g and
![]() $g'$
as follows:
$g'$
as follows:
-
• For
 $z\in G(F)$
, we have
$z\in G(F)$
, we have
 $\operatorname {\mathrm {inv}}[b]((\operatorname {\mathrm {ad}} z)(g),g') = (\operatorname {\mathrm {ad}} z)(\operatorname {\mathrm {inv}}[b](g,g'))$
, a class in
$\operatorname {\mathrm {inv}}[b]((\operatorname {\mathrm {ad}} z)(g),g') = (\operatorname {\mathrm {ad}} z)(\operatorname {\mathrm {inv}}[b](g,g'))$
, a class in
 $B((\operatorname {\mathrm {ad}} z)(T))$
.
$B((\operatorname {\mathrm {ad}} z)(T))$
. -
• For
 $z\in G_b(F)$
, we have
$z\in G_b(F)$
, we have
 $\operatorname {\mathrm {inv}}[b](g,(\operatorname {\mathrm {ad}} z)(g')) = \operatorname {\mathrm {inv}}[b](g,g')$
.
$\operatorname {\mathrm {inv}}[b](g,(\operatorname {\mathrm {ad}} z)(g')) = \operatorname {\mathrm {inv}}[b](g,g')$
.
The image of
![]() $\mathrm {inv}[b](g,g')$
under the composition of
$\mathrm {inv}[b](g,g')$
under the composition of
![]() $B(T) \to B(G)$
and
$B(T) \to B(G)$
and
![]() $\kappa \colon B(G) \to \pi _1(G)_{\Gamma }$
equals
$\kappa \colon B(G) \to \pi _1(G)_{\Gamma }$
equals
![]() $\kappa (b)$
.
$\kappa (b)$
.
Definition 3.2.4. We define a diagram of topological spaces

as follows. The space
![]() $\operatorname {\mathrm {Rel}}_b$
is the set of conjugacy classes of triples
$\operatorname {\mathrm {Rel}}_b$
is the set of conjugacy classes of triples
![]() $(g,g',\lambda )$
, where
$(g,g',\lambda )$
, where
![]() $g\in G(F)_{\operatorname {\mathrm {sr}}}$
and
$g\in G(F)_{\operatorname {\mathrm {sr}}}$
and
![]() $g'\in G_b(F)_{\operatorname {\mathrm {sr}}}$
are related, and
$g'\in G_b(F)_{\operatorname {\mathrm {sr}}}$
are related, and
![]() $\lambda \in X_*(T)$
, where
$\lambda \in X_*(T)$
, where
![]() $T=\operatorname {\mathrm {Cent}}(g,G)$
. It is required that
$T=\operatorname {\mathrm {Cent}}(g,G)$
. It is required that
![]() $\kappa (\operatorname {\mathrm {inv}}[b](g,g'))$
agrees with the image of
$\kappa (\operatorname {\mathrm {inv}}[b](g,g'))$
agrees with the image of
![]() $\lambda $
in
$\lambda $
in
![]() $X_*(T)_{\Gamma }$
. We consider
$X_*(T)_{\Gamma }$
. We consider
![]() $(g,g',\lambda )$
conjugate to
$(g,g',\lambda )$
conjugate to
![]() $((\operatorname {\mathrm {ad}} z)(g),(\operatorname {\mathrm {ad}} z')(g'),(\operatorname {\mathrm {ad}} z)(\lambda ))$
whenever
$((\operatorname {\mathrm {ad}} z)(g),(\operatorname {\mathrm {ad}} z')(g'),(\operatorname {\mathrm {ad}} z)(\lambda ))$
whenever
![]() $z\in G(F)$
and
$z\in G(F)$
and
![]() $z'\in G_b(F)$
. We give
$z'\in G_b(F)$
. We give
![]() $\operatorname {\mathrm {Rel}}_b\subset (G(F) \times G_b(F)\times X_*(G))/(G(F)\times G_b(F))$
the subspace topology, where
$\operatorname {\mathrm {Rel}}_b\subset (G(F) \times G_b(F)\times X_*(G))/(G(F)\times G_b(F))$
the subspace topology, where
![]() $X_*(G)$
is taken to be discrete.
$X_*(G)$
is taken to be discrete.
Remark 3.2.5. Given
![]() $g\in G(F)_{\operatorname {\mathrm {sr}}}$
and
$g\in G(F)_{\operatorname {\mathrm {sr}}}$
and
![]() $\lambda $
a cocharacter of its torus, there is at most one conjugacy class of
$\lambda $
a cocharacter of its torus, there is at most one conjugacy class of
![]() $g'\in G_b(F)$
with
$g'\in G_b(F)$
with
![]() $(g,g',\lambda )\in \operatorname {\mathrm {Rel}}_b$
. In other words, g and
$(g,g',\lambda )\in \operatorname {\mathrm {Rel}}_b$
. In other words, g and
![]() $\operatorname {\mathrm {inv}}[b](g,g')$
determine the conjugacy class of
$\operatorname {\mathrm {inv}}[b](g,g')$
determine the conjugacy class of
![]() $g'$
. Indeed, suppose
$g'$
. Indeed, suppose
![]() $(g,g',\lambda )$
and
$(g,g',\lambda )$
and
![]() $(g,g'',\lambda )$
are both in
$(g,g'',\lambda )$
are both in
![]() $\operatorname {\mathrm {Rel}}_b$
. Then
$\operatorname {\mathrm {Rel}}_b$
. Then
![]() $g'=ygy^{-1}$
and
$g'=ygy^{-1}$
and
![]() $g''=zgz^{-1}$
for some
$g''=zgz^{-1}$
for some
![]() $y,z\in G(F^{\operatorname {\mathrm {nr}}})$
, and
$y,z\in G(F^{\operatorname {\mathrm {nr}}})$
, and
![]() $y^{-1}by^{\sigma }$
and
$y^{-1}by^{\sigma }$
and
![]() $z^{-1}bz^{\sigma }$
are
$z^{-1}bz^{\sigma }$
are
![]() $\sigma $
-conjugate in
$\sigma $
-conjugate in
![]() $T(\breve {F})$
. This means there exists
$T(\breve {F})$
. This means there exists
![]() $t\in T(\breve {F})$
such that
$t\in T(\breve {F})$
such that
![]() $y^{-1}by^{\sigma }=(zt)^{-1}b (zt)^{\sigma }$
. We see that
$y^{-1}by^{\sigma }=(zt)^{-1}b (zt)^{\sigma }$
. We see that
![]() $x=zty^{-1}\in G_b(F)$
, and that x conjugates
$x=zty^{-1}\in G_b(F)$
, and that x conjugates
![]() $g'$
onto
$g'$
onto
![]() $g''$
.
$g''$
.
Lemma 3.2.6. The map
![]() is a homeomorphism locally on the source. Its image consists of those classes that transfer to
is a homeomorphism locally on the source. Its image consists of those classes that transfer to
![]() $G_b$
. In particular, the image is open and closed.
$G_b$
. In particular, the image is open and closed.
The analogous statement is true for
![]() .
.
Proof. The proof of Lemma 3.1.1 shows that
![]() is the disjoint union of spaces
is the disjoint union of spaces
![]() $T(F)_{\operatorname {\mathrm {sr}}}/W_T$
, as
$T(F)_{\operatorname {\mathrm {sr}}}/W_T$
, as
![]() $T\subset G$
runs through the finitely many conjugacy classes of F-rational maximal tori, and
$T\subset G$
runs through the finitely many conjugacy classes of F-rational maximal tori, and
![]() $W_T=N(T,G)(F)/T(F)$
is a finite group. By the above remark,
$W_T=N(T,G)(F)/T(F)$
is a finite group. By the above remark,
![]() $\operatorname {\mathrm {Rel}}_b$
injects into the disjoint union of the spaces
$\operatorname {\mathrm {Rel}}_b$
injects into the disjoint union of the spaces
![]() $T(F)_{\operatorname {\mathrm {sr}}}/W_T\times X_*(T)$
, with the map to
$T(F)_{\operatorname {\mathrm {sr}}}/W_T\times X_*(T)$
, with the map to
![]() corresponding to the projection
corresponding to the projection
![]() $T(F)_{\operatorname {\mathrm {sr}}}/W_T\times X_*(T)\to T(F)_{\operatorname {\mathrm {sr}}}/W_T$
. Since
$T(F)_{\operatorname {\mathrm {sr}}}/W_T\times X_*(T)\to T(F)_{\operatorname {\mathrm {sr}}}/W_T$
. Since
![]() $X_*(T)$
is discrete, this map is a homeomorphism locally on the source. The other statements are evident from the definitions.
$X_*(T)$
is discrete, this map is a homeomorphism locally on the source. The other statements are evident from the definitions.
The definition of
![]() $\operatorname {\mathrm {Rel}}_b$
already suggests a means for transferring functions from
$\operatorname {\mathrm {Rel}}_b$
already suggests a means for transferring functions from
![]() to
to
![]() , namely, by pulling back from
, namely, by pulling back from
![]() to
to
![]() $\operatorname {\mathrm {Rel}}_b$
, multiplying by a compactly supported kernel function and then pushing forward to
$\operatorname {\mathrm {Rel}}_b$
, multiplying by a compactly supported kernel function and then pushing forward to
![]() . We will define one such kernel function for each geometric conjugacy class of cocharacters
. We will define one such kernel function for each geometric conjugacy class of cocharacters
![]() $\mu \colon \mathbf {G}_{\mathrm {m}}\to G_{\overline {F}}$
.
$\mu \colon \mathbf {G}_{\mathrm {m}}\to G_{\overline {F}}$
.
Let
![]() $\widehat {G}$
be the Langlands dual group. It comes equipped with a splitting, in particular with a torus and Borel
$\widehat {G}$
be the Langlands dual group. It comes equipped with a splitting, in particular with a torus and Borel
![]() $\widehat T \subset \widehat B \subset \widehat G$
. Given a conjugacy class of cocharacters
$\widehat T \subset \widehat B \subset \widehat G$
. Given a conjugacy class of cocharacters
![]() $\mu $
for G as above, we obtain a character
$\mu $
for G as above, we obtain a character
![]() $\widehat \mu : \widehat T \to \mathbf {G}_{\mathrm {m}}$
which is
$\widehat \mu : \widehat T \to \mathbf {G}_{\mathrm {m}}$
which is
![]() $\widehat B$
-dominant. Let
$\widehat B$
-dominant. Let
![]() $r_{\mu }$
be the Weyl module of the dual group
$r_{\mu }$
be the Weyl module of the dual group
![]() $\widehat G$
whose highest weight with respect to
$\widehat G$
whose highest weight with respect to
![]() $(\widehat T,\widehat B)$
is
$(\widehat T,\widehat B)$
is
![]() $\widehat \mu $
.
$\widehat \mu $
.
A cocharacter
![]() $\lambda \in X_*(T)$
corresponds to a character
$\lambda \in X_*(T)$
corresponds to a character
![]() $\widehat {\lambda }\in X^*(\widehat {T})$
. Let
$\widehat {\lambda }\in X^*(\widehat {T})$
. Let
![]() $r_{\mu }[\lambda ]$
be the
$r_{\mu }[\lambda ]$
be the
![]() $\widehat {\lambda }$
-weight space of
$\widehat {\lambda }$
-weight space of
![]() $r_{\mu }$
. The quantity
$r_{\mu }$
. The quantity
![]() $\dim r_{\mu }[\lambda ]$
will give us our kernel function. While we will not need it here, we note that there is an explicit formula for
$\dim r_{\mu }[\lambda ]$
will give us our kernel function. While we will not need it here, we note that there is an explicit formula for
![]() $\dim r_{\mu }[\lambda ]$
coming from the Weyl character formula.
$\dim r_{\mu }[\lambda ]$
coming from the Weyl character formula.
We now fix a commutative ring
![]() $\Lambda $
in which p is invertible. For a topological space X, we let
$\Lambda $
in which p is invertible. For a topological space X, we let
![]() $C(X,\Lambda )$
be the space of continuous
$C(X,\Lambda )$
be the space of continuous
![]() $\Lambda $
-valued functions on X, where
$\Lambda $
-valued functions on X, where
![]() $\Lambda $
is given the discrete topology.
$\Lambda $
is given the discrete topology.
Definition 3.2.7. Let
![]() $d=\left < \mu ,2\rho _G \right>$
, where
$d=\left < \mu ,2\rho _G \right>$
, where
![]() $2\rho _G$
is the sum of the positive roots of G. We define the Hecke transfer map
$2\rho _G$
is the sum of the positive roots of G. We define the Hecke transfer map
by
 $$\begin{align*}[T_{b,\mu}^{G\to G_b} f](g') = (-1)^d\sum_{(g,g',\lambda) \in \operatorname{\mathrm{Rel}}_{b}} f(g) \dim r_{\mu}[\lambda]. \end{align*}$$
$$\begin{align*}[T_{b,\mu}^{G\to G_b} f](g') = (-1)^d\sum_{(g,g',\lambda) \in \operatorname{\mathrm{Rel}}_{b}} f(g) \dim r_{\mu}[\lambda]. \end{align*}$$
Analogously, we define
by
 $$\begin{align*}[T_{b,\mu}^{G_b\to G} f'](g) =(-1)^d \sum_{(g,g',\lambda) \in \operatorname{\mathrm{Rel}}_{b}} f'(g') \dim r_{\mu}[\lambda]. \end{align*}$$
$$\begin{align*}[T_{b,\mu}^{G_b\to G} f'](g) =(-1)^d \sum_{(g,g',\lambda) \in \operatorname{\mathrm{Rel}}_{b}} f'(g') \dim r_{\mu}[\lambda]. \end{align*}$$
Since
![]() $r_{\mu }$
is finite-dimensional, the sum is finite. If
$r_{\mu }$
is finite-dimensional, the sum is finite. If
![]() $f'$
has compact support, then so does its image.
$f'$
has compact support, then so does its image.
Lemma 3.2.8. The Hecke transfer map
![]() $T_{b,\mu }^{G\to G_b}$
is zero unless
$T_{b,\mu }^{G\to G_b}$
is zero unless
![]() $[b]$
is the unique basic class in
$[b]$
is the unique basic class in
![]() $B(G,\mu )$
.
$B(G,\mu )$
.
Proof. Suppose there exists an F-rational maximal torus
![]() $T\subset G$
and a cocharacter
$T\subset G$
and a cocharacter
![]() $\lambda \in X_*(T)$
such that
$\lambda \in X_*(T)$
such that
![]() $r_{\mu }[\lambda ]\neq 0$
. Then
$r_{\mu }[\lambda ]\neq 0$
. Then
![]() $\widehat {\mu }$
and
$\widehat {\mu }$
and
![]() $\widehat {\lambda }$
must agree when restricted to the center
$\widehat {\lambda }$
must agree when restricted to the center
![]() $Z(\widehat {G})$
, which is to say that
$Z(\widehat {G})$
, which is to say that
![]() $\widehat {\mu }$
and
$\widehat {\mu }$
and
![]() $\widehat {\lambda }$
have the same image in
$\widehat {\lambda }$
have the same image in
![]() $X^*(Z(\widehat {G}))$
. Equivalently, if we conjugate
$X^*(Z(\widehat {G}))$
. Equivalently, if we conjugate
![]() $\mu $
so as to assume it is a cocharacter of T, then
$\mu $
so as to assume it is a cocharacter of T, then
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
have the same image under
$\lambda $
have the same image under
![]() $X_*(T)\cong \pi _1(T)\to \pi _1(G)$
. By Fact 3.2.3 and the functoriality of
$X_*(T)\cong \pi _1(T)\to \pi _1(G)$
. By Fact 3.2.3 and the functoriality of
![]() $\kappa $
the image of
$\kappa $
the image of
![]() $\lambda $
in
$\lambda $
in
![]() $\pi _1(G)_{\Gamma }$
equals
$\pi _1(G)_{\Gamma }$
equals
![]() $\kappa (b)$
. We conclude that
$\kappa (b)$
. We conclude that
![]() $\kappa ([b])$
equals the image of
$\kappa ([b])$
equals the image of
![]() $\mu $
in
$\mu $
in
![]() $\pi _1(G)_{\Gamma }$
. This means that
$\pi _1(G)_{\Gamma }$
. This means that
![]() $[b]$
is the unique basic class in
$[b]$
is the unique basic class in
![]() $B(G,\mu )$
.
$B(G,\mu )$
.
Assume therefore that
![]() $[b]$
is the unique basic class in
$[b]$
is the unique basic class in
![]() $B(G,\mu )$
. We may define a ‘truncation’
$B(G,\mu )$
. We may define a ‘truncation’
![]() $\operatorname {\mathrm {Rel}}_{b,\mu }\subset \operatorname {\mathrm {Rel}}_b$
, consisting of conjugacy classes of triples
$\operatorname {\mathrm {Rel}}_{b,\mu }\subset \operatorname {\mathrm {Rel}}_b$
, consisting of conjugacy classes of triples
![]() $(g,g',\lambda )$
for which
$(g,g',\lambda )$
for which
![]() $\lambda \leq \mu $
. Then the kernel function
$\lambda \leq \mu $
. Then the kernel function
![]() $(g,g',\lambda )\mapsto \dim r_{\mu }[\lambda ]$
is supported on
$(g,g',\lambda )\mapsto \dim r_{\mu }[\lambda ]$
is supported on
![]() $\operatorname {\mathrm {Rel}}_{b,\mu }$
. In the diagram
$\operatorname {\mathrm {Rel}}_{b,\mu }$
. In the diagram

both maps are finite étale over their respective images.
The following theorem is proved in §3.3. It relates the Hecke transfer map
![]() $T_{b,\mu }^{G\to G_b}$
to the local Jacquet–Langlands correspondence for G.
$T_{b,\mu }^{G\to G_b}$
to the local Jacquet–Langlands correspondence for G.
Theorem 3.2.9. Assume that
![]() $b\in B(G,\mu )$
is basic and that
$b\in B(G,\mu )$
is basic and that
![]() $\Lambda $
is an algebraically closed field of characteristic 0 abstractly isomorphic to
$\Lambda $
is an algebraically closed field of characteristic 0 abstractly isomorphic to
![]() $\mathbf {C}$
. Let
$\mathbf {C}$
. Let
![]() $\phi \colon W_F \times \mathrm {SL}_2 \to \;^LG$
be a discrete L-parameter with coefficients in
$\phi \colon W_F \times \mathrm {SL}_2 \to \;^LG$
be a discrete L-parameter with coefficients in
![]() $\Lambda $
, and let
$\Lambda $
, and let
![]() $\rho \in \Pi _{\phi }(G_b)$
. Let
$\rho \in \Pi _{\phi }(G_b)$
. Let
![]() be its Harish–Chandra character. Then for any
be its Harish–Chandra character. Then for any
![]() $g\in G(F)_{\operatorname {\mathrm {sr}}}$
that transfers to
$g\in G(F)_{\operatorname {\mathrm {sr}}}$
that transfers to
![]() $G_b(F)$
, we have
$G_b(F)$
, we have
 $$ \begin{align} \left[T_{b,\mu}^{G_b\to G}\Theta_{\rho}\right](g)=\sum_{\pi\in \Pi_{\phi}(G)} \dim \operatorname{\mathrm{Hom}}_{S_{\phi}}(\delta_{\pi,\rho},r_{\mu})\Theta_{\pi}(g), \end{align} $$
$$ \begin{align} \left[T_{b,\mu}^{G_b\to G}\Theta_{\rho}\right](g)=\sum_{\pi\in \Pi_{\phi}(G)} \dim \operatorname{\mathrm{Hom}}_{S_{\phi}}(\delta_{\pi,\rho},r_{\mu})\Theta_{\pi}(g), \end{align} $$
assuming the validity of the refined local Langlands conjecture, i.e., [Reference KalethaKal16a, Conjecture G].
Example 3.2.10. Let
![]() $G=\mathrm {GL}_2$
, and let
$G=\mathrm {GL}_2$
, and let
![]() $\mu \colon \bf {G}_m \to G$
the cocharacter sending x to the diagonal matrix with entries
$\mu \colon \bf {G}_m \to G$
the cocharacter sending x to the diagonal matrix with entries
![]() $(x,1)$
. We have
$(x,1)$
. We have
![]() $\pi _1(G)=\mathbf {Z}$
as a trivial
$\pi _1(G)=\mathbf {Z}$
as a trivial
![]() $\Gamma $
-module. Let
$\Gamma $
-module. Let
![]() $b \in B(G,\mu )$
be the basic class. Then b corresponds to the isocrystal of slope
$b \in B(G,\mu )$
be the basic class. Then b corresponds to the isocrystal of slope
![]() $1/2$
, and
$1/2$
, and
![]() $G_b(F)$
is the multiplicative group of the nonsplit quaternion algebra over F. Let
$G_b(F)$
is the multiplicative group of the nonsplit quaternion algebra over F. Let
![]() $\phi $
be a discrete Langlands parameter. The L-packets
$\phi $
be a discrete Langlands parameter. The L-packets
![]() $\Pi _{\phi }(G)=\left \{ \pi \right \}$
and
$\Pi _{\phi }(G)=\left \{ \pi \right \}$
and
![]() $\Pi _{\phi }(G_b)=\left \{ \rho \right \}$
are singletons. We have
$\Pi _{\phi }(G_b)=\left \{ \rho \right \}$
are singletons. We have
![]() $S_{\phi }=Z(\widehat G)=\mathbf {C}^{\times }$
, and
$S_{\phi }=Z(\widehat G)=\mathbf {C}^{\times }$
, and
![]() $\delta _{\pi ,\rho }$
is the identity character of
$\delta _{\pi ,\rho }$
is the identity character of
![]() $S_{\phi }$
. The representation
$S_{\phi }$
. The representation
![]() $r_{\mu }$
is the standard representation of
$r_{\mu }$
is the standard representation of
![]() $\widehat G=\mathrm {GL}_2(\mathbf {C})$
, and
$\widehat G=\mathrm {GL}_2(\mathbf {C})$
, and
![]() $\dim \operatorname {\mathrm {Hom}}_{S_{\phi }}(\delta _{\pi ,\rho },r_{\mu })=2$
. Therefore, the right-hand side of equation (3.2.3) equals
$\dim \operatorname {\mathrm {Hom}}_{S_{\phi }}(\delta _{\pi ,\rho },r_{\mu })=2$
. Therefore, the right-hand side of equation (3.2.3) equals
![]() $2\Theta _{\pi }(g)$
.
$2\Theta _{\pi }(g)$
.
Let
![]() $w\mu $
be the cocharacter sending x to the diagonal matrix with entries
$w\mu $
be the cocharacter sending x to the diagonal matrix with entries
![]() $(1,x)$
. The map
$(1,x)$
. The map
![]() $\lambda \mapsto r_{\mu }[\lambda ]$
sends
$\lambda \mapsto r_{\mu }[\lambda ]$
sends
![]() $\mu $
and
$\mu $
and
![]() $w\mu $
to
$w\mu $
to
![]() $1$
and all other cocharacters to
$1$
and all other cocharacters to
![]() $0$
. For any strongly regular
$0$
. For any strongly regular
![]() $g' \in G_b(F)$
, there is a unique
$g' \in G_b(F)$
, there is a unique
![]() $G(F)$
-conjugacy class of strongly regular
$G(F)$
-conjugacy class of strongly regular
![]() $g \in G(F)$
related to
$g \in G(F)$
related to
![]() $g'$
. Let
$g'$
. Let
![]() $S \subset G$
be the centralizer of one such g. Then
$S \subset G$
be the centralizer of one such g. Then
![]() $X_*(S) \cong \mathbf {Z}[\Gamma _{E/F}]$
for a quadratic extension
$X_*(S) \cong \mathbf {Z}[\Gamma _{E/F}]$
for a quadratic extension
![]() $E/F$
, and the map
$E/F$
, and the map
![]() $\pi _1(S)_{\Gamma } \to \pi _1(G)_{\Gamma }$
is an isomorphism. There are exactly two elements
$\pi _1(S)_{\Gamma } \to \pi _1(G)_{\Gamma }$
is an isomorphism. There are exactly two elements
![]() $\lambda ,w\lambda \in X_*(S)$
that map to
$\lambda ,w\lambda \in X_*(S)$
that map to
![]() $\mathrm {inv}[b](g,g')$
. Finally,
$\mathrm {inv}[b](g,g')$
. Finally,
![]() $d=1$
. Therefore,
$d=1$
. Therefore,
![]() $T_{b,\mu }^{G \to G_b}f(g')=-2f(g)$
. Setting
$T_{b,\mu }^{G \to G_b}f(g')=-2f(g)$
. Setting
![]() $f=\Theta _{\rho }$
, we find that Theorem 3.2.9 reduces to the Jacquet–Langlands character identity
$f=\Theta _{\rho }$
, we find that Theorem 3.2.9 reduces to the Jacquet–Langlands character identity
3.3 Proof of Theorem 3.2.9
We now give the proof of Theorem 3.2.9. We will use the notation and results of §A.1.
We are given a discrete L-parameter
![]() $\phi $
, a representation
$\phi $
, a representation
![]() $\rho \in \Pi _{\phi }(G_b)$
in its L-packet, and an element
$\rho \in \Pi _{\phi }(G_b)$
in its L-packet, and an element
![]() $g\in G(F)_{\operatorname {\mathrm {sr}}}$
. We assume that g is related to an element of
$g\in G(F)_{\operatorname {\mathrm {sr}}}$
. We assume that g is related to an element of
![]() $G_b(F)$
. This means there exists a triple in
$G_b(F)$
. This means there exists a triple in
![]() $\operatorname {\mathrm {Rel}}_b$
of the form
$\operatorname {\mathrm {Rel}}_b$
of the form
![]() $(g,g',\lambda )$
. For the moment, we fix such a triple
$(g,g',\lambda )$
. For the moment, we fix such a triple
![]() $(g,g',\lambda )$
.
$(g,g',\lambda )$
.
Let
![]() $s\in S_{\phi }$
be a semisimple element, and let
$s\in S_{\phi }$
be a semisimple element, and let
![]() $\dot s \in S_{\phi }^+$
be a lift of it. Then we have the refined endoscopic datum
$\dot s \in S_{\phi }^+$
be a lift of it. Then we have the refined endoscopic datum
![]() $\mathfrak {\dot e}=(H,\mathcal {H},\dot s,\eta )$
defined in equation (A.1.1); we choose as in that section a z-pair
$\mathfrak {\dot e}=(H,\mathcal {H},\dot s,\eta )$
defined in equation (A.1.1); we choose as in that section a z-pair
![]() $\mathfrak {z}=(H_1,\eta _1)$
. Then
$\mathfrak {z}=(H_1,\eta _1)$
. Then
 $$ \begin{align*} \begin{array}{cll} &&\; e(G_b)\displaystyle\sum_{\rho'\in \Pi_{\phi}(G_b)} \operatorname{\mathrm{tr}}\tau_{z,\mathfrak{w},\rho'}(\dot s)\Theta_{\rho'}(g')\\[2pt] &\stackrel{(A.1.2)}{=}& \!\! \displaystyle\sum_{h_1\in H_1(F)/\mathrm{st}} \Delta(h_1,g')S\Theta_{\phi^s}(h_1) \\[2pt] &\stackrel{(A.1.4)}{=}&\!\! \displaystyle\sum_{h_1\in H_1(F)/\mathrm{st}} \Delta(h_1,g)\left< \operatorname{\mathrm{inv}}[b](g,g'),s^{\natural}_{h,g} \right>S\Theta_{\phi^s}(h_1) \\[2pt] & \quad = &\!\! \displaystyle\sum_{h_1\in H_1(F)/\mathrm{st}} \Delta(h_1,g)\lambda(s^{\natural}_{h,g})S\Theta_{\phi^s}(h_1). \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{cll} &&\; e(G_b)\displaystyle\sum_{\rho'\in \Pi_{\phi}(G_b)} \operatorname{\mathrm{tr}}\tau_{z,\mathfrak{w},\rho'}(\dot s)\Theta_{\rho'}(g')\\[2pt] &\stackrel{(A.1.2)}{=}& \!\! \displaystyle\sum_{h_1\in H_1(F)/\mathrm{st}} \Delta(h_1,g')S\Theta_{\phi^s}(h_1) \\[2pt] &\stackrel{(A.1.4)}{=}&\!\! \displaystyle\sum_{h_1\in H_1(F)/\mathrm{st}} \Delta(h_1,g)\left< \operatorname{\mathrm{inv}}[b](g,g'),s^{\natural}_{h,g} \right>S\Theta_{\phi^s}(h_1) \\[2pt] & \quad = &\!\! \displaystyle\sum_{h_1\in H_1(F)/\mathrm{st}} \Delta(h_1,g)\lambda(s^{\natural}_{h,g})S\Theta_{\phi^s}(h_1). \end{array} \end{align*} $$
We now multiply this expression by the kernel function
![]() $\dim r_{\mu }[\lambda ]$
and then sum over all
$\dim r_{\mu }[\lambda ]$
and then sum over all
![]() $G_b(F)$
-conjugacy classes of elements
$G_b(F)$
-conjugacy classes of elements
![]() $g' \in G_b(F)$
and all
$g' \in G_b(F)$
and all
![]() $\lambda \in X_*(T_g)$
such that
$\lambda \in X_*(T_g)$
such that
![]() $(g,g',\lambda )$
lies in
$(g,g',\lambda )$
lies in
![]() $\operatorname {\mathrm {Rel}}_b$
. We obtain
$\operatorname {\mathrm {Rel}}_b$
. We obtain
 $$ \begin{align*} \begin{array}{cll} & &\; e(G_b) \displaystyle\sum_{(g',\lambda)}\; \sum_{\rho'\in \Pi_{\phi}(G_b)} \operatorname{\mathrm{tr}}\tau_{z,\mathfrak{w},\rho'}(\dot s)\Theta_{\rho'}(g')\dim r_{\mu}[\lambda]\\[2pt] &\ \ = &\!\displaystyle\sum_{h_1\in H_1(F)/\mathrm{st}}\Delta(h_1,g) S\Theta_{\phi^s}(h_1)\sum_{(g',\lambda)}\lambda(s^{\natural}_{h,g})\dim r_{\mu}[\lambda]\\[2pt] &\ \stackrel{(*)}{=}&\!\!\displaystyle\sum_{h_1\in H_1(F)/\mathrm{st}}\Delta(h_1,g)S\Theta_{\phi^s}(h_1)\operatorname{\mathrm{tr}} r_{\mu}(s^{\natural}_{h,g}) \\[2pt] &\ \stackrel{(**)}{=}&\!\!\operatorname{\mathrm{tr}} r_{\mu}(s^{\natural})\displaystyle\sum_{h_1\in H_1(F)/\mathrm{st}}\Delta(h_1,g)S\Theta_{\phi^s}(h_1)\\[2pt] &\stackrel{(A.1.2)}{=}&\!\! \operatorname{\mathrm{tr}} r_{\mu}(s^{\natural})e(G)\displaystyle\sum_{\pi\in \Pi_{\phi}(G)} \operatorname{\mathrm{tr}}\tau_{z,\mathfrak{w},\pi}(\dot s)\Theta_{\pi}(g).\\[2pt] \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{cll} & &\; e(G_b) \displaystyle\sum_{(g',\lambda)}\; \sum_{\rho'\in \Pi_{\phi}(G_b)} \operatorname{\mathrm{tr}}\tau_{z,\mathfrak{w},\rho'}(\dot s)\Theta_{\rho'}(g')\dim r_{\mu}[\lambda]\\[2pt] &\ \ = &\!\displaystyle\sum_{h_1\in H_1(F)/\mathrm{st}}\Delta(h_1,g) S\Theta_{\phi^s}(h_1)\sum_{(g',\lambda)}\lambda(s^{\natural}_{h,g})\dim r_{\mu}[\lambda]\\[2pt] &\ \stackrel{(*)}{=}&\!\!\displaystyle\sum_{h_1\in H_1(F)/\mathrm{st}}\Delta(h_1,g)S\Theta_{\phi^s}(h_1)\operatorname{\mathrm{tr}} r_{\mu}(s^{\natural}_{h,g}) \\[2pt] &\ \stackrel{(**)}{=}&\!\!\operatorname{\mathrm{tr}} r_{\mu}(s^{\natural})\displaystyle\sum_{h_1\in H_1(F)/\mathrm{st}}\Delta(h_1,g)S\Theta_{\phi^s}(h_1)\\[2pt] &\stackrel{(A.1.2)}{=}&\!\! \operatorname{\mathrm{tr}} r_{\mu}(s^{\natural})e(G)\displaystyle\sum_{\pi\in \Pi_{\phi}(G)} \operatorname{\mathrm{tr}}\tau_{z,\mathfrak{w},\pi}(\dot s)\Theta_{\pi}(g).\\[2pt] \end{array} \end{align*} $$
We justify
![]() $(**)$
: Let
$(**)$
: Let
![]() $T \subset G$
be the centralizer of g. The image of
$T \subset G$
be the centralizer of g. The image of
![]() $s^{\natural }_{h,g}$
under any admissible embedding
$s^{\natural }_{h,g}$
under any admissible embedding
![]() $\widehat T \to \widehat G$
is conjugate to
$\widehat T \to \widehat G$
is conjugate to
![]() $s^{\natural }$
in
$s^{\natural }$
in
![]() $\widehat {G}$
and
$\widehat {G}$
and
![]() $\operatorname {\mathrm {tr}} r_{\mu }$
is conjugation-invariant. Recall here that
$\operatorname {\mathrm {tr}} r_{\mu }$
is conjugation-invariant. Recall here that
![]() $s^{\natural } \in S_{\phi }$
is the image of
$s^{\natural } \in S_{\phi }$
is the image of
![]() $\dot s$
under equation (2.3.2).
$\dot s$
under equation (2.3.2).
We justify
![]() $(*)$
:
$(*)$
:
![]() $\lambda \in X_*(T)$
determines the
$\lambda \in X_*(T)$
determines the
![]() $G_b(F)$
-conjugacy class of
$G_b(F)$
-conjugacy class of
![]() $g'$
since
$g'$
since
![]() $\mathrm {inv}[b](g,g') \in B(T)$
determines it. Therefore, the sum over
$\mathrm {inv}[b](g,g') \in B(T)$
determines it. Therefore, the sum over
![]() $(g',\lambda )$
is in reality a sum only over
$(g',\lambda )$
is in reality a sum only over
![]() $\lambda $
. There exists
$\lambda $
. There exists
![]() $g' \in G_b(F)$
with
$g' \in G_b(F)$
with
![]() $\kappa (\mathrm {inv}[b](g,g'))$
being the image of
$\kappa (\mathrm {inv}[b](g,g'))$
being the image of
![]() $\lambda $
in
$\lambda $
in
![]() $X_*(T)_{\Gamma }$
if and only if the image of
$X_*(T)_{\Gamma }$
if and only if the image of
![]() $\lambda $
under
$\lambda $
under
![]() $X_*(T) \to X_*(T)_{\Gamma } \to \pi _1(G)_{\Gamma }$
equals
$X_*(T) \to X_*(T)_{\Gamma } \to \pi _1(G)_{\Gamma }$
equals
![]() $\kappa (b)$
. Since the image of
$\kappa (b)$
. Since the image of
![]() $\mu $
in
$\mu $
in
![]() $\pi _1(G)_{\Gamma }$
also equals
$\pi _1(G)_{\Gamma }$
also equals
![]() $\kappa (b)$
, the sum over
$\kappa (b)$
, the sum over
![]() $(g',\lambda )$
is in fact the sum over
$(g',\lambda )$
is in fact the sum over
![]() $\lambda \in X_*(T)$
having the same image as
$\lambda \in X_*(T)$
having the same image as
![]() $\mu $
in
$\mu $
in
![]() $\pi _1(G)_{\Gamma }$
. In terms of the dual torus
$\pi _1(G)_{\Gamma }$
. In terms of the dual torus
![]() $\widehat T$
, this is the sum over
$\widehat T$
, this is the sum over
![]() $\lambda \in X^*(\widehat T)$
whose restriction to
$\lambda \in X^*(\widehat T)$
whose restriction to
![]() $Z(\widehat G)^{\Gamma }$
equals that of
$Z(\widehat G)^{\Gamma }$
equals that of
![]() $\mu $
. Since, for
$\mu $
. Since, for
![]() $\lambda $
not satisfying this condition the number
$\lambda $
not satisfying this condition the number
![]() $\mathrm {dim}r_{\mu }[\lambda ]$
is zero, we may extend the sum to be over all
$\mathrm {dim}r_{\mu }[\lambda ]$
is zero, we may extend the sum to be over all
![]() $\lambda \in X_*(T)=X^*(\widehat T)$
.
$\lambda \in X_*(T)=X^*(\widehat T)$
.
We now continue with the equation. Multiply both sides of the above equation by
![]() $\operatorname {\mathrm {tr}}\check \tau _{z,\mathfrak {w},\rho }(\dot s)$
. As functions of
$\operatorname {\mathrm {tr}}\check \tau _{z,\mathfrak {w},\rho }(\dot s)$
. As functions of
![]() $\dot s \in S_{\phi }^+$
, both sides then become invariant under
$\dot s \in S_{\phi }^+$
, both sides then become invariant under
![]() $Z(\widehat {\bar G})^+$
and thus become functions of the finite quotient
$Z(\widehat {\bar G})^+$
and thus become functions of the finite quotient
![]() $\bar S_{\phi } = S_{\phi }^+/Z(\widehat {\bar G})^+=S_{\phi }/Z(\widehat G)^{\Gamma }$
. Now apply
$\bar S_{\phi } = S_{\phi }^+/Z(\widehat {\bar G})^+=S_{\phi }/Z(\widehat G)^{\Gamma }$
. Now apply
![]() $\left \lvert \bar S_{\phi } \right \rvert ^{-1}\sum _{\bar s \in \bar S_{\phi }}$
to both sides to obtain an equality between
$\left \lvert \bar S_{\phi } \right \rvert ^{-1}\sum _{\bar s \in \bar S_{\phi }}$
to both sides to obtain an equality between
 $$ \begin{align} \left\lvert \bar S_{\phi} \right\rvert^{-1} e(G_b)\sum_{\bar s \in \bar S_{\phi}} \sum_{(g',\lambda)} \sum_{\rho'\in \Pi_{\phi}(G_b)} \operatorname{\mathrm{tr}}\check\tau_{z,\mathfrak{w},\rho}(\dot s)\operatorname{\mathrm{tr}}\tau_{z,\mathfrak{w},\rho'}(\dot s)\Theta_{\rho'}(g')\dim r_{\mu}[\lambda] \end{align} $$
$$ \begin{align} \left\lvert \bar S_{\phi} \right\rvert^{-1} e(G_b)\sum_{\bar s \in \bar S_{\phi}} \sum_{(g',\lambda)} \sum_{\rho'\in \Pi_{\phi}(G_b)} \operatorname{\mathrm{tr}}\check\tau_{z,\mathfrak{w},\rho}(\dot s)\operatorname{\mathrm{tr}}\tau_{z,\mathfrak{w},\rho'}(\dot s)\Theta_{\rho'}(g')\dim r_{\mu}[\lambda] \end{align} $$
and
 $$ \begin{align} \left\lvert \bar S_{\phi} \right\rvert^{-1}e(G) \sum_{\bar s \in \bar S_{\phi}}\operatorname{\mathrm{tr}} r_{\mu}(s^{\natural})\sum_{\pi\in \Pi_{\phi}(G)} \operatorname{\mathrm{tr}}\check\tau_{z,\mathfrak{w},\rho}(\dot s) \operatorname{\mathrm{tr}}\tau_{z,\mathfrak{w},\pi}(\dot s)\Theta_{\pi}(g), \end{align} $$
$$ \begin{align} \left\lvert \bar S_{\phi} \right\rvert^{-1}e(G) \sum_{\bar s \in \bar S_{\phi}}\operatorname{\mathrm{tr}} r_{\mu}(s^{\natural})\sum_{\pi\in \Pi_{\phi}(G)} \operatorname{\mathrm{tr}}\check\tau_{z,\mathfrak{w},\rho}(\dot s) \operatorname{\mathrm{tr}}\tau_{z,\mathfrak{w},\pi}(\dot s)\Theta_{\pi}(g), \end{align} $$
where in both formulas
![]() $\dot s$
is an arbitrary lift of
$\dot s$
is an arbitrary lift of
![]() $\bar s$
and
$\bar s$
and
![]() $s^{\natural } \in S_{\phi }$
is the image of
$s^{\natural } \in S_{\phi }$
is the image of
![]() $\dot s$
under equation (2.3.2). Executing the sum over
$\dot s$
under equation (2.3.2). Executing the sum over
![]() $\bar s$
in equation (3.3.1) gives
$\bar s$
in equation (3.3.1) gives
 $$\begin{align*}e(G_b)\sum_{(g',\lambda)} \Theta_{\rho}(g')\dim r_{\mu}[\lambda] = e(G_b)[T^{G_b\to G}_{b,\mu}\Theta_{\rho}](g). \end{align*}$$
$$\begin{align*}e(G_b)\sum_{(g',\lambda)} \Theta_{\rho}(g')\dim r_{\mu}[\lambda] = e(G_b)[T^{G_b\to G}_{b,\mu}\Theta_{\rho}](g). \end{align*}$$
To treat equation (3.3.2) note that
![]() $\check \tau _{z,\mathfrak {w},\rho }\otimes \tau _{z,\mathfrak {w},\pi }(\dot s) = \check {\delta }_{\pi ,\rho }(s^{\natural })$
. Furthermore, the composition of the map (2.3.2) with the natural projection
$\check \tau _{z,\mathfrak {w},\rho }\otimes \tau _{z,\mathfrak {w},\pi }(\dot s) = \check {\delta }_{\pi ,\rho }(s^{\natural })$
. Furthermore, the composition of the map (2.3.2) with the natural projection
![]() $S_{\phi } \to S_{\phi }/Z(\widehat G)^{\Gamma }$
is equal to the natural projection
$S_{\phi } \to S_{\phi }/Z(\widehat G)^{\Gamma }$
is equal to the natural projection
![]() $S_{\phi }^+ \to S_{\phi }^+/Z(\widehat {\bar G})^+ = S_{\phi }/Z(\widehat G)^{\Gamma } = \bar S_{\phi }$
. Thus,
$S_{\phi }^+ \to S_{\phi }^+/Z(\widehat {\bar G})^+ = S_{\phi }/Z(\widehat G)^{\Gamma } = \bar S_{\phi }$
. Thus,
![]() $s^{\natural }$
is simply a lift of
$s^{\natural }$
is simply a lift of
![]() $\bar s$
to
$\bar s$
to
![]() $S_{\phi }$
. We find that equation (3.3.2) equals
$S_{\phi }$
. We find that equation (3.3.2) equals
 $$\begin{align*}e(G)\left\lvert \bar S_{\phi} \right\rvert^{-1} \sum_{\bar s \in \bar S_{\phi}}\operatorname{\mathrm{tr}} r_{\mu}(s^{\natural}) \operatorname{\mathrm{tr}}\check{\delta}_{\pi,\rho}(s^{\natural}) = e(G)\dim \operatorname{\mathrm{Hom}}_{S_{\phi}}(\delta_{\pi,\rho}, r_{\mu}).\end{align*}$$
$$\begin{align*}e(G)\left\lvert \bar S_{\phi} \right\rvert^{-1} \sum_{\bar s \in \bar S_{\phi}}\operatorname{\mathrm{tr}} r_{\mu}(s^{\natural}) \operatorname{\mathrm{tr}}\check{\delta}_{\pi,\rho}(s^{\natural}) = e(G)\dim \operatorname{\mathrm{Hom}}_{S_{\phi}}(\delta_{\pi,\rho}, r_{\mu}).\end{align*}$$
We have now reduced Theorem 3.2.9 to the identity
where
![]() $\rho _G$
is the sum of the positive roots. Recall that
$\rho _G$
is the sum of the positive roots. Recall that
![]() $G^*$
is a quasi-split inner form of G. Let
$G^*$
is a quasi-split inner form of G. Let
![]() $\mu _1,\mu _2 \in X^*(Z(\widehat G_{\mathrm {sc}})^{\Gamma })$
be the elements corresponding to the inner twists
$\mu _1,\mu _2 \in X^*(Z(\widehat G_{\mathrm {sc}})^{\Gamma })$
be the elements corresponding to the inner twists
![]() $G^* \to G$
and
$G^* \to G$
and
![]() $G^* \to G_b$
by Kottwitz’s homomorphism [Reference KottwitzKot86, Theorem 1.2]. By Lemma A.2.1, we have
$G^* \to G_b$
by Kottwitz’s homomorphism [Reference KottwitzKot86, Theorem 1.2]. By Lemma A.2.1, we have
![]() $e(G_b)e(G)=(-1)^{\langle 2\rho ,\mu _2-\mu _1\rangle }$
. But since
$e(G_b)e(G)=(-1)^{\langle 2\rho ,\mu _2-\mu _1\rangle }$
. But since
![]() $G_b$
is obtained from G by twisting by b, the difference
$G_b$
is obtained from G by twisting by b, the difference
![]() $\mu _2-\mu _1$
is equal to the image of
$\mu _2-\mu _1$
is equal to the image of
![]() $\kappa (b) \in X^*(Z(\widehat G)^{\Gamma })$
under the map
$\kappa (b) \in X^*(Z(\widehat G)^{\Gamma })$
under the map
![]() $X^*(Z(\widehat G)^{\Gamma }) \to X^*(Z(\widehat G_{\mathrm {sc}})^{\Gamma })$
dual to the natural map
$X^*(Z(\widehat G)^{\Gamma }) \to X^*(Z(\widehat G_{\mathrm {sc}})^{\Gamma })$
dual to the natural map
![]() $Z(\widehat G_{\mathrm {sc}}) \to Z(\widehat G)$
. Since
$Z(\widehat G_{\mathrm {sc}}) \to Z(\widehat G)$
. Since
![]() $b \in B(G,\mu )$
, we see that
$b \in B(G,\mu )$
, we see that
![]() $\mu _2-\mu _1=\mu $
, and equation (3.3.3) follows. The proof of Theorem 3.2.9 is complete.
$\mu _2-\mu _1=\mu $
, and equation (3.3.3) follows. The proof of Theorem 3.2.9 is complete.
3.4 An adjointness property
In this section, we will discuss an adjointness property of the Hecke transfer maps
![]() $T_{b,\mu }^{G \to G_b}$
. This will be used in §6.3.
$T_{b,\mu }^{G \to G_b}$
. This will be used in §6.3.
Let
![]() $\Lambda $
be an algebraically closed field of characteristic zero. For a topological space X, we let
$\Lambda $
be an algebraically closed field of characteristic zero. For a topological space X, we let
![]() $C_c(X,\Lambda )$
be the space of compactly supported locally constant
$C_c(X,\Lambda )$
be the space of compactly supported locally constant
![]() $\Lambda $
-valued functions. The space of distributions
$\Lambda $
-valued functions. The space of distributions
![]() $\operatorname {\mathrm {Dist}}(G(F),\Lambda )$
is the
$\operatorname {\mathrm {Dist}}(G(F),\Lambda )$
is the
![]() $\Lambda $
-linear dual of
$\Lambda $
-linear dual of
![]() $C_c(G(F),\Lambda )$
. The subspace of invariant distributions
$C_c(G(F),\Lambda )$
. The subspace of invariant distributions
![]() $\operatorname {\mathrm {Dist}}(G(F),\Lambda )^{G(F)}$
is the linear dual of the space of coinvariants
$\operatorname {\mathrm {Dist}}(G(F),\Lambda )^{G(F)}$
is the linear dual of the space of coinvariants
![]() $C_c(G(F),\Lambda )_{G(F)}$
.
$C_c(G(F),\Lambda )_{G(F)}$
.
Given a
![]() $\Lambda $
-valued Haar measure
$\Lambda $
-valued Haar measure
![]() $dx$
on
$dx$
on
![]() $G(F)$
, integration against a function
$G(F)$
, integration against a function
![]() is a
is a
![]() $G(F)$
-invariant distribution on
$G(F)$
-invariant distribution on
![]() $G(F)$
. Due to the functions in
$G(F)$
. Due to the functions in
![]() $C_c(G(F),\Lambda )$
being locally constant and having compact support, the ‘integral’ is in reality a finite sum. For our purposes, we will work with functions
$C_c(G(F),\Lambda )$
being locally constant and having compact support, the ‘integral’ is in reality a finite sum. For our purposes, we will work with functions
![]() and integrate them against test functions in
and integrate them against test functions in
![]() $C_c(G(F)_{\mathrm {sr}})$
.
$C_c(G(F)_{\mathrm {sr}})$
.
The Weyl integration formula can be used to compute this distribution in terms of orbital integrals. In fact, we will need a ‘stable’ variant of this formula. Before we can explain this, we need to discuss choices of measures.
Choose a
![]() $\Lambda $
-valued Haar measure on F. Then a choice of an element
$\Lambda $
-valued Haar measure on F. Then a choice of an element
![]() $\eta \in \bigwedge ^{\dim (G)}(\mathrm {Lie}(G)(F)^*)=\bigwedge ^{\dim (G)}(\mathrm {Lie}(G)^*)(F)$
leads to a
$\eta \in \bigwedge ^{\dim (G)}(\mathrm {Lie}(G)(F)^*)=\bigwedge ^{\dim (G)}(\mathrm {Lie}(G)^*)(F)$
leads to a
![]() $\Lambda $
-valued Haar measure
$\Lambda $
-valued Haar measure
![]() $dx_{\eta }$
on
$dx_{\eta }$
on
![]() $G(F)$
; note that multiplying
$G(F)$
; note that multiplying
![]() $\eta $
by an element of
$\eta $
by an element of
![]() $\mathcal {O}_F^{\times }$
doesn’t affect the measure
$\mathcal {O}_F^{\times }$
doesn’t affect the measure
![]() $dx_{\eta }$
. More generally, any element of
$dx_{\eta }$
. More generally, any element of
![]() $\bigwedge ^{\dim (G)}(\mathrm {Lie}(G)^*)(\breve F)$
leads to a
$\bigwedge ^{\dim (G)}(\mathrm {Lie}(G)^*)(\breve F)$
leads to a
![]() $\Lambda $
-valued Haar measure
$\Lambda $
-valued Haar measure
![]() $dx_{\eta }$
on
$dx_{\eta }$
on
![]() $G(F)$
by choosing
$G(F)$
by choosing
![]() $a \in \mathcal {O}_{\breve F}^{\times }$
with the property that
$a \in \mathcal {O}_{\breve F}^{\times }$
with the property that
![]() $a\eta \in \bigwedge ^{\dim (G)}(\mathrm {Lie}(G)^*)(F)$
and defining
$a\eta \in \bigwedge ^{\dim (G)}(\mathrm {Lie}(G)^*)(F)$
and defining
![]() $dx_{\eta } := dx_{a\eta }$
, noting that this does not depend on the choice of a. In fact, this procedure allows us to even attach a measure to an element
$dx_{\eta } := dx_{a\eta }$
, noting that this does not depend on the choice of a. In fact, this procedure allows us to even attach a measure to an element
![]() $\eta \in \bigwedge ^{\dim (G)}(\mathrm {Lie}(G)^*)(\overline {F})$
by taking
$\eta \in \bigwedge ^{\dim (G)}(\mathrm {Lie}(G)^*)(\overline {F})$
by taking
![]() $a \in \overline {F}^{\times }$
such that
$a \in \overline {F}^{\times }$
such that
![]() $a\eta \in \bigwedge ^{\dim (G)}(\mathrm {Lie}(G)^*)(F)$
and letting
$a\eta \in \bigwedge ^{\dim (G)}(\mathrm {Lie}(G)^*)(F)$
and letting
![]() $dx_{\eta } := |a|_{\Lambda }^{-1}dx_{a\eta }$
. But for this we need to make sense of
$dx_{\eta } := |a|_{\Lambda }^{-1}dx_{a\eta }$
. But for this we need to make sense of
![]() $|a|_{\Lambda }$
, which requires choosing a compatible system of roots of p in
$|a|_{\Lambda }$
, which requires choosing a compatible system of roots of p in
![]() $\Lambda $
. For us, elements of
$\Lambda $
. For us, elements of
![]() $\bigwedge ^{\dim (G)}(\mathrm {Lie}(G)^*)(\breve F)$
will suffice, so we will not make such a choice.
$\bigwedge ^{\dim (G)}(\mathrm {Lie}(G)^*)(\breve F)$
will suffice, so we will not make such a choice.
This procedure allows us to choose Haar measures compatibly in the following two situations. First, consider the inner forms G and
![]() $G_b$
. They are canonically identified over
$G_b$
. They are canonically identified over
![]() $\breve F$
, which gives an identification
$\breve F$
, which gives an identification
![]() $\bigwedge ^{\dim (G)}(\mathrm {Lie}(G)^*)(\breve F)= \bigwedge ^{\dim (G)}(\mathrm {Lie}(G_b)^*)(\breve F)$
. Haar measures on
$\bigwedge ^{\dim (G)}(\mathrm {Lie}(G)^*)(\breve F)= \bigwedge ^{\dim (G)}(\mathrm {Lie}(G_b)^*)(\breve F)$
. Haar measures on
![]() $G(F)$
and
$G(F)$
and
![]() $G_b(F)$
corresponding to the same
$G_b(F)$
corresponding to the same
![]() $\eta $
will be called compatible. Second, consider two maximal F-rational tori
$\eta $
will be called compatible. Second, consider two maximal F-rational tori
![]() $T_1$
and
$T_1$
and
![]() $T_2$
, each either in G or
$T_2$
, each either in G or
![]() $G_b$
. They are called related if there exists
$G_b$
. They are called related if there exists
![]() $g \in G(\overline {F})$
or, equivalently (cf. Lemma 3.2.1)
$g \in G(\overline {F})$
or, equivalently (cf. Lemma 3.2.1)
![]() $g \in G(\breve F)$
such that
$g \in G(\breve F)$
such that
![]() $gT_1g^{-1}=T_2$
and the isomorphism
$gT_1g^{-1}=T_2$
and the isomorphism
![]() $\mathrm {Ad}(g) :T_1 \to T_2$
is F-rational; we are using here the identification
$\mathrm {Ad}(g) :T_1 \to T_2$
is F-rational; we are using here the identification
![]() $G_{\breve F} = (G_b)_{\breve F}$
. We obtain an isomorphism
$G_{\breve F} = (G_b)_{\breve F}$
. We obtain an isomorphism
![]() $\mathrm {Ad}(g) : \bigwedge ^{\dim (G)}(\mathrm {Lie}(T_1)^*)(\breve F)= \bigwedge ^{\dim (G)}(\mathrm {Lie}(T_2)^*)(\breve F)$
, which leads again to the notion of compatible measures on
$\mathrm {Ad}(g) : \bigwedge ^{\dim (G)}(\mathrm {Lie}(T_1)^*)(\breve F)= \bigwedge ^{\dim (G)}(\mathrm {Lie}(T_2)^*)(\breve F)$
, which leads again to the notion of compatible measures on
![]() $T_1(F)$
and
$T_1(F)$
and
![]() $T_2(F)$
. The choice of
$T_2(F)$
. The choice of
![]() $g \in G(\breve F)$
is unique up to multiplication by
$g \in G(\breve F)$
is unique up to multiplication by
![]() $N(T_1,G)(\breve F)$
, and since this group acts on
$N(T_1,G)(\breve F)$
, and since this group acts on
![]() $\bigwedge ^{\dim (G)}(\mathrm {Lie}(T_1)^*)(\breve F)$
via a
$\bigwedge ^{\dim (G)}(\mathrm {Lie}(T_1)^*)(\breve F)$
via a
![]() $\mathcal {O}_{\breve F}^{\times }$
-valued character of the Weyl group, the notion of compatible measures does not depend on the choice of g.
$\mathcal {O}_{\breve F}^{\times }$
-valued character of the Weyl group, the notion of compatible measures does not depend on the choice of g.
From now on, we assume that the Haar measures on
![]() $G(F)$
and
$G(F)$
and
![]() $G_b(F)$
have been chosen compatibly, and the Haar measures on all tori of G and
$G_b(F)$
have been chosen compatibly, and the Haar measures on all tori of G and
![]() $G_b$
that are related to each other have been chosen compatibly.
$G_b$
that are related to each other have been chosen compatibly.
We now return to the discussion of distributions. For
![]() $\phi \in C_c(G(F)_{\mathrm {sr}},\Lambda )$
, let
$\phi \in C_c(G(F)_{\mathrm {sr}},\Lambda )$
, let
![]() be the orbital integral function,
be the orbital integral function,
 $$\begin{align*}\phi_G(y) = \int_{x\in G(F)/G(F)_y} \phi(xyx^{-1})\; dx.\end{align*}$$
$$\begin{align*}\phi_G(y) = \int_{x\in G(F)/G(F)_y} \phi(xyx^{-1})\; dx.\end{align*}$$
As remarked by the referee, the map
![]() $\phi \to \phi _G$
induces an isomorphism
$\phi \to \phi _G$
induces an isomorphism
cf. Lemma 3.1.1. The stable Weyl integration formula states
We explain now the notation
![]() $\left < f,\phi _G \right>_G$
. For a function
$\left < f,\phi _G \right>_G$
. For a function
![]() , we define
, we define
 $$\begin{align*}\left< f,h \right>_G = \sum_{T} \left\lvert W(T,G)(F) \right\rvert^{-1}\int_{t \in T(F)_{\operatorname{\mathrm{sr}}}} \left\lvert D(t) \right\rvert \sum_{t_0 \sim t} f(t_0)h(t_0)dt, \end{align*}$$
$$\begin{align*}\left< f,h \right>_G = \sum_{T} \left\lvert W(T,G)(F) \right\rvert^{-1}\int_{t \in T(F)_{\operatorname{\mathrm{sr}}}} \left\lvert D(t) \right\rvert \sum_{t_0 \sim t} f(t_0)h(t_0)dt, \end{align*}$$
where
-
• T runs over a set of representatives for the stable classes of maximal tori,
-
•
 $W(T,G)=N(T,G)/T$
is the absolute Weyl group,
$W(T,G)=N(T,G)/T$
is the absolute Weyl group, -
•
 $D(t)=\det \left (\operatorname {\mathrm {Ad}}(t)-1\biggm \vert \operatorname {\mathrm {Lie}} G/\operatorname {\mathrm {Lie}} T\right )$
is the usual Weyl discriminant and
$D(t)=\det \left (\operatorname {\mathrm {Ad}}(t)-1\biggm \vert \operatorname {\mathrm {Lie}} G/\operatorname {\mathrm {Lie}} T\right )$
is the usual Weyl discriminant and -
•
 $t_0$
runs over the
$t_0$
runs over the
 $G(F)$
-conjugacy classes inside of the stable class of t.
$G(F)$
-conjugacy classes inside of the stable class of t.
Note that the integral does not depend on the chosen representative since any two are isomorphic over F by definition of stable conjugacy, and the isomorphism is canonical up to the action of the Weyl group
![]() $W(T,G)(F)$
, which is irrelevant given the sum
$W(T,G)(F)$
, which is irrelevant given the sum
![]() $t_0 \sim t$
.
$t_0 \sim t$
.
The following lemma shows that the Hecke transfer maps
![]() $T_{b,\mu }^{G\to G_b}$
and
$T_{b,\mu }^{G\to G_b}$
and
![]() $T_{b,\mu }^{G_b\to G}$
are adjoint with respect to the pairing
$T_{b,\mu }^{G_b\to G}$
are adjoint with respect to the pairing
![]() $\left < \cdot ,\cdot \right>_G$
and its analogue
$\left < \cdot ,\cdot \right>_G$
and its analogue
![]() $\left < \cdot ,\cdot \right>_{G_b}$
, defined similarly.
$\left < \cdot ,\cdot \right>_{G_b}$
, defined similarly.
Lemma 3.4.1. Given
![]() and
and
![]() , one of which has compact support, we have
, one of which has compact support, we have
Proof. By definition
![]() $\langle T_{b,\mu }^{G_b \to G}f',f\rangle _G$
equals
$\langle T_{b,\mu }^{G_b \to G}f',f\rangle _G$
equals
 $$ \begin{align} (-1)^d\sum_T |W(T,G)(F)|^{-1}\int_{t \in T(F)_{\operatorname{\mathrm{sr}}}} |D(t)| \sum_{t_0 \sim t} \sum_{(t_0,t_0',\lambda)}r_{\mu,\lambda}f'(t_0')f(t_0)dt. \end{align} $$
$$ \begin{align} (-1)^d\sum_T |W(T,G)(F)|^{-1}\int_{t \in T(F)_{\operatorname{\mathrm{sr}}}} |D(t)| \sum_{t_0 \sim t} \sum_{(t_0,t_0',\lambda)}r_{\mu,\lambda}f'(t_0')f(t_0)dt. \end{align} $$
The first sum runs over a set of representatives for the stable classes of maximal tori in G. The second sum runs over the set
![]() $t_0$
of
$t_0$
of
![]() $G(F)$
-conjugacy classes of elements that are stably conjugate to t. Let
$G(F)$
-conjugacy classes of elements that are stably conjugate to t. Let
![]() $T_{t_0}$
denote the centralizer of
$T_{t_0}$
denote the centralizer of
![]() $t_0$
. The third sum runs over triples
$t_0$
. The third sum runs over triples
![]() $(t_0,t_0',\lambda )$
, where
$(t_0,t_0',\lambda )$
, where
![]() $t_0'$
is a
$t_0'$
is a
![]() $G_b(F)$
-conjugacy class that is stably conjugate to
$G_b(F)$
-conjugacy class that is stably conjugate to
![]() $t_0$
, and
$t_0$
, and
![]() $\lambda \in X_*(T_{t_0})$
maps to
$\lambda \in X_*(T_{t_0})$
maps to
![]() $\mathrm {inv}(t_0,t_0') \in X_*(T_{t_0})_{\Gamma }$
. Note that if T does not transfer to
$\mathrm {inv}(t_0,t_0') \in X_*(T_{t_0})_{\Gamma }$
. Note that if T does not transfer to
![]() $G_b$
, then it does not contribute to the sum because the sum over
$G_b$
, then it does not contribute to the sum because the sum over
![]() $(t_0,t_0',\lambda )$
is empty. Let
$(t_0,t_0',\lambda )$
is empty. Let
![]() $\mathcal {X}$
be a set of representatives for those stable classes of maximal tori in G that transfer to
$\mathcal {X}$
be a set of representatives for those stable classes of maximal tori in G that transfer to
![]() $G_b$
. The above expression becomes
$G_b$
. The above expression becomes
 $$\begin{align*}(-1)^d\sum_{T \in \mathcal{X}} |W(T,G)(F)|^{-1}\int_{t \in T(F)_{\operatorname{\mathrm{sr}}}} |D(t)| \sum_{(t_0,t_0',\lambda)}r_{\mu,\lambda}f'(t_0')f(t_0)dt, \end{align*}$$
$$\begin{align*}(-1)^d\sum_{T \in \mathcal{X}} |W(T,G)(F)|^{-1}\int_{t \in T(F)_{\operatorname{\mathrm{sr}}}} |D(t)| \sum_{(t_0,t_0',\lambda)}r_{\mu,\lambda}f'(t_0')f(t_0)dt, \end{align*}$$
where now the second sum runs over triples
![]() $(t_0,t_0',\lambda )$
with
$(t_0,t_0',\lambda )$
with
![]() $t_0$
a
$t_0$
a
![]() $G(F)$
-conjugacy class and
$G(F)$
-conjugacy class and
![]() $t_0'$
a
$t_0'$
a
![]() $G_b(F)$
-conjugacy class, both stably conjugate to t, and
$G_b(F)$
-conjugacy class, both stably conjugate to t, and
![]() $\lambda \in X_*(T_{t_0})$
mapping to
$\lambda \in X_*(T_{t_0})$
mapping to
![]() $\mathrm {inv}(t_0,t_0') \in X_*(T_{t_0})_{\Gamma }$
.
$\mathrm {inv}(t_0,t_0') \in X_*(T_{t_0})_{\Gamma }$
.
Let
![]() $\mathcal {X}'$
be a set of representatives for those stable classes of maximal tori of
$\mathcal {X}'$
be a set of representatives for those stable classes of maximal tori of
![]() $G_b$
that transfer to G. We have a bijection
$G_b$
that transfer to G. We have a bijection
![]() $\mathcal {X} \leftrightarrow \mathcal {X}'$
. Fix arbitrarily an admissible isomorphism
$\mathcal {X} \leftrightarrow \mathcal {X}'$
. Fix arbitrarily an admissible isomorphism
![]() $T \to T'$
for any
$T \to T'$
for any
![]() $T \in \mathcal {X}$
and
$T \in \mathcal {X}$
and
![]() $T' \in \mathcal {X}'$
that correspond under this bijection. It induces an isomorphism
$T' \in \mathcal {X}'$
that correspond under this bijection. It induces an isomorphism
![]() $W(T,G) \to W(T',G_b)$
of finite algebraic groups, as well as an isomorphism
$W(T,G) \to W(T',G_b)$
of finite algebraic groups, as well as an isomorphism
![]() $T(F) \to T'(F)$
of toplogical groups that preserves the chosen measures (since we have arranged the measures to be compatible). Given
$T(F) \to T'(F)$
of toplogical groups that preserves the chosen measures (since we have arranged the measures to be compatible). Given
![]() $t \in T(F)_{\operatorname {\mathrm {sr}}}$
, let
$t \in T(F)_{\operatorname {\mathrm {sr}}}$
, let
![]() $t' \in T'(F)_{\operatorname {\mathrm {sr}}}$
be its image under the admissible isomorphism. Then
$t' \in T'(F)_{\operatorname {\mathrm {sr}}}$
be its image under the admissible isomorphism. Then
![]() $|D(t)|=|D(t')|$
, and equation (3.4.3) becomes
$|D(t)|=|D(t')|$
, and equation (3.4.3) becomes
 $$ \begin{align} (-1)^d\sum_{T' \in \mathcal{X}'} |W(T',G_b)(F)|^{-1}\int_{t' \in T^{\prime}_{\operatorname{\mathrm{sr}}}(F)} |D(t')| \sum_{(t_0,t_0',\lambda)}r_{\mu,\lambda}f'(t_0')f(t_0)dt, \end{align} $$
$$ \begin{align} (-1)^d\sum_{T' \in \mathcal{X}'} |W(T',G_b)(F)|^{-1}\int_{t' \in T^{\prime}_{\operatorname{\mathrm{sr}}}(F)} |D(t')| \sum_{(t_0,t_0',\lambda)}r_{\mu,\lambda}f'(t_0')f(t_0)dt, \end{align} $$
where now the second sum runs over triples
![]() $(t_0,t_0',\lambda )$
, where
$(t_0,t_0',\lambda )$
, where
![]() $t_0$
is a
$t_0$
is a
![]() $G(F)$
-conjugacy class,
$G(F)$
-conjugacy class,
![]() $t_0'$
is a
$t_0'$
is a
![]() $G_b(F)$
-conjugacy class, both are stably conjugate to
$G_b(F)$
-conjugacy class, both are stably conjugate to
![]() $t'$
and
$t'$
and
![]() $\lambda \in X_*(T_{t_0})$
maps to
$\lambda \in X_*(T_{t_0})$
maps to
![]() $\mathrm {inv}(t_0,t_0') \in X_*(T_{t_0})_{\Gamma }$
. Reversing the arguments from the beginning of this proof, we see that this expression equals
$\mathrm {inv}(t_0,t_0') \in X_*(T_{t_0})_{\Gamma }$
. Reversing the arguments from the beginning of this proof, we see that this expression equals
![]() $\langle f',T_{b,\mu }^{G \to G_b}f\rangle _{G_b}$
.
$\langle f',T_{b,\mu }^{G \to G_b}f\rangle _{G_b}$
.
In §6.3, we will define by geometric means an operator
and show (Proposition 6.3.3) that
![]() $T_{b,\mu }^{G \to G_b}$
corresponds to
$T_{b,\mu }^{G \to G_b}$
corresponds to
![]() $\widetilde T_{b,\mu }^{G \to G_b}$
under equation (3.4.1).
$\widetilde T_{b,\mu }^{G \to G_b}$
under equation (3.4.1).
4 The Lefschetz–Verdier trace formula for v-stacks
The goal of this section is to build up some machinery related to the Lefschetz–Verdier trace formula.
We briefly review the setup in the context of a separated finite-type morphism of schemes
![]() $p\colon X\to \operatorname {\mathrm {Spec}} k$
, where k is an algebraically closed field. Let
$p\colon X\to \operatorname {\mathrm {Spec}} k$
, where k is an algebraically closed field. Let
![]() $\ell $
be a prime unequal to the characteristic of k, and let A be an object of
$\ell $
be a prime unequal to the characteristic of k, and let A be an object of
![]() $D(X_{\mathrm {\acute {e}t}},\overline {\mathbf {Q}}_{\ell })$
, the derived category of étale
$D(X_{\mathrm {\acute {e}t}},\overline {\mathbf {Q}}_{\ell })$
, the derived category of étale
![]() $\overline {\mathbf {Q}}_{\ell }$
-sheaves on X. Suppose
$\overline {\mathbf {Q}}_{\ell }$
-sheaves on X. Suppose
![]() $f\colon X\to X$
is a k-linear endomorphism. If we are given the additional datum of a morphismFootnote 1
$f\colon X\to X$
is a k-linear endomorphism. If we are given the additional datum of a morphismFootnote 1
![]() $Rf_!A\to A$
, we obtain an operator
$Rf_!A\to A$
, we obtain an operator
![]() $Rp_!A\cong Rp_!Rf_!A\to Rp_!A$
on the compactly supported cohomology
$Rp_!A\cong Rp_!Rf_!A\to Rp_!A$
on the compactly supported cohomology
![]() $Rp_!A=R\Gamma _c(X,A)$
.
$Rp_!A=R\Gamma _c(X,A)$
.
In the special case that X is proper over k so that
![]() $R\Gamma _c(X,A)=R\Gamma (X,A)$
, the Lefschetz–Verdier trace formula [SGA77], [Reference VarshavskyVar07] expresses
$R\Gamma _c(X,A)=R\Gamma (X,A)$
, the Lefschetz–Verdier trace formula [SGA77], [Reference VarshavskyVar07] expresses
![]() $\operatorname {\mathrm {tr}} (f\vert R\Gamma (X,A))$
in terms of data living on the fixed point locus
$\operatorname {\mathrm {tr}} (f\vert R\Gamma (X,A))$
in terms of data living on the fixed point locus
![]() $\operatorname {\mathrm {Fix}}(f)$
of f. In particular, at isolated fixed points
$\operatorname {\mathrm {Fix}}(f)$
of f. In particular, at isolated fixed points
![]() $x\in \operatorname {\mathrm {Fix}}(f)$
, there are local terms
$x\in \operatorname {\mathrm {Fix}}(f)$
, there are local terms
![]() $\operatorname {\mathrm {loc}}_x(f,A) \in \overline {\mathbf {Q}}_{\ell }$
, and if all fixed points are isolated, then
$\operatorname {\mathrm {loc}}_x(f,A) \in \overline {\mathbf {Q}}_{\ell }$
, and if all fixed points are isolated, then
![]() $\operatorname {\mathrm {tr}} (f\vert R\Gamma (X,A))$
is the sum of the
$\operatorname {\mathrm {tr}} (f\vert R\Gamma (X,A))$
is the sum of the
![]() $\operatorname {\mathrm {loc}}_x(f,A)$
.
$\operatorname {\mathrm {loc}}_x(f,A)$
.
In order to apply the Lefschetz–Verdier trace formula, we need to assume that A satisfies a suitable finiteness hypothesis (constructible of bounded amplitude). Under this hypothesis, one establishes an isomorphism [SGA77, Exposé III, (3.1.1)]
in
![]() $D((X\times _k X)_{\mathrm {\acute {e}t}},\overline {\mathbf {Q}}_{\ell })$
, where
$D((X\times _k X)_{\mathrm {\acute {e}t}},\overline {\mathbf {Q}}_{\ell })$
, where
![]() $\operatorname {\mathrm {pr}}_1,\operatorname {\mathrm {pr}}_2\colon X\times _k X\to X$
are the projection maps, and
$\operatorname {\mathrm {pr}}_1,\operatorname {\mathrm {pr}}_2\colon X\times _k X\to X$
are the projection maps, and
![]() $\mathbf {D}$
is Verdier duality relative to k. Once equation (4.0.1) is established, the definition of local terms and the validity of the Lefschetz–Verdier trace formula can be derived by applying Grothendieck’s six functor formalism. The special case where
$\mathbf {D}$
is Verdier duality relative to k. Once equation (4.0.1) is established, the definition of local terms and the validity of the Lefschetz–Verdier trace formula can be derived by applying Grothendieck’s six functor formalism. The special case where
![]() $X=\operatorname {\mathrm {Spec}} k$
is instructive; the finiteness condition on A is that it be a perfect complex of
$X=\operatorname {\mathrm {Spec}} k$
is instructive; the finiteness condition on A is that it be a perfect complex of
![]() $\overline {\mathbf {Q}}_{\ell }$
-vector spaces, and then equation (4.0.1) reduces to the fact that
$\overline {\mathbf {Q}}_{\ell }$
-vector spaces, and then equation (4.0.1) reduces to the fact that
![]() $A^{\vee }\otimes ^{\mathbf {L}} A\to \operatorname {RHom}(A,A)$
is an isomorphism. This allows us to express the trace of an endomorphism
$A^{\vee }\otimes ^{\mathbf {L}} A\to \operatorname {RHom}(A,A)$
is an isomorphism. This allows us to express the trace of an endomorphism
![]() $f\in \operatorname {\mathrm {End}} A$
as the image of f under the evaluation map
$f\in \operatorname {\mathrm {End}} A$
as the image of f under the evaluation map
![]() $A^{\vee }\otimes ^{\mathbf {L}} A\to \overline {\mathbf {Q}}_{\ell }$
.
$A^{\vee }\otimes ^{\mathbf {L}} A\to \overline {\mathbf {Q}}_{\ell }$
.
In this section, we extend the formalism of the Lefschetz–Verdier trace formula to the setting of perfectoid spaces, diamonds and v-stacks. The main result is Theorem 4.3.8 and its Corollary 4.3.9. We very closely follow the approach of [Reference Lu and ZhengLZ22], putting a suitable symmetric monoidal 2-category of cohomological correspondences at center stage. In both the schematic and perfectoid settings, the finiteness condition required of the object A can be stated in terms of the property of universal local acyclicity (ULA); as noted in [Reference Fargues and ScholzeFS21, Theorem IV.2.23], this is precisely the hypothesis necessary to obtain the isomorphism in equation (4.0.1).
The statement of Lefschetz–Verdier is formally identical in the schematic and perfectoid settings. However, in the perfectoid setting, there arises the possibility that the fixed point locus
![]() $\operatorname {\mathrm {Fix}}(f)$
has the structure of a locally profinite set, in which case the local terms appearing in Lefschetz–Verdier are not a function on
$\operatorname {\mathrm {Fix}}(f)$
has the structure of a locally profinite set, in which case the local terms appearing in Lefschetz–Verdier are not a function on
![]() $\operatorname {\mathrm {Fix}}(f)$
, but rather a distribution on
$\operatorname {\mathrm {Fix}}(f)$
, but rather a distribution on
![]() $\operatorname {\mathrm {Fix}}(f)$
. This observation is critical to our applications.
$\operatorname {\mathrm {Fix}}(f)$
. This observation is critical to our applications.
For our applications, we have included two additional theorems concerning local terms in the perfectoid setting, which could also have been stated in the schematic setting and may be of independent interest. Theorem 4.5.3 is a sort of Künneth isomorphism for local terms on a fiber product of stacks. Theorem 4.6.1 states that, in the situation of a smooth group G acting on a diamond X, the local terms corresponding to individual elements
![]() $g\in G$
agree with local terms computed on the quotient stack
$g\in G$
agree with local terms computed on the quotient stack
![]() $[X/G]$
.
$[X/G]$
.
4.1 Decent v-stacks and the six-functor formalism
We recall here some material from [Reference ScholzeSch17] and [Reference Gulotta, Hansen and WeinsteinGHW22] on the main classes of geometric objects we deal with—perfectoid spaces, diamonds and v-stacks—and their associated étale cohomology formalism.
Let
![]() $\operatorname {\mathrm {Perf}}$
be the category of perfectoid spaces in characteristic p. There are four topologies we consider on
$\operatorname {\mathrm {Perf}}$
be the category of perfectoid spaces in characteristic p. There are four topologies we consider on
![]() $\operatorname {\mathrm {Perf}}$
, which we list from coarsest to finest: the analytic topology, the étale topology, the pro-étale topology and the v-topology. The v-topology is a rough analogue of the fpqc topology on schemes. All representable presheaves on
$\operatorname {\mathrm {Perf}}$
, which we list from coarsest to finest: the analytic topology, the étale topology, the pro-étale topology and the v-topology. The v-topology is a rough analogue of the fpqc topology on schemes. All representable presheaves on
![]() $\operatorname {\mathrm {Perf}}$
are sheaves for the v-topology [Reference ScholzeSch17, Theorem 1.2].
$\operatorname {\mathrm {Perf}}$
are sheaves for the v-topology [Reference ScholzeSch17, Theorem 1.2].
A diamond is a pro-étale sheaf on
![]() $\operatorname {\mathrm {Perf}}$
of the form
$\operatorname {\mathrm {Perf}}$
of the form
![]() $X/R$
, where X is a perfectoid space and
$X/R$
, where X is a perfectoid space and
![]() $R\subset X \times X$
is a pro-étale equivalence relation. Diamonds are automatically v-sheaves [Reference ScholzeSch17, Proposition 11.9]. A particularly well-behaved class of diamonds is locally spatial diamonds [Reference ScholzeSch17, Definition 1.4]. There is a natural functor
$R\subset X \times X$
is a pro-étale equivalence relation. Diamonds are automatically v-sheaves [Reference ScholzeSch17, Proposition 11.9]. A particularly well-behaved class of diamonds is locally spatial diamonds [Reference ScholzeSch17, Definition 1.4]. There is a natural functor
![]() $X\mapsto X^{\diamond }$
from analytic adic spaces over
$X\mapsto X^{\diamond }$
from analytic adic spaces over
![]() $\mathbf {Z}_p$
to locally spatial diamonds.
$\mathbf {Z}_p$
to locally spatial diamonds.
A v-sheaf Y on
![]() $\operatorname {\mathrm {Perf}}$
is small if there exists a surjective map
$\operatorname {\mathrm {Perf}}$
is small if there exists a surjective map
![]() $X\to Y$
from a perfectoid space X. A v-stack is a stack over
$X\to Y$
from a perfectoid space X. A v-stack is a stack over
![]() $\operatorname {\mathrm {Perf}}$
with its v-topology. A small v-stack [Reference ScholzeSch17, Definition 12.4] is a v-stack Y on
$\operatorname {\mathrm {Perf}}$
with its v-topology. A small v-stack [Reference ScholzeSch17, Definition 12.4] is a v-stack Y on
![]() $\operatorname {\mathrm {Perf}}$
such that there exists a surjective map
$\operatorname {\mathrm {Perf}}$
such that there exists a surjective map
![]() $X\to Y$
from a perfectoid space X such that
$X\to Y$
from a perfectoid space X such that
![]() $X\times _Y X$
is a small v-sheaf.
$X\times _Y X$
is a small v-sheaf.
As with any category of stacks, v-stacks form a strict
![]() $(2,1)$
-category. The objects of this category are v-stacks X, which are themselves categories fibered in groupoids over
$(2,1)$
-category. The objects of this category are v-stacks X, which are themselves categories fibered in groupoids over
![]() $\operatorname {\mathrm {Perf}}$
. The morphisms between v-stacks
$\operatorname {\mathrm {Perf}}$
. The morphisms between v-stacks
![]() $X\to Y$
are functors between fibered categories. Given two morphisms
$X\to Y$
are functors between fibered categories. Given two morphisms
![]() $f_1,f_2\colon X\to Y$
, a 2-morphism
$f_1,f_2\colon X\to Y$
, a 2-morphism
![]() $\alpha \colon f_1\Rightarrow f_2$
is an invertible natural transformation between functors.
$\alpha \colon f_1\Rightarrow f_2$
is an invertible natural transformation between functors.
Example 4.1.1. Let S be a diamond, and let
![]() $G\to S$
be a group diamond. The stack
$G\to S$
be a group diamond. The stack
![]() $BG=[S/G]$
classifying G-torsors is a small v-stack, as
$BG=[S/G]$
classifying G-torsors is a small v-stack, as
![]() $S\times _{[S/G]} S\cong G$
is already a diamond. Let
$S\times _{[S/G]} S\cong G$
is already a diamond. Let
![]() $H\to S$
be another group diamond. The morphisms
$H\to S$
be another group diamond. The morphisms
![]() $[S/G]\to [S/H]$
correspond to S-homomorphisms
$[S/G]\to [S/H]$
correspond to S-homomorphisms
![]() $G\to H$
. Suppose we are given two homomorphisms
$G\to H$
. Suppose we are given two homomorphisms
![]() $f_1,f_2\colon G\to H$
, inducing morphisms
$f_1,f_2\colon G\to H$
, inducing morphisms
![]() $\phi _1,\phi _2\colon [S/G]\to [S/H]$
. The set of 2-morphisms
$\phi _1,\phi _2\colon [S/G]\to [S/H]$
. The set of 2-morphisms
![]() $\phi _1\Rightarrow \phi _2$
may be identified with the set of
$\phi _1\Rightarrow \phi _2$
may be identified with the set of
![]() $h\in H(S)$
satisfying
$h\in H(S)$
satisfying
![]() $f_1 = (\operatorname {\mathrm {ad}} h)\circ f_2$
.
$f_1 = (\operatorname {\mathrm {ad}} h)\circ f_2$
.
We use the notation
![]() $\ast $
to indicate ‘horizontal’ composition between 2-morphisms. Thus, if
$\ast $
to indicate ‘horizontal’ composition between 2-morphisms. Thus, if
![]() $X,Y,Z$
are v-stacks,
$X,Y,Z$
are v-stacks,
![]() $f_1,f_2\colon X\to Y$
and
$f_1,f_2\colon X\to Y$
and
![]() $g_1,g_2\colon Y\to Z$
are morphisms, and
$g_1,g_2\colon Y\to Z$
are morphisms, and
![]() $\alpha \colon f_1\Rightarrow f_2$
and
$\alpha \colon f_1\Rightarrow f_2$
and
![]() $\beta \colon g_1\Rightarrow g_2$
are 2-morphisms, then
$\beta \colon g_1\Rightarrow g_2$
are 2-morphisms, then
![]() $\beta \ast \alpha \colon g_1\circ f_1\Rightarrow g_2\circ f_2$
is another 2-morphism.
$\beta \ast \alpha \colon g_1\circ f_1\Rightarrow g_2\circ f_2$
is another 2-morphism.
Let
![]() $\Lambda $
be a ring which is n-torsion for some n prime to p. For every small v-stack X, there is a triangulated category
$\Lambda $
be a ring which is n-torsion for some n prime to p. For every small v-stack X, there is a triangulated category
![]() $D_{\mathrm {\acute {e}t}}(X,\Lambda )$
[Reference ScholzeSch17, Definition 1.7]. If X is a locally spatial diamond, then
$D_{\mathrm {\acute {e}t}}(X,\Lambda )$
[Reference ScholzeSch17, Definition 1.7]. If X is a locally spatial diamond, then
![]() $D_{\mathrm {\acute {e}t}}(X,\Lambda )$
is equivalent to the left-completion of the derived category of sheaves of
$D_{\mathrm {\acute {e}t}}(X,\Lambda )$
is equivalent to the left-completion of the derived category of sheaves of
![]() $\Lambda $
-modules on the étale topology of X [Reference ScholzeSch17, Proposition 14.15].
$\Lambda $
-modules on the étale topology of X [Reference ScholzeSch17, Proposition 14.15].
The familiar six functors of Grothendieck have analogues in the world of small v-stacks [Reference ScholzeSch17, Definition 1.7]. There is a derived tensor product
![]() $\otimes _{\Lambda }^{\mathbf {L}}$
and a derived internal hom
$\otimes _{\Lambda }^{\mathbf {L}}$
and a derived internal hom
![]() $\underline {\mathrm {RHom}}_{\Lambda }$
. For any morphism
$\underline {\mathrm {RHom}}_{\Lambda }$
. For any morphism
![]() $f\colon Y\to X$
of small v-stacks, there is a pair of adjoint functors
$f\colon Y\to X$
of small v-stacks, there is a pair of adjoint functors
![]() $f^*$
and
$f^*$
and
![]() $Rf_*$
.
$Rf_*$
.
Remark 4.1.2. The adjointness between
![]() $f^*$
and
$f^*$
and
![]() $Rf_*$
is compatible with 2-morphisms, in the following sense. Suppose
$Rf_*$
is compatible with 2-morphisms, in the following sense. Suppose
![]() $\alpha \colon f\Rightarrow g$
is a 2-morphism between
$\alpha \colon f\Rightarrow g$
is a 2-morphism between
![]() $f,g\colon Y\to X$
. Then there are natural isomorphisms
$f,g\colon Y\to X$
. Then there are natural isomorphisms
![]() $\alpha _*\colon f_*\to g_*$
and
$\alpha _*\colon f_*\to g_*$
and
![]() $\alpha ^*\colon f^*\to g^*$
such that the following diagrams commute:
$\alpha ^*\colon f^*\to g^*$
such that the following diagrams commute:

We propose for convenience the following definition.
Definition 4.1.3. A morphism
![]() $f\colon Y\to X$
is representable in nice diamonds or simply nice if is compactifiable [Reference ScholzeSch17, Definition 22.2], representable in locally spatial diamonds [Reference ScholzeSch17, Definition 13.3] and locally of finite geometric transcendence degree [Reference ScholzeSch17, Definition 21.7].
$f\colon Y\to X$
is representable in nice diamonds or simply nice if is compactifiable [Reference ScholzeSch17, Definition 22.2], representable in locally spatial diamonds [Reference ScholzeSch17, Definition 13.3] and locally of finite geometric transcendence degree [Reference ScholzeSch17, Definition 21.7].
If
![]() $f\colon Y\to X$
is representable in nice diamonds, then there is an adjoint pair of functors
$f\colon Y\to X$
is representable in nice diamonds, then there is an adjoint pair of functors
![]() $Rf_!$
and
$Rf_!$
and
![]() $Rf^!$
[Reference ScholzeSch17, Sections 22 and 23].
$Rf^!$
[Reference ScholzeSch17, Sections 22 and 23].
Theorem 4.1.4 [Reference ScholzeSch17, Theorem 1.8]
The six operations
![]() $\otimes _{\Lambda }$
,
$\otimes _{\Lambda }$
,
![]() $\underline {\mathrm {RHom}}_{\Lambda }$
,
$\underline {\mathrm {RHom}}_{\Lambda }$
,
![]() $f^*$
,
$f^*$
,
![]() $Rf_*$
,
$Rf_*$
,
![]() $Rf_!$
and
$Rf_!$
and
![]() $Rf^!$
obey the rules:
$Rf^!$
obey the rules:
-
(P1.)
 $f^*A \otimes _{\Lambda }^{\mathbf {L}} f^*B \cong f^*(A\otimes _{\Lambda }^{\mathbf {L}} B)$
,
$f^*A \otimes _{\Lambda }^{\mathbf {L}} f^*B \cong f^*(A\otimes _{\Lambda }^{\mathbf {L}} B)$
, (P2.)
 $Rf_*\underline {\mathrm {RHom}}_{\Lambda }(f^*A,B)\cong \underline {\mathrm {RHom}}_{\Lambda }(A,Rf_*B)$
,
$Rf_*\underline {\mathrm {RHom}}_{\Lambda }(f^*A,B)\cong \underline {\mathrm {RHom}}_{\Lambda }(A,Rf_*B)$
,(P3.)
 $Rf_!(A\otimes _{\Lambda }^{\mathbf {L}} f^*B)\cong Rf_!A\otimes _{\Lambda }^{\mathbf {L}} B$
(the projection formula),
$Rf_!(A\otimes _{\Lambda }^{\mathbf {L}} f^*B)\cong Rf_!A\otimes _{\Lambda }^{\mathbf {L}} B$
(the projection formula),-
(P4.)
 $\underline {\mathrm {RHom}}_{\Lambda }(Rf_!A,B)\cong Rf_*\underline {\mathrm {RHom}}_{\Lambda }(A,Rf^!B)$
(local Verdier duality),
$\underline {\mathrm {RHom}}_{\Lambda }(Rf_!A,B)\cong Rf_*\underline {\mathrm {RHom}}_{\Lambda }(A,Rf^!B)$
(local Verdier duality), (P5.)
 $Rf^!\underline {\mathrm {RHom}}_{\Lambda }(A,B)\cong \underline {\mathrm {RHom}}_{\Lambda }(f^*A,Rf^!B)$
.
$Rf^!\underline {\mathrm {RHom}}_{\Lambda }(A,B)\cong \underline {\mathrm {RHom}}_{\Lambda }(f^*A,Rf^!B)$
.
We also need the following base change results.
Theorem 4.1.5 [Reference ScholzeSch17, Theorem 1.9]
Let

be a Cartesian diagram of small v-stacks.
(BC1.) If f is representable in nice diamonds, then
 $g^*Rf_! \cong Rf^{\prime }_!\widetilde {g}^*$
.
$g^*Rf_! \cong Rf^{\prime }_!\widetilde {g}^*$
.-
(BC2.) If g is representable in nice diamonds, then
 $Rg^!Rf_*\cong Rf_*'R\widetilde {g}^!$
.
$Rg^!Rf_*\cong Rf_*'R\widetilde {g}^!$
.
There is a notion of cohomological smoothness [Reference ScholzeSch17, Definition 23.8] for morphisms between small v-stacks which are representable in nice diamonds. Let
![]() $\Lambda $
be an n-torsion ring for some n not divisible by p. For a morphism
$\Lambda $
be an n-torsion ring for some n not divisible by p. For a morphism
![]() $f\colon Y\to X$
of small v-stacks which is representable in nice diamonds, there is a natural map of functors
$f\colon Y\to X$
of small v-stacks which is representable in nice diamonds, there is a natural map of functors
adjoint to
If f is cohomologically smooth, then equation (4.1.2) is an equivalence [Reference ScholzeSch17, Theorem 1.10]. Furthermore, the object
![]() $Rf^!\Lambda _X$
is invertible in the monoidal category
$Rf^!\Lambda _X$
is invertible in the monoidal category
![]() $D_{\mathrm {\acute {e}t}}(Y,\Lambda )$
. (For X a small v-stack, an object A of
$D_{\mathrm {\acute {e}t}}(Y,\Lambda )$
. (For X a small v-stack, an object A of
![]() $D_{\mathrm {\acute {e}t}}(X,\Lambda )$
is invertible if and only if étale locally on X there is an isomorphism
$D_{\mathrm {\acute {e}t}}(X,\Lambda )$
is invertible if and only if étale locally on X there is an isomorphism
![]() $A\cong L[n]$
for some invertible
$A\cong L[n]$
for some invertible
![]() $\Lambda $
-module L.)
$\Lambda $
-module L.)
There is also the following base change theorem for cohomologically smooth morphisms.
Theorem 4.1.6 [Reference ScholzeSch17, Theorem 1.10]
In the Cartesian diagram (4.1.1), assume that f is cohomologically smooth. Then
![]() $\widetilde {g}^*Rf^!\cong R(f')^!g^*$
and
$\widetilde {g}^*Rf^!\cong R(f')^!g^*$
and
![]() $(f')^*Rg^!\cong R\widetilde {g}^! f^*$
.
$(f')^*Rg^!\cong R\widetilde {g}^! f^*$
.
In our applications, we will crucially need to deal with stacky morphisms
![]() $f\colon Y\to X$
between v-stacks. These morphisms are never representable in nice diamonds, and the hoped-for functors
$f\colon Y\to X$
between v-stacks. These morphisms are never representable in nice diamonds, and the hoped-for functors
![]() $Rf_!$
and
$Rf_!$
and
![]() $Rf^!$
were not constructed in [Reference ScholzeSch17]. In the companion paper [Reference Gulotta, Hansen and WeinsteinGHW22], we have extended the
$Rf^!$
were not constructed in [Reference ScholzeSch17]. In the companion paper [Reference Gulotta, Hansen and WeinsteinGHW22], we have extended the
![]() $!$
-functor formalism to certain stacky maps between certain small v-stacks, using the
$!$
-functor formalism to certain stacky maps between certain small v-stacks, using the
![]() $\infty $
-categorical machinery of [Reference Liu and ZhengLZ]. Here, we briefly recall the main results from [Reference Gulotta, Hansen and WeinsteinGHW22], referring the reader to that paper for a more detailed discussion.
$\infty $
-categorical machinery of [Reference Liu and ZhengLZ]. Here, we briefly recall the main results from [Reference Gulotta, Hansen and WeinsteinGHW22], referring the reader to that paper for a more detailed discussion.
Definition 4.1.7 [Reference Gulotta, Hansen and WeinsteinGHW22, Definition 1.1]
A decent v-stack is a small v-stack X such that the diagonal
![]() $\Delta _X \colon X\to X \times X$
is representable in locally separated locally spatial diamonds [Reference Gulotta, Hansen and WeinsteinGHW22, Definition 4.3] and such that there is a locally separated locally spatial diamond U with a morphism
$\Delta _X \colon X\to X \times X$
is representable in locally separated locally spatial diamonds [Reference Gulotta, Hansen and WeinsteinGHW22, Definition 4.3] and such that there is a locally separated locally spatial diamond U with a morphism
![]() $ U\to X$
which is strictly surjective [Reference Gulotta, Hansen and WeinsteinGHW22, Definition 4.1], representable in locally spatial diamonds and which locally on U is compactifiable of finite dim.trg and cohomologically smooth. Any such morphism
$ U\to X$
which is strictly surjective [Reference Gulotta, Hansen and WeinsteinGHW22, Definition 4.1], representable in locally spatial diamonds and which locally on U is compactifiable of finite dim.trg and cohomologically smooth. Any such morphism
![]() $U \to X$
is called a chart for X.
$U \to X$
is called a chart for X.
A morphism
![]() $f:X\to Y$
between decent v-stacks is fine if there exists a commutative diagram
$f:X\to Y$
between decent v-stacks is fine if there exists a commutative diagram

where the vertical maps are charts and g is locally on W compactifiable of finite dim.trg.
Note that these definitions rely on the notion of cohomological smoothness for morphisms representable in nice diamonds.
In our applications, we will often need to deal with decent v-stacks equipped with a structure map to a fixed v-stack S. We refer to such objects as decent S-v-stacks.
In [Reference Gulotta, Hansen and WeinsteinGHW22], we showed that decent v-stacks and fine morphisms between them are very reasonable notions:
-
• Any locally separated locally spatial diamond is a decent v-stack. In particular, if X is any analytic adic space over
 $\operatorname {\mathrm {Spa}} \mathbf {Z}_p$
, the associated diamond
$\operatorname {\mathrm {Spa}} \mathbf {Z}_p$
, the associated diamond
 $X^{\lozenge }$
is a decent v-stack.
$X^{\lozenge }$
is a decent v-stack. -
• Decent v-stacks are Artin v-stacks in the sense of [Reference Fargues and ScholzeFS21].
-
• Any absolute product or fiber product of decent v-stacks is decent.
-
• Fine morphisms are stable under composition and (decent) base change.
-
• Any morphism of decent v-stacks which is representable in nice diamonds is fine.
The key motivation for singling out fine morphisms of decent v-stacks is the following result.
Theorem 4.1.8 [Reference Gulotta, Hansen and WeinsteinGHW22, Theorem 1.4]
If
![]() $f\colon Y\to X$
is any fine map of decent v-stacks, there exist functors
$f\colon Y\to X$
is any fine map of decent v-stacks, there exist functors
![]() $Rf_!$
and
$Rf_!$
and
![]() $Rf^!$
satisfying the properties listed in Theorems 4.1.4 and 4.1.5 and agreeing with the constructions in [Reference ScholzeSch17] when f is representable in nice diamonds. Moreover, the associations
$Rf^!$
satisfying the properties listed in Theorems 4.1.4 and 4.1.5 and agreeing with the constructions in [Reference ScholzeSch17] when f is representable in nice diamonds. Moreover, the associations
![]() $f \rightsquigarrow Rf_!$
and
$f \rightsquigarrow Rf_!$
and
![]() $f \rightsquigarrow Rf^!$
naturally have the structure of pseudo-functors, and on the class of proper morphisms, there is a pseudo-natural isomorphism
$f \rightsquigarrow Rf^!$
naturally have the structure of pseudo-functors, and on the class of proper morphisms, there is a pseudo-natural isomorphism
![]() $Rf_! \to Rf_*$
.
$Rf_! \to Rf_*$
.
Finally, there is a notion of cohomological smoothness for fine maps between decent v-stacks, which can be defined extrinsically in terms of charts or intrinsically in terms of the
![]() $!$
-functors [Reference Gulotta, Hansen and WeinsteinGHW22, Proposition 4.17], agreeing with the notion discussed above for morphisms representable in nice diamonds and with the same formal properties as in the representable case. In particular, the map (4.1.2) is an isomorphism for cohomologically smooth morphisms, and the evident analogue of Theorem 4.1.6 holds.
$!$
-functors [Reference Gulotta, Hansen and WeinsteinGHW22, Proposition 4.17], agreeing with the notion discussed above for morphisms representable in nice diamonds and with the same formal properties as in the representable case. In particular, the map (4.1.2) is an isomorphism for cohomologically smooth morphisms, and the evident analogue of Theorem 4.1.6 holds.
Again, we refer the reader to [Reference Gulotta, Hansen and WeinsteinGHW22] for a complete discussion.
Finally, we need the notion of the relative dualising complex for v-stacks.
Definition 4.1.9 (The dualising complex)
Let
![]() $f\colon X\to S$
be a fine morphism of decent v-stacks. We define
$f\colon X\to S$
be a fine morphism of decent v-stacks. We define
![]() $K_{X/S}=Rf^!\Lambda $
, an object in
$K_{X/S}=Rf^!\Lambda $
, an object in
![]() $D_{\mathrm {\acute {e}t}}(X,\Lambda )$
.
$D_{\mathrm {\acute {e}t}}(X,\Lambda )$
.
Suppose that S is connected, and that f is proper. Then
![]() $Rf_*=Rf_!$
, and so there is a morphism
$Rf_*=Rf_!$
, and so there is a morphism
![]() $Rf_*K_{X/S}=Rf_!Rf^!\Lambda \overset {\mathrm {counit}}{\longrightarrow } \Lambda $
, which induces a morphism on the level of global sectionsFootnote 2
$Rf_*K_{X/S}=Rf_!Rf^!\Lambda \overset {\mathrm {counit}}{\longrightarrow } \Lambda $
, which induces a morphism on the level of global sectionsFootnote 2
which we notate as
![]() $\omega \mapsto \int _X \omega $
.
$\omega \mapsto \int _X \omega $
.
We record the following lemmas for convenience.
Lemma 4.1.10. Let
![]() $f\colon Y\to X$
be a fine morphism of decent v-stacks, and let
$f\colon Y\to X$
be a fine morphism of decent v-stacks, and let
![]() $A,I\in D_{\mathrm {\acute {e}t}}(X,\Lambda )$
be any objects with I invertible. The natural map
$A,I\in D_{\mathrm {\acute {e}t}}(X,\Lambda )$
be any objects with I invertible. The natural map
![]() $Rf^!A\otimes ^{\mathbf {L}}_{\Lambda } f^*I \to Rf^!(A\otimes ^{\mathbf {L}}_{\Lambda } I)$
of equation (4.1.2) is an isomorphism.
$Rf^!A\otimes ^{\mathbf {L}}_{\Lambda } f^*I \to Rf^!(A\otimes ^{\mathbf {L}}_{\Lambda } I)$
of equation (4.1.2) is an isomorphism.
Proof. Let
![]() $w_{A,I}$
be this morphism. We also get a map
$w_{A,I}$
be this morphism. We also get a map
![]() $w_{A\otimes ^{\mathbf {L}}_{\Lambda } I,I^{-1}}\colon Rf^!(A \otimes ^{\mathbf {L}}_{\Lambda } I) \otimes ^{\mathbf {L}}_{\Lambda } f^*I^{-1} \to Rf^!A$
, which induces
$w_{A\otimes ^{\mathbf {L}}_{\Lambda } I,I^{-1}}\colon Rf^!(A \otimes ^{\mathbf {L}}_{\Lambda } I) \otimes ^{\mathbf {L}}_{\Lambda } f^*I^{-1} \to Rf^!A$
, which induces
![]() $Rf^!(A\otimes ^{\mathbf {L}}_{\Lambda } I)\to Rf^!A \otimes ^{\mathbf {L}}_{\Lambda } f^*I$
. This is the inverse to
$Rf^!(A\otimes ^{\mathbf {L}}_{\Lambda } I)\to Rf^!A \otimes ^{\mathbf {L}}_{\Lambda } f^*I$
. This is the inverse to
![]() $w_{A,I}$
.
$w_{A,I}$
.
Lemma 4.1.11. Let
![]() $f\colon Y\to X$
be a fine morphism of decent v-stacks which is cohomologically smooth. Then there is a canonical isomorphism
$f\colon Y\to X$
be a fine morphism of decent v-stacks which is cohomologically smooth. Then there is a canonical isomorphism
so that
![]() $K_{Y/Y\times _X Y} \cong K_{Y/X}^{-1}$
is invertible.
$K_{Y/Y\times _X Y} \cong K_{Y/X}^{-1}$
is invertible.
Proof. Let
![]() $\operatorname {\mathrm {pr}}_1,\operatorname {\mathrm {pr}}_2\colon Y\times _X Y\to Y$
be the projection morphisms; each is cohomologically smooth. We have
$\operatorname {\mathrm {pr}}_1,\operatorname {\mathrm {pr}}_2\colon Y\times _X Y\to Y$
be the projection morphisms; each is cohomologically smooth. We have
where in the last isomorphism we used Lemma 4.1.10 combined with the cohomological smoothness of
![]() $\operatorname {\mathrm {pr}}_1$
. Now use Theorem 4.1.6 to obtain an isomorphism
$\operatorname {\mathrm {pr}}_1$
. Now use Theorem 4.1.6 to obtain an isomorphism
![]() $\Delta _{Y/X}^*R\operatorname {\mathrm {pr}}_1^!f^*\Lambda _X \cong \Delta _{Y/X}^*\operatorname {\mathrm {pr}}_2^*Rf^!\Lambda _X\cong Rf^!\Lambda _X$
.
$\Delta _{Y/X}^*R\operatorname {\mathrm {pr}}_1^!f^*\Lambda _X \cong \Delta _{Y/X}^*\operatorname {\mathrm {pr}}_2^*Rf^!\Lambda _X\cong Rf^!\Lambda _X$
.
For the remainder of the section, we fix
![]() $\Lambda $
, an n-torsion ring for some n not divisible by p. We will now start writing
$\Lambda $
, an n-torsion ring for some n not divisible by p. We will now start writing
![]() $f_!$
for
$f_!$
for
![]() $Rf_!$
and
$Rf_!$
and
![]() $\otimes $
for
$\otimes $
for
![]() $\otimes ^{\mathbf {L}}_{\Lambda }$
, etc.
$\otimes ^{\mathbf {L}}_{\Lambda }$
, etc.
4.2 Examples
We wish to illustrate the behavior of the functors
![]() $f_!$
and
$f_!$
and
![]() $f^!$
through a long list of examples. In the following, assume
$f^!$
through a long list of examples. In the following, assume
![]() $S=\operatorname {\mathrm {Spd}} C$
for an algebraically closed perfectoid field C or else
$S=\operatorname {\mathrm {Spd}} C$
for an algebraically closed perfectoid field C or else
![]() $S=\operatorname {\mathrm {Spd}} k$
for an algebraically closed discrete field of characteristic p. In both cases, we freely identify
$S=\operatorname {\mathrm {Spd}} k$
for an algebraically closed discrete field of characteristic p. In both cases, we freely identify
![]() $D_{\mathrm {\acute {e}t}}(S,\Lambda )$
with the derived category of
$D_{\mathrm {\acute {e}t}}(S,\Lambda )$
with the derived category of
![]() $\Lambda $
-modules. Observe that, in both cases, S is decent: This is trivial for
$\Lambda $
-modules. Observe that, in both cases, S is decent: This is trivial for
![]() $S=\operatorname {\mathrm {Spd}} C$
, while for
$S=\operatorname {\mathrm {Spd}} C$
, while for
![]() $S=\operatorname {\mathrm {Spd}} k$
the condition on the diagonal is easy to check, and one can show that
$S=\operatorname {\mathrm {Spd}} k$
the condition on the diagonal is easy to check, and one can show that
![]() $U = S \times \operatorname {\mathrm {Spd}} \mathbf {F}_p((t^{1/p^{\infty }}))\to S$
is a chart.
$U = S \times \operatorname {\mathrm {Spd}} \mathbf {F}_p((t^{1/p^{\infty }}))\to S$
is a chart.
Example 4.2.1. Let T be a locally profinite set, and let
![]() $T_S=\underline {T} \times S$
be the associated constant diamond over S. Then
$T_S=\underline {T} \times S$
be the associated constant diamond over S. Then
![]() $f\colon T_S\to S$
is representable in nice diamonds. Let
$f\colon T_S\to S$
is representable in nice diamonds. Let
![]() $C(T,\Lambda )$
be the ring of continuous functions
$C(T,\Lambda )$
be the ring of continuous functions
![]() $T\to \Lambda $
, for the discrete topology on
$T\to \Lambda $
, for the discrete topology on
![]() $\Lambda $
. We may naturally identify
$\Lambda $
. We may naturally identify
![]() $D_{\mathrm {\acute {e}t}}(T_S,\Lambda )$
with the derived category of the abelian category of smooth
$D_{\mathrm {\acute {e}t}}(T_S,\Lambda )$
with the derived category of the abelian category of smooth
![]() $C(T,\Lambda )$
-modules in the sense of §B.2. Indeed,
$C(T,\Lambda )$
-modules in the sense of §B.2. Indeed,
![]() $D_{\mathrm {\acute {e}t}}(T_S,\Lambda ) \cong D(T_{S,\mathrm {\acute {e}t}},\Lambda )$
since
$D_{\mathrm {\acute {e}t}}(T_S,\Lambda ) \cong D(T_{S,\mathrm {\acute {e}t}},\Lambda )$
since
![]() $T_S$
locally has cohomological dimension zero, and then the site
$T_S$
locally has cohomological dimension zero, and then the site
![]() $T_{S,\mathrm {\acute {e}t}}$
agrees with the site associated with the topological space T. Finally, Lemma B.2.5 identifies
$T_{S,\mathrm {\acute {e}t}}$
agrees with the site associated with the topological space T. Finally, Lemma B.2.5 identifies
![]() $\operatorname {\mathrm {Sh}}(T,\Lambda )$
with the category of smooth
$\operatorname {\mathrm {Sh}}(T,\Lambda )$
with the category of smooth
![]() $C(T,\Lambda )$
-modules. This identification matches the constant sheaf
$C(T,\Lambda )$
-modules. This identification matches the constant sheaf
![]() $\Lambda $
with the smooth
$\Lambda $
with the smooth
![]() $C(T,\Lambda )$
-module
$C(T,\Lambda )$
-module
![]() $C_c(T,\Lambda )$
. Under this identification, we have concrete descriptions of the four operations associated with
$C_c(T,\Lambda )$
. Under this identification, we have concrete descriptions of the four operations associated with
![]() $f\colon T_S\to S$
. Here, we freely use some language and notation from §B.2.
$f\colon T_S\to S$
. Here, we freely use some language and notation from §B.2.
-
•
 $f^*$
sends a
$f^*$
sends a
 $\Lambda $
-module M to the smooth
$\Lambda $
-module M to the smooth
 $C(T,\Lambda )$
-module
$C(T,\Lambda )$
-module
 $C_c(T,\Lambda )\otimes _{\Lambda } M$
.
$C_c(T,\Lambda )\otimes _{\Lambda } M$
. -
•
 $f_*$
sends a smooth
$f_*$
sends a smooth
 $C(T,\Lambda )$
-module M to
$C(T,\Lambda )$
-module M to
 $M^c$
regarded as a
$M^c$
regarded as a
 $\Lambda $
-module.
$\Lambda $
-module. -
•
 $f_!$
sends a smooth
$f_!$
sends a smooth
 $C(T,\Lambda )$
-module M to its underlying
$C(T,\Lambda )$
-module M to its underlying
 $\Lambda $
-module.
$\Lambda $
-module. -
•
 $f^!$
sends a
$f^!$
sends a
 $\Lambda $
-module M to
$\Lambda $
-module M to
 $\mathrm {RHom}_{\Lambda }(C_c(T,\Lambda ),M)^s$
. In particular,
$\mathrm {RHom}_{\Lambda }(C_c(T,\Lambda ),M)^s$
. In particular,
 $H^0(T_S, f^!\Lambda _S) \cong \operatorname {\mathrm {Dist}}(T,\Lambda )$
, the module of
$H^0(T_S, f^!\Lambda _S) \cong \operatorname {\mathrm {Dist}}(T,\Lambda )$
, the module of
 $\Lambda $
-valued distributions on T.
$\Lambda $
-valued distributions on T.
Example 4.2.2. Suppose G is a locally pro-p group. Let
![]() $[S/G_S]$
be the classifying v-stack of
$[S/G_S]$
be the classifying v-stack of
![]() $G_S$
-torsors. Assume that there is a separated locally spatial diamond X together with a strictly surjective cohomologically smooth map
$G_S$
-torsors. Assume that there is a separated locally spatial diamond X together with a strictly surjective cohomologically smooth map
![]() $X\to S$
and admitting a free
$X\to S$
and admitting a free
![]() $G_S$
-action.Footnote 3 Then
$G_S$
-action.Footnote 3 Then
![]() $[S/G_S]$
is a decent v-stack. Indeed, the condition on the diagonal is easy to check, and one can also check that the natural map
$[S/G_S]$
is a decent v-stack. Indeed, the condition on the diagonal is easy to check, and one can also check that the natural map
![]() $X/G_S \to [S/G_S]$
is a chart.
$X/G_S \to [S/G_S]$
is a chart.
Let
![]() $q\colon S\to [S/G_S]$
be the quotient map. Then q is representable in nice diamonds. The functor
$q\colon S\to [S/G_S]$
be the quotient map. Then q is representable in nice diamonds. The functor
![]() $q^*$
is an equivalence of monoidal categories between
$q^*$
is an equivalence of monoidal categories between
![]() $D_{\mathrm {\acute {e}t}}([S/G_S],\Lambda )$
and the derived category of
$D_{\mathrm {\acute {e}t}}([S/G_S],\Lambda )$
and the derived category of
![]() $\Lambda $
-modules with a smooth G-action [Reference Fargues and ScholzeFS21, Theorem V.1.1]. (Strictly speaking, if M is an object of
$\Lambda $
-modules with a smooth G-action [Reference Fargues and ScholzeFS21, Theorem V.1.1]. (Strictly speaking, if M is an object of
![]() $D_{\mathrm {\acute {e}t}}([S/G_S],\Lambda )$
, then
$D_{\mathrm {\acute {e}t}}([S/G_S],\Lambda )$
, then
![]() $q^*M$
is a bare
$q^*M$
is a bare
![]() $\Lambda $
-module, but then for each
$\Lambda $
-module, but then for each
![]() $g\in G$
there is a 2-morphism
$g\in G$
there is a 2-morphism
![]() $\alpha _g\colon q\implies q$
as in Example 4.1.1, inducing an automorphism of
$\alpha _g\colon q\implies q$
as in Example 4.1.1, inducing an automorphism of
![]() $q^*M$
.)
$q^*M$
.)
With respect to this equivalence of categories, the functors
![]() $q^*,q^!$
(resp.,
$q^*,q^!$
(resp.,
![]() $q_*,q_!$
) take the following values on a
$q_*,q_!$
) take the following values on a
![]() $\Lambda $
-module M (resp., a
$\Lambda $
-module M (resp., a
![]() $\Lambda $
-module M with smooth G-action).
$\Lambda $
-module M with smooth G-action).
-
•
 $q^*M=M$
with its G-action forgotten.
$q^*M=M$
with its G-action forgotten. -
•
 $q_*M=C(G,M)^{G\text {-sm}}$
, the module of continuous M-valued functions on G which are smooth with respect to the action of G by right translation.
$q_*M=C(G,M)^{G\text {-sm}}$
, the module of continuous M-valued functions on G which are smooth with respect to the action of G by right translation. -
•
 $q_!M=C_c(G,M)=C_c(G,\Lambda )\otimes M$
.
$q_!M=C_c(G,M)=C_c(G,\Lambda )\otimes M$
. -
•
 $q^!M=\operatorname {\mathrm {Hom}}_G(C_c(G,\Lambda ),M)$
. In particular,
$q^!M=\operatorname {\mathrm {Hom}}_G(C_c(G,\Lambda ),M)$
. In particular,
 $q^!\Lambda =\mathrm {Haar}(G,\Lambda )$
is the module of left-invariant Haar measures on G.
$q^!\Lambda =\mathrm {Haar}(G,\Lambda )$
is the module of left-invariant Haar measures on G.
We give justifications for these expressions in the next example, which is more general.
Example 4.2.3. This example generalizes the previous one. Let G be a locally pro-p group as in Example 4.2.2. Suppose
![]() $H\subset G$
is a closed subgroup. Then
$H\subset G$
is a closed subgroup. Then
![]() $[S/H_S]$
is also a decent v-stack. Let
$[S/H_S]$
is also a decent v-stack. Let
be the quotient map, so q is representable in nice diamonds. The functors
![]() $q^*,q^!$
(resp.,
$q^*,q^!$
(resp.,
![]() $q_*,q_!$
) take the following values on a
$q_*,q_!$
) take the following values on a
![]() $\Lambda $
-module M with smooth G-action (resp., smooth H-action):
$\Lambda $
-module M with smooth G-action (resp., smooth H-action):
-
•
 $q^*M$
is the restriction of M from G to H.
$q^*M$
is the restriction of M from G to H. -
•
 $q_*M=\mathrm {Ind}_H^G M$
is the smooth induction of M from H to G.
$q_*M=\mathrm {Ind}_H^G M$
is the smooth induction of M from H to G. -
•
 $q_!M=\mathrm {cInd}_H^G M$
is the compact induction of M from H to G.
$q_!M=\mathrm {cInd}_H^G M$
is the compact induction of M from H to G. -
•
 $q^!M$
seems difficult to describe explicitly in general, but there are two special cases:
$q^!M$
seems difficult to describe explicitly in general, but there are two special cases:-
1. If
 $H\subset G$
is open, then
$H\subset G$
is open, then
 $q^!M\cong q^*M$
is the restriction of M from G to H.
$q^!M\cong q^*M$
is the restriction of M from G to H. -
2. If H is a direct factor of G so that
 $G=H\times H'$
, then
$G=H\times H'$
, then  $$\begin{align*}q^!M= \operatorname{\mathrm{Hom}}_{H'}(C_c(H',\Lambda),M)^{H\mathrm{-sm}}. \end{align*}$$
$$\begin{align*}q^!M= \operatorname{\mathrm{Hom}}_{H'}(C_c(H',\Lambda),M)^{H\mathrm{-sm}}. \end{align*}$$
-
For the claims regarding
![]() $q^*$
and
$q^*$
and
![]() $q_*$
: Let
$q_*$
: Let
![]() $q_H\colon S\to [S/H_S]$
be the quotient map for H and similarly for
$q_H\colon S\to [S/H_S]$
be the quotient map for H and similarly for
![]() $q_G\colon S\to [S/G_S]$
. Then the underlying module of
$q_G\colon S\to [S/G_S]$
. Then the underlying module of
![]() $q^*M$
is
$q^*M$
is
![]() $q_H^*q^*M=q_G^*M$
, which we have identified with M itself. For
$q_H^*q^*M=q_G^*M$
, which we have identified with M itself. For
![]() $h\in H$
, we have a 2-morphism
$h\in H$
, we have a 2-morphism
![]() $\beta _h\colon q_H\implies q_H$
, which induces an action of
$\beta _h\colon q_H\implies q_H$
, which induces an action of
![]() $h\in H$
on
$h\in H$
on
![]() $q_G^*M$
, as well as the 2-morphism
$q_G^*M$
, as well as the 2-morphism
![]() $\alpha _h\colon q_G\implies q_G$
inducing the action of
$\alpha _h\colon q_G\implies q_G$
inducing the action of
![]() $h\in G$
on
$h\in G$
on
![]() $q_G^*M$
as discussed in Example 4.2.2; these actions agree because
$q_G^*M$
as discussed in Example 4.2.2; these actions agree because
![]() $\alpha _h = \operatorname {\mathrm {id}}_q\ast \beta _h$
. Since
$\alpha _h = \operatorname {\mathrm {id}}_q\ast \beta _h$
. Since
![]() $q^*$
is restriction,
$q^*$
is restriction,
![]() $q_*$
must be its right adjoint, which is smooth induction.
$q_*$
must be its right adjoint, which is smooth induction.
For the claim about
![]() $q_!$
, consider the Cartesian diagram:
$q_!$
, consider the Cartesian diagram:

The underlying module of
![]() $q_!M$
is
$q_!M$
is
![]() $q_G^*q_!M$
. By base change property (BC1), we have
$q_G^*q_!M$
. By base change property (BC1), we have
![]() $q_G^*q_!M \cong \widetilde {q}_!\widetilde {q}_G^*M$
, which by Example 4.2.1 is identified with the underlying
$q_G^*q_!M \cong \widetilde {q}_!\widetilde {q}_G^*M$
, which by Example 4.2.1 is identified with the underlying
![]() $\Lambda $
-module of
$\Lambda $
-module of
![]() $\widetilde {q}_G^*M$
. The latter is the descent of M along the H-torsor in topological spaces
$\widetilde {q}_G^*M$
. The latter is the descent of M along the H-torsor in topological spaces
![]() $G\to G/H$
. In our dictionary between sheaves on
$G\to G/H$
. In our dictionary between sheaves on
![]() $G/H$
and smooth
$G/H$
and smooth
![]() $C(G/H,\Lambda )$
-modules,
$C(G/H,\Lambda )$
-modules,
![]() $\widetilde {q}_G^*M$
is the module of smooth H-equivariant functions
$\widetilde {q}_G^*M$
is the module of smooth H-equivariant functions
![]() $G\to M$
which are compactly supported modulo H. This is none other than the compact induction of M from H to G. (To show that the action of G is by right translation on such functions, one has to appeal to the compatibility of base change with the 2-isomorphisms
$G\to M$
which are compactly supported modulo H. This is none other than the compact induction of M from H to G. (To show that the action of G is by right translation on such functions, one has to appeal to the compatibility of base change with the 2-isomorphisms
![]() $\alpha _g\colon q_G\implies q_G$
.)
$\alpha _g\colon q_G\implies q_G$
.)
We now turn to the claims for
![]() $q^!$
. In the case that
$q^!$
. In the case that
![]() $H\subset G$
is open, q is étale, and so
$H\subset G$
is open, q is étale, and so
![]() $q^!\cong q^*$
. In the case that
$q^!\cong q^*$
. In the case that
![]() $G=H\times H'$
, suppose M is a smooth H-module; we have an isomorphism of smooth G-modules
$G=H\times H'$
, suppose M is a smooth H-module; we have an isomorphism of smooth G-modules
from which it is easy to see that the right adjoint to
![]() $q_!M$
is as claimed.
$q_!M$
is as claimed.
Example 4.2.4. Suppose G is a locally pro-p-group as in Example 4.2.2. Let
![]() $f\colon [S/G_S]\to S$
be the structure morphism. Then f is fine and, in fact, is cohomologically smooth. The functors associated with f have the following descriptions:
$f\colon [S/G_S]\to S$
be the structure morphism. Then f is fine and, in fact, is cohomologically smooth. The functors associated with f have the following descriptions:
-
•
 $f^*M=M$
with trivial G-action.
$f^*M=M$
with trivial G-action. -
•
 $f_*M=M^G$
is the (derived) G-invariants of M, that is, the group cohomology.
$f_*M=M^G$
is the (derived) G-invariants of M, that is, the group cohomology. -
•
 $f_!M = (M\otimes \mathrm {Haar}(G,\Lambda ))_G$
is the group homology of M twisted by the module of Haar measures.
$f_!M = (M\otimes \mathrm {Haar}(G,\Lambda ))_G$
is the group homology of M twisted by the module of Haar measures. -
•
 $f^!M = \mathrm {Haar}(G,\Lambda )^* \otimes M$
is M (with trivial G-action) twisted by the dual of the module of Haar measures. In particular,
$f^!M = \mathrm {Haar}(G,\Lambda )^* \otimes M$
is M (with trivial G-action) twisted by the dual of the module of Haar measures. In particular,
 $K_{[S/G_S]/S}=\mathrm {Haar}(G,\Lambda )^*$
.
$K_{[S/G_S]/S}=\mathrm {Haar}(G,\Lambda )^*$
.
The claim about
![]() $f^*$
is clear from the definitions, and
$f^*$
is clear from the definitions, and
![]() $f_*$
is the right adjoint to
$f_*$
is the right adjoint to
![]() $f^*$
. Next, we consider
$f^*$
. Next, we consider
![]() $f^!$
. Since f is cohomologically smooth, we have
$f^!$
. Since f is cohomologically smooth, we have
![]() $f^!M\cong f^*M\otimes f^!\Lambda $
. Let
$f^!M\cong f^*M\otimes f^!\Lambda $
. Let
![]() $q\colon S\to [S/G_S]$
be as in Example 4.2.2 so that
$q\colon S\to [S/G_S]$
be as in Example 4.2.2 so that
![]() $f\circ q = \operatorname {\mathrm {id}}_S$
. We have
$f\circ q = \operatorname {\mathrm {id}}_S$
. We have
![]() $M=q^!f^!M=\mathrm {Haar}(G,\Lambda )\otimes f^!M$
so that
$M=q^!f^!M=\mathrm {Haar}(G,\Lambda )\otimes f^!M$
so that
![]() $f^!M=\mathrm {Haar}(G,\Lambda )^* \otimes M$
as claimed. From here, it is easy to compute
$f^!M=\mathrm {Haar}(G,\Lambda )^* \otimes M$
as claimed. From here, it is easy to compute
![]() $f_!$
as the left adjoint of
$f_!$
as the left adjoint of
![]() $f^!$
.
$f^!$
.
Example 4.2.5. This example combines Examples 4.2.1 with 4.2.4. Let G be a locally pro-p group as in Example 4.2.2. Let T be a locally profinite set equipped with a continuous action of G, and let
![]() $T_S$
be the constant diamond over S. Then the stacky quotient
$T_S$
be the constant diamond over S. Then the stacky quotient
![]() $[T_S/G_S]$
is a decent v-stack, and the structure map
$[T_S/G_S]$
is a decent v-stack, and the structure map
![]() $[T_S/G_S] \to S$
is fine. Indeed, we have already seen that
$[T_S/G_S] \to S$
is fine. Indeed, we have already seen that
![]() $[S/G_S]$
is a decent v-stack fine over S, and the evident morphism
$[S/G_S]$
is a decent v-stack fine over S, and the evident morphism
![]() $[T_S/G_S] \to [S/G_S]$
is representable in nice diamonds, so the claim immediately follows from [Reference Gulotta, Hansen and WeinsteinGHW22, Proposition 4.11]. The stack
$[T_S/G_S] \to [S/G_S]$
is representable in nice diamonds, so the claim immediately follows from [Reference Gulotta, Hansen and WeinsteinGHW22, Proposition 4.11]. The stack
![]() $[T_S/G_S]$
is not in general cohomologically smooth over S. The category
$[T_S/G_S]$
is not in general cohomologically smooth over S. The category
![]() $D_{\mathrm {\acute {e}t}}([T_S/G_S],\Lambda )$
may be identified with the derived category of G-equivariant smooth
$D_{\mathrm {\acute {e}t}}([T_S/G_S],\Lambda )$
may be identified with the derived category of G-equivariant smooth
![]() $C(T,\Lambda )$
-modules. Using this identification, we get a natural isomorphism
$C(T,\Lambda )$
-modules. Using this identification, we get a natural isomorphism
which we can think of as the space of G-invariant distributions on T with values in
![]() $\mathrm {Haar}(G,\Lambda )^*$
. If G is unimodular and if we choose a Haar measure on G, then
$\mathrm {Haar}(G,\Lambda )^*$
. If G is unimodular and if we choose a Haar measure on G, then
![]() $H^0([T_S / G_S],K_{[T_S/G_S]/S})$
becomes isomorphic to
$H^0([T_S / G_S],K_{[T_S/G_S]/S})$
becomes isomorphic to
![]() $\operatorname {\mathrm {Dist}}(T,\Lambda )^G$
, the module of G-invariant distributions on T.
$\operatorname {\mathrm {Dist}}(T,\Lambda )^G$
, the module of G-invariant distributions on T.
4.3 The category of cohomological correspondences
The Lefschetz–Verdier trace formula was expressed elegantly by Lu and Zheng [Reference Lu and ZhengLZ22] in the language of symmetric monoidal 2-categories. In brief, [Reference Lu and ZhengLZ22] constructs such a category of cohomological correspondences, where the objects are pairs
![]() $(X,A)$
, where X is a scheme over a fixed base scheme S and A is an object of
$(X,A)$
, where X is a scheme over a fixed base scheme S and A is an object of
![]() $D(X_{\mathrm {\acute {e}t}},\Lambda )$
, and a morphism
$D(X_{\mathrm {\acute {e}t}},\Lambda )$
, and a morphism
![]() $(X,A)\to (X',A')$
is a correspondence
$(X,A)\to (X',A')$
is a correspondence
![]() $c=(c_1,c_2)\colon C\to X\times _S X'$
together with a morphism
$c=(c_1,c_2)\colon C\to X\times _S X'$
together with a morphism
![]() $c_1^*A\to c_2^!A'$
. An endomorphism of a dualizable object
$c_1^*A\to c_2^!A'$
. An endomorphism of a dualizable object
![]() $(X,A)$
has a categorical trace, which lives over the fixed point locus of c. In the special case that
$(X,A)$
has a categorical trace, which lives over the fixed point locus of c. In the special case that
![]() $X=X'=C=S$
and A is a perfect complex of
$X=X'=C=S$
and A is a perfect complex of
![]() $\Lambda $
-modules, the categorical trace is just the Euler characteristic of an endomorphism of A. The trace formula is interpreted as the statement that the categorical trace is compatible with proper pushforwards.
$\Lambda $
-modules, the categorical trace is just the Euler characteristic of an endomorphism of A. The trace formula is interpreted as the statement that the categorical trace is compatible with proper pushforwards.
We adapt here [Reference Lu and ZhengLZ22] to the setting of v-stacks, but the same language could be used in the world of stacks in the scheme setting. The main point of departure from [Reference Lu and ZhengLZ22] is that stacks form a 2-category, and so one must keep track of the 2-morphisms witnessing commutativity of diagrams of stacks. This means that the definition of cohomological correspondences we give (Definition 4.3.4) is a little more delicate than its analogue in [Reference Lu and ZhengLZ22].
First, we recall some definitions and constructions concerning the categorical trace.
Definition 4.3.1 [Reference Lu and ZhengLZ22, Definition 1.1, Construction 1.6]
An object X of a symmetric monoidal 2-category
![]() $(\mathcal {C},\otimes ,1_{\mathcal {C}})$
is dualizable if there exists an object
$(\mathcal {C},\otimes ,1_{\mathcal {C}})$
is dualizable if there exists an object
![]() $X^{\vee }$
together with morphisms
$X^{\vee }$
together with morphisms
![]() $\text {ev}_X\colon X^{\vee }\otimes X \to 1_{\mathcal {C}}$
and
$\text {ev}_X\colon X^{\vee }\otimes X \to 1_{\mathcal {C}}$
and
![]() $\text {coev}_X\colon 1_{\mathcal {C}} \to X\otimes X^{\vee }$
such that the compositions
$\text {coev}_X\colon 1_{\mathcal {C}} \to X\otimes X^{\vee }$
such that the compositions
and
are isomorphic to the identities on X and
![]() $X^{\vee }$
, respectively. Consequently, the functor
$X^{\vee }$
, respectively. Consequently, the functor
![]() $Y\mapsto X\otimes Y$
has right adjoint
$Y\mapsto X\otimes Y$
has right adjoint
![]() $Y\mapsto X^{\vee }\otimes Y$
. If X is dualizable, then
$Y\mapsto X^{\vee }\otimes Y$
. If X is dualizable, then
![]() $X^{\vee }\otimes Y$
serves as an internal mapping object
$X^{\vee }\otimes Y$
serves as an internal mapping object
![]() $\underline {\mathrm {Hom}}(X,Y)$
.
$\underline {\mathrm {Hom}}(X,Y)$
.
Let
![]() $\Omega \mathcal {C}=\operatorname {\mathrm {End}}(1_{\mathcal {C}})$
be the (1-)category of endomorphisms of the unit object of
$\Omega \mathcal {C}=\operatorname {\mathrm {End}}(1_{\mathcal {C}})$
be the (1-)category of endomorphisms of the unit object of
![]() $\mathcal {C}$
. Let
$\mathcal {C}$
. Let
![]() $f\in \operatorname {\mathrm {End}} X$
be an endomorphism of a dualizable object X. Define the categorical trace
$f\in \operatorname {\mathrm {End}} X$
be an endomorphism of a dualizable object X. Define the categorical trace
![]() $\operatorname {\mathrm {tr}}(f)$
as the composite:
$\operatorname {\mathrm {tr}}(f)$
as the composite:
so that
![]() $\operatorname {\mathrm {tr}}(f)$
is an object of
$\operatorname {\mathrm {tr}}(f)$
is an object of
![]() $\Omega \mathcal {C}$
.
$\Omega \mathcal {C}$
.
Example 4.3.2. Let
![]() $\Lambda $
be an arbitrary ring, and let
$\Lambda $
be an arbitrary ring, and let
![]() $D(\Lambda )$
be the derived category of
$D(\Lambda )$
be the derived category of
![]() $\Lambda $
-modules. An object A of
$\Lambda $
-modules. An object A of
![]() $D(\Lambda )$
is dualizable if and only if it is a perfect complex, in which case
$D(\Lambda )$
is dualizable if and only if it is a perfect complex, in which case
![]() $\mathbf {D} A=\underline {\mathrm {RHom}}(A,\Lambda [0])$
is a dual object. (See Lemma B.1.2 in the Appendix for a proof of this claim and related conditions.) If f is an endomorphism of the perfect complex of A, then the categorical trace
$\mathbf {D} A=\underline {\mathrm {RHom}}(A,\Lambda [0])$
is a dual object. (See Lemma B.1.2 in the Appendix for a proof of this claim and related conditions.) If f is an endomorphism of the perfect complex of A, then the categorical trace
![]() $\operatorname {\mathrm {tr}}(f)$
agrees with the Euler characteristic
$\operatorname {\mathrm {tr}}(f)$
agrees with the Euler characteristic
![]() $\operatorname {\mathrm {tr}}(f\vert A)$
of f.
$\operatorname {\mathrm {tr}}(f\vert A)$
of f.
Next, we define the symmetric monoidal 2-category
![]() $\operatorname {\mathrm {Corr}}_S$
of correspondences of v-stacks and its cohomological enhancement
$\operatorname {\mathrm {Corr}}_S$
of correspondences of v-stacks and its cohomological enhancement
![]() $\operatorname {\mathrm {CoCorr}}_S\to \operatorname {\mathrm {Corr}}_S$
. In the following discussion, we fix a decent v-stack S.
$\operatorname {\mathrm {CoCorr}}_S\to \operatorname {\mathrm {Corr}}_S$
. In the following discussion, we fix a decent v-stack S.
Definition 4.3.3 (The category of correspondences)
We define a symmetric monoidal 2-category
![]() $\operatorname {\mathrm {Corr}}_S$
as follows:
$\operatorname {\mathrm {Corr}}_S$
as follows:
-
• The objects of
 $\operatorname {\mathrm {Corr}}_S$
are decent S-v-stacks X whose structure map
$\operatorname {\mathrm {Corr}}_S$
are decent S-v-stacks X whose structure map
 $X \to S$
is fine.
$X \to S$
is fine. -
• Given objects X and
 $X'$
, the category
$X'$
, the category
 $\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {Corr}}_S}(X,X')$
has for its objects the correspondences: (4.3.1)where each
$\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {Corr}}_S}(X,X')$
has for its objects the correspondences: (4.3.1)where each
 $c_i$
a morphism of decent v-stacks, and
$c_i$
a morphism of decent v-stacks, and
 $c_2$
is assumed to be fine.Footnote 4 The composition of
$c_2$
is assumed to be fine.Footnote 4 The composition of
 $(c_1,c_2)\colon C\to X\times _S X'$
with
$(c_1,c_2)\colon C\to X\times _S X'$
with
 $(d_1,d_2)\colon D\to X'\times _S X''$
is the correspondence
$(d_1,d_2)\colon D\to X'\times _S X''$
is the correspondence
 $(c_1d_1',d_2c_2')$
defined by the diagram: (4.3.2)
$(c_1d_1',d_2c_2')$
defined by the diagram: (4.3.2)
-
• If
 $c=(c_1,c_2)\colon C\to X\times _S X'$
and
$c=(c_1,c_2)\colon C\to X\times _S X'$
and
 $d=(d_1,d_2)\colon D\to X\times _S X'$
represent two objects in
$d=(d_1,d_2)\colon D\to X\times _S X'$
represent two objects in
 $\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {Corr}}_S}(X,X')$
, a 2-morphism
$\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {Corr}}_S}(X,X')$
, a 2-morphism
 $c\Rightarrow d$
is an equivalence class of 2-commutative diagrams (4.3.3)where p is proper and
$c\Rightarrow d$
is an equivalence class of 2-commutative diagrams (4.3.3)where p is proper and
 $\alpha _i\colon c_i\Rightarrow d_i\circ p$
(for
$\alpha _i\colon c_i\Rightarrow d_i\circ p$
(for
 $i=1,2$
) is a 2-isomorphism witnessing the 2-commutativity of the appropriate triangle. We write
$i=1,2$
) is a 2-isomorphism witnessing the 2-commutativity of the appropriate triangle. We write
 $(p,\alpha _1,\alpha _2)$
as shorthand for the datum of such a diagram or just p if the 2-isomorphisms are clear from context.
$(p,\alpha _1,\alpha _2)$
as shorthand for the datum of such a diagram or just p if the 2-isomorphisms are clear from context.
We declare two such diagrams
 $(p,\alpha _1,\alpha _2)$
and
$(p,\alpha _1,\alpha _2)$
and
 $(q,\beta _1,\beta _2)$
equivalent if there is a 2-isomorphism
$(q,\beta _1,\beta _2)$
equivalent if there is a 2-isomorphism
 $\gamma \colon p\Rightarrow q$
such that
$\gamma \colon p\Rightarrow q$
such that
 $\beta _i=(\operatorname {\mathrm {id}}_{d_i}\ast \gamma )\circ \alpha _i$
for
$\beta _i=(\operatorname {\mathrm {id}}_{d_i}\ast \gamma )\circ \alpha _i$
for
 $i=1,2$
.
$i=1,2$
. -
• The monoidal structure is defined by
 $X\otimes Y = X\times _S Y$
, with unit object S. Given
$X\otimes Y = X\times _S Y$
, with unit object S. Given
 $c=(c_1,c_2)\colon C\to X\times _S X'$
and
$c=(c_1,c_2)\colon C\to X\times _S X'$
and
 $d=(d_1,d_2)\colon D\to Y\times _S Y'$
representing objects in
$d=(d_1,d_2)\colon D\to Y\times _S Y'$
representing objects in
 $\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {Corr}}_S}(X,X')$
and
$\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {Corr}}_S}(X,X')$
and
 $\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {Corr}}_S}(Y,Y')$
, respectively, we define the object
$\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {Corr}}_S}(Y,Y')$
, respectively, we define the object
 $c\otimes d$
of
$c\otimes d$
of
 $\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {Corr}}_S}(X\times _S Y,X'\times _S Y')$
as the correspondence: (4.3.4)
$\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {Corr}}_S}(X\times _S Y,X'\times _S Y')$
as the correspondence: (4.3.4)
The next thing to do is to construct a symmetric monoidal 2-category
![]() $\operatorname {\mathrm {CoCorr}}_S$
of cohomological correspondences, which lies over
$\operatorname {\mathrm {CoCorr}}_S$
of cohomological correspondences, which lies over
![]() $\operatorname {\mathrm {Corr}}_S$
.
$\operatorname {\mathrm {Corr}}_S$
.
Definition 4.3.4 (The category of cohomological correspondences)
We define a symmetric monoidal 2-category
![]() $\operatorname {\mathrm {CoCorr}}_S$
, which comes equipped with a functor to
$\operatorname {\mathrm {CoCorr}}_S$
, which comes equipped with a functor to
![]() $\operatorname {\mathrm {Corr}}_S$
.
$\operatorname {\mathrm {Corr}}_S$
.
-
• An object of
 $\operatorname {\mathrm {CoCorr}}_S$
is a pair
$\operatorname {\mathrm {CoCorr}}_S$
is a pair
 $\mathfrak {X}=(X,A)$
, where X is a decent S-v-stack whose structure map
$\mathfrak {X}=(X,A)$
, where X is a decent S-v-stack whose structure map
 $X \to S$
is fine, and
$X \to S$
is fine, and
 $A\in D_{\mathrm {\acute {e}t}}(X,\Lambda )$
is arbitrary.
$A\in D_{\mathrm {\acute {e}t}}(X,\Lambda )$
is arbitrary. -
• Given objects
 $\mathfrak {X}=(X,A)$
and
$\mathfrak {X}=(X,A)$
and
 $\mathfrak {X}'=(X',A')$
of
$\mathfrak {X}'=(X',A')$
of
 $\operatorname {\mathrm {CoCorr}}_S$
, the category
$\operatorname {\mathrm {CoCorr}}_S$
, the category
 $\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {CoCorr}}_S}(\mathfrak {X},\mathfrak {X}')$
consists of pairs
$\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {CoCorr}}_S}(\mathfrak {X},\mathfrak {X}')$
consists of pairs
 $\mathfrak {c}=(c,u)$
, where
$\mathfrak {c}=(c,u)$
, where
 $c=(c_1,c_2)$
is a correspondence as in equation (4.3.1), and
$c=(c_1,c_2)$
is a correspondence as in equation (4.3.1), and
 $u\colon c_1^*A\to c_2^!A'$
is a morphism in
$u\colon c_1^*A\to c_2^!A'$
is a morphism in
 $D_{\mathrm {\acute {e}t}}(C,\Lambda )$
. The composition of
$D_{\mathrm {\acute {e}t}}(C,\Lambda )$
. The composition of
 $\mathfrak {c}=(c,u)\colon (X,A)\to (X',A')$
with
$\mathfrak {c}=(c,u)\colon (X,A)\to (X',A')$
with
 $\mathfrak {d}=(d,v)\colon (X',A')\to (X'',A'')$
is
$\mathfrak {d}=(d,v)\colon (X',A')\to (X'',A'')$
is
 $\mathfrak {d}\circ \mathfrak {c}=(e,w)$
, where
$\mathfrak {d}\circ \mathfrak {c}=(e,w)$
, where
 $e\colon C\times _{X'} D\to X\times _S X''$
is the correspondence in equation (4.3.2), and w is the composition where the map labeled a is adjoint to the base change isomorphism
$e\colon C\times _{X'} D\to X\times _S X''$
is the correspondence in equation (4.3.2), and w is the composition where the map labeled a is adjoint to the base change isomorphism $$\begin{align*}(d_1')^*c_1^*A\stackrel{u}{\to} (d_1')^*c_2^! A' \stackrel{a}{\to} (c_2')^!d_1^*A' \stackrel{v}{\to} (c_2')^! d_2^! A'', \end{align*}$$
$$\begin{align*}(d_1')^*c_1^*A\stackrel{u}{\to} (d_1')^*c_2^! A' \stackrel{a}{\to} (c_2')^!d_1^*A' \stackrel{v}{\to} (c_2')^! d_2^! A'', \end{align*}$$
 $(c_2')_!(d_1')^* \cong d_1^* (c_2)_!$
.
$(c_2')_!(d_1')^* \cong d_1^* (c_2)_!$
.
-
• Let
 $\mathfrak {X}=(X,A)$
and
$\mathfrak {X}=(X,A)$
and
 $\mathfrak {X}'=(X',A')$
be two objects of
$\mathfrak {X}'=(X',A')$
be two objects of
 $\operatorname {\mathrm {CoCorr}}_S$
. Let
$\operatorname {\mathrm {CoCorr}}_S$
. Let
 $\mathfrak {c}=(c,u)$
and
$\mathfrak {c}=(c,u)$
and
 $\mathfrak {d}=(d,v)$
be two objects in
$\mathfrak {d}=(d,v)$
be two objects in
 $\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {CoCorr}}_S}(\mathfrak {X},\mathfrak {X}')$
, where
$\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {CoCorr}}_S}(\mathfrak {X},\mathfrak {X}')$
, where
 $c=(c_1,c_2)\colon C\to X\times _S X'$
and
$c=(c_1,c_2)\colon C\to X\times _S X'$
and
 $d=(d_1,d_2)\colon D\to X\times _S X'$
are correspondences, and
$d=(d_1,d_2)\colon D\to X\times _S X'$
are correspondences, and
 $u\colon c_1^*A\to c_2^!A'$
and
$u\colon c_1^*A\to c_2^!A'$
and
 $v\colon d_1^*A\to d_2^!A'$
are morphisms. A 2-morphism
$v\colon d_1^*A\to d_2^!A'$
are morphisms. A 2-morphism
 $\mathfrak {p}\colon \mathfrak {c}\implies \mathfrak {d}$
is an equivalence class of triples
$\mathfrak {p}\colon \mathfrak {c}\implies \mathfrak {d}$
is an equivalence class of triples
 $(p,\alpha _1,\alpha _2)$
as in the diagram (4.3.3) such that the composition
$(p,\alpha _1,\alpha _2)$
as in the diagram (4.3.3) such that the composition  $$ \begin{align*} \begin{array}{lcl} d_1^* A &\! \stackrel{\text{unit}}{\longrightarrow}&\!\! p_*p^*d_1^* A \\ &\!\stackrel{(\alpha_1^*)^{-1}}{\longrightarrow}&\!\! p_*c_1^* A \\ &\!\stackrel{u}{\to}&\!\! p_* c_2^! A' \\ &\!\stackrel{\alpha_2^!}{\longrightarrow} &\!\!p_*p^! d_2^! A' \cong p_!p^!d_2^! A'\\ &\!\stackrel{\text{counit}}{\longrightarrow}&\!\! d_2^!A'\\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{lcl} d_1^* A &\! \stackrel{\text{unit}}{\longrightarrow}&\!\! p_*p^*d_1^* A \\ &\!\stackrel{(\alpha_1^*)^{-1}}{\longrightarrow}&\!\! p_*c_1^* A \\ &\!\stackrel{u}{\to}&\!\! p_* c_2^! A' \\ &\!\stackrel{\alpha_2^!}{\longrightarrow} &\!\!p_*p^! d_2^! A' \cong p_!p^!d_2^! A'\\ &\!\stackrel{\text{counit}}{\longrightarrow}&\!\! d_2^!A'\\ \end{array} \end{align*} $$
agrees with
 $v\colon d_1^*A\to d_2^!A'$
. Here,
$v\colon d_1^*A\to d_2^!A'$
. Here,
 $\alpha _1^*$
and
$\alpha _1^*$
and
 $\alpha _2^!$
are the natural isomorphisms
$\alpha _2^!$
are the natural isomorphisms
 $c_1^*\stackrel {\cong }{\longrightarrow } p^*d_1^*$
and
$c_1^*\stackrel {\cong }{\longrightarrow } p^*d_1^*$
and
 $c_2^!\stackrel {\cong }{\longrightarrow } p^!d_2^!$
, respectively.
$c_2^!\stackrel {\cong }{\longrightarrow } p^!d_2^!$
, respectively.We need to check that the condition on the aforementioned composition depends only on the equivalence class of the triple
 $(p,\alpha _1,\alpha _2)$
. To check this, let
$(p,\alpha _1,\alpha _2)$
. To check this, let
 $(q,\beta _1,\beta _2)$
be another triple which is equivalent to
$(q,\beta _1,\beta _2)$
be another triple which is equivalent to
 $(p,\alpha _1,\alpha _2)$
by a 2-isomorphism
$(p,\alpha _1,\alpha _2)$
by a 2-isomorphism
 $\gamma \colon p\Rightarrow q$
in the sense of Definition 4.3.3, so assume that
$\gamma \colon p\Rightarrow q$
in the sense of Definition 4.3.3, so assume that
 $\beta _i=(\operatorname {\mathrm {id}}_{d_i}\ast \gamma )\circ \alpha _i$
for
$\beta _i=(\operatorname {\mathrm {id}}_{d_i}\ast \gamma )\circ \alpha _i$
for
 $i=1,2$
. Consider the diagram in
$i=1,2$
. Consider the diagram in
 $D_{\mathrm {\acute {e}t}}(D,\Lambda )$
: The first and fifth squares commute by the compatibility described in Remark 4.1.2, the second and fourth squares commute because of the condition
$D_{\mathrm {\acute {e}t}}(D,\Lambda )$
: The first and fifth squares commute by the compatibility described in Remark 4.1.2, the second and fourth squares commute because of the condition
 $\beta _i=(\operatorname {\mathrm {id}}_{d_i}\ast \gamma )\circ \alpha _i$
, taking into account the pseudo-functor structures on the four nonbinary operations and the third square commutes because of the equalities
$\beta _i=(\operatorname {\mathrm {id}}_{d_i}\ast \gamma )\circ \alpha _i$
, taking into account the pseudo-functor structures on the four nonbinary operations and the third square commutes because of the equalities
 $p_*=p_!$
,
$p_*=p_!$
,
 $q_*=q_!$
, and
$q_*=q_!$
, and
 $\gamma _*=\gamma _!$
. The commutativity of the outside rectangle says that if the composition along the left vertical arrow is v, then so is the composition along the right vertical arrow. This shows that our notion of 2-morphsm in
$\gamma _*=\gamma _!$
. The commutativity of the outside rectangle says that if the composition along the left vertical arrow is v, then so is the composition along the right vertical arrow. This shows that our notion of 2-morphsm in
 $\operatorname {\mathrm {CoCorr}}_S$
is well-defined.
$\operatorname {\mathrm {CoCorr}}_S$
is well-defined.
-
• The symmetric monoidal structure on
 $\operatorname {\mathrm {CoCorr}}_S$
is given by
$\operatorname {\mathrm {CoCorr}}_S$
is given by
 $(X,A)\otimes (X',A')= (X\times _S X', A\boxtimes _S A')$
. The unit object is
$(X,A)\otimes (X',A')= (X\times _S X', A\boxtimes _S A')$
. The unit object is
 $1_{\operatorname {\mathrm {CoCorr}}_S}=(S,\Lambda _S)$
. Finally, given
$1_{\operatorname {\mathrm {CoCorr}}_S}=(S,\Lambda _S)$
. Finally, given
 $(c,u)\colon (X_1,A_1)\to (X^{\prime }_1,A^{\prime }_1)$
and
$(c,u)\colon (X_1,A_1)\to (X^{\prime }_1,A^{\prime }_1)$
and
 $(d,v)\colon (X_2,A_2)\to (X^{\prime }_2,A^{\prime }_2)$
, the tensor product
$(d,v)\colon (X_2,A_2)\to (X^{\prime }_2,A^{\prime }_2)$
, the tensor product
 $(c,u)\otimes (d,v)$
is
$(c,u)\otimes (d,v)$
is
 $(c\otimes d, w)$
, where
$(c\otimes d, w)$
, where
 $c\otimes d$
is the correspondence in equation (4.3.4), and w is the composition where
$c\otimes d$
is the correspondence in equation (4.3.4), and w is the composition where $$\begin{align*}(c_1\times_S d_1)^*(A_1\boxtimes_S A_2)\cong c_1^*A_1 \boxtimes d_1^*A_2 \stackrel{u\boxtimes_S v}{\to} c_2^!A_1' \boxtimes_S d_2^!A_2' \stackrel{\kappa}{\to} (c_2\times_S d_2)^! (A_2\boxtimes A_2'), \end{align*}$$
$$\begin{align*}(c_1\times_S d_1)^*(A_1\boxtimes_S A_2)\cong c_1^*A_1 \boxtimes d_1^*A_2 \stackrel{u\boxtimes_S v}{\to} c_2^!A_1' \boxtimes_S d_2^!A_2' \stackrel{\kappa}{\to} (c_2\times_S d_2)^! (A_2\boxtimes A_2'), \end{align*}$$
 $\kappa $
is adjoint to the Künneth isomorphism
$\kappa $
is adjoint to the Künneth isomorphism
 $(c_2\times d_2)_!(B_1\boxtimes _S B_2)\cong (c_2)_!B_1 \boxtimes _S (d_2)_!B_2$
.
$(c_2\times d_2)_!(B_1\boxtimes _S B_2)\cong (c_2)_!B_1 \boxtimes _S (d_2)_!B_2$
.
The category
![]() $\operatorname {\mathrm {CoCorr}}_S$
has internal mapping objects: if
$\operatorname {\mathrm {CoCorr}}_S$
has internal mapping objects: if
![]() $\mathfrak {X}_1=(X_1,A_1)$
and
$\mathfrak {X}_1=(X_1,A_1)$
and
![]() $\mathfrak {X}_2=(X_2,A_2)$
, then
$\mathfrak {X}_2=(X_2,A_2)$
, then
![]() $\underline {\mathrm {Hom}}(\mathfrak {X}_1,\mathfrak {X}_2)=(X_1\times _S X_2,\underline {\mathrm {RHom}}(\operatorname {\mathrm {pr}}_1^*A_1,\operatorname {\mathrm {pr}}_2^!A_2))$
, where
$\underline {\mathrm {Hom}}(\mathfrak {X}_1,\mathfrak {X}_2)=(X_1\times _S X_2,\underline {\mathrm {RHom}}(\operatorname {\mathrm {pr}}_1^*A_1,\operatorname {\mathrm {pr}}_2^!A_2))$
, where
![]() $\operatorname {\mathrm {pr}}_i\colon X_1\times _S X_2\to X_i$
is the projection.
$\operatorname {\mathrm {pr}}_i\colon X_1\times _S X_2\to X_i$
is the projection.
We have the following characterization of dualizable objects in
![]() $\operatorname {\mathrm {CoCorr}}_S$
.
$\operatorname {\mathrm {CoCorr}}_S$
.
Proposition 4.3.5. Let X be a decent S-v-stack whose structure map
![]() $\pi \colon X\to S$
is fine, and let
$\pi \colon X\to S$
is fine, and let
![]() $A\in D_{\mathrm {\acute {e}t}}(X,\Lambda )$
be any object. The following are equivalent.
$A\in D_{\mathrm {\acute {e}t}}(X,\Lambda )$
be any object. The following are equivalent.
-
1. The object
 $(X,A)$
is dualizable in
$(X,A)$
is dualizable in
 $\operatorname {\mathrm {CoCorr}}_S$
.
$\operatorname {\mathrm {CoCorr}}_S$
. -
2. The natural map
 $m\colon \mathbf {D}_{X/S} A\boxtimes _S A \to \underline {\mathrm {RHom}}(\operatorname {\mathrm {pr}}_1^*A,\operatorname {\mathrm {pr}}_2^!A)$
(see proof for construction) is an isomorphism.
$m\colon \mathbf {D}_{X/S} A\boxtimes _S A \to \underline {\mathrm {RHom}}(\operatorname {\mathrm {pr}}_1^*A,\operatorname {\mathrm {pr}}_2^!A)$
(see proof for construction) is an isomorphism.
In this situation, the dual of
![]() $(X,A)$
is
$(X,A)$
is
![]() $(X,\mathbf {D}_{X/S}A)$
.
$(X,\mathbf {D}_{X/S}A)$
.
Proof. Let
![]() $\mathfrak {X}=(X,A)$
, and let
$\mathfrak {X}=(X,A)$
, and let
![]() $\mathfrak {X}'=(X,\mathbf {D}_{X/S}A)$
. There is a morphism
$\mathfrak {X}'=(X,\mathbf {D}_{X/S}A)$
. There is a morphism
![]() $\mathfrak {e}\colon \mathfrak {X}'\otimes \mathfrak {X}\to 1_{\operatorname {\mathrm {CoCorr}}_S}$
, defined as the pair
$\mathfrak {e}\colon \mathfrak {X}'\otimes \mathfrak {X}\to 1_{\operatorname {\mathrm {CoCorr}}_S}$
, defined as the pair
![]() $(c,u)$
, where
$(c,u)$
, where
![]() $c=(\Delta _{X/S},\pi )$
and u is the composition
$c=(\Delta _{X/S},\pi )$
and u is the composition
Then
![]() $\mathfrak {e}$
induces a morphism
$\mathfrak {e}$
induces a morphism
![]() $\mathfrak {X}'\otimes \mathfrak {Y}\to \underline {\mathrm {Hom}}(\mathfrak {X},\mathfrak {Y})$
for any object
$\mathfrak {X}'\otimes \mathfrak {Y}\to \underline {\mathrm {Hom}}(\mathfrak {X},\mathfrak {Y})$
for any object
![]() $\mathfrak {Y}$
of
$\mathfrak {Y}$
of
![]() $\operatorname {\mathrm {CoCorr}}_S$
. For
$\operatorname {\mathrm {CoCorr}}_S$
. For
![]() $\mathfrak {Y}=\mathfrak {X}$
, the map u becomes the map m in (2).
$\mathfrak {Y}=\mathfrak {X}$
, the map u becomes the map m in (2).
Suppose
![]() $\mathfrak {X}$
is dualizable, with witnesses
$\mathfrak {X}$
is dualizable, with witnesses
![]() $\mathfrak {X}^{\vee }$
,
$\mathfrak {X}^{\vee }$
,
![]() $\operatorname {\mathrm {ev}}_{\mathfrak {X}}$
, and
$\operatorname {\mathrm {ev}}_{\mathfrak {X}}$
, and
![]() $\operatorname {\mathrm {coev}}_{\mathfrak {X}}$
. Then
$\operatorname {\mathrm {coev}}_{\mathfrak {X}}$
. Then
![]() $\mathfrak {X}^{\vee }\otimes \mathfrak {Y}\to \underline {\mathrm {Hom}}(\mathfrak {X},\mathfrak {Y})$
is an isomorphism for all objects
$\mathfrak {X}^{\vee }\otimes \mathfrak {Y}\to \underline {\mathrm {Hom}}(\mathfrak {X},\mathfrak {Y})$
is an isomorphism for all objects
![]() $\mathfrak {Y}$
. Setting
$\mathfrak {Y}$
. Setting
![]() $\mathfrak {Y}=1_{\operatorname {\mathrm {CoCorr}}_S}$
, we find an isomorphism
$\mathfrak {Y}=1_{\operatorname {\mathrm {CoCorr}}_S}$
, we find an isomorphism
![]() $\mathfrak {X}^{\vee }\cong \mathfrak {X}'$
which identifies
$\mathfrak {X}^{\vee }\cong \mathfrak {X}'$
which identifies
![]() $\operatorname {\mathrm {ev}}_{\mathfrak {X}}$
with
$\operatorname {\mathrm {ev}}_{\mathfrak {X}}$
with
![]() $\mathfrak {e}$
. Setting
$\mathfrak {e}$
. Setting
![]() $\mathfrak {Y}=\mathfrak {X}$
, we find that m is an isomorphism.
$\mathfrak {Y}=\mathfrak {X}$
, we find that m is an isomorphism.
Conversely, if m is an isomorphism, let
![]() $\operatorname {\mathrm {coev}}_{\mathfrak {X}}=(d,w)$
, where
$\operatorname {\mathrm {coev}}_{\mathfrak {X}}=(d,w)$
, where
![]() $d=(\pi ,\Delta _{X/S})$
and w is the composition
$d=(\pi ,\Delta _{X/S})$
and w is the composition
followed by
![]() $m^{-1}\colon \Delta _{X/S}^!\underline {\mathrm {RHom}}_{\Lambda }(\operatorname {\mathrm {pr}}_1^*A, \operatorname {\mathrm {pr}}_2^!A)\to \Delta _{X/S}^!(A\boxtimes _S \mathbf {D}_{X/S}A)$
. Here,
$m^{-1}\colon \Delta _{X/S}^!\underline {\mathrm {RHom}}_{\Lambda }(\operatorname {\mathrm {pr}}_1^*A, \operatorname {\mathrm {pr}}_2^!A)\to \Delta _{X/S}^!(A\boxtimes _S \mathbf {D}_{X/S}A)$
. Here,
![]() $\epsilon $
is adjoint to
$\epsilon $
is adjoint to
![]() $\operatorname {\mathrm {id}}_A\colon A\to A$
. A diagram chase now shows that
$\operatorname {\mathrm {id}}_A\colon A\to A$
. A diagram chase now shows that
![]() $\operatorname {\mathrm {coev}}_{\mathfrak {X}}$
and
$\operatorname {\mathrm {coev}}_{\mathfrak {X}}$
and
![]() $\operatorname {\mathrm {ev}}_{\mathfrak {X}}$
witness the dualizability of
$\operatorname {\mathrm {ev}}_{\mathfrak {X}}$
witness the dualizability of
![]() $\mathfrak {X}$
.
$\mathfrak {X}$
.
In the scheme setting, a pair
![]() $(X,A)$
is dualizable if and only if A is locally acyclic over S [Reference Lu and ZhengLZ22, Theorem 2.16], under some mild assumptions. Similarly, if
$(X,A)$
is dualizable if and only if A is locally acyclic over S [Reference Lu and ZhengLZ22, Theorem 2.16], under some mild assumptions. Similarly, if
![]() $f:X\to S$
is a morphism of v-stacks which is representable in nice diamonds, then
$f:X\to S$
is a morphism of v-stacks which is representable in nice diamonds, then
![]() $(X,A)$
is dualizable in
$(X,A)$
is dualizable in
![]() $\operatorname {\mathrm {CoCorr}}_S$
if and only if A is f-universally locally acyclic [Reference Fargues and ScholzeFS21, Theorem IV.2.24]. This result extends immediately to the situation of fine morphisms between decent v-stacks, using that universal local acyclicity is cohomologically smooth-local on the source.
$\operatorname {\mathrm {CoCorr}}_S$
if and only if A is f-universally locally acyclic [Reference Fargues and ScholzeFS21, Theorem IV.2.24]. This result extends immediately to the situation of fine morphisms between decent v-stacks, using that universal local acyclicity is cohomologically smooth-local on the source.
If
![]() $\mathfrak {X}$
is a dualizable object of
$\mathfrak {X}$
is a dualizable object of
![]() $\operatorname {\mathrm {CoCorr}}_S$
, and
$\operatorname {\mathrm {CoCorr}}_S$
, and
![]() $\mathfrak {f}\colon \mathfrak {X}\to \mathfrak {X}$
is an endomorphism, we may define the categorical trace
$\mathfrak {f}\colon \mathfrak {X}\to \mathfrak {X}$
is an endomorphism, we may define the categorical trace
![]() $\operatorname {\mathrm {tr}}(\mathfrak {f})$
, an object of
$\operatorname {\mathrm {tr}}(\mathfrak {f})$
, an object of
![]() $\Omega \operatorname {\mathrm {CoCorr}}_S=\operatorname {\mathrm {End}} 1_{\operatorname {\mathrm {CoCorr}}_S}$
. Let us make this explicit. The category
$\Omega \operatorname {\mathrm {CoCorr}}_S=\operatorname {\mathrm {End}} 1_{\operatorname {\mathrm {CoCorr}}_S}$
. Let us make this explicit. The category
![]() $\Omega \operatorname {\mathrm {CoCorr}}_S$
has objects
$\Omega \operatorname {\mathrm {CoCorr}}_S$
has objects
![]() $(X,\omega )$
, where X is a decent S-v-stack with fine structure map
$(X,\omega )$
, where X is a decent S-v-stack with fine structure map
![]() $X\to S$
, and
$X\to S$
, and
![]() $\omega \in H^0(X,K_{X/S})$
is arbitrary. A morphism
$\omega \in H^0(X,K_{X/S})$
is arbitrary. A morphism
![]() $(X,\omega )\to (X',\omega ')$
is a diagram
$(X,\omega )\to (X',\omega ')$
is a diagram

with p proper such that
![]() $\omega '=p_*\omega $
. Here,
$\omega '=p_*\omega $
. Here,
is induced from
![]() $\pi _*K_{X/S}\cong \pi ^{\prime }_*p_*p^!K_{X'/S} \cong \pi ^{\prime }_*p_!p^!K_{X'/S} \stackrel {\text {counit}}{\to } \pi ^{\prime }_*K_{X'/S}$
.
$\pi _*K_{X/S}\cong \pi ^{\prime }_*p_*p^!K_{X'/S} \cong \pi ^{\prime }_*p_!p^!K_{X'/S} \stackrel {\text {counit}}{\to } \pi ^{\prime }_*K_{X'/S}$
.
Now let
![]() $\mathfrak {X}=(X,A)$
be a dualizable object in
$\mathfrak {X}=(X,A)$
be a dualizable object in
![]() $\operatorname {\mathrm {CoCorr}}_S$
, and let
$\operatorname {\mathrm {CoCorr}}_S$
, and let
![]() $\mathfrak {f}=(c,u)\colon \mathfrak {X}\to \mathfrak {X}$
be an endomorphism, with
$\mathfrak {f}=(c,u)\colon \mathfrak {X}\to \mathfrak {X}$
be an endomorphism, with
![]() $c=(c_1,c_2)\colon C\to X\times _S X$
and
$c=(c_1,c_2)\colon C\to X\times _S X$
and
![]() $u\colon c_1^*A\to c_2^!A$
. By definition,
$u\colon c_1^*A\to c_2^!A$
. By definition,
![]() $\operatorname {\mathrm {tr}}(\mathfrak {f}) = \operatorname {\mathrm {ev}}_{\mathfrak {X}}\circ (f\otimes \operatorname {\mathrm {id}}_{\mathfrak {X}^{\vee }}) \circ \operatorname {\mathrm {coev}}_{\mathfrak {X}}$
. The object
$\operatorname {\mathrm {tr}}(\mathfrak {f}) = \operatorname {\mathrm {ev}}_{\mathfrak {X}}\circ (f\otimes \operatorname {\mathrm {id}}_{\mathfrak {X}^{\vee }}) \circ \operatorname {\mathrm {coev}}_{\mathfrak {X}}$
. The object
![]() $\operatorname {\mathrm {tr}}(\mathfrak {f})$
is represented by a pair
$\operatorname {\mathrm {tr}}(\mathfrak {f})$
is represented by a pair
![]() $(\operatorname {\mathrm {tr}}(c),\operatorname {\mathrm {tr}}(u))$
. Here,
$(\operatorname {\mathrm {tr}}(c),\operatorname {\mathrm {tr}}(u))$
. Here,
![]() $\operatorname {\mathrm {tr}}(c)\in \Omega 1_{\operatorname {\mathrm {Corr}}_S}$
is the correspondence
$\operatorname {\mathrm {tr}}(c)\in \Omega 1_{\operatorname {\mathrm {Corr}}_S}$
is the correspondence
![]() $\operatorname {\mathrm {Fix}}(c)\to S\times _S S = S$
, where
$\operatorname {\mathrm {Fix}}(c)\to S\times _S S = S$
, where
![]() $\operatorname {\mathrm {Fix}}(c)$
is the fixed-point locus of the correspondence c, as in the Cartesian diagram:
$\operatorname {\mathrm {Fix}}(c)$
is the fixed-point locus of the correspondence c, as in the Cartesian diagram:

For its part, the element
![]() $\operatorname {\mathrm {tr}}(u)$
is an element of
$\operatorname {\mathrm {tr}}(u)$
is an element of
![]() $H^0(\operatorname {\mathrm {Fix}}(c),K_{\operatorname {\mathrm {Fix}}(c)/S})$
. Footnote 5It is the image of
$H^0(\operatorname {\mathrm {Fix}}(c),K_{\operatorname {\mathrm {Fix}}(c)/S})$
. Footnote 5It is the image of
![]() $u\in \operatorname {\mathrm {Hom}}(c_1^*A,c_2^!A)$
under
$u\in \operatorname {\mathrm {Hom}}(c_1^*A,c_2^!A)$
under
 $$ \begin{align*} \begin{array}{lcl} H^0(C,\underline{\mathrm{RHom}}(c_1^*A, c_2^!A)) &\stackrel{(P5)}{\stackrel{\cong}{\longrightarrow}} &\!\!H^0(C,c^!\underline{\mathrm{RHom}}(\operatorname{\mathrm{pr}}_1^*A, \operatorname{\mathrm{pr}}_2^!A)) \\[2pt] &\stackrel{(4.0.1)}{\stackrel{\cong}{\longrightarrow}}&\!\! H^0(C,c^!(\mathbf{D}_{X/S}A \boxtimes_S A)) \\[2pt] &\stackrel{\alpha}{\to}&\!\! H^0(C,c^!(\Delta_{X/S})_* (\mathbf{D}_{X/S}A \otimes A) ) \\[2pt] &\stackrel{\operatorname{\mathrm{ev}}_A}{\to}&\!\! H^0(C,c^!(\Delta_{X/S})_* K_{X/S} )\\[2pt] &\stackrel{{\text{(BC2)}}}{\stackrel{\cong}{\longrightarrow}} &\!\! H^0(C,(\Delta^{\prime}_{X/S})_* (c')^! K_{X/S}) \\[2pt] &\cong &\!\! H^0(\operatorname{\mathrm{Fix}}(c),K_{\operatorname{\mathrm{Fix}}(c)/S}). \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{lcl} H^0(C,\underline{\mathrm{RHom}}(c_1^*A, c_2^!A)) &\stackrel{(P5)}{\stackrel{\cong}{\longrightarrow}} &\!\!H^0(C,c^!\underline{\mathrm{RHom}}(\operatorname{\mathrm{pr}}_1^*A, \operatorname{\mathrm{pr}}_2^!A)) \\[2pt] &\stackrel{(4.0.1)}{\stackrel{\cong}{\longrightarrow}}&\!\! H^0(C,c^!(\mathbf{D}_{X/S}A \boxtimes_S A)) \\[2pt] &\stackrel{\alpha}{\to}&\!\! H^0(C,c^!(\Delta_{X/S})_* (\mathbf{D}_{X/S}A \otimes A) ) \\[2pt] &\stackrel{\operatorname{\mathrm{ev}}_A}{\to}&\!\! H^0(C,c^!(\Delta_{X/S})_* K_{X/S} )\\[2pt] &\stackrel{{\text{(BC2)}}}{\stackrel{\cong}{\longrightarrow}} &\!\! H^0(C,(\Delta^{\prime}_{X/S})_* (c')^! K_{X/S}) \\[2pt] &\cong &\!\! H^0(\operatorname{\mathrm{Fix}}(c),K_{\operatorname{\mathrm{Fix}}(c)/S}). \\ \end{array} \end{align*} $$
Here, the map labeled
![]() $\alpha $
is adjoint to
$\alpha $
is adjoint to
![]() $(\Delta _{X/S})^*(\mathbf {D}_{X/S}A \boxtimes _S A)\stackrel {\cong }{\longrightarrow } \mathbf {D}_{X/S} A \otimes A$
.
$(\Delta _{X/S})^*(\mathbf {D}_{X/S}A \boxtimes _S A)\stackrel {\cong }{\longrightarrow } \mathbf {D}_{X/S} A \otimes A$
.
Definition 4.3.6 (Inertia stack, characteristic class)
In the special case that
![]() $\mathfrak {f}=\operatorname {\mathrm {id}}_{\mathfrak {X}}=(\Delta _{X/S},\operatorname {\mathrm {id}}_A)$
, the object
$\mathfrak {f}=\operatorname {\mathrm {id}}_{\mathfrak {X}}=(\Delta _{X/S},\operatorname {\mathrm {id}}_A)$
, the object
![]() $\operatorname {\mathrm {tr}}(\Delta _{X/S})=X\times _{X\times _S X} X$
is the inertia stack of X, which we notate as
$\operatorname {\mathrm {tr}}(\Delta _{X/S})=X\times _{X\times _S X} X$
is the inertia stack of X, which we notate as
![]() $\operatorname {\mathrm {In}}_S(X)$
. Its objects are pairs
$\operatorname {\mathrm {In}}_S(X)$
. Its objects are pairs
![]() $(x,g)$
, where
$(x,g)$
, where
![]() $x\in X$
and
$x\in X$
and
![]() $g\in \operatorname {\mathrm {Aut}} x$
. Then
$g\in \operatorname {\mathrm {Aut}} x$
. Then
![]() $\operatorname {\mathrm {tr}}(\operatorname {\mathrm {id}}_A)$
is an element of
$\operatorname {\mathrm {tr}}(\operatorname {\mathrm {id}}_A)$
is an element of
![]() $H^0(\operatorname {\mathrm {In}}_S(X),K_{\operatorname {\mathrm {In}}_S(X)})$
, which we call the characteristic class of A. We notate this element as
$H^0(\operatorname {\mathrm {In}}_S(X),K_{\operatorname {\mathrm {In}}_S(X)})$
, which we call the characteristic class of A. We notate this element as
![]() $\operatorname {\mathrm {cc}}_{X/S}(A)$
.
$\operatorname {\mathrm {cc}}_{X/S}(A)$
.
We record one lemma here for later reference.
Lemma 4.3.7. Let
![]() $i\colon U\to X$
be an open immersion of decent S-v-stacks fine over S. Then
$i\colon U\to X$
be an open immersion of decent S-v-stacks fine over S. Then
![]() $\operatorname {\mathrm {In}}_S(i)\colon \operatorname {\mathrm {In}}_S(U)\to \operatorname {\mathrm {In}}_S(X)$
is also an open immersion. If
$\operatorname {\mathrm {In}}_S(i)\colon \operatorname {\mathrm {In}}_S(U)\to \operatorname {\mathrm {In}}_S(X)$
is also an open immersion. If
![]() $A\in D_{\mathrm {\acute {e}t}}(X,\Lambda )$
is ULA over S, then so is
$A\in D_{\mathrm {\acute {e}t}}(X,\Lambda )$
is ULA over S, then so is
![]() $i^*A$
, and then
$i^*A$
, and then
Proof. All constructions are local on X.
Theorem 4.3.8 (Relative Lefschetz–Verdier trace formula)
Let
![]() $\mathfrak {X}=(X,A)$
be a dualizable object in
$\mathfrak {X}=(X,A)$
be a dualizable object in
![]() $\operatorname {\mathrm {CoCorr}}_S$
, and let
$\operatorname {\mathrm {CoCorr}}_S$
, and let
![]() $\mathfrak {f}\in \operatorname {\mathrm {End}} \mathfrak {X}$
lie over the correspondence
$\mathfrak {f}\in \operatorname {\mathrm {End}} \mathfrak {X}$
lie over the correspondence
![]() $c\colon C\to X\times _S X$
. Suppose we are given a diagram
$c\colon C\to X\times _S X$
. Suppose we are given a diagram

with
![]() $p,q$
proper. Then
$p,q$
proper. Then
![]() $\mathfrak {X}'=(X',q_*A)$
is also dualizable. Let
$\mathfrak {X}'=(X',q_*A)$
is also dualizable. Let
![]() $\mathfrak {q}\colon \mathfrak {X}\to \mathfrak {X}'$
be the evident 1-morphism lying over q. There is a unique morphism
$\mathfrak {q}\colon \mathfrak {X}\to \mathfrak {X}'$
be the evident 1-morphism lying over q. There is a unique morphism
![]() $\mathfrak {f}'\in \operatorname {\mathrm {End}}\mathfrak {X}'$
lying over
$\mathfrak {f}'\in \operatorname {\mathrm {End}}\mathfrak {X}'$
lying over
![]() $C'\to X'\times _S X'$
such that p defines a 2-morphism
$C'\to X'\times _S X'$
such that p defines a 2-morphism
![]() $\widetilde {p}$
filling in the square
$\widetilde {p}$
filling in the square

Finally, there exists a (necessarily unique) 2-morphism
![]() $\operatorname {\mathrm {tr}}(\widetilde {p})\colon \operatorname {\mathrm {tr}}(\mathfrak {f})\implies \operatorname {\mathrm {tr}}(\mathfrak {f}')$
lying over
$\operatorname {\mathrm {tr}}(\widetilde {p})\colon \operatorname {\mathrm {tr}}(\mathfrak {f})\implies \operatorname {\mathrm {tr}}(\mathfrak {f}')$
lying over
![]() $\operatorname {\mathrm {tr}}(p)\colon \operatorname {\mathrm {tr}}(c)\implies \operatorname {\mathrm {tr}}(c')$
.
$\operatorname {\mathrm {tr}}(p)\colon \operatorname {\mathrm {tr}}(c)\implies \operatorname {\mathrm {tr}}(c')$
.
Proof. This is formally the same as the proof of (a special case of) [Reference Lu and ZhengLZ22, Theorem 2.21], so we give a brief sketch. (In [Reference Lu and ZhengLZ22] one gets a statement about the more general Lefschetz–Verdier pairing, which we also could have established.) The existence and uniqueness of
![]() $\mathfrak {f}'\in \operatorname {\mathrm {End}}\mathfrak {X}'$
follows from the definition of 2-morphisms in
$\mathfrak {f}'\in \operatorname {\mathrm {End}}\mathfrak {X}'$
follows from the definition of 2-morphisms in
![]() $\operatorname {\mathrm {CoCorr}}_S$
. The dualizability of
$\operatorname {\mathrm {CoCorr}}_S$
. The dualizability of
![]() $\mathfrak {X}'$
is [Reference Lu and ZhengLZ22, Proposition 2.23]. The dual of
$\mathfrak {X}'$
is [Reference Lu and ZhengLZ22, Proposition 2.23]. The dual of
![]() $\mathfrak {X}'$
is
$\mathfrak {X}'$
is
![]() $(\mathfrak {X}')^{\vee }=(X',q_*\mathbf {D}_{X/S}A)$
; there is another natural map
$(\mathfrak {X}')^{\vee }=(X',q_*\mathbf {D}_{X/S}A)$
; there is another natural map
![]() $\mathfrak {q}^{\vee }\colon \mathfrak {X}^{\vee }\to (\mathfrak {X}')^{\vee }$
defined similarly to
$\mathfrak {q}^{\vee }\colon \mathfrak {X}^{\vee }\to (\mathfrak {X}')^{\vee }$
defined similarly to
![]() $\mathfrak {q}$
.
$\mathfrak {q}$
.
Consider the diagram:

The two outer triangles can be filled in with a 2-morphism, as can the inner square (via
![]() $p\otimes \operatorname {\mathrm {id}}_{\mathfrak {q}^{\vee }}$
). See [Reference Lu and ZhengLZ22, Construction 1.7] for details. Composing, we find the required 2-morphism
$p\otimes \operatorname {\mathrm {id}}_{\mathfrak {q}^{\vee }}$
). See [Reference Lu and ZhengLZ22, Construction 1.7] for details. Composing, we find the required 2-morphism
![]() $\operatorname {\mathrm {tr}}(\widetilde {p})\colon \operatorname {\mathrm {tr}}(\mathfrak {f})\implies \operatorname {\mathrm {tr}}(\mathfrak {f}')$
.
$\operatorname {\mathrm {tr}}(\widetilde {p})\colon \operatorname {\mathrm {tr}}(\mathfrak {f})\implies \operatorname {\mathrm {tr}}(\mathfrak {f}')$
.
Corollary 4.3.9. Let
![]() $(X,A)$
be a dualizable object, and let
$(X,A)$
be a dualizable object, and let
![]() $p\colon X\to X'$
be proper. Then
$p\colon X\to X'$
be proper. Then
![]() $(X',p_!A)$
is dualizable. The morphism
$(X',p_!A)$
is dualizable. The morphism
![]() $\operatorname {\mathrm {In}}_S(p)\colon \operatorname {\mathrm {In}}_S(X)\to \operatorname {\mathrm {In}}_S(X')$
is proper, and
$\operatorname {\mathrm {In}}_S(p)\colon \operatorname {\mathrm {In}}_S(X)\to \operatorname {\mathrm {In}}_S(X')$
is proper, and
Example 4.3.10. We can immediately deduce a familiar-looking trace formula from Theorem 4.3.8 in the case of proper diamonds. Suppose
![]() $S=\operatorname {\mathrm {Spd}} C$
for an algebraically closed perfectoid field C, and suppose
$S=\operatorname {\mathrm {Spd}} C$
for an algebraically closed perfectoid field C, and suppose
![]() $q\colon X\to S$
is a nice diamond. Let
$q\colon X\to S$
is a nice diamond. Let
![]() $A\in D_{\mathrm {\acute {e}t}}(X,\Lambda )$
be ULA over S. Then
$A\in D_{\mathrm {\acute {e}t}}(X,\Lambda )$
be ULA over S. Then
![]() $\mathfrak {X}=(X,A)$
is a dualizable object of
$\mathfrak {X}=(X,A)$
is a dualizable object of
![]() $\operatorname {\mathrm {CoCorr}}_S$
. Let
$\operatorname {\mathrm {CoCorr}}_S$
. Let
![]() $\mathfrak {f}=(c,u)$
be an endomorphism of
$\mathfrak {f}=(c,u)$
be an endomorphism of
![]() $\mathfrak {X}$
lying over a correspondence
$\mathfrak {X}$
lying over a correspondence
![]() $c\colon Y\to X\times _S X$
. The categorical trace
$c\colon Y\to X\times _S X$
. The categorical trace
![]() $\operatorname {\mathrm {tr}}(\mathfrak {f})$
is an endomorphism of
$\operatorname {\mathrm {tr}}(\mathfrak {f})$
is an endomorphism of
![]() $1_{\operatorname {\mathrm {CoCorr}}_S}$
consisting of the pair
$1_{\operatorname {\mathrm {CoCorr}}_S}$
consisting of the pair
![]() $(\operatorname {\mathrm {Fix}}(c),\omega )$
, where
$(\operatorname {\mathrm {Fix}}(c),\omega )$
, where
![]() $\operatorname {\mathrm {Fix}}(c)=Y\times _{c,X\times _S X,\Delta _{X/S}} X$
is the fixed point locus of the correspondence, and
$\operatorname {\mathrm {Fix}}(c)=Y\times _{c,X\times _S X,\Delta _{X/S}} X$
is the fixed point locus of the correspondence, and
![]() $\omega $
is a global section of
$\omega $
is a global section of
![]() $K_{\operatorname {\mathrm {Fix}}(c)/S}$
.
$K_{\operatorname {\mathrm {Fix}}(c)/S}$
.
Now suppose that X is proper over S. In the setting of Theorem 4.3.8, we put
![]() $\mathfrak {X}'=(S,q_*A)$
and
$\mathfrak {X}'=(S,q_*A)$
and
![]() $C'=S$
. The dualizability of
$C'=S$
. The dualizability of
![]() $\mathfrak {X}'$
means that
$\mathfrak {X}'$
means that
![]() $q_*A=R\Gamma (X,A)$
is a perfect complex. The morphism
$q_*A=R\Gamma (X,A)$
is a perfect complex. The morphism
![]() $\mathfrak {f}'\colon \mathfrak {X}'\to \mathfrak {X}'$
supplied by Theorem 4.3.8 is the endomorphism
$\mathfrak {f}'\colon \mathfrak {X}'\to \mathfrak {X}'$
supplied by Theorem 4.3.8 is the endomorphism
![]() $q_*(\mathfrak {f})\colon q_*A \to q_*A$
. Finally, the existence of
$q_*(\mathfrak {f})\colon q_*A \to q_*A$
. Finally, the existence of
![]() $\operatorname {\mathrm {tr}}(\widetilde {p})\colon \operatorname {\mathrm {tr}}(\mathfrak {f})\implies \operatorname {\mathrm {tr}}(\mathfrak {f}')$
lying over
$\operatorname {\mathrm {tr}}(\widetilde {p})\colon \operatorname {\mathrm {tr}}(\mathfrak {f})\implies \operatorname {\mathrm {tr}}(\mathfrak {f}')$
lying over
![]() $\operatorname {\mathrm {tr}}(p)\colon \operatorname {\mathrm {tr}}(c)\implies \operatorname {\mathrm {tr}}(\operatorname {\mathrm {id}}_S)$
implies that
$\operatorname {\mathrm {tr}}(p)\colon \operatorname {\mathrm {tr}}(c)\implies \operatorname {\mathrm {tr}}(\operatorname {\mathrm {id}}_S)$
implies that
 $$ \begin{align} \operatorname{\mathrm{tr}}\left(q_*(\mathfrak{f})\biggm\vert R\Gamma(X,A)\right) = \int_{\operatorname{\mathrm{Fix}}(c)} \omega. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{tr}}\left(q_*(\mathfrak{f})\biggm\vert R\Gamma(X,A)\right) = \int_{\operatorname{\mathrm{Fix}}(c)} \omega. \end{align} $$
Definition 4.3.11. Let
![]() $x\in \operatorname {\mathrm {Fix}}(c)$
be an isolated point such that
$x\in \operatorname {\mathrm {Fix}}(c)$
be an isolated point such that
![]() $x\to S$
an isomorphism. The local term
$x\to S$
an isomorphism. The local term
![]() $\operatorname {\mathrm {loc}}_x(\mathfrak {f})$
is the restriction of
$\operatorname {\mathrm {loc}}_x(\mathfrak {f})$
is the restriction of
![]() $\omega $
to x, considered as an element of
$\omega $
to x, considered as an element of
![]() $\Lambda $
.
$\Lambda $
.
If
![]() $\mathfrak {f}$
arises from an automorphism
$\mathfrak {f}$
arises from an automorphism
![]() $g\colon X\to X$
along with a morphism
$g\colon X\to X$
along with a morphism
![]() $u\colon g^*A\to A$
, we write the local term as
$u\colon g^*A\to A$
, we write the local term as
![]() $\operatorname {\mathrm {loc}}_x(g,A)$
(the dependence on u being implicit).
$\operatorname {\mathrm {loc}}_x(g,A)$
(the dependence on u being implicit).
In the latter situation, if it so happens that
![]() $\operatorname {\mathrm {Fix}}(g)$
consists of finitely many isolated S-points
$\operatorname {\mathrm {Fix}}(g)$
consists of finitely many isolated S-points
![]() $x_1,\dots ,x_n$
, then equation (4.3.5) reduces to
$x_1,\dots ,x_n$
, then equation (4.3.5) reduces to
 $$\begin{align*}\operatorname{\mathrm{tr}}\left(q_*(g)\biggm\vert R\Gamma(X,A)\right) = \sum_{i=1}^n \operatorname{\mathrm{loc}}_x(g,A).\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{tr}}\left(q_*(g)\biggm\vert R\Gamma(X,A)\right) = \sum_{i=1}^n \operatorname{\mathrm{loc}}_x(g,A).\end{align*}$$
4.4 The trace distribution as a characteristic class
Let S be a geometric point, and let G be a locally pro-p group as in Example 4.2.2 so that
![]() $[S/G_S]$
is a decent v-stack and
$[S/G_S]$
is a decent v-stack and
![]() $f\colon [S/G_S]\to S$
is fine and cohomologically smooth. As in that example, we freely identify
$f\colon [S/G_S]\to S$
is fine and cohomologically smooth. As in that example, we freely identify
![]() $D_{\mathrm {\acute {e}t}}([S/G_S],\Lambda )$
with the derived category of
$D_{\mathrm {\acute {e}t}}([S/G_S],\Lambda )$
with the derived category of
![]() $\Lambda $
-modules with a smooth G-action. For an object
$\Lambda $
-modules with a smooth G-action. For an object
![]() $M\in D_{\mathrm {\acute {e}t}}([S/G_S],\Lambda )$
, we let
$M\in D_{\mathrm {\acute {e}t}}([S/G_S],\Lambda )$
, we let
![]() $M^{\vee } = \underline {\mathrm {RHom}}(M,\Lambda )$
; by [Reference Fargues and ScholzeFS21, Corollary V.1.4], this is just the usual (derived) smooth dual.
$M^{\vee } = \underline {\mathrm {RHom}}(M,\Lambda )$
; by [Reference Fargues and ScholzeFS21, Corollary V.1.4], this is just the usual (derived) smooth dual.
For a compact open subgroup
![]() $K\subset G$
, we let
$K\subset G$
, we let
![]() $M^K$
be the complex of derived K-invariants. If K is pro-p, the map of complexes
$M^K$
be the complex of derived K-invariants. If K is pro-p, the map of complexes
![]() $M^K\to M$
admits a section, namely, averaging over K with respect to a normalized Haar measure. Thus,
$M^K\to M$
admits a section, namely, averaging over K with respect to a normalized Haar measure. Thus,
![]() $M^K$
is naturally a summand of M.
$M^K$
is naturally a summand of M.
Proposition 4.4.1. Let M be an object of
![]() $D_{\mathrm {\acute {e}t}}([S/G_S],\Lambda )$
. The following are equivalent:
$D_{\mathrm {\acute {e}t}}([S/G_S],\Lambda )$
. The following are equivalent:
-
1. The object
 $([S/G_S],M)$
of
$([S/G_S],M)$
of
 $\operatorname {\mathrm {CoCorr}}_S$
is dualizable, with dual
$\operatorname {\mathrm {CoCorr}}_S$
is dualizable, with dual
 $([S/G_S],\mathbf {D} M)$
, where
$([S/G_S],\mathbf {D} M)$
, where
 $\mathbf {D} M=\mathrm {Haar}(G,\Lambda )^* \otimes M^{\vee }$
.
$\mathbf {D} M=\mathrm {Haar}(G,\Lambda )^* \otimes M^{\vee }$
. -
2. The object M is ULA over S.
-
3. For all compact open pro-p subgroups
 $K\subset G$
, the (derived) K-invariants
$K\subset G$
, the (derived) K-invariants
 $M^K$
are a perfect complex of
$M^K$
are a perfect complex of
 $\Lambda $
-modules.
$\Lambda $
-modules.
Proof. The equivalence between (1) dualizability in
![]() $\operatorname {\mathrm {CoCorr}}_S$
and (2) the ULA property is [Reference Fargues and ScholzeFS21, Theorem IV.2.23]. For the equivalence between (2) and (3), see [Reference Fargues and ScholzeFS21, V.7.1]. (There, the authors work in the more general context of
$\operatorname {\mathrm {CoCorr}}_S$
and (2) the ULA property is [Reference Fargues and ScholzeFS21, Theorem IV.2.23]. For the equivalence between (2) and (3), see [Reference Fargues and ScholzeFS21, V.7.1]. (There, the authors work in the more general context of
![]() $\operatorname {\mathrm {Bun}}_G$
, but the method of proof can be used in our situation of
$\operatorname {\mathrm {Bun}}_G$
, but the method of proof can be used in our situation of
![]() $[S/G_S]$
.) The Verdier dual of M is
$[S/G_S]$
.) The Verdier dual of M is
![]() $\underline {\mathrm {RHom}}(M,f^!\Lambda )$
, and
$\underline {\mathrm {RHom}}(M,f^!\Lambda )$
, and
![]() $f^!\Lambda = \mathrm {Haar}(G,\Lambda )^*$
by Example 4.2.4.
$f^!\Lambda = \mathrm {Haar}(G,\Lambda )^*$
by Example 4.2.4.
We note that is possible to give a direct proof of the implication (3)
![]() $\implies $
(1). Let
$\implies $
(1). Let
![]() $\mathfrak {X}=([S/G_S],M)$
and
$\mathfrak {X}=([S/G_S],M)$
and
![]() $\mathfrak {X}^{\vee }=([S/G_S],\mathbf {D} M)$
. The evaluation map
$\mathfrak {X}^{\vee }=([S/G_S],\mathbf {D} M)$
. The evaluation map
![]() $\mathfrak {X}^{\vee }\otimes \mathfrak {X} \to 1_{\operatorname {\mathrm {CoCorr}}_S}$
lies over the correspondence
$\mathfrak {X}^{\vee }\otimes \mathfrak {X} \to 1_{\operatorname {\mathrm {CoCorr}}_S}$
lies over the correspondence
![]() $\Delta _f\times f\colon [S/G_S]\to [S/G_S]^2 \times S$
; on the level of sheaves, it is a twist of the evaluation map
$\Delta _f\times f\colon [S/G_S]\to [S/G_S]^2 \times S$
; on the level of sheaves, it is a twist of the evaluation map
![]() $M^{\vee } \otimes M \to \Lambda $
. The coevaluation map
$M^{\vee } \otimes M \to \Lambda $
. The coevaluation map
![]() $1_{\operatorname {\mathrm {CoCorr}}_S} \to \mathfrak {X}\otimes \mathfrak {X}^{\vee }$
lies over the correspondence
$1_{\operatorname {\mathrm {CoCorr}}_S} \to \mathfrak {X}\otimes \mathfrak {X}^{\vee }$
lies over the correspondence
![]() $f\times \Delta _f\colon [S/G_S] \to S\times [S/G_S]^2$
. Note that the diagonal map presents G as a direct factor of
$f\times \Delta _f\colon [S/G_S] \to S\times [S/G_S]^2$
. Note that the diagonal map presents G as a direct factor of
![]() $G^2$
so that Example 4.2.3 applies to give an explicit description of
$G^2$
so that Example 4.2.3 applies to give an explicit description of
![]() $\Delta _f^!$
. The result is that the
$\Delta _f^!$
. The result is that the
![]() $\Lambda $
-module of cohomological correspondences lying over
$\Lambda $
-module of cohomological correspondences lying over
![]() $f\times \Delta _f$
:
$f\times \Delta _f$
:
may be identified with the
![]() $\Lambda $
-module
$\Lambda $
-module
In the latter expression,
![]() $G\times G$
acts on
$G\times G$
acts on
![]() $C_c(G,\Lambda )$
by left and right translation. We describe the coevaluation map as a
$C_c(G,\Lambda )$
by left and right translation. We describe the coevaluation map as a
![]() $G\times G$
-equivariant function
$G\times G$
-equivariant function
Let
![]() $h\in C_c(G,\Lambda )$
and
$h\in C_c(G,\Lambda )$
and
![]() $\mu \in \mathrm {Haar}(G,\Lambda )$
; then integration against
$\mu \in \mathrm {Haar}(G,\Lambda )$
; then integration against
![]() $h\;d\mu $
describes an endomorphism
$h\;d\mu $
describes an endomorphism
![]() $I_{h,\mu }\in \operatorname {\mathrm {End}} M$
:
$I_{h,\mu }\in \operatorname {\mathrm {End}} M$
:
 $$\begin{align*}I_{h,\mu}(v) = \int_{g\in G} h(g)gv \; d\mu(g). \end{align*}$$
$$\begin{align*}I_{h,\mu}(v) = \int_{g\in G} h(g)gv \; d\mu(g). \end{align*}$$
The function h is left and right K-invariant for some sufficiently small pro-p open subgroup
![]() $K\subset G$
, in which case
$K\subset G$
, in which case
![]() $I_{h,\mu }$
factors through a map
$I_{h,\mu }$
factors through a map
![]() $M^K\to M^K$
. Since
$M^K\to M^K$
. Since
![]() $M^K$
is perfect by hypothesis, we have described an element of
$M^K$
is perfect by hypothesis, we have described an element of
Then
![]() $I(h\otimes \mu )$
is the image of
$I(h\otimes \mu )$
is the image of
![]() $I_{h,\mu }$
in
$I_{h,\mu }$
in
![]() $H^0(M\otimes M^{\vee })$
.
$H^0(M\otimes M^{\vee })$
.
Definition 4.4.2. The object M of
![]() $D_{\mathrm {\acute {e}t}}([S/G_S],\Lambda )$
is admissible if it satisfies the equivalent conditions of Proposition 4.4.1.
$D_{\mathrm {\acute {e}t}}([S/G_S],\Lambda )$
is admissible if it satisfies the equivalent conditions of Proposition 4.4.1.
Suppose M is an admissible object of
![]() $D_{\mathrm {\acute {e}t}}([S/G_S],\Lambda )$
. The trace distribution of M is a canonical element
$D_{\mathrm {\acute {e}t}}([S/G_S],\Lambda )$
. The trace distribution of M is a canonical element
where G is meant to act on
![]() $C_c(G,\Lambda )$
by conjugation and on
$C_c(G,\Lambda )$
by conjugation and on
![]() $\mathrm {Haar}(G,\Lambda )$
by the modular character. Namely,
$\mathrm {Haar}(G,\Lambda )$
by the modular character. Namely,
![]() $\operatorname {\mathrm {tr.dist}}(M)$
sends
$\operatorname {\mathrm {tr.dist}}(M)$
sends
![]() $h\otimes \mu $
(where
$h\otimes \mu $
(where
![]() $h\in C_c(G,\Lambda )$
and
$h\in C_c(G,\Lambda )$
and
![]() $\mu \in \mathrm {Haar}(G,\Lambda )$
to the Euler characteristic of the operator
$\mu \in \mathrm {Haar}(G,\Lambda )$
to the Euler characteristic of the operator
![]() $I_{h,\mu }$
described in the proof of Proposition 4.4.1.
$I_{h,\mu }$
described in the proof of Proposition 4.4.1.
On the other hand, we have the inertia stack
![]() $\operatorname {\mathrm {In}}_S([S/G_S])$
and the characteristic class
$\operatorname {\mathrm {In}}_S([S/G_S])$
and the characteristic class
![]() $\operatorname {\mathrm {cc}}_{[S/G_S]/S}(M)$
as in Definition 4.3.6. We have
$\operatorname {\mathrm {cc}}_{[S/G_S]/S}(M)$
as in Definition 4.3.6. We have
the stack of conjugacy classes of G. (Reasoning: For a perfectoid space
![]() $Y\to S$
, a Y-point of
$Y\to S$
, a Y-point of
![]() $\operatorname {\mathrm {In}}_S([S/G_S])$
is a
$\operatorname {\mathrm {In}}_S([S/G_S])$
is a
![]() $G_S$
-torsor
$G_S$
-torsor
![]() $\widetilde {Y}\to Y$
together with a
$\widetilde {Y}\to Y$
together with a
![]() $G_S$
-equivariant automorphism
$G_S$
-equivariant automorphism
![]() $i\colon \widetilde {Y}\to \widetilde {Y}$
. Such an automorphism arises as
$i\colon \widetilde {Y}\to \widetilde {Y}$
. Such an automorphism arises as
![]() $i(y)=f(y).y$
, where
$i(y)=f(y).y$
, where
![]() $f\colon \widetilde {Y}\to G_S$
is a morphism satisfying
$f\colon \widetilde {Y}\to G_S$
is a morphism satisfying
![]() $f(gy)=gf(y)g^{-1}$
. The pair
$f(gy)=gf(y)g^{-1}$
. The pair
![]() $(\widetilde {Y},f)$
then constitutes a Y-point of
$(\widetilde {Y},f)$
then constitutes a Y-point of
.) For its part, the characteristic class
![]() $\operatorname {\mathrm {cc}}_{[S/G_S]/S}(M)$
lies in
$\operatorname {\mathrm {cc}}_{[S/G_S]/S}(M)$
lies in
![]() $H^0(\operatorname {\mathrm {In}}_S([S/G_S]), K_{\operatorname {\mathrm {In}}_S([S/G_S])/S})$
, and by Example 4.2.5 we have an isomorphism
$H^0(\operatorname {\mathrm {In}}_S([S/G_S]), K_{\operatorname {\mathrm {In}}_S([S/G_S])/S})$
, and by Example 4.2.5 we have an isomorphism
onto the same module appearing in equation (4.4.1).
Proposition 4.4.3. Let G be a locally pro-p group satisfying the hypotheses of Example 4.2.2. Let M be an admissible object of
![]() $D_{\mathrm {\acute {e}t}}([S/G_S],\Lambda )$
. Then
$D_{\mathrm {\acute {e}t}}([S/G_S],\Lambda )$
. Then
Proof. The characteristic class of M is the categorical trace of the identity on the object
![]() $\mathfrak {X}=([S/G_S],M)$
, which is
$\mathfrak {X}=([S/G_S],M)$
, which is
![]() $\operatorname {\mathrm {ev}}_{\mathfrak {X}}\circ \operatorname {\mathrm {coev}}_{\mathfrak {X}}$
. This equals the image of the identity map through the left side of the following commutative diagram:
$\operatorname {\mathrm {ev}}_{\mathfrak {X}}\circ \operatorname {\mathrm {coev}}_{\mathfrak {X}}$
. This equals the image of the identity map through the left side of the following commutative diagram:

whereas on the right side of the diagram, the map labeled
![]() $\operatorname {\mathrm {coev}}_M$
carries the identity to the integration map I described in the proof of Proposition 4.4.1, and then
$\operatorname {\mathrm {coev}}_M$
carries the identity to the integration map I described in the proof of Proposition 4.4.1, and then
![]() $\operatorname {\mathrm {ev}}_M$
carries I onto
$\operatorname {\mathrm {ev}}_M$
carries I onto
![]() $\operatorname {\mathrm {tr.dist}}(M)$
by definition of the latter.
$\operatorname {\mathrm {tr.dist}}(M)$
by definition of the latter.
4.5 A Künneth theorem for characteristic classes
The goal of this section is to prove the compatibility of the categorical trace with fiber products to get an analogue of the relation
![]() $\operatorname {\mathrm {tr}}(A\otimes B)=\operatorname {\mathrm {tr}}(A) \operatorname {\mathrm {tr}}(B)$
for square matrices. Again, throughout this section we fix a decent base v-stack S.
$\operatorname {\mathrm {tr}}(A\otimes B)=\operatorname {\mathrm {tr}}(A) \operatorname {\mathrm {tr}}(B)$
for square matrices. Again, throughout this section we fix a decent base v-stack S.
As an example of what we will do, suppose
![]() $X_1,X_2\to S$
are two fine morphisms of decent v-stacks, and suppose
$X_1,X_2\to S$
are two fine morphisms of decent v-stacks, and suppose
![]() $A_i\in D_{\mathrm {\acute {e}t}}(X_i,\Lambda )$
is ULA over S for
$A_i\in D_{\mathrm {\acute {e}t}}(X_i,\Lambda )$
is ULA over S for
![]() $i=1,2$
. Then
$i=1,2$
. Then
![]() $A_1\boxtimes _S A_2$
is ULA over S, so we may define the characteristic class
$A_1\boxtimes _S A_2$
is ULA over S, so we may define the characteristic class
![]() $\operatorname {\mathrm {cc}}_{X_1\times _S X_2/S}(A_1\boxtimes _S A_2)$
in
$\operatorname {\mathrm {cc}}_{X_1\times _S X_2/S}(A_1\boxtimes _S A_2)$
in
![]() $H^0(\operatorname {\mathrm {In}}_S(X_1\times _S X_2),K_{\operatorname {\mathrm {In}}_S(X_1\times _S X_2)})$
. We have an isomorphism
$H^0(\operatorname {\mathrm {In}}_S(X_1\times _S X_2),K_{\operatorname {\mathrm {In}}_S(X_1\times _S X_2)})$
. We have an isomorphism
![]() $\operatorname {\mathrm {In}}_S(X_1\times _S X_2)\cong \operatorname {\mathrm {In}}_S(X_1)\times _S \operatorname {\mathrm {In}}_S(X_2)$
and therefore a Künneth map
$\operatorname {\mathrm {In}}_S(X_1\times _S X_2)\cong \operatorname {\mathrm {In}}_S(X_1)\times _S \operatorname {\mathrm {In}}_S(X_2)$
and therefore a Künneth map
which we notate as
![]() $\mu _1\otimes \mu _2\mapsto \mu _1\boxtimes _S \mu _2$
for global sections
$\mu _1\otimes \mu _2\mapsto \mu _1\boxtimes _S \mu _2$
for global sections
![]() $\mu _i$
of
$\mu _i$
of
![]() $K_{\operatorname {\mathrm {In}}_S(X_i)/S}$
. Then it is straightforward to show (and a corollary of Theorem 4.5.3 below) that
$K_{\operatorname {\mathrm {In}}_S(X_i)/S}$
. Then it is straightforward to show (and a corollary of Theorem 4.5.3 below) that
For our applications, we need a more general result involving fiber products over bases other than S. First, we need a modification of the above Künneth map in a general setting.
Definition 4.5.1 Modified Künneth map
Let
![]() $U\to T$
be a cohomologically smooth morphism of decent S-v-stacks. Suppose we are given a 2-commutative diagram of decent S-v-stacks
$U\to T$
be a cohomologically smooth morphism of decent S-v-stacks. Suppose we are given a 2-commutative diagram of decent S-v-stacks

for
![]() $i=1,2$
such that
$i=1,2$
such that
![]() $f_1$
and
$f_1$
and
![]() $f_2$
are fine. Let
$f_2$
are fine. Let
![]() $f\colon Y_1\times _U Y_2\to X_1\times _T X_2$
and
$f\colon Y_1\times _U Y_2\to X_1\times _T X_2$
and
![]() $g\colon Y_1\times _U Y_2 \to U$
be the induced product maps. Let
$g\colon Y_1\times _U Y_2 \to U$
be the induced product maps. Let
![]() $A_i$
be an object of
$A_i$
be an object of
![]() $D_{\mathrm {\acute {e}t}}(X_i,\Lambda )$
for
$D_{\mathrm {\acute {e}t}}(X_i,\Lambda )$
for
![]() $i=1,2$
. We define a map
$i=1,2$
. We define a map
as follows. There is a Cartesian diagram

The map
![]() $\kappa _{U/T}$
is defined as the composition
$\kappa _{U/T}$
is defined as the composition
 $$ \begin{align*} & f_1^!A_1\boxtimes_U f_2^!A_2 \\[2pt] \cong & (\Delta_{U/T}')^*(f_1^!A_1 \boxtimes_T f_2^!A_2) \\[2pt] \to & (\Delta_{U/T}')^*(f_1\times_T f_2)^!(A_1\boxtimes_T A_2) \\[2pt] \stackrel{(4.1.3)}{\cong} & (\Delta_{U/T}')^*(f_1\times_T f_2)^!(A_1\boxtimes_T A_2) \otimes g^*(\Delta_{U/T})^!\Lambda_T \otimes g^*K_{U/T} \\[2pt] \to & (\Delta_{U/T}')^*(f_1\times_T f_2)^! (A_1\boxtimes_T A_2) \otimes (\Delta_{U/T}')^!\Lambda_{Y_1\times_T Y_2} \otimes g^*K_{U/T} \\[2pt] \to & (\Delta_{U/T}')^!(f_1\times_T f_2)^!(A_1\boxtimes_T A_2) \otimes g^*K_{U/T} \\[2pt] \cong & f^!(A_1\boxtimes_T A_2) \otimes g^*K_{U/T}. \end{align*} $$
$$ \begin{align*} & f_1^!A_1\boxtimes_U f_2^!A_2 \\[2pt] \cong & (\Delta_{U/T}')^*(f_1^!A_1 \boxtimes_T f_2^!A_2) \\[2pt] \to & (\Delta_{U/T}')^*(f_1\times_T f_2)^!(A_1\boxtimes_T A_2) \\[2pt] \stackrel{(4.1.3)}{\cong} & (\Delta_{U/T}')^*(f_1\times_T f_2)^!(A_1\boxtimes_T A_2) \otimes g^*(\Delta_{U/T})^!\Lambda_T \otimes g^*K_{U/T} \\[2pt] \to & (\Delta_{U/T}')^*(f_1\times_T f_2)^! (A_1\boxtimes_T A_2) \otimes (\Delta_{U/T}')^!\Lambda_{Y_1\times_T Y_2} \otimes g^*K_{U/T} \\[2pt] \to & (\Delta_{U/T}')^!(f_1\times_T f_2)^!(A_1\boxtimes_T A_2) \otimes g^*K_{U/T} \\[2pt] \cong & f^!(A_1\boxtimes_T A_2) \otimes g^*K_{U/T}. \end{align*} $$
In particular, the case
![]() $X_1=X_2=T=S$
yields a map
$X_1=X_2=T=S$
yields a map
We can now introduce the setup of the main theorem of this section. We consider bases
![]() $T\to S$
satisfying two hypotheses: (1)
$T\to S$
satisfying two hypotheses: (1)
![]() $T\to S$
is cohomologically smooth, and (2)
$T\to S$
is cohomologically smooth, and (2)
![]() $\Delta _{T/S}\colon T\to T\times _S T$
is cohomologically smooth. These are satisfied for instance when
$\Delta _{T/S}\colon T\to T\times _S T$
is cohomologically smooth. These are satisfied for instance when
![]() $T=[S/G]$
, where G is a cohomologically smooth locally spatial group diamond over S. Considering the diagram
$T=[S/G]$
, where G is a cohomologically smooth locally spatial group diamond over S. Considering the diagram

in which both squares are Cartesian, we see that
![]() $\operatorname {\mathrm {In}}_S(T)\to S$
is also cohomologically smooth. Furthermore, we can trivialize the dualizing complex
$\operatorname {\mathrm {In}}_S(T)\to S$
is also cohomologically smooth. Furthermore, we can trivialize the dualizing complex
![]() $K_{\operatorname {\mathrm {In}}_S(T)/S}$
.
$K_{\operatorname {\mathrm {In}}_S(T)/S}$
.
Lemma 4.5.2. Let T be a decent S-v-stack such that the structure map
![]() $\pi \colon T\to S$
and diagonal
$\pi \colon T\to S$
and diagonal
![]() $\Delta _{T/S} \colon T\to T\times _S T$
are both cohomologically smooth. Then the object
$\Delta _{T/S} \colon T\to T\times _S T$
are both cohomologically smooth. Then the object
![]() $\mathfrak {T}=(T,\Lambda _T)\in \operatorname {\mathrm {CoCorr}}_S$
is dualizable, and its characteristic class
$\mathfrak {T}=(T,\Lambda _T)\in \operatorname {\mathrm {CoCorr}}_S$
is dualizable, and its characteristic class
![]() $\operatorname {\mathrm {cc}}_{T/S}(\Lambda _T)$
, considered as a morphism
$\operatorname {\mathrm {cc}}_{T/S}(\Lambda _T)$
, considered as a morphism
![]() $\Lambda _{\operatorname {\mathrm {In}}_S(T)} \to K_{\operatorname {\mathrm {In}}_S(T)/S}$
, is an isomorphism.
$\Lambda _{\operatorname {\mathrm {In}}_S(T)} \to K_{\operatorname {\mathrm {In}}_S(T)/S}$
, is an isomorphism.
In the case
![]() $T=[S/G]$
, where G is a cohomologically smooth locally spatial group diamond over S, the inertia stack is
$T=[S/G]$
, where G is a cohomologically smooth locally spatial group diamond over S, the inertia stack is
![]() , the stack of conjugacy classes of G. This is a cohomologically smooth stack of dimension 0, so perhaps it is unsurprising that it has trivial dualizing complex; the lemma states that the trivialization is in fact canonical.
, the stack of conjugacy classes of G. This is a cohomologically smooth stack of dimension 0, so perhaps it is unsurprising that it has trivial dualizing complex; the lemma states that the trivialization is in fact canonical.
Proof. Let
![]() $\operatorname {\mathrm {pr}}_1,\operatorname {\mathrm {pr}}_2\colon T\times _S T\to T$
be the projection morphisms. The morphism in
$\operatorname {\mathrm {pr}}_1,\operatorname {\mathrm {pr}}_2\colon T\times _S T\to T$
be the projection morphisms. The morphism in
![]() $D_{\mathrm {\acute {e}t}}(T,\Lambda )$
associated with the cohomological correspondence
$D_{\mathrm {\acute {e}t}}(T,\Lambda )$
associated with the cohomological correspondence
![]() $\operatorname {\mathrm {coev}}_{\mathfrak {T}}\colon (S,\Lambda _S)\to (T\times _S T, \operatorname {\mathrm {pr}}_2^*K_{T/S})$
is an isomorphism:
$\operatorname {\mathrm {coev}}_{\mathfrak {T}}\colon (S,\Lambda _S)\to (T\times _S T, \operatorname {\mathrm {pr}}_2^*K_{T/S})$
is an isomorphism:
Here, we the use cohomological smoothness of
![]() $\pi $
to get the isomorphism
$\pi $
to get the isomorphism
![]() $\alpha $
, as in Theorem 4.1.6. The morphism
$\alpha $
, as in Theorem 4.1.6. The morphism
![]() $\Delta _{T/S}^*\operatorname {\mathrm {pr}}_2^*K_{T/S}\to \pi ^!\Lambda _S$
associated with
$\Delta _{T/S}^*\operatorname {\mathrm {pr}}_2^*K_{T/S}\to \pi ^!\Lambda _S$
associated with
![]() $\operatorname {\mathrm {ev}}_{\mathfrak {T}}\colon (T\times _S T,\operatorname {\mathrm {pr}}_2^*K_{T/S})\to (S,\Lambda _S)$
is also an isomorphism (this is true without any hypotheses on
$\operatorname {\mathrm {ev}}_{\mathfrak {T}}\colon (T\times _S T,\operatorname {\mathrm {pr}}_2^*K_{T/S})\to (S,\Lambda _S)$
is also an isomorphism (this is true without any hypotheses on
![]() $\pi $
or
$\pi $
or
![]() $\Delta _{T/S}$
). Referring to the diagram
$\Delta _{T/S}$
). Referring to the diagram

we may describe the characteristic class
![]() $\operatorname {\mathrm {cc}}_{T/S}(\Lambda _T)$
as the composition
$\operatorname {\mathrm {cc}}_{T/S}(\Lambda _T)$
as the composition
 $$ \begin{align*} h^*\pi^*\Lambda_S &\cong h^*\Delta_{T/S}^!\operatorname{\mathrm{pr}}_2^*K_{T/S}\\ &\stackrel{\beta}{\cong} h^!\Delta_{T/S}^*\operatorname{\mathrm{pr}}_2^* K_{T/S}\cong h^!K_{T/S}\cong K_{\operatorname{\mathrm{In}}_S(T)/S}, \end{align*} $$
$$ \begin{align*} h^*\pi^*\Lambda_S &\cong h^*\Delta_{T/S}^!\operatorname{\mathrm{pr}}_2^*K_{T/S}\\ &\stackrel{\beta}{\cong} h^!\Delta_{T/S}^*\operatorname{\mathrm{pr}}_2^* K_{T/S}\cong h^!K_{T/S}\cong K_{\operatorname{\mathrm{In}}_S(T)/S}, \end{align*} $$
which is an isomorphism. Here, we once again applied Theorem 4.1.6, using the cohomological smoothness of
![]() $\Delta _{T/S}$
.
$\Delta _{T/S}$
.
Now suppose
![]() $p_i\colon X_i\to T$
(
$p_i\colon X_i\to T$
(
![]() $i=1,2$
) is a fine morphism of decent S-v-stacks, with fiber product
$i=1,2$
) is a fine morphism of decent S-v-stacks, with fiber product
![]() $p\colon X_1\times _T X_2\to T$
. Then there is an isomorphism
$p\colon X_1\times _T X_2\to T$
. Then there is an isomorphism
and therefore by the discussion above we have a modified Künneth map
Using the trivialization
![]() $\Lambda _{\operatorname {\mathrm {In}}_S(T)/S}\cong K_{\operatorname {\mathrm {In}}_S(T)/S}$
from Lemma 4.5.2, we obtain a map
$\Lambda _{\operatorname {\mathrm {In}}_S(T)/S}\cong K_{\operatorname {\mathrm {In}}_S(T)/S}$
from Lemma 4.5.2, we obtain a map
which on global sections we notate as
![]() $\mu _1\otimes \mu _2\mapsto \mu _1\boxtimes _{\operatorname {\mathrm {In}}_S(T)} \mu _2$
.
$\mu _1\otimes \mu _2\mapsto \mu _1\boxtimes _{\operatorname {\mathrm {In}}_S(T)} \mu _2$
.
Finally, we can state the main theorem of the section.
Theorem 4.5.3. Let T be a decent S-v-stack such that the structure map
![]() $\pi \colon T\to S$
and the diagonal
$\pi \colon T\to S$
and the diagonal
![]() $\Delta _{T/S}\colon T\to T\times _S T$
are both cohomologically smooth. Let
$\Delta _{T/S}\colon T\to T\times _S T$
are both cohomologically smooth. Let
![]() $X_1,X_2\to T$
be two fine morphisms of decent v-stacks (so also the induced morphisms
$X_1,X_2\to T$
be two fine morphisms of decent v-stacks (so also the induced morphisms
![]() $X_1,X_2 \to S$
are fine), and let
$X_1,X_2 \to S$
are fine), and let
![]() $A_i\in D_{\mathrm {\acute {e}t}}(X_i,\Lambda )$
be a sheaf which is ULA over S. Then
$A_i\in D_{\mathrm {\acute {e}t}}(X_i,\Lambda )$
be a sheaf which is ULA over S. Then
![]() $A_1\boxtimes _T A_2$
is ULA over S, and
$A_1\boxtimes _T A_2$
is ULA over S, and
In order to prove Theorem 4.5.3, we need to enhance the category
![]() $\operatorname {\mathrm {CoCorr}}_S$
to include data coming from a smooth base v-stack, which we allow to vary. At a first pass, one might think that such a category would have objects
$\operatorname {\mathrm {CoCorr}}_S$
to include data coming from a smooth base v-stack, which we allow to vary. At a first pass, one might think that such a category would have objects
![]() $(X\to T,A)$
, where
$(X\to T,A)$
, where
![]() $T\to S$
is cohomologically smooth,
$T\to S$
is cohomologically smooth,
![]() $X\to T$
is a morphism of v-stacks and
$X\to T$
is a morphism of v-stacks and
![]() $A\in D_{\mathrm {\acute {e}t}}(X,\Lambda )$
. The morphisms
$A\in D_{\mathrm {\acute {e}t}}(X,\Lambda )$
. The morphisms
![]() $(X\to T,A)\to (X'\to T',A')$
would be pairs
$(X\to T,A)\to (X'\to T',A')$
would be pairs
![]() $(q^{\natural },\alpha )$
, where
$(q^{\natural },\alpha )$
, where
![]() $q^{\natural } =(p,q,p')$
is a morphism of correspondences as in a 2-commutative diagram:
$q^{\natural } =(p,q,p')$
is a morphism of correspondences as in a 2-commutative diagram:

and
![]() $\alpha \colon c^*A\to (c')^!A'$
is a morphism. We assume that
$\alpha \colon c^*A\to (c')^!A'$
is a morphism. We assume that
![]() $u'$
is cohomologically smooth. Given pairs
$u'$
is cohomologically smooth. Given pairs
![]() $\mathfrak {X}_1=(X_1\to T,A_1)$
and
$\mathfrak {X}_1=(X_1\to T,A_1)$
and
![]() $\mathfrak {X}_2=(X_2\to T,A_2)$
with common base T, we could then define
$\mathfrak {X}_2=(X_2\to T,A_2)$
with common base T, we could then define
![]() $\mathfrak {X}_1\boxtimes _T \mathfrak {X}_2 = (X_1\times _T X_2\to T,A_1\boxtimes _T A_2)$
.
$\mathfrak {X}_1\boxtimes _T \mathfrak {X}_2 = (X_1\times _T X_2\to T,A_1\boxtimes _T A_2)$
.
However, it turns out that this definition is not functorial in
![]() $\mathfrak {X}_1$
and
$\mathfrak {X}_1$
and
![]() $\mathfrak {X}_2$
. That is, given a morphism
$\mathfrak {X}_2$
. That is, given a morphism
![]() $e\colon T\to T'$
in
$e\colon T\to T'$
in
![]() $\operatorname {\mathrm {Corr}}_S$
and morphisms
$\operatorname {\mathrm {Corr}}_S$
and morphisms
![]() $f_i\colon \mathfrak {X}_i\to \mathfrak {X}_i'$
lying over e, one cannot in general define a map
$f_i\colon \mathfrak {X}_i\to \mathfrak {X}_i'$
lying over e, one cannot in general define a map
![]() $f_1\otimes _e f_2\colon \mathfrak {X}_1\boxtimes _T \mathfrak {X}_2\to \mathfrak {X}_1'\boxtimes _{T'} \mathfrak {X}_2'$
. Essentially, this is due to the appearance of the invertible sheaf
$f_1\otimes _e f_2\colon \mathfrak {X}_1\boxtimes _T \mathfrak {X}_2\to \mathfrak {X}_1'\boxtimes _{T'} \mathfrak {X}_2'$
. Essentially, this is due to the appearance of the invertible sheaf
![]() $K_{U/S}$
appearing in the modified Künneth map (4.5.1).
$K_{U/S}$
appearing in the modified Künneth map (4.5.1).
To obtain a functorial definition of
![]() $\mathfrak {X}_1\boxtimes _T \mathfrak {X}_2$
, we need to define an enhancement of the category which keeps track of an invertible sheaf living on the base.
$\mathfrak {X}_1\boxtimes _T \mathfrak {X}_2$
, we need to define an enhancement of the category which keeps track of an invertible sheaf living on the base.
Definition 4.5.4 (The category of based cohomological correspondences)
We define a symmetric monoidal 2-category
![]() $\operatorname {\mathrm {BCoCorr}}_S$
. The objects of
$\operatorname {\mathrm {BCoCorr}}_S$
. The objects of
![]() $\operatorname {\mathrm {BCoCorr}}_S$
are triples
$\operatorname {\mathrm {BCoCorr}}_S$
are triples
![]() $(X\to T,A,B)$
, where
$(X\to T,A,B)$
, where
![]() $X\to T$
is a (fine) morphism of decent S-v-stacks whose structure maps to S are fine, where A is an object of
$X\to T$
is a (fine) morphism of decent S-v-stacks whose structure maps to S are fine, where A is an object of
![]() $D_{\mathrm {\acute {e}t}}(X,\Lambda )$
and where B is an invertible object of
$D_{\mathrm {\acute {e}t}}(X,\Lambda )$
and where B is an invertible object of
![]() $D_{\mathrm {\acute {e}t}}(T,\Lambda )$
. We assume that the structure map
$D_{\mathrm {\acute {e}t}}(T,\Lambda )$
. We assume that the structure map
![]() $T\to S$
is cohomologically smooth.
$T\to S$
is cohomologically smooth.
Given objects
![]() $\mathfrak {X}=(X\to T,A,B)$
and
$\mathfrak {X}=(X\to T,A,B)$
and
![]() $\mathfrak {X}'=(X'\to T',A',B')$
, an object of the category
$\mathfrak {X}'=(X'\to T',A',B')$
, an object of the category
![]() $\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {BCoCorr}}_S}(\mathfrak {X},\mathfrak {X}')$
is a triple
$\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {BCoCorr}}_S}(\mathfrak {X},\mathfrak {X}')$
is a triple
![]() $(q^{\natural },\alpha ,\beta )$
. The first element in the triple is a morphism
$(q^{\natural },\alpha ,\beta )$
. The first element in the triple is a morphism
![]() $q^{\natural }=(p,q,p')$
between correspondences as in equation (4.5.3), where
$q^{\natural }=(p,q,p')$
between correspondences as in equation (4.5.3), where
![]() $u'$
is cohomologically smooth. The second element is a morphism
$u'$
is cohomologically smooth. The second element is a morphism
![]() $\alpha \colon c^*A \to (c')^!A'$
, and the third is an isomorphism
$\alpha \colon c^*A \to (c')^!A'$
, and the third is an isomorphism
![]() $\beta \colon u^*B\stackrel {\cong }{\longrightarrow } (u')^! B'$
. Compositions of morphisms are defined similarly as in Definition 4.3.4. (Note that the cohomological smoothness of
$\beta \colon u^*B\stackrel {\cong }{\longrightarrow } (u')^! B'$
. Compositions of morphisms are defined similarly as in Definition 4.3.4. (Note that the cohomological smoothness of
![]() $u'$
is preserved under composition of correspondences.) Given objects
$u'$
is preserved under composition of correspondences.) Given objects
![]() $(X\to T,A,B)$
and
$(X\to T,A,B)$
and
![]() $(X'\to T',A',B')$
, and morphisms between them represented by
$(X'\to T',A',B')$
, and morphisms between them represented by
![]() $C\to X\times _U X'$
(lying over
$C\to X\times _U X'$
(lying over
![]() $U\to T\times _S T'$
) and
$U\to T\times _S T'$
) and
![]() $D\to X\times _V X'$
(lying over
$D\to X\times _V X'$
(lying over
![]() $V\to T\times _S T'$
), a 2-morphism is an equivalence class of 2-commutative diagrams as in equation (4.3.3), together with a similar one involving morphisms
$V\to T\times _S T'$
), a 2-morphism is an equivalence class of 2-commutative diagrams as in equation (4.3.3), together with a similar one involving morphisms
![]() $U\to V$
.
$U\to V$
.
The monoidal structure on
![]() $\operatorname {\mathrm {BCoCorr}}_S$
is defined by
$\operatorname {\mathrm {BCoCorr}}_S$
is defined by
The unit object is
![]() $(S \overset {\mathrm {id}}{\to } S,\Lambda _S,\Lambda _S)$
.
$(S \overset {\mathrm {id}}{\to } S,\Lambda _S,\Lambda _S)$
.
Finally, we introduce the obvious monoidal functors
![]() $\mathcal {B},\mathcal {S}\colon \operatorname {\mathrm {BCoCorr}}_S\to \operatorname {\mathrm {CoCorr}}_S$
, with
$\mathcal {B},\mathcal {S}\colon \operatorname {\mathrm {BCoCorr}}_S\to \operatorname {\mathrm {CoCorr}}_S$
, with
![]() $\mathcal {B}(X\to T,A,B)=(T,B)$
(the base) and
$\mathcal {B}(X\to T,A,B)=(T,B)$
(the base) and
![]() $\mathcal {S}(X\to T,A,B)=(X,A)$
(the source).
$\mathcal {S}(X\to T,A,B)=(X,A)$
(the source).
So far, the objects A and B in Definition 4.5.4 have nothing to do with each other. They only begin to interact when we talk about fiber products of objects of
![]() $\operatorname {\mathrm {BCoCorr}}_S$
over common bases. Given objects
$\operatorname {\mathrm {BCoCorr}}_S$
over common bases. Given objects
![]() $\mathfrak {X}_i=(X_i\stackrel {p_i}{\to } T,A_i,B)$
for
$\mathfrak {X}_i=(X_i\stackrel {p_i}{\to } T,A_i,B)$
for
![]() $i=1,2$
with common base
$i=1,2$
with common base
![]() $\mathfrak {T}=(T,B)$
, we define
$\mathfrak {T}=(T,B)$
, we define
We claim that
![]() $\boxtimes _{\mathfrak {T}}$
defines a monoidal functor
$\boxtimes _{\mathfrak {T}}$
defines a monoidal functor
A morphism in the category
![]() $\operatorname {\mathrm {BCoCorr}}_S \times _{\mathcal {B},\operatorname {\mathrm {CoCorr}}_S} \operatorname {\mathrm {BCoCorr}}_S$
is a morphism
$\operatorname {\mathrm {BCoCorr}}_S \times _{\mathcal {B},\operatorname {\mathrm {CoCorr}}_S} \operatorname {\mathrm {BCoCorr}}_S$
is a morphism
![]() $e\colon \mathfrak {T}\to \mathfrak {T}'$
in
$e\colon \mathfrak {T}\to \mathfrak {T}'$
in
![]() $\operatorname {\mathrm {CoCorr}}_S$
together with a pair of morphisms
$\operatorname {\mathrm {CoCorr}}_S$
together with a pair of morphisms
![]() $\mathfrak {f}_i\colon \mathfrak {X}_i\to \mathfrak {X}_i'$
(
$\mathfrak {f}_i\colon \mathfrak {X}_i\to \mathfrak {X}_i'$
(
![]() $i=1,2$
) lying over e. We may represent this state of affairs with a diagram
$i=1,2$
) lying over e. We may represent this state of affairs with a diagram

for
![]() $i=1,2$
, with
$i=1,2$
, with
![]() $u'$
cohomologically smooth, together with morphisms
$u'$
cohomologically smooth, together with morphisms
![]() $\alpha _i\colon c_i^*A_i\to (c_i')^!A_i'$
for
$\alpha _i\colon c_i^*A_i\to (c_i')^!A_i'$
for
![]() $i=1,2$
and an isomorphism
$i=1,2$
and an isomorphism
![]() $\beta \colon u^*B\stackrel {\cong }{\longrightarrow } (u')^! B'$
. Taking fiber products over the base correspondence, we obtain a morphism of correspondences
$\beta \colon u^*B\stackrel {\cong }{\longrightarrow } (u')^! B'$
. Taking fiber products over the base correspondence, we obtain a morphism of correspondences
![]() $q^{\natural }=(p,q,p')$
fitting into a diagram
$q^{\natural }=(p,q,p')$
fitting into a diagram

The required morphism
is defined as the composition
 $$ \begin{align*} \begin{array}{lcl} c^*\left((A_1\boxtimes_T A_2)\otimes p^*B^{-1}\right) &\cong &\!\! (c_1^*A_1 \boxtimes_U c_2^* A_2)\otimes q^*u^*B^{-1} \\[2pt] &\stackrel{(\alpha_1\boxtimes_U\alpha_2)\otimes \beta}{\to} &\!\! (c_1')^!A_1' \boxtimes_U (c_2')^!A_2' \otimes q^*((u')^!B')^{-1} \\[2pt] &\stackrel{\kappa_{U/T'}}{\to} &\!\! (c')^!(A_1' \boxtimes_{T'} A_2') \otimes q^*(K_{U/T'}\otimes ((u')^!B')^{-1}) \\[2pt] &\cong &\!\! (c')^!(A_1' \boxtimes_{T'} A_2') \otimes q^*(u')^*(B')^{-1} \\[2pt] &\cong &\!\! (c')^!\left((A_1'\boxtimes_{T'} A_2') \otimes (p')^*(B')^{-1}\right), \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{lcl} c^*\left((A_1\boxtimes_T A_2)\otimes p^*B^{-1}\right) &\cong &\!\! (c_1^*A_1 \boxtimes_U c_2^* A_2)\otimes q^*u^*B^{-1} \\[2pt] &\stackrel{(\alpha_1\boxtimes_U\alpha_2)\otimes \beta}{\to} &\!\! (c_1')^!A_1' \boxtimes_U (c_2')^!A_2' \otimes q^*((u')^!B')^{-1} \\[2pt] &\stackrel{\kappa_{U/T'}}{\to} &\!\! (c')^!(A_1' \boxtimes_{T'} A_2') \otimes q^*(K_{U/T'}\otimes ((u')^!B')^{-1}) \\[2pt] &\cong &\!\! (c')^!(A_1' \boxtimes_{T'} A_2') \otimes q^*(u')^*(B')^{-1} \\[2pt] &\cong &\!\! (c')^!\left((A_1'\boxtimes_{T'} A_2') \otimes (p')^*(B')^{-1}\right), \end{array} \end{align*} $$
where in the last step we used Lemma 4.1.10.
To completely justify that equation (4.5.4) is a functor, one must also produce a 2-isomorphism
whenever all compositions are defined. Furthermore, one must also show that equation (4.5.4) is a monoidal functor; that is, we have an isomorphism
The details are straightforward but tedious.
We can now prove Theorem 4.5.3. Let
![]() $X_1,X_2\to T$
be two morphisms satisfying the assumptions of that theorem, and let
$X_1,X_2\to T$
be two morphisms satisfying the assumptions of that theorem, and let
![]() $A_i\in D_{\mathrm {\acute {e}t}}(X_i,\Lambda )$
be two sheaves which are ULA over S. Assume that the structure map
$A_i\in D_{\mathrm {\acute {e}t}}(X_i,\Lambda )$
be two sheaves which are ULA over S. Assume that the structure map
![]() $\pi \colon T\to S$
and the diagonal
$\pi \colon T\to S$
and the diagonal
![]() $\Delta _{T/S}$
are both cohomologically smooth.
$\Delta _{T/S}$
are both cohomologically smooth.
Let
![]() $\mathfrak {X}_i=(X_i\to T, A_i,\Lambda _T)\in \operatorname {\mathrm {BCoCorr}}_S$
for
$\mathfrak {X}_i=(X_i\to T, A_i,\Lambda _T)\in \operatorname {\mathrm {BCoCorr}}_S$
for
![]() $i=1,2$
so that
$i=1,2$
so that
![]() $\mathcal {B}(\mathfrak {X}_1)=\mathcal {B}(\mathfrak {X}_2)=\mathfrak {T}=(T,\Lambda _T)$
. Then
$\mathcal {B}(\mathfrak {X}_1)=\mathcal {B}(\mathfrak {X}_2)=\mathfrak {T}=(T,\Lambda _T)$
. Then
![]() $\mathfrak {X}_i$
is dualizable, with dual
$\mathfrak {X}_i$
is dualizable, with dual
![]() $\mathfrak {X}_i^{\vee }=(X_i\to T,\mathbf {D}_{X_i/S}A_i,K_{T/S})$
, as witnessed by
$\mathfrak {X}_i^{\vee }=(X_i\to T,\mathbf {D}_{X_i/S}A_i,K_{T/S})$
, as witnessed by
![]() $\operatorname {\mathrm {coev}}_{\mathfrak {X}_i}\colon 1_{\operatorname {\mathrm {BCoCorr}}_S}\to \mathfrak {X}_i\otimes \mathfrak {X}_i^{\vee }$
and
$\operatorname {\mathrm {coev}}_{\mathfrak {X}_i}\colon 1_{\operatorname {\mathrm {BCoCorr}}_S}\to \mathfrak {X}_i\otimes \mathfrak {X}_i^{\vee }$
and
![]() $\operatorname {\mathrm {ev}}_{\mathfrak {X}_i}\colon \mathfrak {X}_i^{\vee } \otimes \mathfrak {X}_i \to 1_{\operatorname {\mathrm {BCoCorr}}_S}$
. Note that
$\operatorname {\mathrm {ev}}_{\mathfrak {X}_i}\colon \mathfrak {X}_i^{\vee } \otimes \mathfrak {X}_i \to 1_{\operatorname {\mathrm {BCoCorr}}_S}$
. Note that
![]() $\mathcal {B}(\operatorname {\mathrm {coev}}_{\mathfrak {X}_i})=\operatorname {\mathrm {coev}}_{\mathfrak {T}}$
and
$\mathcal {B}(\operatorname {\mathrm {coev}}_{\mathfrak {X}_i})=\operatorname {\mathrm {coev}}_{\mathfrak {T}}$
and
![]() $\mathcal {S}(\operatorname {\mathrm {coev}}_{\mathfrak {X}_i})=\operatorname {\mathrm {coev}}_{\mathcal {S}(\mathfrak {X}_i)}$
, and similarly for
$\mathcal {S}(\operatorname {\mathrm {coev}}_{\mathfrak {X}_i})=\operatorname {\mathrm {coev}}_{\mathcal {S}(\mathfrak {X}_i)}$
, and similarly for
![]() $\operatorname {\mathrm {ev}}$
. Then the categorical trace of
$\operatorname {\mathrm {ev}}$
. Then the categorical trace of
![]() $1_{\mathfrak {X}_i}$
is
$1_{\mathfrak {X}_i}$
is
![]() $\operatorname {\mathrm {tr}}(1_{\mathfrak {X}_i})=\operatorname {\mathrm {ev}}_{\mathfrak {X}_i}\circ \operatorname {\mathrm {coev}}_{\mathfrak {X}_i}$
so that
$\operatorname {\mathrm {tr}}(1_{\mathfrak {X}_i})=\operatorname {\mathrm {ev}}_{\mathfrak {X}_i}\circ \operatorname {\mathrm {coev}}_{\mathfrak {X}_i}$
so that
![]() $\mathcal {S}(\operatorname {\mathrm {tr}}(1_{\mathfrak {X}_i}))=\operatorname {\mathrm {tr}}(1_{\mathcal {S}(\mathfrak {X}_i)})=\operatorname {\mathrm {cc}}_{X_i/S}(A_i)$
.
$\mathcal {S}(\operatorname {\mathrm {tr}}(1_{\mathfrak {X}_i}))=\operatorname {\mathrm {tr}}(1_{\mathcal {S}(\mathfrak {X}_i)})=\operatorname {\mathrm {cc}}_{X_i/S}(A_i)$
.
Now consider
![]() $\mathfrak {X}=\mathfrak {X}_1\boxtimes _{\mathfrak {T}} \mathfrak {X}_2=(X_1\boxtimes _T X_2\to T, A_1\boxtimes _T A_2,\Lambda _T)$
. Define an object
$\mathfrak {X}=\mathfrak {X}_1\boxtimes _{\mathfrak {T}} \mathfrak {X}_2=(X_1\boxtimes _T X_2\to T, A_1\boxtimes _T A_2,\Lambda _T)$
. Define an object
![]() $\mathfrak {X}^{\vee } = \mathfrak {X}_1^{\vee }\boxtimes _{\mathfrak {T}^{\vee }} \mathfrak {X}_2^{\vee }$
, and define morphisms
$\mathfrak {X}^{\vee } = \mathfrak {X}_1^{\vee }\boxtimes _{\mathfrak {T}^{\vee }} \mathfrak {X}_2^{\vee }$
, and define morphisms
![]() $\operatorname {\mathrm {coev}}_{\mathfrak {X}}$
and
$\operatorname {\mathrm {coev}}_{\mathfrak {X}}$
and
![]() $\operatorname {\mathrm {ev}}_{\mathfrak {X}}$
via the diagrams
$\operatorname {\mathrm {ev}}_{\mathfrak {X}}$
via the diagrams

and

Then
![]() $\mathfrak {X}^{\vee }$
,
$\mathfrak {X}^{\vee }$
,
![]() $\operatorname {\mathrm {coev}}_{\mathfrak {X}}$
and
$\operatorname {\mathrm {coev}}_{\mathfrak {X}}$
and
![]() $\operatorname {\mathrm {ev}}_{\mathfrak {X}}$
witness the dualizability of
$\operatorname {\mathrm {ev}}_{\mathfrak {X}}$
witness the dualizability of
![]() $\mathfrak {X}$
. It follows that
$\mathfrak {X}$
. It follows that
![]() $\mathcal {S}(\mathfrak {X})=(X_1\times _T X_2,A_1\boxtimes _T A_2)$
is dualizable so that
$\mathcal {S}(\mathfrak {X})=(X_1\times _T X_2,A_1\boxtimes _T A_2)$
is dualizable so that
![]() $A_1\boxtimes _T A_2$
is ULA over S. Now consider
$A_1\boxtimes _T A_2$
is ULA over S. Now consider
![]() $\operatorname {\mathrm {tr}}(1_{\mathfrak {X}})=\operatorname {\mathrm {ev}}_{\mathfrak {X}}\circ \operatorname {\mathrm {coev}}_{\mathfrak {X}}$
, an endomorphism of
$\operatorname {\mathrm {tr}}(1_{\mathfrak {X}})=\operatorname {\mathrm {ev}}_{\mathfrak {X}}\circ \operatorname {\mathrm {coev}}_{\mathfrak {X}}$
, an endomorphism of
![]() $1_{\operatorname {\mathrm {BCoCorr}}_S}$
. On the one hand,
$1_{\operatorname {\mathrm {BCoCorr}}_S}$
. On the one hand,
![]() $\mathcal {S}(\operatorname {\mathrm {tr}}(1_{\mathfrak {X}}))=\operatorname {\mathrm {tr}}(1_{\mathcal {S}(\mathfrak {X})})\in \operatorname {\mathrm {End}} 1_{\operatorname {\mathrm {CoCorr}}_S}$
is the datum of the inertia stack
$\mathcal {S}(\operatorname {\mathrm {tr}}(1_{\mathfrak {X}}))=\operatorname {\mathrm {tr}}(1_{\mathcal {S}(\mathfrak {X})})\in \operatorname {\mathrm {End}} 1_{\operatorname {\mathrm {CoCorr}}_S}$
is the datum of the inertia stack
![]() $\operatorname {\mathrm {In}}_S(X_1\times _T X_2)$
together with the characteristic class
$\operatorname {\mathrm {In}}_S(X_1\times _T X_2)$
together with the characteristic class
![]() $\operatorname {\mathrm {cc}}_{X_1\times _T X_2/S}(A)\in H^0(\operatorname {\mathrm {In}}_S(X_1\times _T X_2),K_{\operatorname {\mathrm {In}}_S(X_1\times _T X_2)/S})$
. On the other hand, equation (4.5.8) gives a 2-isomorphism
$\operatorname {\mathrm {cc}}_{X_1\times _T X_2/S}(A)\in H^0(\operatorname {\mathrm {In}}_S(X_1\times _T X_2),K_{\operatorname {\mathrm {In}}_S(X_1\times _T X_2)/S})$
. On the other hand, equation (4.5.8) gives a 2-isomorphism
The source of this morphism is the correspondence
![]() $\operatorname {\mathrm {In}}_S(X_1)\times _{\operatorname {\mathrm {In}}_S(T_1)} \operatorname {\mathrm {In}}_S(X_2)\to S\times _S S \cong S$
together with a global section of
$\operatorname {\mathrm {In}}_S(X_1)\times _{\operatorname {\mathrm {In}}_S(T_1)} \operatorname {\mathrm {In}}_S(X_2)\to S\times _S S \cong S$
together with a global section of
![]() $K_{\operatorname {\mathrm {In}}_S(X_1\times _T X_2)/S}$
. Reviewing the definition of
$K_{\operatorname {\mathrm {In}}_S(X_1\times _T X_2)/S}$
. Reviewing the definition of
![]() $\boxtimes $
for morphisms in
$\boxtimes $
for morphisms in
![]() $\operatorname {\mathrm {BCoCorr}}_S$
as in equation (4.5.7), we see that this section is the image of
$\operatorname {\mathrm {BCoCorr}}_S$
as in equation (4.5.7), we see that this section is the image of
![]() $\operatorname {\mathrm {cc}}_{X_1/S}(A_1)\otimes \operatorname {\mathrm {cc}}_{X_2/S}(A_2)$
under
$\operatorname {\mathrm {cc}}_{X_1/S}(A_1)\otimes \operatorname {\mathrm {cc}}_{X_2/S}(A_2)$
under
 $$ \begin{align*} \begin{array}{lcl} K_{\operatorname{\mathrm{In}}_S(X_1)/S}\boxtimes_{\operatorname{\mathrm{In}}_S(T)} K_{\operatorname{\mathrm{In}}_S(X_2)/S} &\stackrel{\kappa_{\operatorname{\mathrm{In}}_S(T)/S}}{\to} &\!\! K_{\operatorname{\mathrm{In}}_S(X_1\times_T X_2)/S} \otimes \operatorname{\mathrm{In}}(p)^*K_{\operatorname{\mathrm{In}}_S(T)} \\[2pt] &\cong &\!\! K_{\operatorname{\mathrm{In}}_S(X_1\times_T X_2)/S}, \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{lcl} K_{\operatorname{\mathrm{In}}_S(X_1)/S}\boxtimes_{\operatorname{\mathrm{In}}_S(T)} K_{\operatorname{\mathrm{In}}_S(X_2)/S} &\stackrel{\kappa_{\operatorname{\mathrm{In}}_S(T)/S}}{\to} &\!\! K_{\operatorname{\mathrm{In}}_S(X_1\times_T X_2)/S} \otimes \operatorname{\mathrm{In}}(p)^*K_{\operatorname{\mathrm{In}}_S(T)} \\[2pt] &\cong &\!\! K_{\operatorname{\mathrm{In}}_S(X_1\times_T X_2)/S}, \end{array} \end{align*} $$
where the last isomorphism is induced from the inverse to
![]() $\operatorname {\mathrm {cc}}_{T/S}(\Lambda _T)\colon \Lambda _{\operatorname {\mathrm {In}}_S(T)} \to K_{\operatorname {\mathrm {In}}_S(T)/S}$
. The result is exactly
$\operatorname {\mathrm {cc}}_{T/S}(\Lambda _T)\colon \Lambda _{\operatorname {\mathrm {In}}_S(T)} \to K_{\operatorname {\mathrm {In}}_S(T)/S}$
. The result is exactly
![]() $\operatorname {\mathrm {cc}}_{X_1/S}(A_1)\boxtimes _{\operatorname {\mathrm {In}}_S(T)} \operatorname {\mathrm {cc}}_{X_2/S}(A_2)$
as defined in Theorem 4.5.3.
$\operatorname {\mathrm {cc}}_{X_1/S}(A_1)\boxtimes _{\operatorname {\mathrm {In}}_S(T)} \operatorname {\mathrm {cc}}_{X_2/S}(A_2)$
as defined in Theorem 4.5.3.
4.6 The case of
 $[X/G]$
for G smooth
$[X/G]$
for G smooth
Let X be a nice diamond over S which is equipped with an action of a cohomologically smooth S-group diamond G. Let
![]() $\alpha \colon X\times _S G\to X$
be the action map
$\alpha \colon X\times _S G\to X$
be the action map
![]() $(x,g)\mapsto g(x)$
. Let
$(x,g)\mapsto g(x)$
. Let
![]() $Y=[X/G]$
be the stack quotient; this is a decent S-v-stack whose structure map to S is fine. The point of this section is to compare two contexts for the Lefschetz–Verdier trace formula: one for the identity correspondence on
$Y=[X/G]$
be the stack quotient; this is a decent S-v-stack whose structure map to S is fine. The point of this section is to compare two contexts for the Lefschetz–Verdier trace formula: one for the identity correspondence on
![]() $[X/G]$
and the other for the morphism
$[X/G]$
and the other for the morphism
![]() $g\colon X\to X$
for an individual
$g\colon X\to X$
for an individual
![]() $g\in G(S)$
.
$g\in G(S)$
.
Let
![]() $A\in D_{\mathrm {\acute {e}t}}(Y,\Lambda )$
be ULA over S. Then the pair
$A\in D_{\mathrm {\acute {e}t}}(Y,\Lambda )$
be ULA over S. Then the pair
![]() $(Y,A)$
is dualizable in
$(Y,A)$
is dualizable in
![]() $\operatorname {\mathrm {CoCorr}}_S$
, and we obtain a characteristic class
$\operatorname {\mathrm {CoCorr}}_S$
, and we obtain a characteristic class
On the other hand, the pullback
![]() $A_X$
of A along
$A_X$
of A along
![]() $X\to Y$
is also ULA over S (because
$X\to Y$
is also ULA over S (because
![]() $G\to S$
is cohomologically smooth). For each element
$G\to S$
is cohomologically smooth). For each element
![]() $g\in G(S)$
, we have an isomorphism
$g\in G(S)$
, we have an isomorphism
![]() $u_g\colon A_X\to g^*A_X$
lying over
$u_g\colon A_X\to g^*A_X$
lying over
![]() $g\colon X\to X$
. The pair
$g\colon X\to X$
. The pair
![]() $(g,u_g)$
constitutes an endomorphism of the dualizable object
$(g,u_g)$
constitutes an endomorphism of the dualizable object
![]() $(X,A_X)$
in
$(X,A_X)$
in
![]() $\operatorname {\mathrm {CoCorr}}_S$
, so we may define the categorical trace
$\operatorname {\mathrm {CoCorr}}_S$
, so we may define the categorical trace
![]() $\operatorname {\mathrm {tr}}(g,u_g)\in H^0(\operatorname {\mathrm {Fix}}(g),K_{\operatorname {\mathrm {Fix}}(g)/S})$
. Here,
$\operatorname {\mathrm {tr}}(g,u_g)\in H^0(\operatorname {\mathrm {Fix}}(g),K_{\operatorname {\mathrm {Fix}}(g)/S})$
. Here,
![]() $\operatorname {\mathrm {Fix}}(g)=X\times _{g,X\times _S X,\Delta _{X/S}} X$
is the fixed-point locus of g on X. The object is to show how the
$\operatorname {\mathrm {Fix}}(g)=X\times _{g,X\times _S X,\Delta _{X/S}} X$
is the fixed-point locus of g on X. The object is to show how the
![]() $\operatorname {\mathrm {tr}}(g,u_g)$
can be derived from
$\operatorname {\mathrm {tr}}(g,u_g)$
can be derived from
![]() $\mathrm {cc}_{Y/S}(A)$
.
$\mathrm {cc}_{Y/S}(A)$
.
First, we give a concrete presentation of
![]() $\mathrm {In}_{S}(Y)$
. Define a correspondence c on X by
$\mathrm {In}_{S}(Y)$
. Define a correspondence c on X by
 $$ \begin{align*} c=\operatorname{\mathrm{pr}}_X\times_S \alpha:X\times_S G&\to X\times_S X\\ (x,g)&\mapsto (x,g(x)). \end{align*} $$
$$ \begin{align*} c=\operatorname{\mathrm{pr}}_X\times_S \alpha:X\times_S G&\to X\times_S X\\ (x,g)&\mapsto (x,g(x)). \end{align*} $$
Then the fixed-point locus
![]() $\operatorname {\mathrm {Fix}}(c)\subset X\times _S G$
is G-stable for the G-action on
$\operatorname {\mathrm {Fix}}(c)\subset X\times _S G$
is G-stable for the G-action on
![]() $X\times _S G$
given by
$X\times _S G$
given by
![]() $h(x,g)=(h(x),hgh^{-1})$
, and then
$h(x,g)=(h(x),hgh^{-1})$
, and then
![]() $\operatorname {\mathrm {In}}_S(Y)\cong [\operatorname {\mathrm {Fix}}(c)/G]$
. With respect to this isomorphism, the canonical map
$\operatorname {\mathrm {In}}_S(Y)\cong [\operatorname {\mathrm {Fix}}(c)/G]$
. With respect to this isomorphism, the canonical map
![]() is the quotient by G of the projection map
is the quotient by G of the projection map
![]() $\operatorname {\mathrm {Fix}}(c)\to G$
.
$\operatorname {\mathrm {Fix}}(c)\to G$
.
The G-equivariance of
![]() $A\vert _X$
may be expressed an isomorphism
$A\vert _X$
may be expressed an isomorphism
![]() $u\colon A\vert _{X\times G} \to \alpha ^*A\vert _X$
. This is not a cohomological correspondence in general (as
$u\colon A\vert _{X\times G} \to \alpha ^*A\vert _X$
. This is not a cohomological correspondence in general (as
![]() $\alpha ^*\neq \alpha ^!$
). To obtain a cohomological correspondence on nonstacky objects, we work over the base G. Let
$\alpha ^*\neq \alpha ^!$
). To obtain a cohomological correspondence on nonstacky objects, we work over the base G. Let
![]() $X_G=X\times _S G$
, and consider the correspondence
$X_G=X\times _S G$
, and consider the correspondence
![]() $\widetilde {c}$
defined by the diagram of diamonds over G:
$\widetilde {c}$
defined by the diagram of diamonds over G:

By design, the fiber of this correspondence over
![]() $g\in G(S)$
is automorphism
$g\in G(S)$
is automorphism
![]() $g\colon X\to X$
. Moreover, there is a natural isomorphism
$g\colon X\to X$
. Moreover, there is a natural isomorphism
![]() $\operatorname {\mathrm {Fix}}(c)\cong \operatorname {\mathrm {Fix}}(\widetilde {c})$
, and the fiber of
$\operatorname {\mathrm {Fix}}(c)\cong \operatorname {\mathrm {Fix}}(\widetilde {c})$
, and the fiber of
![]() $\mathrm {Fix}(\widetilde {c})$
over any
$\mathrm {Fix}(\widetilde {c})$
over any
![]() $g\in G(S)$
is exactly
$g\in G(S)$
is exactly
![]() $\mathrm {Fix}(g)$
. The G-equivariance of
$\mathrm {Fix}(g)$
. The G-equivariance of
![]() $A\vert _{X}$
is encoded by an isomorphism
$A\vert _{X}$
is encoded by an isomorphism
![]() $\widetilde {u}\colon A\vert _{X_G}\to \widetilde {\alpha }^*A\vert _{X_G}$
. Since
$\widetilde {u}\colon A\vert _{X_G}\to \widetilde {\alpha }^*A\vert _{X_G}$
. Since
![]() $\widetilde {\alpha }$
is an isomorphism, we have
$\widetilde {\alpha }$
is an isomorphism, we have
![]() $\widetilde {\alpha }^*\cong \widetilde {\alpha }^!$
, and therefore, the pair
$\widetilde {\alpha }^*\cong \widetilde {\alpha }^!$
, and therefore, the pair
![]() $(\widetilde {c},\widetilde {u})$
constitutes an endomorphism of the dualizable object
$(\widetilde {c},\widetilde {u})$
constitutes an endomorphism of the dualizable object
![]() $(X_G,A\vert _{X_G})$
of
$(X_G,A\vert _{X_G})$
of
![]() $\operatorname {\mathrm {CoCorr}}_G$
. The categorical trace of
$\operatorname {\mathrm {CoCorr}}_G$
. The categorical trace of
![]() $(\widetilde {c},\widetilde {u})$
is an element
$(\widetilde {c},\widetilde {u})$
is an element
This is the ‘universal local term’ for the action of G on X, in the sense that, for any
![]() $g\in G(S)$
, the restriction map
$g\in G(S)$
, the restriction map
carries
![]() $\operatorname {\mathrm {tr}}(\widetilde {c},\widetilde {u})$
onto
$\operatorname {\mathrm {tr}}(\widetilde {c},\widetilde {u})$
onto
![]() $\operatorname {\mathrm {tr}}(g,u_g)$
.
$\operatorname {\mathrm {tr}}(g,u_g)$
.
We want to compare the characteristic class
![]() $\mathrm {cc}_{Y/S}(A)$
with the universal local term
$\mathrm {cc}_{Y/S}(A)$
with the universal local term
![]() $\operatorname {\mathrm {tr}}(\widetilde {c},\widetilde {u})$
. To do this, we first observe that from the Cartesian square
$\operatorname {\mathrm {tr}}(\widetilde {c},\widetilde {u})$
. To do this, we first observe that from the Cartesian square

we obtain a canonical map
, and thus a canonical pullback map
Next, Lemma 4.5.2 applied to
![]() $T=[S/G]$
shows that
$T=[S/G]$
shows that
![]() $\operatorname {\mathrm {cc}}_{T/S}(\Lambda _T)$
is an isomorphism
$\operatorname {\mathrm {cc}}_{T/S}(\Lambda _T)$
is an isomorphism
. This induces an isomorphism
Combining equations (4.6.1) and (4.6.2), we obtain a canonical map
The main result of this section is the following theorem.
Theorem 4.6.1. Notation and assumptions as above, we have an equality
Proof. We restate the theorem in the language of based cohomological correspondences. The main players are
-
•
 $T=([S/G],\Lambda _{[S/G]})$
, a dualizable object of
$T=([S/G],\Lambda _{[S/G]})$
, a dualizable object of
 $\operatorname {\mathrm {CoCorr}}_S$
.
$\operatorname {\mathrm {CoCorr}}_S$
. -
•
 $\mathfrak {Y}=(Y\to [S/G],A,\Lambda _{[S/G]})$
, a dualizable object of
$\mathfrak {Y}=(Y\to [S/G],A,\Lambda _{[S/G]})$
, a dualizable object of
 $\operatorname {\mathrm {BCoCorr}}_S$
with base T.
$\operatorname {\mathrm {BCoCorr}}_S$
with base T. -
•
 $\mathfrak {X}_G=(X_G,A_{X_G})$
, a dualizable object of
$\mathfrak {X}_G=(X_G,A_{X_G})$
, a dualizable object of
 $\operatorname {\mathrm {CoCorr}}_G$
with base
$\operatorname {\mathrm {CoCorr}}_G$
with base
 $1_{\operatorname {\mathrm {CoCorr}}_G}$
.
$1_{\operatorname {\mathrm {CoCorr}}_G}$
. -
•
 $\alpha \in \operatorname {\mathrm {End}} \mathfrak {X}_G$
, the endomorphism described by the pair
$\alpha \in \operatorname {\mathrm {End}} \mathfrak {X}_G$
, the endomorphism described by the pair
 $(\widetilde {c},\widetilde {u})$
.
$(\widetilde {c},\widetilde {u})$
.
We would like to relate
![]() $\operatorname {\mathrm {tr}}(\operatorname {\mathrm {id}}_{\mathfrak {Y}})$
to
$\operatorname {\mathrm {tr}}(\operatorname {\mathrm {id}}_{\mathfrak {Y}})$
to
![]() $\operatorname {\mathrm {tr}}(\alpha )$
. The idea is to promote
$\operatorname {\mathrm {tr}}(\alpha )$
. The idea is to promote
![]() $\alpha $
to an endomorphism of based cohomological correspondences which lies over
$\alpha $
to an endomorphism of based cohomological correspondences which lies over
![]() $\operatorname {\mathrm {id}}_{T}$
. To this end, we introduce some more objects in
$\operatorname {\mathrm {id}}_{T}$
. To this end, we introduce some more objects in
![]() $\operatorname {\mathrm {BCoCorr}}_S$
:
$\operatorname {\mathrm {BCoCorr}}_S$
:
-
•
 $\mathfrak {G}=(G\to S,\Lambda _G,\Lambda _S)$
with base
$\mathfrak {G}=(G\to S,\Lambda _G,\Lambda _S)$
with base
 $1_{\operatorname {\mathrm {CoCorr}}_S}$
,
$1_{\operatorname {\mathrm {CoCorr}}_S}$
, -
•
 $\mathfrak {G}'=(G\to [S/G]\times _S [S/G],\Lambda _G,\Lambda _{[S/G]}\boxtimes _S K_{[S/G]/S})$
, with base
$\mathfrak {G}'=(G\to [S/G]\times _S [S/G],\Lambda _G,\Lambda _{[S/G]}\boxtimes _S K_{[S/G]/S})$
, with base
 $T\otimes T^{\vee }$
, where the morphism
$T\otimes T^{\vee }$
, where the morphism
 $G\to [S/G]\times _S [S/G]$
is defined as the trivial
$G\to [S/G]\times _S [S/G]$
is defined as the trivial
 $G\times _S G$
-torsor
$G\times _S G$
-torsor
 $G_{G\times _S G}=G\times _S G\times _S G$
.
$G_{G\times _S G}=G\times _S G\times _S G$
.
We also define morphisms in
![]() $\operatorname {\mathrm {BCoCorr}}_S$
:
$\operatorname {\mathrm {BCoCorr}}_S$
:
-
•
 $\operatorname {\mathrm {coev}}_G \colon \mathfrak {G}\to \mathfrak {G}'$
, which has base
$\operatorname {\mathrm {coev}}_G \colon \mathfrak {G}\to \mathfrak {G}'$
, which has base
 $\operatorname {\mathrm {coev}}_T$
and source
$\operatorname {\mathrm {coev}}_T$
and source
 $1_{(G,\Lambda _G)}$
,
$1_{(G,\Lambda _G)}$
, -
•
 $\operatorname {\mathrm {ev}}_G\colon \mathfrak {G}'\to \mathfrak {G}$
, which has base
$\operatorname {\mathrm {ev}}_G\colon \mathfrak {G}'\to \mathfrak {G}$
, which has base
 $\operatorname {\mathrm {ev}}_T$
and source
$\operatorname {\mathrm {ev}}_T$
and source
 $1_{(G,\Lambda _G)}$
.
$1_{(G,\Lambda _G)}$
. -
• An automorphism
 $\alpha _0\in \operatorname {\mathrm {Aut}} \mathfrak {G}'$
lying over the identity on both base and source, coming from a 2-isomorphism of
$\alpha _0\in \operatorname {\mathrm {Aut}} \mathfrak {G}'$
lying over the identity on both base and source, coming from a 2-isomorphism of
 $G\to [S/G]^2$
corresponding to the automorphism of the trivial torsor
$G\to [S/G]^2$
corresponding to the automorphism of the trivial torsor
 $G_{G\times G}\to G_{G\times G}$
defined by
$G_{G\times G}\to G_{G\times G}$
defined by
 $(x,g,h)\mapsto (x,gx,h)$
.
$(x,g,h)\mapsto (x,gx,h)$
.
Now observe that
![]() $\operatorname {\mathrm {tr}}_G:=\operatorname {\mathrm {ev}}_G\circ \alpha _0\circ \operatorname {\mathrm {coev}}_G$
is an endomorphism of
$\operatorname {\mathrm {tr}}_G:=\operatorname {\mathrm {ev}}_G\circ \alpha _0\circ \operatorname {\mathrm {coev}}_G$
is an endomorphism of
![]() $\mathfrak {G}$
with base
$\mathfrak {G}$
with base
![]() $\operatorname {\mathrm {tr}}(\operatorname {\mathrm {id}}_T)$
and source
$\operatorname {\mathrm {tr}}(\operatorname {\mathrm {id}}_T)$
and source
![]() $\operatorname {\mathrm {id}}_{\mathcal {S}(\mathfrak {G})}$
, whose underlying based correspondence is shown in the diagram:
$\operatorname {\mathrm {id}}_{\mathcal {S}(\mathfrak {G})}$
, whose underlying based correspondence is shown in the diagram:

where the central horizontal arrow sends g to its own conjugacy class. (If we had omitted
![]() $\alpha _0$
from the definition of
$\alpha _0$
from the definition of
![]() $\operatorname {\mathrm {tr}}_G$
, the central horizontal arrow would send everything to the identity of G.)
$\operatorname {\mathrm {tr}}_G$
, the central horizontal arrow would send everything to the identity of G.)
Recall that
![]() $\mathcal {S}\colon \operatorname {\mathrm {BCoCorr}}_S\to \operatorname {\mathrm {CoCorr}}_S$
takes a based cohomological corresponce onto its source. Let
$\mathcal {S}\colon \operatorname {\mathrm {BCoCorr}}_S\to \operatorname {\mathrm {CoCorr}}_S$
takes a based cohomological corresponce onto its source. Let
![]() $\mathcal {F}\colon \operatorname {\mathrm {CoCorr}}_G\to \operatorname {\mathrm {CoCorr}}_S$
be the functor which forgets the base G. We have a diagram in
$\mathcal {F}\colon \operatorname {\mathrm {CoCorr}}_G\to \operatorname {\mathrm {CoCorr}}_S$
be the functor which forgets the base G. We have a diagram in
![]() $\operatorname {\mathrm {CoCorr}}_S$
:
$\operatorname {\mathrm {CoCorr}}_S$
:

where all squares are filled in with 2-isomorpisms. The functoriality property of
![]() $\boxtimes $
from equation (4.5.8) now gives a 2-isomorphism
$\boxtimes $
from equation (4.5.8) now gives a 2-isomorphism
The isomorphism of v-stacks implicit in equation (4.6.4) is expressed by the fact that we have a Cartesian diagram:

On the level of cohomology classes, equation (4.6.4) tells us that
![]() $\operatorname {\mathrm {tr}}(\alpha )$
, considered as an element of
$\operatorname {\mathrm {tr}}(\alpha )$
, considered as an element of
![]() $H^0(\operatorname {\mathrm {Fix}}(\widetilde {c}),K_{\operatorname {\mathrm {Fix}}(\widetilde {c})/S})$
, can be derived from
$H^0(\operatorname {\mathrm {Fix}}(\widetilde {c}),K_{\operatorname {\mathrm {Fix}}(\widetilde {c})/S})$
, can be derived from
![]() $\operatorname {\mathrm {cc}}_{Y/S}(A)$
in the manner described by the theorem.
$\operatorname {\mathrm {cc}}_{Y/S}(A)$
in the manner described by the theorem.
We conclude the section with a remark about isolated fixed points. Assume there exists a conjugacy-invariant open subset
![]() $U\subset G$
whose elements act on X with only isolated fixed points. (This is the case for the action of the positive loop group on the affine Grassmannian. We study that scenario in the next section.) Write
$U\subset G$
whose elements act on X with only isolated fixed points. (This is the case for the action of the positive loop group on the affine Grassmannian. We study that scenario in the next section.) Write
![]() $\operatorname {\mathrm {In}}_S([X/G])_U$
for the pullback of
$\operatorname {\mathrm {In}}_S([X/G])_U$
for the pullback of
![]() under
under
![]() . Then
. Then
![]() is étale over
is étale over
![]() ; as such, we have a canonical trivialization
; as such, we have a canonical trivialization
![]() $K_{\operatorname {\mathrm {In}}_S([X/G])_U/S}\cong \Lambda _{\operatorname {\mathrm {In}}_S([X/G])_U}$
. Therefore, the restriction over U of the characteristic class of A is an element
$K_{\operatorname {\mathrm {In}}_S([X/G])_U/S}\cong \Lambda _{\operatorname {\mathrm {In}}_S([X/G])_U}$
. Therefore, the restriction over U of the characteristic class of A is an element
that is, it is a continuous function on the space of pairs
![]() $(x,g)\in X\times _S U$
with
$(x,g)\in X\times _S U$
with
![]() $g(x)=x$
. Theorem 4.6.1 implies that this function is
$g(x)=x$
. Theorem 4.6.1 implies that this function is
![]() $(x,g)\mapsto \operatorname {\mathrm {loc}}_x(g,A)$
.
$(x,g)\mapsto \operatorname {\mathrm {loc}}_x(g,A)$
.
5 Local terms on the
 $B_{\mathrm {dR}}$
-affine Grassmannian
$B_{\mathrm {dR}}$
-affine Grassmannian
The goal of this chapter is to explicitly compute certain local terms on the
![]() $B_{\operatorname {\mathrm {dR}}}$
-affine Grassmannian in terms of the geometric Satake equivalence.
$B_{\operatorname {\mathrm {dR}}}$
-affine Grassmannian in terms of the geometric Satake equivalence.
5.1 The main result
To explain the main result, let us fix some notation. Let
![]() $F/\mathbf {Q}_{p}$
be a finite extension with residue field
$F/\mathbf {Q}_{p}$
be a finite extension with residue field
![]() $\mathbf {F}_q$
. Let C be the completion of an algebraic closure of F. Let
$\mathbf {F}_q$
. Let C be the completion of an algebraic closure of F. Let
![]() $G/F$
be a connected reductive group, and let
$G/F$
be a connected reductive group, and let
![]() $\mathrm {Gr}_{G}=LG/L^{+}G$
be the associated
$\mathrm {Gr}_{G}=LG/L^{+}G$
be the associated
![]() $B_{\mathrm {dR}}$
-affine Grassmannian over
$B_{\mathrm {dR}}$
-affine Grassmannian over
![]() $\operatorname {\mathrm {Spd}} C$
. We explain the notation: For a perfectoid C-algebra R, we have the loop group
$\operatorname {\mathrm {Spd}} C$
. We explain the notation: For a perfectoid C-algebra R, we have the loop group
![]() $LG(R)=B_{\operatorname {\mathrm {dR}}}(R)$
and its positive subgroup
$LG(R)=B_{\operatorname {\mathrm {dR}}}(R)$
and its positive subgroup
![]() $L^+G(R)=B_{\operatorname {\mathrm {dR}}}^+(R)$
. Then
$L^+G(R)=B_{\operatorname {\mathrm {dR}}}^+(R)$
. Then
![]() $\operatorname {\mathrm {Gr}}_G$
is an ind-spatial diamond admitting an action of
$\operatorname {\mathrm {Gr}}_G$
is an ind-spatial diamond admitting an action of
![]() $L^+G$
and in particular its subgroup
$L^+G$
and in particular its subgroup
![]() $G(F)$
. For a cocharacter
$G(F)$
. For a cocharacter
![]() $\mu $
of
$\mu $
of
![]() $G_{\overline {F}}$
, we let
$G_{\overline {F}}$
, we let
![]() $\operatorname {\mathrm {Gr}}_{G,\leq \mu }$
be the corresponding closed Schubert cell; this is a proper diamond. Finally, define the local Hecke stack by
$\operatorname {\mathrm {Gr}}_{G,\leq \mu }$
be the corresponding closed Schubert cell; this is a proper diamond. Finally, define the local Hecke stack by
We remark that there are versions of these objects living over
![]() $\operatorname {\mathrm {Spd}} F$
, but we will not need these for our results.
$\operatorname {\mathrm {Spd}} F$
, but we will not need these for our results.
Fix a coefficient ring
![]() $\Lambda \in \left \{ \mathbf {Z}/\ell ^{n}\mathbf {Z}[\sqrt {q}],\mathbf {Z}_{\ell }[\sqrt {q}\right \} $
. The Satake category
$\Lambda \in \left \{ \mathbf {Z}/\ell ^{n}\mathbf {Z}[\sqrt {q}],\mathbf {Z}_{\ell }[\sqrt {q}\right \} $
. The Satake category
is the subcategory of objects which are perverse,
![]() $\Lambda $
-flat and ULA over
$\Lambda $
-flat and ULA over
![]() $\operatorname {\mathrm {Spd}} C$
[Reference Fargues and ScholzeFS21, Definition I.6.2]. It is a symmetric monoidal category under the convolution product.
$\operatorname {\mathrm {Spd}} C$
[Reference Fargues and ScholzeFS21, Definition I.6.2]. It is a symmetric monoidal category under the convolution product.
Theorem 5.1.1 [Reference Fargues and ScholzeFS21, Theorem I.6.3]
There is an equivalence of symmetric monoidal categories:
 $$ \begin{align*} \operatorname{\mathrm{Rep}}_{\widehat{G}}(\Lambda) &\stackrel{\cong}{\longrightarrow} \operatorname{\mathrm{Sat}}_G(\Lambda) \\ V &\;\mapsto \ \mathcal{S}_V, \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Rep}}_{\widehat{G}}(\Lambda) &\stackrel{\cong}{\longrightarrow} \operatorname{\mathrm{Sat}}_G(\Lambda) \\ V &\;\mapsto \ \mathcal{S}_V, \end{align*} $$
where
![]() $\widehat {G}$
is the Langlands dual group (considered over
$\widehat {G}$
is the Langlands dual group (considered over
![]() $\Lambda $
), and
$\Lambda $
), and
![]() $\operatorname {\mathrm {Rep}}_{\widehat {G}}(\Lambda )$
is the category of representations of
$\operatorname {\mathrm {Rep}}_{\widehat {G}}(\Lambda )$
is the category of representations of
![]() $\widehat {G}$
on finite projective
$\widehat {G}$
on finite projective
![]() $\Lambda $
-modules.
$\Lambda $
-modules.
We continue to write
![]() $\mathcal {S}_V$
for the pullback of this object along the quotient
$\mathcal {S}_V$
for the pullback of this object along the quotient
![]() $\operatorname {\mathrm {Gr}}_G\to [L^+G \backslash \operatorname {\mathrm {Gr}}_G]$
.
$\operatorname {\mathrm {Gr}}_G\to [L^+G \backslash \operatorname {\mathrm {Gr}}_G]$
.
Our next order of business is to determine, for
![]() $g\in G(F)_{\operatorname {\mathrm {sr}}}$
, the fixed point locus
$g\in G(F)_{\operatorname {\mathrm {sr}}}$
, the fixed point locus
![]() $\operatorname {\mathrm {Gr}}_G^g$
. The answer is the same regardless of which sort of affine Grassmannian we consider (classical, Witt vector,
$\operatorname {\mathrm {Gr}}_G^g$
. The answer is the same regardless of which sort of affine Grassmannian we consider (classical, Witt vector,
![]() $B_{\operatorname {\mathrm {dR}}}$
), as the following proposition shows.
$B_{\operatorname {\mathrm {dR}}}$
), as the following proposition shows.
Proposition 5.1.2. Let
![]() $K^+$
be a discrete valuation ring with algebraically closed residue field k and fraction field K. Let G be a reductive group over
$K^+$
be a discrete valuation ring with algebraically closed residue field k and fraction field K. Let G be a reductive group over
![]() $K^+$
. Let
$K^+$
. Let
![]() $g\in G(K^+)$
be an element whose image in
$g\in G(K^+)$
be an element whose image in
![]() $G(k)$
is strongly regular, and let
$G(k)$
is strongly regular, and let
![]() $T=\operatorname {\mathrm {Cent}}(g,G)$
. The inclusion
$T=\operatorname {\mathrm {Cent}}(g,G)$
. The inclusion
![]() $T\subset G$
induces a bijection
$T\subset G$
induces a bijection
so that the fixed point locus of g may be identified with
![]() $X_*(T)$
.
$X_*(T)$
.
Consequently, if
![]() $\operatorname {\mathrm {Gr}}_G$
is any incarnation of the affine Grassmannian, then
$\operatorname {\mathrm {Gr}}_G$
is any incarnation of the affine Grassmannian, then
![]() $\operatorname {\mathrm {Gr}}_{G,\leq \mu }^g$
is finite over its base with underlying set
$\operatorname {\mathrm {Gr}}_{G,\leq \mu }^g$
is finite over its base with underlying set
![]() $X_*(T)_{\leq \mu }$
.
$X_*(T)_{\leq \mu }$
.
Proof. Let
![]() $\mathcal {B}$
be the (reduced) Bruhat–Tits building of the split reductive group
$\mathcal {B}$
be the (reduced) Bruhat–Tits building of the split reductive group
![]() $G_K$
over the discretely valued field K. Thus,
$G_K$
over the discretely valued field K. Thus,
![]() $\mathcal {B}$
is a locally finite simplicial complex admitting an action of
$\mathcal {B}$
is a locally finite simplicial complex admitting an action of
![]() $LG=G(K)$
. We will identify the
$LG=G(K)$
. We will identify the
![]() $LG$
-set
$LG$
-set
![]() $\operatorname {\mathrm {Gr}}_G$
with a piece of this building.
$\operatorname {\mathrm {Gr}}_G$
with a piece of this building.
By [Reference Bruhat and TitsBT84, 5.1.40], there exists a hyperspecial point
![]() $\bar o \in \mathcal {B}$
corresponding to
$\bar o \in \mathcal {B}$
corresponding to
![]() $L^+G=G(K^+)$
. The point
$L^+G=G(K^+)$
. The point
![]() $\bar o$
can be characterized by [Reference Bruhat and TitsBT84, 4.6.29] as the unique fixed point of
$\bar o$
can be characterized by [Reference Bruhat and TitsBT84, 4.6.29] as the unique fixed point of
![]() $L^+G$
. Let
$L^+G$
. Let
![]() $\mathcal {B}^{\mathrm {ext}}$
be the extended Bruhat–Tits building of
$\mathcal {B}^{\mathrm {ext}}$
be the extended Bruhat–Tits building of
![]() $G_K$
. Recall that
$G_K$
. Recall that
![]() $\mathcal {B}^{\mathrm {ext}}=\mathcal {B} \times X_*(A_G)_{\mathbf {R}}$
, where
$\mathcal {B}^{\mathrm {ext}}=\mathcal {B} \times X_*(A_G)_{\mathbf {R}}$
, where
![]() $A_G$
is the connected center of G. The group
$A_G$
is the connected center of G. The group
![]() $LG$
acts on
$LG$
acts on
![]() $X_*(A_G)_{\mathbf {R}}$
via the isomorphism
$X_*(A_G)_{\mathbf {R}}$
via the isomorphism
![]() $X_*(A_G)_{\mathbf {R}} \to X_*(A_G')_{\mathbf {R}}$
, where
$X_*(A_G)_{\mathbf {R}} \to X_*(A_G')_{\mathbf {R}}$
, where
![]() $A_G'$
is the maximal abelian quotient of G. Let
$A_G'$
is the maximal abelian quotient of G. Let
![]() $o=(\bar o,z)$
be any point in
$o=(\bar o,z)$
be any point in
![]() $\mathcal {B}^{\mathrm {ext}}$
lying over
$\mathcal {B}^{\mathrm {ext}}$
lying over
![]() $\bar o$
. Then
$\bar o$
. Then
![]() $L^+G$
can be characterized as the full stabilizer of o in
$L^+G$
can be characterized as the full stabilizer of o in
![]() $G(K)$
: It is clear that
$G(K)$
: It is clear that
![]() $L^+G$
stabilizes o, and the reverse inclusion follows from the Cartan decomposition
$L^+G$
stabilizes o, and the reverse inclusion follows from the Cartan decomposition
![]() $LG = L^+G \cdot X_*(T) \cdot L^+G$
(which relies on
$LG = L^+G \cdot X_*(T) \cdot L^+G$
(which relies on
![]() $\bar o$
being hyperspecial) and the fact that
$\bar o$
being hyperspecial) and the fact that
![]() $X_*(T)$
acts on the apartment of T in
$X_*(T)$
acts on the apartment of T in
![]() $\mathcal {B}^{\mathrm {ext}}$
by translations. It follows that the action of
$\mathcal {B}^{\mathrm {ext}}$
by translations. It follows that the action of
![]() $LG$
on
$LG$
on
![]() $\mathcal {B}^{\mathrm {ext}}$
provides an
$\mathcal {B}^{\mathrm {ext}}$
provides an
![]() $LG$
-equivariant bijection from
$LG$
-equivariant bijection from
![]() $\operatorname {\mathrm {Gr}}_G$
to the orbit of
$\operatorname {\mathrm {Gr}}_G$
to the orbit of
![]() $LG$
through o.
$LG$
through o.
Now suppose
![]() $x\in \operatorname {\mathrm {Gr}}_G$
is fixed by a strongly regular element
$x\in \operatorname {\mathrm {Gr}}_G$
is fixed by a strongly regular element
![]() $g\in L^+T_{\operatorname {\mathrm {sr}}}$
. Then its image in
$g\in L^+T_{\operatorname {\mathrm {sr}}}$
. Then its image in
![]() $\mathcal {B}^{\mathrm {ext}}$
is a g-fixed point belonging to the orbit of o, and we can write
$\mathcal {B}^{\mathrm {ext}}$
is a g-fixed point belonging to the orbit of o, and we can write
![]() $x=ho$
for some
$x=ho$
for some
![]() $h\in LG$
. For every root
$h\in LG$
. For every root
![]() $\alpha \colon T\to \mathbf {G}_{\mathrm {m}}$
, the element
$\alpha \colon T\to \mathbf {G}_{\mathrm {m}}$
, the element
![]() $\alpha (g)$
does not lie in the kernel of
$\alpha (g)$
does not lie in the kernel of
![]() $L^+\mathbf {G}_{\mathrm {m}}\to \mathbf {G}_{\mathrm {m}}$
. According to [Reference TitsTit79, 3.6.1], the image of x in
$L^+\mathbf {G}_{\mathrm {m}}\to \mathbf {G}_{\mathrm {m}}$
. According to [Reference TitsTit79, 3.6.1], the image of x in
![]() $\mathcal {B}$
belongs to the apartment
$\mathcal {B}$
belongs to the apartment
![]() $\mathcal {A}$
of T. At the same time,
$\mathcal {A}$
of T. At the same time,
![]() $g\in L^+G$
also fixes
$g\in L^+G$
also fixes
![]() $\bar o$
, so for the same reason,
$\bar o$
, so for the same reason,
![]() $\bar o \in \mathcal {A}$
. Thus,
$\bar o \in \mathcal {A}$
. Thus,
![]() $\bar o$
belongs to both apartments
$\bar o$
belongs to both apartments
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $h^{-1}\mathcal {A}$
. Since
$h^{-1}\mathcal {A}$
. Since
![]() $L^+G$
acts transitively on the apartments containing
$L^+G$
acts transitively on the apartments containing
![]() $\bar o$
[Reference Bruhat and TitsBT84, 4.6.28], we can multiply h on the right by an element of
$\bar o$
[Reference Bruhat and TitsBT84, 4.6.28], we can multiply h on the right by an element of
![]() $L^+G$
to ensure that
$L^+G$
to ensure that
![]() $h^{-1}\mathcal {A}=\mathcal {A}$
. By [Reference Bruhat and TitsBT72, 7.4.10], we then have
$h^{-1}\mathcal {A}=\mathcal {A}$
. By [Reference Bruhat and TitsBT72, 7.4.10], we then have
![]() $h \in L^+N(T,G)$
. Since
$h \in L^+N(T,G)$
. Since
![]() $\bar o$
is hyperspecial, every Weyl reflection is realized in
$\bar o$
is hyperspecial, every Weyl reflection is realized in
![]() $L^+G$
, and hence, we may again modify h on the right to achieve
$L^+G$
, and hence, we may again modify h on the right to achieve
![]() $h \in LT$
. We see now that
$h \in LT$
. We see now that
![]() $x=ho$
is fixed by all of
$x=ho$
is fixed by all of
![]() $LT$
and that furthermore the coset
$LT$
and that furthermore the coset
![]() $x=hL^+G$
is the image of the coset
$x=hL^+G$
is the image of the coset
![]() $hL^+T$
.
$hL^+T$
.
Proposition 5.1.2 shows that, if we fix a split maximal torus
![]() $\widehat {T}\subset \widehat {G}$
, there is a natural finite-to-one map
$\widehat {T}\subset \widehat {G}$
, there is a natural finite-to-one map
 $$ \begin{align*} \mathrm{Gr}_{G}^{g} & \to X_{+}^{\ast}(\widehat{T})\\ x & \mapsto \,\nu_{x}. \end{align*} $$
$$ \begin{align*} \mathrm{Gr}_{G}^{g} & \to X_{+}^{\ast}(\widehat{T})\\ x & \mapsto \,\nu_{x}. \end{align*} $$
Note that
![]() $\nu _{x}$
simply records which open Schubert cell of
$\nu _{x}$
simply records which open Schubert cell of
![]() $\mathrm {Gr}_{G}$
contains the point x.
$\mathrm {Gr}_{G}$
contains the point x.
Now, for any
![]() $V\in \mathrm {Rep}(\widehat {G})$
and any
$V\in \mathrm {Rep}(\widehat {G})$
and any
![]() $x\in \mathrm {Gr}_{G}^{g}$
, there is an associated local term
$x\in \mathrm {Gr}_{G}^{g}$
, there is an associated local term
![]() $\mathrm {loc}_{x}(g,\mathcal {S}_{V})\in \Lambda $
. The main result of this chapter is the following theorem, giving an explicit computation of these local terms.
$\mathrm {loc}_{x}(g,\mathcal {S}_{V})\in \Lambda $
. The main result of this chapter is the following theorem, giving an explicit computation of these local terms.
Theorem 5.1.3. Let
![]() $V\in \mathrm {Rep}(\widehat {G})$
be an object of the Satake category, and let
$V\in \mathrm {Rep}(\widehat {G})$
be an object of the Satake category, and let
![]() $g\in G(F)_{\mathrm {sr}}$
be a strongly regular semisimple element. Then for any
$g\in G(F)_{\mathrm {sr}}$
be a strongly regular semisimple element. Then for any
![]() $x\in \mathrm {Gr}_{G}^{g}$
, there is an equality in
$x\in \mathrm {Gr}_{G}^{g}$
, there is an equality in
![]() $\Lambda $
:
$\Lambda $
:
Note that, since V is (by hypothesis) a finite projective
![]() $\Lambda $
-module and tori are reductive in the strongest sense, the weight space
$\Lambda $
-module and tori are reductive in the strongest sense, the weight space
![]() $V[\nu _{x}]$
is a finite projective
$V[\nu _{x}]$
is a finite projective
![]() $\Lambda $
-module, so the right-hand side of this equality is well-defined.
$\Lambda $
-module, so the right-hand side of this equality is well-defined.
Due to the highly inexplicit nature of local terms, the proof of Theorem 5.1.3 is rather indirect. Indeed, we would be able to give a simple proof of Theorem 5.1.3 if we knew the equality between ‘true’ and ‘naive’ local terms on
![]() $\mathrm {Gr}_{G}$
. Unfortunately, this equality seems to be a very difficult problem. Even for schemes, the problem of comparing true and naive local terms was only settled very recently by Varshavsky. Instead, our strategy reduces the computation of the local terms in Theorem 5.1.3 to an analogous computation on the Witt vector affine Grassmannian, where a global-to-local argument can be pushed through. The key theme in the proof is the idea that local terms are constant in families.
$\mathrm {Gr}_{G}$
. Unfortunately, this equality seems to be a very difficult problem. Even for schemes, the problem of comparing true and naive local terms was only settled very recently by Varshavsky. Instead, our strategy reduces the computation of the local terms in Theorem 5.1.3 to an analogous computation on the Witt vector affine Grassmannian, where a global-to-local argument can be pushed through. The key theme in the proof is the idea that local terms are constant in families.
For our applications, the following restatement of the main results of this section in terms of characteristic classes on the quotient
![]() $[\operatorname {\mathrm {Gr}}_{G,\leq \mu }/L_m^+G]$
will be useful.
$[\operatorname {\mathrm {Gr}}_{G,\leq \mu }/L_m^+G]$
will be useful.
Theorem 5.1.4. Let V be such that
![]() $\mathcal {S}_V$
is supported on some Schubert cell
$\mathcal {S}_V$
is supported on some Schubert cell
![]() $\operatorname {\mathrm {Gr}}_{G,\leq \mu }$
. Choose some large m such that the
$\operatorname {\mathrm {Gr}}_{G,\leq \mu }$
. Choose some large m such that the
![]() $L^+ G$
-action on this cell factors through the quotient
$L^+ G$
-action on this cell factors through the quotient
![]() $L_m^+G$
, and set
$L_m^+G$
, and set
![]() $X=[\operatorname {\mathrm {Gr}}_{G,\leq \mu }/L_m^+G]$
.
$X=[\operatorname {\mathrm {Gr}}_{G,\leq \mu }/L_m^+G]$
.
Then the set of connected components of
![]() $\operatorname {\mathrm {In}}_S(X)_{\operatorname {\mathrm {sr}}}$
may be identified with
$\operatorname {\mathrm {In}}_S(X)_{\operatorname {\mathrm {sr}}}$
may be identified with
![]() $X_*^+(T)_{\leq \mu }/W$
, and the dualizing complex of
$X_*^+(T)_{\leq \mu }/W$
, and the dualizing complex of
![]() $\operatorname {\mathrm {In}}_S(X)_{\operatorname {\mathrm {sr}}}$
has a canonical trivialization. With respect to those identifications, the restriction of
$\operatorname {\mathrm {In}}_S(X)_{\operatorname {\mathrm {sr}}}$
has a canonical trivialization. With respect to those identifications, the restriction of
![]() $\operatorname {\mathrm {cc}}_{X/S}(\mathcal {S}_V)$
to
$\operatorname {\mathrm {cc}}_{X/S}(\mathcal {S}_V)$
to
![]() $\operatorname {\mathrm {In}}_S(X)_{\operatorname {\mathrm {sr}}}$
is the function sending
$\operatorname {\mathrm {In}}_S(X)_{\operatorname {\mathrm {sr}}}$
is the function sending
![]() $\lambda \in X_*(T)$
to
$\lambda \in X_*(T)$
to
![]() $(-1)^{\left < 2\rho _G,\lambda \right>}\operatorname {\mathrm {rank}}_{\Lambda } V[\lambda ]$
.
$(-1)^{\left < 2\rho _G,\lambda \right>}\operatorname {\mathrm {rank}}_{\Lambda } V[\lambda ]$
.
Proof. The first claim is proved in §5.4 below. Since
![]() $L_m^+G$
is a cohomologically smooth group diamond, Theorem 4.6.1 applies to the quotient
$L_m^+G$
is a cohomologically smooth group diamond, Theorem 4.6.1 applies to the quotient
![]() $X=[\operatorname {\mathrm {Gr}}_{G,\leq \mu }/L_m^+G]$
. The remark following the proof of that theorem applies to the locus
$X=[\operatorname {\mathrm {Gr}}_{G,\leq \mu }/L_m^+G]$
. The remark following the proof of that theorem applies to the locus
![]() $L_m^+G_{\operatorname {\mathrm {sr}}}$
so that we may relate
$L_m^+G_{\operatorname {\mathrm {sr}}}$
so that we may relate
![]() $\operatorname {\mathrm {cc}}_{X/S}(\mathcal {S}_V)$
to the local terms
$\operatorname {\mathrm {cc}}_{X/S}(\mathcal {S}_V)$
to the local terms
![]() $\operatorname {\mathrm {loc}}_x(g,\mathcal {S}_V)$
. The latter have been computed by Theorem 5.1.3.
$\operatorname {\mathrm {loc}}_x(g,\mathcal {S}_V)$
. The latter have been computed by Theorem 5.1.3.
5.2 Strategy of proof
In this section, we reduce Theorem 5.1.3 to four auxiliary propositions stated below. The proofs of these propositions will occupy the remainder of this chapter.
As a preliminary observation, note that all of the objects appearing in Theorem 5.1.3 depend on G only through its base change to
![]() $\overline {F}$
, so we may enlarge F whenever convenient in the argument. In particular, we can and do assume that G admits a split reductive model
$\overline {F}$
, so we may enlarge F whenever convenient in the argument. In particular, we can and do assume that G admits a split reductive model
![]() $\mathcal {G} / \mathcal {O}_F$
, and that
$\mathcal {G} / \mathcal {O}_F$
, and that
![]() $\mathcal {G}(\mathcal {O}_F)$
contains elements of finite prime-to-p order with strongly regular semisimple image in
$\mathcal {G}(\mathcal {O}_F)$
contains elements of finite prime-to-p order with strongly regular semisimple image in
![]() $\mathcal {G}(\mathbf {F}_q)$
.
$\mathcal {G}(\mathbf {F}_q)$
.
Now we begin the argument. First, we show that the local terms appearing in Theorem 5.1.3 are essentially independent of g.
Proposition 5.2.1. In the notation and setup of Theorem 5.1.3,
![]() $\mathrm {loc}_{x}(g,\mathcal {S}_{V})$
depends on g and x only through the cocharacter
$\mathrm {loc}_{x}(g,\mathcal {S}_{V})$
depends on g and x only through the cocharacter
![]() $\nu _{x}$
. More precisely, if
$\nu _{x}$
. More precisely, if
![]() $g,g'\in G(F)_{\mathrm {sr}}$
are two strongly regular semisimple elements and
$g,g'\in G(F)_{\mathrm {sr}}$
are two strongly regular semisimple elements and
![]() $x\in \mathrm {Gr}_{G}^{g}$
, resp.,
$x\in \mathrm {Gr}_{G}^{g}$
, resp.,
![]() $x'\in \mathrm {Gr}_{G}^{g'}$
are fixed points such that
$x'\in \mathrm {Gr}_{G}^{g'}$
are fixed points such that
![]() $\nu _{x}=\nu _{x'}$
, then
$\nu _{x}=\nu _{x'}$
, then
Next, we are going to degenerate from characteristic zero into characteristic p. For this, fix a split reductive model
![]() $\mathcal {G}/\mathcal {O}_{F}$
of G, and let
$\mathcal {G}/\mathcal {O}_{F}$
of G, and let
![]() $\mathrm {Gr}_{\mathcal {G}}$
be the associated Beilinson–Drinfeld affine Grassmannian over
$\mathrm {Gr}_{\mathcal {G}}$
be the associated Beilinson–Drinfeld affine Grassmannian over
![]() $S=\operatorname {\mathrm {Spd}} \mathcal {O}_C$
. Recall that this is a small v-sheaf which interpolates between the
$S=\operatorname {\mathrm {Spd}} \mathcal {O}_C$
. Recall that this is a small v-sheaf which interpolates between the
![]() $B_{\mathrm {dR}}$
-affine Grassmannian
$B_{\mathrm {dR}}$
-affine Grassmannian
![]() $\mathrm {Gr}_{G}$
and the Witt vector affine Grassmannian
$\mathrm {Gr}_{G}$
and the Witt vector affine Grassmannian
![]() $\mathrm {Gr}_{\mathcal {G}}^{W}$
, in the sense that we have a commutative diagram
$\mathrm {Gr}_{\mathcal {G}}^{W}$
, in the sense that we have a commutative diagram

with Cartesian squares. We will crucially use the fact that all of these Grassmannians satisfy compatible forms of geometric Satake, in the sense that there are natural monoidal functors

such that the vertical arrows are equivalences of categories on the essential images of
![]() $\mathrm {Rep}(\widehat {G})$
.
$\mathrm {Rep}(\widehat {G})$
.
Proposition 5.2.2. Let
![]() $g\in \mathcal {G}(\mathcal {O}_{F})$
be an element such that
$g\in \mathcal {G}(\mathcal {O}_{F})$
be an element such that
![]() $\overline {g}\in \mathcal {G}(\mathbf {F}_q)$
is strongly regular semisimple. Then
$\overline {g}\in \mathcal {G}(\mathbf {F}_q)$
is strongly regular semisimple. Then
![]() $\mathcal {T}=\mathrm {Cent}(g,\mathcal {G})$
is a maximal torus, and there is a natural isomorphism
$\mathcal {T}=\mathrm {Cent}(g,\mathcal {G})$
is a maximal torus, and there is a natural isomorphism
In particular, if
![]() $\beta \simeq S\subset \mathrm {Gr}_{\mathcal {G}}^{g}$
is any connected component, then
$\beta \simeq S\subset \mathrm {Gr}_{\mathcal {G}}^{g}$
is any connected component, then
![]() $\beta _{\eta }$
and
$\beta _{\eta }$
and
![]() $\beta _{s}$
are isolated fixed points for the g-action in the generic and special fiber, respectively.
$\beta _{s}$
are isolated fixed points for the g-action in the generic and special fiber, respectively.
Proposition 5.2.3. Let
![]() $g\in \mathcal {G}(\mathcal {O}_{F})$
be an element such that
$g\in \mathcal {G}(\mathcal {O}_{F})$
be an element such that
![]() $\overline {g}\in \mathcal {G}(\mathbf {F}_q)$
is strongly regular semisimple. Then for any
$\overline {g}\in \mathcal {G}(\mathbf {F}_q)$
is strongly regular semisimple. Then for any
![]() $V\in \mathrm {Rep}(\widehat {G})$
and any connected component
$V\in \mathrm {Rep}(\widehat {G})$
and any connected component
![]() $\beta \subset \mathrm {Gr}_{\mathcal {G}}^{g}$
, we have the equality
$\beta \subset \mathrm {Gr}_{\mathcal {G}}^{g}$
, we have the equality
of local terms.
Finally, we compute the local terms on the Witt vector affine Grassmannian by a direct argument.
Proposition 5.2.4. Let
![]() $g\in \mathcal {G}(\mathcal {O}_{F})$
be an element with finite prime-to-p order such that
$g\in \mathcal {G}(\mathcal {O}_{F})$
be an element with finite prime-to-p order such that
![]() $\overline {g}\in \mathcal {G}(\mathbf {F}_q)$
is strongly regular semisimple. Then for any
$\overline {g}\in \mathcal {G}(\mathbf {F}_q)$
is strongly regular semisimple. Then for any
![]() $x\in \mathrm {Gr}_{\mathcal {G}}^{W,g}$
and any
$x\in \mathrm {Gr}_{\mathcal {G}}^{W,g}$
and any
![]() $V\in \mathrm {Rep}(\widehat {G})$
,
$V\in \mathrm {Rep}(\widehat {G})$
,
where
![]() $\nu _{x}\in X_{+}^{\ast }(\widehat {T})$
is as before.
$\nu _{x}\in X_{+}^{\ast }(\widehat {T})$
is as before.
5.3 Local terms and base change
In this section, we prove two key technical results, namely that formation of local terms commutes with any base change and with passage from perfect schemes to v-sheaves.
In order to fix notation, we briefly recall the key definitions concerning local terms; we apologize for the overlap with Chapter 4. Let S be a small v-sheaf, which will be our base object. Let
![]() $f:X\to S$
be a map of v-sheaves representable in nice diamonds. Consider a correspondence
$f:X\to S$
be a map of v-sheaves representable in nice diamonds. Consider a correspondence
![]() $c=(c_1,c_2)\colon C\to X\times _{S}X$
given by a map of v-sheaves representable in nice diamonds. This gives rise to a Cartesian diagram
$c=(c_1,c_2)\colon C\to X\times _{S}X$
given by a map of v-sheaves representable in nice diamonds. This gives rise to a Cartesian diagram

of small v-sheaves. We will sometimes assume that
![]() $c_{1}$
is proper and that
$c_{1}$
is proper and that
![]() $\mathrm {Fix}(c)$
is a disjoint union of open-closed subspaces which are proper over S. These conditions will hold, e.g., if f and c are proper.
$\mathrm {Fix}(c)$
is a disjoint union of open-closed subspaces which are proper over S. These conditions will hold, e.g., if f and c are proper.
Let
![]() $\mathcal {F}\in D_{\mathrm {\acute {e}t}}(X,\Lambda )$
be an f-ULA object. Recall that a cohomological correspondence over c is a map
$\mathcal {F}\in D_{\mathrm {\acute {e}t}}(X,\Lambda )$
be an f-ULA object. Recall that a cohomological correspondence over c is a map
![]() $u:Rc_{2!}c_{1}^{\ast }\mathcal {F}\to \mathcal {F}$
, i.e., an element
$u:Rc_{2!}c_{1}^{\ast }\mathcal {F}\to \mathcal {F}$
, i.e., an element
![]() $u\in \mathrm {Hom}(c_{1}^{\ast }\mathcal {F},Rc_{2}^{!}\mathcal {F})$
. If
$u\in \mathrm {Hom}(c_{1}^{\ast }\mathcal {F},Rc_{2}^{!}\mathcal {F})$
. If
![]() $c_{1}$
is proper, then applying
$c_{1}$
is proper, then applying
![]() $Rf_{!}$
induces an endomorphism
$Rf_{!}$
induces an endomorphism
 $$ \begin{align*} Rf_{!}u:Rf_{!}\mathcal{F} & \to Rf_{!}Rc_{1\ast}c_{1}^{\ast}\mathcal{F}=Rf_{!}Rc_{1!}c_{1}^{\ast}\mathcal{F}\\ & \;\;\;\cong Rf_{!}Rc_{2!}c_{1}^{\ast}\mathcal{F}\overset{u}{\to}Rf_{!}\mathcal{F} \end{align*} $$
$$ \begin{align*} Rf_{!}u:Rf_{!}\mathcal{F} & \to Rf_{!}Rc_{1\ast}c_{1}^{\ast}\mathcal{F}=Rf_{!}Rc_{1!}c_{1}^{\ast}\mathcal{F}\\ & \;\;\;\cong Rf_{!}Rc_{2!}c_{1}^{\ast}\mathcal{F}\overset{u}{\to}Rf_{!}\mathcal{F} \end{align*} $$
of
![]() $Rf_{!}\mathcal {F}$
. On the other hand, there is a natural map
$Rf_{!}\mathcal {F}$
. On the other hand, there is a natural map
cf. the discussion immediately before Definition 4.3.5, and we write
![]() $\mathrm {tr}_{c}(u,\mathcal {F})\in H^{0}(\mathrm {Fix}(c),K_{\mathrm {Fix}(c)/S})$
for the image of u under this map.
$\mathrm {tr}_{c}(u,\mathcal {F})\in H^{0}(\mathrm {Fix}(c),K_{\mathrm {Fix}(c)/S})$
for the image of u under this map.
If
![]() $\beta \subset \mathrm {Fix}(c)$
is a closed-open subspace with proper structure map
$\beta \subset \mathrm {Fix}(c)$
is a closed-open subspace with proper structure map
![]() $g:\beta \to S$
, then
$g:\beta \to S$
, then
![]() $H^{0}(\beta ,K_{\beta /S})=H^{0}(\beta ,Rg^{!}\Lambda )$
is canonically a direct summand of
$H^{0}(\beta ,K_{\beta /S})=H^{0}(\beta ,Rg^{!}\Lambda )$
is canonically a direct summand of
![]() $H^{0}(\mathrm {Fix}(c),K_{\mathrm {Fix}(c)/S})$
, and we can further consider the image of
$H^{0}(\mathrm {Fix}(c),K_{\mathrm {Fix}(c)/S})$
, and we can further consider the image of
![]() $\mathrm {tr}_{c}(u,\mathcal {F})$
under the map
$\mathrm {tr}_{c}(u,\mathcal {F})$
under the map
 $$ \begin{align*} H^{0}(\mathrm{Fix}(c),K_{\mathrm{Fix}(c)/S}) & \to H^{0}(\beta,Rg^{!}\Lambda)\cong H^{0}(S,Rg_{\ast}Rg^{!}\Lambda)\\ & \;\;\;\;\;\cong H^{0}(S,Rg_{!}Rg^{!}\Lambda)\to H^{0}(S,\Lambda). \end{align*} $$
$$ \begin{align*} H^{0}(\mathrm{Fix}(c),K_{\mathrm{Fix}(c)/S}) & \to H^{0}(\beta,Rg^{!}\Lambda)\cong H^{0}(S,Rg_{\ast}Rg^{!}\Lambda)\\ & \;\;\;\;\;\cong H^{0}(S,Rg_{!}Rg^{!}\Lambda)\to H^{0}(S,\Lambda). \end{align*} $$
By definition, this is the local term
![]() $\mathrm {loc}_{\beta }(u,\mathcal {F})$
. In most situations we care about, S is connected, so
$\mathrm {loc}_{\beta }(u,\mathcal {F})$
. In most situations we care about, S is connected, so
![]() $H^{0}(S,\Lambda )=\Lambda $
, and we simply regard
$H^{0}(S,\Lambda )=\Lambda $
, and we simply regard
![]() $\mathrm {loc}_{\beta }(u,\mathcal {F})$
as an element of
$\mathrm {loc}_{\beta }(u,\mathcal {F})$
as an element of
![]() $\Lambda $
. Note that local terms are additive in the sense that if
$\Lambda $
. Note that local terms are additive in the sense that if
![]() $\beta =\beta _{1}\coprod \beta _{2}$
, then
$\beta =\beta _{1}\coprod \beta _{2}$
, then
![]() $\mathrm {loc}_{\beta }(u,\mathcal {F})=\mathrm {loc}_{\beta _{1}}(u,\mathcal {F})+\mathrm {loc}_{\beta _{2}}(u,\mathcal {F})$
. If S is a geometric point, f and c are proper, and
$\mathrm {loc}_{\beta }(u,\mathcal {F})=\mathrm {loc}_{\beta _{1}}(u,\mathcal {F})+\mathrm {loc}_{\beta _{2}}(u,\mathcal {F})$
. If S is a geometric point, f and c are proper, and
![]() $\pi _{0}(\mathrm {Fix}(c))$
is a discrete (and therefore finite) set, the usual Lefschetz trace formula holds, and says that
$\pi _{0}(\mathrm {Fix}(c))$
is a discrete (and therefore finite) set, the usual Lefschetz trace formula holds, and says that
 $$\begin{align*}\mathrm{tr}(u|R\Gamma_{c}(X,\mathcal{F}))=\sum_{\beta\in\pi_{0}(\mathrm{Fix}(c))}\mathrm{loc}_{\beta}(u,\mathcal{F}). \end{align*}$$
$$\begin{align*}\mathrm{tr}(u|R\Gamma_{c}(X,\mathcal{F}))=\sum_{\beta\in\pi_{0}(\mathrm{Fix}(c))}\mathrm{loc}_{\beta}(u,\mathcal{F}). \end{align*}$$
We need to understand how local terms interact with base change on S. More precisely, assume we are given a morphism
![]() $a:T\to S$
. Then all objects and morphisms above naturally base change to objects over T. Note that
$a:T\to S$
. Then all objects and morphisms above naturally base change to objects over T. Note that
![]() $\mathrm {Fix}(c)_{T}=\mathrm {Fix}(c_{T})$
. We write
$\mathrm {Fix}(c)_{T}=\mathrm {Fix}(c_{T})$
. We write
![]() $a_{X}:X_{T}\to X$
,
$a_{X}:X_{T}\to X$
,
![]() $a_{C}:C_{T}\to C$
, etc. for the base changes of a. We naturally get a cohomological correspondence
$a_{C}:C_{T}\to C$
, etc. for the base changes of a. We naturally get a cohomological correspondence
![]() $u_{T}$
on
$u_{T}$
on
![]() $\mathcal {F}_{T}=a_{X}^{\ast }\mathcal {F}$
over
$\mathcal {F}_{T}=a_{X}^{\ast }\mathcal {F}$
over
![]() $c_{T}$
by taking the image of u under the map
$c_{T}$
by taking the image of u under the map
 $$ \begin{align*} \mathrm{Hom}(c_{1}^{\ast}\mathcal{F},Rc_{2}^{!}\mathcal{F}) & \to\mathrm{Hom}(a_{C}^{\ast}c_{1}^{\ast}\mathcal{F},a_{C}^{\ast}Rc_{2}^{!}\mathcal{F})\cong\mathrm{Hom}(c_{1,T}^{\ast}a_{X}^{\ast}\mathcal{F},a_{C}^{\ast}Rc_{2}^{!}\mathcal{F})\\ & \;\;\;\;\to\mathrm{Hom}(c_{1,T}^{\ast}a_{X}^{\ast}\mathcal{F},Rc_{2,T}^{!}a_{X}^{\ast}\mathcal{F}). \end{align*} $$
$$ \begin{align*} \mathrm{Hom}(c_{1}^{\ast}\mathcal{F},Rc_{2}^{!}\mathcal{F}) & \to\mathrm{Hom}(a_{C}^{\ast}c_{1}^{\ast}\mathcal{F},a_{C}^{\ast}Rc_{2}^{!}\mathcal{F})\cong\mathrm{Hom}(c_{1,T}^{\ast}a_{X}^{\ast}\mathcal{F},a_{C}^{\ast}Rc_{2}^{!}\mathcal{F})\\ & \;\;\;\;\to\mathrm{Hom}(c_{1,T}^{\ast}a_{X}^{\ast}\mathcal{F},Rc_{2,T}^{!}a_{X}^{\ast}\mathcal{F}). \end{align*} $$
The final arrow here is induced by the canonical map
![]() $a_{C}^{\ast }Rc_{2}^{!}\mathcal {F}\to Rc_{2,T}^{!}a_{X}^{\ast }\mathcal {F}$
. This map is a special case of the natural transformation
$a_{C}^{\ast }Rc_{2}^{!}\mathcal {F}\to Rc_{2,T}^{!}a_{X}^{\ast }\mathcal {F}$
. This map is a special case of the natural transformation
![]() $\beta _{f,g}:\widetilde {f}^{\ast }Rg^{!}\to R\widetilde {g}^{!}f^{\ast }$
which exists for any Cartesian diagram
$\beta _{f,g}:\widetilde {f}^{\ast }Rg^{!}\to R\widetilde {g}^{!}f^{\ast }$
which exists for any Cartesian diagram

with g representable in nice diamonds. The transformation in question is adjoint to the map
![]() $R\widetilde {g}_{!}\widetilde {f}^{\ast }Rg^{!}\cong f^{\ast }Rg_{!}Rg^{!}\to f^{\ast }$
(it is also adjoint to the map
$R\widetilde {g}_{!}\widetilde {f}^{\ast }Rg^{!}\cong f^{\ast }Rg_{!}Rg^{!}\to f^{\ast }$
(it is also adjoint to the map
![]() $Rg^{!}\to Rg^{!}Rf_{\ast }f^{\ast }\cong R\widetilde {f}_{\ast }R\widetilde {g}^{!}f^{\ast }$
).
$Rg^{!}\to Rg^{!}Rf_{\ast }f^{\ast }\cong R\widetilde {f}_{\ast }R\widetilde {g}^{!}f^{\ast }$
).
In this setup, the next proposition says that formation of local terms commutes with base change along
![]() $T\to S$
.
$T\to S$
.
Proposition 5.3.1. For any given
![]() $\beta \subset \mathrm {Fix}(c)$
as above, the natural map
$\beta \subset \mathrm {Fix}(c)$
as above, the natural map
sends
![]() $\mathrm {loc}_{\beta }(u,\mathcal {F})$
to
$\mathrm {loc}_{\beta }(u,\mathcal {F})$
to
![]() $\mathrm {loc}_{\beta _{T}}(u_{T},\mathcal {F}_{T})$
. In particular, if S and T are connected, then
$\mathrm {loc}_{\beta _{T}}(u_{T},\mathcal {F}_{T})$
. In particular, if S and T are connected, then
![]() $\mathrm {loc}_{\beta }(u,\mathcal {F})=\mathrm {loc}_{\beta _{T}}(u_{T},\mathcal {F}_{T})$
as elements of
$\mathrm {loc}_{\beta }(u,\mathcal {F})=\mathrm {loc}_{\beta _{T}}(u_{T},\mathcal {F}_{T})$
as elements of
![]() $\Lambda $
.
$\Lambda $
.
Proof. By a straightforward argument, this reduces to showing that there is a natural map
compatible with the map
![]() $H^{0}(S,\Lambda )\to H^{0}(T,\Lambda )$
and sending
$H^{0}(S,\Lambda )\to H^{0}(T,\Lambda )$
and sending
![]() $\mathrm {tr}_{c}(u,\mathcal {F})$
to
$\mathrm {tr}_{c}(u,\mathcal {F})$
to
![]() $\mathrm {tr}_{c_{T}}(u_{T},\mathcal {F}_{T})$
. To obtain the map itself, apply
$\mathrm {tr}_{c_{T}}(u_{T},\mathcal {F}_{T})$
. To obtain the map itself, apply
![]() $H^{0}(\mathrm {Fix}(c),-)$
to the composition
$H^{0}(\mathrm {Fix}(c),-)$
to the composition
 $$ \begin{align*} K_{\mathrm{Fix}(c)/S} & =R(f\circ c')^{!}\Lambda\to Ra_{\mathrm{Fix}(c)\ast}a_{\mathrm{Fix}(c)}^{\ast}R(f\circ c')^{!}\Lambda\\ & \;\overset{\beta_{a,f\circ c'}}{\longrightarrow}Ra_{\mathrm{Fix}(c)\ast}R(f_{T}\circ c^{\prime}_{T})^{!}a^{\ast}\Lambda=Ra_{\mathrm{Fix}(c)\ast}K_{\mathrm{Fix}(c)_{T}/T}. \end{align*} $$
$$ \begin{align*} K_{\mathrm{Fix}(c)/S} & =R(f\circ c')^{!}\Lambda\to Ra_{\mathrm{Fix}(c)\ast}a_{\mathrm{Fix}(c)}^{\ast}R(f\circ c')^{!}\Lambda\\ & \;\overset{\beta_{a,f\circ c'}}{\longrightarrow}Ra_{\mathrm{Fix}(c)\ast}R(f_{T}\circ c^{\prime}_{T})^{!}a^{\ast}\Lambda=Ra_{\mathrm{Fix}(c)\ast}K_{\mathrm{Fix}(c)_{T}/T}. \end{align*} $$
The claim about the relation between
![]() $\mathrm {tr}_{c}$
and
$\mathrm {tr}_{c}$
and
![]() $\mathrm {tr}_{c_{T}}$
now follows from the fact that the base change functor
$\mathrm {tr}_{c_{T}}$
now follows from the fact that the base change functor
![]() $\mathrm {CoCorr}_{S}\to \mathrm {CoCorr}_{T}$
is symmetric monoidal and therefore preserves dualizable objects and traces of endomorphisms thereof.
$\mathrm {CoCorr}_{S}\to \mathrm {CoCorr}_{T}$
is symmetric monoidal and therefore preserves dualizable objects and traces of endomorphisms thereof.
We will also need to compare local terms associated with perfect schemes and with v-sheaves. More precisely, fix a perfect field
![]() $k/\mathbf {F}_{p}$
, and let
$k/\mathbf {F}_{p}$
, and let
![]() $\mathrm {PSch}_{k}$
be the category of perfect schemes over k. There is a natural functor
$\mathrm {PSch}_{k}$
be the category of perfect schemes over k. There is a natural functor
![]() $X\mapsto X^{\lozenge }$
from
$X\mapsto X^{\lozenge }$
from
![]() $\mathrm {PSch}_{k}$
to small v-sheaves over
$\mathrm {PSch}_{k}$
to small v-sheaves over
![]() $\mathrm {Spd}\,k$
, characterized by
$\mathrm {Spd}\,k$
, characterized by
![]() $(\mathrm {Spec}\,R)^{\lozenge }(A,A^{+})=\mathrm {Hom}_{k}(R,A)$
. Said differently,
$(\mathrm {Spec}\,R)^{\lozenge }(A,A^{+})=\mathrm {Hom}_{k}(R,A)$
. Said differently,
![]() $X^{\lozenge }$
sends
$X^{\lozenge }$
sends
![]() $\operatorname {\mathrm {Spec}} R$
to
$\operatorname {\mathrm {Spec}} R$
to
![]() $\operatorname {\mathrm {Spa}}(R,R^{+})^{\lozenge }$
where
$\operatorname {\mathrm {Spa}}(R,R^{+})^{\lozenge }$
where
![]() $R^{+}$
is the integral closure of k in R. This functor commutes with finite limits. Moreover, if
$R^{+}$
is the integral closure of k in R. This functor commutes with finite limits. Moreover, if
![]() $f:X\to Y$
is separated and perfectly of finite type, then
$f:X\to Y$
is separated and perfectly of finite type, then
![]() $f^{\lozenge }$
is representable in locally spatial diamonds and compactifiable with finite dim.trg. By [Reference ScholzeSch17, §27], for any X there is a fully faithful symmetric monoidal functor
$f^{\lozenge }$
is representable in locally spatial diamonds and compactifiable with finite dim.trg. By [Reference ScholzeSch17, §27], for any X there is a fully faithful symmetric monoidal functor
![]() $c_{X}^{\ast }:D_{\mathrm {\acute {e}t}}(X,\Lambda )\to D_{\mathrm {\acute {e}t}}(X^{\lozenge },\Lambda )$
compatible with
$c_{X}^{\ast }:D_{\mathrm {\acute {e}t}}(X,\Lambda )\to D_{\mathrm {\acute {e}t}}(X^{\lozenge },\Lambda )$
compatible with
![]() $f^{\ast }$
and
$f^{\ast }$
and
![]() $Rf_{!}$
in the evident senses. Moreover, one has canonical natural transformations
$Rf_{!}$
in the evident senses. Moreover, one has canonical natural transformations
and
![]() $c_{X}^{\ast }Rf^{!}\to Rf^{\lozenge !}c_{Y}^{\ast }$
for f separated and perfectly of finite type.
$c_{X}^{\ast }Rf^{!}\to Rf^{\lozenge !}c_{Y}^{\ast }$
for f separated and perfectly of finite type.
Now let
![]() $\mathrm {PSch}_{k}^{\mathrm {ft}}$
be the full subcategory of schemes separated and perfectly of finite type over k. Fix
$\mathrm {PSch}_{k}^{\mathrm {ft}}$
be the full subcategory of schemes separated and perfectly of finite type over k. Fix
![]() $X\in \mathrm {PSch}_{k}^{\mathrm {ft}}$
with structure map
$X\in \mathrm {PSch}_{k}^{\mathrm {ft}}$
with structure map
![]() $f:X\to \operatorname {\mathrm {Spec}} k$
, and let
$f:X\to \operatorname {\mathrm {Spec}} k$
, and let
![]() $c:C\to X\times _{k}X$
be a correspondence in
$c:C\to X\times _{k}X$
be a correspondence in
![]() $\mathrm {PSch}_{k}^{\mathrm {ft}}$
such that
$\mathrm {PSch}_{k}^{\mathrm {ft}}$
such that
![]() $c_{1}$
and
$c_{1}$
and
![]() $f\circ c'$
are perfectly proper. Let
$f\circ c'$
are perfectly proper. Let
![]() $\mathcal {F}\in D_{\mathrm {\acute {e}t}}(X,\Lambda )$
be an f-ULA object equipped with a cohomological correspondence u lying over c, so we get local terms
$\mathcal {F}\in D_{\mathrm {\acute {e}t}}(X,\Lambda )$
be an f-ULA object equipped with a cohomological correspondence u lying over c, so we get local terms
![]() $\mathrm {loc}_{\beta }(u,\mathcal {F})\in H^{0}(\mathrm {Spec}k,\Lambda )=\Lambda $
by the schematic version of the recipe recalled above.
$\mathrm {loc}_{\beta }(u,\mathcal {F})\in H^{0}(\mathrm {Spec}k,\Lambda )=\Lambda $
by the schematic version of the recipe recalled above.
On the other hand, applying
![]() $(-)^{\lozenge }$
and using commutation with finite limits, we get a correspondence
$(-)^{\lozenge }$
and using commutation with finite limits, we get a correspondence
![]() $c^{\lozenge }:C^{\lozenge }\to X^{\lozenge }\times _{\mathrm {Spd}\,k}X^{\lozenge }$
of v-sheaves over
$c^{\lozenge }:C^{\lozenge }\to X^{\lozenge }\times _{\mathrm {Spd}\,k}X^{\lozenge }$
of v-sheaves over
![]() $S=\mathrm {Spd}\,k$
with
$S=\mathrm {Spd}\,k$
with
![]() $\mathrm {Fix}(c)^{\lozenge }=\mathrm {Fix}(c^{\lozenge })$
, satisfying all of our assumptions from above. Moreover, u naturally induces a cohomological correspondence
$\mathrm {Fix}(c)^{\lozenge }=\mathrm {Fix}(c^{\lozenge })$
, satisfying all of our assumptions from above. Moreover, u naturally induces a cohomological correspondence
![]() $u^{\lozenge }$
on
$u^{\lozenge }$
on
![]() $c_{X}^{\ast }\mathcal {F}$
lying over
$c_{X}^{\ast }\mathcal {F}$
lying over
![]() $c^{\lozenge }$
, by taking the image of u under the natural map
$c^{\lozenge }$
, by taking the image of u under the natural map
 $$ \begin{align*} \mathrm{Hom}(c_{1}^{\ast}\mathcal{F},Rc_{2}^{!}\mathcal{F}) & \to\mathrm{Hom}(c_{C}^{\ast}c_{1}^{\ast}\mathcal{F},c_{C}^{\ast}Rc_{2}^{!}\mathcal{F})\cong\mathrm{Hom}(c_{1}^{\lozenge\ast}c_{X}^{\ast}\mathcal{F},c_{C}^{\ast}Rc_{2}^{!}\mathcal{F})\\ & \;\;\;\;\to\mathrm{Hom}(c_{1}^{\lozenge\ast}c_{X}^{\ast}\mathcal{F},Rc_{2}^{\lozenge!}c_{X}^{\ast}\mathcal{F}). \end{align*} $$
$$ \begin{align*} \mathrm{Hom}(c_{1}^{\ast}\mathcal{F},Rc_{2}^{!}\mathcal{F}) & \to\mathrm{Hom}(c_{C}^{\ast}c_{1}^{\ast}\mathcal{F},c_{C}^{\ast}Rc_{2}^{!}\mathcal{F})\cong\mathrm{Hom}(c_{1}^{\lozenge\ast}c_{X}^{\ast}\mathcal{F},c_{C}^{\ast}Rc_{2}^{!}\mathcal{F})\\ & \;\;\;\;\to\mathrm{Hom}(c_{1}^{\lozenge\ast}c_{X}^{\ast}\mathcal{F},Rc_{2}^{\lozenge!}c_{X}^{\ast}\mathcal{F}). \end{align*} $$
Proposition 5.3.2. Maintain the previous setup and notation. Then
![]() $c_{X}^{\ast }\mathcal {F}$
is
$c_{X}^{\ast }\mathcal {F}$
is
![]() $f^{\lozenge }$
-ULA, and for any open-closed
$f^{\lozenge }$
-ULA, and for any open-closed
![]() $\beta \subset \mathrm {Fix}(c)$
, we have an equality
$\beta \subset \mathrm {Fix}(c)$
, we have an equality
of local terms.
Proof. This is formally identical to the proof of Proposition 5.3.1, using the fact that
![]() $(-)^{\lozenge }$
induces a symmetric monoidal functor on the appropriate categories of cohomological correspondences.
$(-)^{\lozenge }$
induces a symmetric monoidal functor on the appropriate categories of cohomological correspondences.
5.4 Independence of g
In this section, we prove Proposition 5.2.1. In this section only, we set
![]() $S=\operatorname {\mathrm {Spd}} C$
.
$S=\operatorname {\mathrm {Spd}} C$
.
Fix V as in the proposition. Decomposing V into isotypic summands for the action of
![]() $Z(\widehat {G})^{\circ }$
, we can assume that
$Z(\widehat {G})^{\circ }$
, we can assume that
![]() $\mathcal {S}_{V}$
is supported on a single connected component of
$\mathcal {S}_{V}$
is supported on a single connected component of
![]() $\mathrm {Gr}_{G}$
. We can then pick some
$\mathrm {Gr}_{G}$
. We can then pick some
![]() $\mu $
such that
$\mu $
such that
![]() $\mathcal {S}_{V}$
is supported on the Schubert cell
$\mathcal {S}_{V}$
is supported on the Schubert cell
![]() $\mathrm {Gr}_{G,\leq \mu }$
. Choose some large m such that the
$\mathrm {Gr}_{G,\leq \mu }$
. Choose some large m such that the
![]() $L^{+}G$
action on
$L^{+}G$
action on
![]() $\mathrm {Gr}_{G,\leq \mu }$
factors over the truncated loop group
$\mathrm {Gr}_{G,\leq \mu }$
factors over the truncated loop group
![]() $L_{m}^{+}G$
. The sheaf
$L_{m}^{+}G$
. The sheaf
![]() $\mathcal {S}_{V}$
is naturally the pullback of a sheaf again denoted
$\mathcal {S}_{V}$
is naturally the pullback of a sheaf again denoted
![]() $\mathcal {S}_{V}$
on the quotient stack
$\mathcal {S}_{V}$
on the quotient stack
![]() $X=[\mathrm {Gr}_{G,\leq \mu }/L_{m}^{+}G]$
, so we can consider the characteristic class
$X=[\mathrm {Gr}_{G,\leq \mu }/L_{m}^{+}G]$
, so we can consider the characteristic class
![]() $\mathrm {cc}_{X/S}(\mathcal {S}_{V})$
.
$\mathrm {cc}_{X/S}(\mathcal {S}_{V})$
.
To analyze this class, we need to understand the inertia stack of X. For this, we need some notation. Let
![]() $L_{m}^{+}G_{\mathrm {sr}}$
be the preimage of the strongly regular semisimple locus
$L_{m}^{+}G_{\mathrm {sr}}$
be the preimage of the strongly regular semisimple locus
![]() $G_{\mathrm {sr}}\subset G$
under the theta map
$G_{\mathrm {sr}}\subset G$
under the theta map
![]() $L_{m}^{+}G\to G$
. Pick any maximal torus
$L_{m}^{+}G\to G$
. Pick any maximal torus
![]() $T\subset G$
with Weyl group W, and set
$T\subset G$
with Weyl group W, and set
![]() $L_{m}^{+}T_{\mathrm {sr}}=L_{m}^{+}T\cap L_{m}^{+}G_{\mathrm {sr}}$
.
$L_{m}^{+}T_{\mathrm {sr}}=L_{m}^{+}T\cap L_{m}^{+}G_{\mathrm {sr}}$
.
Proposition 5.4.1. 1. The open substack
is canonically identified with
![]() $[L_{m}^{+}T_{\mathrm {sr}}/(W\ltimes L_{m}^{+}T)]$
via the natural map.
$[L_{m}^{+}T_{\mathrm {sr}}/(W\ltimes L_{m}^{+}T)]$
via the natural map.
2. The open substack
is canonically identified with
such that the natural map
![]() $\mathrm {In}_{S}(X)_{\mathrm {sr}}\to \mathrm {In}_{S}([S/L_{m}^{+}G])_{\mathrm {sr}}$
coincides via the identification in part (1) with the evident projection onto
$\mathrm {In}_{S}(X)_{\mathrm {sr}}\to \mathrm {In}_{S}([S/L_{m}^{+}G])_{\mathrm {sr}}$
coincides via the identification in part (1) with the evident projection onto
![]() $[L_{m}^{+}T_{\mathrm {sr}}/(W\ltimes L_{m}^{+}T)]$
.
$[L_{m}^{+}T_{\mathrm {sr}}/(W\ltimes L_{m}^{+}T)]$
.
Proof. The idea behind (1) is that any
![]() $g\in L^+G_{\operatorname {\mathrm {sr}}}$
is conjugate to an element of
$g\in L^+G_{\operatorname {\mathrm {sr}}}$
is conjugate to an element of
![]() $L^+T_{\operatorname {\mathrm {sr}}}$
, which is well-defined up to the action of the normalizer of this group, which is
$L^+T_{\operatorname {\mathrm {sr}}}$
, which is well-defined up to the action of the normalizer of this group, which is
![]() $W\ltimes L^+T$
.
$W\ltimes L^+T$
.
For (2), we observe that an object of
![]() $\operatorname {\mathrm {In}}_S(X)_{\operatorname {\mathrm {sr}}}$
is a pair
$\operatorname {\mathrm {In}}_S(X)_{\operatorname {\mathrm {sr}}}$
is a pair
![]() $(x,g)$
, where
$(x,g)$
, where
![]() $g\in L_m^+G_{\operatorname {\mathrm {sr}}}$
fixes
$g\in L_m^+G_{\operatorname {\mathrm {sr}}}$
fixes
![]() $x\in \operatorname {\mathrm {Gr}}_{G,\leq \mu }$
; the automorphisms of this object are
$x\in \operatorname {\mathrm {Gr}}_{G,\leq \mu }$
; the automorphisms of this object are
![]() $L^+_mG$
. The g can be conjugated to lie in
$L^+_mG$
. The g can be conjugated to lie in
![]() $L^+T_{\operatorname {\mathrm {sr}}}$
, and then by Proposition 5.1.2, the x can be identified with an element of
$L^+T_{\operatorname {\mathrm {sr}}}$
, and then by Proposition 5.1.2, the x can be identified with an element of
![]() $X_*(T)_{\leq \mu }$
, which is well-defined up to an element of W.
$X_*(T)_{\leq \mu }$
, which is well-defined up to an element of W.
Corollary 5.4.2. There is a natural isomorphism
which sends
![]() $\operatorname {\mathrm {cc}}_{X/S}(\mathcal {S}_V)$
to the function sending
$\operatorname {\mathrm {cc}}_{X/S}(\mathcal {S}_V)$
to the function sending
![]() $\lambda \in X_*(T)_{\leq \mu }$
to
$\lambda \in X_*(T)_{\leq \mu }$
to
![]() $\operatorname {\mathrm {loc}}_{x_{\lambda }}(g,\mathcal {S}_V)$
, where
$\operatorname {\mathrm {loc}}_{x_{\lambda }}(g,\mathcal {S}_V)$
, where
![]() $x_{\lambda }\in \operatorname {\mathrm {Gr}}_{G,\leq \mu }$
is the T-fixed point corresponding to
$x_{\lambda }\in \operatorname {\mathrm {Gr}}_{G,\leq \mu }$
is the T-fixed point corresponding to
![]() $\lambda $
, and
$\lambda $
, and
![]() $g\in L_m^+T_{\operatorname {\mathrm {sr}}}$
. In particular,
$g\in L_m^+T_{\operatorname {\mathrm {sr}}}$
. In particular,
![]() $\operatorname {\mathrm {loc}}_{x_{\lambda }}(g,\mathcal {S}_V)$
does not depend on the choice of
$\operatorname {\mathrm {loc}}_{x_{\lambda }}(g,\mathcal {S}_V)$
does not depend on the choice of
![]() $g\in L_m^+T_{\operatorname {\mathrm {sr}}}$
.
$g\in L_m^+T_{\operatorname {\mathrm {sr}}}$
.
5.5 Degeneration to characteristic p
In this section, we prove Propositions 5.2.2 and 5.2.3.
Proof of Proposition 5.2.2
The isomorphism
![]() $\mathrm {Gr}_{\mathcal {T}}\cong {X_{\ast }(\mathcal {T})}_S$
is [Reference Scholze and WeinsteinSW20, Proposition 21.3.1]. There is an evident map
$\mathrm {Gr}_{\mathcal {T}}\cong {X_{\ast }(\mathcal {T})}_S$
is [Reference Scholze and WeinsteinSW20, Proposition 21.3.1]. There is an evident map
![]() $f: \mathrm {Gr}_{\mathcal {T}}\to \mathrm {Gr}_{\mathcal {\mathcal {G}}}^{g}$
, and it remains to see that f is an isomorphism. For this, we first note that f is a closed immersion. This follows from the observation the source and target of f are both closed subfunctors of
$f: \mathrm {Gr}_{\mathcal {T}}\to \mathrm {Gr}_{\mathcal {\mathcal {G}}}^{g}$
, and it remains to see that f is an isomorphism. For this, we first note that f is a closed immersion. This follows from the observation the source and target of f are both closed subfunctors of
![]() $\mathrm {Gr}_{\mathcal {G}}$
. For the source, this follows from [Reference Scholze and WeinsteinSW20, Proposition 20.3.7], while for the target this follows from the fact that
$\mathrm {Gr}_{\mathcal {G}}$
. For the source, this follows from [Reference Scholze and WeinsteinSW20, Proposition 20.3.7], while for the target this follows from the fact that
![]() $\mathrm {Gr}_{\mathcal {G}} \to S$
is separated.
$\mathrm {Gr}_{\mathcal {G}} \to S$
is separated.
Since f is a closed immersion, it is both qcqs and specializing. By [Reference ScholzeSch17, Lemma 12.5], it is enough to check that f is a bijection on rank one geometric points. This can be checked separately on the generic and special fibers. Both cases are handled by Proposition 5.1.2.
Proof of Proposition 5.2.3
By two applications of (the connected case of) Proposition 5.3.1, applied to the maps
![]() $\eta \to S$
and
$\eta \to S$
and
![]() $s \to S$
, we get equalities
$s \to S$
, we get equalities
and the result follows.
5.6 Local terms on the Witt vector affine Grassmannian
Proof of Proposition 5.2.4
Fix g and V as in the statement, and let
![]() $\mathcal {T}\subset \mathcal {G}$
be the connected centralizer of g. For every
$\mathcal {T}\subset \mathcal {G}$
be the connected centralizer of g. For every
![]() $\nu \in X_{\ast }(\mathcal {T})$
, let
$\nu \in X_{\ast }(\mathcal {T})$
, let
![]() $S_{\nu }\subset \mathrm {Gr}_{\mathcal {G}}^{W}$
be the associated semi-infinite orbit, with closure
$S_{\nu }\subset \mathrm {Gr}_{\mathcal {G}}^{W}$
be the associated semi-infinite orbit, with closure
![]() $\overline {S_{\nu }}=\cup _{\nu '\leq \nu }S_{\nu }$
.
$\overline {S_{\nu }}=\cup _{\nu '\leq \nu }S_{\nu }$
.
Let
![]() $X\subset \mathrm {Gr}_{\mathcal {G}}^{W}$
be a finite union of closed Schubert cells containing the support of
$X\subset \mathrm {Gr}_{\mathcal {G}}^{W}$
be a finite union of closed Schubert cells containing the support of
![]() $\mathcal {S}_{V}$
, so X is a perfectly projective k-scheme by the results in [Reference Bhatt and ScholzeBS17]. Write
$\mathcal {S}_{V}$
, so X is a perfectly projective k-scheme by the results in [Reference Bhatt and ScholzeBS17]. Write
![]() $X_{\nu }=X\cap S_{\nu }$
,
$X_{\nu }=X\cap S_{\nu }$
,
![]() $X_{\leq \nu }=X\cap \overline {S_{\nu }}$
, and
$X_{\leq \nu }=X\cap \overline {S_{\nu }}$
, and
![]() $\partial X_{\leq \nu }=X_{\leq \nu }\smallsetminus X_{\nu }$
. Note that all of these spaces are stable under g and in fact under
$\partial X_{\leq \nu }=X_{\leq \nu }\smallsetminus X_{\nu }$
. Note that all of these spaces are stable under g and in fact under
![]() $\mathcal {T}$
. Note also that each
$\mathcal {T}$
. Note also that each
![]() $X_{\nu }$
contains a unique g-fixed point
$X_{\nu }$
contains a unique g-fixed point
![]() $x_{\nu }$
.
$x_{\nu }$
.
Proposition 5.6.1. The compactly supported Euler characteristic of
![]() $\mathcal {S}_V$
on
$\mathcal {S}_V$
on
![]() $X_{\nu }$
is
$X_{\nu }$
is
Proof. This is a consequence of the integral-coefficients version of the geometric Satake equivalence for the Witt vector affine Grassmannian given in [Reference YuYu19]. There it is shown (Proposition 4.2) that
![]() $H^d_c(X_{\nu }, \mathcal {S}_V)$
is zero unless
$H^d_c(X_{\nu }, \mathcal {S}_V)$
is zero unless
![]() $d=\left < 2\rho ,\nu \right>$
, and in that degree it corresponds exactly to the
$d=\left < 2\rho ,\nu \right>$
, and in that degree it corresponds exactly to the
![]() $\nu $
-weight functor in the Satake category.
$\nu $
-weight functor in the Satake category.
Any
![]() $t\in \mathcal {T}$
must act trivially on
$t\in \mathcal {T}$
must act trivially on
![]() $H^d_c(X_{\nu },\mathcal {S}_V)$
, so
$H^d_c(X_{\nu },\mathcal {S}_V)$
, so
![]() $\chi _{c}(U,\mathcal {S}_{V})$
coincides with the trace of g on
$\chi _{c}(U,\mathcal {S}_{V})$
coincides with the trace of g on
![]() $R\Gamma _{c}(X_{\nu },\mathcal {S}_{V})$
. The same is true for
$R\Gamma _{c}(X_{\nu },\mathcal {S}_{V})$
. The same is true for
![]() $X_{\leq \nu }$
and
$X_{\leq \nu }$
and
![]() $\partial X_{\leq \nu }$
. We compute:
$\partial X_{\leq \nu }$
. We compute:
 $$ \begin{align*} (-1)^{\left\langle 2\rho,\nu\right\rangle }\operatorname{\mathrm{rank}} V[\nu] & =\chi_{c}(X_{\nu},\mathcal{S}_{V})\\ & =\chi_{c}(X_{\leq\nu},\mathcal{S}_{V})-\chi_{c}(\partial X_{\leq\nu},\mathcal{S}_{V})\\ & =\mathrm{tr}(g|R\Gamma_{c}(X_{\leq\nu},\mathcal{S}_{V}))-\mathrm{tr}(g|R\Gamma_{c}(\partial X_{\leq\nu},\mathcal{S}_{V}))\\ & =\sum_{\nu'\leq\nu}\mathrm{loc}_{x_{\nu'}}(g,\mathcal{S}_{V}|_{X_{\leq\nu}})-\sum_{\nu'\leq\nu,\nu'\neq\nu}\mathrm{loc}_{x_{\nu'}}(g,\mathcal{S}_{V}|_{\partial X_{\leq\nu}})\\ & =\sum_{\nu'\leq\nu}\mathrm{loc}_{x_{\nu'}}(g,\mathcal{S}_{V})-\sum_{\nu'\leq\nu,\nu'\neq\nu}\mathrm{loc}_{x_{\nu'}}(g,\mathcal{S}_{V})\\ & =\mathrm{loc}_{x_{\nu}}(g,\mathcal{S}_{V}). \end{align*} $$
$$ \begin{align*} (-1)^{\left\langle 2\rho,\nu\right\rangle }\operatorname{\mathrm{rank}} V[\nu] & =\chi_{c}(X_{\nu},\mathcal{S}_{V})\\ & =\chi_{c}(X_{\leq\nu},\mathcal{S}_{V})-\chi_{c}(\partial X_{\leq\nu},\mathcal{S}_{V})\\ & =\mathrm{tr}(g|R\Gamma_{c}(X_{\leq\nu},\mathcal{S}_{V}))-\mathrm{tr}(g|R\Gamma_{c}(\partial X_{\leq\nu},\mathcal{S}_{V}))\\ & =\sum_{\nu'\leq\nu}\mathrm{loc}_{x_{\nu'}}(g,\mathcal{S}_{V}|_{X_{\leq\nu}})-\sum_{\nu'\leq\nu,\nu'\neq\nu}\mathrm{loc}_{x_{\nu'}}(g,\mathcal{S}_{V}|_{\partial X_{\leq\nu}})\\ & =\sum_{\nu'\leq\nu}\mathrm{loc}_{x_{\nu'}}(g,\mathcal{S}_{V})-\sum_{\nu'\leq\nu,\nu'\neq\nu}\mathrm{loc}_{x_{\nu'}}(g,\mathcal{S}_{V})\\ & =\mathrm{loc}_{x_{\nu}}(g,\mathcal{S}_{V}). \end{align*} $$
The penultimate equality is the key technical fact and follows from Proposition 5.6.2 below together with the assumptions on g.
Proposition 5.6.2. Let
![]() $k/\mathbf {F}_{p}$
be an algebraically closed field, and let X be a perfectly finite type k-scheme with an automorphism
$k/\mathbf {F}_{p}$
be an algebraically closed field, and let X be a perfectly finite type k-scheme with an automorphism
![]() $g:X\to X$
of finite prime-to-p order. Let
$g:X\to X$
of finite prime-to-p order. Let
![]() $A\in D_{c}^{b}(X,\mathbf {Z}_{\ell })$
be an object equipped with a morphism
$A\in D_{c}^{b}(X,\mathbf {Z}_{\ell })$
be an object equipped with a morphism
![]() $u:g^{\ast }A\to A$
. Then for every isolated g-fixed point x, the true local term
$u:g^{\ast }A\to A$
. Then for every isolated g-fixed point x, the true local term
![]() $\mathrm {loc}_{x}(g,A)$
equals the naive local term
$\mathrm {loc}_{x}(g,A)$
equals the naive local term
![]() $\mathrm {tr}(g|A_{x})$
.
$\mathrm {tr}(g|A_{x})$
.
In particular, if
![]() $Z\subset X$
is a g-stable closed subscheme, then
$Z\subset X$
is a g-stable closed subscheme, then
![]() $\mathrm {loc}_{x}(g,A)=\mathrm {loc}_{x}(g,A|_{Z})$
.
$\mathrm {loc}_{x}(g,A)=\mathrm {loc}_{x}(g,A|_{Z})$
.
Proof. With the word ‘perfectly’ deleted, this is a recent result of Varshavsky [Reference VarshavskyVar20] (combine Theorem 4.10(b) and Corollary 5.4(b)). We will reduce to Varshavsky’s result by deperfecting.
Precisely, since
![]() $\mathrm {loc}_{x}(g,A)$
is insensitive to replacing
$\mathrm {loc}_{x}(g,A)$
is insensitive to replacing
![]() $X,A$
by
$X,A$
by
![]() $U,A|U$
for
$U,A|U$
for
![]() $U\subset X$
any g-invariant open neighborhood of x, we can assume that X is affine, so
$U\subset X$
any g-invariant open neighborhood of x, we can assume that X is affine, so
![]() $X=\operatorname {\mathrm {Spec}} R$
with R perfectly of finite type. Let
$X=\operatorname {\mathrm {Spec}} R$
with R perfectly of finite type. Let
![]() $R_{0}\subset R$
be a finite type k-algebra with
$R_{0}\subset R$
be a finite type k-algebra with
![]() $R_{0}^{\mathrm {perf}}=R$
, and let
$R_{0}^{\mathrm {perf}}=R$
, and let
![]() $R_1\subset R$
be the k-algebra generated by
$R_1\subset R$
be the k-algebra generated by
![]() $g^{i}R_{0}$
for all
$g^{i}R_{0}$
for all
![]() $1\leq i\leq \operatorname {\mathrm {ord}}(g)$
. Then
$1\leq i\leq \operatorname {\mathrm {ord}}(g)$
. Then
![]() $R_1\subset R$
is a finite-type k-algebra stable under g, with
$R_1\subset R$
is a finite-type k-algebra stable under g, with
![]() $R_1^{\mathrm {perf}}=A$
, so
$R_1^{\mathrm {perf}}=A$
, so
![]() $X_{1}=\operatorname {\mathrm {Spec}} R_1$
is a deperfection of X equipped with an automorphism
$X_{1}=\operatorname {\mathrm {Spec}} R_1$
is a deperfection of X equipped with an automorphism
![]() $g_{1}$
deperfecting g; since
$g_{1}$
deperfecting g; since
![]() $X\to X_{1}$
is a homeomorphism, there is a unique
$X\to X_{1}$
is a homeomorphism, there is a unique
![]() $g_{1}$
-fixed point
$g_{1}$
-fixed point
![]() $x_{1}$
under x. Next,
$x_{1}$
under x. Next,
![]() $g^{\ast }A \to A$
deperfects uniquely to a complex
$g^{\ast }A \to A$
deperfects uniquely to a complex
![]() $A_{1}$
on
$A_{1}$
on
![]() $X_1$
equipped with a map
$X_1$
equipped with a map
![]() $g_{1}^{\ast }A_{1}\to A_{1}$
, using the equivalence of categories
$g_{1}^{\ast }A_{1}\to A_{1}$
, using the equivalence of categories
![]() $D(X_{\mathrm {et}},\Lambda )\cong D(X_{1,\mathrm {\acute {e}t}},\Lambda )$
. Finally, we compute that
$D(X_{\mathrm {et}},\Lambda )\cong D(X_{1,\mathrm {\acute {e}t}},\Lambda )$
. Finally, we compute that
where the first equality is formal nonsense (the six functors on k-varieties and on perfectly finite type k-schemes are compatible under perfection), the second equality is Varshavsky’s theorem and the third equality is trivial.
6 Application to the Hecke stacks
In this final, chapter we prove Theorem 1.0.2 by applying the technology of the Lefschetz–Verdier trace formula to the Hecke stacks over
![]() $\operatorname {\mathrm {Bun}}_G$
.
$\operatorname {\mathrm {Bun}}_G$
.
6.1
 $\operatorname {\mathrm {Bun}}_G$
, the local and global Hecke stacks and their relation to shtuka spaces
$\operatorname {\mathrm {Bun}}_G$
, the local and global Hecke stacks and their relation to shtuka spaces
Let
![]() $F/\mathbf {Q}_p$
be a finite extension, and let
$F/\mathbf {Q}_p$
be a finite extension, and let
![]() $G/F$
be a connected reductive group. Let k be an algebraically closed perfectoid field containing the residue field of F.
$G/F$
be a connected reductive group. Let k be an algebraically closed perfectoid field containing the residue field of F.
For an algebraically closed perfectoid field
![]() $C/k$
, there is a bijection [Reference FarguesFar20]
$C/k$
, there is a bijection [Reference FarguesFar20]
between Kottwitz’ set
![]() $B(G)$
and isomorphism classes of G-bundles on the Fargues–Fontaine curve
$B(G)$
and isomorphism classes of G-bundles on the Fargues–Fontaine curve
![]() $X_C$
. Therefore, the moduli stack of G-bundles is some geometric version of the set
$X_C$
. Therefore, the moduli stack of G-bundles is some geometric version of the set
![]() $B(G)$
.
$B(G)$
.
Definition 6.1.1 [Reference Fargues and ScholzeFS21, Definition III.0.1 and Theorem III.0.2]
Let
![]() $\operatorname {\mathrm {Bun}}_G$
be the v-stack which assigns to a perfectoid space
$\operatorname {\mathrm {Bun}}_G$
be the v-stack which assigns to a perfectoid space
![]() $S/k$
the groupoid of G-bundles on
$S/k$
the groupoid of G-bundles on
![]() $X_S$
. Given a class
$X_S$
. Given a class
![]() $b\in B(G)$
, let
$b\in B(G)$
, let
![]() $i_b\colon \operatorname {\mathrm {Bun}}_G^b\to \operatorname {\mathrm {Bun}}_G$
be the locally closed substack classifying G-bundles which are isomorphic to
$i_b\colon \operatorname {\mathrm {Bun}}_G^b\to \operatorname {\mathrm {Bun}}_G$
be the locally closed substack classifying G-bundles which are isomorphic to
![]() $\mathcal {E}^b$
at every geometric point.
$\mathcal {E}^b$
at every geometric point.
Then
![]() $\operatorname {\mathrm {Bun}}_G$
is a cohomologically smooth Artin v-stack over
$\operatorname {\mathrm {Bun}}_G$
is a cohomologically smooth Artin v-stack over
![]() $\operatorname {\mathrm {Spd}} k$
[Reference Fargues and ScholzeFS21, Theorem I.4.1(vii)]. Central to its study are the substacks
$\operatorname {\mathrm {Spd}} k$
[Reference Fargues and ScholzeFS21, Theorem I.4.1(vii)]. Central to its study are the substacks
![]() $\operatorname {\mathrm {Bun}}_G^b$
. For each
$\operatorname {\mathrm {Bun}}_G^b$
. For each
![]() $b\in B(G)$
, we have an isomorphism
$b\in B(G)$
, we have an isomorphism
![]() $\operatorname {\mathrm {Bun}}_G^b\cong [\operatorname {\mathrm {Spd}} k/\widetilde {G}_b]$
, where
$\operatorname {\mathrm {Bun}}_G^b\cong [\operatorname {\mathrm {Spd}} k/\widetilde {G}_b]$
, where
is a group diamond over
![]() $\operatorname {\mathrm {Spd}} k$
. This fits in an exact sequence of group diamonds over
$\operatorname {\mathrm {Spd}} k$
. This fits in an exact sequence of group diamonds over
![]() $\operatorname {\mathrm {Spd}} k$
:
$\operatorname {\mathrm {Spd}} k$
:
Here, the neutral component
![]() $\widetilde {G}_b^{\circ }\subset \widetilde {G}_b$
is a cohomologically smooth group diamond over
$\widetilde {G}_b^{\circ }\subset \widetilde {G}_b$
is a cohomologically smooth group diamond over
![]() $\operatorname {\mathrm {Spd}} k$
, and
$\operatorname {\mathrm {Spd}} k$
, and
![]() $G_b$
is the automorphism group of the isocrystal b. The group
$G_b$
is the automorphism group of the isocrystal b. The group
![]() $G_b$
is an inner form of a Levi subgroup of the quasisplit inner form of G. If b is basic, then
$G_b$
is an inner form of a Levi subgroup of the quasisplit inner form of G. If b is basic, then
![]() $i_b$
is an open immersion, and
$i_b$
is an open immersion, and
![]() $\widetilde {G}_b=G_b(F)_{\operatorname {\mathrm {Spd}} k}$
.
$\widetilde {G}_b=G_b(F)_{\operatorname {\mathrm {Spd}} k}$
.
We next recall the Hecke correspondence on
![]() $\operatorname {\mathrm {Bun}}_G$
and its relation to the local shtuka spaces
$\operatorname {\mathrm {Bun}}_G$
and its relation to the local shtuka spaces
![]() $\operatorname {\mathrm {Sht}}_{G,b,\mu }$
. Since our main result on the cohomology of local Shimura varieties does not concern the action of a Weil group, all objects in this discussion will live over the base
$\operatorname {\mathrm {Sht}}_{G,b,\mu }$
. Since our main result on the cohomology of local Shimura varieties does not concern the action of a Weil group, all objects in this discussion will live over the base
![]() $S=\operatorname {\mathrm {Spd}} C$
, where C is an algebraically closed perfectoid field containing F, whose residue field contains k. In particular, we have
$S=\operatorname {\mathrm {Spd}} C$
, where C is an algebraically closed perfectoid field containing F, whose residue field contains k. In particular, we have
![]() $\operatorname {\mathrm {Bun}}_{G,C}=\operatorname {\mathrm {Bun}}_G \times _{\operatorname {\mathrm {Spd}} k} S$
. If T is a perfectoid space over C, the Fargues–Fontaine curve
$\operatorname {\mathrm {Bun}}_{G,C}=\operatorname {\mathrm {Bun}}_G \times _{\operatorname {\mathrm {Spd}} k} S$
. If T is a perfectoid space over C, the Fargues–Fontaine curve
![]() $X_T$
comes equipped with a degree 1 Cartier divisor
$X_T$
comes equipped with a degree 1 Cartier divisor
![]() $D_T$
, corresponding to the untilt T of
$D_T$
, corresponding to the untilt T of
![]() $T^{\flat }$
.
$T^{\flat }$
.
We introduce now a diagram of v-stacks over
![]() $\operatorname {\mathrm {Spd}} C$
containing both local and global Hecke correspondences:
$\operatorname {\mathrm {Spd}} C$
containing both local and global Hecke correspondences:

We explain below the objects and morphisms appearing in equation (6.1.1). Let
![]() $T=\operatorname {\mathrm {Spa}}(R,R^+)$
be an affinoid perfectoid space over
$T=\operatorname {\mathrm {Spa}}(R,R^+)$
be an affinoid perfectoid space over
![]() $\operatorname {\mathrm {Spa}} C$
.
$\operatorname {\mathrm {Spa}} C$
.
-
• The T-points of the stack
 $\operatorname {\mathrm {Hecke}}_{G,C}$
classify triples
$\operatorname {\mathrm {Hecke}}_{G,C}$
classify triples
 $(\mathcal {E}_1,\mathcal {E}_2,f)$
, where
$(\mathcal {E}_1,\mathcal {E}_2,f)$
, where
 $\mathcal {E}_1$
and
$\mathcal {E}_1$
and
 $\mathcal {E}_2$
are G-bundles on
$\mathcal {E}_2$
are G-bundles on
 $X_T$
, and is an isomorphism which is meromorphic along
$X_T$
, and is an isomorphism which is meromorphic along $$\begin{align*}f\colon \mathcal{E}_1\vert_{X_T\backslash D_T} \cong \mathcal{E}_2\vert_{X_T\backslash D_T} \end{align*}$$
$$\begin{align*}f\colon \mathcal{E}_1\vert_{X_T\backslash D_T} \cong \mathcal{E}_2\vert_{X_T\backslash D_T} \end{align*}$$
 $D_T$
.
$D_T$
.
-
• The morphism
 $h_i$
sends a triple as above to
$h_i$
sends a triple as above to
 $\mathcal {E}_i$
for
$\mathcal {E}_i$
for
 $i=1,2$
.
$i=1,2$
. -
• The T-points of
 $\operatorname {\mathrm {Bun}}_{G,C}^{\operatorname {\mathrm {loc}}}$
classify G-bundles on
$\operatorname {\mathrm {Bun}}_{G,C}^{\operatorname {\mathrm {loc}}}$
classify G-bundles on
 $\operatorname {\mathrm {Spec}} B_{\operatorname {\mathrm {dR}}}^+(R)$
, this being the completion of
$\operatorname {\mathrm {Spec}} B_{\operatorname {\mathrm {dR}}}^+(R)$
, this being the completion of
 $X_T$
along
$X_T$
along
 $D_T$
. Such G-bundles are v-locally trivial on T so that we have an isomorphism where
$D_T$
. Such G-bundles are v-locally trivial on T so that we have an isomorphism where $$\begin{align*}\operatorname{\mathrm{Bun}}_{G,C}^{\operatorname{\mathrm{loc}}} \cong [\operatorname{\mathrm{Spd}} C / L^+G], \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Bun}}_{G,C}^{\operatorname{\mathrm{loc}}} \cong [\operatorname{\mathrm{Spd}} C / L^+G], \end{align*}$$
 $L^+G = G(B_{\operatorname {\mathrm {dR}}}^+)$
is the positive loop group.
$L^+G = G(B_{\operatorname {\mathrm {dR}}}^+)$
is the positive loop group.
-
• The T-points of
 $\operatorname {\mathrm {Hecke}}^{\operatorname {\mathrm {loc}}}_{G,C}$
classify triples
$\operatorname {\mathrm {Hecke}}^{\operatorname {\mathrm {loc}}}_{G,C}$
classify triples
 $(\mathcal {E}_1,\mathcal {E}_2,f)$
, where
$(\mathcal {E}_1,\mathcal {E}_2,f)$
, where
 $\mathcal {E}_1$
and
$\mathcal {E}_1$
and
 $\mathcal {E}_2$
are G-bundles on
$\mathcal {E}_2$
are G-bundles on
 $\operatorname {\mathrm {Spec}} B_{\operatorname {\mathrm {dR}}}^+(R)$
, and f is an isomorphism between their restrictions to
$\operatorname {\mathrm {Spec}} B_{\operatorname {\mathrm {dR}}}^+(R)$
, and f is an isomorphism between their restrictions to
 $\operatorname {\mathrm {Spec}} B_{\operatorname {\mathrm {dR}}}(R)$
, meromorphic along
$\operatorname {\mathrm {Spec}} B_{\operatorname {\mathrm {dR}}}(R)$
, meromorphic along
 $D_T$
. We have an isomorphism where
$D_T$
. We have an isomorphism where $$\begin{align*}\operatorname{\mathrm{Hecke}}_{G,C}^{\operatorname{\mathrm{loc}}} \cong [L^+G \backslash LG / L^+G ],\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Hecke}}_{G,C}^{\operatorname{\mathrm{loc}}} \cong [L^+G \backslash LG / L^+G ],\end{align*}$$
 $LG=G(B_{\operatorname {\mathrm {dR}}})$
is the full loop group. Put another way, we have the
$LG=G(B_{\operatorname {\mathrm {dR}}})$
is the full loop group. Put another way, we have the
 $B_{\operatorname {\mathrm {dR}}}$
-affine Grassmannian
$B_{\operatorname {\mathrm {dR}}}$
-affine Grassmannian
 $\operatorname {\mathrm {Gr}}_{G,C}=LG/L^+G$
and then
$\operatorname {\mathrm {Gr}}_{G,C}=LG/L^+G$
and then
 $\operatorname {\mathrm {Hecke}}_{G,C}^{\operatorname {\mathrm {loc}}}=[L^+G \backslash \operatorname {\mathrm {Gr}}_{G,C}]$
.
$\operatorname {\mathrm {Hecke}}_{G,C}^{\operatorname {\mathrm {loc}}}=[L^+G \backslash \operatorname {\mathrm {Gr}}_{G,C}]$
.
-
• The morphism
 $h_i^{\operatorname {\mathrm {loc}}}$
sends such a triple to
$h_i^{\operatorname {\mathrm {loc}}}$
sends such a triple to
 $\mathcal {E}_i$
for
$\mathcal {E}_i$
for
 $i=1,2$
.
$i=1,2$
. -
• The vertical maps send an object to its completion along
 $D_T$
in the evident manner.
$D_T$
in the evident manner.
The squares in equation (6.1.1) are Cartesian by Beauville–Laszlo gluing.
It is a basic fact that
![]() $\operatorname {\mathrm {Bun}}_{G,C}$
is a decent v-stack, and the structure map
$\operatorname {\mathrm {Bun}}_{G,C}$
is a decent v-stack, and the structure map
![]() $\operatorname {\mathrm {Bun}}_{G,C} \to S=\operatorname {\mathrm {Spd}} C$
is fine. With some care, it is possible to ‘truncate’ some of the other objects appearing in equation (6.1.1) to obtain decent S-v-stacks with fine structure maps to S. In particular, let
$\operatorname {\mathrm {Bun}}_{G,C} \to S=\operatorname {\mathrm {Spd}} C$
is fine. With some care, it is possible to ‘truncate’ some of the other objects appearing in equation (6.1.1) to obtain decent S-v-stacks with fine structure maps to S. In particular, let
![]() $\mu $
be a dominant cocharacter of G, and let
$\mu $
be a dominant cocharacter of G, and let
![]() $\operatorname {\mathrm {Hecke}}_{G,\leq \mu ,C}$
be the substack of
$\operatorname {\mathrm {Hecke}}_{G,\leq \mu ,C}$
be the substack of
![]() $\operatorname {\mathrm {Hecke}}_{G,\mu }$
consisting of triples
$\operatorname {\mathrm {Hecke}}_{G,\mu }$
consisting of triples
![]() $(\mathcal {E}_1,\mathcal {E}_2,f)$
, where the meromorphy of f is fiberwise bounded by
$(\mathcal {E}_1,\mathcal {E}_2,f)$
, where the meromorphy of f is fiberwise bounded by
![]() $\mu $
. Then
$\mu $
. Then
![]() $\operatorname {\mathrm {Hecke}}_{G,\leq \mu ,C}$
is decent, and the maps to
$\operatorname {\mathrm {Hecke}}_{G,\leq \mu ,C}$
is decent, and the maps to
![]() $\operatorname {\mathrm {Bun}}_{G,C}$
induced by restricting
$\operatorname {\mathrm {Bun}}_{G,C}$
induced by restricting
![]() $h_1$
and
$h_1$
and
![]() $h_2$
are fine. We may define
$h_2$
are fine. We may define
![]() $\operatorname {\mathrm {Hecke}}_{G,\leq \mu ,C}^{\operatorname {\mathrm {loc}}}$
analogously; this is isomorphic to
$\operatorname {\mathrm {Hecke}}_{G,\leq \mu ,C}^{\operatorname {\mathrm {loc}}}$
analogously; this is isomorphic to
![]() $[\operatorname {\mathrm {Gr}}_{G,\leq \mu ,C}/L^+G]$
, where
$[\operatorname {\mathrm {Gr}}_{G,\leq \mu ,C}/L^+G]$
, where
![]() $\operatorname {\mathrm {Gr}}_{G,\leq \mu ,C}$
is the bounded Grassmannian. This is not quite a decent v-stack. However, if we instead form the quotient
$\operatorname {\mathrm {Gr}}_{G,\leq \mu ,C}$
is the bounded Grassmannian. This is not quite a decent v-stack. However, if we instead form the quotient
![]() $[\operatorname {\mathrm {Gr}}_{G,\leq \mu ,C}/L^{+}_{m}G]$
for some sufficiently large truncation as in Theorem 5.1.4, we do obtain a decent S-v-stack with fine structure map. This is sufficient for our purposes.
$[\operatorname {\mathrm {Gr}}_{G,\leq \mu ,C}/L^{+}_{m}G]$
for some sufficiently large truncation as in Theorem 5.1.4, we do obtain a decent S-v-stack with fine structure map. This is sufficient for our purposes.
Now let
![]() $b\in B(G,\mu )$
be basic. We explain the relation between Hecke stacks and local shtuka spaces. It will be helpful to refer to the commutative diagram of stacks
$b\in B(G,\mu )$
be basic. We explain the relation between Hecke stacks and local shtuka spaces. It will be helpful to refer to the commutative diagram of stacks

in which all squares are Cartesian, the morphisms labeled with i are open immersions and the morphisms
![]() $h_1$
and
$h_1$
and
![]() $h_2$
are proper.
$h_2$
are proper.
The top row of equation (6.1.2) can be described via the diagram:

Explanation:
![]() $\operatorname {\mathrm {Gr}}_{G,\leq \mu ,C}^1$
assigns to
$\operatorname {\mathrm {Gr}}_{G,\leq \mu ,C}^1$
assigns to
![]() $T=\operatorname {\mathrm {Spa}}(R,R^+)$
the set of pairs
$T=\operatorname {\mathrm {Spa}}(R,R^+)$
the set of pairs
![]() $(\mathcal {E},f)$
, where
$(\mathcal {E},f)$
, where
![]() $\mathcal {E}$
is a G-bundle on
$\mathcal {E}$
is a G-bundle on
![]() $X_S$
, and
$X_S$
, and
![]() $f\colon \mathcal {E}^1\vert _{X_T\backslash D_T}\cong \mathcal {E}\vert _{X_T\backslash D_T}$
is an isomorphism, which is bounded by
$f\colon \mathcal {E}^1\vert _{X_T\backslash D_T}\cong \mathcal {E}\vert _{X_T\backslash D_T}$
is an isomorphism, which is bounded by
![]() $\mu $
along
$\mu $
along
![]() $D_T$
. The bundle
$D_T$
. The bundle
![]() $\mathcal {E}^1$
can be canonically trivialized over
$\mathcal {E}^1$
can be canonically trivialized over
![]() $\operatorname {\mathrm {Spa}} B_{\operatorname {\mathrm {dR}}}^+(R)$
, and in so doing, we obtain an isomorphism
$\operatorname {\mathrm {Spa}} B_{\operatorname {\mathrm {dR}}}^+(R)$
, and in so doing, we obtain an isomorphism
![]() $\operatorname {\mathrm {Gr}}^1_{G,\leq \mu ,C}\cong \operatorname {\mathrm {Gr}}_{G,\leq \mu ,C}$
. Within
$\operatorname {\mathrm {Gr}}^1_{G,\leq \mu ,C}\cong \operatorname {\mathrm {Gr}}_{G,\leq \mu ,C}$
. Within
![]() $\operatorname {\mathrm {Gr}}_{G,\leq \mu }^1$
, we have the open locus
$\operatorname {\mathrm {Gr}}_{G,\leq \mu }^1$
, we have the open locus
![]() $\operatorname {\mathrm {Gr}}_{G,\leq \mu }^{1,\operatorname {\mathrm {adm}}}$
, consisting of those pairs
$\operatorname {\mathrm {Gr}}_{G,\leq \mu }^{1,\operatorname {\mathrm {adm}}}$
, consisting of those pairs
![]() $(\mathcal {E},\gamma )$
, where
$(\mathcal {E},\gamma )$
, where
![]() $\mathcal {E}$
is everywhere isomorphic to
$\mathcal {E}$
is everywhere isomorphic to
![]() $\mathcal {E}^b$
.
$\mathcal {E}^b$
.
Similarly, the leftmost column of equation (6.1.2) can be described via the diagram:

Explanation:
![]() $\operatorname {\mathrm {Gr}}_{G,\leq \mu ,C}^b$
assigns to
$\operatorname {\mathrm {Gr}}_{G,\leq \mu ,C}^b$
assigns to
![]() $T=\operatorname {\mathrm {Spa}}(R,R^+)$
the set of pairs
$T=\operatorname {\mathrm {Spa}}(R,R^+)$
the set of pairs
![]() $(\mathcal {E},f)$
, where
$(\mathcal {E},f)$
, where
![]() $\mathcal {E}$
is a G-bundle, and
$\mathcal {E}$
is a G-bundle, and
![]() $f\colon \mathcal {E}\vert _{X_T\backslash D_T}\cong \mathcal {E}^b\vert _{X_T\backslash D_T}$
is an isomorphism, which is bounded by
$f\colon \mathcal {E}\vert _{X_T\backslash D_T}\cong \mathcal {E}^b\vert _{X_T\backslash D_T}$
is an isomorphism, which is bounded by
![]() $\mu $
along
$\mu $
along
![]() $D_T$
. We have an isomorphism
$D_T$
. We have an isomorphism
![]() $\operatorname {\mathrm {Gr}}_{G,\leq \mu ,C}^b\cong \operatorname {\mathrm {Gr}}_{G,\leq -\mu ,C}$
. Within
$\operatorname {\mathrm {Gr}}_{G,\leq \mu ,C}^b\cong \operatorname {\mathrm {Gr}}_{G,\leq -\mu ,C}$
. Within
![]() $\operatorname {\mathrm {Gr}}_{G,\leq \mu ,C}^b$
, we have the open admissible locus
$\operatorname {\mathrm {Gr}}_{G,\leq \mu ,C}^b$
, we have the open admissible locus
![]() $\operatorname {\mathrm {Gr}}_{G,\leq \mu ,C}^{b,\operatorname {\mathrm {adm}}}$
consisting of pairs
$\operatorname {\mathrm {Gr}}_{G,\leq \mu ,C}^{b,\operatorname {\mathrm {adm}}}$
consisting of pairs
![]() $(\mathcal {E},f)$
, where
$(\mathcal {E},f)$
, where
![]() $\mathcal {E}$
is everywhere isomorphic to
$\mathcal {E}$
is everywhere isomorphic to
![]() $\mathcal {E}^1$
.
$\mathcal {E}^1$
.
The moduli space of local shtukas
![]() $\operatorname {\mathrm {Sht}}_{G,b,\mu ,C}$
appears as the fiber product:
$\operatorname {\mathrm {Sht}}_{G,b,\mu ,C}$
appears as the fiber product:

where the right vertical morphism corresponds to
![]() $\mathcal {E}^b\times \mathcal {E}^1$
. This is evident from the definition of
$\mathcal {E}^b\times \mathcal {E}^1$
. This is evident from the definition of
![]() $\operatorname {\mathrm {Sht}}_{G,b,\mu }$
: Its S-points are morphisms
$\operatorname {\mathrm {Sht}}_{G,b,\mu }$
: Its S-points are morphisms
![]() $f\colon \mathcal {E}^1_{X_S\backslash D_S}\cong \mathcal {E}^b_{X_S\backslash D_S}$
which are bounded by
$f\colon \mathcal {E}^1_{X_S\backslash D_S}\cong \mathcal {E}^b_{X_S\backslash D_S}$
which are bounded by
![]() $\mu $
on
$\mu $
on
![]() $D_S$
.
$D_S$
.
We also have the period morphisms:

The morphism
![]() $\pi _1$
is a
$\pi _1$
is a
![]() $G_b(F)_S$
-equivariant
$G_b(F)_S$
-equivariant
![]() $G(F)_S$
-torsor over the admissible locus
$G(F)_S$
-torsor over the admissible locus
![]() $\operatorname {\mathrm {Gr}}^{b,\operatorname {\mathrm {adm}}}_{G,\leq \mu ,C}$
. Similarly,
$\operatorname {\mathrm {Gr}}^{b,\operatorname {\mathrm {adm}}}_{G,\leq \mu ,C}$
. Similarly,
![]() $\pi _2$
is a
$\pi _2$
is a
![]() $G(F)_S$
-equivariant
$G(F)_S$
-equivariant
![]() $G_b(F)_S$
-torsor over the admissible locus
$G_b(F)_S$
-torsor over the admissible locus
![]() $\operatorname {\mathrm {Gr}}^{1,\operatorname {\mathrm {adm}}}_{G,\leq \mu ,C}$
.
$\operatorname {\mathrm {Gr}}^{1,\operatorname {\mathrm {adm}}}_{G,\leq \mu ,C}$
.
6.2 The inertia stack of the Hecke stack; admissibility of elliptic fixed points
We continue to put
![]() $S=\operatorname {\mathrm {Spd}} C$
. Here, we investigate the inertia stack
$S=\operatorname {\mathrm {Spd}} C$
. Here, we investigate the inertia stack
![]() $\operatorname {\mathrm {In}}_S(\operatorname {\mathrm {Hecke}}_{G,\leq \mu ,C})$
, or at least the part of it lying over the strongly regular locus in
$\operatorname {\mathrm {In}}_S(\operatorname {\mathrm {Hecke}}_{G,\leq \mu ,C})$
, or at least the part of it lying over the strongly regular locus in
![]() .
.
It will help to introduce some notation. Suppose
![]() $\mathcal {E}$
is a G-bundle on
$\mathcal {E}$
is a G-bundle on
![]() $X_C$
equipped with a trivialization over the completion at
$X_C$
equipped with a trivialization over the completion at
![]() $\infty =D_C$
. Let
$\infty =D_C$
. Let
![]() $T\subset G$
be a maximal torus. We have seen in Proposition 5.1.2 that there is a bijection
$T\subset G$
be a maximal torus. We have seen in Proposition 5.1.2 that there is a bijection
![]() $\lambda \mapsto L_{\lambda }$
between
$\lambda \mapsto L_{\lambda }$
between
![]() $X_*(T)$
and the set of T-fixed points of
$X_*(T)$
and the set of T-fixed points of
![]() $\operatorname {\mathrm {Gr}}_{G}$
. Given
$\operatorname {\mathrm {Gr}}_{G}$
. Given
![]() $\lambda \in X_*(T)$
, we let
$\lambda \in X_*(T)$
, we let
![]() $\mathcal {E}[\lambda ]$
be the modification of
$\mathcal {E}[\lambda ]$
be the modification of
![]() $\mathcal {E}$
corresponding to
$\mathcal {E}$
corresponding to
![]() $L_{\lambda }$
.
$L_{\lambda }$
.
Lemma 6.2.1 [Reference Caraiani and ScholzeCS17, Lemma 3.5.5], see also [Reference Chen, Fargues and ShenCFS21, §2.2], but note that we use the opposite convention concerning Schubert cells
Let
![]() $\mathcal {E}$
be a G-bundle on
$\mathcal {E}$
be a G-bundle on
![]() $X_{C}$
equipped with a trivialization at
$X_{C}$
equipped with a trivialization at
![]() $\infty $
, let
$\infty $
, let
![]() $T\subset G$
be a maximal torus, let
$T\subset G$
be a maximal torus, let
![]() $\lambda \in X_*(T)$
be a cocharacter and let
$\lambda \in X_*(T)$
be a cocharacter and let
![]() $\widehat {\lambda }\in X^*(\widehat {T})$
be the corresponding character. In the group
$\widehat {\lambda }\in X^*(\widehat {T})$
be the corresponding character. In the group
![]() $X^*(Z(\widehat {G})^{\Gamma })$
, we have
$X^*(Z(\widehat {G})^{\Gamma })$
, we have
Proposition 6.2.2. Suppose a pair
![]() $(g,g')\in G(F)_{\operatorname {\mathrm {sr}}}\times G_b(F)_{\operatorname {\mathrm {sr}}}$
fixes a point
$(g,g')\in G(F)_{\operatorname {\mathrm {sr}}}\times G_b(F)_{\operatorname {\mathrm {sr}}}$
fixes a point
![]() $x\in \operatorname {\mathrm {Sht}}_{G,b, \mu }(C)$
. Let
$x\in \operatorname {\mathrm {Sht}}_{G,b, \mu }(C)$
. Let
![]() $T=\operatorname {\mathrm {Cent}}(g,G)$
and
$T=\operatorname {\mathrm {Cent}}(g,G)$
and
![]() $T'=\operatorname {\mathrm {Cent}}(g',G_b)$
. Then
$T'=\operatorname {\mathrm {Cent}}(g',G_b)$
. Then
![]() $\pi _1(x)\in \operatorname {\mathrm {Gr}}_{G,\leq -\mu }^{g'}$
and
$\pi _1(x)\in \operatorname {\mathrm {Gr}}_{G,\leq -\mu }^{g'}$
and
![]() $\pi _2(x)\in \operatorname {\mathrm {Gr}}_{G,\leq \mu }^g$
correspond to cocharacters
$\pi _2(x)\in \operatorname {\mathrm {Gr}}_{G,\leq \mu }^g$
correspond to cocharacters
![]() $\lambda '\in X_*(T')_{\leq -\mu }$
and
$\lambda '\in X_*(T')_{\leq -\mu }$
and
![]() $\lambda \in X_*(T)_{\leq \mu }$
, respectively.
$\lambda \in X_*(T)_{\leq \mu }$
, respectively.
There exists
![]() $y\in G(\breve {F})$
such that
$y\in G(\breve {F})$
such that
![]() $\operatorname {\mathrm {ad}} y$
is an F-rational isomorphism
$\operatorname {\mathrm {ad}} y$
is an F-rational isomorphism
![]() $T\to T'$
, which carries g to
$T\to T'$
, which carries g to
![]() $g'$
and
$g'$
and
![]() $\lambda $
onto
$\lambda $
onto
![]() $-\lambda '$
. The invariant
$-\lambda '$
. The invariant
![]() $\operatorname {\mathrm {inv}}[b](g,g')\in B(T)\cong X_*(T)_{\Gamma }$
agrees with the image of
$\operatorname {\mathrm {inv}}[b](g,g')\in B(T)\cong X_*(T)_{\Gamma }$
agrees with the image of
![]() $\lambda $
under
$\lambda $
under
![]() $X_*(T)\to X_*(T)_{\Gamma }$
. Therefore,
$X_*(T)\to X_*(T)_{\Gamma }$
. Therefore,
![]() $(g,g',\lambda )$
lies in
$(g,g',\lambda )$
lies in
![]() $\operatorname {\mathrm {Rel}}_{b,\mu }$
.
$\operatorname {\mathrm {Rel}}_{b,\mu }$
.
Proof. The point x corresponds to an isomorphism
![]() $\gamma \colon \mathcal {E}^1[\lambda ]\to \mathcal {E}^b$
and also to an isomorphism
$\gamma \colon \mathcal {E}^1[\lambda ]\to \mathcal {E}^b$
and also to an isomorphism
![]() $\gamma '\colon \mathcal {E}^1\to \mathcal {E}^b[\lambda ']$
. Each of these interlaces the action of g with
$\gamma '\colon \mathcal {E}^1\to \mathcal {E}^b[\lambda ']$
. Each of these interlaces the action of g with
![]() $g'$
and furthermore
$g'$
and furthermore
![]() $\gamma =\gamma '$
away from
$\gamma =\gamma '$
away from
![]() $\infty $
. Trivializing
$\infty $
. Trivializing
![]() $\mathcal {E}^1$
and
$\mathcal {E}^1$
and
![]() $\mathcal {E}^b$
away from
$\mathcal {E}^b$
away from
![]() $\infty $
, we see that g and
$\infty $
, we see that g and
![]() $g'$
become conjugate over the ring
$g'$
become conjugate over the ring
![]() $B_e=H^0(X_C\backslash \left \{ \infty \right \},\mathcal {O}_{X_C})$
, which implies they are conjugate over
$B_e=H^0(X_C\backslash \left \{ \infty \right \},\mathcal {O}_{X_C})$
, which implies they are conjugate over
![]() $\overline {F}$
and (by Lemma 3.2.1) they are even conjugate over
$\overline {F}$
and (by Lemma 3.2.1) they are even conjugate over
![]() $\breve {F}$
. Let
$\breve {F}$
. Let
![]() $y\in G(\breve {F})$
be an element such that
$y\in G(\breve {F})$
be an element such that
![]() $(\operatorname {\mathrm {ad}} y)(g) = g'$
. Then
$(\operatorname {\mathrm {ad}} y)(g) = g'$
. Then
![]() $\operatorname {\mathrm {ad}} y$
is a
$\operatorname {\mathrm {ad}} y$
is a
![]() $\breve {F}$
-rational isomorphism
$\breve {F}$
-rational isomorphism
![]() $T\to T'$
which carries g onto
$T\to T'$
which carries g onto
![]() $g'$
. In fact, since there is only one such isomorphism, we can conclude that
$g'$
. In fact, since there is only one such isomorphism, we can conclude that
![]() $\operatorname {\mathrm {ad}} y$
is an F-rational isomorphism
$\operatorname {\mathrm {ad}} y$
is an F-rational isomorphism
![]() $T\to T'$
. Let
$T\to T'$
. Let
![]() $\lambda _0=(\operatorname {\mathrm {ad}} y^{-1})(\lambda ')\in X_*(T)$
.
$\lambda _0=(\operatorname {\mathrm {ad}} y^{-1})(\lambda ')\in X_*(T)$
.
Let
![]() $b_0=y^{-1}by^{\sigma }$
. Then (cf. Definition 3.2.2) we have
$b_0=y^{-1}by^{\sigma }$
. Then (cf. Definition 3.2.2) we have
![]() $b_0\in T(F)$
. The element y induces isomorphisms
$b_0\in T(F)$
. The element y induces isomorphisms
![]() $y\colon \mathcal {E}^{b_0}\to \mathcal {E}^b$
and
$y\colon \mathcal {E}^{b_0}\to \mathcal {E}^b$
and
![]() $y\colon \mathcal {E}^{b_0}[\lambda _0]\to \mathcal {E}^b[\lambda ']$
. Then the isomorphism
$y\colon \mathcal {E}^{b_0}[\lambda _0]\to \mathcal {E}^b[\lambda ']$
. Then the isomorphism
![]() $y^{-1}\gamma '\colon \mathcal {E}^1\to \mathcal {E}^{b_0}[\lambda _0]$
descends to an isomorphism of T-bundles; comparing this with the isomorphism
$y^{-1}\gamma '\colon \mathcal {E}^1\to \mathcal {E}^{b_0}[\lambda _0]$
descends to an isomorphism of T-bundles; comparing this with the isomorphism
![]() $\gamma y^{-1}\colon \mathcal {E}^1[\lambda ]\to \mathcal {E}^{b_0}$
shows that
$\gamma y^{-1}\colon \mathcal {E}^1[\lambda ]\to \mathcal {E}^{b_0}$
shows that
![]() $\lambda _0=-\lambda $
. In light of the isomorphism of T-bundles
$\lambda _0=-\lambda $
. In light of the isomorphism of T-bundles
![]() $\mathcal {E}^1[\lambda ]\cong \mathcal {E}^{b_0}$
, Lemma 6.2.1 implies that the identity
$\mathcal {E}^1[\lambda ]\cong \mathcal {E}^{b_0}$
, Lemma 6.2.1 implies that the identity
![]() $\kappa (\mathcal {E}^{b_0})=\lambda $
holds in
$\kappa (\mathcal {E}^{b_0})=\lambda $
holds in
![]() $B(T)$
. But also
$B(T)$
. But also
![]() $\kappa (\mathcal {E}^{b_0})$
is the class of
$\kappa (\mathcal {E}^{b_0})$
is the class of
![]() $[b_0]$
in
$[b_0]$
in
![]() $B(T)$
, which is
$B(T)$
, which is
![]() $\operatorname {\mathrm {inv}}[b](g,g')$
by definition.
$\operatorname {\mathrm {inv}}[b](g,g')$
by definition.
Proposition 6.2.2 shows that if
![]() $(g,g')\in G(F)_{\operatorname {\mathrm {sr}}}\times G_b(F)_{\operatorname {\mathrm {sr}}}$
fixes a point of
$(g,g')\in G(F)_{\operatorname {\mathrm {sr}}}\times G_b(F)_{\operatorname {\mathrm {sr}}}$
fixes a point of
![]() $\operatorname {\mathrm {Sht}}_{G,b,\mu }$
, then g and
$\operatorname {\mathrm {Sht}}_{G,b,\mu }$
, then g and
![]() $g'$
are related. However the converse may fail: If a pair of related strongly regular elements
$g'$
are related. However the converse may fail: If a pair of related strongly regular elements
![]() $(g,g')$
is given, it is not necessarily true that
$(g,g')$
is given, it is not necessarily true that
![]() $(g,g')$
fixes a point of
$(g,g')$
fixes a point of
![]() $\operatorname {\mathrm {Sht}}_{G,b, \mu }$
. Indeed, a necessary condition for this is that the action of
$\operatorname {\mathrm {Sht}}_{G,b, \mu }$
. Indeed, a necessary condition for this is that the action of
![]() $g'$
on
$g'$
on
![]() $\operatorname {\mathrm {Gr}}_{G,\leq -\mu }^b$
has a fixed point in the admissible locus, and this is not automatic.
$\operatorname {\mathrm {Gr}}_{G,\leq -\mu }^b$
has a fixed point in the admissible locus, and this is not automatic.
This converse result is always true, however, if g (or equivalently,
![]() $g'$
) is an elliptic element.
$g'$
) is an elliptic element.
Theorem 6.2.3. Let
![]() $g\in G(F)_{\operatorname {\mathrm {ell}}}$
. Then the fixed points of g acting on
$g\in G(F)_{\operatorname {\mathrm {ell}}}$
. Then the fixed points of g acting on
![]() $\operatorname {\mathrm {Gr}}_{G,\leq \mu }^1$
lie in the admissible locus
$\operatorname {\mathrm {Gr}}_{G,\leq \mu }^1$
lie in the admissible locus
![]() $\operatorname {\mathrm {Gr}}_{G,\leq \mu }^{1,\operatorname {\mathrm {adm}}}$
. Similarly, if
$\operatorname {\mathrm {Gr}}_{G,\leq \mu }^{1,\operatorname {\mathrm {adm}}}$
. Similarly, if
![]() $g'\in G_b(F)_{\operatorname {\mathrm {ell}}}$
, then the fixed points of
$g'\in G_b(F)_{\operatorname {\mathrm {ell}}}$
, then the fixed points of
![]() $g'$
acting on
$g'$
acting on
![]() $\operatorname {\mathrm {Gr}}_{G,\leq -\mu }^b$
lie in the admissible locus
$\operatorname {\mathrm {Gr}}_{G,\leq -\mu }^b$
lie in the admissible locus
![]() $\operatorname {\mathrm {Gr}}_{G,\leq -\mu }^{b,\operatorname {\mathrm {adm}}}$
.
$\operatorname {\mathrm {Gr}}_{G,\leq -\mu }^{b,\operatorname {\mathrm {adm}}}$
.
Proof. We prove the first statement; the second is similar. Let
![]() $g\in G(F)_{\operatorname {\mathrm {ell}}}$
, and let
$g\in G(F)_{\operatorname {\mathrm {ell}}}$
, and let
![]() $T=\operatorname {\mathrm {Cent}}(g,G)$
be the elliptic maximal torus containing g. Suppose we are given a g-fixed point
$T=\operatorname {\mathrm {Cent}}(g,G)$
be the elliptic maximal torus containing g. Suppose we are given a g-fixed point
![]() $x\in \operatorname {\mathrm {Gr}}_{G,\leq \mu }(C)$
. Then x corresponds to a cocharacter
$x\in \operatorname {\mathrm {Gr}}_{G,\leq \mu }(C)$
. Then x corresponds to a cocharacter
![]() $\lambda \in X_*(T)$
, which in turn corresponds to a modification
$\lambda \in X_*(T)$
, which in turn corresponds to a modification
![]() $\mathcal {E}^1[\lambda ]$
of the trivial G-bundle
$\mathcal {E}^1[\lambda ]$
of the trivial G-bundle
![]() $\mathcal {E}^1$
. We wish to show that
$\mathcal {E}^1$
. We wish to show that
![]() $\mathcal {E}^1[\lambda ]\cong \mathcal {E}^b$
. First, we will show that it is semistable.
$\mathcal {E}^1[\lambda ]\cong \mathcal {E}^b$
. First, we will show that it is semistable.
Let
![]() $b'\in G(\breve {F})$
be an element whose class in
$b'\in G(\breve {F})$
be an element whose class in
![]() $B(G)$
corresponds to the isomorphism class of
$B(G)$
corresponds to the isomorphism class of
![]() $\mathcal {E}^1[\lambda ]$
. We wish to show that
$\mathcal {E}^1[\lambda ]$
. We wish to show that
![]() $b'$
is basic. We have the algebraic group
$b'$
is basic. We have the algebraic group
![]() $G_{b'}/F$
, which is a priori an inner form of a Levi subgroup
$G_{b'}/F$
, which is a priori an inner form of a Levi subgroup
![]() $M^*$
of
$M^*$
of
![]() $G^*$
, where
$G^*$
, where
![]() $G^*$
is the quasi-split inner form of G. Showing that
$G^*$
is the quasi-split inner form of G. Showing that
![]() $b'$
is basic is equivalent to showing that
$b'$
is basic is equivalent to showing that
![]() $M^*=G^*$
.
$M^*=G^*$
.
We have an isomorphism
![]() $\gamma \colon \mathcal {E}^1[\lambda ]\cong \mathcal {E}^{b'}$
. The action of
$\gamma \colon \mathcal {E}^1[\lambda ]\cong \mathcal {E}^{b'}$
. The action of
![]() $g\in T(F)$
on
$g\in T(F)$
on
![]() $\mathcal {E}^1$
extends to an action on
$\mathcal {E}^1$
extends to an action on
![]() $\mathcal {E}^1[\lambda ]$
, which can be transported via
$\mathcal {E}^1[\lambda ]$
, which can be transported via
![]() $\gamma $
to obtain an automorphism
$\gamma $
to obtain an automorphism
![]() $g'\in \widetilde {G}_{b'}(C)=\operatorname {\mathrm {Aut}} \mathcal {E}_{b'}$
. Let
$g'\in \widetilde {G}_{b'}(C)=\operatorname {\mathrm {Aut}} \mathcal {E}_{b'}$
. Let
![]() $\overline {g}'$
be the image of
$\overline {g}'$
be the image of
![]() $g'$
under the projection
$g'$
under the projection
![]() $\widetilde {G}_{b'}(C)\to G_{b'}(F)$
.
$\widetilde {G}_{b'}(C)\to G_{b'}(F)$
.
The G-bundles
![]() $\mathcal {E}^1$
and
$\mathcal {E}^1$
and
![]() $\mathcal {E}^{b'}$
may be trivialized over
$\mathcal {E}^{b'}$
may be trivialized over
![]() $\operatorname {\mathrm {Spec}} B_{\operatorname {\mathrm {dR}}}^+(C)$
. In doing so, we obtain embeddings of
$\operatorname {\mathrm {Spec}} B_{\operatorname {\mathrm {dR}}}^+(C)$
. In doing so, we obtain embeddings of
![]() $G(F)=\operatorname {\mathrm {Aut}} \mathcal {E}^1$
and
$G(F)=\operatorname {\mathrm {Aut}} \mathcal {E}^1$
and
![]() $\widetilde {G}_{b'}(C)=\operatorname {\mathrm {Aut}} \mathcal {E}^{b'}$
into
$\widetilde {G}_{b'}(C)=\operatorname {\mathrm {Aut}} \mathcal {E}^{b'}$
into
![]() $G(B_{\operatorname {\mathrm {dR}}}^+(C))$
; we denote both of these by
$G(B_{\operatorname {\mathrm {dR}}}^+(C))$
; we denote both of these by
![]() $h\mapsto h_{\infty }$
. We also have the isomorphism
$h\mapsto h_{\infty }$
. We also have the isomorphism
![]() $\gamma _{\infty }$
between
$\gamma _{\infty }$
between
![]() $\mathcal {E}^1$
and
$\mathcal {E}^1$
and
![]() $\mathcal {E}^{b'}$
over
$\mathcal {E}^{b'}$
over
![]() $\operatorname {\mathrm {Spec}} B_{\operatorname {\mathrm {dR}}}(C)$
; we may identify
$\operatorname {\mathrm {Spec}} B_{\operatorname {\mathrm {dR}}}(C)$
; we may identify
![]() $\gamma _{\infty }$
with an element of
$\gamma _{\infty }$
with an element of
![]() $G(B_{\operatorname {\mathrm {dR}}}(C))$
, and then
$G(B_{\operatorname {\mathrm {dR}}}(C))$
, and then
![]() $g^{\prime }_{\infty } =\gamma _{\infty } g_{\infty } \gamma _{\infty }^{-1}$
holds in
$g^{\prime }_{\infty } =\gamma _{\infty } g_{\infty } \gamma _{\infty }^{-1}$
holds in
![]() $G(B_{\operatorname {\mathrm {dR}}}(C))$
.
$G(B_{\operatorname {\mathrm {dR}}}(C))$
.
The element
![]() $\bar g^{\prime }_{\infty }$
is conjugate to
$\bar g^{\prime }_{\infty }$
is conjugate to
![]() $g^{\prime }_{\infty }$
, so
$g^{\prime }_{\infty }$
, so
![]() $\bar g^{\prime }_{\infty }$
is conjugate to
$\bar g^{\prime }_{\infty }$
is conjugate to
![]() $g_{\infty }$
in
$g_{\infty }$
in
![]() $G(B_{\operatorname {\mathrm {dR}}})$
. Since g and
$G(B_{\operatorname {\mathrm {dR}}})$
. Since g and
![]() $\overline {g}'$
are both regular semisimple
$\overline {g}'$
are both regular semisimple
![]() $\bar F$
-points of G, being conjugate in
$\bar F$
-points of G, being conjugate in
![]() $G(B_{\operatorname {\mathrm {dR}}})$
is the same as being conjugate in
$G(B_{\operatorname {\mathrm {dR}}})$
is the same as being conjugate in
![]() $G(\bar F)$
. Their centralizers, being F-rational tori, are thus isomorphic over F. Thus,
$G(\bar F)$
. Their centralizers, being F-rational tori, are thus isomorphic over F. Thus,
![]() $G_{b'}$
contains a maximal torus that is elliptic for G. Elliptic maximal tori transfer across inner forms [Reference KottwitzKot86, §10], which means that the Levi subgroup
$G_{b'}$
contains a maximal torus that is elliptic for G. Elliptic maximal tori transfer across inner forms [Reference KottwitzKot86, §10], which means that the Levi subgroup
![]() $M^* \subset G^*$
of which
$M^* \subset G^*$
of which
![]() $G_{b'}$
is an inner form contains a maximal torus that is elliptic for
$G_{b'}$
is an inner form contains a maximal torus that is elliptic for
![]() $G^*$
. Therefore,
$G^*$
. Therefore,
![]() $M^*=G^*$
.
$M^*=G^*$
.
We have shown that
![]() $\mathcal {E}^1[\lambda ]\cong \mathcal {E}_{b'}$
is semistable, implying that
$\mathcal {E}^1[\lambda ]\cong \mathcal {E}_{b'}$
is semistable, implying that
![]() $\operatorname {\mathrm {Aut}} \mathcal {E}^{b'}=G_{b'}(F)$
and that
$\operatorname {\mathrm {Aut}} \mathcal {E}^{b'}=G_{b'}(F)$
and that
![]() $g'\in G_{b'}(F)$
. Lemma 6.2.1 shows that
$g'\in G_{b'}(F)$
. Lemma 6.2.1 shows that
![]() $\kappa ([b'])$
equals the image of
$\kappa ([b'])$
equals the image of
![]() $\lambda $
in
$\lambda $
in
![]() $\pi _1(G)_{\Gamma }$
; this is the same as the image of
$\pi _1(G)_{\Gamma }$
; this is the same as the image of
![]() $\mu $
, which in turn is the same as
$\mu $
, which in turn is the same as
![]() $\kappa ([b])$
because
$\kappa ([b])$
because
![]() $b\in B(G,\mu )$
. Since
$b\in B(G,\mu )$
. Since
![]() $b'$
is basic, we have
$b'$
is basic, we have
![]() $[b']=[b]$
by [Reference KottwitzKot85, Proposition 5.6].
$[b']=[b]$
by [Reference KottwitzKot85, Proposition 5.6].
Recall the locally profinite set
![]() $\operatorname {\mathrm {Rel}}_{b,\leq \mu }$
from Definition 3.2.4. This is the set of conjugacy classes of triples
$\operatorname {\mathrm {Rel}}_{b,\leq \mu }$
from Definition 3.2.4. This is the set of conjugacy classes of triples
![]() $(g,g',\lambda )$
, where
$(g,g',\lambda )$
, where
![]() $g\in G(F)$
and
$g\in G(F)$
and
![]() $g'\in G_b(F)$
are related strongly regular elements, and
$g'\in G_b(F)$
are related strongly regular elements, and
![]() $\lambda $
is a cocharacter of
$\lambda $
is a cocharacter of
![]() $T=\operatorname {\mathrm {Cent}}(g,G)$
, bounded by
$T=\operatorname {\mathrm {Cent}}(g,G)$
, bounded by
![]() $\mu $
such that
$\mu $
such that
![]() $\kappa (\operatorname {\mathrm {inv}}[b](g,g'))$
agrees with the image of
$\kappa (\operatorname {\mathrm {inv}}[b](g,g'))$
agrees with the image of
![]() $\lambda $
in
$\lambda $
in
![]() $X_*(T)_{\Gamma }$
. Let
$X_*(T)_{\Gamma }$
. Let
![]() $\operatorname {\mathrm {Rel}}_{b,\leq \mu ,\operatorname {\mathrm {ell}}}$
be the subset, where g (equivalently,
$\operatorname {\mathrm {Rel}}_{b,\leq \mu ,\operatorname {\mathrm {ell}}}$
be the subset, where g (equivalently,
![]() $g'$
) is elliptic.
$g'$
) is elliptic.
Theorem 6.2.3 has the following corollary. For a v-stack X, we write
![]() $\left \lvert X \right \rvert $
for the underlying topological space.
$\left \lvert X \right \rvert $
for the underlying topological space.
Corollary 6.2.4. Let
![]() $\operatorname {\mathrm {In}}_S(\operatorname {\mathrm {Hecke}}^{b,\ast }_{G,\leq \mu ,S})_{\operatorname {\mathrm {ell}}}$
be the preimage under
$\operatorname {\mathrm {In}}_S(\operatorname {\mathrm {Hecke}}^{b,\ast }_{G,\leq \mu ,S})_{\operatorname {\mathrm {ell}}}$
be the preimage under
![]() $\operatorname {\mathrm {In}}_S(h_1)$
of
$\operatorname {\mathrm {In}}_S(h_1)$
of
![]() $\operatorname {\mathrm {In}}_S(\operatorname {\mathrm {Bun}}^b_{G,S})_{\operatorname {\mathrm {ell}}}$
. Similarly let
$\operatorname {\mathrm {In}}_S(\operatorname {\mathrm {Bun}}^b_{G,S})_{\operatorname {\mathrm {ell}}}$
. Similarly let
![]() $\operatorname {\mathrm {In}}_S(\operatorname {\mathrm {Hecke}}^{\ast ,1}_{G,\leq \mu ,S})_{\operatorname {\mathrm {ell}}}$
be the preimage under
$\operatorname {\mathrm {In}}_S(\operatorname {\mathrm {Hecke}}^{\ast ,1}_{G,\leq \mu ,S})_{\operatorname {\mathrm {ell}}}$
be the preimage under
![]() $\operatorname {\mathrm {In}}_S(h_2)$
of
$\operatorname {\mathrm {In}}_S(h_2)$
of
![]() $\operatorname {\mathrm {In}}_S(\operatorname {\mathrm {Bun}}^1_{G,S})_{\operatorname {\mathrm {ell}}}$
. Then
$\operatorname {\mathrm {In}}_S(\operatorname {\mathrm {Bun}}^1_{G,S})_{\operatorname {\mathrm {ell}}}$
. Then
There is a homeomorphism
![]() $\left \lvert \operatorname {\mathrm {In}}_S(\operatorname {\mathrm {Hecke}}_{G,b,\leq \mu ,S}^{b,1})_{\operatorname {\mathrm {ell}}} \right \rvert \cong \operatorname {\mathrm {Rel}}_{b,\mu ,\operatorname {\mathrm {ell}}}$
.
$\left \lvert \operatorname {\mathrm {In}}_S(\operatorname {\mathrm {Hecke}}_{G,b,\leq \mu ,S}^{b,1})_{\operatorname {\mathrm {ell}}} \right \rvert \cong \operatorname {\mathrm {Rel}}_{b,\mu ,\operatorname {\mathrm {ell}}}$
.
Proof. The first claim is just the statement that fixed points of elliptic elements on
![]() $\operatorname {\mathrm {Gr}}^b_G$
and
$\operatorname {\mathrm {Gr}}^b_G$
and
![]() $\operatorname {\mathrm {Gr}}^1_G$
are admissible. For the second claim: Since
$\operatorname {\mathrm {Gr}}^1_G$
are admissible. For the second claim: Since
![]() $\operatorname {\mathrm {Hecke}}^{\ast ,1}_{G,\leq \mu ,S} \cong [\operatorname {\mathrm {Gr}}_{G,\leq \mu ,S}/G(F)_S]$
, we can think of
$\operatorname {\mathrm {Hecke}}^{\ast ,1}_{G,\leq \mu ,S} \cong [\operatorname {\mathrm {Gr}}_{G,\leq \mu ,S}/G(F)_S]$
, we can think of
![]() $\left \lvert \operatorname {\mathrm {In}}_S(\operatorname {\mathrm {Hecke}}_{G,b,\leq \mu }^{b,1})_{\operatorname {\mathrm {ell}}} \right \rvert $
as the set of conjugacy classes of pairs
$\left \lvert \operatorname {\mathrm {In}}_S(\operatorname {\mathrm {Hecke}}_{G,b,\leq \mu }^{b,1})_{\operatorname {\mathrm {ell}}} \right \rvert $
as the set of conjugacy classes of pairs
![]() $(g,\lambda )$
, where
$(g,\lambda )$
, where
![]() $g\in G(F)_{\operatorname {\mathrm {ell}}}$
and
$g\in G(F)_{\operatorname {\mathrm {ell}}}$
and
![]() $\lambda \in X_*(T)_{\leq \mu }$
, where
$\lambda \in X_*(T)_{\leq \mu }$
, where
![]() $T=\operatorname {\mathrm {Cent}}(g,G)$
. We have an isomorphism
$T=\operatorname {\mathrm {Cent}}(g,G)$
. We have an isomorphism
![]() $\mathcal {E}^1[\lambda ]\cong \mathcal {E}^b$
. The element
$\mathcal {E}^1[\lambda ]\cong \mathcal {E}^b$
. The element
![]() $g\in G(F)\cong \operatorname {\mathrm {Aut}} \mathcal {E}^1$
determines an element
$g\in G(F)\cong \operatorname {\mathrm {Aut}} \mathcal {E}^1$
determines an element
![]() $g'\in G_b(F)\cong \operatorname {\mathrm {Aut}}\mathcal {E}^b$
, up to conjugacy. By Proposition 6.2.2, the triple
$g'\in G_b(F)\cong \operatorname {\mathrm {Aut}}\mathcal {E}^b$
, up to conjugacy. By Proposition 6.2.2, the triple
![]() $(g,g',\lambda )$
determines an element of
$(g,g',\lambda )$
determines an element of
![]() $\operatorname {\mathrm {Rel}}_{b,\mu ,\operatorname {\mathrm {ell}}}$
. Conversely, given such a triple
$\operatorname {\mathrm {Rel}}_{b,\mu ,\operatorname {\mathrm {ell}}}$
. Conversely, given such a triple
![]() $(g,g',\lambda )$
, the pair
$(g,g',\lambda )$
, the pair
![]() $(g,\lambda )$
determines an element
$(g,\lambda )$
determines an element
![]() $g''\in G_b(F)$
as we have just argued, but then
$g''\in G_b(F)$
as we have just argued, but then
![]() $g'$
and
$g'$
and
![]() $g''$
are conjugate by Remark 3.2.5.
$g''$
are conjugate by Remark 3.2.5.
6.3 Transfer of distributions from
 $G_b$
to G
$G_b$
to G
We continue to let b be a basic element of
![]() $B(G)$
. Let
$B(G)$
. Let
![]() $\Lambda $
be a ring in which p is invertible. Recall the Hecke transfer map
$\Lambda $
be a ring in which p is invertible. Recall the Hecke transfer map
from 3.2.7. As promised, we can now promote this to a transfer of distributions, at least after restriction to elliptic loci (and assuming, as we have been doing all along, that the
![]() $\Lambda $
-valued Haar measures on
$\Lambda $
-valued Haar measures on
![]() $G(F)$
and
$G(F)$
and
![]() $G_b(F)$
are chosen compatibly).
$G_b(F)$
are chosen compatibly).
Recall the period morphisms:
in which
![]() $\pi _1$
is a
$\pi _1$
is a
![]() $G(F)_S$
-torsor over its image, and
$G(F)_S$
-torsor over its image, and
![]() $\pi _2$
is a
$\pi _2$
is a
![]() $G_b(F)_S$
-torsor over its image. Consider the action map on
$G_b(F)_S$
-torsor over its image. Consider the action map on
![]() $\operatorname {\mathrm {Sht}}_{G,b,\mu ,C}$
:
$\operatorname {\mathrm {Sht}}_{G,b,\mu ,C}$
:
and also those on the period domains:
 $$ \begin{align*} \alpha_1\colon G(F)_S\times \operatorname{\mathrm{Gr}}^1_{G,\leq\mu,C} &\to \operatorname{\mathrm{Gr}}^1_{G,\leq\mu,C} \\ \alpha_b\colon G_b(F)_S\times \operatorname{\mathrm{Gr}}^b_{G,\leq\mu,C} &\to \operatorname{\mathrm{Gr}}^b_{G,\leq\mu,C}. \end{align*} $$
$$ \begin{align*} \alpha_1\colon G(F)_S\times \operatorname{\mathrm{Gr}}^1_{G,\leq\mu,C} &\to \operatorname{\mathrm{Gr}}^1_{G,\leq\mu,C} \\ \alpha_b\colon G_b(F)_S\times \operatorname{\mathrm{Gr}}^b_{G,\leq\mu,C} &\to \operatorname{\mathrm{Gr}}^b_{G,\leq\mu,C}. \end{align*} $$
For
![]() $?\in \left \{ \operatorname {\mathrm {Sht}},1,b \right \}$
we can define the elliptic fixed-point locus
$?\in \left \{ \operatorname {\mathrm {Sht}},1,b \right \}$
we can define the elliptic fixed-point locus
![]() $\operatorname {\mathrm {Fix}}(\alpha _?)_{\operatorname {\mathrm {ell}}}$
of the corresponding action map, consisting of pairs
$\operatorname {\mathrm {Fix}}(\alpha _?)_{\operatorname {\mathrm {ell}}}$
of the corresponding action map, consisting of pairs
![]() $(g,x)$
with g elliptic and
$(g,x)$
with g elliptic and
![]() $g.x=x$
; let us think of each
$g.x=x$
; let us think of each
![]() $\operatorname {\mathrm {Fix}}(\alpha _?)$
as a locally profinite set. For instance,
$\operatorname {\mathrm {Fix}}(\alpha _?)$
as a locally profinite set. For instance,
![]() $\operatorname {\mathrm {Fix}}(\alpha _1)_{\operatorname {\mathrm {ell}}}$
is the set of pairs
$\operatorname {\mathrm {Fix}}(\alpha _1)_{\operatorname {\mathrm {ell}}}$
is the set of pairs
![]() $(g,\lambda )$
, where
$(g,\lambda )$
, where
![]() $g\in G(F)_{\operatorname {\mathrm {ell}}}$
, and
$g\in G(F)_{\operatorname {\mathrm {ell}}}$
, and
![]() $\lambda \in X_*(T_g)$
(
$\lambda \in X_*(T_g)$
(
![]() $T_g=\operatorname {\mathrm {Cent}}(g,G)$
) is bounded by
$T_g=\operatorname {\mathrm {Cent}}(g,G)$
) is bounded by
![]() $\mu $
. These fit into a diagram
$\mu $
. These fit into a diagram

of locally profinite sets, in which
![]() $p_1$
is a
$p_1$
is a
![]() $G_b(F)$
-equivariant
$G_b(F)$
-equivariant
![]() $G(F)$
-torsor,
$G(F)$
-torsor,
![]() $p_2$
is a
$p_2$
is a
![]() $G(F)$
-equivariant
$G(F)$
-equivariant
![]() $G_b(F)$
-torsor and
$G_b(F)$
-torsor and
![]() $q_1$
and
$q_1$
and
![]() $q_2$
are finite étale. (The maps
$q_2$
are finite étale. (The maps
![]() $p_i$
are surjective by Theorem 6.2.3.) Furthermore, let us observe that, for
$p_i$
are surjective by Theorem 6.2.3.) Furthermore, let us observe that, for
![]() $(g,g',x)\in \operatorname {\mathrm {Fix}}(\alpha _{\operatorname {\mathrm {Sht}}})$
, the image of x in
$(g,g',x)\in \operatorname {\mathrm {Fix}}(\alpha _{\operatorname {\mathrm {Sht}}})$
, the image of x in
![]() $\operatorname {\mathrm {Gr}}_G^1(C)^g$
may be identified with a cocharacter
$\operatorname {\mathrm {Gr}}_G^1(C)^g$
may be identified with a cocharacter
![]() $\lambda \in X_*(T)$
of
$\lambda \in X_*(T)$
of
![]() $T=\operatorname {\mathrm {Cent}}(g,G)$
, and then the triple
$T=\operatorname {\mathrm {Cent}}(g,G)$
, and then the triple
![]() $(g,g',\lambda )$
lies in
$(g,g',\lambda )$
lies in
![]() $\operatorname {\mathrm {Rel}}_{b,\mu }$
by Proposition 6.2.2. A key observation is that we have a diagram of stacks in locally profinite sets, in which both squares are Cartesian:
$\operatorname {\mathrm {Rel}}_{b,\mu }$
by Proposition 6.2.2. A key observation is that we have a diagram of stacks in locally profinite sets, in which both squares are Cartesian:

Thus, at least over the elliptic locus, we have promoted a correspondence between sets of conjugacy classes to a correspondence between stacks of conjugacy classes. Formally, this is exactly what is required to promote our transfer of functions to a transfer of distributions.
Lemma 6.3.1. Let H be a locally pro-p group, and let
![]() $\Lambda $
be a commutative ring in which p is invertible. Choose a
$\Lambda $
be a commutative ring in which p is invertible. Choose a
![]() $\Lambda $
-valued Haar measure on H. Let
$\Lambda $
-valued Haar measure on H. Let
![]() $h\colon \widetilde {T}\to T$
be an H-torsor in locally profinite sets. The integration-along-fibers map
$h\colon \widetilde {T}\to T$
be an H-torsor in locally profinite sets. The integration-along-fibers map
![]() $C_c(\widetilde {T},\Lambda ) \to C_c(T,\Lambda )$
induces an isomorphism of
$C_c(\widetilde {T},\Lambda ) \to C_c(T,\Lambda )$
induces an isomorphism of
![]() $C(T,\Lambda )$
-modules
$C(T,\Lambda )$
-modules
and, dually, an isomorphism of
![]() $C(T,\Lambda )$
-modules
$C(T,\Lambda )$
-modules
Proof. The
![]() $C(T,\Lambda )$
-modules
$C(T,\Lambda )$
-modules
![]() $C_c(T,\Lambda )$
and
$C_c(T,\Lambda )$
and
![]() $C_c(\widetilde T,\Lambda )$
are smooth in the sense of Definition B.2.1. Therefore, by Lemma B.2.5 the statement is local on T, so we may assume that the torsor
$C_c(\widetilde T,\Lambda )$
are smooth in the sense of Definition B.2.1. Therefore, by Lemma B.2.5 the statement is local on T, so we may assume that the torsor
![]() $\widetilde {T}=T\times H$
is split. Then
$\widetilde {T}=T\times H$
is split. Then
![]() $C_c(\widetilde T,\Lambda )_H=C_c(T,\Lambda ) \otimes _{\Lambda } C_c(H,\Lambda )_H$
. The integration map
$C_c(\widetilde T,\Lambda )_H=C_c(T,\Lambda ) \otimes _{\Lambda } C_c(H,\Lambda )_H$
. The integration map
![]() $C_c(H,\Lambda )_H \to \Lambda $
is an isomorphism so that
$C_c(H,\Lambda )_H \to \Lambda $
is an isomorphism so that
![]() $C_c(\widetilde {T},\Lambda )_H\cong C_c(T,\Lambda )$
.
$C_c(\widetilde {T},\Lambda )_H\cong C_c(T,\Lambda )$
.
Recall from §3.4 that we have chosen compatible Haar measures on
![]() $G(F)$
and
$G(F)$
and
![]() $G_b(F)$
.
$G_b(F)$
.
Definition 6.3.2. With notation as in equation (6.3.1), we define a
![]() $\Lambda $
-linear map
$\Lambda $
-linear map
as the composition
 $$ \begin{align*} \begin{array}{lcl} C_c(G(F)_{\operatorname{\mathrm{ell}}},\Lambda)_{G(F)} &\stackrel{q_2^*}{\to} &\!\! C_c(\operatorname{\mathrm{Fix}}(\alpha_1)_{\operatorname{\mathrm{ell}}},\Lambda)_{G(F)} \\[2pt] &\stackrel{(p_2)_*^{-1}}{\stackrel{\cong}{\longrightarrow}} &\!\! C_c(\operatorname{\mathrm{Fix}}(\alpha_{\operatorname{\mathrm{Sht}}})_{\operatorname{\mathrm{ell}}},\Lambda)_{G(F)\times G_b(F)} \\[2pt] &\stackrel{(p_1)_*}{\stackrel{\cong}{\longrightarrow}} &\!\! C_c(\operatorname{\mathrm{Fix}}(\alpha_b)_{\operatorname{\mathrm{ell}}},\Lambda)_{G_b(F)} \\[2pt] &\stackrel{\cdot K_{\mu}}{\to} &\!\! C_c(\operatorname{\mathrm{Fix}}(\alpha_b)_{\operatorname{\mathrm{ell}}},\Lambda)_{G_b(F)} \\[2pt] &\stackrel{q_{1*}}{\to} &\!\! C_c(G_b(F)_{\operatorname{\mathrm{ell}}},\Lambda)_{G_b(F)}, \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{lcl} C_c(G(F)_{\operatorname{\mathrm{ell}}},\Lambda)_{G(F)} &\stackrel{q_2^*}{\to} &\!\! C_c(\operatorname{\mathrm{Fix}}(\alpha_1)_{\operatorname{\mathrm{ell}}},\Lambda)_{G(F)} \\[2pt] &\stackrel{(p_2)_*^{-1}}{\stackrel{\cong}{\longrightarrow}} &\!\! C_c(\operatorname{\mathrm{Fix}}(\alpha_{\operatorname{\mathrm{Sht}}})_{\operatorname{\mathrm{ell}}},\Lambda)_{G(F)\times G_b(F)} \\[2pt] &\stackrel{(p_1)_*}{\stackrel{\cong}{\longrightarrow}} &\!\! C_c(\operatorname{\mathrm{Fix}}(\alpha_b)_{\operatorname{\mathrm{ell}}},\Lambda)_{G_b(F)} \\[2pt] &\stackrel{\cdot K_{\mu}}{\to} &\!\! C_c(\operatorname{\mathrm{Fix}}(\alpha_b)_{\operatorname{\mathrm{ell}}},\Lambda)_{G_b(F)} \\[2pt] &\stackrel{q_{1*}}{\to} &\!\! C_c(G_b(F)_{\operatorname{\mathrm{ell}}},\Lambda)_{G_b(F)}, \end{array} \end{align*} $$
where
![]() $q_2^*$
means pullback,
$q_2^*$
means pullback,
![]() $q_{1*}$
means pushforward (i.e., sum over fibers), the isomorphisms
$q_{1*}$
means pushforward (i.e., sum over fibers), the isomorphisms
![]() $(p_i)_*$
are induced by our choices of Haar measures as in Lemma 6.3.1, and finally
$(p_i)_*$
are induced by our choices of Haar measures as in Lemma 6.3.1, and finally
![]() $K_{\mu }\in C(\operatorname {\mathrm {Fix}}(\alpha _b),\Lambda )^{G_b(F)}$
is the function
$K_{\mu }\in C(\operatorname {\mathrm {Fix}}(\alpha _b),\Lambda )^{G_b(F)}$
is the function
![]() $(g',\lambda ')\mapsto (-1)^d\operatorname {\mathrm {rank}} V_{\mu }^{\vee }[\lambda ']$
, where
$(g',\lambda ')\mapsto (-1)^d\operatorname {\mathrm {rank}} V_{\mu }^{\vee }[\lambda ']$
, where
![]() $d=\left < \mu ,2\rho _G \right>$
.
$d=\left < \mu ,2\rho _G \right>$
.
Proposition 6.3.3. Assume that
![]() $\Lambda = \overline {\mathbf {Q}_{\ell }}$
. Let
$\Lambda = \overline {\mathbf {Q}_{\ell }}$
. Let
![]() $\phi \in C_c(G(F)_{\operatorname {\mathrm {ell}}},\Lambda )$
, and let
$\phi \in C_c(G(F)_{\operatorname {\mathrm {ell}}},\Lambda )$
, and let
![]() $\phi '\in C_c(G_b(F)_{\operatorname {\mathrm {ell}}},\Lambda )$
be any lift of
$\phi '\in C_c(G_b(F)_{\operatorname {\mathrm {ell}}},\Lambda )$
be any lift of
![]() $\widetilde {T}^{G\to G_b}_{b,\mu }\phi $
. Then the orbital integrals of
$\widetilde {T}^{G\to G_b}_{b,\mu }\phi $
. Then the orbital integrals of
![]() $\phi $
and
$\phi $
and
![]() $\phi '$
are related by
$\phi '$
are related by
Proof. For
![]() $g'\in G_b(F)_{\operatorname {\mathrm {ell}}}$
, with centralizer
$g'\in G_b(F)_{\operatorname {\mathrm {ell}}}$
, with centralizer
![]() $T'$
, we have:
$T'$
, we have:
 $$ \begin{align*} &\; \phi^{\prime}_{G_b}(g') \\ =&\int_{h'\in G_b(F)/T'(F)} \phi'(h'g'(h')^{-1})\;dh'\\ =&\; (-1)^d \sum_{\lambda'\in X_*(T')_{\leq -\mu}} \operatorname{\mathrm{rank}} V_{\mu}^{\vee}[\lambda'] \int_{h'\in \frac{G_b(F)}{T'(F)}} [(p_1)_*(p_2)_*^{-1}q_2^*\phi](h'.(g',\lambda')) dh\;dh'. \end{align*} $$
$$ \begin{align*} &\; \phi^{\prime}_{G_b}(g') \\ =&\int_{h'\in G_b(F)/T'(F)} \phi'(h'g'(h')^{-1})\;dh'\\ =&\; (-1)^d \sum_{\lambda'\in X_*(T')_{\leq -\mu}} \operatorname{\mathrm{rank}} V_{\mu}^{\vee}[\lambda'] \int_{h'\in \frac{G_b(F)}{T'(F)}} [(p_1)_*(p_2)_*^{-1}q_2^*\phi](h'.(g',\lambda')) dh\;dh'. \end{align*} $$
Let T be a transfer of the elliptic torus
![]() $T'$
to G. Since
$T'$
to G. Since
![]() $\operatorname {\mathrm {Fix}}(\alpha _{\operatorname {\mathrm {Sht}}})_{\operatorname {\mathrm {ell}}}\to \operatorname {\mathrm {Fix}}(\alpha _b)_{\operatorname {\mathrm {ell}}}$
is a
$\operatorname {\mathrm {Fix}}(\alpha _{\operatorname {\mathrm {Sht}}})_{\operatorname {\mathrm {ell}}}\to \operatorname {\mathrm {Fix}}(\alpha _b)_{\operatorname {\mathrm {ell}}}$
is a
![]() $G(F)$
-torsor, we may choose for each
$G(F)$
-torsor, we may choose for each
![]() $\lambda '$
a lift
$\lambda '$
a lift
![]() $y_{\lambda '}=(g_{\lambda '},g',x_{\lambda '})$
of
$y_{\lambda '}=(g_{\lambda '},g',x_{\lambda '})$
of
![]() $(g',\lambda ')$
to
$(g',\lambda ')$
to
![]() $\operatorname {\mathrm {Fix}}(\alpha _{\operatorname {\mathrm {Sht}}})$
with
$\operatorname {\mathrm {Fix}}(\alpha _{\operatorname {\mathrm {Sht}}})$
with
![]() $g_{\lambda '}\in T(F)$
. Then
$g_{\lambda '}\in T(F)$
. Then
![]() $\phi ^{\prime }_{G_b}(g')$
equals
$\phi ^{\prime }_{G_b}(g')$
equals
 $$\begin{align*}(-1)^d\sum_{\lambda'\in X_*(T')_{\leq -\mu}}\operatorname{\mathrm{rank}} V_{\mu}^{\vee}[\lambda'] \int_{h'\in G_b(F)/T'(F)} \int_{h\in G(F)} [(p_2)_*^{-1}q_2^*\phi] \left((h,h').(y_{\lambda'})\right) \; dh\;dh'. \end{align*}$$
$$\begin{align*}(-1)^d\sum_{\lambda'\in X_*(T')_{\leq -\mu}}\operatorname{\mathrm{rank}} V_{\mu}^{\vee}[\lambda'] \int_{h'\in G_b(F)/T'(F)} \int_{h\in G(F)} [(p_2)_*^{-1}q_2^*\phi] \left((h,h').(y_{\lambda'})\right) \; dh\;dh'. \end{align*}$$
We rewrite the inner integral as a nested integral so that our expression for
![]() $\phi ^{\prime }_{G_b}(g')$
equals:
$\phi ^{\prime }_{G_b}(g')$
equals:
 $$ \begin{align*} &(-1)^d\!\sum_{\lambda'}\! \operatorname{\mathrm{rank}} V_{\mu}^{\vee}[\lambda'] \!\int_{h'\in G_b(F)/T'(F)} \!\int_{h\in G(F)/T(F)} \!\int_{t\in T(F)} [(p_2)_*^{-1}q_2^*\phi]\!\left((ht^{-1},h'). y_{\lambda'}\right) dt\;dh\;dh' \\ = \; &(-1)^d\! \sum_{\lambda'}\! \operatorname{\mathrm{rank}} V_{\mu}^{\vee}[\lambda']\!\int_{h'\in G_b(F)/T'(F)}\! \int_{h\in G(F)/T(F)}\! \int_{t'\in T'(F)}\! [(p_2)_*^{-1}q_2^*\phi]\!\left((h,h't').y_{\lambda'}\right)dt'\;dh\;dh'. \end{align*} $$
$$ \begin{align*} &(-1)^d\!\sum_{\lambda'}\! \operatorname{\mathrm{rank}} V_{\mu}^{\vee}[\lambda'] \!\int_{h'\in G_b(F)/T'(F)} \!\int_{h\in G(F)/T(F)} \!\int_{t\in T(F)} [(p_2)_*^{-1}q_2^*\phi]\!\left((ht^{-1},h'). y_{\lambda'}\right) dt\;dh\;dh' \\ = \; &(-1)^d\! \sum_{\lambda'}\! \operatorname{\mathrm{rank}} V_{\mu}^{\vee}[\lambda']\!\int_{h'\in G_b(F)/T'(F)}\! \int_{h\in G(F)/T(F)}\! \int_{t'\in T'(F)}\! [(p_2)_*^{-1}q_2^*\phi]\!\left((h,h't').y_{\lambda'}\right)dt'\;dh\;dh'. \end{align*} $$
Here, we have used Proposition 6.2.2: There is an isomorphism
![]() $\iota \colon t\mapsto t'$
between
$\iota \colon t\mapsto t'$
between
![]() $T(F)$
and
$T(F)$
and
![]() $T'(F)$
satisfying
$T'(F)$
satisfying
![]() $(t,t').y_{\lambda '}=y_{\lambda '}$
. This induces a bijection
$(t,t').y_{\lambda '}=y_{\lambda '}$
. This induces a bijection
![]() $\lambda \mapsto \lambda '=-\iota _*\lambda $
between
$\lambda \mapsto \lambda '=-\iota _*\lambda $
between
![]() $X_*(T)_{\leq \mu }$
and
$X_*(T)_{\leq \mu }$
and
![]() $X_*(T')_{\leq -\mu }$
. Given
$X_*(T')_{\leq -\mu }$
. Given
![]() $\lambda \in X_*(T)_{\leq \mu }$
, we let
$\lambda \in X_*(T)_{\leq \mu }$
, we let
![]() $g_{\lambda }=g_{\lambda '}$
. Then by Proposition 6.2.2, the preimage of
$g_{\lambda }=g_{\lambda '}$
. Then by Proposition 6.2.2, the preimage of
![]() $g'$
in
$g'$
in
![]() $\operatorname {\mathrm {Rel}}_{b,\mu }$
is exactly
$\operatorname {\mathrm {Rel}}_{b,\mu }$
is exactly
![]() $\left \{ (g_{\lambda },g,\lambda ) \right \}_{\lambda \in X_*(T)_{\leq \mu }}$
.
$\left \{ (g_{\lambda },g,\lambda ) \right \}_{\lambda \in X_*(T)_{\leq \mu }}$
.
Noting that
![]() $\operatorname {\mathrm {rank}} V_{\mu }[\lambda ]=\operatorname {\mathrm {rank}} V_{\mu }^{\vee }[\lambda ']$
, we exchange the order of the first two integrals above to obtain
$\operatorname {\mathrm {rank}} V_{\mu }[\lambda ]=\operatorname {\mathrm {rank}} V_{\mu }^{\vee }[\lambda ']$
, we exchange the order of the first two integrals above to obtain
 $$ \begin{align*} \phi^{\prime}_{G_b}(g') &= (-1)^d\sum_{\lambda\in X_*(T)_{\leq\mu}} \operatorname{\mathrm{rank}} V_{\mu}[\lambda] \int_{h\in G(F)/T(F)}\int_{h'\in G_b(F)} [(p_2)_*^{-1}q_2^*\phi]\left((h,h')\cdot y_{\lambda'}\right)\;dh'\;dh \\ &= (-1)^d\sum_{\lambda\in X_*(T)_{\leq\mu}} \operatorname{\mathrm{rank}} V_{\mu}[\lambda']\int_{h\in G(F)/T(F)} \phi(hg_{\lambda} h^{-1})\;dh\\ &=(-1)^d\sum_{\lambda\in X_*(T)_{\leq\mu}} \operatorname{\mathrm{rank}} V_{\mu}[\lambda] \phi_G(g_{\lambda}) \\ &= [T_{b,\mu}^{G\to G_b}\phi_G](g').\\[-32pt] \end{align*} $$
$$ \begin{align*} \phi^{\prime}_{G_b}(g') &= (-1)^d\sum_{\lambda\in X_*(T)_{\leq\mu}} \operatorname{\mathrm{rank}} V_{\mu}[\lambda] \int_{h\in G(F)/T(F)}\int_{h'\in G_b(F)} [(p_2)_*^{-1}q_2^*\phi]\left((h,h')\cdot y_{\lambda'}\right)\;dh'\;dh \\ &= (-1)^d\sum_{\lambda\in X_*(T)_{\leq\mu}} \operatorname{\mathrm{rank}} V_{\mu}[\lambda']\int_{h\in G(F)/T(F)} \phi(hg_{\lambda} h^{-1})\;dh\\ &=(-1)^d\sum_{\lambda\in X_*(T)_{\leq\mu}} \operatorname{\mathrm{rank}} V_{\mu}[\lambda] \phi_G(g_{\lambda}) \\ &= [T_{b,\mu}^{G\to G_b}\phi_G](g').\\[-32pt] \end{align*} $$
Definition 6.3.4. Let
be the
![]() $\Lambda $
-linear dual of
$\Lambda $
-linear dual of
![]() $\widetilde {T}_{b,\mu }^{G\to G_b}$
.
$\widetilde {T}_{b,\mu }^{G\to G_b}$
.
Proposition 6.3.5. Assume that
![]() $\Lambda = \overline {\mathbf {Q}_{\ell }}$
. Then the transfer of distributions
$\Lambda = \overline {\mathbf {Q}_{\ell }}$
. Then the transfer of distributions
![]() $\mathcal {T}^{G_b\to G}_{b,\mu }$
extends the transfer of functions
$\mathcal {T}^{G_b\to G}_{b,\mu }$
extends the transfer of functions
![]() $T^{G_b\to G}_{b,\mu }$
from Definition 3.2.7.
$T^{G_b\to G}_{b,\mu }$
from Definition 3.2.7.
Proof. Let
![]() $f\in C(G_b(F)_{\operatorname {\mathrm {ell}}},\Lambda )^{G_b(F)}$
be a conjugation-invariant function. Let
$f\in C(G_b(F)_{\operatorname {\mathrm {ell}}},\Lambda )^{G_b(F)}$
be a conjugation-invariant function. Let
![]() $\phi \in C_c(G(F)_{\operatorname {\mathrm {ell}}},\Lambda )$
, and let
$\phi \in C_c(G(F)_{\operatorname {\mathrm {ell}}},\Lambda )$
, and let
![]() $\phi '\in C_c(G_b(F)_{\operatorname {\mathrm {ell}}},\Lambda )$
be a lift of
$\phi '\in C_c(G_b(F)_{\operatorname {\mathrm {ell}}},\Lambda )$
be a lift of
![]() $\widetilde {T}^{G\to G_b}_{b,\mu }\phi $
. Using the Weyl integration formula (3.4.2), Lemma 3.4.1 and Proposition 6.3.3, we compute
$\widetilde {T}^{G\to G_b}_{b,\mu }\phi $
. Using the Weyl integration formula (3.4.2), Lemma 3.4.1 and Proposition 6.3.3, we compute
 $$ \begin{align*} \int_{g\in G(F)_{\operatorname{\mathrm{ell}}}} \phi(g)\mathcal{T}_{b,\mu}^{\kern3pt G_b\to G}(f\;dg') &= \int_{g'\in G_b(F)_{\operatorname{\mathrm{ell}}}} f(g')\phi'(g')\; dg' \\ &=\left< f,\phi^{\prime}_{G_b} \right>_{G_b}\\ &= \left< f,T_{b,\mu}^{G\to G_b}\phi_G \right>_{G_b} \\ &= \left< T_{b,\mu}^{G_b\to G} f, \phi_G \right>_{G}\\ &= \int_{g\in G(F)_{\operatorname{\mathrm{ell}}}} \phi(g)(T_{b,\mu}^{G_b\to G} f)\; dg \end{align*} $$
$$ \begin{align*} \int_{g\in G(F)_{\operatorname{\mathrm{ell}}}} \phi(g)\mathcal{T}_{b,\mu}^{\kern3pt G_b\to G}(f\;dg') &= \int_{g'\in G_b(F)_{\operatorname{\mathrm{ell}}}} f(g')\phi'(g')\; dg' \\ &=\left< f,\phi^{\prime}_{G_b} \right>_{G_b}\\ &= \left< f,T_{b,\mu}^{G\to G_b}\phi_G \right>_{G_b} \\ &= \left< T_{b,\mu}^{G_b\to G} f, \phi_G \right>_{G}\\ &= \int_{g\in G(F)_{\operatorname{\mathrm{ell}}}} \phi(g)(T_{b,\mu}^{G_b\to G} f)\; dg \end{align*} $$
so that
as desired.
6.4 Hecke operators on
 $\operatorname {\mathrm {Bun}}_G$
and the cohomology of shtuka spaces
$\operatorname {\mathrm {Bun}}_G$
and the cohomology of shtuka spaces
We are finally ready to reap our rewards. For the remainder of this chapter, we fix a prime
![]() $\ell \neq p$
and write
$\ell \neq p$
and write
![]() $\Lambda $
for a
$\Lambda $
for a
![]() $\mathbf {Z}_{\ell }$
-algebra. Let
$\mathbf {Z}_{\ell }$
-algebra. Let
![]() $\widehat {G}$
be the Langlands dual group over
$\widehat {G}$
be the Langlands dual group over
![]() $\mathbf {Z}_{\ell }$
.
$\mathbf {Z}_{\ell }$
.
We begin by quickly reviewing the results of [Reference Fargues and ScholzeFS21] on the categories
![]() $D_{\operatorname {\mathrm {lis}}}(\operatorname {\mathrm {Bun}}_G,\Lambda )$
and
$D_{\operatorname {\mathrm {lis}}}(\operatorname {\mathrm {Bun}}_G,\Lambda )$
and
![]() $D_{\operatorname {\mathrm {lis}}}(\operatorname {\mathrm {Bun}}_G^{b},\Lambda )$
, and the action of Hecke operators on
$D_{\operatorname {\mathrm {lis}}}(\operatorname {\mathrm {Bun}}_G^{b},\Lambda )$
, and the action of Hecke operators on
![]() $D_{\operatorname {\mathrm {lis}}}(\operatorname {\mathrm {Bun}}_G,\Lambda )$
.
$D_{\operatorname {\mathrm {lis}}}(\operatorname {\mathrm {Bun}}_G,\Lambda )$
.
The first key fact is that, for any
![]() $b \in B(G)$
, there is a natural equivalence of categories
$b \in B(G)$
, there is a natural equivalence of categories
[Reference Fargues and ScholzeFS21, Theorem I.5.1]. For a complex
![]() $\rho $
of smooth representations of
$\rho $
of smooth representations of
![]() $G_b(F)$
, we will slightly abusively also write
$G_b(F)$
, we will slightly abusively also write
![]() $\rho $
for the corresponding object of
$\rho $
for the corresponding object of
![]() $D_{\operatorname {\mathrm {lis}}}(\operatorname {\mathrm {Bun}}_G^b,\Lambda )$
.
$D_{\operatorname {\mathrm {lis}}}(\operatorname {\mathrm {Bun}}_G^b,\Lambda )$
.
Next, recall that there is a notion of ULA objects in
![]() $D_{\operatorname {\mathrm {lis}}}(\operatorname {\mathrm {Bun}}_G,\Lambda )$
. These admit the following concrete characterization.
$D_{\operatorname {\mathrm {lis}}}(\operatorname {\mathrm {Bun}}_G,\Lambda )$
. These admit the following concrete characterization.
Theorem 6.4.1 [Reference Fargues and ScholzeFS21, Theorem I.5.1(v)]
The following are equivalent for an object
![]() $A\in D_{\operatorname {\mathrm {lis}}}(\operatorname {\mathrm {Bun}}_G,\Lambda )$
.
$A\in D_{\operatorname {\mathrm {lis}}}(\operatorname {\mathrm {Bun}}_G,\Lambda )$
.
-
1. A is ULA over
 $\operatorname {\mathrm {Spd}} k$
.
$\operatorname {\mathrm {Spd}} k$
. -
2. For all
 $b\in B(G)$
, the restriction
$b\in B(G)$
, the restriction
 $i_b^*A$
, considered as an object of
$i_b^*A$
, considered as an object of
 $D(G_b(F),\Lambda )$
via equation (6.4.1), is admissible in the sense that
$D(G_b(F),\Lambda )$
via equation (6.4.1), is admissible in the sense that
 $(i_b^*A)^K$
is a perfect complex for all pro-p open subgroups
$(i_b^*A)^K$
is a perfect complex for all pro-p open subgroups
 $K\subset G_b(F)$
.
$K\subset G_b(F)$
.
Moreover, ULA objects are preserved under Verdier duality
![]() $\mathbf {D}=\mathbf {D}_{\operatorname {\mathrm {Bun}}_G/\operatorname {\mathrm {Spd}} k}$
and satisfy Verdier biduality.
$\mathbf {D}=\mathbf {D}_{\operatorname {\mathrm {Bun}}_G/\operatorname {\mathrm {Spd}} k}$
and satisfy Verdier biduality.
Corollary 6.4.2. Let
![]() $b\in B(G)$
, and let
$b\in B(G)$
, and let
![]() $\rho $
be an admissible complex in
$\rho $
be an admissible complex in
![]() $D(G_b(F),\Lambda )$
. The objects
$D(G_b(F),\Lambda )$
. The objects
![]() $(i_b)_*\rho $
and
$(i_b)_*\rho $
and
![]() $(i_b)_!\rho $
of
$(i_b)_!\rho $
of
![]() $D_{\operatorname {\mathrm {lis}}}(\operatorname {\mathrm {Bun}}_G,\Lambda )$
are ULA over
$D_{\operatorname {\mathrm {lis}}}(\operatorname {\mathrm {Bun}}_G,\Lambda )$
are ULA over
![]() $\operatorname {\mathrm {Spd}} k$
.
$\operatorname {\mathrm {Spd}} k$
.
Proof. The object
![]() $(i_b)_!\rho $
is ULA by the criterion in Theorem 6.4.1. Using Verdier duality (P4.) we have
$(i_b)_!\rho $
is ULA by the criterion in Theorem 6.4.1. Using Verdier duality (P4.) we have
![]() $\mathbf {D}((i_b)_!\rho ^{\vee })\cong (i_b)_* \rho $
so that
$\mathbf {D}((i_b)_!\rho ^{\vee })\cong (i_b)_* \rho $
so that
![]() $(i_b)_* \rho $
is also ULA.
$(i_b)_* \rho $
is also ULA.
Next, recall that any object V of
![]() $\operatorname {\mathrm {Rep}}_{\widehat {G}}(\Lambda )$
gives rise to a Hecke operator
$\operatorname {\mathrm {Rep}}_{\widehat {G}}(\Lambda )$
gives rise to a Hecke operator
![]() $T_V$
, which is an endofunctor of
$T_V$
, which is an endofunctor of
![]() $D_{\operatorname {\mathrm {lis}}}(\operatorname {\mathrm {Bun}}_{G,C},\Lambda )$
. When
$D_{\operatorname {\mathrm {lis}}}(\operatorname {\mathrm {Bun}}_{G,C},\Lambda )$
. When
![]() $\Lambda $
is a torsion ring, there is a natural equivalence
$\Lambda $
is a torsion ring, there is a natural equivalence
![]() $D_{\operatorname {\mathrm {lis}}}(\operatorname {\mathrm {Bun}}_{G,C},\Lambda ) \cong D_{\mathrm {\acute {e}t}}(\operatorname {\mathrm {Bun}}_{G,C},\Lambda )$
, and the operator
$D_{\operatorname {\mathrm {lis}}}(\operatorname {\mathrm {Bun}}_{G,C},\Lambda ) \cong D_{\mathrm {\acute {e}t}}(\operatorname {\mathrm {Bun}}_{G,C},\Lambda )$
, and the operator
![]() $T_V$
is defined concretely as the operation
$T_V$
is defined concretely as the operation
 $$ \begin{align*} T_V\colon D_{\mathrm{\acute{e}t}}(\operatorname{\mathrm{Bun}}_{G,C},\Lambda) &\to D_{\mathrm{\acute{e}t}}(\operatorname{\mathrm{Bun}}_{G,C}, \Lambda) \\ \mathcal{F} &\mapsto h_{2!}(h_1^* \mathcal{F}\otimes \mathcal{S}_V). \end{align*} $$
$$ \begin{align*} T_V\colon D_{\mathrm{\acute{e}t}}(\operatorname{\mathrm{Bun}}_{G,C},\Lambda) &\to D_{\mathrm{\acute{e}t}}(\operatorname{\mathrm{Bun}}_{G,C}, \Lambda) \\ \mathcal{F} &\mapsto h_{2!}(h_1^* \mathcal{F}\otimes \mathcal{S}_V). \end{align*} $$
Here,
![]() $\mathcal {S}_V\in D_{\mathrm {\acute {e}t}}(\operatorname {\mathrm {Hecke}}_{G,C},\Lambda )$
is pulled back from the object
$\mathcal {S}_V\in D_{\mathrm {\acute {e}t}}(\operatorname {\mathrm {Hecke}}_{G,C},\Lambda )$
is pulled back from the object
![]() $\mathcal {S}_V\in D_{\mathrm {\acute {e}t}}(\operatorname {\mathrm {Hecke}}_{G,C}^{\operatorname {\mathrm {loc}}},\Lambda )$
corresponding to V under the Satake equivalence (Theorem 5.1.1).
$\mathcal {S}_V\in D_{\mathrm {\acute {e}t}}(\operatorname {\mathrm {Hecke}}_{G,C}^{\operatorname {\mathrm {loc}}},\Lambda )$
corresponding to V under the Satake equivalence (Theorem 5.1.1).
Theorem 6.4.3 [Reference Fargues and ScholzeFS21, Theorem IX.0.1]
The Hecke operators preserve the subcategories of ULA and compact objects in
![]() $D_{\operatorname {\mathrm {lis}}}(\operatorname {\mathrm {Bun}}_{G,C},\Lambda )$
. For any V,
$D_{\operatorname {\mathrm {lis}}}(\operatorname {\mathrm {Bun}}_{G,C},\Lambda )$
. For any V,
![]() $T_V$
has left and right adjoint given by
$T_V$
has left and right adjoint given by
![]() $T_{V^{\vee }}$
, where
$T_{V^{\vee }}$
, where
![]() $V^{\vee }$
is the dual representation of
$V^{\vee }$
is the dual representation of
![]() $\widehat {G}$
. The actions of Hecke operators are compatible with extension of scalars along any ring map
$\widehat {G}$
. The actions of Hecke operators are compatible with extension of scalars along any ring map
![]() $\Lambda \to \Lambda '$
.
$\Lambda \to \Lambda '$
.
Next, we explain the relation between the Hecke operators
![]() $T_V$
and the cohomology of local shtuka spaces. Let
$T_V$
and the cohomology of local shtuka spaces. Let
![]() $\mu $
be a dominant cocharacter of G, and let
$\mu $
be a dominant cocharacter of G, and let
![]() $V_{\mu } \in \operatorname {\mathrm {Rep}}(\widehat {G})$
be the associated Weyl module. For any
$V_{\mu } \in \operatorname {\mathrm {Rep}}(\widehat {G})$
be the associated Weyl module. For any
![]() $\mathbf {Z}_{\ell }$
-algebra
$\mathbf {Z}_{\ell }$
-algebra
![]() $\Lambda $
, we write
$\Lambda $
, we write
![]() $V_{\mu ,\Lambda } \in \operatorname {\mathrm {Rep}}(\widehat {G}_{\Lambda })$
for the base change of
$V_{\mu ,\Lambda } \in \operatorname {\mathrm {Rep}}(\widehat {G}_{\Lambda })$
for the base change of
![]() $V_{\mu }$
. Let
$V_{\mu }$
. Let
![]() $\mathcal {S}_{\mu }=\mathcal {S}_{V_{\mu }}$
be the corresponding object in the Satake category with
$\mathcal {S}_{\mu }=\mathcal {S}_{V_{\mu }}$
be the corresponding object in the Satake category with
![]() $\mathbf {Z}_{\ell }$
-coefficients; similarly, if
$\mathbf {Z}_{\ell }$
-coefficients; similarly, if
![]() $\Lambda $
is a torsion ring, we write
$\Lambda $
is a torsion ring, we write
![]() $\mathcal {S}_{\mu ,\Lambda }=\mathcal {S}_{V_{\mu },\Lambda }$
for the corresponding object with
$\mathcal {S}_{\mu ,\Lambda }=\mathcal {S}_{V_{\mu },\Lambda }$
for the corresponding object with
![]() $\Lambda $
-coefficients. We will slightly abuse notation by using the same notations for the pullbacks of
$\Lambda $
-coefficients. We will slightly abuse notation by using the same notations for the pullbacks of
![]() $\mathcal {S}_{\mu }$
and
$\mathcal {S}_{\mu }$
and
![]() $\mathcal {S}_{\mu ,\Lambda }$
to various other v-stacks, including
$\mathcal {S}_{\mu ,\Lambda }$
to various other v-stacks, including
![]() $\operatorname {\mathrm {Gr}}_{G,\leq \mu ,C}$
and
$\operatorname {\mathrm {Gr}}_{G,\leq \mu ,C}$
and
![]() $\operatorname {\mathrm {Sht}}_{G,b,\mu ,C}$
(along the period morphism
$\operatorname {\mathrm {Sht}}_{G,b,\mu ,C}$
(along the period morphism
![]() $\pi _1$
from equation (6.1.4)).
$\pi _1$
from equation (6.1.4)).
Lemma 6.4.4. Let
![]() $\Lambda $
be a
$\Lambda $
be a
![]() $\mathbf {Z}_{\ell }$
-algebra, let
$\mathbf {Z}_{\ell }$
-algebra, let
![]() $K\subset G(F)$
be an open compact subgroup and let
$K\subset G(F)$
be an open compact subgroup and let
![]() $I_{K,\Lambda }={\operatorname {\mathrm {cInd}}}_K^{G(F)} \Lambda $
, where
$I_{K,\Lambda }={\operatorname {\mathrm {cInd}}}_K^{G(F)} \Lambda $
, where
![]() $\operatorname {\mathrm {cInd}}$
is compactly supported induction. Then there is a natural isomorphism
$\operatorname {\mathrm {cInd}}$
is compactly supported induction. Then there is a natural isomorphism
in
![]() $D(G_b(F),\Lambda )$
.
$D(G_b(F),\Lambda )$
.
Proof. When
![]() $\Lambda $
is a torsion ring, we can give the following direct argument. The global sections of
$\Lambda $
is a torsion ring, we can give the following direct argument. The global sections of
![]() $i_b^{\ast } T_{V_{\mu ,\Lambda }} (i_1)_!I_{K,\Lambda }$
over
$i_b^{\ast } T_{V_{\mu ,\Lambda }} (i_1)_!I_{K,\Lambda }$
over
![]() $\operatorname {\mathrm {Spd}} C\to \operatorname {\mathrm {Bun}}_G^b$
are
$\operatorname {\mathrm {Spd}} C\to \operatorname {\mathrm {Bun}}_G^b$
are
Now use
![]() $I_{K,\Lambda } \cong (j_K)_! \Lambda $
along with proper base change to get the result.
$I_{K,\Lambda } \cong (j_K)_! \Lambda $
along with proper base change to get the result.
The general case follows from the proof of [Reference Fargues and ScholzeFS21, Proposition IX.3.2].
Recall that, when
![]() $\rho $
is any smooth
$\rho $
is any smooth
![]() $G_b(F)$
-representation with
$G_b(F)$
-representation with
![]() $\overline {\mathbf {Q}_{\ell }}$
-coefficients, we defined an object
$\overline {\mathbf {Q}_{\ell }}$
-coefficients, we defined an object
in
![]() $D(G(F),\overline {\mathbf {Q}_{\ell }})$
, cf. Definition 2.4.3. The association
$D(G(F),\overline {\mathbf {Q}_{\ell }})$
, cf. Definition 2.4.3. The association
![]() $\rho \mapsto R\Gamma (G,b,\mu )[\rho ]$
clearly extends to a functor
$\rho \mapsto R\Gamma (G,b,\mu )[\rho ]$
clearly extends to a functor
![]() $D(G_b(F),\overline {\mathbf {Q}_{\ell }}) \to D(G(F),\overline {\mathbf {Q}_{\ell }})$
. Our next goal is to give an alternative approach to this construction, which is valid for more general coefficient rings and which makes the finiteness properties of this construction transparent.
$D(G_b(F),\overline {\mathbf {Q}_{\ell }}) \to D(G(F),\overline {\mathbf {Q}_{\ell }})$
. Our next goal is to give an alternative approach to this construction, which is valid for more general coefficient rings and which makes the finiteness properties of this construction transparent.
Proposition 6.4.5. Let
![]() $\rho $
be any object of
$\rho $
be any object of
![]() $D(G_b(F),\overline {\mathbf {Q}_{\ell }})$
. Then there is a natural isomorphism
$D(G_b(F),\overline {\mathbf {Q}_{\ell }})$
. Then there is a natural isomorphism
in
![]() $D(G(F),\overline {\mathbf {Q}_{\ell }})$
.
$D(G(F),\overline {\mathbf {Q}_{\ell }})$
.
If
![]() $\rho $
is admissible, then so is
$\rho $
is admissible, then so is
![]() $R\Gamma (G,b,\mu )[\rho ]$
. If
$R\Gamma (G,b,\mu )[\rho ]$
. If
![]() $\rho $
is of finite length, then so is
$\rho $
is of finite length, then so is
![]() $R\Gamma (G,b,\mu )[\rho ]$
.
$R\Gamma (G,b,\mu )[\rho ]$
.
Proof. Let
![]() $K\subset G(F)$
be a compact open subgroup. Using Lemma 6.4.4, various adjunctions and the compatibility of Hecke operators with extension of scalars, we have
$K\subset G(F)$
be a compact open subgroup. Using Lemma 6.4.4, various adjunctions and the compatibility of Hecke operators with extension of scalars, we have
 $$ \begin{align*} R\operatorname{\mathrm{Hom}}_{G_b(F)}(R\Gamma_c(\operatorname{\mathrm{Sht}}_{G,b,\mu,K,C},\mathcal{S}_V) \otimes \overline{\mathbf{Q}_{\ell}},\rho) &\cong R\operatorname{\mathrm{Hom}}_{G_b(F)}(i_b^{\ast} T_{V_{\mu}} (i_1)_! {\operatorname{\mathrm{cInd}}}_K^{G(F)} \mathbf{Z}_{\ell} \otimes \overline{\mathbf{Q}_{\ell}}, \rho) \\ & \cong R\operatorname{\mathrm{Hom}}_{G_b(F)}(i_b^{\ast} T_{V_{\mu,\overline{\mathbf{Q}_{\ell}}}} (i_1)_! {\operatorname{\mathrm{cInd}}}_{K}^{G(F)} \overline{\mathbf{Q}_{\ell}}, \rho) \\ &\cong (i_1^* T_{{V^{\vee}_{\mu,\overline{\mathbf{Q}_{\ell}}}}} (i_b)_*\rho)^K. \end{align*} $$
$$ \begin{align*} R\operatorname{\mathrm{Hom}}_{G_b(F)}(R\Gamma_c(\operatorname{\mathrm{Sht}}_{G,b,\mu,K,C},\mathcal{S}_V) \otimes \overline{\mathbf{Q}_{\ell}},\rho) &\cong R\operatorname{\mathrm{Hom}}_{G_b(F)}(i_b^{\ast} T_{V_{\mu}} (i_1)_! {\operatorname{\mathrm{cInd}}}_K^{G(F)} \mathbf{Z}_{\ell} \otimes \overline{\mathbf{Q}_{\ell}}, \rho) \\ & \cong R\operatorname{\mathrm{Hom}}_{G_b(F)}(i_b^{\ast} T_{V_{\mu,\overline{\mathbf{Q}_{\ell}}}} (i_1)_! {\operatorname{\mathrm{cInd}}}_{K}^{G(F)} \overline{\mathbf{Q}_{\ell}}, \rho) \\ &\cong (i_1^* T_{{V^{\vee}_{\mu,\overline{\mathbf{Q}_{\ell}}}}} (i_b)_*\rho)^K. \end{align*} $$
Taking the colimit over K gives the first claim. The claim about preservation of admissibility now follows from Theorem 6.4.1 combined with Theorem 6.4.3. For the final claim, fix some
![]() $\rho $
of finite length. Note that
$\rho $
of finite length. Note that
![]() $i_1^*T_{{V^{\vee }_{\mu ,\overline {\mathbf {Q}_{\ell }}}}} (i_b)_*\rho $
is the smooth dual of
$i_1^*T_{{V^{\vee }_{\mu ,\overline {\mathbf {Q}_{\ell }}}}} (i_b)_*\rho $
is the smooth dual of
![]() $i_1^*T_{{V^{\vee }_{\mu ,\overline {\mathbf {Q}_{\ell }}}}} (i_b)_! \rho ^{\vee }$
, so it’s enough to show that
$i_1^*T_{{V^{\vee }_{\mu ,\overline {\mathbf {Q}_{\ell }}}}} (i_b)_! \rho ^{\vee }$
, so it’s enough to show that
![]() $i_1^*T_{{V^{\vee }_{\mu ,\overline {\mathbf {Q}_{\ell }}}}} (i_b)_! \rho ^{\vee }$
is of finite length. But finite length is equivalent to being both compact and admissible, so we conclude by observing that the operation
$i_1^*T_{{V^{\vee }_{\mu ,\overline {\mathbf {Q}_{\ell }}}}} (i_b)_! \rho ^{\vee }$
is of finite length. But finite length is equivalent to being both compact and admissible, so we conclude by observing that the operation
![]() $i_1^*T_{{V^{\vee }_{\mu ,\overline {\mathbf {Q}_{\ell }}}}} (i_b)_!(-)$
preserves compact objects.
$i_1^*T_{{V^{\vee }_{\mu ,\overline {\mathbf {Q}_{\ell }}}}} (i_b)_!(-)$
preserves compact objects.
Definition 6.4.6. For any
![]() $\mathbf {Z}_{\ell }$
-algebra
$\mathbf {Z}_{\ell }$
-algebra
![]() $\Lambda $
, we write
$\Lambda $
, we write
for the functor
![]() $i_1^* T_{{V^{\vee }_{\mu ,\Lambda }}} (i_b)_*(-)$
.
$i_1^* T_{{V^{\vee }_{\mu ,\Lambda }}} (i_b)_*(-)$
.
By the previous discussion, this functor is compatible with extension of scalars along any map
![]() $\Lambda \to \Lambda '$
and preserves admissible objects. Moreover, if
$\Lambda \to \Lambda '$
and preserves admissible objects. Moreover, if
![]() $\Lambda $
is Artinian and
$\Lambda $
is Artinian and
![]() $\rho \in D(G_b(F),\Lambda )$
is admissible of finite length, then
$\rho \in D(G_b(F),\Lambda )$
is admissible of finite length, then
![]() $R\Gamma (G,b,\mu )[\rho ]$
is also of finite length by the same argument as in the proof of Proposition 6.4.5.
$R\Gamma (G,b,\mu )[\rho ]$
is also of finite length by the same argument as in the proof of Proposition 6.4.5.
We now come to the technical heart of this paper. Choose
![]() $\mathbf {Z}_{\ell }$
-valued Haar measures on
$\mathbf {Z}_{\ell }$
-valued Haar measures on
![]() $G(F)$
and
$G(F)$
and
![]() $G_b(F)$
, compatibly as in §3.4. These induce
$G_b(F)$
, compatibly as in §3.4. These induce
![]() $\Lambda $
-valued Haar measures on the same groups compatibly with varying
$\Lambda $
-valued Haar measures on the same groups compatibly with varying
![]() $\Lambda $
. Then for any
$\Lambda $
. Then for any
![]() $\Lambda $
, any admissible representation
$\Lambda $
, any admissible representation
![]() $\pi $
of
$\pi $
of
![]() $G(F)$
with coefficients in
$G(F)$
with coefficients in
![]() $\Lambda $
has a corresponding
$\Lambda $
has a corresponding
![]() $\Lambda $
-valued trace distribution
$\Lambda $
-valued trace distribution
![]() $\operatorname {\mathrm {tr.dist}}(\pi )$
, and similarly for
$\operatorname {\mathrm {tr.dist}}(\pi )$
, and similarly for
![]() $G_b(F)$
. Recall also that we defined a transfer of
$G_b(F)$
. Recall also that we defined a transfer of
![]() $\Lambda $
-valued distributions
$\Lambda $
-valued distributions
![]() $\mathcal {T}_{b,\mu }^{\kern3pt G_b\to G}$
, Definition 6.3.4.
$\mathcal {T}_{b,\mu }^{\kern3pt G_b\to G}$
, Definition 6.3.4.
Proposition 6.4.7. Let
![]() $\Lambda $
be any torsion
$\Lambda $
be any torsion
![]() $\mathbf {Z}_{\ell }$
-algebra, and let
$\mathbf {Z}_{\ell }$
-algebra, and let
![]() $\rho $
be any admissible representation of
$\rho $
be any admissible representation of
![]() $G_b(F)$
with coefficients in
$G_b(F)$
with coefficients in
![]() $\Lambda $
. Then have an equality
$\Lambda $
. Then have an equality
in
![]() $\operatorname {\mathrm {Dist}}(G(F)_{\operatorname {\mathrm {ell}}},\Lambda )^{G(F)}$
.
$\operatorname {\mathrm {Dist}}(G(F)_{\operatorname {\mathrm {ell}}},\Lambda )^{G(F)}$
.
Proof. In the following proof, we set
![]() $S=\operatorname {\mathrm {Spd}} C$
and
$S=\operatorname {\mathrm {Spd}} C$
and
![]() $V=V_{\mu ,\Lambda }$
for brevity.
$V=V_{\mu ,\Lambda }$
for brevity.
We have an isomorphism
and similarly for
![]() $G_b(F)$
. With respect those isomorphisms, the left side of the desired equality is the characteristic class
$G_b(F)$
. With respect those isomorphisms, the left side of the desired equality is the characteristic class
restricted to
![]() $\operatorname {\mathrm {Dist}}(G(F)_{\operatorname {\mathrm {ell}}},\Lambda )^{G(F)}$
.
$\operatorname {\mathrm {Dist}}(G(F)_{\operatorname {\mathrm {ell}}},\Lambda )^{G(F)}$
.
For the remainder of the proof, we introduce the abbreviations
![]() $B=\operatorname {\mathrm {Bun}}_{G,C}$
and
$B=\operatorname {\mathrm {Bun}}_{G,C}$
and
![]() $H=\operatorname {\mathrm {Hecke}}_{G,\leq \mu ,C}$
and
$H=\operatorname {\mathrm {Hecke}}_{G,\leq \mu ,C}$
and
![]() $\operatorname {\mathrm {In}}=\operatorname {\mathrm {In}}_S$
. Let us also use a subscript ‘ell’ to mean restriction to the appropriate elliptic locus. Taking inertia stacks in equation (6.1.2), we obtain a commutative diagram
$\operatorname {\mathrm {In}}=\operatorname {\mathrm {In}}_S$
. Let us also use a subscript ‘ell’ to mean restriction to the appropriate elliptic locus. Taking inertia stacks in equation (6.1.2), we obtain a commutative diagram

in which all squares are Cartesian, and the morphism labeled
![]() $\operatorname {\mathrm {id}}$
is the equality from Corollary 6.2.4. The characteristic class in question is
$\operatorname {\mathrm {id}}$
is the equality from Corollary 6.2.4. The characteristic class in question is
 $$ \begin{align*} \begin{array}{lcl} j_1^*\operatorname{\mathrm{cc}}_{B^1/S}(i_1^*T_{V^{\vee}}(i_b)_*\rho ) &\stackrel{\text{Lem. }4.3.7}{=} &\!\! j_1^*\operatorname{\mathrm{In}}(i_1)^*\operatorname{\mathrm{cc}}_{B/S}\left((h_2)_!(h_1^*(i_b)_*\rho \otimes \mathcal{S}_{V^{\vee}}\right) \\[2pt] &\stackrel{\text{Cor.} 4.3.9}{=} &\!\! j_1^*\operatorname{\mathrm{In}}(i_1)^*\operatorname{\mathrm{In}}(h_2)_*\operatorname{\mathrm{cc}}_{H/S}(h_1^*(i_b)_*\rho \otimes \mathcal{S}_{V^{\vee}})\\[2pt] &= &\!\! (\operatorname{\mathrm{In}}(h_2^{\ast,1})_{\operatorname{\mathrm{ell}}})_*(j_1')^*\operatorname{\mathrm{In}}(i_1')^*\operatorname{\mathrm{cc}}_{H/S}(h_1^*(i_b)_*\rho \otimes\mathcal{S}_{V^{\vee}})\\[2pt] &= &\!\! (\operatorname{\mathrm{In}}(h_2^{\ast,1})_{\operatorname{\mathrm{ell}}})_*(j_b')^*\operatorname{\mathrm{In}}(i_b')^*\operatorname{\mathrm{cc}}_{H/S}(h_1^*(i_b)_*\rho \otimes\mathcal{S}_{V^{\vee}})\\[2pt] &\stackrel{\text{Lem. }4.3.7}{=} &\!\! (\operatorname{\mathrm{In}}(h_2^{\ast,1})_{\operatorname{\mathrm{ell}}})_*(j_b')^*\operatorname{\mathrm{cc}}_{H^{b,\ast}/S}((i_b')^*h_1^*(i_b)_*\rho \otimes\mathcal{S}_{V^{\vee}}) \\[2pt] &= &\!\! (\operatorname{\mathrm{In}}(h_2^{\ast,1})_{\operatorname{\mathrm{ell}}})_*(j_b')^* \operatorname{\mathrm{cc}}_{H^{b,\ast}/S} ((h_1^{b,\ast})^*\rho \otimes \mathcal{S}_{V^{\vee}}). \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{lcl} j_1^*\operatorname{\mathrm{cc}}_{B^1/S}(i_1^*T_{V^{\vee}}(i_b)_*\rho ) &\stackrel{\text{Lem. }4.3.7}{=} &\!\! j_1^*\operatorname{\mathrm{In}}(i_1)^*\operatorname{\mathrm{cc}}_{B/S}\left((h_2)_!(h_1^*(i_b)_*\rho \otimes \mathcal{S}_{V^{\vee}}\right) \\[2pt] &\stackrel{\text{Cor.} 4.3.9}{=} &\!\! j_1^*\operatorname{\mathrm{In}}(i_1)^*\operatorname{\mathrm{In}}(h_2)_*\operatorname{\mathrm{cc}}_{H/S}(h_1^*(i_b)_*\rho \otimes \mathcal{S}_{V^{\vee}})\\[2pt] &= &\!\! (\operatorname{\mathrm{In}}(h_2^{\ast,1})_{\operatorname{\mathrm{ell}}})_*(j_1')^*\operatorname{\mathrm{In}}(i_1')^*\operatorname{\mathrm{cc}}_{H/S}(h_1^*(i_b)_*\rho \otimes\mathcal{S}_{V^{\vee}})\\[2pt] &= &\!\! (\operatorname{\mathrm{In}}(h_2^{\ast,1})_{\operatorname{\mathrm{ell}}})_*(j_b')^*\operatorname{\mathrm{In}}(i_b')^*\operatorname{\mathrm{cc}}_{H/S}(h_1^*(i_b)_*\rho \otimes\mathcal{S}_{V^{\vee}})\\[2pt] &\stackrel{\text{Lem. }4.3.7}{=} &\!\! (\operatorname{\mathrm{In}}(h_2^{\ast,1})_{\operatorname{\mathrm{ell}}})_*(j_b')^*\operatorname{\mathrm{cc}}_{H^{b,\ast}/S}((i_b')^*h_1^*(i_b)_*\rho \otimes\mathcal{S}_{V^{\vee}}) \\[2pt] &= &\!\! (\operatorname{\mathrm{In}}(h_2^{\ast,1})_{\operatorname{\mathrm{ell}}})_*(j_b')^* \operatorname{\mathrm{cc}}_{H^{b,\ast}/S} ((h_1^{b,\ast})^*\rho \otimes \mathcal{S}_{V^{\vee}}). \end{array} \end{align*} $$
Noting that
![]() $H^{b,\ast }\cong [\operatorname {\mathrm {Gr}}^b_{G,\leq -\mu ,C}/G_b(F)_S]$
, we have a Cartesian diagram of decent S-v-stacks:
$H^{b,\ast }\cong [\operatorname {\mathrm {Gr}}^b_{G,\leq -\mu ,C}/G_b(F)_S]$
, we have a Cartesian diagram of decent S-v-stacks:

Here,
![]() $B^b\cong [S/G_b(F)_S]$
,
$B^b\cong [S/G_b(F)_S]$
,
![]() $H^{\operatorname {\mathrm {loc}}}_m\cong [\operatorname {\mathrm {Gr}}_{G,\leq -\mu ,C}/L^+_mG]$
, and
$H^{\operatorname {\mathrm {loc}}}_m\cong [\operatorname {\mathrm {Gr}}_{G,\leq -\mu ,C}/L^+_mG]$
, and
![]() $B_m^{\operatorname {\mathrm {loc}}}\cong [S/L^+_mG]$
; the m here is chosen large enough so that the action of
$B_m^{\operatorname {\mathrm {loc}}}\cong [S/L^+_mG]$
; the m here is chosen large enough so that the action of
![]() $L^+G$
on
$L^+G$
on
![]() $\operatorname {\mathrm {Gr}}_{G,\leq -\mu ,C}$
factors through the quotient
$\operatorname {\mathrm {Gr}}_{G,\leq -\mu ,C}$
factors through the quotient
![]() $L^+_mG$
. Through this, we can identify
$L^+_mG$
. Through this, we can identify
![]() $(h_1^{b,\ast })^*\rho \otimes \mathcal {S}_{V^{\vee }}$
with
$(h_1^{b,\ast })^*\rho \otimes \mathcal {S}_{V^{\vee }}$
with
![]() $\rho \boxtimes _{B^{\operatorname {\mathrm {loc}}}_m} \mathcal {S}_{V^{\vee }}$
. It is at this point we apply Theorem 4.5.3, valid because the base
$\rho \boxtimes _{B^{\operatorname {\mathrm {loc}}}_m} \mathcal {S}_{V^{\vee }}$
. It is at this point we apply Theorem 4.5.3, valid because the base
![]() $B_m^{\operatorname {\mathrm {loc}}}=[S/L^+_mG]$
satisfies the hypotheses of Lemma 4.5.2. We get
$B_m^{\operatorname {\mathrm {loc}}}=[S/L^+_mG]$
satisfies the hypotheses of Lemma 4.5.2. We get
 $$ \begin{align*} j_1^*\operatorname{\mathrm{cc}}_{B^1/S}(i_1^*T_{V^{\vee}}(i_b)_*\rho) &= (\operatorname{\mathrm{In}}(h_2^{\ast,1})_{\operatorname{\mathrm{ell}}})_*(j_b')^*\left(\operatorname{\mathrm{cc}}_{B^b/S}\rho \boxtimes_{\operatorname{\mathrm{In}}(B^{\operatorname{\mathrm{loc}}}_m)} \operatorname{\mathrm{cc}}_{H_m^{\operatorname{\mathrm{loc}}}/S}(\mathcal{S}_{V^{\vee}}) \right) \\ &= (\operatorname{\mathrm{In}}(h_2^{\ast,1})_{\operatorname{\mathrm{ell}}})_*\left(\operatorname{\mathrm{cc}}_{B^b/S}\rho_{\operatorname{\mathrm{ell}}} \boxtimes_{\operatorname{\mathrm{In}}(B^{\operatorname{\mathrm{loc}}}_m)_{\operatorname{\mathrm{sr}}}} \operatorname{\mathrm{cc}}_{H_m^{\operatorname{\mathrm{loc}}}/S}(\mathcal{S}_{V^{\vee}})_{\operatorname{\mathrm{sr}}}\right). \end{align*} $$
$$ \begin{align*} j_1^*\operatorname{\mathrm{cc}}_{B^1/S}(i_1^*T_{V^{\vee}}(i_b)_*\rho) &= (\operatorname{\mathrm{In}}(h_2^{\ast,1})_{\operatorname{\mathrm{ell}}})_*(j_b')^*\left(\operatorname{\mathrm{cc}}_{B^b/S}\rho \boxtimes_{\operatorname{\mathrm{In}}(B^{\operatorname{\mathrm{loc}}}_m)} \operatorname{\mathrm{cc}}_{H_m^{\operatorname{\mathrm{loc}}}/S}(\mathcal{S}_{V^{\vee}}) \right) \\ &= (\operatorname{\mathrm{In}}(h_2^{\ast,1})_{\operatorname{\mathrm{ell}}})_*\left(\operatorname{\mathrm{cc}}_{B^b/S}\rho_{\operatorname{\mathrm{ell}}} \boxtimes_{\operatorname{\mathrm{In}}(B^{\operatorname{\mathrm{loc}}}_m)_{\operatorname{\mathrm{sr}}}} \operatorname{\mathrm{cc}}_{H_m^{\operatorname{\mathrm{loc}}}/S}(\mathcal{S}_{V^{\vee}})_{\operatorname{\mathrm{sr}}}\right). \end{align*} $$
Considering the diagram

our characteristic class is the image of
![]() $\operatorname {\mathrm {cc}}_{B^b/S}(\rho )_{\operatorname {\mathrm {ell}}}$
under the composite vertical map on the left. The diagram is commutative; the hardest thing to check is the commutativity of the top square, which follows from Proposition 6.4.8 below. The composition along the right column is
$\operatorname {\mathrm {cc}}_{B^b/S}(\rho )_{\operatorname {\mathrm {ell}}}$
under the composite vertical map on the left. The diagram is commutative; the hardest thing to check is the commutativity of the top square, which follows from Proposition 6.4.8 below. The composition along the right column is
![]() $\mathcal {T}^{G_b\to G}_{b,\mu }$
, giving us the desired equality of distributions.
$\mathcal {T}^{G_b\to G}_{b,\mu }$
, giving us the desired equality of distributions.
It remains to justify one step in this computation. Maintain the notation and assumptions of the previous theorem. The v-stack
![]() $H^{b,\ast }$
can be expressed as a fiber product as in equation (6.4.3); we have the ULA object
$H^{b,\ast }$
can be expressed as a fiber product as in equation (6.4.3); we have the ULA object
![]() $\rho \boxtimes _{B_m^{\operatorname {\mathrm {loc}}}} \mathcal {S}_{V^{\vee }}$
, whose characteristic class can be calculated using Theorem 4.5.3.
$\rho \boxtimes _{B_m^{\operatorname {\mathrm {loc}}}} \mathcal {S}_{V^{\vee }}$
, whose characteristic class can be calculated using Theorem 4.5.3.
Let
be the action map so that we have an isomorphism
Let
![]() $\operatorname {\mathrm {Fix}}(\alpha _b)_{\operatorname {\mathrm {sr}}}$
be the open subset lying over
$\operatorname {\mathrm {Fix}}(\alpha _b)_{\operatorname {\mathrm {sr}}}$
be the open subset lying over
![]() $G_b(F)_{\operatorname {\mathrm {sr}}}$
(and use the same convention for other objects); then
$G_b(F)_{\operatorname {\mathrm {sr}}}$
(and use the same convention for other objects); then
![]() $\operatorname {\mathrm {Fix}}(\alpha _b)_{\operatorname {\mathrm {sr}}}$
is a locally profinite set, which is finite over
$\operatorname {\mathrm {Fix}}(\alpha _b)_{\operatorname {\mathrm {sr}}}$
is a locally profinite set, which is finite over
![]() $G_b(F)_{\operatorname {\mathrm {sr}}}$
with fibers
$G_b(F)_{\operatorname {\mathrm {sr}}}$
with fibers
![]() $X_*(T)_{\leq -\mu }$
.
$X_*(T)_{\leq -\mu }$
.
Proposition 6.4.8. The characteristic class
equals the image of
![]() $\operatorname {\mathrm {tr.dist}}(\rho ) \otimes (-1)^{\left < 2\rho _G,- \right>}\operatorname {\mathrm {rank}} V^{\vee }[-]$
under the evident map
$\operatorname {\mathrm {tr.dist}}(\rho ) \otimes (-1)^{\left < 2\rho _G,- \right>}\operatorname {\mathrm {rank}} V^{\vee }[-]$
under the evident map
Proof. Take inertia stacks in equation (6.4.3), and restrict to the strongly regular locus in
![]() $\operatorname {\mathrm {In}}_S[S/L^+_mG]$
to obtain a Cartesian diagram
$\operatorname {\mathrm {In}}_S[S/L^+_mG]$
to obtain a Cartesian diagram

The Künneth map (4.5.2) in this situation reduces to equation (6.4.4) on the level of global sections. The result now follows from Theorems 4.5.3 and 5.1.4.
This formally implies the following theorem.
Theorem 6.4.9. Let
![]() $\rho $
be any finite length admissible
$\rho $
be any finite length admissible
![]() $G_b(F)$
-representation with
$G_b(F)$
-representation with
![]() $\overline {\mathbf {Q}_{\ell }}$
-coefficients. Assume that
$\overline {\mathbf {Q}_{\ell }}$
-coefficients. Assume that
![]() $\rho $
admits a
$\rho $
admits a
![]() $\overline {\mathbf {Z}_{\ell }}$
-lattice in the sense of Definition C.2.1. Then for all
$\overline {\mathbf {Z}_{\ell }}$
-lattice in the sense of Definition C.2.1. Then for all
![]() $\phi \in C_c(G(F)_{\operatorname {\mathrm {ell}}},\overline {\mathbf {Q}_{\ell }})$
, the equality
$\phi \in C_c(G(F)_{\operatorname {\mathrm {ell}}},\overline {\mathbf {Q}_{\ell }})$
, the equality
holds.
Recall that by definition,
![]() $\mathcal {T}_{b,\mu }^{\kern3pt G_b\to G} (\operatorname {\mathrm {tr.dist}}\rho )(\phi )$
depends only on
$\mathcal {T}_{b,\mu }^{\kern3pt G_b\to G} (\operatorname {\mathrm {tr.dist}}\rho )(\phi )$
depends only on
![]() $(\operatorname {\mathrm {tr.dist}}\rho )_{\operatorname {\mathrm {ell}}}$
.
$(\operatorname {\mathrm {tr.dist}}\rho )_{\operatorname {\mathrm {ell}}}$
.
Proof. Fix
![]() $\rho $
and
$\rho $
and
![]() $\phi $
as in the theorem, and fix a
$\phi $
as in the theorem, and fix a
![]() $\overline {\mathbf {Z}_{\ell }}$
-lattice
$\overline {\mathbf {Z}_{\ell }}$
-lattice
![]() $\rho ^{\circ } \subset \rho $
. After rescaling, we may also assume
$\rho ^{\circ } \subset \rho $
. After rescaling, we may also assume
![]() $\phi $
is valued in
$\phi $
is valued in
![]() $\overline {\mathbf {Z}_{\ell }}$
. It is clear from the definitions that
$\overline {\mathbf {Z}_{\ell }}$
. It is clear from the definitions that
![]() $\operatorname {\mathrm {tr}} (\phi | \operatorname {\mathrm {Mant}}_{b,\mu }(\rho )) = \operatorname {\mathrm {tr}} (\phi | R\Gamma (G,b,\mu )[\rho ^{\circ }])$
and
$\operatorname {\mathrm {tr}} (\phi | \operatorname {\mathrm {Mant}}_{b,\mu }(\rho )) = \operatorname {\mathrm {tr}} (\phi | R\Gamma (G,b,\mu )[\rho ^{\circ }])$
and
For all
![]() $n\geq 1$
, set
$n\geq 1$
, set
![]() $\rho ^{\circ }_{n} = \rho ^{\circ } \otimes \mathbf {Z}/\ell ^n$
, and write
$\rho ^{\circ }_{n} = \rho ^{\circ } \otimes \mathbf {Z}/\ell ^n$
, and write
![]() $\phi _n \in C_c(G(F)_{\operatorname {\mathrm {ell}}},\overline {\mathbf {Z}_{\ell }}/\ell ^n)$
for the obvious reductions of
$\phi _n \in C_c(G(F)_{\operatorname {\mathrm {ell}}},\overline {\mathbf {Z}_{\ell }}/\ell ^n)$
for the obvious reductions of
![]() $\phi $
. Applying Proposition 6.4.7 with
$\phi $
. Applying Proposition 6.4.7 with
![]() $\Lambda = \overline {\mathbf {Z}_{\ell }}/\ell ^n$
, we get equalities
$\Lambda = \overline {\mathbf {Z}_{\ell }}/\ell ^n$
, we get equalities
for all
![]() $n\geq 1$
. The result now follows by taking the inverse limit over n.
$n\geq 1$
. The result now follows by taking the inverse limit over n.
6.5 Proof of Theorem 1.0.2
We are finally ready to prove the main theorem of the paper, which we restate for the convenience of the reader.
Theorem 6.5.1. Assume the refined local Langlands correspondence [Reference KalethaKal16a, Conjecture G]. Let
![]() $\phi \colon W_F \times \mathrm {SL}_2 \to {^LG}$
be a discrete Langlands parameter with coefficients in
$\phi \colon W_F \times \mathrm {SL}_2 \to {^LG}$
be a discrete Langlands parameter with coefficients in
![]() $\overline {\mathbf {Q}}_{\ell }$
, and let
$\overline {\mathbf {Q}}_{\ell }$
, and let
![]() $\rho \in \Pi _{\phi }(G_b)$
be a member of its L-packet. After ignoring the action of
$\rho \in \Pi _{\phi }(G_b)$
be a member of its L-packet. After ignoring the action of
![]() $W_E$
, we have an equality
$W_E$
, we have an equality
 $$\begin{align*}\operatorname{\mathrm{Mant}}_{b,\mu}(\rho)=\sum_{\pi\in\Pi_{\phi}(G)} \left[\dim \operatorname{\mathrm{Hom}}_{S_{\phi}}(\delta_{\pi,\rho},r_{\mu})\right]\pi + \mathrm{err} \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Mant}}_{b,\mu}(\rho)=\sum_{\pi\in\Pi_{\phi}(G)} \left[\dim \operatorname{\mathrm{Hom}}_{S_{\phi}}(\delta_{\pi,\rho},r_{\mu})\right]\pi + \mathrm{err} \end{align*}$$
in
![]() $\operatorname {\mathrm {Groth}}(G(F))$
, where
$\operatorname {\mathrm {Groth}}(G(F))$
, where
![]() $\mathrm {err} \in \operatorname {\mathrm {Groth}}(G(F))$
is a virtual representation whose character vanishes on the locus of elliptic elements of
$\mathrm {err} \in \operatorname {\mathrm {Groth}}(G(F))$
is a virtual representation whose character vanishes on the locus of elliptic elements of
![]() $G(F)$
.
$G(F)$
.
If the packet
![]() $\Pi _{\phi }(G)$
consists entirely of supercuspidal representations and the semisimple L-parameter
$\Pi _{\phi }(G)$
consists entirely of supercuspidal representations and the semisimple L-parameter
![]() $\varphi _{\rho }$
associated with
$\varphi _{\rho }$
associated with
![]() $\rho $
as in [Reference Fargues and ScholzeFS21, §I.9.6] is supercuspidal, then in fact
$\rho $
as in [Reference Fargues and ScholzeFS21, §I.9.6] is supercuspidal, then in fact
![]() $\mathrm {err}=0$
.
$\mathrm {err}=0$
.
The main ingredient in the proof is the following extension of Theorem 6.4.9 to its natural level of generality.
Theorem 6.5.2. Let
![]() $\rho $
be any finite length admissible
$\rho $
be any finite length admissible
![]() $G_b(F)$
-representation with
$G_b(F)$
-representation with
![]() $\overline {\mathbf {Q}_{\ell }}$
-coefficients. Then for all
$\overline {\mathbf {Q}_{\ell }}$
-coefficients. Then for all
![]() $\phi \in C_c(G(F)_{\operatorname {\mathrm {ell}}},\overline {\mathbf {Q}_{\ell }})$
, the equality
$\phi \in C_c(G(F)_{\operatorname {\mathrm {ell}}},\overline {\mathbf {Q}_{\ell }})$
, the equality
holds.
In particular, the virtual character of
![]() $\operatorname {\mathrm {Mant}}_{b,\mu }(\rho )$
restricted to
$\operatorname {\mathrm {Mant}}_{b,\mu }(\rho )$
restricted to
![]() $G(F)_{\operatorname {\mathrm {ell}}}$
is equal to
$G(F)_{\operatorname {\mathrm {ell}}}$
is equal to
![]() $T_{b,\mu }^{G_b \to G}(\Theta _{\rho })$
.
$T_{b,\mu }^{G_b \to G}(\Theta _{\rho })$
.
We will formally deduce this from Theorem 6.4.9 by a continuity argument.
For the proof of this theorem, it will be convenient to use the language of Grothendieck groups. In particular, by the finiteness results mentioned above,
![]() $\operatorname {\mathrm {Mant}}_{b,\mu }(-)$
can be regarded as a group homomorphism
$\operatorname {\mathrm {Mant}}_{b,\mu }(-)$
can be regarded as a group homomorphism
![]() $\operatorname {\mathrm {Mant}}_{b,\mu }(-): \operatorname {\mathrm {Groth}}(G_b(F)) \to \operatorname {\mathrm {Groth}}(G(F))$
. Recall that any element
$\operatorname {\mathrm {Mant}}_{b,\mu }(-): \operatorname {\mathrm {Groth}}(G_b(F)) \to \operatorname {\mathrm {Groth}}(G(F))$
. Recall that any element
![]() $\phi \in C_c(G(F),\overline {\mathbf {Q}_{\ell }})$
defines a linear form
$\phi \in C_c(G(F),\overline {\mathbf {Q}_{\ell }})$
defines a linear form
![]() $\operatorname {\mathrm {tr}}(\phi | -): \operatorname {\mathrm {Groth}}(G(F)) \to \overline {\mathbf {Q}_{\ell }}$
. By definition, a linear form
$\operatorname {\mathrm {tr}}(\phi | -): \operatorname {\mathrm {Groth}}(G(F)) \to \overline {\mathbf {Q}_{\ell }}$
. By definition, a linear form
![]() $f: \operatorname {\mathrm {Groth}}(G(F)) \to \overline {\mathbf {Q}_{\ell }}$
is a trace form if it can be written as
$f: \operatorname {\mathrm {Groth}}(G(F)) \to \overline {\mathbf {Q}_{\ell }}$
is a trace form if it can be written as
![]() $\operatorname {\mathrm {tr}}( \phi | -)$
for some
$\operatorname {\mathrm {tr}}( \phi | -)$
for some
![]() $\phi \in C_c(G(F),\overline {\mathbf {Q}_{\ell }})$
. The key ingredient in the proof of Theorem 6.5.2 is the following result, which roughly says that
$\phi \in C_c(G(F),\overline {\mathbf {Q}_{\ell }})$
. The key ingredient in the proof of Theorem 6.5.2 is the following result, which roughly says that
![]() $\operatorname {\mathrm {Mant}}_{b,\mu }(\rho )$
is a continuous function of
$\operatorname {\mathrm {Mant}}_{b,\mu }(\rho )$
is a continuous function of
![]() $\rho $
.
$\rho $
.
Theorem 6.5.3. For any
![]() $\phi \in C_c(G(F),\overline {\mathbf {Q}_{\ell }})$
, the linear form
$\phi \in C_c(G(F),\overline {\mathbf {Q}_{\ell }})$
, the linear form
is a trace form.
With future applications in mind, we’ll actually prove the following refined form of this theorem which also accounts for the Weil group action.
Theorem 6.5.4. For any fixed
![]() $\phi \in C_{c}(G(F),\overline {\mathbf {Q}_{\ell }})$
and
$\phi \in C_{c}(G(F),\overline {\mathbf {Q}_{\ell }})$
and
![]() $w\in W_{E}$
, the linear form
$w\in W_{E}$
, the linear form
![]() $\operatorname {\mathrm {Groth}}(G_{b}(F))\to \overline {\mathbf {Q}_{\ell }}$
defined by
$\operatorname {\mathrm {Groth}}(G_{b}(F))\to \overline {\mathbf {Q}_{\ell }}$
defined by
is a trace form.
In the classical setting of Rapoport–Zink spaces, this was conjectured by Taylor, cf. [Reference ShinShi12, Conjecture 8.3]. Taking
![]() $w=1$
, we deduce Theorem 6.5.3.
$w=1$
, we deduce Theorem 6.5.3.
Proof. For any reductive group
![]() $H/F$
, the trace Paley–Wiener theorem of Bernstein–Deligne–Kazhdan, [Reference Bernstein, Deligne and KazhdanBDK86], characterizes trace forms among all linear forms on
$H/F$
, the trace Paley–Wiener theorem of Bernstein–Deligne–Kazhdan, [Reference Bernstein, Deligne and KazhdanBDK86], characterizes trace forms among all linear forms on
![]() $\operatorname {\mathrm {Groth}}(H(F))$
by the following two conditions:
$\operatorname {\mathrm {Groth}}(H(F))$
by the following two conditions:
-
1. There is some open compact subgroup
 $K\subset H(F)$
such that
$K\subset H(F)$
such that
 $f(\pi )\neq 0$
only if
$f(\pi )\neq 0$
only if
 $\pi ^{K}\ne 0$
.
$\pi ^{K}\ne 0$
. -
2. For any parabolic
 $P=MU\subset H$
and any irreducible smooth
$P=MU\subset H$
and any irreducible smooth
 $M(F)$
-representation
$M(F)$
-representation
 $\sigma $
,
$\sigma $
,
 $f(i_{M}^{H}(\sigma \psi ))$
is an algebraic function of
$f(i_{M}^{H}(\sigma \psi ))$
is an algebraic function of
 $\psi $
, where
$\psi $
, where
 $\psi $
varies over the unramified characters of
$\psi $
varies over the unramified characters of
 $M(F)$
. Here,
$M(F)$
. Here,
 $i_{M}^{H}(-)$
denotes normalizes parabolic induction.
$i_{M}^{H}(-)$
denotes normalizes parabolic induction.
We’ll prove the theorem by showing that the linear form
![]() $\mathrm {tr}(\phi \times w | R\Gamma (G,b,\mu )[-])$
satisfies the conditions of the trace Paley–Wiener theorem, applied to the group
$\mathrm {tr}(\phi \times w | R\Gamma (G,b,\mu )[-])$
satisfies the conditions of the trace Paley–Wiener theorem, applied to the group
![]() $H=G_b$
.
$H=G_b$
.
Verification of Condition 1. Fix a pro-p open compact subgroup
![]() $K\subset G(F)$
such that
$K\subset G(F)$
such that
![]() $\phi $
is bi-K-invariant. If
$\phi $
is bi-K-invariant. If
![]() $\mathrm {tr}(\phi \times w| R\Gamma (G,b,\mu )[\rho ])\neq 0$
, then
$\mathrm {tr}(\phi \times w| R\Gamma (G,b,\mu )[\rho ])\neq 0$
, then
![]() $(i_{\mathbf {1}}^{\ast }T_{V^{\vee }_{\mu ,\overline {\mathbf {Q}_{\ell }}}}i_{b \ast }\rho )^{K}\neq 0$
. Therefore, it suffices to see that there is some open compact
$(i_{\mathbf {1}}^{\ast }T_{V^{\vee }_{\mu ,\overline {\mathbf {Q}_{\ell }}}}i_{b \ast }\rho )^{K}\neq 0$
. Therefore, it suffices to see that there is some open compact
![]() $K'\subset G_{b}(F)$
such that
$K'\subset G_{b}(F)$
such that
![]() $(i_{\mathbf {1}}^{\ast }T_{V^{\vee }_{\mu ,\overline {\mathbf {Q}_{\ell }}}}i_{b \ast }\rho )^{K}\neq 0$
only if
$(i_{\mathbf {1}}^{\ast }T_{V^{\vee }_{\mu ,\overline {\mathbf {Q}_{\ell }}}}i_{b \ast }\rho )^{K}\neq 0$
only if
![]() $\rho ^{K'}\neq 0$
. For this, write
$\rho ^{K'}\neq 0$
. For this, write
 $$ \begin{align*} (i_{\mathbf{1}}^{\ast}T_{V^{\vee}_{\mu,\overline{\mathbf{Q}_{\ell}}}}i_{b \ast}\rho)^{K} & \cong R\mathrm{Hom}(i_{\mathbf{1}!}\operatorname{\mathrm{cInd}}_{K}^{G(F)}\overline{\mathbf{Q}_{\ell}},T_{V^{\vee}_{\mu,\overline{\mathbf{Q}_{\ell}}}}i_{b \ast}\rho)\\ & \cong R\mathrm{Hom}(T_{V_{\mu,\overline{\mathbf{Q}_{\ell}}}}i_{\mathbf{1}!}\operatorname{\mathrm{cInd}}_{K}^{G(F)}\overline{\mathbf{Q}_{\ell}},i_{b \ast}\rho)\\ & \cong R\mathrm{Hom}(i_{b}^{\ast}T_{V_{\mu,\overline{\mathbf{Q}_{\ell}}}}i_{\mathbf{1}!}\operatorname{\mathrm{cInd}}_{K}^{G(F)}\overline{\mathbf{Q}_{\ell}},\rho). \end{align*} $$
$$ \begin{align*} (i_{\mathbf{1}}^{\ast}T_{V^{\vee}_{\mu,\overline{\mathbf{Q}_{\ell}}}}i_{b \ast}\rho)^{K} & \cong R\mathrm{Hom}(i_{\mathbf{1}!}\operatorname{\mathrm{cInd}}_{K}^{G(F)}\overline{\mathbf{Q}_{\ell}},T_{V^{\vee}_{\mu,\overline{\mathbf{Q}_{\ell}}}}i_{b \ast}\rho)\\ & \cong R\mathrm{Hom}(T_{V_{\mu,\overline{\mathbf{Q}_{\ell}}}}i_{\mathbf{1}!}\operatorname{\mathrm{cInd}}_{K}^{G(F)}\overline{\mathbf{Q}_{\ell}},i_{b \ast}\rho)\\ & \cong R\mathrm{Hom}(i_{b}^{\ast}T_{V_{\mu,\overline{\mathbf{Q}_{\ell}}}}i_{\mathbf{1}!}\operatorname{\mathrm{cInd}}_{K}^{G(F)}\overline{\mathbf{Q}_{\ell}},\rho). \end{align*} $$
But now
![]() $i_{b}^{\ast }T_{V_{\mu ,\overline {\mathbf {Q}_{\ell }}}}i_{\mathbf {1}!}\operatorname {\mathrm {cInd}}_{K}^{G(F)}\overline {\mathbf {Q}_{\ell }}$
is compact and hence supported on only finitely many Bernstein components for
$i_{b}^{\ast }T_{V_{\mu ,\overline {\mathbf {Q}_{\ell }}}}i_{\mathbf {1}!}\operatorname {\mathrm {cInd}}_{K}^{G(F)}\overline {\mathbf {Q}_{\ell }}$
is compact and hence supported on only finitely many Bernstein components for
![]() $G_{b}(F)$
. This shows that the irreducible
$G_{b}(F)$
. This shows that the irreducible
![]() $\rho $
’s with
$\rho $
’s with
![]() $(i_{\mathbf {1}}^{\ast }T_{V^{\vee }_{\mu ,\overline {\mathbf {Q}_{\ell }}}}i_{b \ast }\rho )^{K}\neq 0$
are supported on finitely many Bernstein components for
$(i_{\mathbf {1}}^{\ast }T_{V^{\vee }_{\mu ,\overline {\mathbf {Q}_{\ell }}}}i_{b \ast }\rho )^{K}\neq 0$
are supported on finitely many Bernstein components for
![]() $G_{b}(F)$
. Quite generally, if
$G_{b}(F)$
. Quite generally, if
![]() $\Theta $
is any finite union of Bernstein components for
$\Theta $
is any finite union of Bernstein components for
![]() $G_{b}(F)$
, we can choose an open compact subgroup
$G_{b}(F)$
, we can choose an open compact subgroup
![]() $K'\subset G_{b}(F)$
such that
$K'\subset G_{b}(F)$
such that
![]() $\rho ^{K'}\neq 0$
if
$\rho ^{K'}\neq 0$
if
![]() $\rho $
is supported on
$\rho $
is supported on
![]() $\Theta $
. This gives the result.
$\Theta $
. This gives the result.
Verification of Condition 2. Fix
![]() $P=MU\subset G_{b}$
and
$P=MU\subset G_{b}$
and
![]() $\sigma $
as in Condition 2. Let
$\sigma $
as in Condition 2. Let
![]() $X=\mathrm {Spec}R$
be the smooth affine algebraic variety over
$X=\mathrm {Spec}R$
be the smooth affine algebraic variety over
![]() $\overline {\mathbf {Q}_{\ell }}$
parametrizing unramified characters of
$\overline {\mathbf {Q}_{\ell }}$
parametrizing unramified characters of
![]() $M(F)$
. Let
$M(F)$
. Let
![]() $\boldsymbol {\psi }:M(F)\to R^{\times }$
be the universal character and form
$\boldsymbol {\psi }:M(F)\to R^{\times }$
be the universal character and form
![]() $\Pi =i_{M}^{G_{b}}(\sigma \boldsymbol {\psi })$
. This is an admissible smooth
$\Pi =i_{M}^{G_{b}}(\sigma \boldsymbol {\psi })$
. This is an admissible smooth
![]() $R[G_{b}(F)]$
-module interpolating the parabolic inductions
$R[G_{b}(F)]$
-module interpolating the parabolic inductions
![]() $i_{M}^{G_{b}}(\sigma \psi )$
over varying unramified characters
$i_{M}^{G_{b}}(\sigma \psi )$
over varying unramified characters
![]() $\psi $
in the evident sense.Footnote 6 Since
$\psi $
in the evident sense.Footnote 6 Since
![]() $\Pi $
is admissible, the pushforward
$\Pi $
is admissible, the pushforward
![]() $i_{b \ast }\Pi \in D_{\mathrm {lis}}(\mathrm {Bun}_{G},R)$
is ULA. Since Hecke operators preserve ULA complexes, we deduce that
$i_{b \ast }\Pi \in D_{\mathrm {lis}}(\mathrm {Bun}_{G},R)$
is ULA. Since Hecke operators preserve ULA complexes, we deduce that
![]() $i_{\mathbf {1}}^{\ast }T_{V^{\vee }_{\mu ,R}}i_{b \ast }\Pi \in D(G(F),R)^{BW_{E}}$
is an admissible complex of smooth
$i_{\mathbf {1}}^{\ast }T_{V^{\vee }_{\mu ,R}}i_{b \ast }\Pi \in D(G(F),R)^{BW_{E}}$
is an admissible complex of smooth
![]() $R[G(F)]$
-modules with
$R[G(F)]$
-modules with
![]() $W_{E}$
-action, which interpolates the individual complexes
$W_{E}$
-action, which interpolates the individual complexes
in the evident sense.
Now fix a pro-p open compact subgroup
![]() $K \subset G(F)$
such that
$K \subset G(F)$
such that
![]() $\phi $
is bi-K-invariant, so
$\phi $
is bi-K-invariant, so
![]() $\phi \times w$
defines an endomorphism of the perfect complex
$\phi \times w$
defines an endomorphism of the perfect complex
Let
![]() $f\in R$
be the trace of this endomorphism. Unwinding definitions, we see that, for any unramified character
$f\in R$
be the trace of this endomorphism. Unwinding definitions, we see that, for any unramified character
![]() $\psi :M(F)\to \overline {\mathbf {Q}_{\ell }}^{\times }$
with associated point
$\psi :M(F)\to \overline {\mathbf {Q}_{\ell }}^{\times }$
with associated point
![]() $x_{\psi }\in X(\overline {\mathbf {Q}_{\ell }})$
, there is an equality
$x_{\psi }\in X(\overline {\mathbf {Q}_{\ell }})$
, there is an equality
This shows that
![]() $\mathrm {tr}(\phi \times w|R\Gamma (G,b,\mu )[i_{M}^{G_{b}}(\sigma \psi )])$
is an algebraic function of
$\mathrm {tr}(\phi \times w|R\Gamma (G,b,\mu )[i_{M}^{G_{b}}(\sigma \psi )])$
is an algebraic function of
![]() $\psi $
, as desired.
$\psi $
, as desired.
Let us say a subset
![]() $S\subset \mathrm {Irr}_{\overline {\mathbf {Q}_{\ell }}}(G(F))$
is dense if any trace form on
$S\subset \mathrm {Irr}_{\overline {\mathbf {Q}_{\ell }}}(G(F))$
is dense if any trace form on
![]() $\operatorname {\mathrm {Groth}}(G(F))$
which vanishes on S vanishes identically. For instance, the Langlands classification implies that (for any fixed choice of isomorphism
$\operatorname {\mathrm {Groth}}(G(F))$
which vanishes on S vanishes identically. For instance, the Langlands classification implies that (for any fixed choice of isomorphism
![]() $\mathbf {C}\simeq \overline {\mathbf {Q}_{\ell }}$
) tempered representations are dense, cf. [Reference KazhdanKaz86, Theorem 0].
$\mathbf {C}\simeq \overline {\mathbf {Q}_{\ell }}$
) tempered representations are dense, cf. [Reference KazhdanKaz86, Theorem 0].
Lemma 6.5.5. The subset of irreducible representations
![]() $\pi \in \mathrm {Irr}_{\overline {\mathbf {Q}_{\ell }}}(G(F))$
admitting
$\pi \in \mathrm {Irr}_{\overline {\mathbf {Q}_{\ell }}}(G(F))$
admitting
![]() $\overline {\mathbf {Z}_{\ell }}$
-lattices is dense.
$\overline {\mathbf {Z}_{\ell }}$
-lattices is dense.
It seems reasonable to think of this lemma as an
![]() $\ell $
-adic analogue of the density of tempered representations.
$\ell $
-adic analogue of the density of tempered representations.
Proof. Let f be a trace form, and assume that
![]() $f(\tau )=0$
for every
$f(\tau )=0$
for every
![]() $\tau \in \mathrm {Irr}_{\overline {\mathbf {Q}_{\ell }}}(G(F))$
admitting a
$\tau \in \mathrm {Irr}_{\overline {\mathbf {Q}_{\ell }}}(G(F))$
admitting a
![]() $\overline {\mathbf {Z}_{\ell }}$
-lattice.
$\overline {\mathbf {Z}_{\ell }}$
-lattice.
By Proposition C.2.2, it’s enough to show that
![]() $f( i_{M}^{G}(\sigma \psi ))=0$
for any parabolic
$f( i_{M}^{G}(\sigma \psi ))=0$
for any parabolic
![]() $P=MU \subset G$
, any unramified character
$P=MU \subset G$
, any unramified character
![]() $\psi $
of
$\psi $
of
![]() $M(F)$
and any
$M(F)$
and any
![]() $\sigma \in \mathrm {Irr}_{\overline {\mathbf {Q}_{\ell }}}(M(F))$
admitting a
$\sigma \in \mathrm {Irr}_{\overline {\mathbf {Q}_{\ell }}}(M(F))$
admitting a
![]() $\overline {\mathbf {Z}_{\ell }}$
-lattice. Fix P and
$\overline {\mathbf {Z}_{\ell }}$
-lattice. Fix P and
![]() $\sigma $
, and consider the function g on unramified characters of
$\sigma $
, and consider the function g on unramified characters of
![]() $M(F)$
sending
$M(F)$
sending
![]() $\psi $
to
$\psi $
to
![]() $f \left ( i_{M}^{G}(\sigma \psi ) \right )$
. By the easy direction of the trace Paley–Wiener theorem, g is a regular function on the variety of unramified characters of
$f \left ( i_{M}^{G}(\sigma \psi ) \right )$
. By the easy direction of the trace Paley–Wiener theorem, g is a regular function on the variety of unramified characters of
![]() $M(F)$
.
$M(F)$
.
Let us say an unramified character
![]() $\psi $
is integral if it takes values in
$\psi $
is integral if it takes values in
![]() $\overline {\mathbf {Z}_{\ell }}^{\times }$
. If
$\overline {\mathbf {Z}_{\ell }}^{\times }$
. If
![]() $\psi $
is integral, then
$\psi $
is integral, then
![]() $\sigma \psi $
admits a
$\sigma \psi $
admits a
![]() $\overline {\mathbf {Z}_{\ell }}$
-lattice, and hence also
$\overline {\mathbf {Z}_{\ell }}$
-lattice, and hence also
![]() $i_{M}^{G}(\sigma \psi )$
admits a
$i_{M}^{G}(\sigma \psi )$
admits a
![]() $\overline {\mathbf {Z}_{\ell }}$
-lattice. In particular, if
$\overline {\mathbf {Z}_{\ell }}$
-lattice. In particular, if
![]() $\psi $
is integral and
$\psi $
is integral and
![]() $i_{M}^{G}(\sigma \psi )$
is irreducible, then
$i_{M}^{G}(\sigma \psi )$
is irreducible, then
![]() $g(\psi )=0$
by combining these observations with our assumption on f. Now integral characters are Zariski-dense in the variety of unramified characters of
$g(\psi )=0$
by combining these observations with our assumption on f. Now integral characters are Zariski-dense in the variety of unramified characters of
![]() $M(F)$
, and the subset T of integral characters such that
$M(F)$
, and the subset T of integral characters such that
![]() $i_{M}^{G}(\sigma \psi )$
is irreducible is also Zariski-dense (use [Reference DatDat05, Theorem 5.1]). Since
$i_{M}^{G}(\sigma \psi )$
is irreducible is also Zariski-dense (use [Reference DatDat05, Theorem 5.1]). Since
![]() $g(\psi )=0$
for all
$g(\psi )=0$
for all
![]() $\psi \in T$
, we deduce that
$\psi \in T$
, we deduce that
![]() $g \equiv 0$
, so in particular
$g \equiv 0$
, so in particular
for all
![]() $\psi $
. This gives the result.
$\psi $
. This gives the result.
Proof of Theorem 6.5.2
Fix
![]() $\phi $
as in the statement of the theorem, and consider the linear form
$\phi $
as in the statement of the theorem, and consider the linear form
on
![]() $\operatorname {\mathrm {Groth}}(G_b(F))$
. By Theorem 6.4.9, we know that
$\operatorname {\mathrm {Groth}}(G_b(F))$
. By Theorem 6.4.9, we know that
![]() $f(\rho )=0$
if
$f(\rho )=0$
if
![]() $\rho $
admits a lattice. We need to show that f vanishes identically.
$\rho $
admits a lattice. We need to show that f vanishes identically.
The key observation is that f is a trace form. Indeed,
![]() $\operatorname {\mathrm {tr}}(\phi | \operatorname {\mathrm {Mant}}_{b,\mu }(-))$
is a trace form by Theorem 6.5.3. Moreover,
$\operatorname {\mathrm {tr}}(\phi | \operatorname {\mathrm {Mant}}_{b,\mu }(-))$
is a trace form by Theorem 6.5.3. Moreover,
![]() $\left [\mathcal {T}_{b,\mu }^{\kern3pt G_b\to G} (\operatorname {\mathrm {tr.dist}} - )\right ](\phi )$
is a trace form since we can rewrite
$\left [\mathcal {T}_{b,\mu }^{\kern3pt G_b\to G} (\operatorname {\mathrm {tr.dist}} - )\right ](\phi )$
is a trace form since we can rewrite
![]() $\left [\mathcal {T}_{b,\mu }^{\kern3pt G_b\to G} (\operatorname {\mathrm {tr.dist}} \rho )\right ](\phi )$
as the trace of
$\left [\mathcal {T}_{b,\mu }^{\kern3pt G_b\to G} (\operatorname {\mathrm {tr.dist}} \rho )\right ](\phi )$
as the trace of
![]() $\widetilde {T}_{b,\mu }^{G\to G_b}(\phi ) \in C_c(G_b(F)_{\operatorname {\mathrm {ell}}},\overline {\mathbf {Q}_{\ell }})_{G_b(F)}$
acting on
$\widetilde {T}_{b,\mu }^{G\to G_b}(\phi ) \in C_c(G_b(F)_{\operatorname {\mathrm {ell}}},\overline {\mathbf {Q}_{\ell }})_{G_b(F)}$
acting on
![]() $\rho $
. Thus, f is a difference of trace forms and hence a trace form. Since
$\rho $
. Thus, f is a difference of trace forms and hence a trace form. Since
![]() $f(\rho )=0$
for any
$f(\rho )=0$
for any
![]() $\rho $
admitting a lattice, Lemma 6.5.5 now implies the desired result.
$\rho $
admitting a lattice, Lemma 6.5.5 now implies the desired result.
For the final claim about virtual characters, choose compatible
![]() $\overline {\mathbf {Q}_{\ell }}$
-valued Haar measures
$\overline {\mathbf {Q}_{\ell }}$
-valued Haar measures
![]() $dg$
and
$dg$
and
![]() $dg'$
on
$dg'$
on
![]() $G(F)$
and
$G(F)$
and
![]() $G_b(F)$
. Fix some
$G_b(F)$
. Fix some
![]() $\rho $
, and let
$\rho $
, and let
![]() be the virtual character of
be the virtual character of
![]() $\operatorname {\mathrm {Mant}}_{b,\mu }(\rho )$
. Pick any
$\operatorname {\mathrm {Mant}}_{b,\mu }(\rho )$
. Pick any
![]() $\phi \in C_c(G(F)_{\operatorname {\mathrm {ell}}},\overline {\mathbf {Q}_{\ell }})$
. Then
$\phi \in C_c(G(F)_{\operatorname {\mathrm {ell}}},\overline {\mathbf {Q}_{\ell }})$
. Then
by definition. On the other hand,
by compatibility of the Haar measures and Proposition 6.3.5. Combining these observations, we get an equality
for any
![]() $\phi \in C_c(G(F)_{\operatorname {\mathrm {ell}}},\overline {\mathbf {Q}_{\ell }})$
. The result now follows by varying
$\phi \in C_c(G(F)_{\operatorname {\mathrm {ell}}},\overline {\mathbf {Q}_{\ell }})$
. The result now follows by varying
![]() $\phi $
.
$\phi $
.
Proof of Theorem 6.5.1
The claimed equality in
![]() $\operatorname {\mathrm {Groth}}(G(F))$
is an immediate consequence of Theorem 6.5.2 and Theorem 3.2.9.
$\operatorname {\mathrm {Groth}}(G(F))$
is an immediate consequence of Theorem 6.5.2 and Theorem 3.2.9.
For the claim regarding the error term, consider the virtual representation
 $$\begin{align*}\mathrm{err}=\operatorname{\mathrm{Mant}}_{b,\mu}(\rho)- \sum_{\pi\in \Pi_{\phi}(G)} \dim \operatorname{\mathrm{Hom}}_{S_{\phi}}(\delta_{\pi,\rho},r_{\mu})\pi. \end{align*}$$
$$\begin{align*}\mathrm{err}=\operatorname{\mathrm{Mant}}_{b,\mu}(\rho)- \sum_{\pi\in \Pi_{\phi}(G)} \dim \operatorname{\mathrm{Hom}}_{S_{\phi}}(\delta_{\pi,\rho},r_{\mu})\pi. \end{align*}$$
By the first half of the theorem, we know that
![]() $\mathrm {err}$
is nonelliptic. By Theorem C.1.1, it thus suffices to show that
$\mathrm {err}$
is nonelliptic. By Theorem C.1.1, it thus suffices to show that
![]() $\mathrm {err}$
is a virtual sum of supercuspidal representations. Since the packet
$\mathrm {err}$
is a virtual sum of supercuspidal representations. Since the packet
![]() $\Pi _{\phi }(G)$
is supercuspidal by assumption, we’re reduced to showing that
$\Pi _{\phi }(G)$
is supercuspidal by assumption, we’re reduced to showing that
![]() $\operatorname {\mathrm {Mant}}_{b,\mu }(\rho )$
is a virtual supercuspidal representation. By definition, this is the Grothendieck class of the complex
$\operatorname {\mathrm {Mant}}_{b,\mu }(\rho )$
is a virtual supercuspidal representation. By definition, this is the Grothendieck class of the complex
![]() $A = i_{\mathbf {1}}^{\ast } T_{V^{\vee }_{\mu ,\overline {\mathbf {Q}_{\ell }}}} i_{b \ast } \rho \in D(G(F),\overline {\mathbf {Q}_{\ell }})$
, so we need to see that any irreducible
$A = i_{\mathbf {1}}^{\ast } T_{V^{\vee }_{\mu ,\overline {\mathbf {Q}_{\ell }}}} i_{b \ast } \rho \in D(G(F),\overline {\mathbf {Q}_{\ell }})$
, so we need to see that any irreducible
![]() $\tau $
occurring in the Jordan-Hölder series of
$\tau $
occurring in the Jordan-Hölder series of
![]() $H^{\ast } (A)$
is supercuspidal. Since
$H^{\ast } (A)$
is supercuspidal. Since
![]() $\varphi _{\tau } = \varphi _{\rho }$
by the commutation of Hecke operators with excursion operators, the claim now follows from the assumption on
$\varphi _{\tau } = \varphi _{\rho }$
by the commutation of Hecke operators with excursion operators, the claim now follows from the assumption on
![]() $\varphi _{\rho }$
and [Reference Fargues and ScholzeFS21, Theorem I.9.6.viii].
$\varphi _{\rho }$
and [Reference Fargues and ScholzeFS21, Theorem I.9.6.viii].
6.6 Application to inner forms of
 $\operatorname {\mathrm {GL}}_n$
$\operatorname {\mathrm {GL}}_n$
We give an application to the local Langlands correspondence. Recall that, for any
![]() $G/F$
, any
$G/F$
, any
![]() $b\in B(G)$
and any
$b\in B(G)$
and any
![]() $\tau \in \mathrm {Irr}(G_b(F))$
, the construction in [Reference Fargues and ScholzeFS21, Proposition I.9.1] (applied to
$\tau \in \mathrm {Irr}(G_b(F))$
, the construction in [Reference Fargues and ScholzeFS21, Proposition I.9.1] (applied to
![]() $A= i_{b!} \tau $
) gives rise to a semisimple L-parameter
$A= i_{b!} \tau $
) gives rise to a semisimple L-parameter
![]() $\varphi _{\tau }:W_F \to \phantom {}^L G(\overline {\mathbf {Q}_{\ell }})$
associated with
$\varphi _{\tau }:W_F \to \phantom {}^L G(\overline {\mathbf {Q}_{\ell }})$
associated with
![]() $\tau $
. This construction is canonical and satisfies a long list of desirable properties [Reference Fargues and ScholzeFS21, Theorem I.9.6]. However, it is a highly nontrivial problem to compare this construction with ‘previously known’ realizations of the local Langlands correspondence.
$\tau $
. This construction is canonical and satisfies a long list of desirable properties [Reference Fargues and ScholzeFS21, Theorem I.9.6]. However, it is a highly nontrivial problem to compare this construction with ‘previously known’ realizations of the local Langlands correspondence.
Theorem 6.6.1. Let G be any inner form of
![]() $\mathrm {GL}_n/F$
, and let
$\mathrm {GL}_n/F$
, and let
![]() $\pi $
be an irreducible smooth representation of
$\pi $
be an irreducible smooth representation of
![]() $G(F)$
. Then the L-parameter
$G(F)$
. Then the L-parameter
![]() $\varphi _{\pi }$
associated with
$\varphi _{\pi }$
associated with
![]() $\pi $
as in [Reference Fargues and ScholzeFS21, §I.9] agrees with the usual semisimplified L-parameter attached to
$\pi $
as in [Reference Fargues and ScholzeFS21, §I.9] agrees with the usual semisimplified L-parameter attached to
![]() $\pi $
.
$\pi $
.
Proof. By [Reference Fargues and ScholzeFS21, Theorem I.9.6.viii], we can assume
![]() $\pi $
is supercuspidal. Pick some basic b with
$\pi $
is supercuspidal. Pick some basic b with
![]() $G_b = \mathrm {GL}_{n}/F$
, and let
$G_b = \mathrm {GL}_{n}/F$
, and let
![]() $\rho \in \mathrm {Irr}(G_b(F))$
be the Jacquet–Langlands transfer of
$\rho \in \mathrm {Irr}(G_b(F))$
be the Jacquet–Langlands transfer of
![]() $\pi $
[Reference Deligne, Kazhdan and VignérasDKV84], so the (usual) semisimple L-parameters of
$\pi $
[Reference Deligne, Kazhdan and VignérasDKV84], so the (usual) semisimple L-parameters of
![]() $\rho $
and
$\rho $
and
![]() $\pi $
agree. By [Reference Fargues and ScholzeFS21, Theorem 1.9.6.viii-ix], we know that
$\pi $
agree. By [Reference Fargues and ScholzeFS21, Theorem 1.9.6.viii-ix], we know that
![]() $\varphi _{\rho }$
agrees with the usual semisimple L-parameter of
$\varphi _{\rho }$
agrees with the usual semisimple L-parameter of
![]() $\rho $
. To prove the theorem, it thus suffices to show that
$\rho $
. To prove the theorem, it thus suffices to show that
![]() $\varphi _{\pi } = \varphi _{\rho }$
.
$\varphi _{\pi } = \varphi _{\rho }$
.
Pick any
![]() $\mu $
such that
$\mu $
such that
![]() $b \in B(G,\mu )$
. By Theorem 6.5.2 and the usual character relation characterizing the Jacquet–Langlands correspondence, we have an equality
$b \in B(G,\mu )$
. By Theorem 6.5.2 and the usual character relation characterizing the Jacquet–Langlands correspondence, we have an equality
![]() $\operatorname {\mathrm {Mant}}_{b,\mu }(\rho ) = \dim V_{\mu } \cdot \pi + e$
in
$\operatorname {\mathrm {Mant}}_{b,\mu }(\rho ) = \dim V_{\mu } \cdot \pi + e$
in
![]() $\operatorname {\mathrm {Groth}}(G(F))$
, where e is a nonelliptic virtual representation. Since
$\operatorname {\mathrm {Groth}}(G(F))$
, where e is a nonelliptic virtual representation. Since
![]() $\pi $
is supercuspidal, this implies that
$\pi $
is supercuspidal, this implies that
![]() $\pi $
occurs as a subquotient of some cohomology group of the complex
$\pi $
occurs as a subquotient of some cohomology group of the complex
![]() $A = i_{\mathbf {1}}^{\ast } T_{V^{\vee }_{\mu ,\overline {\mathbf {Q}_{\ell }}}} i_{b \ast } \rho \in D(G(F),\overline {\mathbf {Q}_{\ell }})$
. But Hecke operators commute with excursion operators, so
$A = i_{\mathbf {1}}^{\ast } T_{V^{\vee }_{\mu ,\overline {\mathbf {Q}_{\ell }}}} i_{b \ast } \rho \in D(G(F),\overline {\mathbf {Q}_{\ell }})$
. But Hecke operators commute with excursion operators, so
![]() $\varphi _{\tau } = \varphi _{\rho }$
for any irreducible
$\varphi _{\tau } = \varphi _{\rho }$
for any irreducible
![]() $\tau $
occurring in the Jordan–Holder series of
$\tau $
occurring in the Jordan–Holder series of
![]() $H^{\ast } (A)$
.
$H^{\ast } (A)$
.
A Endoscopy
A.1 Endoscopic character relations
We recall here the endoscopic character identities, which are part of the refined local Langlands correspondence, following the formulation of [Reference KalethaKal16b, §5.4], also recalled in [Reference KalethaKal16a, §4.2]. They play a key role in the proof of Theorem 3.2.9. We recall the notation established before the statement of that theorem.
-
•
 $F/\mathbf {Q}_p$
is a finite extension,
$F/\mathbf {Q}_p$
is a finite extension,
 $F^{\mathrm {nr}}/F$
a maximal unramified extension.
$F^{\mathrm {nr}}/F$
a maximal unramified extension. -
• G is a connected reductive group defined over F.
-
•
 $G^*$
is a quasi-split connected reductive group defined over F.
$G^*$
is a quasi-split connected reductive group defined over F. -
•
 $\Psi $
is a
$\Psi $
is a
 $G^*$
-conjugacy class of inner twists
$G^*$
-conjugacy class of inner twists
 $\psi \colon G^*\to G$
.
$\psi \colon G^*\to G$
. -
•
 $\bar z_{\sigma }=\psi ^{-1}\sigma (\psi )\in G^*_{\mathrm {ad}}$
so that
$\bar z_{\sigma }=\psi ^{-1}\sigma (\psi )\in G^*_{\mathrm {ad}}$
so that
 $\bar z\in Z^1(F,G^*_{\mathrm {ad}})$
.
$\bar z\in Z^1(F,G^*_{\mathrm {ad}})$
. -
•
 $z\in Z^1(u\to W,Z(G^*)\to G^*)$
is a lift of
$z\in Z^1(u\to W,Z(G^*)\to G^*)$
is a lift of
 $\bar z$
.
$\bar z$
. -
•
 $b\in G(F^{\mathrm {nr}})$
is a decent basic element.
$b\in G(F^{\mathrm {nr}})$
is a decent basic element. -
•
 $G_b$
is the corresponding inner form of G.
$G_b$
is the corresponding inner form of G. -
•
 $\xi \colon G_{F^{\mathrm {nr}}}\to G_{b,F^{\mathrm {nr}}}$
is the identity map.
$\xi \colon G_{F^{\mathrm {nr}}}\to G_{b,F^{\mathrm {nr}}}$
is the identity map. -
•
 $z_b \in Z^1(u\to W,Z(G)\to G)$
and
$z_b \in Z^1(u\to W,Z(G)\to G)$
and
 $g \in G(\overline {\breve F})$
satisfy equation (2.3.1).
$g \in G(\overline {\breve F})$
satisfy equation (2.3.1). -
•
 $\mathfrak {w}$
is a Whittaker datum for
$\mathfrak {w}$
is a Whittaker datum for
 $G^*$
.
$G^*$
. -
•
 $\phi \colon W_F \times \mathrm {SL}_2 \to {^LG}$
is a discrete L-parameter.
$\phi \colon W_F \times \mathrm {SL}_2 \to {^LG}$
is a discrete L-parameter. -
•
 $S_{\phi }=\operatorname {\mathrm {Cent}}(\phi ,\widehat {G})$
.
$S_{\phi }=\operatorname {\mathrm {Cent}}(\phi ,\widehat {G})$
. -
•
 $S_{\phi }^+$
is the group defined in Definition 2.3.1.
$S_{\phi }^+$
is the group defined in Definition 2.3.1. -
•
 $\lambda _z$
, resp.,
$\lambda _z$
, resp.,
 $\lambda _{z_b}$
the image of the class of z, resp.,
$\lambda _{z_b}$
the image of the class of z, resp.,
 $z_b$
under the isomorphism
$z_b$
under the isomorphism
 $H^1(u \to W,Z(G^*) \to G^*) \to \pi _0(Z(\widehat {\bar G})^+)^*$
.
$H^1(u \to W,Z(G^*) \to G^*) \to \pi _0(Z(\widehat {\bar G})^+)^*$
.
Recall that
![]() $\mathrm {Ad}(g) : G_{z_b} \to G_b$
is an F-isomorphism. We will use it to identify the two groups and drop g from the notation. We will use the letter g for a different purpose below.
$\mathrm {Ad}(g) : G_{z_b} \to G_b$
is an F-isomorphism. We will use it to identify the two groups and drop g from the notation. We will use the letter g for a different purpose below.
Associated to
![]() $\phi $
are the L-packets
$\phi $
are the L-packets
![]() $\Pi _{\phi }(G)$
and
$\Pi _{\phi }(G)$
and
![]() $\Pi _{\phi }(G_{z_b})$
and the bijections
$\Pi _{\phi }(G_{z_b})$
and the bijections
denoted by
![]() $\pi \mapsto \tau _{z,\mathfrak {w},\pi }$
and
$\pi \mapsto \tau _{z,\mathfrak {w},\pi }$
and
![]() $\rho \mapsto \tau _{z,\mathfrak {w},\rho }$
.
$\rho \mapsto \tau _{z,\mathfrak {w},\rho }$
.
We now choose a semisimple element
![]() $s \in S_{\phi }$
and an element
$s \in S_{\phi }$
and an element
![]() $\dot s \in S_{\phi }^+$
which lifts s. Let
$\dot s \in S_{\phi }^+$
which lifts s. Let
![]() $e(G)$
and
$e(G)$
and
![]() $e(G_{z_b})$
be the Kottwitz signs of the groups G and
$e(G_{z_b})$
be the Kottwitz signs of the groups G and
![]() $G_{z_b}$
, as defined in [Reference KottwitzKot83]. Of course,
$G_{z_b}$
, as defined in [Reference KottwitzKot83]. Of course,
![]() $e(G_{z_b})=e(G_b)$
. Consider the virtual characters
$e(G_{z_b})=e(G_b)$
. Consider the virtual characters
 $$\begin{align*}e(G)\sum_{\pi \in \Pi_{\phi}(G)} \operatorname{\mathrm{tr}}\tau_{z,\mathfrak{w},\pi}(\dot s) \cdot \Theta_{\pi}\qquad\mathrm{and}\qquad e(G_{z_b})\sum_{\rho \in \Pi_{\phi}(G_{z_b})} \operatorname{\mathrm{tr}}\tau_{z,\mathfrak{w},\rho}(\dot s) \cdot \Theta_{\rho}.\end{align*}$$
$$\begin{align*}e(G)\sum_{\pi \in \Pi_{\phi}(G)} \operatorname{\mathrm{tr}}\tau_{z,\mathfrak{w},\pi}(\dot s) \cdot \Theta_{\pi}\qquad\mathrm{and}\qquad e(G_{z_b})\sum_{\rho \in \Pi_{\phi}(G_{z_b})} \operatorname{\mathrm{tr}}\tau_{z,\mathfrak{w},\rho}(\dot s) \cdot \Theta_{\rho}.\end{align*}$$
The endoscopic character identities are equations which relate these two virtual characters to virtual characters on an endoscopic group
![]() $H_1$
. From the pair
$H_1$
. From the pair
![]() $(\phi ,\dot s)$
, one obtains a refined elliptic endoscopic datum
$(\phi ,\dot s)$
, one obtains a refined elliptic endoscopic datum
in the sense of [Reference KalethaKal16b, §5.3] as follows. Let
![]() $\widehat H=\mathrm {Cent}(s,\widehat G)^{\circ }$
. The image of
$\widehat H=\mathrm {Cent}(s,\widehat G)^{\circ }$
. The image of
![]() $\phi $
is contained in
$\phi $
is contained in
![]() $\mathrm {Cent}(s,\widehat G)$
, which in turns acts by conjugation on its connected component
$\mathrm {Cent}(s,\widehat G)$
, which in turns acts by conjugation on its connected component
![]() $\widehat H$
. This gives a homomorphism
$\widehat H$
. This gives a homomorphism
![]() $W_F \to \mathrm {Aut}(\widehat H)$
. Letting
$W_F \to \mathrm {Aut}(\widehat H)$
. Letting
![]() $\Psi _0(\widehat H)$
be the based root datum of
$\Psi _0(\widehat H)$
be the based root datum of
![]() $\widehat H$
[Reference KottwitzKot84b, §1.1] and
$\widehat H$
[Reference KottwitzKot84b, §1.1] and
![]() $\Psi _0^{\vee }(\widehat H)$
its dual, we obtain the homomorphism
$\Psi _0^{\vee }(\widehat H)$
its dual, we obtain the homomorphism
Since the target is finite, this homomorphism extends to
![]() $\Gamma _F$
, and we obtain a based root datum with Galois action, hence a quasi-split connected reductive group H defined over F. Its dual group is by construction equal to
$\Gamma _F$
, and we obtain a based root datum with Galois action, hence a quasi-split connected reductive group H defined over F. Its dual group is by construction equal to
![]() $\widehat H$
. We let
$\widehat H$
. We let
![]() $\mathcal {H}=\widehat H \cdot \phi (W_F)$
, noting that the right factor normalizes the left, so their product
$\mathcal {H}=\widehat H \cdot \phi (W_F)$
, noting that the right factor normalizes the left, so their product
![]() $\mathcal {H}$
is a subgroup of
$\mathcal {H}$
is a subgroup of
![]() $^LG$
. Finally, we let
$^LG$
. Finally, we let
![]() $\eta : \mathcal {H} \to {^LG}$
be the natural inclusion. Note that by construction
$\eta : \mathcal {H} \to {^LG}$
be the natural inclusion. Note that by construction
![]() $\phi $
takes image in
$\phi $
takes image in
![]() $\mathcal {H}$
, i.e., it factors through
$\mathcal {H}$
, i.e., it factors through
![]() $\eta $
.
$\eta $
.
We can realize the L-group of H as
![]() $^LH = \widehat H \rtimes W_F$
, but we caution the reader that
$^LH = \widehat H \rtimes W_F$
, but we caution the reader that
![]() $W_F$
does not act on
$W_F$
does not act on
![]() $\widehat H$
via the map
$\widehat H$
via the map
![]() $W_F \to \mathrm {Aut}(\widehat H)$
given by
$W_F \to \mathrm {Aut}(\widehat H)$
given by
![]() $\phi $
as above. Rather, we have to modify this action to ensure that it preserves a pinning of
$\phi $
as above. Rather, we have to modify this action to ensure that it preserves a pinning of
![]() $\widehat H$
. More precisely, after fixing an arbitrary pinning of
$\widehat H$
. More precisely, after fixing an arbitrary pinning of
![]() $\widehat H$
, we obtain a splitting
$\widehat H$
, we obtain a splitting
![]() $\mathrm {Out}(\widehat H) \to \mathrm {Aut}(\widehat H)$
of the projection
$\mathrm {Out}(\widehat H) \to \mathrm {Aut}(\widehat H)$
of the projection
![]() $\mathrm {Aut}(\widehat H) \to \mathrm {Out}(\widehat H)$
, and the action of
$\mathrm {Aut}(\widehat H) \to \mathrm {Out}(\widehat H)$
, and the action of
![]() $W_F$
on
$W_F$
on
![]() $\widehat H$
we use to form
$\widehat H$
we use to form
![]() $^LH$
is given by composing the above map
$^LH$
is given by composing the above map
![]() $W_F \to \mathrm {Out}(\widehat H)$
with this splitting.
$W_F \to \mathrm {Out}(\widehat H)$
with this splitting.
Both
![]() $^LH$
and
$^LH$
and
![]() $\mathcal {H}$
are thus extensions of
$\mathcal {H}$
are thus extensions of
![]() $W_F$
by
$W_F$
by
![]() $\widehat H$
, but they need not be isomorphic. If they are, we fix arbitrarily an isomorphism
$\widehat H$
, but they need not be isomorphic. If they are, we fix arbitrarily an isomorphism
![]() $\eta _1 : \mathcal {H} \to {^LH}$
of extensions. Then
$\eta _1 : \mathcal {H} \to {^LH}$
of extensions. Then
![]() $\phi ^s = \eta _1 \circ \phi $
is a discrete parameter for H.
$\phi ^s = \eta _1 \circ \phi $
is a discrete parameter for H.
In the general case, we need to introduce a z-pair
![]() $\mathfrak {z}=(H_1,\eta _1)$
as in [Reference Kottwitz and ShelstadKS99, §2]. It consists of a z-extension
$\mathfrak {z}=(H_1,\eta _1)$
as in [Reference Kottwitz and ShelstadKS99, §2]. It consists of a z-extension
![]() $H_1 \to H$
(recall this means that
$H_1 \to H$
(recall this means that
![]() $H_1$
has a simply connected derived subgroup and the kernel of
$H_1$
has a simply connected derived subgroup and the kernel of
![]() $H_1 \to H$
is an induced torus) and
$H_1 \to H$
is an induced torus) and
![]() $\eta _1 : \mathcal {H} \to {^LH_1}$
is an L-embedding that extends the natural embedding
$\eta _1 : \mathcal {H} \to {^LH_1}$
is an L-embedding that extends the natural embedding
![]() $\widehat H \to \widehat H_1$
. As is shown in [Reference Kottwitz and ShelstadKS99, §2.2], such a z-pair always exists. Again, we set
$\widehat H \to \widehat H_1$
. As is shown in [Reference Kottwitz and ShelstadKS99, §2.2], such a z-pair always exists. Again, we set
![]() $\phi ^s = \eta _1 \circ \phi $
and obtain a discrete parameter for
$\phi ^s = \eta _1 \circ \phi $
and obtain a discrete parameter for
![]() $H_1$
. In the situation where an isomorphism
$H_1$
. In the situation where an isomorphism
![]() $\eta _1 : \mathcal {H} \to {^LH}$
does exist, we will allows ourselves to take
$\eta _1 : \mathcal {H} \to {^LH}$
does exist, we will allows ourselves to take
![]() $H=H_1$
and so regard
$H=H_1$
and so regard
![]() $\mathfrak {z}=(H,\eta _1)$
as a z-pair, even though in general H will not have a simply connected derived subgroup.
$\mathfrak {z}=(H,\eta _1)$
as a z-pair, even though in general H will not have a simply connected derived subgroup.
The virtual character on
![]() $H_1$
that the above virtual characters on G and
$H_1$
that the above virtual characters on G and
![]() $G_{z_b}$
are to be related to is
$G_{z_b}$
are to be related to is
 $$\begin{align*}S\Theta_{\phi^s} := \sum_{\pi^s \in \Pi_{\phi^s}(H_1)} \mathrm{dim}(\tau_{\pi^s})\Theta_{\pi^s}. \end{align*}$$
$$\begin{align*}S\Theta_{\phi^s} := \sum_{\pi^s \in \Pi_{\phi^s}(H_1)} \mathrm{dim}(\tau_{\pi^s})\Theta_{\pi^s}. \end{align*}$$
Here,
![]() $\pi ^s \mapsto \tau _{\pi ^s}$
is a bijection
$\pi ^s \mapsto \tau _{\pi ^s}$
is a bijection
![]() $\Pi _{\phi ^s}(H_1) \to \mathrm {Irr}(\pi _0(\mathrm {Cent}(\phi ^s,\widehat H_1)/Z(\widehat H_1)^{\Gamma }))$
determined by an arbitrary choice of Whittaker datum for
$\Pi _{\phi ^s}(H_1) \to \mathrm {Irr}(\pi _0(\mathrm {Cent}(\phi ^s,\widehat H_1)/Z(\widehat H_1)^{\Gamma }))$
determined by an arbitrary choice of Whittaker datum for
![]() $H_1$
. The argument in the proof of Lemma 2.3.3 shows the independence of
$H_1$
. The argument in the proof of Lemma 2.3.3 shows the independence of
![]() $\mathrm {dim}(\tau _{\pi ^s})$
of the choice of a Whittaker datum for
$\mathrm {dim}(\tau _{\pi ^s})$
of the choice of a Whittaker datum for
![]() $H_1$
.
$H_1$
.
The relationship between the virtual characters on G,
![]() $G_{z_b}$
and
$G_{z_b}$
and
![]() $H_1$
is expressed in terms of the Langlands–Shelstad transfer factor
$H_1$
is expressed in terms of the Langlands–Shelstad transfer factor
![]() $\Delta _{\mathrm {abs}}'[\mathfrak {\dot e},\mathfrak {z},\mathfrak {w},(\psi ,z)]$
for the pair of groups
$\Delta _{\mathrm {abs}}'[\mathfrak {\dot e},\mathfrak {z},\mathfrak {w},(\psi ,z)]$
for the pair of groups
![]() $(H_1,G)$
and the corresponding Langlands–Shelstad transfer factor
$(H_1,G)$
and the corresponding Langlands–Shelstad transfer factor
![]() $\Delta _{\mathrm {abs}}'[\mathfrak {\dot e},\mathfrak {z},\mathfrak {w},(\xi \circ \psi ,\psi ^{-1}(z_b)\cdot z)]$
for the pair of groups
$\Delta _{\mathrm {abs}}'[\mathfrak {\dot e},\mathfrak {z},\mathfrak {w},(\xi \circ \psi ,\psi ^{-1}(z_b)\cdot z)]$
for the pair of groups
![]() $(H_1,G_{z_b})$
, both of which are defined by [Reference KalethaKal16b, (5.10)]. We will abbreviate both of them to just
$(H_1,G_{z_b})$
, both of which are defined by [Reference KalethaKal16b, (5.10)]. We will abbreviate both of them to just
![]() $\Delta $
. It is a simple consequence of the Weyl integration formula that the character relation [Reference KalethaKal16b, (5.11)] can be restated in terms of character functions (rather than character distributions) as
$\Delta $
. It is a simple consequence of the Weyl integration formula that the character relation [Reference KalethaKal16b, (5.11)] can be restated in terms of character functions (rather than character distributions) as
 $$ \begin{align} e(G)\sum_{\pi\in \Pi_{\phi}(G)} \operatorname{\mathrm{tr}}\tau_{z,\mathfrak{w},\pi}(\dot s)\Theta_{\pi}(g)= \sum_{h_1\in H_1(F)/\mathrm{st.}} \Delta(h_1,g)S\Theta_{\phi^s}(h_1) \end{align} $$
$$ \begin{align} e(G)\sum_{\pi\in \Pi_{\phi}(G)} \operatorname{\mathrm{tr}}\tau_{z,\mathfrak{w},\pi}(\dot s)\Theta_{\pi}(g)= \sum_{h_1\in H_1(F)/\mathrm{st.}} \Delta(h_1,g)S\Theta_{\phi^s}(h_1) \end{align} $$
for any strongly regular semisimple element
![]() $g \in G(F)$
. The sum on the right runs over stable conjugacy classes of strongly regular semisimple elements of
$g \in G(F)$
. The sum on the right runs over stable conjugacy classes of strongly regular semisimple elements of
![]() $H_1(F)$
. We also have the analogous identity for
$H_1(F)$
. We also have the analogous identity for
![]() $G_{z_b}$
:
$G_{z_b}$
:
 $$ \begin{align} e(G_{z_b})\sum_{\rho\in \Pi_{\phi}(G_{z_b})} \operatorname{\mathrm{tr}}\tau_{z,\mathfrak{w},\rho}(\dot s)\Theta_{\rho}(g')= \sum_{h_1\in H_1(F)/\mathrm{st.}} \Delta(h_1,g')S\Theta_{\phi^s}(h_1). \end{align} $$
$$ \begin{align} e(G_{z_b})\sum_{\rho\in \Pi_{\phi}(G_{z_b})} \operatorname{\mathrm{tr}}\tau_{z,\mathfrak{w},\rho}(\dot s)\Theta_{\rho}(g')= \sum_{h_1\in H_1(F)/\mathrm{st.}} \Delta(h_1,g')S\Theta_{\phi^s}(h_1). \end{align} $$
For the purposes of this paper, we are only interested in the right-hand sides of these two equations as a bridge between their left-hand sides. Essential for this bridge is a certain compatibility between the transfer factors appearing on both right-hand sides:
Lemma A.1.1.
We need to explain the second factor. Given maximal tori
![]() $T_H \subset H$
and
$T_H \subset H$
and
![]() $T \subset G$
, there is a notion of an admissible isomorphism
$T \subset G$
, there is a notion of an admissible isomorphism
![]() $T_H \to T$
, for which we refer the reader to [Reference KalethaKal16a, §1.3]. Two strongly regular semisimple elements
$T_H \to T$
, for which we refer the reader to [Reference KalethaKal16a, §1.3]. Two strongly regular semisimple elements
![]() $h\in H(\mathbf {Q}_p)$
and
$h\in H(\mathbf {Q}_p)$
and
![]() $g\in G(\mathbf {Q}_p)$
are called related if there exists an admissible isomorphism
$g\in G(\mathbf {Q}_p)$
are called related if there exists an admissible isomorphism
![]() $T_h \to T_g$
between their centralizers mapping h to g. If such an isomorphism exists, it is unique, and in particular defined over F, and shall be called
$T_h \to T_g$
between their centralizers mapping h to g. If such an isomorphism exists, it is unique, and in particular defined over F, and shall be called
![]() $\varphi _{h,g}$
. An element
$\varphi _{h,g}$
. An element
![]() $h_1 \in H_1(F)$
is called related to
$h_1 \in H_1(F)$
is called related to
![]() $g \in G(F)$
if and only if its image
$g \in G(F)$
if and only if its image
![]() $h \in H(F)$
is so. Since g and
$h \in H(F)$
is so. Since g and
![]() $g'$
are stably conjugate, an element
$g'$
are stably conjugate, an element
![]() $h_1 \in H_1(F)$
is related to g if and only if it is related to
$h_1 \in H_1(F)$
is related to g if and only if it is related to
![]() $g'$
. If that is not the case, both
$g'$
. If that is not the case, both
![]() $\Delta (h_1,g')$
and
$\Delta (h_1,g')$
and
![]() $\Delta (h_1,g)$
are zero, and equation (A.1.4) is trivially true. Thus, assume that
$\Delta (h_1,g)$
are zero, and equation (A.1.4) is trivially true. Thus, assume that
![]() $h_1$
is related to both g and
$h_1$
is related to both g and
![]() $g'$
. Let
$g'$
. Let
![]() $s^{\natural } \in S_{\phi }$
be the image of
$s^{\natural } \in S_{\phi }$
be the image of
![]() $\dot s$
under equation (2.3.2). Note that
$\dot s$
under equation (2.3.2). Note that
![]() $s^{\natural } \in s \cdot Z(\widehat G)^{\circ ,\Gamma }$
, and hence, the preimage of
$s^{\natural } \in s \cdot Z(\widehat G)^{\circ ,\Gamma }$
, and hence, the preimage of
![]() $s^{\natural }$
under
$s^{\natural }$
under
![]() $\eta $
belongs to
$\eta $
belongs to
![]() $Z(\widehat H)^{\Gamma }$
, which in turns embeds naturally into
$Z(\widehat H)^{\Gamma }$
, which in turns embeds naturally into
![]() $\widehat T_h^{\Gamma }$
. Using the admissible isomorphism
$\widehat T_h^{\Gamma }$
. Using the admissible isomorphism
![]() $\varphi _{h,g}$
, we transport
$\varphi _{h,g}$
, we transport
![]() $s^{\natural }$
into
$s^{\natural }$
into
![]() $\widehat T_g^{\Gamma }$
and denote it by
$\widehat T_g^{\Gamma }$
and denote it by
![]() $s^{\natural }_{h,g}$
. It is then paired with
$s^{\natural }_{h,g}$
. It is then paired with
![]() $\mathrm {inv}[b](g,g')$
via the isomorphism
$\mathrm {inv}[b](g,g')$
via the isomorphism
![]() $B(T_g) \cong X^*(\widehat T_g^{\Gamma })$
of [Reference KottwitzKot85, §2.4].
$B(T_g) \cong X^*(\widehat T_g^{\Gamma })$
of [Reference KottwitzKot85, §2.4].
Proof. For every finite subgroup
![]() $Z \subset Z(G) \subset T_g$
one obtains from
$Z \subset Z(G) \subset T_g$
one obtains from
![]() $\varphi _{h,g}$
an isomorphism
$\varphi _{h,g}$
an isomorphism
![]() $T_h/\varphi _{h,g}^{-1}(Z) \to T_g/Z$
. Using the subgroups
$T_h/\varphi _{h,g}^{-1}(Z) \to T_g/Z$
. Using the subgroups
![]() $Z_n$
from §2.3, we form the quotients
$Z_n$
from §2.3, we form the quotients
![]() $T_{h,n}=T_h/\varphi _{h,g}^{-1}(Z_n)$
and
$T_{h,n}=T_h/\varphi _{h,g}^{-1}(Z_n)$
and
![]() $T_{g,n}=T_g/Z_n$
. From
$T_{g,n}=T_g/Z_n$
. From
![]() $\varphi _{h,g}$
we obtain an isomorphism
$\varphi _{h,g}$
we obtain an isomorphism
between the limits over n of the tori dual to
![]() $T_{h,n}$
and
$T_{h,n}$
and
![]() $T_{g,n}$
. Let
$T_{g,n}$
. Let
![]() $\dot s_{h,g} \in [\widehat {\bar T_g}]^+$
be the image of
$\dot s_{h,g} \in [\widehat {\bar T_g}]^+$
be the image of
![]() $\dot s$
under this isomorphism. Let
$\dot s$
under this isomorphism. Let
![]() $\mathrm {inv}[z_b](g,g') \in H^1(u \to W,Z(G) \to T_g)$
be the invariant defined in [Reference KalethaKal16b, §5.1]. If we replace
$\mathrm {inv}[z_b](g,g') \in H^1(u \to W,Z(G) \to T_g)$
be the invariant defined in [Reference KalethaKal16b, §5.1]. If we replace
![]() $\langle \mathrm {inv}[b](g,g'),s^{\natural }_{h,g}\rangle $
by
$\langle \mathrm {inv}[b](g,g'),s^{\natural }_{h,g}\rangle $
by
![]() $\langle \mathrm {inv}[z_b](g,g'),\dot s_{h,g}\rangle $
then the lemma follows immediately from the defining formula [Reference KalethaKal16b, (5.10)] of the transfer factors. The lemma follows from the equality
$\langle \mathrm {inv}[z_b](g,g'),\dot s_{h,g}\rangle $
then the lemma follows immediately from the defining formula [Reference KalethaKal16b, (5.10)] of the transfer factors. The lemma follows from the equality
![]() $\langle \mathrm {inv}[b](g,g'),s^{\natural }_{h,g}\rangle = \langle \mathrm {inv}[z_b](g,g'),\dot s_{h,g}\rangle $
proved in [Reference KalethaKal18, §4.2].
$\langle \mathrm {inv}[b](g,g'),s^{\natural }_{h,g}\rangle = \langle \mathrm {inv}[z_b](g,g'),\dot s_{h,g}\rangle $
proved in [Reference KalethaKal18, §4.2].
A.2 The Kottwitz sign
We will give a formula for the Kottwitz sign
![]() $e(G)$
in terms of the dual group
$e(G)$
in terms of the dual group
![]() $\widehat G$
. Fix a quasi-split inner form
$\widehat G$
. Fix a quasi-split inner form
![]() $G^*$
and an inner twisting
$G^*$
and an inner twisting
![]() $\psi \colon G^* \to G$
. Let
$\psi \colon G^* \to G$
. Let
![]() $h \in H^1(\Gamma ,G^*_{\mathrm {ad}})$
be the class of
$h \in H^1(\Gamma ,G^*_{\mathrm {ad}})$
be the class of
![]() $\sigma \mapsto \psi ^{-1}\sigma (\psi )$
. Via the Kottwitz homomorphism [Reference KottwitzKot86, Theorem 1.2] the class h corresponds to a character
$\sigma \mapsto \psi ^{-1}\sigma (\psi )$
. Via the Kottwitz homomorphism [Reference KottwitzKot86, Theorem 1.2] the class h corresponds to a character
![]() $\nu \in X^*(Z(\widehat G_{\mathrm {sc}})^{\Gamma })$
.
$\nu \in X^*(Z(\widehat G_{\mathrm {sc}})^{\Gamma })$
.
Choose an arbitrary Borel pair
![]() $(\widehat T_{\mathrm {sc}},\widehat B_{\mathrm {sc}})$
of
$(\widehat T_{\mathrm {sc}},\widehat B_{\mathrm {sc}})$
of
![]() $\widehat G_{\mathrm {sc}}$
and let
$\widehat G_{\mathrm {sc}}$
and let
![]() $2\rho \in X_*(\widehat T_{\mathrm {sc}})$
be the sum of the
$2\rho \in X_*(\widehat T_{\mathrm {sc}})$
be the sum of the
![]() $\widehat B_{\mathrm {sc}}$
-positive coroots. The restriction map
$\widehat B_{\mathrm {sc}}$
-positive coroots. The restriction map
![]() $X^*(\widehat T_{\mathrm {sc}}) \to X^*(Z(\widehat G_{\mathrm {sc}}))$
is surjective and we can lift
$X^*(\widehat T_{\mathrm {sc}}) \to X^*(Z(\widehat G_{\mathrm {sc}}))$
is surjective and we can lift
![]() $\nu $
to
$\nu $
to
![]() $\dot \nu \in X^*(\widehat T_{\mathrm {sc}})$
and form
$\dot \nu \in X^*(\widehat T_{\mathrm {sc}})$
and form
![]() $\langle 2\rho ,\dot \nu \rangle \in \mathbf {Z}$
. A different lift
$\langle 2\rho ,\dot \nu \rangle \in \mathbf {Z}$
. A different lift
![]() $\dot \nu $
would differ by an element of
$\dot \nu $
would differ by an element of
![]() $X^*(\widehat T_{\mathrm {ad}})$
, and since
$X^*(\widehat T_{\mathrm {ad}})$
, and since
![]() $\rho \in X_*(\widehat T_{\mathrm {ad}})$
we see that the image of
$\rho \in X_*(\widehat T_{\mathrm {ad}})$
we see that the image of
![]() $\langle 2\rho ,\dot \nu \rangle $
in
$\langle 2\rho ,\dot \nu \rangle $
in
![]() $\mathbf {Z}/2\mathbf {Z}$
is independent of the choice of lift
$\mathbf {Z}/2\mathbf {Z}$
is independent of the choice of lift
![]() $\dot \nu $
. We thus write
$\dot \nu $
. We thus write
![]() $\langle 2\rho ,\nu \rangle \in \mathbf {Z}/2\mathbf {Z}$
. Since any two Borel pairs in
$\langle 2\rho ,\nu \rangle \in \mathbf {Z}/2\mathbf {Z}$
. Since any two Borel pairs in
![]() $\widehat G_{\mathrm {sc}}$
are conjugate,
$\widehat G_{\mathrm {sc}}$
are conjugate,
![]() $\langle 2\rho ,\nu \rangle $
does not depend on the choice of
$\langle 2\rho ,\nu \rangle $
does not depend on the choice of
![]() $(\widehat T_{\mathrm {sc}},\widehat B_{\mathrm {sc}})$
.
$(\widehat T_{\mathrm {sc}},\widehat B_{\mathrm {sc}})$
.
Lemma A.2.1.
Proof. We fix
![]() $\Gamma $
-invariant Borel pairs
$\Gamma $
-invariant Borel pairs
![]() $(T_{\mathrm {ad}},B_{\mathrm {ad}})$
in
$(T_{\mathrm {ad}},B_{\mathrm {ad}})$
in
![]() $G^*_{\mathrm {ad}}$
and
$G^*_{\mathrm {ad}}$
and
![]() $(\widehat T_{\mathrm {sc}},\widehat B_{\mathrm {sc}})$
in
$(\widehat T_{\mathrm {sc}},\widehat B_{\mathrm {sc}})$
in
![]() $\widehat G_{\mathrm {sc}}$
. Then we have the identification
$\widehat G_{\mathrm {sc}}$
. Then we have the identification
![]() $X^*(T_{\mathrm {ad}})=X_*(\widehat T_{\mathrm {sc}})$
. Let
$X^*(T_{\mathrm {ad}})=X_*(\widehat T_{\mathrm {sc}})$
. Let
![]() $(T_{\mathrm {sc}},B_{\mathrm {sc}})$
be the preimage in
$(T_{\mathrm {sc}},B_{\mathrm {sc}})$
be the preimage in
![]() $G^*_{\mathrm {sc}}$
of
$G^*_{\mathrm {sc}}$
of
![]() $(T_{\mathrm {ad}},B_{\mathrm {ad}})$
.
$(T_{\mathrm {ad}},B_{\mathrm {ad}})$
.
By definition, the Kottwitz sign is the image of h under
where
![]() $\rho \in X^*(T_{\mathrm {sc}})$
is half the sum of the
$\rho \in X^*(T_{\mathrm {sc}})$
is half the sum of the
![]() $B_{\mathrm {sc}}$
-positive roots and its restriction to
$B_{\mathrm {sc}}$
-positive roots and its restriction to
![]() $Z(G^*_{\mathrm {sc}})$
is independent of the choice of
$Z(G^*_{\mathrm {sc}})$
is independent of the choice of
![]() $(T_{\mathrm {ad}},B_{\mathrm {ad}})$
. By functoriality of the Tate–Nakayama pairing, this is the same as pairing
$(T_{\mathrm {ad}},B_{\mathrm {ad}})$
. By functoriality of the Tate–Nakayama pairing, this is the same as pairing
![]() $\delta h \in H^2(\Gamma ,Z(G^*_{\mathrm {sc}}))$
with
$\delta h \in H^2(\Gamma ,Z(G^*_{\mathrm {sc}}))$
with
![]() $\rho \in H^0(\Gamma ,X^*(Z(G^*_{\mathrm {sc}})))$
. The canonical pairing
$\rho \in H^0(\Gamma ,X^*(Z(G^*_{\mathrm {sc}})))$
. The canonical pairing
![]() $X^*(T_{\mathrm {ad}}) \otimes X^*(\widehat T_{\mathrm {sc}}) \to \mathbf {Z}$
induces the perfect pairing
$X^*(T_{\mathrm {ad}}) \otimes X^*(\widehat T_{\mathrm {sc}}) \to \mathbf {Z}$
induces the perfect pairing
![]() $X^*(T_{\mathrm {sc}})/X^*(T_{\mathrm {ad}}) \otimes X^*(\widehat T_{\mathrm {sc}})/X^*(\widehat T_{\mathrm {ad}}) \to \mathbf {Q}/\mathbf {Z}$
and hence the isomorphism
$X^*(T_{\mathrm {sc}})/X^*(T_{\mathrm {ad}}) \otimes X^*(\widehat T_{\mathrm {sc}})/X^*(\widehat T_{\mathrm {ad}}) \to \mathbf {Q}/\mathbf {Z}$
and hence the isomorphism
![]() $X^*(Z(G^*_{\mathrm {sc}})) \to \mathrm {Hom}_{\mathbf {Z}}(X^*(Z(\widehat G_{\mathrm {sc}})),\mathbf {Q}/\mathbf {Z}) = Z(\widehat G_{\mathrm {sc}})$
, where the last equality uses the exponential map. Under this isomorphism,
$X^*(Z(G^*_{\mathrm {sc}})) \to \mathrm {Hom}_{\mathbf {Z}}(X^*(Z(\widehat G_{\mathrm {sc}})),\mathbf {Q}/\mathbf {Z}) = Z(\widehat G_{\mathrm {sc}})$
, where the last equality uses the exponential map. Under this isomorphism,
![]() $\rho \in X^*(Z(G^*_{\mathrm {sc}}))^{\Gamma }$
maps to the element
$\rho \in X^*(Z(G^*_{\mathrm {sc}}))^{\Gamma }$
maps to the element
![]() $(-1)^{2\rho } \in Z(\widehat G_{\mathrm {sc}})^{\Gamma }$
obtained by mapping
$(-1)^{2\rho } \in Z(\widehat G_{\mathrm {sc}})^{\Gamma }$
obtained by mapping
![]() $(-1) \in \mathbf {C}^{\times }$
under
$(-1) \in \mathbf {C}^{\times }$
under
![]() $2\rho \in X^*(T_{\mathrm {ad}})=X_*(\widehat T_{\mathrm {sc}})$
. The lemma now follows from [Reference KottwitzKot86, Lemma 1.8].
$2\rho \in X^*(T_{\mathrm {ad}})=X_*(\widehat T_{\mathrm {sc}})$
. The lemma now follows from [Reference KottwitzKot86, Lemma 1.8].
B Elementary Lemmas
B.1 Homological algebra
Lemma B.1.1. Let R be a discrete valuation ring with maximal ideal
![]() $\mathfrak {m}$
. Let
$\mathfrak {m}$
. Let
![]() $\kappa =R/\mathfrak {m}$
be the residue field, and let
$\kappa =R/\mathfrak {m}$
be the residue field, and let
![]() $\Lambda =R/\mathfrak {m}^k$
for some
$\Lambda =R/\mathfrak {m}^k$
for some
![]() $k>0$
. For a
$k>0$
. For a
![]() $\Lambda $
-module M, we have the dual module
$\Lambda $
-module M, we have the dual module
![]() $M^*=\mathrm {Hom}_{\Lambda }(M,\Lambda )$
and the natural morphisms
$M^*=\mathrm {Hom}_{\Lambda }(M,\Lambda )$
and the natural morphisms
![]() $M \to M^{**}$
and
$M \to M^{**}$
and
![]() $(M^* \otimes M) \to (M \otimes M^*)^*$
.
$(M^* \otimes M) \to (M \otimes M^*)^*$
.
The morphism
![]() $M \to M^{**}$
is an isomorphism if and only if M is finitely generated.
$M \to M^{**}$
is an isomorphism if and only if M is finitely generated.
Proof. For the ‘if’ direction of the first point, we note that the structure theorem for R-modules implies that a finitely generated
![]() $\Lambda $
-module is a direct sum of finitely many cyclic
$\Lambda $
-module is a direct sum of finitely many cyclic
![]() $\Lambda $
-modules, and each cyclic
$\Lambda $
-modules, and each cyclic
![]() $\Lambda $
-module is isomorphic to its own double dual.
$\Lambda $
-module is isomorphic to its own double dual.
Conversely, assume that
![]() $M\to M^{**}$
is an isomorphism. We induct on k. If
$M\to M^{**}$
is an isomorphism. We induct on k. If
![]() $k=1$
, then
$k=1$
, then
![]() $\Lambda $
is a field, and this is well-known. For general k, we consider
$\Lambda $
is a field, and this is well-known. For general k, we consider
![]() $N=M/\mathfrak {m} M$
. The ring
$N=M/\mathfrak {m} M$
. The ring
![]() $\Lambda $
is an Artinian serial ring, and hence, it is injective as a module over itself. Thus, the dualization functor is exact, and we get a commutative diagram
$\Lambda $
is an Artinian serial ring, and hence, it is injective as a module over itself. Thus, the dualization functor is exact, and we get a commutative diagram

which shows that the right-most vertical map is surjective and the left-most vertical map is injective.
We have an isomorphism of
![]() $\Lambda $
-modules
$\Lambda $
-modules
![]() $\mathfrak {m}^{m-1}\Lambda \to \kappa $
, from which we obtain
$\mathfrak {m}^{m-1}\Lambda \to \kappa $
, from which we obtain
Thus,
![]() $N^{**}$
is also the double dual of N in the category of
$N^{**}$
is also the double dual of N in the category of
![]() $\kappa $
-vector spaces, and it is easy to check that the right-most vertical map in equation (B.1.1) is the canonical map in that category. Thus, this map is an isomorphism, and N is fintely generated as a
$\kappa $
-vector spaces, and it is easy to check that the right-most vertical map in equation (B.1.1) is the canonical map in that category. Thus, this map is an isomorphism, and N is fintely generated as a
![]() $\kappa $
-vector space.
$\kappa $
-vector space.
By the Snake lemma, the left-most vertical arrow in equation (B.1.1) is an isomorphism. We can apply the inductive hypothesis to the
![]() $(\Lambda /\mathfrak {m}^{m-1})$
-module
$(\Lambda /\mathfrak {m}^{m-1})$
-module
![]() $\mathfrak {m} M$
and conclude that it is finitely generated. Thus, so is M.
$\mathfrak {m} M$
and conclude that it is finitely generated. Thus, so is M.
Lemma B.1.2. Let
![]() $\Lambda $
be an arbitrary ring, and let
$\Lambda $
be an arbitrary ring, and let
![]() $D(\Lambda )$
be the derived category of
$D(\Lambda )$
be the derived category of
![]() $\Lambda $
-modules. For an object M of
$\Lambda $
-modules. For an object M of
![]() $D(\Lambda )$
, let
$D(\Lambda )$
, let
![]() $\mathbf {D} M=\mathrm {RHom}(M,\Lambda [0])$
.
$\mathbf {D} M=\mathrm {RHom}(M,\Lambda [0])$
.
-
1. Assume that
 $\Lambda =R/\mathfrak {m}^k$
for a discrete valuation ring R with maximal ideal
$\Lambda =R/\mathfrak {m}^k$
for a discrete valuation ring R with maximal ideal
 $\mathfrak {m}$
. Then the natural morphism
$\mathfrak {m}$
. Then the natural morphism
 $M\to \mathbf {D}\mathbf {D} M$
is an isomorphism if and only if each
$M\to \mathbf {D}\mathbf {D} M$
is an isomorphism if and only if each
 $H^i(M)$
is finitely generated.
$H^i(M)$
is finitely generated. -
2. For general
 $\Lambda $
, the following are equivalent:
$\Lambda $
, the following are equivalent:-
(a) The natural maps
 $M\to \mathbf {D}\mathbf {D} M$
and
$M\to \mathbf {D}\mathbf {D} M$
and
 $\mathbf {D} M\otimes M\to \mathbf {D}(M\otimes \mathbf {D} M)$
are isomorphisms.
$\mathbf {D} M\otimes M\to \mathbf {D}(M\otimes \mathbf {D} M)$
are isomorphisms. -
(b) The natural map
 $M\otimes \mathbf {D} M\to \mathrm {RHom}(M,M)$
is an isomorphism.
$M\otimes \mathbf {D} M\to \mathrm {RHom}(M,M)$
is an isomorphism. -
(c) M is strongly dualizable; that is, for any object N,
 $N\otimes \mathbf {D} M\to \mathrm {RHom}(M,N)$
is an isomorphism.
$N\otimes \mathbf {D} M\to \mathrm {RHom}(M,N)$
is an isomorphism. -
(d) M is a compact object; that is, the functor
 $N\mapsto \mathrm {RHom}(M,N)$
commutes with colimits.
$N\mapsto \mathrm {RHom}(M,N)$
commutes with colimits. -
(e) M is a perfect complex; that is, M is isomorphic to a bounded complex of finitely generated projective
 $\Lambda $
-modules.
$\Lambda $
-modules.
-
(Throughout, the
![]() $\otimes $
means derived tensor product.)
$\otimes $
means derived tensor product.)
Proof. For the first statement, the self-injectivity of
![]() $\Lambda $
implies that
$\Lambda $
implies that
![]() $H^i(\mathbf {D} M)\cong H^{-i}(M)^*$
so that
$H^i(\mathbf {D} M)\cong H^{-i}(M)^*$
so that
![]() $H^i(\mathbf {D} \mathbf {D} M)\cong H^i(M)^{**}$
. Therefore,
$H^i(\mathbf {D} \mathbf {D} M)\cong H^i(M)^{**}$
. Therefore,
![]() $M\to \mathbf {D}\mathbf {D} M$
is an isomorphism if and only if each
$M\to \mathbf {D}\mathbf {D} M$
is an isomorphism if and only if each
![]() $H^i(M)\to H^i(M)^{**}$
is an isomorphism. By Lemma B.1.1, this is equivalent to each
$H^i(M)\to H^i(M)^{**}$
is an isomorphism. By Lemma B.1.1, this is equivalent to each
![]() $H^i(M)$
being finitely generated.
$H^i(M)$
being finitely generated.
We now turn to the second statement. For (a)
![]() $\implies $
(b), assume that
$\implies $
(b), assume that
![]() $M\to \mathbf {D} \mathbf {D} M$
and
$M\to \mathbf {D} \mathbf {D} M$
and
![]() $\mathbf {D} M\otimes M\to \mathbf {D}(M\otimes \mathbf {D} M)$
are isomorphisms. Then
$\mathbf {D} M\otimes M\to \mathbf {D}(M\otimes \mathbf {D} M)$
are isomorphisms. Then
![]() $\mathrm {RHom}(M,M)\cong \mathrm {RHom}(M,\mathbf {D} \mathbf {D} M)\cong \mathrm {RHom}(M\otimes \mathbf {D} M, \Lambda )\cong \mathbf {D}(M\otimes \mathbf {D} M)\cong \mathbf {D} M\otimes M$
.
$\mathrm {RHom}(M,M)\cong \mathrm {RHom}(M,\mathbf {D} \mathbf {D} M)\cong \mathrm {RHom}(M\otimes \mathbf {D} M, \Lambda )\cong \mathbf {D}(M\otimes \mathbf {D} M)\cong \mathbf {D} M\otimes M$
.
For (b)
![]() $\implies $
(c), the identity map on M induces a morphism
$\implies $
(c), the identity map on M induces a morphism
![]() $\varepsilon \colon \Lambda [0]\to \mathrm {RHom}(M,M)\stackrel {\cong }{\longrightarrow } M\otimes \mathbf {D} M$
(the coevaluation map). The required inverse to
$\varepsilon \colon \Lambda [0]\to \mathrm {RHom}(M,M)\stackrel {\cong }{\longrightarrow } M\otimes \mathbf {D} M$
(the coevaluation map). The required inverse to
![]() $N\otimes \mathbf {D} M\to \mathrm {RHom}(M,N)$
is
$N\otimes \mathbf {D} M\to \mathrm {RHom}(M,N)$
is
For (c)
![]() $\implies $
(d), we use the fact that
$\implies $
(d), we use the fact that
![]() $\otimes $
commutes with colimits.
$\otimes $
commutes with colimits.
For (d)
![]() $\implies $
(e), we use the fact that compact objects of
$\implies $
(e), we use the fact that compact objects of
![]() $D(\Lambda )$
are perfect [Sta21, Tag 07LT].
$D(\Lambda )$
are perfect [Sta21, Tag 07LT].
Finally, for (e) implies (a), we can write M as a bounded complex of finitely generated projective
![]() $\Lambda $
-modules. Then duals and derived tensor products can be computed on the level of chain complexes. We are reduced to showing, for finitely generated projective
$\Lambda $
-modules. Then duals and derived tensor products can be computed on the level of chain complexes. We are reduced to showing, for finitely generated projective
![]() $\Lambda $
-modules A and B, that
$\Lambda $
-modules A and B, that
![]() $A\to A^{**}$
and
$A\to A^{**}$
and
![]() $A^*\otimes B\to (A\otimes B^*)^*$
are isomorphisms. After localizing on
$A^*\otimes B\to (A\otimes B^*)^*$
are isomorphisms. After localizing on
![]() $\Lambda $
, we may assume that A and B are free of finite rank (since duals commute over direct sums), where these statements are easy to check.
$\Lambda $
, we may assume that A and B are free of finite rank (since duals commute over direct sums), where these statements are easy to check.
We thank Bhargav Bhatt for helping us with the above proof.
B.2 Sheaves on locally profinite sets
Let S be a locally profinite set and
![]() $\Lambda $
a discrete ring. We have the ring
$\Lambda $
a discrete ring. We have the ring
![]() $C(S,\Lambda )$
of locally constant functions on S, and the nonunital ring
$C(S,\Lambda )$
of locally constant functions on S, and the nonunital ring
![]() $C_c(S,\Lambda )$
of locally constant compactly supported functions on S. For each compact open subset
$C_c(S,\Lambda )$
of locally constant compactly supported functions on S. For each compact open subset
![]() $U \subset S$
, let
$U \subset S$
, let
![]() $\textbf {1}_U$
denote the characteristic function. Then
$\textbf {1}_U$
denote the characteristic function. Then
![]() $C(U,\Lambda )$
is a principal ideal of both
$C(U,\Lambda )$
is a principal ideal of both
![]() $C_c(S,\Lambda )$
and
$C_c(S,\Lambda )$
and
![]() $C(S,\Lambda )$
generated by
$C(S,\Lambda )$
generated by
![]() $\textbf {1}_U$
. Multiplication by
$\textbf {1}_U$
. Multiplication by
![]() $\textbf {1}_U$
is a homomorphism
$\textbf {1}_U$
is a homomorphism
![]() $C(S,\Lambda ) \to C(U,\Lambda )$
of rings with unity. In this way, every
$C(S,\Lambda ) \to C(U,\Lambda )$
of rings with unity. In this way, every
![]() $C(U,\Lambda )$
-module becomes a
$C(U,\Lambda )$
-module becomes a
![]() $C(S,\Lambda )$
-module.
$C(S,\Lambda )$
-module.
Definition B.2.1. We call a
![]() $C(S,\Lambda )$
-module M
$C(S,\Lambda )$
-module M
-
1. smooth if it satisfies the following equivalent conditions
-
(a) The multiplication map
 $M \otimes _{C(S,\Lambda )}C_c(S,\Lambda ) \to M$
is an isomorphism.
$M \otimes _{C(S,\Lambda )}C_c(S,\Lambda ) \to M$
is an isomorphism. -
(b) The natural map
 $\varinjlim (\textbf {1}_U \cdot M) \to M$
is an isomorphism, where the colimit runs over the open compact subsets
$\varinjlim (\textbf {1}_U \cdot M) \to M$
is an isomorphism, where the colimit runs over the open compact subsets
 $U \subset S$
and the transition map
$U \subset S$
and the transition map
 $\textbf {1}_U\cdot M \to \textbf {1}_V\cdot M$
for
$\textbf {1}_U\cdot M \to \textbf {1}_V\cdot M$
for
 $U \subset V$
is given by the natural inclusion.
$U \subset V$
is given by the natural inclusion.
-
-
2. complete if the natural map
 $M \to \varprojlim _U (\textbf {1}_U \cdot M)$
is an isomorphism, where again U runs over the open compact subsets of S and the transition map
$M \to \varprojlim _U (\textbf {1}_U \cdot M)$
is an isomorphism, where again U runs over the open compact subsets of S and the transition map
 $\textbf {1}_U\cdot M \to \textbf {1}_V\cdot M$
for
$\textbf {1}_U\cdot M \to \textbf {1}_V\cdot M$
for
 $V \subset U$
is multiplication by
$V \subset U$
is multiplication by
 $\textbf {1}_V$
.
$\textbf {1}_V$
.
Lemma B.2.2. Let
![]() $V \subset S$
be compact open, and let M be any
$V \subset S$
be compact open, and let M be any
![]() $C(S,\Lambda )$
-module. Then
$C(S,\Lambda )$
-module. Then
-
1.
 $\textbf {1}_{V}\cdot M$
is a submodule of
$\textbf {1}_{V}\cdot M$
is a submodule of
 $\varinjlim _U (\textbf {1}_U \cdot M)$
and equals
$\varinjlim _U (\textbf {1}_U \cdot M)$
and equals
 $\textbf {1}_V\cdot \varinjlim (\textbf {1}_U\cdot M)$
.
$\textbf {1}_V\cdot \varinjlim (\textbf {1}_U\cdot M)$
. -
2.
 $\textbf {1}_{V}\cdot M$
is a submodule of
$\textbf {1}_{V}\cdot M$
is a submodule of
 $\varprojlim _U (\textbf {1}_U \cdot M)$
and equals
$\varprojlim _U (\textbf {1}_U \cdot M)$
and equals
 $\textbf {1}_V\cdot \varprojlim (\textbf {1}_U\cdot M)$
.
$\textbf {1}_V\cdot \varprojlim (\textbf {1}_U\cdot M)$
.
Lemma B.2.3.
-
1. The functor
 $M \mapsto M^s:=\varinjlim (\textbf {1}_U \cdot M)$
is a projector onto the category of smooth modules.
$M \mapsto M^s:=\varinjlim (\textbf {1}_U \cdot M)$
is a projector onto the category of smooth modules. -
2. The functor
 $M \mapsto M^c:=\varprojlim (\textbf {1}_U \cdot M)$
is a projector onto the category of complete modules.
$M \mapsto M^c:=\varprojlim (\textbf {1}_U \cdot M)$
is a projector onto the category of complete modules. -
3. The two functors give mutually inverse equivalences of categories between the categories of smooth and complete modules.
Let
![]() $\mathcal {B}$
the set of open compact subsets of S. Then
$\mathcal {B}$
the set of open compact subsets of S. Then
![]() $\mathcal {B}$
is a basis for the topology of S and is closed under taking finite intersections and finite unions. Restriction gives an equivalence between the category of sheaves on S and the category of sheaves on
$\mathcal {B}$
is a basis for the topology of S and is closed under taking finite intersections and finite unions. Restriction gives an equivalence between the category of sheaves on S and the category of sheaves on
![]() $\mathcal {B}$
. Define
$\mathcal {B}$
. Define
![]() $R(U)=C(U,\Lambda )$
. This is a sheaf of rings on S.
$R(U)=C(U,\Lambda )$
. This is a sheaf of rings on S.
Let
![]() $\mathcal {F}$
be an R-module sheaf on S. For
$\mathcal {F}$
be an R-module sheaf on S. For
![]() $U \in \mathcal {B}$
we extend the
$U \in \mathcal {B}$
we extend the
![]() $R(U)$
-module structure on
$R(U)$
-module structure on
![]() $\mathcal {F}(U)$
to a
$\mathcal {F}(U)$
to a
![]() $C(S,\Lambda )$
-module structure as remarked above. Then the restriction map
$C(S,\Lambda )$
-module structure as remarked above. Then the restriction map
![]() $\mathcal {F}(S) \to \mathcal {F}(U)$
becomes a morphism of
$\mathcal {F}(S) \to \mathcal {F}(U)$
becomes a morphism of
![]() $C(S,\Lambda )$
-modules.
$C(S,\Lambda )$
-modules.
Lemma B.2.4.
-
1. For any
 $U \in \mathcal {B}$
the restriction map
$U \in \mathcal {B}$
the restriction map
 $\mathcal {F}(S) \to \mathcal {F}(U)$
is surjective and its restriction to
$\mathcal {F}(S) \to \mathcal {F}(U)$
is surjective and its restriction to
 $\textbf {1}_U \cdot \mathcal {F}(S)$
is an isomorphism
$\textbf {1}_U \cdot \mathcal {F}(S)$
is an isomorphism
 $\textbf {1}_U \cdot \mathcal {F}(S) \to \mathcal {F}(U)$
.
$\textbf {1}_U \cdot \mathcal {F}(S) \to \mathcal {F}(U)$
. -
2. We have
 $\mathcal {F}(S) = \varprojlim _U \mathcal {F}(U)$
, where the transition maps are the restriction maps.
$\mathcal {F}(S) = \varprojlim _U \mathcal {F}(U)$
, where the transition maps are the restriction maps.
Let M be an
![]() $C(S,\Lambda )$
-module. Let
$C(S,\Lambda )$
-module. Let
![]() $\mathcal {F}_M(U)=R(U)M=\textbf {1}_UM$
. This is a
$\mathcal {F}_M(U)=R(U)M=\textbf {1}_UM$
. This is a
![]() $C(S,\Lambda )$
-submodule of M. Given
$C(S,\Lambda )$
-submodule of M. Given
![]() $V,U \in \mathcal {B}$
with
$V,U \in \mathcal {B}$
with
![]() $V \subset U$
we have the map
$V \subset U$
we have the map
![]() $\mathcal {F}_M(U) \to \mathcal {F}_M(V)$
defined by multiplication by
$\mathcal {F}_M(U) \to \mathcal {F}_M(V)$
defined by multiplication by
![]() $\textbf {1}_V$
. In this way,
$\textbf {1}_V$
. In this way,
![]() $\mathcal {F}_M$
becomes an R-module sheaf.
$\mathcal {F}_M$
becomes an R-module sheaf.
Let
![]() $f : M \to N$
be a morphism of
$f : M \to N$
be a morphism of
![]() $C(S,\Lambda )$
-modules. We define for each U the morphism
$C(S,\Lambda )$
-modules. We define for each U the morphism
![]() $f_U : \mathcal {F}_M(U) \to \mathcal {F}_N(U)$
simply by restricting f to
$f_U : \mathcal {F}_M(U) \to \mathcal {F}_N(U)$
simply by restricting f to
![]() $\mathcal {F}_M(U)$
. One checks immediately that
$\mathcal {F}_M(U)$
. One checks immediately that
![]() $(f_U)_U$
is a morphism of sheaves of R-modules. Therefore, we obtain a functor from the category of
$(f_U)_U$
is a morphism of sheaves of R-modules. Therefore, we obtain a functor from the category of
![]() $C(S,\Lambda )$
-modules to the category of sheaves of R-modules.
$C(S,\Lambda )$
-modules to the category of sheaves of R-modules.
Given a sheaf
![]() $\mathcal {F}$
on S, we can define the smooth module
$\mathcal {F}$
on S, we can define the smooth module
![]() $M_{\mathcal {F}}^s$
and the complete module
$M_{\mathcal {F}}^s$
and the complete module
![]() $M_{\mathcal {F}}^c$
by
$M_{\mathcal {F}}^c$
by
where the limit is taken over the restriction maps, and the colimit is taken over their sections given by Lemma B.2.4, and in both cases U runs over
![]() $\mathcal {B}$
. Conversely, given any
$\mathcal {B}$
. Conversely, given any
![]() $C(S,\Lambda )$
-module M, we have the sheaf
$C(S,\Lambda )$
-module M, we have the sheaf
![]() $\mathcal {F}_M$
.
$\mathcal {F}_M$
.
Lemma B.2.5. These functors give mutually inverse equivalences of categories from the category of smooth (resp., complete)
![]() $C(S,\Lambda )$
-modules to the category of R-module sheaves. These equivalences commute with the equivalence between the categories of smooth and complete modules. Furthermore,
$C(S,\Lambda )$
-modules to the category of R-module sheaves. These equivalences commute with the equivalence between the categories of smooth and complete modules. Furthermore,
![]() $\mathcal {F}_M(S)=M^c$
.
$\mathcal {F}_M(S)=M^c$
.
C Some representation theory
Let G be a reductive group over a finite extension
![]() $F/\mathbf {Q}_p$
. For a parabolic subgroup P of G, we write
$F/\mathbf {Q}_p$
. For a parabolic subgroup P of G, we write
![]() $i_P^G$
for the functor of normalized parabolic induction and
$i_P^G$
for the functor of normalized parabolic induction and
![]() $r_G^P$
for the normalized Jacquet module functor.
$r_G^P$
for the normalized Jacquet module functor.
Fix a minimal parabolic
![]() $P_0=M_0 U_0$
. A parabolic subgroup P is called standard if it contains
$P_0=M_0 U_0$
. A parabolic subgroup P is called standard if it contains
![]() $P_0$
. There is a unique Levi factor M of P that contains
$P_0$
. There is a unique Levi factor M of P that contains
![]() $M_0$
, and conversely M determines P. In that situation, we may write
$M_0$
, and conversely M determines P. In that situation, we may write
![]() $i_M^G$
and
$i_M^G$
and
![]() $r_G^M$
in place of
$r_G^M$
in place of
![]() $i_P^G$
and
$i_P^G$
and
![]() $r_G^P$
.
$r_G^P$
.
C.1 Nonelliptic representations
Recall that a finite-length (virtual)
![]() $G(F)$
-representation is nonelliptic if its Harish–Chandra character vanishes on all elliptic elements. Our goal in this section is the following result.
$G(F)$
-representation is nonelliptic if its Harish–Chandra character vanishes on all elliptic elements. Our goal in this section is the following result.
Theorem C.1.1. Let
![]() $\pi \in \operatorname {\mathrm {Groth}}(G(F))$
be any finite-length virtual
$\pi \in \operatorname {\mathrm {Groth}}(G(F))$
be any finite-length virtual
![]() $G(F)$
-representation with
$G(F)$
-representation with
![]() $\mathbf {C}$
-coefficients, or with
$\mathbf {C}$
-coefficients, or with
![]() $\overline {\mathbf {Q}_{\ell }}$
-coefficients. Then
$\overline {\mathbf {Q}_{\ell }}$
-coefficients. Then
![]() $\pi $
is nonelliptic if and only if it can be expressed as a
$\pi $
is nonelliptic if and only if it can be expressed as a
![]() $\mathbf {Q}$
-linear virtual combination of representations induced from proper parabolic subgroups of G.
$\mathbf {Q}$
-linear virtual combination of representations induced from proper parabolic subgroups of G.
When
![]() $G(F)$
has compact center, this is (a weaker version of) a classical result of Kazhdan [Reference KazhdanKaz86]. The general statement seems to be well-known to experts, but we were unable to find an explicit formulation in the literature.
$G(F)$
has compact center, this is (a weaker version of) a classical result of Kazhdan [Reference KazhdanKaz86]. The general statement seems to be well-known to experts, but we were unable to find an explicit formulation in the literature.
Proof. It suffices to treat the case of complex coefficients. Parabolic inductions are nonelliptic by van Dijk’s formula [Reference van DijkvD72], so the ‘if’ direction is clear. We will deduce the ‘only if’ direction from [Reference DatDat00]; in what follows, we freely use various notations from loc. cit., in particular writing
![]() $\mathscr {R}(G)$
for the Grothendieck group of finite length smooth
$\mathscr {R}(G)$
for the Grothendieck group of finite length smooth
![]() $\mathbf {C}$
-representations of
$\mathbf {C}$
-representations of
![]() $G(F)$
.
$G(F)$
.
Suppose that
![]() $\pi \in \mathscr {R}(G)$
is nonelliptic. Following the notation of [Reference DatDat00], pick any
$\pi \in \mathscr {R}(G)$
is nonelliptic. Following the notation of [Reference DatDat00], pick any
![]() $f \in \overline {\mathscr {H}}^{d(G)}(G)$
. Then all regular semisimple nonelliptic orbital integrals of f vanish by [Reference DatDat00, Theorem 3.2.iii], so
$f \in \overline {\mathscr {H}}^{d(G)}(G)$
. Then all regular semisimple nonelliptic orbital integrals of f vanish by [Reference DatDat00, Theorem 3.2.iii], so
![]() $\operatorname {\mathrm {tr}} (f | \pi ) = 0$
by our assumption on
$\operatorname {\mathrm {tr}} (f | \pi ) = 0$
by our assumption on
![]() $\pi $
and the Weyl integration formula. Therefore,
$\pi $
and the Weyl integration formula. Therefore,
![]() $\pi \in \overline {\mathscr {H}}^{d(G)} (G)^{\perp }$
, so
$\pi \in \overline {\mathscr {H}}^{d(G)} (G)^{\perp }$
, so
![]() $\pi \in \mathscr {R}_{\mathbf {C}_{d(G)}}(G)$
by [Reference DatDat00, Theorem 3.2.ii]. Now applying [Reference DatDat00, Proposition 2.5.i] to the Hopf system
$\pi \in \mathscr {R}_{\mathbf {C}_{d(G)}}(G)$
by [Reference DatDat00, Theorem 3.2.ii]. Now applying [Reference DatDat00, Proposition 2.5.i] to the Hopf system
![]() $\mathscr {A}(-) = \mathscr {R}(-) \otimes \mathbf {Q}$
with
$\mathscr {A}(-) = \mathscr {R}(-) \otimes \mathbf {Q}$
with
![]() $d=d(G)$
, we see that
$d=d(G)$
, we see that
![]() $\pi \in \mathscr {R}(G) \otimes \mathbf {Q}$
is annihilated by the operator
$\pi \in \mathscr {R}(G) \otimes \mathbf {Q}$
is annihilated by the operator
![]() $1-\sum _{d(M)>d(G)}c_d(M) i_{M}^{G} r_{G}^{M}$
for some rational numbers
$1-\sum _{d(M)>d(G)}c_d(M) i_{M}^{G} r_{G}^{M}$
for some rational numbers
![]() $c_d(M)$
. Therefore,
$c_d(M)$
. Therefore,
and the right-hand side is a
![]() $\mathbf {Q}$
-linear virtual combination of proper parabolic inductions, giving the result.
$\mathbf {Q}$
-linear virtual combination of proper parabolic inductions, giving the result.
C.2 Integral representations and parabolic inductions
Fix a prime
![]() $\ell \neq p$
. As usual, let
$\ell \neq p$
. As usual, let
![]() $\operatorname {\mathrm {Groth}}(G(F))$
be the Grothendieck group of finite-length smooth
$\operatorname {\mathrm {Groth}}(G(F))$
be the Grothendieck group of finite-length smooth
![]() $\overline {\mathbf {Q}_{\ell }}$
-representations of
$\overline {\mathbf {Q}_{\ell }}$
-representations of
![]() $G(F)$
.
$G(F)$
.
Definition C.2.1. Let
![]() $\pi $
be an admissible smooth
$\pi $
be an admissible smooth
![]() $\overline {\mathbf {Q}_{\ell }}$
-representation of
$\overline {\mathbf {Q}_{\ell }}$
-representation of
![]() $G(F)$
. We say
$G(F)$
. We say
![]() $\pi $
admits a
$\pi $
admits a
![]() $\overline {\mathbf {Z}_{\ell }}$
-lattice if there exists an admissible smooth
$\overline {\mathbf {Z}_{\ell }}$
-lattice if there exists an admissible smooth
![]() $\ell $
-torsion-free
$\ell $
-torsion-free
![]() $\overline {\mathbf {Z}_{\ell }}[G(F)]$
-module L together with an isomorphism
$\overline {\mathbf {Z}_{\ell }}[G(F)]$
-module L together with an isomorphism
![]() $L[1/\ell ] \simeq \pi $
.
$L[1/\ell ] \simeq \pi $
.
Recall that our convention on the meaning of admissible is slightly nonstandard, so in particular any such L has the property that
![]() $L^{K}$
is a finite free
$L^{K}$
is a finite free
![]() $\overline {\mathbf {Z}_{\ell }}$
-module for all open compact pro-p subgroups
$\overline {\mathbf {Z}_{\ell }}$
-module for all open compact pro-p subgroups
![]() $K \subset G(F)$
, and whence L is a free
$K \subset G(F)$
, and whence L is a free
![]() $\overline {\mathbf {Z}_{\ell }}$
-module. The existence of a
$\overline {\mathbf {Z}_{\ell }}$
-module. The existence of a
![]() $\overline {\mathbf {Z}_{\ell }}$
-lattice in our sense implies, but is strictly stronger than, the existence of a ‘
$\overline {\mathbf {Z}_{\ell }}$
-lattice in our sense implies, but is strictly stronger than, the existence of a ‘
![]() $\overline {\mathbf {Z}_{\ell }}G(F)$
-réseau’ in the sense of [Reference VignérasVig96]. Note also that if
$\overline {\mathbf {Z}_{\ell }}G(F)$
-réseau’ in the sense of [Reference VignérasVig96]. Note also that if
![]() $\pi $
is a finite-length admissible representation admitting a
$\pi $
is a finite-length admissible representation admitting a
![]() $\overline {\mathbf {Z}_{\ell }}$
-lattice, then any such lattice is finitely generated as a
$\overline {\mathbf {Z}_{\ell }}$
-lattice, then any such lattice is finitely generated as a
![]() $\overline {\mathbf {Z}_{\ell }}[G(F)]$
-module by [Reference VignérasVig04].
$\overline {\mathbf {Z}_{\ell }}[G(F)]$
-module by [Reference VignérasVig04].
The goal of this section is to prove the following result.
Proposition C.2.2. The group
![]() $\operatorname {\mathrm {Groth}}(G(F))$
is generated by representations of the form
$\operatorname {\mathrm {Groth}}(G(F))$
is generated by representations of the form
![]() $ i_{M}^{G}(\sigma \otimes \psi )$
, where
$ i_{M}^{G}(\sigma \otimes \psi )$
, where
![]() $i_{M}^{G}(-)$
is the normalized parabolic induction functor associated with a standard Levi subgroup M,
$i_{M}^{G}(-)$
is the normalized parabolic induction functor associated with a standard Levi subgroup M,
![]() $\psi $
is an unramified character of
$\psi $
is an unramified character of
![]() $M(F)$
, and
$M(F)$
, and
![]() $\sigma $
is an irreducible admissible
$\sigma $
is an irreducible admissible
![]() $\overline {\mathbf {Q}_{\ell }}$
-representation of
$\overline {\mathbf {Q}_{\ell }}$
-representation of
![]() $M(F)$
admitting a
$M(F)$
admitting a
![]() $\overline {\mathbf {Z}_{\ell }}$
-lattice.
$\overline {\mathbf {Z}_{\ell }}$
-lattice.
We will deduce this from Dat’s theory of
![]() $\nu $
-tempered representations [Reference DatDat05]. In particular, we will apply the theory from [Reference DatDat05] with
$\nu $
-tempered representations [Reference DatDat05]. In particular, we will apply the theory from [Reference DatDat05] with
![]() $\mathcal {K} = \overline {\mathbf {Q}_{\ell }}$
or with
$\mathcal {K} = \overline {\mathbf {Q}_{\ell }}$
or with
![]() $\mathcal {K}=E \subset \overline {\mathbf {Q}_{\ell }}$
a finite extension of
$\mathcal {K}=E \subset \overline {\mathbf {Q}_{\ell }}$
a finite extension of
![]() $\mathbf {Q}_{\ell }$
, equipped with the usual norms, so
$\mathbf {Q}_{\ell }$
, equipped with the usual norms, so
![]() $\nu $
is a positive multiple of the usual
$\nu $
is a positive multiple of the usual
![]() $\ell $
-adic valuation.
$\ell $
-adic valuation.
Lemma C.2.3. Let
![]() $\pi $
be any irreducible smooth
$\pi $
be any irreducible smooth
![]() $\overline {\mathbf {Q}_{\ell }}$
-representation of
$\overline {\mathbf {Q}_{\ell }}$
-representation of
![]() $G(F)$
. If
$G(F)$
. If
![]() $\pi $
is
$\pi $
is
![]() $\nu $
-tempered, then
$\nu $
-tempered, then
![]() $\pi $
admits a
$\pi $
admits a
![]() $\overline {\mathbf {Z}_{\ell }}$
-lattice.
$\overline {\mathbf {Z}_{\ell }}$
-lattice.
Proof. Suppose given
![]() $\pi $
as in the lemma. By [Reference VignérasVig96, II.4.7], we may choose some E and some admissible E-representation
$\pi $
as in the lemma. By [Reference VignérasVig96, II.4.7], we may choose some E and some admissible E-representation
![]() $\pi _E$
together with an isomorphism
$\pi _E$
together with an isomorphism
![]() $\pi _E \otimes _E \overline {\mathbf {Q}_{\ell }} = \pi $
. By definition,
$\pi _E \otimes _E \overline {\mathbf {Q}_{\ell }} = \pi $
. By definition,
![]() $\pi $
is
$\pi $
is
![]() $\nu $
-tempered if and only if
$\nu $
-tempered if and only if
![]() $\pi _E$
is
$\pi _E$
is
![]() $\nu $
-tempered, [Reference DatDat05, Lemma 3.3]. Since
$\nu $
-tempered, [Reference DatDat05, Lemma 3.3]. Since
![]() $\pi _E$
is
$\pi _E$
is
![]() $\nu $
-tempered, it admits an
$\nu $
-tempered, it admits an
![]() $\mathcal {O}_E$
-lattice L by [Reference DatDat05, Proposition 6.3]. Then
$\mathcal {O}_E$
-lattice L by [Reference DatDat05, Proposition 6.3]. Then
![]() $L \otimes _{\mathcal {O}_E} \overline {\mathbf {Z}_{\ell }}$
is the desired
$L \otimes _{\mathcal {O}_E} \overline {\mathbf {Z}_{\ell }}$
is the desired
![]() $\overline {\mathbf {Z}_{\ell }}$
-lattice in
$\overline {\mathbf {Z}_{\ell }}$
-lattice in
![]() $\pi $
.
$\pi $
.
We will now freely use all the notation and results of [Reference DatDat05, §2-3], with
![]() $\mathcal {K} = \overline {\mathbf {Q}_{\ell }}$
. A triple
$\mathcal {K} = \overline {\mathbf {Q}_{\ell }}$
. A triple
![]() $(M,\sigma ,\psi )$
consisting of a standard Levi subgroup
$(M,\sigma ,\psi )$
consisting of a standard Levi subgroup
![]() $M \subset G$
, a
$M \subset G$
, a
![]() $\nu $
-tempered irreducible representation
$\nu $
-tempered irreducible representation
![]() $\sigma $
of
$\sigma $
of
![]() $M(F)$
and an unramified character
$M(F)$
and an unramified character
![]() $\psi $
of
$\psi $
of
![]() $M(F)$
with
$M(F)$
with
![]() $-\nu (\psi ) \in (\mathfrak {a}_P)^{*,+}$
is called a Langlands triple. The corresponding representation
$-\nu (\psi ) \in (\mathfrak {a}_P)^{*,+}$
is called a Langlands triple. The corresponding representation
![]() $i_P^G(\sigma \otimes \psi )$
has a unique irreducible quotient, which we will denote by
$i_P^G(\sigma \otimes \psi )$
has a unique irreducible quotient, which we will denote by
![]() $j_P^G(\sigma \otimes \psi )$
. Every irreducible smooth representation
$j_P^G(\sigma \otimes \psi )$
. Every irreducible smooth representation
![]() $\pi $
of
$\pi $
of
![]() $G(F)$
is isomorphic to
$G(F)$
is isomorphic to
![]() $j_P^G(\sigma \otimes \psi )$
for a (essentially) unique Langlands triple, cf. [Reference DatDat05, Theorem 3.11]. The uniqueness of the triple
$j_P^G(\sigma \otimes \psi )$
for a (essentially) unique Langlands triple, cf. [Reference DatDat05, Theorem 3.11]. The uniqueness of the triple
![]() $(M,\sigma ,\psi )$
with a given irreducible quotient
$(M,\sigma ,\psi )$
with a given irreducible quotient
![]() $\pi $
allows us to index the representation
$\pi $
allows us to index the representation
![]() $i_P^G(\sigma \otimes \psi )$
by
$i_P^G(\sigma \otimes \psi )$
by
![]() $\pi $
. We shall write
$\pi $
. We shall write
![]() $I(\pi )$
for this representation and refer to it as the standard representation associated with
$I(\pi )$
for this representation and refer to it as the standard representation associated with
![]() $\pi $
. Note that there is a natural surjection
$\pi $
. Note that there is a natural surjection
![]() $I(\pi ) \to \pi $
.
$I(\pi ) \to \pi $
.
On the other hand, by [Reference DatDat05, Theorem 3.11.ii],
![]() $\lambda _{\pi }:= -\nu (\psi ) \in \mathfrak {a}_{M_0}^{\ast }$
is also a well-defined invariant of
$\lambda _{\pi }:= -\nu (\psi ) \in \mathfrak {a}_{M_0}^{\ast }$
is also a well-defined invariant of
![]() $\pi $
. Note that
$\pi $
. Note that
![]() $\pi $
is
$\pi $
is
![]() $\nu $
-tempered if and only if
$\nu $
-tempered if and only if
![]() $\lambda _{\pi }=0$
and that M can be read off from
$\lambda _{\pi }=0$
and that M can be read off from
![]() $\lambda _{\pi }$
. The following key lemma is the analogue of [Reference Borel and WallachBW00, Lemma XI.2.13] in our setting.
$\lambda _{\pi }$
. The following key lemma is the analogue of [Reference Borel and WallachBW00, Lemma XI.2.13] in our setting.
Lemma C.2.4. Let
![]() $\pi $
be any irreducible representation. Write
$\pi $
be any irreducible representation. Write
![]() $\pi = j_P^G(\sigma \otimes \psi )$
, and let
$\pi = j_P^G(\sigma \otimes \psi )$
, and let
![]() $\pi '$
be any nonzero irreducible subquotient of
$\pi '$
be any nonzero irreducible subquotient of
![]() $I(\pi ) = i_{M}^{G}(\sigma \otimes \psi )$
. Then
$I(\pi ) = i_{M}^{G}(\sigma \otimes \psi )$
. Then
![]() $\lambda _{\pi '} \leq \lambda _{\pi }$
in the usual partial ordering on
$\lambda _{\pi '} \leq \lambda _{\pi }$
in the usual partial ordering on
![]() $\mathfrak {a}_{M_0}^{\ast }$
, and
$\mathfrak {a}_{M_0}^{\ast }$
, and
![]() $\lambda _{\pi '} < \lambda _{\pi }$
if
$\lambda _{\pi '} < \lambda _{\pi }$
if
![]() $\pi '$
is a subquotient of
$\pi '$
is a subquotient of
![]() $\mathrm {ker}(I(\pi ) \to \pi )$
.
$\mathrm {ker}(I(\pi ) \to \pi )$
.
Proof. After twisting, we may assume
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
have integral central characters. Write
$\pi '$
have integral central characters. Write
![]() $\pi ' = j_Q^G(\sigma '\otimes \psi ')$
for some Langlands triple
$\pi ' = j_Q^G(\sigma '\otimes \psi ')$
for some Langlands triple
![]() $(L,\sigma ',\psi ')$
. By the proof of [Reference DatDat05, Theorem 3.11.i],
$(L,\sigma ',\psi ')$
. By the proof of [Reference DatDat05, Theorem 3.11.i],
![]() $\lambda _{\pi '}$
occurs in
$\lambda _{\pi '}$
occurs in
![]() $-\nu (\mathcal {E}(A_L,r^{\overline {Q}}_{G}(\pi ')))$
, so the result now follows from the subsequent proposition.
$-\nu (\mathcal {E}(A_L,r^{\overline {Q}}_{G}(\pi ')))$
, so the result now follows from the subsequent proposition.
Proposition C.2.5. Let
![]() $MU=P$
and
$MU=P$
and
![]() $LN=Q$
be standard parabolic subgroups of G. Let
$LN=Q$
be standard parabolic subgroups of G. Let
![]() $\sigma $
be a
$\sigma $
be a
![]() $\nu $
-tempered irreducible representation of
$\nu $
-tempered irreducible representation of
![]() $M(F)$
, and
$M(F)$
, and
![]() $\psi : M(F) \to \overline {\mathbf {Q}_{\ell }}^{\times }$
an unramified character with
$\psi : M(F) \to \overline {\mathbf {Q}_{\ell }}^{\times }$
an unramified character with
![]() $\mu =-\nu (\psi ) \in (\mathfrak {a}_P^G)^{*,+}$
. Let
$\mu =-\nu (\psi ) \in (\mathfrak {a}_P^G)^{*,+}$
. Let
![]() $\pi '$
be a subquotient of
$\pi '$
be a subquotient of
![]() $i_P^G(\sigma \otimes \psi )$
, and let
$i_P^G(\sigma \otimes \psi )$
, and let
![]() $\mu ' \in -\nu (\mathcal {E}(A_L,r^{\overline {Q}}_G(\pi ')))$
. Then
$\mu ' \in -\nu (\mathcal {E}(A_L,r^{\overline {Q}}_G(\pi ')))$
. Then
-
1.
 $\mu ' \leq \mu $
.
$\mu ' \leq \mu $
. -
2. If
 $\pi '$
is a subquotient of
$\pi '$
is a subquotient of
 $\mathrm {ker}(i_P^G(\sigma \otimes \psi ) \to j_P^G(\sigma \otimes \psi ))$
, then
$\mathrm {ker}(i_P^G(\sigma \otimes \psi ) \to j_P^G(\sigma \otimes \psi ))$
, then
 $\mu ' < \mu $
.
$\mu ' < \mu $
.
Proof. The exponents of
![]() $\pi '$
are a subset of the exponents of
$\pi '$
are a subset of the exponents of
![]() $r^{\overline {Q}}_{G}(i_P^G(\sigma \otimes \psi ))$
. These were analyzed in the proof of [Reference DatDat05, Lemma 3.7], where it was shown that if
$r^{\overline {Q}}_{G}(i_P^G(\sigma \otimes \psi ))$
. These were analyzed in the proof of [Reference DatDat05, Lemma 3.7], where it was shown that if
![]() $\psi '$
is such an exponent and
$\psi '$
is such an exponent and
![]() $\mu '=-\nu (\psi ')$
is such an exponent, then
$\mu '=-\nu (\psi ')$
is such an exponent, then
for some
![]() $w \in W_M \setminus W/ W_L$
. It was moreover shown that
$w \in W_M \setminus W/ W_L$
. It was moreover shown that
![]() $\mu -[\mu ]_L^G$
and
$\mu -[\mu ]_L^G$
and
![]() $[\mu -w^{-1}\mu ]_L^G$
belong to
$[\mu -w^{-1}\mu ]_L^G$
belong to
![]() $\overline {^+(\mathfrak {a}_M^G)^*}$
, which shows
$\overline {^+(\mathfrak {a}_M^G)^*}$
, which shows
![]() $\mu -\mu ' \geq 0$
, hence (1).
$\mu -\mu ' \geq 0$
, hence (1).
For (2), we may replace
![]() $\pi '$
with
$\pi '$
with
![]() $\mathrm {ker}(i_P^G(\sigma \otimes \psi ) \to j_P^G(\sigma \otimes \psi ))$
since the exponents of the former are again a subset of the exponents of the latter. We assume by way of contradiction that
$\mathrm {ker}(i_P^G(\sigma \otimes \psi ) \to j_P^G(\sigma \otimes \psi ))$
since the exponents of the former are again a subset of the exponents of the latter. We assume by way of contradiction that
![]() $\mu =\mu '$
. We have
$\mu =\mu '$
. We have
![]() $\mu \in (\mathfrak {a}_P^G)^{*,+}$
and
$\mu \in (\mathfrak {a}_P^G)^{*,+}$
and
![]() $\mu ' \in (\mathfrak {a}_L^G)^*$
, so
$\mu ' \in (\mathfrak {a}_L^G)^*$
, so
![]() $\mu ' = \mu $
implies that the intersection
$\mu ' = \mu $
implies that the intersection
![]() $(\mathfrak {a}_P^G)^* \cap (\mathfrak {a}_L^G)^*$
is nonempty. Since
$(\mathfrak {a}_P^G)^* \cap (\mathfrak {a}_L^G)^*$
is nonempty. Since
![]() $(\mathfrak {a}_P^G)^{*,+}$
is an open subset of
$(\mathfrak {a}_P^G)^{*,+}$
is an open subset of
![]() $(\mathfrak {a}_M^G)^*$
, we see that
$(\mathfrak {a}_M^G)^*$
, we see that
![]() $(\mathfrak {a}_M^G)^* \subset (\mathfrak {a}_L^G)^*$
, hence
$(\mathfrak {a}_M^G)^* \subset (\mathfrak {a}_L^G)^*$
, hence
![]() $Q \subset P$
. According to the formula
$Q \subset P$
. According to the formula
![]() $r^{\overline {Q}}_{G}(\pi ') = r^{\overline {Q}\cap M}_{M}(r^{\overline {P}}_{G}(\pi '))$
,
$r^{\overline {Q}}_{G}(\pi ') = r^{\overline {Q}\cap M}_{M}(r^{\overline {P}}_{G}(\pi '))$
,
![]() $\mu ' \in -\nu (\mathcal {E}(A_M,r^{\overline {P}}_{G}(\pi '))$
.
$\mu ' \in -\nu (\mathcal {E}(A_M,r^{\overline {P}}_{G}(\pi '))$
.
By construction of the Langlands quotient
![]() $j_P^G(\sigma \otimes \psi )$
, we have the exact sequence
$j_P^G(\sigma \otimes \psi )$
, we have the exact sequence
where the map between the two parabolic inductions is the intertwining operator
![]() $J_{\overline {P},P}$
of [Reference DatDat05, Lemma 3.7]. We recall that this intertwining operator was obtained via Frobenius reciprocity from the unique (up to scalar) element of
$J_{\overline {P},P}$
of [Reference DatDat05, Lemma 3.7]. We recall that this intertwining operator was obtained via Frobenius reciprocity from the unique (up to scalar) element of
![]() $\mathrm {Hom}_M(r^{\overline {P}}_G(i_P^G(\sigma \otimes \psi )),\sigma \otimes \psi )$
. This element is the unique retraction of the natural embedding of
$\mathrm {Hom}_M(r^{\overline {P}}_G(i_P^G(\sigma \otimes \psi )),\sigma \otimes \psi )$
. This element is the unique retraction of the natural embedding of
![]() $\sigma \otimes \psi $
into
$\sigma \otimes \psi $
into
![]() $r^{\overline {P}}_G(i_P^G(\sigma \otimes \psi ))$
.
$r^{\overline {P}}_G(i_P^G(\sigma \otimes \psi ))$
.
We can describe this element in a slightly different way that is more suitable for our purposes. The representation
![]() $r^{\overline {P}}_G(i_P^G(\sigma \otimes \psi ))$
has a filtration indexed by elements of
$r^{\overline {P}}_G(i_P^G(\sigma \otimes \psi ))$
has a filtration indexed by elements of
![]() $W_M \setminus W_G / W_M$
(strictly speaking, one has to choose a total order that refines the Bruhat order), and the natural embedding of
$W_M \setminus W_G / W_M$
(strictly speaking, one has to choose a total order that refines the Bruhat order), and the natural embedding of
![]() $\sigma \otimes \psi $
into
$\sigma \otimes \psi $
into
![]() $r^{\overline {P}}_G(i_P^G(\sigma \otimes \psi ))$
identifies
$r^{\overline {P}}_G(i_P^G(\sigma \otimes \psi ))$
identifies
![]() $\sigma \otimes \psi $
with the beginning part of this filtration, indexed by
$\sigma \otimes \psi $
with the beginning part of this filtration, indexed by
![]() $w=1$
. It is shown in equation (3.9) of the proof of [Reference DatDat05, Lemma 3.7] that, for any exponent
$w=1$
. It is shown in equation (3.9) of the proof of [Reference DatDat05, Lemma 3.7] that, for any exponent
![]() $\psi ''$
of a subqoutient corresponding to
$\psi ''$
of a subqoutient corresponding to
![]() $w \neq 1$
,
$w \neq 1$
,
![]() $\mu ''=-\nu (\psi '')$
satisfies
$\mu ''=-\nu (\psi '')$
satisfies
![]() $\mu '' < \mu $
. On the other hand, all exponents of
$\mu '' < \mu $
. On the other hand, all exponents of
![]() $\sigma \otimes \psi $
have image
$\sigma \otimes \psi $
have image
![]() $\mu $
under
$\mu $
under
![]() $-\nu $
. Therefore, the retraction
$-\nu $
. Therefore, the retraction
![]() $r^{\overline {P}}_G(i_P^G(\sigma \otimes \psi )) \to \sigma \otimes \psi $
is simply the projection onto the
$r^{\overline {P}}_G(i_P^G(\sigma \otimes \psi )) \to \sigma \otimes \psi $
is simply the projection onto the
![]() $\mu $
-direct summand of the the exponent decomposition of
$\mu $
-direct summand of the the exponent decomposition of
![]() $r^{\overline {P}}_G(i_P^G(\sigma \otimes \psi ))$
.
$r^{\overline {P}}_G(i_P^G(\sigma \otimes \psi ))$
.
Applying
![]() $r^{\overline {P}}_G$
to the above displayed exact sequence, we obtain the exact sequence
$r^{\overline {P}}_G$
to the above displayed exact sequence, we obtain the exact sequence
Therefore,
![]() $r^{\overline {P}}_G(\pi ')$
, being the kernel of
$r^{\overline {P}}_G(\pi ')$
, being the kernel of
![]() $r^{\overline {P}}_G(i_P^G(\sigma \otimes \psi )) \to r^{\overline {P}}_G(i_{\overline {P}}^G(\sigma \otimes \psi ))$
, is contained in the kernel of the composition of this map with the evaluation-at-
$r^{\overline {P}}_G(i_P^G(\sigma \otimes \psi )) \to r^{\overline {P}}_G(i_{\overline {P}}^G(\sigma \otimes \psi ))$
, is contained in the kernel of the composition of this map with the evaluation-at-
![]() $1$
map
$1$
map
![]() $r^{\overline {P}}_G(i_{\overline {P}}^G(\sigma \otimes \psi )) \to \sigma \otimes \psi $
. But that composition is, by construction of
$r^{\overline {P}}_G(i_{\overline {P}}^G(\sigma \otimes \psi )) \to \sigma \otimes \psi $
. But that composition is, by construction of
![]() $J_{\overline {P},P}$
via Frobenius reciprocity, equal to the projection
$J_{\overline {P},P}$
via Frobenius reciprocity, equal to the projection
![]() $r^{\overline {P}}_G(i_P^G(\sigma \otimes \psi )) \to (r^{\overline {P}}_G(i_P^G(\sigma \otimes \psi )))_{\mu }$
. Thus, the exponents of the kernel of that projection are those exponents of
$r^{\overline {P}}_G(i_P^G(\sigma \otimes \psi )) \to (r^{\overline {P}}_G(i_P^G(\sigma \otimes \psi )))_{\mu }$
. Thus, the exponents of the kernel of that projection are those exponents of
![]() $r^{\overline {P}}_G(i_P^G(\sigma \otimes \psi ))$
whose image
$r^{\overline {P}}_G(i_P^G(\sigma \otimes \psi ))$
whose image
![]() $\mu ''$
under
$\mu ''$
under
![]() $-\nu $
is not equal to
$-\nu $
is not equal to
![]() $\mu $
. By what was said in the previous paragraph, these satisfy
$\mu $
. By what was said in the previous paragraph, these satisfy
![]() $\mu '' < \mu $
.
$\mu '' < \mu $
.
Proof of Proposition C.2.2
Fix a point
![]() $\theta $
in the Bernstein variety for
$\theta $
in the Bernstein variety for
![]() $G(F)$
, and let
$G(F)$
, and let
![]() $\operatorname {\mathrm {Irr}}(G(F))_{\theta } \subset \operatorname {\mathrm {Irr}}(G(F))$
be the finite set of irreducible representations with cuspidal support
$\operatorname {\mathrm {Irr}}(G(F))_{\theta } \subset \operatorname {\mathrm {Irr}}(G(F))$
be the finite set of irreducible representations with cuspidal support
![]() $\theta $
. Let
$\theta $
. Let
be the subgroup generated by
![]() $\operatorname {\mathrm {Irr}}(G(F))_{\theta }$
, so
$\operatorname {\mathrm {Irr}}(G(F))_{\theta }$
, so
By Lemma C.2.3, it suffices to prove that
![]() $\operatorname {\mathrm {Groth}}(G(F))_{\theta }$
is generated by representations
$\operatorname {\mathrm {Groth}}(G(F))_{\theta }$
is generated by representations
![]() $i_{M}^{G}(\sigma \otimes \psi )$
for Langlands triples
$i_{M}^{G}(\sigma \otimes \psi )$
for Langlands triples
![]() $(M,\sigma ,\psi )$
, i.e., by standard representations. Note that
$(M,\sigma ,\psi )$
, i.e., by standard representations. Note that
![]() $\pi \in \operatorname {\mathrm {Irr}}(G(F))_{\theta }$
implies
$\pi \in \operatorname {\mathrm {Irr}}(G(F))_{\theta }$
implies
![]() $I(\pi ) \in \operatorname {\mathrm {Groth}}(G(F))_{\theta }$
, cf. [Reference Bernstein, Deligne and KazhdanBDK86, Proposition 2.4]. We will prove the finer result that the standard representations
$I(\pi ) \in \operatorname {\mathrm {Groth}}(G(F))_{\theta }$
, cf. [Reference Bernstein, Deligne and KazhdanBDK86, Proposition 2.4]. We will prove the finer result that the standard representations
![]() $I(\pi ), \pi \in \operatorname {\mathrm {Irr}}(G(F))_{\theta }$
give a basis for
$I(\pi ), \pi \in \operatorname {\mathrm {Irr}}(G(F))_{\theta }$
give a basis for
![]() $\operatorname {\mathrm {Groth}}(G(F))_{\theta }$
.
$\operatorname {\mathrm {Groth}}(G(F))_{\theta }$
.
Set
Note that S is a finite set and inherits a natural partial order from the partial order on
![]() $\mathfrak {a}_{M_0}^{\ast }$
. Pick any
$\mathfrak {a}_{M_0}^{\ast }$
. Pick any
![]() $\pi \in \operatorname {\mathrm {Irr}}(G(F))_{\theta }$
. If
$\pi \in \operatorname {\mathrm {Irr}}(G(F))_{\theta }$
. If
![]() $\lambda _{\pi }$
is minimal in S, then the natural map
$\lambda _{\pi }$
is minimal in S, then the natural map
![]() $I(\pi ) \to \pi $
is an isomorphism by Lemma C.2.4. In general, if
$I(\pi ) \to \pi $
is an isomorphism by Lemma C.2.4. In general, if
![]() $\lambda _{\pi }$
is not minimal in S, then by Lemma C.2.4 and induction on S, we may assume that
$\lambda _{\pi }$
is not minimal in S, then by Lemma C.2.4 and induction on S, we may assume that
![]() $\mathrm {ker}(I(\pi ) \to \pi )$
is a
$\mathrm {ker}(I(\pi ) \to \pi )$
is a
![]() $\mathbf {Z}$
-linear combination of standard representations
$\mathbf {Z}$
-linear combination of standard representations
![]() $I(\pi '), \pi ' \in \operatorname {\mathrm {Irr}}(G(F))_{\theta }$
. Then also
$I(\pi '), \pi ' \in \operatorname {\mathrm {Irr}}(G(F))_{\theta }$
. Then also
![]() $\pi = I(\pi ) - \mathrm {ker}(I(\pi ) \to \pi )$
is a
$\pi = I(\pi ) - \mathrm {ker}(I(\pi ) \to \pi )$
is a
![]() $\mathbf {Z}$
-linear combination of standard representations, giving the desired result.
$\mathbf {Z}$
-linear combination of standard representations, giving the desired result.
Acknowledgements
We are grateful to Peter Scholze for explaining to us some of the material on inertia stacks that appears in §4. We also thank Jean-François Dat, Laurent Fargues, Martin Olsson, Jack Thorne and Yakov Varshavsky for many helpful conversations. Additionally, DH is grateful to Marie-France Vignéras for sharing a scanned copy of her book [Reference VignérasVig96]. Finally, we are very grateful to the referee for their detailed comments and feedback on earlier versions of this paper.
Funding statement
T.K. was supported in part by NSF grants DMS-1161489, DMS-1801687, and a Sloan Fellowship. J.W. was supported by NSF grants DMS-1303312, DMS-1902148, and a Sloan Fellowship.
Competing interests
None.