Hostname: page-component-788cddb947-pt5lt Total loading time: 0 Render date: 2024-10-14T21:11:34.788Z Has data issue: false hasContentIssue false
  • English
  • Français

Analysis of crack singularities in an aging elastic material

Published online by Cambridge University Press:  22 July 2006

Martin Costabel ,
Monique Dauge ,
SergeïA. Nazarov  and
Jan Sokolowski
Martin Costabel
Affiliation:
Institut de Recherche Mathématique de Rennes, Université de Rennes 1, Campus de Beaulieu, 35042 Rennes Cedex, France. Martin.Costabel@univ-rennes1.fr; Monique.Dauge@univ-rennes1.fr
Monique Dauge
Affiliation:
Institut de Recherche Mathématique de Rennes, Université de Rennes 1, Campus de Beaulieu, 35042 Rennes Cedex, France. Martin.Costabel@univ-rennes1.fr; Monique.Dauge@univ-rennes1.fr
SergeïA. Nazarov
Affiliation:
Institute of Mechanical Engineering Problems, Laboratory of Mathematical Methods, Russian Academy of Sciences, V.O. Bol'shoi 61, 199178 St. Petersburg, Russia. serna@snark.ipme.ru
Jan Sokolowski
Affiliation:
Institut Élie Cartan, Laboratoire de Mathématiques, Université Henri Poincaré Nancy I, B.P. 239, 54506 Vandoeuvre-lès-Nancy Cedex, France. Jan.Sokolowski@iecn.u-nancy.fr
Get access

Abstract

We consider a quasistatic system involving a Volterra kernel modelling an hereditarily-elastic aging body. We are concerned with the behavior of displacement and stress fields in the neighborhood of cracks. In this paper, we investigate the case of a straight crack in a two-dimensional domain with a possibly anisotropic material law. We study the asymptotics of the time dependent solution near the crack tips. We prove that, depending on the regularity of the material law and the Volterra kernel, these asymptotics contain singular functions which are simple homogeneous functions of degree $\frac12$ 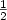or have a more complicated dependence on the distance variable r to the crack tips. In the latter situation, we observe a novel behavior of the singular functions, incompatible with the usual fracture criteria, involving super polynomial functions of ln r growing in time.

Keywords

Crack singularitiescreep theoryVolterra kernelhereditarily-elastic.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 40 , Issue 3 , May 2006 , pp. 553 - 595
Copyright
© EDP Sciences, SMAI, 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agranovich, M.S. and Vishik, M.I., Elliptic problems with the parameter and parabolic problems of general type. Uspekhi Mat. Nauk 19 (1963) 53–161 (English transl.: Russ. Math. Surv. 19 (1964) 53–157).
N.Kh. Arutyunyan and V.B. Kolmanovskii, The theory of creeping heterogeneous bodies. Nauka, Moscow (1983) 336.
Arutyunyan, N.Kh., Nazarov, S.A. and Shoikhet, B.A., Bounds and the asymptote of the stress-strain state of a threedimensional body with a crack in elasticity theory and creep theory. Dokl. Akad. Nauk SSSR 266 (1982) 1361–1366 (English transl.: Sov. Phys. Dokl. 27 (1982) 817–819).
N.Kh. Arutyunyan, A.D. Drozdov and V.E. Naumov, Mechanics of growing visco-elasto-plastic bodies. Nauka, Moscow (1987) 472.
Atkinson, C. and Bourne, J.P., Stress singularities in viscoelastic media. Q. J. Mech. Appl. Math. 42 (1989) 385–412. CrossRef
Atkinson, C. and Bourne, J.P., Stress singularities in angular sectors of viscoelastic media. Int. J. Eng. Sci. 28 (1990) 615–650. CrossRef
Bourne, J.P. and Atkinson, C., Stress singularities in viscoelastic media. II. Plane-strain stress singularities at corners. IMA J. Appl. Math. 44 (1990) 163–180. CrossRef
Costabel, M. and Dauge, M., Construction of corner singularities for Agmon-Douglis-Nirenberg elliptic systems. Math. Nachr. 162 (1993) 209–237. CrossRef
Costabel, M. and Dauge, M., Crack singularities for general elliptic systems. Math. Nachr. 235 (2002) 29–49. 3.0.CO;2-6>CrossRef
Costabel, M., Dauge, M. and Duduchava, R., Asymptotics without logarithmic terms for crack problems. Comm. Partial Differential Equations 28 (2003) 869–926. CrossRef
Duduchava, R. and Wendland, W.L., The Wiener-Hopf method for systems of pseudodifferential equations with an application to crack problems. Integr. Equat. Oper. Th. 23 (1995) 294–335. CrossRef
Duduchava, R., Sändig, A.M. and Wendland, W.L., Interface cracks in anisotropic composites. Math. Method. Appl. Sci. 22 (1999) 1413–1446. 3.0.CO;2-M>CrossRef
Dundurs, J., Effect of elastic constants on stress in composite under plane deformations. J. Compos. Mater. 1 (1967) 310. CrossRef
G. Gripenberg, S.-O. Londen and O. Staffans, Volterra Integral and Functional equations. Cambridge Univ. Press, Cambridge (1990).
Kondratiev, V.A., Boundary problems for elliptic equations in domains with conical or angular points. Trudy Moskov. Mat. Obshch. 16 (1967) 209–292 (English transl.: Trans. Moscow Math. Soc. 16 (1967) 227–313).
Kondratiev, V.A. and Oleinik, O.A., Boundary-value problems for the system of elasticity theory in unbounded domains. Korn's inequalities. Uspehi Mat. Nauk 43 (1988) 55–98 (English transl.: Russ. Math. Surv. 43 (1988) 65–119).
V.A. Kozlov, V.G. Maz'ya and J. Rossmann, Elliptic boundary value problems in domains with point singularities. Amer. Math. Soc., Providence (1997).
M.A. Krasnosel'skii, G.M. Vainikko and P.P. Zabreiko, Approximate solutions to integral equations. Nauka, Moscow (1969) 455.
V.G. Maz'ya and B.A. Plamenevskii, Weighted spaces with nonhomogeneous norms and boundary value problems in domains with conical points. In: Elliptische Differentialgleichungen (Meeting in Rostock, 1977), Wilhelm-Pieck-Univ., Rostock (1978) 161–189 (English transl.: Amer. Math. Soc. Transl. Ser. 2 123 (1984) 89–107).
Maz'ya, V.G. and Plamenevskii, B.A., The coefficients in the asymptotics of solutions of elliptic boundary value problems in domains with conical points. Math. Nachr. 76 (1997) 29–60 (English transl.: Amer. Math. Soc. Transl. Ser. 2 123 (1984) 57–88).
Mikhailov, S.E., Singularities of stresses in a plane hereditarily-elastic aging solid with corner points. Mech. Solids (Izv. AN SSSR. MTT) 19 (1984) 126–139.
Mikhailov, S.E., Singular stress behavior in a bonded hereditarily-elastic aging wedge. Part. I: Problem statement and degenerate case. Math. Method. Appl. Sci. 20 (1997) 13–30. 3.0.CO;2-T>CrossRef
Mikhailov, S.E., Singular stress behavior in a bonded hereditarily-elastic aging wedge. Part. II: General heredity. Math. Method. Appl. Sci. 20 (1997) 31–45. 3.0.CO;2-#>CrossRef
Nazarov, S.A., Vishik-Lyusternik method for elliptic boundary-value problems in regions with conical points. 1. The problem in a cone. Sibirsk. Mat. Zh. 22 (1981) 142–163 (English transl.: Siberian Math. J. 22 (1982) 594–611).
Nazarov, S.A., Weight functions and invariant integrals. Vychisl. Mekh. Deform. Tverd. Tela. 1 (1990) 17–31. (Russian)
S.A. Nazarov, Self-adjoint boundary value problems. The polynomial property and formal positive operators. St.-Petersburg Univ., Probl. Mat. Anal. 16 (1997) 167–192. (Russian)
Nazarov, S.A., The interface crack in anisotropic bodies. Stress singularities and invariant integrals. Prikl. Mat. Mekh. 62 (1998) 489–502 (English transl.: J. Appl. Math. Mech. 62 (1998) 453–464).
Nazarov, S.A., The polynomial property of self-adjoint elliptic boundary-value problems and the algebraic description of their attributes. Uspekhi mat. nauk 54 (1999) 77–142 (English transl.: Russ. Math. Surv. 54 (1999) 947–1014). CrossRef
Nazarov, S.A. and Shoikhet, B.A., Asymptotic behavior of the solution of a certain integro-differential equation near an angular point of the boundary. Mat. Zametki. 33 (1983) 583–594 (English transl.: Math. Notes 33 (1983) 300–306).
Nazarov, S.A. and Plamenevskii, B.A., Neumann problem for selfadjoint elliptic systems in a domain with piecewise smooth boundary. Trudy Leningrad. Mat. Obshch. 1 (1990) 174–211 (English transl.: Amer. Math. Soc. Transl. Ser. 2 155 (1993) 169–206).
S.A. Nazarov and B.A. Plamenevsky, Elliptic problems in domains with piecewise smooth boundaries. Walter de Gruyter, Berlin, New York (1994) 525.
Nazarov, S.A., Trapeznikov, L.P. and Shoikhet, B.A., On the correspondence principle in the plane creep problem of aging homogeneous media with developing slits and cavities. Prikl. Mat. Mekh. 51 (1987) 504–512 (English transl.: J. Appl. Math. Mech. 51 (1987) 392–399).
J. Nečas, Les méthodes directes en théorie des équations elliptiques. Masson-Academia, Paris-Prague (1967).
A.C. Pipkin, Lectures on viscoelasticity theory. Springer, NY (1972) 180.
Vardanyan, G.S. and Sheremet, V.D., On certain theorems in the plane problem of the creep theory. Izvestia AN Arm. SSR. Mechanics 4 (1973) 60–76.
Zhuravlev, V.P., Nazarov, S.A. and Shoikhet, B.A., Asymptotics of the stress-strain state near the tip of a crack in an inhomogeneously aging bodies. Dokl. Akad. Nauk Armenian SSR 74 (1982) 26–29. (Russian)
Zhuravlev, V.P., Nazarov, S.A. and Shoikhet, B.A., Asymptotics near the tip of a crack of the state of stress and strain of inhomogeneously aging bodies. Prikl. Mat. Mekh. 47 (1983) 200–208 (English transl.: J. Appl. Math. Mech. 47 (1984) 162–170).