Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-01T21:11:09.116Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixing constructions with infinite invariant measure and spectral multiplicities

Published online by Cambridge University Press:  10 May 2010

ALEXANDRE I. DANILENKO  and
VALERY V. RYZHIKOV
ALEXANDRE I. DANILENKO
Affiliation:
Max Planck Institute for Mathematics, Vivatsgasse 7, D-53111 Bonn, Germany (email: alexandre.danilenko@gmail.com)
VALERY V. RYZHIKOV
Affiliation:
Department of Mechanics and Mathematics, Lomonosov Moscow State University, GSP-1, Leninskie Gory, Moscow, 119991, Russian Federation (email: vryzh@mail.ru)
Get access Rights & Permissions [Opens in a new window]

Abstract

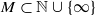We introduce high staircase infinite measure preserving transformations and prove that they are mixing under a restricted growth condition. This is used to (i) realize each subset as the set of essential values of the multiplicity function for the Koopman operator of a mixing ergodic infinite measure preserving transformation, (ii) construct mixing power weakly mixing infinite measure preserving transformations, and (iii) construct mixing Poissonian automorphisms with a simple spectrum, etc.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 31 , Issue 3 , June 2011 , pp. 853 - 873
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Aaronson, J.. An Introduction to Infinite Ergodic Theory. American Mathematical Society, Providence, RI, 1997.CrossRefGoogle Scholar
[2]Adams, T. M.. Smorodinsky’s conjecture on rank one systems. Proc. Amer. Math. Soc. 126 (1998), 739–744.CrossRefGoogle Scholar
[3]Adams, T., Friedman, N. and Silva, C. E.. Rank-one power weak mixing nonsingular transformations. Ergod. Th. & Dynam. Sys. 21 (2001), 1321–1332.CrossRefGoogle Scholar
[4]Ageev, O. N.. Mixing with staircase multiplicity function. Ergod. Th. & Dynam. Sys. 28 (2008), 1687–1700.CrossRefGoogle Scholar
[5]Choksi, J. and Kakutani, S.. Residuality of ergodic measure transformations and of ergodic transformations which preserve an infinite measure. Indiana Univ. Math. J. 28 (1979), 453–469.CrossRefGoogle Scholar
[6]Cornfeld, I. P., Fomin, V. S. and Sinai, Ya. G.. Ergodic Theory. Springer, New York, 1982.CrossRefGoogle Scholar
[7]Danilenko, A. I.. Funny rank one weak mixing for nonsingular Abelian actions. Israel J. Math. 121 (2001), 29–54.CrossRefGoogle Scholar
[8]Danilenko, A. I.. Infinite rank one actions and nonsingular Chacon transformations. Illinois J. Math. 48 (2004), 769–786.CrossRefGoogle Scholar
[9]Danilenko, A. I.. (C,F)-actions in ergodic theory. Geometry and Dynamics of Groups and Spaces (Progress in Mathematics, 265). Birkhäuser, Basel, 2008, pp. 325–351.CrossRefGoogle Scholar
[10]Danilenko, A. I.. New spectral multiplicities for mixing transformations. Preprint, arXiv:0908.1640.Google Scholar
[11]Danilenko, A. I. and Ryzhikov, V. V.. Spectral multiplicities for infinite measure preserving transformations. Funct. Anal. Appl. to appear.Google Scholar
[12]Danilenko, A. I. and Silva, C. E.. Multiple and polynomial recurrence for Abelian actions in infinite measure. J. Lond. Math. Soc. 69 (2004), 183–200.CrossRefGoogle Scholar
[13]Danilenko, A. I. and Silva, C. E.. Ergodic Theory: Non-Singular Transformations (Encyclopedia of Complexity and Systems Science). Springer, New York, 2009, pp. 3055–3083.Google Scholar
[14]del Junco, A.. A simple map with no prime factors. Israel J. Math. 104 (1998), 301–320.CrossRefGoogle Scholar
[15]Furstenberg, H. and Weiss, B.. The finite multipliers of infinite ergodic transformations. The Structure of Attractors in Dynamical Systems (Lecture Notes in Mathematics, 668). Springer, Berlin, 1978, pp. 127–132.CrossRefGoogle Scholar
[16]Krengel, U. and Sucheston, L.. On mixing in infinite measure spaces. Z. Wahrscheinlichkeitstheorie Verw. Gebiete 13 (1969), 150–164.CrossRefGoogle Scholar
[17]Nadkarni, M. G.. Spectral theory of dynamical systems (Birkhäuser Advanced Texts: Basler Lehrbücher). Birkhäuser, Basel, 1998.Google Scholar
[18]Neretin, Yu.. Categories of Symmetries and Infinite Dimensional Groups. Oxford University Press, Oxford, 1986.Google Scholar
[19]Newton, D.. On Gaussian processes with simple spectrum. Z. Wahrscheinlichkeitstheorie Verw. Gebiete 5 (1966), 207–209.CrossRefGoogle Scholar
[20]Ornstein, D. S.. On the root problem in ergodic theory. Proc. Sixth Berkley Symp. Math. Stat. Prob. (Univ. California, Berkeley, Calif., 1970/1971) (Vol II: Probability Theory). University of California Press, Berkeley, 1972, pp. 347–356.Google Scholar
[21]Parry, W.. Ergodic and spectral analysis of certain infinite measure preserving transformations. Proc. Amer. Math. Soc. 16 (1965), 960–966.CrossRefGoogle Scholar
[22]Roy, E.. Ergodic properties of Poissonian ID-processes. Ann. Probab. 35 (2007), 551–576.CrossRefGoogle Scholar
[23]Roy, E.. Poisson suspensions and infinite ergodic theory. Ergod. Th. & Dynam. Sys. 29 (2009), 667–683.CrossRefGoogle Scholar
[24]Ryzhikov, V. V.. Homogeneous spectrum, disjointness of convolutions, and mixing properties of dynamical systems. Selected Russian Mathematics 1 (1999), 13–24.Google Scholar
[25]Ryzhikov, V. V.. Weak limits of powers, the simple spectrum of symmetric products and mixing constructions of rank 1. Sb. Math. 198 (2007), 733–754.CrossRefGoogle Scholar
[26]Ryzhikov, V. V.. Spectral multiplicities and asymptotic operator properties of actions with invariant measure. Sb. Math. 200 (2009), 1833–1845.CrossRefGoogle Scholar