Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-18T05:52:08.212Z Has data issue: false hasContentIssue false
  • English
  • Français

Subgroups of the Adjoint Group of a Radical Ring

Published online by Cambridge University Press:  20 November 2018

B. Amberg ,
O. Dickenschied  and
YA. P. Sysak
B. Amberg
Affiliation:
Fachbereich Mathematik der Universität Mainz D-55099 Mainz Germany, e-mail: amberg@mat.mathematik.uni-mainz.de, e-mail: dickenschied@mat.mathematik.uni-mainz.de
O. Dickenschied
Affiliation:
Fachbereich Mathematik der Universität Mainz D-55099 Mainz Germany, e-mail: amberg@mat.mathematik.uni-mainz.de, e-mail: dickenschied@mat.mathematik.uni-mainz.de
YA. P. Sysak
Affiliation:
Institute of Mathematics Ukrainian Academy of Science 252601 Kiev Ukraine, e-mail: mathkiev@imat.gluk.apc.org
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

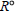It is shown that the adjoint group ${{R}^{{}^\circ }}$ of an arbitrary radical ring $R$ has a series with abelian factors and that its finite subgroups are nilpotent. Moreover, some criteria for subgroups of 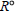${{R}^{{}^\circ }}$ to be locally nilpotent are given.

Keywords

16N2020F19
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 1 , 01 February 1998 , pp. 3 - 15
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Amberg, B. and Dickenschied, O., On the adjoint group of a radical ring. Canad.Math. Bull. (3) 38 (1995), 262–270.Google Scholar
2. Amberg, B., Franciosi, S., and de Giovanni, F., Products of groups.Oxford University Press, New York, 1992.Google Scholar
3. Amberg, B. and Ya. Sysak, P., Locally soluble products of two minimax subgroups. Proceedings of ‘Groups-Korea 1994’, W. de Gruyter, Berlin, 1995. 8–14.Google Scholar
4. Brown, K.A., The Nullstellensatz for certain group rings. J. LondonMath. Soc. (2), 26 (1982), 425–434.Google Scholar
5. Jacobson, N., Structure of Rings. Amer. Math. Soc. Colloq. Publ. 37 , 1964.Google Scholar
6. Kim, Y.K. and Rhemtulla, A.H., Weak maximality condition and polycyclic groups. Proc. Amer. Math. Soc. (3) 123 (1995), 711–714.Google Scholar
7. Kropholler, P.H., Linnel, P.A., and Moody, J.A., Applications of a new K-theoretic theorem to soluble group rings. Proc. Amer. Math. Soc. (3) 104 (1988), 675–684.Google Scholar
8. Neroslavskii, O.M., Structures that are connected with radical rings (Russian). Vesci Akad. Navuk BSSR Ser. Fiz.-Mat. Navuk (2) 134 (1973), 5–10.Google Scholar
9. Robinson, D.J.S., Finiteness Conditions and Generalized Soluble Groups.Springer-Verlag, Berlin- Heidelberg-New York, 1972.Google Scholar
10. Rowen, L.H., Ring Theory.Academic Press, New York, 1988.Google Scholar
11. Watters, J.F., On the adjoint group of a radical ring. J. London Math. Soc. 43 (1968), 725–729.Google Scholar
12. Wehrfritz, B.A.F., Infinite Linear Groups.Springer-Verlag, Berlin, 1973.Google Scholar
13. Wilson, J.S., Two-generator conditions for residually finite groups. Bull. London Math. Soc. 23 (1991), 239–248.Google Scholar
14. Zelmanov, E., The solution of the restricted Burnside problem for groups of odd exponent. Izv. Akad. Nauk SSSR, Ser.Mat. (1) 54 (1990), 42–59.Google Scholar
15. Zelmanov, E., The solution of the restricted Burnside problem for 2-groups. Mat. Sb. (4)182 (1991), 568–592..Google Scholar