Hostname: page-component-f554764f5-rj9fg Total loading time: 0 Render date: 2025-04-10T14:31:50.592Z Has data issue: false hasContentIssue false
  • English
  • Français

Weighted normal numbers

Published online by Cambridge University Press:  17 April 2009

Geon H. Choe
Geon H. Choe
Affiliation:
Department of Mathematics, Korea Advanced Institute of Science and Technology, Taejon 305–701, Korea, e-mail: choe@euclid.kaist.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that if {ak}k is bounded then 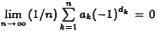for almost every 0 < x < 1 where 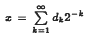is the dyadic expansion of x. It is also shown that 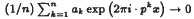almost everywhere where p > 1 is any fixed integer.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 52 , Issue 2 , October 1995 , pp. 177 - 181
Copyright
Copyright © Australian Mathematical Society 1995

References

[1]Bellow, A. and Losert, V., ‘The weighted pointwise ergodic theorem and the individual ergodic theorem along subsequences’, Trans. Amer. Math. Soc. 288 (1985), 307–345.CrossRefGoogle Scholar
[2]Choe, G.H., ‘Spectral types of uniform distribution’, Proc. Amer. Math. Soc. 120 (1994), 715–722.CrossRefGoogle Scholar
[3]Helson, H., Harmonic analysis (Addison-Wesley, 1983).Google Scholar
[4]Katznelson, Y., An introduction to Harmonic analysis (Dover, New York, 1976).Google Scholar
[5]Nair, R., ‘On the metrical theory of continued fractions’, Proc. Amer. Math. Soc. 120 (1994), 1041–1046.CrossRefGoogle Scholar
[6]Petersen, K., Ergodic theory (Cambridge University Press, Cambridge, London, 1983).CrossRefGoogle Scholar
[7]Walters, P., An introduction to Ergodic theory (Springer-Verlag, New York, 1982).CrossRefGoogle Scholar