Hostname: page-component-76fb5796d-5g6vh Total loading time: 0 Render date: 2024-04-26T14:57:45.287Z Has data issue: false hasContentIssue false
  • English
  • Français

GROUPS WHOSE NONNORMAL SUBGROUPS ARE METAHAMILTONIAN

Part of: Special aspects of infinite or finite groups

Published online by Cambridge University Press:  08 October 2019

DARIO ESPOSITO Open the ORCID record for DARIO ESPOSITO [Opens in a new window] ,
FRANCESCO DE GIOVANNI Open the ORCID record for FRANCESCO DE GIOVANNI [Opens in a new window]  and
MARCO TROMBETTI Open the ORCID record for MARCO TROMBETTI [Opens in a new window]
DARIO ESPOSITO
Affiliation:
Dipartimento di Matematica e Applicazioni, Università di Napoli Federico II, Napoli, Italy email esposito.dario94@gmail.com
FRANCESCO DE GIOVANNI*
Affiliation:
Dipartimento di Matematica e Applicazioni, Università di Napoli Federico II, Napoli, Italy email degiovan@unina.it
MARCO TROMBETTI
Affiliation:
Dipartimento di Matematica e Applicazioni, Università di Napoli Federico II, Napoli, Italy email marco.trombetti@unina.it
*
✉degiovan@unina.it
Get access Rights & Permissions [Opens in a new window]

Abstract

If 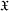$\mathfrak{X}$ is a class of groups, we define a sequence $\mathfrak{X}_{1},\mathfrak{X}_{2},\ldots ,\mathfrak{X}_{k},\ldots$ of group classes by putting 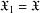$\mathfrak{X}_{1}=\mathfrak{X}$ and choosing 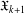$\mathfrak{X}_{k+1}$ as the class of all groups whose nonnormal subgroups belong to 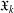$\mathfrak{X}_{k}$. In particular, if 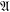$\mathfrak{A}$ is the class of abelian groups, 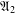$\mathfrak{A}_{2}$ is the class of metahamiltonian groups, that is, groups whose nonnormal subgroups are abelian. The aim of this paper is to study the structure of 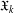$\mathfrak{X}_{k}$-groups, with special emphasis on the case 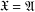$\mathfrak{X}=\mathfrak{A}$. Among other results, it will be proved that a group has a finite commutator subgroup if and only if it is locally graded and belongs to 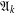$\mathfrak{A}_{k}$ for some positive integer 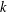$k$.

Keywords

metahamiltonian groupk-hamiltonian groupfinite-by-abelian group

MSC classification

Primary: 20F24: FC-groups and their generalizations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 1 , August 2020 , pp. 96 - 103
Check for updates
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The authors are supported by GNSAGA (INdAM); the last two authors are members of AGTA—Advances in Group Theory and Applications (www.advgrouptheory.com).

References

Baer, R., ‘Überauflösbare Gruppen’, Abh. Math. Sem. Univ. Hamburg 23 (1957), 11–28.10.1007/BF02941022CrossRefGoogle Scholar
De Falco, M., de Giovanni, F. and Musella, C., ‘Groups whose finite homomorphic images are metahamiltonian’, Comm. Algebra 37 (2009), 2468–2476.CrossRefGoogle Scholar
De Falco, M., de Giovanni, F. and Musella, C., ‘Metahamiltonian groups and related topics’, Int. J. Group Theory 2 (2013), 117–129.Google Scholar
De Mari, F. and de Giovanni, F., ‘Groups with few normalizer subgroups’, Irish Math. Soc. Bull. 56 (2005), 103–113.CrossRefGoogle Scholar
de Giovanni, F. and Trombetti, M., ‘Groups with restrictions on proper uncountable subgroups’, Studia Sci. Math. Hungar. 56 (2019), 154–165.Google Scholar
de Giovanni, F. and Trombetti, M., ‘Groups whose proper subgroups are metahamiltonian-by-finite’, Rocky Mountain J. Math., to appear.Google Scholar
de Giovanni, F. and Trombetti, M., ‘Cohopfian groups and accessible group classes’, to appear.Google Scholar
Kuzennyi, N. F. and Semko, N. N., ‘Structure of solvable nonilpotent metahamiltonian groups’, Math. Notes 34 (1983), 572–577.CrossRefGoogle Scholar
Lennox, J. C., ‘Finite Frattini factors in finitely generated soluble groups’, Proc. Amer. Math. Soc. 41 (1973), 356–360.10.1090/S0002-9939-1973-0333003-XCrossRefGoogle Scholar
Neumann, B. H., ‘Groups with finite classes of conjugate subgroups’, Math. Z. 63 (1955), 76–96.CrossRefGoogle Scholar
Robinson, D. J. S., ‘A theorem on finitely generated hyperabelian groups’, Invent. Math. 10 (1970), 38–43.CrossRefGoogle Scholar
Robinson, D. J. S., Finiteness Conditions and Generalized Soluble Groups (Springer, Berlin, 1972).10.1007/978-3-662-07241-7CrossRefGoogle Scholar
Robinson, D. J . S., A Course in the Theory of Groups, 2nd edn (Springer, Berlin, 1996).10.1007/978-1-4419-8594-1CrossRefGoogle Scholar
Romalis, G. M. and Sesekin, N. F., ‘Metahamiltonian groups’, Ural. Gos. Univ. Mat. Zap. 5 (1966), 101–106.Google Scholar
Romalis, G. M. and Sesekin, N. F., ‘Metahamiltonian groups II’, Ural. Gos. Univ. Mat. Zap. 6 (1968), 50–52.Google Scholar
Romalis, G. M. and Sesekin, N. F., ‘Metahamiltonian groups III’, Ural. Gos. Univ. Mat. Zap. 7 (1969/70), 195–199.Google Scholar