Hostname: page-component-f554764f5-8cg97 Total loading time: 0 Render date: 2025-04-12T04:58:02.275Z Has data issue: false hasContentIssue false
  • English
  • Français

BLOCKS WITH SMALL-DIMENSIONAL BASIC ALGEBRA

Part of: Modules, bimodules and ideals Representation theory of groups

Published online by Cambridge University Press:  21 September 2020

BENJAMIN SAMBALE Open the ORCID record for BENJAMIN SAMBALE [Opens in a new window]
BENJAMIN SAMBALE*
Affiliation:
Institut für Algebra, Zahlentheorie und Diskrete Mathematik, Leibniz Universität Hannover, Welfengarten 1, 30167 Hannover, Germany
*
e-mail: sambale@math.uni-hannover.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Linckelmann and Murphy have classified the Morita equivalence classes of p-blocks of finite groups whose basic algebra has dimension at most 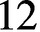$12$ . We extend their classification to dimension 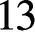$13$ and 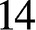$14$ . As predicted by Donovan’s conjecture, we obtain only finitely many such Morita equivalence classes.

Keywords

basic block algebraMorita equivalenceDonovan’s conjecture

MSC classification

Primary: 20C05: Group rings of finite groups and their modules
Secondary: 16D90: Module categories ; module theory in a category-theoretic context; Morita equivalence and duality
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 3 , June 2021 , pp. 461 - 474
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BYCreative Common License - NCCreative Common License - ND
This is an Open Access article, distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives licence (http://creativecommons.org/licenses/by-nc-nd/4.0/), which permits non-commercial re-use, distribution, and reproduction in any medium, provided the original work is unaltered and is properly cited. The written permission of Cambridge University Press must be obtained for commercial re-use or in order to create a derivative work.
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Footnotes

This work is supported by the German Research Foundation (SA 2864/1-2 and SA 2864/3-1).

References

Ardito, C. G. and Sambale, B., ‘Cartan matrices and Brauer’s $k(B)$ -Conjecture V’, Preprint, https://arxiv.org/abs/1911.10710v1.Google Scholar
Bonnafé, C., Representations of SL2 (Fq), Algebra and Applications, 13 (Springer-Verlag, London, UK, 2011).CrossRefGoogle Scholar
Eaton, C., ‘Morita equivalence classes of blocks with elementary abelian defect groups of order 16’, Preprint, https://arxiv.org/abs/1612.03485v4.Google Scholar
Eaton, C. W. and Livesey, M., ‘Donovan’s conjecture and blocks with abelian defect groups’, Proc. Amer. Math. Soc. 147 (2019), 963–970.CrossRefGoogle Scholar
Erdmann, K., Blocks of Tame Representation Type and Related Algebras, Lecture Notes in Mathematics, 1428 (Springer-Verlag, Berlin, 1990).CrossRefGoogle Scholar
Fong, P. and Srinivasan, B., ‘Brauer trees in $\mathrm{GL}\left(n,q\right)$ ’, Math. Z. 187 (1984), 81–88.CrossRefGoogle Scholar
The GAP Group, GAP – Groups, Algorithms, and Programming, Version 4.11.0 (2020), http://www.gap-system.org.Google Scholar
Hendren, S., ‘Extra special defect groups of order ${p}^3$ and exponent $p$ ’, J. Algebra 313 (2007), 724–760.CrossRefGoogle Scholar
Holm, T., Blocks of Tame Representation Type and Related Algebras: Derived Equivalences and Hochschild Cohomology, Habilitationsschrift, Magdeburg, 2001.Google Scholar
Kessar, R. and Malle, G., ‘Quasi-isolated blocks and Brauer’s height zero conjecture’, Ann. Math. (2) 178 (2013), 321–384.CrossRefGoogle Scholar
Linckelmann, M., ‘Finite-dimensional algebras arising as blocks of finite group algebras’, in: Representations of Algebras, Contemporary Mathematics, 705 (American Mathematical Society, Providence, RI, 2018), 155–188.CrossRefGoogle Scholar
Linckelmann, M. and Murphy, W., ‘A 9-dimensional algebra which is not a block of a finite group’, Preprint, https://arxiv.org/abs/2005.02223v1.Google Scholar
Naehrig, N., ‘A construction of almost all Brauer trees’, J. Group Theory 11 (2008), 813–829.CrossRefGoogle Scholar
Navarro, G., Characters and Blocks of Finite Groups, London Mathematical Society Lecture Note Series, 250 (Cambridge University Press, Cambridge, UK, 1998).CrossRefGoogle Scholar
Plesken, W., ‘Solving $X{X}^{\mathsf{tr}}=A$ over the integers’, Linear Algebra Appl. 226/228 (1995), 331–344.CrossRefGoogle Scholar
Ruiz, A. and Viruel, A., ‘The classification of $p$ -local finite groups over the extraspecial group of order ${p}^3$ and exponent $p$ ’, Math. Z. 248 (2004), 45–65.CrossRefGoogle Scholar
Sambale, B., Blocks of Finite Groups and their Invariants, Springer Lecture Notes in Mathematics, 2127 (Springer-Verlag, Cham, 2014).CrossRefGoogle Scholar
Sambale, B., ‘Cartan matrices and Brauer’s $k(B)$ -Conjecture IV’, J. Math. Soc. Jpn. 69 (2017), 1–20.CrossRefGoogle Scholar
Wilson, R. A., Thackray, J. G., Parker, R. A., Noeske, F., Müller, J., Lux, K., Lübeck, F., Jansen, C., Hiss, G. and Breuer, T., The Modular Atlas homepage, http://www.math.rwth-aachen.de/∼MOC/decomposition/tex/A7/A7mod7.pdf.Google Scholar