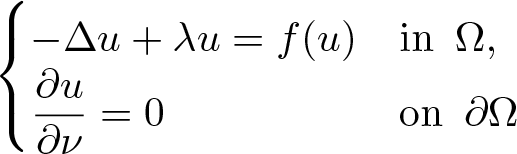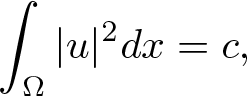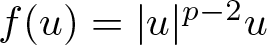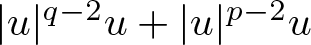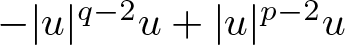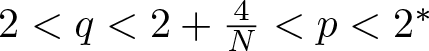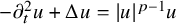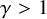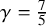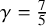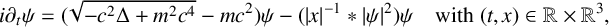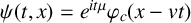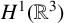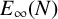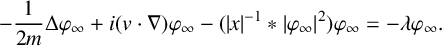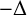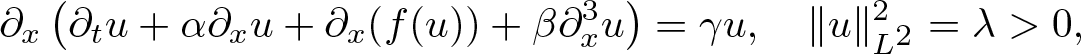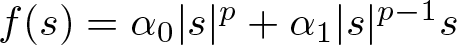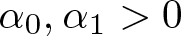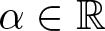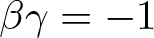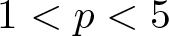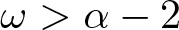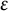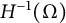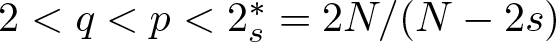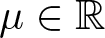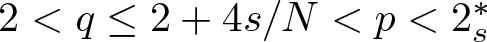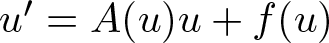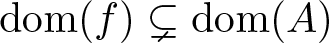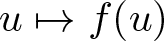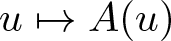335 results in 35Qxx
Remark on the local well-posedness for NLS with the modulated dispersion
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-12
-
- Article
- Export citation
Numerical solution of a PDE arising from prediction with expert advice
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Solutions with prescribed mass for L2-supercritical NLS equations under Neumann boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On blow-up for the supercritical defocusing nonlinear wave equation
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 31 March 2025, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
3D Navier–Stokes–Voigt equations with damping and double delays on unbounded domains: Well-posedness, pullback attractors, and limit measures
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 March 2025, pp. 1-39
-
- Article
- Export citation
Rigorous derivation of a binary-ternary Boltzmann equation for a non ideal gas of hard spheres
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 05 March 2025, e52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unique compact representation of magnetic fields using truncated solid harmonic expansions
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 03 March 2025, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Well-posedness for the 3-D generalized micropolar system in critical Fourier–Besov–Morrey spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 26 February 2025, pp. 1-17
-
- Article
- Export citation
Global well-posedness and Turing–Hopf bifurcation of prey-taxis systems with hunting cooperation
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A sharp threshold for Trudinger–Moser type inequalities with logarithmic kernels in dimension N
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 17 February 2025, pp. 1-39
-
- Article
- Export citation
Smooth imploding solutions for 3D compressible fluids
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 February 2025, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spatio-temporal behaviour of SIR models with cross-diffusion and vital dynamics
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NONRELATIVISTIC LIMIT FOR THE TRAVELLING WAVES OF THE PSEUDORELATIVISTIC HARTREE EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 26 December 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
Fractional time differential equations as a singular limit of the Kobayashi–Warren–Carter system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 December 2024, pp. 1-37
-
- Article
-
- You have access
- HTML
- Export citation
SYMMETRY RESTORATION IN COLLISIONS OF SOLITONS IN FRACTIONAL COUPLERS
- Part of
-
- Journal:
- The ANZIAM Journal , First View
- Published online by Cambridge University Press:
- 03 December 2024, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral stability of constrained solitary waves for a generalized Ostrovsky equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 November 2024, pp. 1-32
-
- Article
-
- You have access
- HTML
- Export citation
Stability conditions for mean-field limiting vorticities of the Ginzburg-Landau equations in 2D
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 27 November 2024, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Instability of standing waves for fractional NLS with combined nonlinearities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 November 2024, pp. 1-29
-
- Article
-
- You have access
- HTML
- Export citation
Well-posedness of quasilinear parabolic equations in time-weighted spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-33
-
- Article
-
- You have access
- HTML
- Export citation
On Riemann–Hilbert problem and multiple high-order pole solutions to the cubic Camassa–Holm equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-51
-
- Article
-
- You have access
- HTML
- Export citation