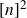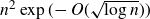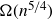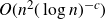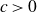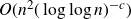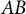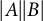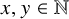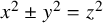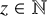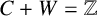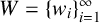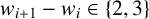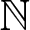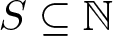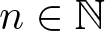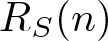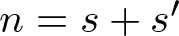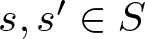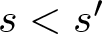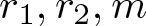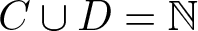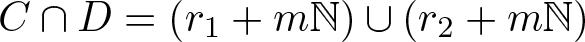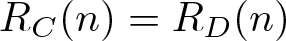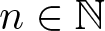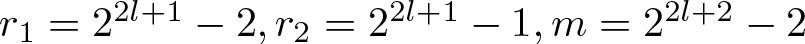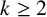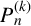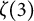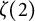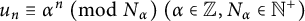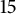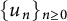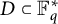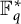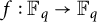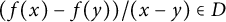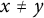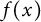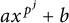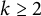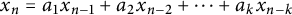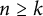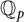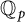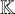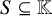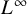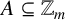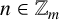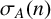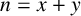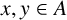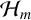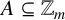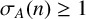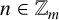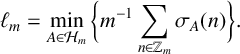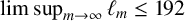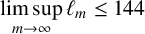319 results in 11Bxx
Improved bounds for skew corner-free sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 04 April 2025, pp. 1-16
-
- Article
- Export citation
Semisimple random walks on the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 03 March 2025, pp. 1-58
-
- Article
- Export citation
Multiplicative structure of shifted multiplicative subgroups and its applications to Diophantine tuples
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 19 February 2025, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Partition regularity of Pythagorean pairs
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 February 2025, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON MINIMAL ADDITIVE COMPLEMENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 February 2025, pp. 1-8
-
- Article
- Export citation
An efficient asymmetric removal lemma and its limitations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 February 2025, e38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CORRECTION TO ‘ADDITIVE AND SUBTRACTIVE BASES OF
 $ \mathbb {Z}_m$ IN AVERAGE’
$ \mathbb {Z}_m$ IN AVERAGE’
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1-2
-
- Article
- Export citation
On the structure of non-negative integer sets which have identical representation functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 February 2025, pp. 1-20
-
- Article
- Export citation
Finding product sets in some classes of amenable groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON PERFECT POWERS AS SUMS OR DIFFERENCES OF TWO k-GENERALISED PELL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 20 January 2025, pp. 1-10
-
- Article
- Export citation
Restricted sumsets in multiplicative subgroups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the binomial transforms of Apéry-like sequences
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 08 January 2025, pp. 1-18
-
- Article
- Export citation
A NOTE ON THE LARGE SIEVE INEQUALITY FOR MODULI GENERATED BY A QUADRATIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 26 December 2024, pp. 1-6
-
- Article
-
- You have access
- HTML
- Export citation
A Szemerédi type theorem for sets of positive density in approximate lattices
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A strengthening of McConnel’s theorem on permutations over finite fields
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 213-218
- Print publication:
- March 2025
-
- Article
-
- You have access
- HTML
- Export citation
p-Adic quotient sets: Linear recurrence sequences with reducible characteristic polynomials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 11 December 2024, pp. 177-186
- Print publication:
- March 2025
-
- Article
-
- You have access
- HTML
- Export citation
Simplices in large sets and directional expansion in ergodic actions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e121
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Polynomial progressions in topological fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 November 2024, e106
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ADDITIVE AND SUBTRACTIVE BASES OF
 $\mathbb {Z}_m$ IN AVERAGE
$\mathbb {Z}_m$ IN AVERAGE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-10
-
- Article
-
- You have access
- HTML
- Export citation
Arithmetic Ramsey theory over the primes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 November 2024, pp. 1-47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation