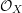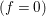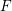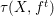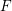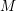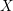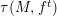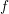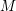121 results in 13Axx
GRADED UNIPOTENT GROUPS AND GROSSHANS THEORY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 04 September 2017, e21
-
- Article
-
- You have access
- Open access
- Export citation
Local cohomology of Du Bois singularities and applications to families
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 10 / October 2017
- Published online by Cambridge University Press:
- 27 July 2017, pp. 2147-2170
- Print publication:
- October 2017
-
- Article
- Export citation
Invariants of GLn(𝔽q) in polynomials modulo Frobenius powers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 05 July 2017, pp. 831-873
- Print publication:
- August 2017
-
- Article
- Export citation
ESSENTIAL DIMENSION OF GENERIC SYMBOLS IN CHARACTERISTIC
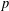 $p$
$p$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 22 June 2017, e14
-
- Article
-
- You have access
- Open access
- Export citation
On log del Pezzo surfaces in large characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 08 March 2017, pp. 820-850
- Print publication:
- April 2017
-
- Article
- Export citation
Towards a symplectic version of the Chevalley restriction theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 647-666
- Print publication:
- March 2017
-
- Article
- Export citation
RELATIVE HILBERT CO-EFFICIENTS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 01 March 2017, pp. 729-741
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
An intrinsic definition of the Rees algebra of a module
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 22 February 2017, pp. 13-30
-
- Article
- Export citation
On the Universal SL2-Representation Rings of Free Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 30 January 2017, pp. 973-1001
-
- Article
- Export citation
F-THRESHOLDS OF GRADED RINGS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 229 / March 2018
- Published online by Cambridge University Press:
- 07 December 2016, pp. 141-168
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation
GENERALIZED HILBERT–KUNZ FUNCTION IN GRADED DIMENSION 2
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 05 December 2016, pp. 1-17
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
WHEN IS THE INTEGRAL CLOSURE COMPARABLE TO ALL INTERMEDIATE RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 14-21
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
LOCAL COHOMOLOGY OF MULTI-REES ALGEBRAS, JOINT REDUCTION NUMBERS AND PRODUCT OF COMPLETE IDEALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 228 / December 2017
- Published online by Cambridge University Press:
- 18 October 2016, pp. 1-20
- Print publication:
- December 2017
-
- Article
-
- You have access
- HTML
- Export citation
Degree bounds on homology and a conjecture of Derksen
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 10 / October 2016
- Published online by Cambridge University Press:
- 21 September 2016, pp. 2041-2049
- Print publication:
- October 2016
-
- Article
- Export citation
BLOWUPS AND FIBERS OF MORPHISMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 224 / Issue 1 / December 2016
- Published online by Cambridge University Press:
- 13 September 2016, pp. 168-201
- Print publication:
- December 2016
-
- Article
-
- You have access
- HTML
- Export citation
A TORSION-FREE ABELIAN GROUP EXISTS WHOSE QUOTIENT GROUP MODULO THE SQUARE SUBGROUP IS NOT A NIL-GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 30 August 2016, pp. 449-456
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
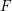 $F$-PURITY VERSUS LOG CANONICITY FOR POLYNOMIALS
$F$-PURITY VERSUS LOG CANONICITY FOR POLYNOMIALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 224 / Issue 1 / December 2016
- Published online by Cambridge University Press:
- 23 August 2016, pp. 10-36
- Print publication:
- December 2016
-
- Article
-
- You have access
- HTML
- Export citation
THE
 ${\it\alpha}$ -INVARIANT AND THOMPSON’S CONJECTURE
${\it\alpha}$ -INVARIANT AND THOMPSON’S CONJECTURE
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 4 / 2016
- Published online by Cambridge University Press:
- 08 July 2016, e5
-
- Article
-
- You have access
- Open access
- Export citation
Symbolic Powers of Monomial Ideals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 13 June 2016, pp. 39-55
-
- Article
- Export citation
BERNSTEIN–SATO POLYNOMIALS AND TEST MODULES IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 222 / Issue 1 / June 2016
- Published online by Cambridge University Press:
- 13 May 2016, pp. 74-99
- Print publication:
- June 2016
-
- Article
-
- You have access
- HTML
- Export citation

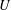
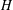

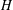
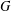
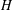

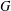
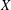
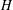
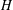
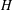
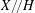
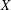
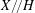
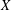
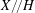
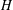
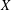
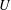
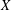
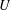
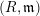
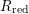
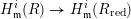
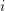
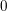
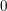
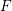
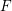
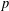
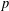
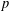
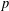
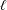
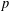
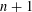
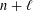
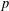
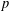
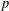
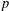
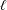
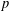
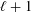
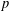
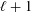
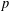
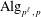
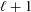
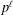
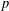
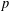
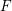
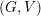

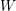
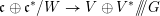
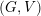
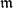

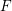
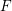
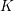
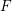
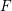

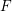
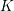
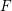
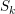
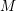
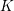
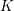
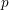
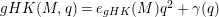
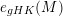
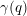
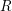
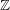
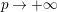
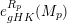
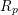
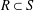
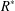
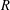
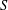
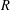
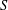
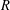
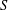
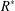
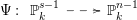 defined by homogeneous forms
defined by homogeneous forms 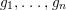
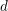
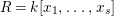
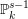
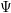
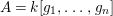
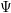
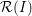
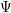
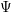
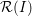
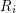
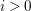
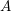
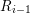
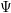
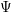
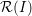
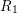
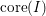
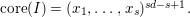
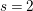
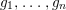
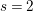
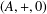
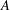
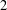
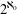
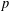
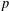
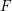
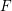
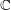
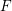
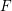
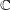
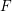

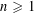
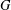
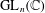
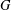
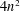
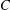
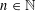
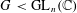
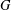
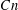

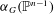
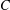
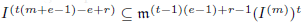 for all positive integers
for all positive integers 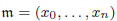 . This captures two conjectures (
. This captures two conjectures (