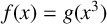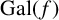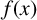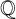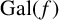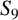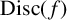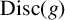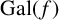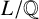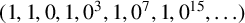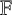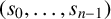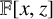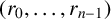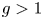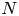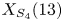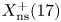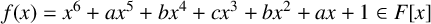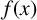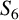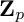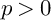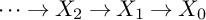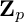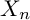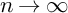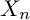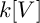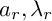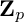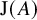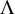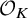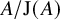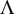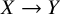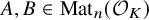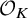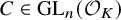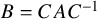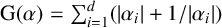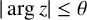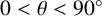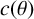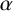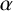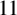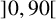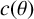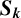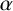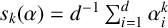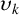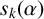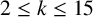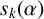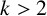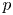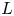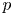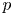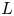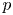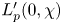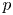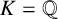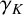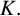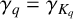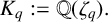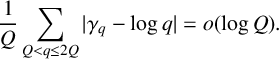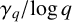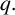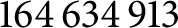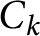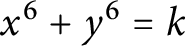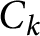122 results in 11Yxx
ON SOME EFFECTIVE RESULTS INVOLVING ZEROS OF THE RIEMANN ZETA FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 March 2025, pp. 1-3
-
- Article
-
- You have access
- HTML
- Export citation
ON GALOIS GROUPS OF POWER COMPOSITIONAL NONIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1-15
-
- Article
- Export citation
PARITY BIAS IN FUNDAMENTAL UNITS OF REAL QUADRATIC FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 February 2025, pp. 1-4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE BINARY SEQUENCE
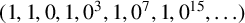 $(1,1,0,1,0^3,1,0^7,1,0^{15},\ldots )$
$(1,1,0,1,0^3,1,0^7,1,0^{15},\ldots )$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 23 October 2024, pp. 260-271
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximizing weighted sums of binomial coefficients using generalized continued fractions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 August 2024, pp. 1-16
-
- Article
-
- You have access
- HTML
- Export citation
CHARACTERISATION OF PRIMES DIVIDING THE INDEX OF A CLASS OF POLYNOMIALS AND ITS APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 01 April 2024, pp. 460-467
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
Leopoldt-type theorems for non-abelian extensions of
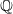 $\mathbb{Q}$
$\mathbb{Q}$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 22 January 2024, pp. 308-337
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOUNDING ZETA ON THE 1-LINE UNDER THE PARTIAL RIEMANN HYPOTHESIS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 10 January 2024, pp. 244-251
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NEW EFFECTIVE RESULTS IN THE THEORY OF THE RIEMANN ZETA-FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 12 December 2023, pp. 403-406
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
SHORT CHARACTER SUMS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 11 July 2023, pp. 339-340
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
Quadratic Chabauty for modular curves: algorithms and examples
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1111-1152
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXPLICIT MERTENS’ THEOREMS FOR NUMBER FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 169-172
- Print publication:
- August 2023
-
- Article
-
- You have access
- HTML
- Export citation
GALOIS GROUPS OF RECIPROCAL SEXTIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 37-44
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
IWASAWA THEORY FOR p-TORSION CLASS GROUP SCHEMES IN CHARACTERISTIC p
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 22 November 2022, pp. 298-351
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Computation of lattice isomorphisms and the integral matrix similarity problem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 October 2022, e87
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN ANALOGUE OF THE SCHUR–SIEGEL–SMYTH TRACE PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 30 August 2022, pp. 227-238
- Print publication:
- April 2023
-
- Article
- Export citation
THE ABSOLUTE
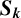 $\boldsymbol {S_k}$
-MEASURE OF TOTALLY POSITIVE ALGEBRAIC INTEGERS
$\boldsymbol {S_k}$
-MEASURE OF TOTALLY POSITIVE ALGEBRAIC INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 11 August 2022, pp. 239-249
- Print publication:
- April 2023
-
- Article
- Export citation
Sum expressions for Kubota–Leopoldt $p$
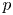 -adic $L$
-adic $L$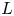 -functions
-functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 10 June 2022, pp. 460-479
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EULER–KRONECKER CONSTANTS FOR CYCLOTOMIC FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 30 May 2022, pp. 79-84
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integers that are sums of two rational sixth powers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 07 March 2022, pp. 166-177
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation