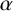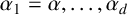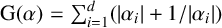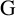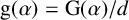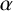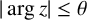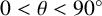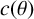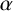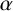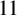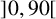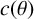1 Introduction
Let
![]() $\alpha $
be a nonzero algebraic integer of degree
$\alpha $
be a nonzero algebraic integer of degree
![]() $d \geq 1$
with conjugates
$d \geq 1$
with conjugates
![]() $\alpha _1=\alpha , \ldots , \alpha _d$
. By analogy with the trace,
$\alpha _1=\alpha , \ldots , \alpha _d$
. By analogy with the trace,
![]() $ {\mathrm {Tr}}(\alpha )=\sum _{i=1}^d \alpha _i$
, we define the G-measure of
$ {\mathrm {Tr}}(\alpha )=\sum _{i=1}^d \alpha _i$
, we define the G-measure of
![]() $\alpha $
by
$\alpha $
by
 $$ \begin{align*} {\mathrm{G}} (\alpha)= \sum_{i=1}^d ( |\alpha_i| + 1/ | \alpha_i | ) \end{align*} $$
$$ \begin{align*} {\mathrm{G}} (\alpha)= \sum_{i=1}^d ( |\alpha_i| + 1/ | \alpha_i | ) \end{align*} $$
and the absolute
![]() ${\mathrm G}$
-measure of
${\mathrm G}$
-measure of
![]() $\alpha $
by
$\alpha $
by
![]() ${\mathrm {g}}(\alpha )={\mathrm {G}}(\alpha )/d$
. It is obvious that
${\mathrm {g}}(\alpha )={\mathrm {G}}(\alpha )/d$
. It is obvious that
![]() $\mathrm {g}(\alpha ) \geq 2$
, with equality if and only if
$\mathrm {g}(\alpha ) \geq 2$
, with equality if and only if
![]() $\alpha $
is a root of unity. Indeed, if
$\alpha $
is a root of unity. Indeed, if
![]() $g(\alpha )=2$
, then
$g(\alpha )=2$
, then
![]() $|\alpha _i|=1$
for
$|\alpha _i|=1$
for
![]() $i=1, \ldots , d$
. By Kronecker’s theorem, we deduce that
$i=1, \ldots , d$
. By Kronecker’s theorem, we deduce that
![]() $\alpha $
is a root of unity.
$\alpha $
is a root of unity.
The absolute trace of
![]() $\alpha $
is
$\alpha $
is
![]() ${\mathrm {tr}}(\alpha ) \displaystyle = {\mathrm {Tr}}(\alpha )/d$
. The Schur–Siegel–Smyth trace problem is formulated as follows: fix
${\mathrm {tr}}(\alpha ) \displaystyle = {\mathrm {Tr}}(\alpha )/d$
. The Schur–Siegel–Smyth trace problem is formulated as follows: fix
![]() $\rho < 2$
and show that all but finitely many totally positive algebraic integers
$\rho < 2$
and show that all but finitely many totally positive algebraic integers
![]() $\alpha $
have
$\alpha $
have
![]() ${\mathrm {tr}}(\alpha )> \rho $
. This problem were studied by Schur [Reference Schur13], Siegel [Reference Siegel14] and Smyth [Reference Smyth15]. In 2016, we solved it for
${\mathrm {tr}}(\alpha )> \rho $
. This problem were studied by Schur [Reference Schur13], Siegel [Reference Siegel14] and Smyth [Reference Smyth15]. In 2016, we solved it for
![]() $\rho < 1.792812$
[Reference Flammang5]. Recently, in 2021, Wang et al. solved it for 1.793145 [Reference Wang, Wu and Wu17]. On the other hand, Serre [Reference Aguirre, Peral, McKee and Smyth1] showed that the method of explicit auxiliary functions used in all attacks on the problem since [Reference Smyth15] does not give such an inequality for any
$\rho < 1.792812$
[Reference Flammang5]. Recently, in 2021, Wang et al. solved it for 1.793145 [Reference Wang, Wu and Wu17]. On the other hand, Serre [Reference Aguirre, Peral, McKee and Smyth1] showed that the method of explicit auxiliary functions used in all attacks on the problem since [Reference Smyth15] does not give such an inequality for any
![]() $\rho $
larger than
$\rho $
larger than
![]() $1.8983021\ldots .$
Therefore, this method cannot be used to prove that 2 is the smallest limit point of the set of numbers
$1.8983021\ldots .$
Therefore, this method cannot be used to prove that 2 is the smallest limit point of the set of numbers
![]() $\{ {\mathrm {tr}}(\alpha ) : \alpha {\ } {\text {is a totally positive algebraic integer}} \}$
.
$\{ {\mathrm {tr}}(\alpha ) : \alpha {\ } {\text {is a totally positive algebraic integer}} \}$
.
The aim of this paper is to search for the supremum, say s, of all
![]() $\rho>0$
such that all but finitely many totally positive algebraic numbers satisfy
$\rho>0$
such that all but finitely many totally positive algebraic numbers satisfy
![]() ${\mathrm {g}}(\alpha )> \rho $
. The following theorem, using the algebraic numbers
${\mathrm {g}}(\alpha )> \rho $
. The following theorem, using the algebraic numbers
![]() $\beta _n$
defined by Smyth [Reference Smyth15], proves that
$\beta _n$
defined by Smyth [Reference Smyth15], proves that
![]() $s \leq 4$
.
$s \leq 4$
.
Theorem 1.1. Let
![]() $\beta _n^2$
be a totally positive algebraic integer of degree
$\beta _n^2$
be a totally positive algebraic integer of degree
![]() $2^n$
, defined by
$2^n$
, defined by
Then
![]() $\lim _{ n \rightarrow + \infty } {\mathrm {g}}({\kern1pt}\beta _n^2)=4$
.
$\lim _{ n \rightarrow + \infty } {\mathrm {g}}({\kern1pt}\beta _n^2)=4$
.
Let
![]() ${\cal {G}} = \{ {\mathrm {g}}(\alpha ) : \alpha {\ } {\text {is a totally positive algebraic integer}} \}$
. Theorem 1.1 shows that 4 is a limit point of this set. Thus, the analogue of the Schur–Siegel–Smyth trace problem for the G-measure is: fix
${\cal {G}} = \{ {\mathrm {g}}(\alpha ) : \alpha {\ } {\text {is a totally positive algebraic integer}} \}$
. Theorem 1.1 shows that 4 is a limit point of this set. Thus, the analogue of the Schur–Siegel–Smyth trace problem for the G-measure is: fix
![]() $\rho <4$
and prove that all but finitely many totally positive algebraic numbers satisfy
$\rho <4$
and prove that all but finitely many totally positive algebraic numbers satisfy
![]() ${\mathrm {g}}(\alpha )> \rho $
. The following theorem solves the problem for
${\mathrm {g}}(\alpha )> \rho $
. The following theorem solves the problem for
![]() $\rho \leq 3.024561$
.
$\rho \leq 3.024561$
.
Theorem 1.2. If
![]() $\alpha $
is a nonzero totally positive algebraic integer whose minimal polynomial is different from
$\alpha $
is a nonzero totally positive algebraic integer whose minimal polynomial is different from
![]() $x-1$
,
$x-1$
,
![]() $x-2$
,
$x-2$
,
![]() $x^2-3x+1$
,
$x^2-3x+1$
,
![]() $x^2-4x+2$
,
$x^2-4x+2$
,
![]() $x^2 - 5x + 5$
,
$x^2 - 5x + 5$
,
![]() $x^3 - 6x^2 + 9x - 3$
,
$x^3 - 6x^2 + 9x - 3$
,
![]() $x^3 - 7x^2 + 14x - 7$
,
$x^3 - 7x^2 + 14x - 7$
,
![]() $x^4 - 9x^3 + 27x^2 - 31x + 11$
and
$x^4 - 9x^3 + 27x^2 - 31x + 11$
and
![]() $x^6 - 13x^5 + 64x^4 - 151x^3 + 177x^2 - 96x + 19$
, then
$x^6 - 13x^5 + 64x^4 - 151x^3 + 177x^2 - 96x + 19$
, then
![]() ${\mathrm {g}}(\alpha ) \geq 3.024561.$
Moreover, the first five points of
${\mathrm {g}}(\alpha ) \geq 3.024561.$
Moreover, the first five points of
![]() ${\cal {G}}$
are:
${\cal {G}}$
are:
 $$ \begin{align*} \begin{array}{ll} 2& = g(x-1),\\ 2.5& = g(x-2),\\ 2.954545& = g(x^4 - 9x^3 + 27x^2 - 31x + 11),\\ 3& = g(x^2-3x+1)= g(x^2-4x+2)= g(x^2 - 5x + 5)\\ & = g(x^3 - 6x^2 + 9x - 3)= g(x^3 - 7x^2 + 14x - 7),\\ 3.008771& = g(x^6 - 13x^5 + 64x^4 - 151x^3 + 177x^2 - 96x + 19). \end{array}\end{align*} $$
$$ \begin{align*} \begin{array}{ll} 2& = g(x-1),\\ 2.5& = g(x-2),\\ 2.954545& = g(x^4 - 9x^3 + 27x^2 - 31x + 11),\\ 3& = g(x^2-3x+1)= g(x^2-4x+2)= g(x^2 - 5x + 5)\\ & = g(x^3 - 6x^2 + 9x - 3)= g(x^3 - 7x^2 + 14x - 7),\\ 3.008771& = g(x^6 - 13x^5 + 64x^4 - 151x^3 + 177x^2 - 96x + 19). \end{array}\end{align*} $$
From now on, we consider a nonzero algebraic integer
![]() $\alpha $
, not a root of unity, all of whose conjugates lie in a sector
$\alpha $
, not a root of unity, all of whose conjugates lie in a sector
![]() $S_{\theta }= \{ z \in \mathbb {C}: | \arg z | \leq \theta \}$
,
$S_{\theta }= \{ z \in \mathbb {C}: | \arg z | \leq \theta \}$
,
![]() $0 < \theta < 90$
. We first recall a result of Langevin [Reference Langevin10] on the Mahler measure M: there is a function
$0 < \theta < 90$
. We first recall a result of Langevin [Reference Langevin10] on the Mahler measure M: there is a function
![]() $c(\theta )$
on [0,
$c(\theta )$
on [0,
![]() $\mathrm {180}^{\circ }$
), always greater than
$\mathrm {180}^{\circ }$
), always greater than
![]() $1$
, such that if all the conjugates of
$1$
, such that if all the conjugates of
![]() $\alpha $
lie in
$\alpha $
lie in
![]() $S_{\theta }$
, then
$S_{\theta }$
, then
![]() ${\mbox {M}}(\alpha )^{1/d} \geq c(\theta )$
where d denotes the degree of
${\mbox {M}}(\alpha )^{1/d} \geq c(\theta )$
where d denotes the degree of
![]() $\alpha $
. In 1995, Rhin and Smyth [Reference Rhin and Smyth11] were the first to make this result effective. More precisely, they succeeded in finding the exact value of
$\alpha $
. In 1995, Rhin and Smyth [Reference Rhin and Smyth11] were the first to make this result effective. More precisely, they succeeded in finding the exact value of
![]() $c(\theta )$
for
$c(\theta )$
for
![]() $\theta $
in nine subintervals of [0,
$\theta $
in nine subintervals of [0,
![]() $\mathrm {120}^{\circ }$
]. They used the method of explicit auxiliary functions with polynomials found by heuristic search. They conjectured that
$\mathrm {120}^{\circ }$
]. They used the method of explicit auxiliary functions with polynomials found by heuristic search. They conjectured that
![]() $c(\theta )$
is a ‘staircase’ decreasing function of
$c(\theta )$
is a ‘staircase’ decreasing function of
![]() $\theta $
, which is constant except for finitely many left discontinuities in any closed subinterval of [0,
$\theta $
, which is constant except for finitely many left discontinuities in any closed subinterval of [0,
![]() $\mathrm {180}^{\circ }$
). In 2004, thanks to Wu’s algorithm [Reference Wu18], Rhin and Wu [Reference Rhin and Wu12] gave the exact value of
$\mathrm {180}^{\circ }$
). In 2004, thanks to Wu’s algorithm [Reference Wu18], Rhin and Wu [Reference Rhin and Wu12] gave the exact value of
![]() $c(\theta )$
for four new subintervals of [0,
$c(\theta )$
for four new subintervals of [0,
![]() $\mathrm {140}^{\circ }$
] and extended four existing subintervals. In 2013, the author and Rhin [Reference Flammang and Rhin9] found for the first time a complete subinterval and a
$\mathrm {140}^{\circ }$
] and extended four existing subintervals. In 2013, the author and Rhin [Reference Flammang and Rhin9] found for the first time a complete subinterval and a
![]() $14$
th subinterval. A complete subinterval is an interval on which the function
$14$
th subinterval. A complete subinterval is an interval on which the function
![]() $c(\theta )$
describing the minimum on the sector
$c(\theta )$
describing the minimum on the sector
![]() $|\arg z | \leq \theta $
is constant, with jump discontinuities at each end. These improvements came from our recursive algorithm, based on Wu’s algorithm but where the polynomials are found by induction. We applied this method to measures such as the trace [Reference Flammang2], the length [Reference Flammang3] and the house [Reference Flammang4], as well as to unusual measures (see [Reference Flammang6–Reference Flammang8]). Here we prove the following result.
$|\arg z | \leq \theta $
is constant, with jump discontinuities at each end. These improvements came from our recursive algorithm, based on Wu’s algorithm but where the polynomials are found by induction. We applied this method to measures such as the trace [Reference Flammang2], the length [Reference Flammang3] and the house [Reference Flammang4], as well as to unusual measures (see [Reference Flammang6–Reference Flammang8]). Here we prove the following result.
Theorem 1.3. There exist a left discontinuous, strictly positive, staircase function h on
![]() $\displaystyle [0, 90^{\circ })$
and a positive, continuous, monotonically decreasing function f on
$\displaystyle [0, 90^{\circ })$
and a positive, continuous, monotonically decreasing function f on
![]() $\displaystyle [0, 90^{\circ })$
such that
$\displaystyle [0, 90^{\circ })$
such that
Moreover, the exact value of
![]() $\displaystyle c(\theta )$
is known on
$\displaystyle c(\theta )$
is known on
![]() $11$
subintervals of
$11$
subintervals of
![]() $\displaystyle [0, 90^{\circ })$
.
$\displaystyle [0, 90^{\circ })$
.
The function
![]() $h(\theta )$
is the smallest value of
$h(\theta )$
is the smallest value of
![]() ${\mathrm {g}} (\alpha )$
that could be found for
${\mathrm {g}} (\alpha )$
that could be found for
![]() $\alpha $
having all its conjugates in
$\alpha $
having all its conjugates in
![]() $| \arg z | \leq \theta $
. The function
$| \arg z | \leq \theta $
. The function
![]() $f( \theta )$
is given by
$f( \theta )$
is given by
![]() $ f( \theta ) = \max _{1 \leq i \leq 11} (f_i(\theta ))$
, where the functions
$ f( \theta ) = \max _{1 \leq i \leq 11} (f_i(\theta ))$
, where the functions
![]() $f_i ( \theta )$
are defined by
$f_i ( \theta )$
are defined by
 $$ \begin{align*} f_i ( \theta) = \displaystyle \min_{z \in S_{\theta}} \bigg ( | z| + \frac{1}{ |z|} - \sum_{1\leq j \leq J} c_{ij}\log | Q_{ij} (z) | \bigg). \end{align*} $$
$$ \begin{align*} f_i ( \theta) = \displaystyle \min_{z \in S_{\theta}} \bigg ( | z| + \frac{1}{ |z|} - \sum_{1\leq j \leq J} c_{ij}\log | Q_{ij} (z) | \bigg). \end{align*} $$
Table 1 summarises our results. One can read off the
![]() $11$
intervals
$11$
intervals
![]() $[\theta _i, {\theta '}_i)$
where
$[\theta _i, {\theta '}_i)$
where
![]() $f(\theta )> g(\theta )$
so that
$f(\theta )> g(\theta )$
so that
![]() $c(\theta )=h(\theta )=h(\theta _i)$
for
$c(\theta )=h(\theta )=h(\theta _i)$
for
![]() $\theta $
in these intervals. Also
$\theta $
in these intervals. Also
![]() $c(\theta )=c(\theta _i)={\mathrm {g}}(P_i)$
. The real numbers
$c(\theta )=c(\theta _i)={\mathrm {g}}(P_i)$
. The real numbers
![]() $ c_{ij}$
and the polynomials
$ c_{ij}$
and the polynomials
![]() $Q_{ij}$
are given in Table 3.
$Q_{ij}$
are given in Table 3.
Table 1 Intervals where
![]() $c(\theta )$
is known exactly.
$c(\theta )$
is known exactly.

What is remarkable here and appears for the first time is that we are able to find complete and consecutive subintervals from 0 to
![]() $\mathrm {86.24}^{\circ }$
. This supports the Rhin–Smyth conjecture that
$\mathrm {86.24}^{\circ }$
. This supports the Rhin–Smyth conjecture that
![]() $c(\theta )$
is a ‘staircase’ decreasing function of
$c(\theta )$
is a ‘staircase’ decreasing function of
![]() $\theta $
, which is constant except for finitely many left discontinuities in any closed subinterval of [0,
$\theta $
, which is constant except for finitely many left discontinuities in any closed subinterval of [0,
![]() $\mathrm {90^{\circ }}$
).
$\mathrm {90^{\circ }}$
).
2 Proof of Theorem 1.1
The sequence of totally positive algebraic integers
![]() $({\kern1pt}\beta _n^2)_{n \geq 0}$
is defined by
$({\kern1pt}\beta _n^2)_{n \geq 0}$
is defined by
By induction, we can easily prove that
On the other hand,
 $$ \begin{align*} {\mathrm{G}}({\kern1pt}\beta_n^2) & = \sum_{i=1}^{2^n} ( \beta_{n,i}^2 + \beta_{n,i}^{-2})= 2 \sum_{i=1}^{2^{n-1}} ( \beta_{n,i}^2 + \beta_{n,i}^{-2})= 2 \sum_{i=1}^{2^{n-1}} ({\kern1pt}\beta_{n-1,i}^2 + 2 ) \\ & = 2 {\mathrm{Tr}}({\kern1pt}\beta_{n-1,i}^2) + 2^{n+1}= 2 ( 2^n -1) + 2^{n+1}= 2^{n+2}-1. \end{align*} $$
$$ \begin{align*} {\mathrm{G}}({\kern1pt}\beta_n^2) & = \sum_{i=1}^{2^n} ( \beta_{n,i}^2 + \beta_{n,i}^{-2})= 2 \sum_{i=1}^{2^{n-1}} ( \beta_{n,i}^2 + \beta_{n,i}^{-2})= 2 \sum_{i=1}^{2^{n-1}} ({\kern1pt}\beta_{n-1,i}^2 + 2 ) \\ & = 2 {\mathrm{Tr}}({\kern1pt}\beta_{n-1,i}^2) + 2^{n+1}= 2 ( 2^n -1) + 2^{n+1}= 2^{n+2}-1. \end{align*} $$
Therefore,
![]() $ \displaystyle {\mathrm {g}} ({\kern1pt}\beta _n^2)= 4- 2^{-n}$
. This proves Theorem 1.1.
$ \displaystyle {\mathrm {g}} ({\kern1pt}\beta _n^2)= 4- 2^{-n}$
. This proves Theorem 1.1.
3 Proof of Theorem 1.2
3.1 The principle of auxiliary functions
The auxiliary function involved in the study of the
![]() ${\mathrm {G}}$
-measure is
${\mathrm {G}}$
-measure is
 $$ \begin{align*} f(x) = x + \frac{1}{x} - \sum_{ 1\leq j \leq J} c_j \log | Q_j(x)| \quad\mbox{for}\ x>0, \end{align*} $$
$$ \begin{align*} f(x) = x + \frac{1}{x} - \sum_{ 1\leq j \leq J} c_j \log | Q_j(x)| \quad\mbox{for}\ x>0, \end{align*} $$
where the
![]() $c_j$
are positive real numbers and the polynomials
$c_j$
are positive real numbers and the polynomials
![]() $Q_j$
are nonzero polynomials in
$Q_j$
are nonzero polynomials in
![]() $\mathbb {Z}[x]$
.
$\mathbb {Z}[x]$
.
Let m denote the minimum of the function f and P the minimal polynomial of
![]() $\alpha $
. If P does not divide any
$\alpha $
. If P does not divide any
![]() $Q_j$
, then
$Q_j$
, then
 $$ \begin{align*} \displaystyle \sum_{i=1}^{d} f( {\alpha}_i) \geq md, \end{align*} $$
$$ \begin{align*} \displaystyle \sum_{i=1}^{d} f( {\alpha}_i) \geq md, \end{align*} $$
that is,
 $$ \begin{align*} {\text{G}}(\alpha) \geq md + \sum_{ 1\leq j \leq J} c_j \log \bigg| \prod_{i=1}^{d} Q_j( {\alpha}_i)\bigg|. \end{align*} $$
$$ \begin{align*} {\text{G}}(\alpha) \geq md + \sum_{ 1\leq j \leq J} c_j \log \bigg| \prod_{i=1}^{d} Q_j( {\alpha}_i)\bigg|. \end{align*} $$
Since P is monic and does not divide any
![]() $Q_j$
, it follows that
$Q_j$
, it follows that
![]() $\prod _{i=1}^{d} Q_j( {\alpha }_i)$
is a nonzero integer because it is the resultant of P and
$\prod _{i=1}^{d} Q_j( {\alpha }_i)$
is a nonzero integer because it is the resultant of P and
![]() $Q_j$
. Hence, if
$Q_j$
. Hence, if
![]() $\alpha $
is not a root of
$\alpha $
is not a root of
![]() $Q_j$
, then
$Q_j$
, then
Remark 3.1. In order to ensure a better convergence in our program with Pascal, we have reduced the size of the coefficients of the polynomials involved in the auxiliary function by working on
![]() $[-1, \infty )$
. Thus, the auxiliary function becomes
$[-1, \infty )$
. Thus, the auxiliary function becomes
 $$ \begin{align} f(x) = x +1 + \frac{1}{x+1 } - \sum_{ 1\leq j \leq J} c_j \log | Q_j(x) | \quad \mbox{for}{\ } x> -1, \end{align} $$
$$ \begin{align} f(x) = x +1 + \frac{1}{x+1 } - \sum_{ 1\leq j \leq J} c_j \log | Q_j(x) | \quad \mbox{for}{\ } x> -1, \end{align} $$
where the polynomials
![]() $Q_j$
and the real numbers
$Q_j$
and the real numbers
![]() $c_j$
are given in Table 2.
$c_j$
are given in Table 2.
Table 2 Coefficients and polynomials involved in Theorem 1.2.

Table 3 The polynomials
![]() $Q_j$
and their coefficients
$Q_j$
and their coefficients
![]() $c_j$
involved in the functions
$c_j$
involved in the functions
![]() $f_i$
,
$f_i$
,
![]() $1 \leq i \leq 11$
.
$1 \leq i \leq 11$
.

3.2 Auxiliary functions and generalised integer transfinite diameter
This and the following sections reproduce the corresponding sections of [Reference Flammang5].
Let K be a compact subset of
![]() $\mathbb {C}$
. The transfinite diameter of K is defined by
$\mathbb {C}$
. The transfinite diameter of K is defined by
 $$ \begin{align*} t(K) = \liminf_{\substack{n \geq 1\\ n \rightarrow \infty}} \inf_{\substack{P \in \mathbb{C}[X]\\ P\ {\mathrm{monic}}\\ \deg(P)=n}} |P |_{ \infty, K} ^{{1}/{n}}, \end{align*} $$
$$ \begin{align*} t(K) = \liminf_{\substack{n \geq 1\\ n \rightarrow \infty}} \inf_{\substack{P \in \mathbb{C}[X]\\ P\ {\mathrm{monic}}\\ \deg(P)=n}} |P |_{ \infty, K} ^{{1}/{n}}, \end{align*} $$
where
![]() $|P |_{ \infty , K} = \sup _{z \in K} |P(z) |$
for
$|P |_{ \infty , K} = \sup _{z \in K} |P(z) |$
for
![]() $P \in \mathbb {C} [X]$
. The integer transfinite diameter of K is defined by
$P \in \mathbb {C} [X]$
. The integer transfinite diameter of K is defined by
 $$ \begin{align*} t_{\mathbb{Z}}(K) = \liminf_{\substack{n \geq 1\\ n \rightarrow \infty}} \inf_{\substack{P \in \mathbb{Z}[X]\\ \deg(P)=n}} | P |_{\infty, K}^{{1}/{n}}. \end{align*} $$
$$ \begin{align*} t_{\mathbb{Z}}(K) = \liminf_{\substack{n \geq 1\\ n \rightarrow \infty}} \inf_{\substack{P \in \mathbb{Z}[X]\\ \deg(P)=n}} | P |_{\infty, K}^{{1}/{n}}. \end{align*} $$
Finally, if
![]() $\varphi $
is a positive function defined on K, the
$\varphi $
is a positive function defined on K, the
![]() $\varphi $
-generalised integer transfinite diameter of K is defined by
$\varphi $
-generalised integer transfinite diameter of K is defined by
 $$ \begin{align*} t_{\mathbb{Z}, \varphi}(K) = \liminf_{\substack{ n \geq 1\\ n \rightarrow \infty}} \inf_{\substack{P \in \mathbb{Z}[X]\\ \deg(P)=n}} \sup _{z \in K} \,( | P(z) |^{{1}/{n}} \varphi(z)). \end{align*} $$
$$ \begin{align*} t_{\mathbb{Z}, \varphi}(K) = \liminf_{\substack{ n \geq 1\\ n \rightarrow \infty}} \inf_{\substack{P \in \mathbb{Z}[X]\\ \deg(P)=n}} \sup _{z \in K} \,( | P(z) |^{{1}/{n}} \varphi(z)). \end{align*} $$
In the auxiliary function (3.1), we replace the coefficients
![]() $c_j$
by rational numbers
$c_j$
by rational numbers
![]() $a_j/q$
where q is a positive integer such that
$a_j/q$
where q is a positive integer such that
![]() $qc_j$
is an integer for
$qc_j$
is an integer for
![]() $1\leq j \leq J$
. Then, for
$1\leq j \leq J$
. Then, for
![]() $x>-1$
,
$x>-1$
,
where
![]() $Q=\prod _{j=1}^J Q_j^{a_j} \in \mathbb {Z}[X]$
is of degree
$Q=\prod _{j=1}^J Q_j^{a_j} \in \mathbb {Z}[X]$
is of degree
![]() $r = \sum _{j=1}^J a_j \deg Q_j$
and
$r = \sum _{j=1}^J a_j \deg Q_j$
and
![]() $t= \sum _{j=1}^J c_j \deg Q_j$
(this formulation was introduced by Serre). Thus we seek a polynomial
$t= \sum _{j=1}^J c_j \deg Q_j$
(this formulation was introduced by Serre). Thus we seek a polynomial
![]() $Q \in \mathbb {Z}[X]$
such that
$Q \in \mathbb {Z}[X]$
such that
If we suppose that t is fixed, this is equivalent to finding an effective upper bound for the weighted integer transfinite diameter over the interval
![]() $[-1, \infty [$
with the weight
$[-1, \infty [$
with the weight
![]() $\varphi (x) = e^{-(x+1+ 1/(x+1))} $
, that is,
$\varphi (x) = e^{-(x+1+ 1/(x+1))} $
, that is,
 $$ \begin{align*} t_{\mathbb{Z},\varphi}([-1,\infty )) = \liminf _{\substack{r \geq 1\\ r \rightarrow \infty}} \inf_{\substack{P \in \mathbb{Z}[X]\\ \deg(P)=r}} \sup_{x>-1} \,( | P(x) |^{{t}/{r}} \varphi(x) ). \end{align*} $$
$$ \begin{align*} t_{\mathbb{Z},\varphi}([-1,\infty )) = \liminf _{\substack{r \geq 1\\ r \rightarrow \infty}} \inf_{\substack{P \in \mathbb{Z}[X]\\ \deg(P)=r}} \sup_{x>-1} \,( | P(x) |^{{t}/{r}} \varphi(x) ). \end{align*} $$
Even though we have replaced the compact set K by the infinite interval
![]() $[-1, \infty [$
, the weight
$[-1, \infty [$
, the weight
![]() $\varphi $
ensures that the quantity
$\varphi $
ensures that the quantity
![]() $t_{\mathbb {Z},\varphi }([-1, \infty ) )$
is finite.
$t_{\mathbb {Z},\varphi }([-1, \infty ) )$
is finite.
3.3 Construction of an auxiliary function
The main point is to find a set of ‘good’ polynomials
![]() $Q_j$
to give the best possible value for m. Until 2003, the polynomials were found heuristically. In 2003, Wu [Reference Wu18] developed an algorithm that allows a systematic search for ‘good’ polynomials. For an auxiliary function as defined by (3.1), we fix a set
$Q_j$
to give the best possible value for m. Until 2003, the polynomials were found heuristically. In 2003, Wu [Reference Wu18] developed an algorithm that allows a systematic search for ‘good’ polynomials. For an auxiliary function as defined by (3.1), we fix a set
![]() $E_0$
of control points, uniformly distributed on the real interval
$E_0$
of control points, uniformly distributed on the real interval
![]() $I=[-1, A]$
where A is ‘sufficiently large’. Using the LLL algorithm, we find a polynomial Q small on
$I=[-1, A]$
where A is ‘sufficiently large’. Using the LLL algorithm, we find a polynomial Q small on
![]() $E_0$
in terms of the quadratic norm. We test this polynomial in the auxiliary function and keep only the factors of Q which have a nonzero exponent. The convergence of this new function gives local minima that we add to the set of points
$E_0$
in terms of the quadratic norm. We test this polynomial in the auxiliary function and keep only the factors of Q which have a nonzero exponent. The convergence of this new function gives local minima that we add to the set of points
![]() $E_0$
to get a new set of control points
$E_0$
to get a new set of control points
![]() $E_1$
. We use the LLL algorithm again with the set
$E_1$
. We use the LLL algorithm again with the set
![]() $E_1$
and the process is repeated.
$E_1$
and the process is repeated.
In 2006, we made two improvements to Wu’s algorithm in the use of the LLL algorithm. The first is, at each step, to take into account not only the new control points but also the new polynomials of the best auxiliary function. The second is the introduction of a corrective coefficient t. The idea is to get good polynomials
![]() $Q_j$
by induction. Thus, we call this algorithm the recursive algorithm. The first step is the optimisation of the auxiliary function
$Q_j$
by induction. Thus, we call this algorithm the recursive algorithm. The first step is the optimisation of the auxiliary function
![]() $f_1= x +1 + {1}/{(x+1) } - t \log x $
. We take
$f_1= x +1 + {1}/{(x+1) } - t \log x $
. We take
![]() $t=c_1$
where
$t=c_1$
where
![]() $c_1$
gives the best function
$c_1$
gives the best function
![]() $f_1$
. We suppose that we have some polynomials
$f_1$
. We suppose that we have some polynomials
![]() $Q_1$
,
$Q_1$
,
![]() $Q_2$
, …,
$Q_2$
, …,
![]() $Q_J$
and a function f as good as possible for this set of polynomials in the form (3.2). We seek a polynomial
$Q_J$
and a function f as good as possible for this set of polynomials in the form (3.2). We seek a polynomial
![]() $R \in \mathbb {Z}[x]$
of degree k such that
$R \in \mathbb {Z}[x]$
of degree k such that
where
![]() $Q= \prod _{j=1}^J Q_j$
. We want the quantity
$Q= \prod _{j=1}^J Q_j$
. We want the quantity
to be as small as possible. We apply the LLL algorithm to the linear forms
The
![]() $x_i$
are control points uniformly distributed on the interval I to which we have added points where f has local minima. Thus we find a polynomial R whose irreducible factors
$x_i$
are control points uniformly distributed on the interval I to which we have added points where f has local minima. Thus we find a polynomial R whose irreducible factors
![]() $R_j$
are good candidates to enlarge the set
$R_j$
are good candidates to enlarge the set
![]() $\{Q_1, \ldots , Q_J\}$
. We only keep the factors
$\{Q_1, \ldots , Q_J\}$
. We only keep the factors
![]() $R_j$
that have a nonzero coefficient in the newly optimised auxiliary function f. After optimisation, some of the previous polynomials
$R_j$
that have a nonzero coefficient in the newly optimised auxiliary function f. After optimisation, some of the previous polynomials
![]() $Q_j$
may have a zero exponent and so are removed.
$Q_j$
may have a zero exponent and so are removed.
We applied this recursive algorithm for
![]() $k=\deg R$
running from 4 to 25. We stop there because at that point the minimum m only varies in the fifth decimal place.
$k=\deg R$
running from 4 to 25. We stop there because at that point the minimum m only varies in the fifth decimal place.
3.4 Optimization of the
 $c_j$
$c_j$
We have to solve a problem of the following form: find
where
![]() $f(x,C)$
is a linear form with respect to
$f(x,C)$
is a linear form with respect to
![]() $C=(c_0, c_1,\ldots , c_k)$
(
$C=(c_0, c_1,\ldots , c_k)$
(
![]() $c_0$
is the coefficient of x and is equal to 1), X is a compact domain of
$c_0$
is the coefficient of x and is equal to 1), X is a compact domain of
![]() $\mathbb {C}$
and the maximum is taken over
$\mathbb {C}$
and the maximum is taken over
![]() $c_j \geq 0$
for
$c_j \geq 0$
for
![]() $j=0,\ldots , k$
. A classical solution involves taking very many control points
$j=0,\ldots , k$
. A classical solution involves taking very many control points
![]() $\displaystyle (x_i)_{1 \leq i \leq N} $
and solving the standard problem of linear programming:
$\displaystyle (x_i)_{1 \leq i \leq N} $
and solving the standard problem of linear programming:
The result then depends on the choice of the control points.
The idea of semi-infinite linear programming (introduced into number theory by Smyth [Reference Smyth16]) involves repeating the previous process, adding new control points at each step and verifying that this process converges to m, the value of the linear form for an optimum choice of C. The algorithm is as follows.
-
(1) Choose an initial value
 $C^0$
for C and calculate
$C^0$
for C and calculate
 $ m^{\prime }_0= \min _{x \in X} f(x, C^0)$
.
$ m^{\prime }_0= \min _{x \in X} f(x, C^0)$
. -
(2) Choose a finite set
 $X_0$
of control points belonging to X and set
$X_0$
of control points belonging to X and set  $$ \begin{align*} m^{\prime}_0 \leq m \leq m_0= \min_{x \in X_0}f(x, C^0). \end{align*} $$
$$ \begin{align*} m^{\prime}_0 \leq m \leq m_0= \min_{x \in X_0}f(x, C^0). \end{align*} $$
-
(3) Add to
 $X_0$
the points where
$X_0$
the points where
 $f(x,C^0)$
has local minima to get a new set
$f(x,C^0)$
has local minima to get a new set
 $X_1$
of control points.
$X_1$
of control points. -
(4) Solve the usual linear programming problem
 $ \max _{C} \min _{x \in X_1} f(x,C).$
We get a new value for C denoted by
$ \max _{C} \min _{x \in X_1} f(x,C).$
We get a new value for C denoted by
 $C^1$
and a result from the linear programming problem equal to
$C^1$
and a result from the linear programming problem equal to
 $m^{\prime }_1 = \min _{x \in X} f(x, C^1)$
. Then
$m^{\prime }_1 = \min _{x \in X} f(x, C^1)$
. Then  $$ \begin{align*} m^{\prime}_0 \leq m^{\prime}_1 \leq m \leq m_1=\displaystyle \min_{x \in X_1}f(x, C^1) \leq m_0. \end{align*} $$
$$ \begin{align*} m^{\prime}_0 \leq m^{\prime}_1 \leq m \leq m_1=\displaystyle \min_{x \in X_1}f(x, C^1) \leq m_0. \end{align*} $$
-
(5) Repeat steps 2–4, giving two sequences
 $(m_i)$
and
$(m_i)$
and
 $(m^{\prime }_i)$
which satisfy
$(m^{\prime }_i)$
which satisfy  $$ \begin{align*} m^{\prime}_0 \leq m^{\prime}_1 \leq \cdots \leq m^{\prime}_i \leq m \leq m_i \leq \cdots \leq m_1 \leq m_0.\end{align*} $$
$$ \begin{align*} m^{\prime}_0 \leq m^{\prime}_1 \leq \cdots \leq m^{\prime}_i \leq m \leq m_i \leq \cdots \leq m_1 \leq m_0.\end{align*} $$
We stop when there is a good enough convergence, for example when
![]() $m_i-m^{\prime }_i \leq 10^{-6}$
. If p iterations are sufficient then we take
$m_i-m^{\prime }_i \leq 10^{-6}$
. If p iterations are sufficient then we take
![]() $m=m^{\prime }_p$
.
$m=m^{\prime }_p$
.
4 Proof of Theorem 1.3
We assume that
![]() $\alpha $
is an algebraic integer all of whose conjugates
$\alpha $
is an algebraic integer all of whose conjugates
![]() $\alpha _1=\alpha , \ldots , \alpha _d$
lie in
$\alpha _1=\alpha , \ldots , \alpha _d$
lie in
![]() $S_{\theta }$
. The auxiliary functions
$S_{\theta }$
. The auxiliary functions
![]() $f_i$
,
$f_i$
,
![]() $1 \leq i \leq 11$
, are of the form
$1 \leq i \leq 11$
, are of the form
 $$ \begin{align*} f_i(z)= |z| + 1/ |z | -\sum_{1 \leq j \leq J} c_{ij }\log | Q_{ij}(z)| \quad \mbox{for all } z \in S_{\theta}, \end{align*} $$
$$ \begin{align*} f_i(z)= |z| + 1/ |z | -\sum_{1 \leq j \leq J} c_{ij }\log | Q_{ij}(z)| \quad \mbox{for all } z \in S_{\theta}, \end{align*} $$
where the coefficients
![]() $c_{ij}$
are positive real numbers and the polynomials
$c_{ij}$
are positive real numbers and the polynomials
![]() $Q_{ij}$
are nonzero in
$Q_{ij}$
are nonzero in
![]() $\mathbb {Z}[z]$
.
$\mathbb {Z}[z]$
.
Since the function
![]() $f_i$
is invariant under complex conjugation, we can limit ourselves to
$f_i$
is invariant under complex conjugation, we can limit ourselves to
![]() $0 \leq \arg z \leq \theta $
. Moreover, the function
$0 \leq \arg z \leq \theta $
. Moreover, the function
![]() $f_i$
is harmonic outside the union of arbitrary small discs around the roots of the polynomials
$f_i$
is harmonic outside the union of arbitrary small discs around the roots of the polynomials
![]() $Q_{ij}$
, so the minimum is taken on the upper edge of
$Q_{ij}$
, so the minimum is taken on the upper edge of
![]() $S_{\theta }$
where
$S_{\theta }$
where
![]() $z=x e^{i \theta }$
with
$z=x e^{i \theta }$
with
![]() $x>0$
.
$x>0$
.
The auxiliary function on the half line
![]() $ R_{\theta }=\{ z \in \mathbb {C}, z=x e^{i \theta }, x>0\}$
is
$ R_{\theta }=\{ z \in \mathbb {C}, z=x e^{i \theta }, x>0\}$
is
 $$ \begin{align*}f_i(z) = x + 1/x - \sum_{1 \leq j \leq J} c_j \log |Q_j(z) |.\end{align*} $$
$$ \begin{align*}f_i(z) = x + 1/x - \sum_{1 \leq j \leq J} c_j \log |Q_j(z) |.\end{align*} $$
We proceed as in the Section 3.3. For several values of k, we search for a polynomial
![]() $R(z)= \sum _{l=0}^k a_l z^l \in \mathbb {Z} [z]$
such that
$R(z)= \sum _{l=0}^k a_l z^l \in \mathbb {Z} [z]$
such that
 $$ \begin{align*} \sup_{x>0} \vert Q(z)R(z) \vert \exp \bigg( \frac{-(x+ 1/x)(r+k)}{t} \bigg) \end{align*} $$
$$ \begin{align*} \sup_{x>0} \vert Q(z)R(z) \vert \exp \bigg( \frac{-(x+ 1/x)(r+k)}{t} \bigg) \end{align*} $$
is as small as possible. But, here,
![]() $R(z)$
is not a real linear form in the unknown coefficients
$R(z)$
is not a real linear form in the unknown coefficients
![]() $a_i$
. So, we replace it by its real part and its imaginary part. Then, we apply LLL to the two linear forms
$a_i$
. So, we replace it by its real part and its imaginary part. Then, we apply LLL to the two linear forms
 $$ \begin{align*} & | Q(z_n)| \cdot {\text{Re}}(R(z_n)) \cdot \exp \bigg( \frac{-(x_n+ 1/x_n)(r+k)}{t} \bigg), \\[5pt] &| Q(z_n)| \cdot {\text{Im}}(R(z_n))\cdot \exp \bigg( \frac{-(x_n+ 1/x_n)(r+k)}{t} \bigg), \end{align*} $$
$$ \begin{align*} & | Q(z_n)| \cdot {\text{Re}}(R(z_n)) \cdot \exp \bigg( \frac{-(x_n+ 1/x_n)(r+k)}{t} \bigg), \\[5pt] &| Q(z_n)| \cdot {\text{Im}}(R(z_n))\cdot \exp \bigg( \frac{-(x_n+ 1/x_n)(r+k)}{t} \bigg), \end{align*} $$
where
![]() $z_n=x_n e^{i \theta }$
. The
$z_n=x_n e^{i \theta }$
. The
![]() $x_n$
are suitable control points in
$x_n$
are suitable control points in
![]() $[0,50]$
, including the points where
$[0,50]$
, including the points where
![]() $f_i$
has its least local minima. Then we proceed as described above.
$f_i$
has its least local minima. Then we proceed as described above.