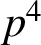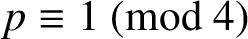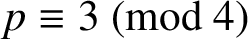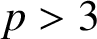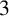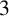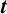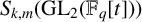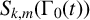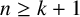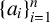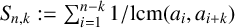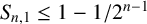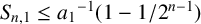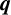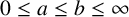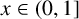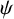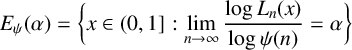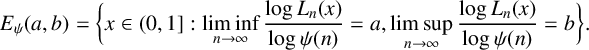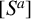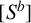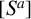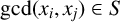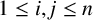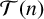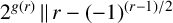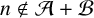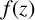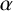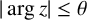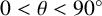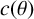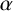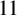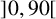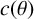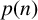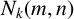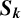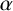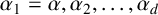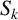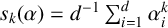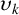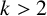Research Article
NEW GENERALISATIONS OF VAN HAMME’S (G.2) SUPERCONGRUENCE
- Part of:
-
- Published online by Cambridge University Press:
- 18 May 2022, pp. 177-183
-
- Article
- Export citation
REGULARITY OF POWERS OF BIPARTITE GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 19 September 2022, pp. 1-9
-
- Article
- Export citation
NOWHERE-ZERO
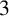 $3$
-FLOWS IN TWO FAMILIES OF VERTEX-TRANSITIVE GRAPHS
$3$
-FLOWS IN TWO FAMILIES OF VERTEX-TRANSITIVE GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 15 September 2022, pp. 353-360
-
- Article
- Export citation
HECKE OPERATORS AND DRINFELD CUSP FORMS OF LEVEL
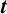 $\boldsymbol {t}$
$\boldsymbol {t}$
- Part of:
-
- Published online by Cambridge University Press:
- 15 June 2022, pp. 184-195
-
- Article
- Export citation
ON THE EUCLIDEAN ALGORITHM: RHYTHM WITHOUT RECURSION
- Part of:
-
- Published online by Cambridge University Press:
- 22 September 2022, pp. 361-367
-
- Article
- Export citation
A SHARP UPPER BOUND FOR THE SUM OF RECIPROCALS OF LEAST COMMON MULTIPLES II
- Part of:
-
- Published online by Cambridge University Press:
- 09 June 2022, pp. 10-21
-
- Article
- Export citation
ON MINIMAL RESTRICTED ASYMPTOTIC BASES
- Part of:
-
- Published online by Cambridge University Press:
- 06 October 2022, pp. 368-373
-
- Article
- Export citation
A NEW
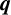 $\boldsymbol {q}$
-ANALOGUE OF VAN HAMME’S (A.2) SUPERCONGRUENCE
$\boldsymbol {q}$
-ANALOGUE OF VAN HAMME’S (A.2) SUPERCONGRUENCE
- Part of:
-
- Published online by Cambridge University Press:
- 20 May 2022, pp. 22-30
-
- Article
- Export citation
APPROXIMATING NUMBERS OF THE CANTOR SET BY ALGEBRAIC NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 03 October 2022, pp. 196-203
-
- Article
- Export citation
ZAREMBA, SALEM AND THE FRACTAL NATURE OF GHOST DISTRIBUTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 06 October 2022, pp. 374-389
-
- Article
- Export citation
ON LÜROTH EXPANSIONS IN WHICH THE LARGEST DIGIT GROWS WITH SLOWLY INCREASING SPEED
- Part of:
-
- Published online by Cambridge University Press:
- 23 June 2022, pp. 204-214
-
- Article
- Export citation
ON THE DIVISIBILITY AMONG POWER LCM MATRICES ON GCD-CLOSED SETS
- Part of:
-
- Published online by Cambridge University Press:
- 19 May 2022, pp. 31-39
-
- Article
- Export citation
OHNO–ZAGIER TYPE RELATIONS FOR MULTIPLE t-VALUES
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2022, pp. 215-226
-
- Article
- Export citation
TIGHT UNIVERSAL SUMS OF m-GONAL NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 13 July 2022, pp. 40-52
-
- Article
- Export citation
SINGULAR DIRECTIONS IN VEECH SURFACES
- Part of:
-
- Published online by Cambridge University Press:
- 16 September 2022, pp. 390-397
-
- Article
- Export citation
A NOTE ON THE NUMBER OF SOLUTIONS OF TERNARY PURELY EXPONENTIAL DIOPHANTINE EQUATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2022, pp. 53-65
-
- Article
- Export citation
A NOTE ON AN ASYMPTOTIC VERSION OF A PROBLEM OF MAHLER
- Part of:
-
- Published online by Cambridge University Press:
- 15 September 2022, pp. 398-402
-
- Article
- Export citation
AN ANALOGUE OF THE SCHUR–SIEGEL–SMYTH TRACE PROBLEM
- Part of:
-
- Published online by Cambridge University Press:
- 30 August 2022, pp. 227-238
-
- Article
- Export citation
THE SECOND SHIFTED DIFFERENCE OF PARTITIONS AND ITS APPLICATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 25 August 2022, pp. 66-78
-
- Article
- Export citation
THE ABSOLUTE
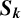 $\boldsymbol {S_k}$
-MEASURE OF TOTALLY POSITIVE ALGEBRAIC INTEGERS
$\boldsymbol {S_k}$
-MEASURE OF TOTALLY POSITIVE ALGEBRAIC INTEGERS
- Part of:
-
- Published online by Cambridge University Press:
- 11 August 2022, pp. 239-249
-
- Article
- Export citation