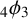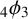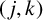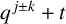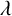FirstView articles
Research Article
ISOMORPHISM OF RELATIVE HOLOMORPHS AND MATRIX SIMILARITY
- Part of:
-
- Published online by Cambridge University Press:
- 23 September 2024, pp. 1-16
-
- Article
-
- You have access
- HTML
- Export citation
PhD Abstract
COMPUTATIONAL FLUID DYNAMICS SIMULATION OF OSCILLATORY FLOW IN PERIODIC MICROPORE STRUCTURES
-
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-3
-
- Article
-
- You have access
- HTML
- Export citation
Research Article
EXTREMAL GRAPHS FOR DEGREE SUMS AND DOMINATING CYCLES
- Part of:
-
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-7
-
- Article
-
- You have access
- HTML
- Export citation
GRAPHS WITH SEMITOTAL DOMINATION NUMBER HALF THEIR ORDER
- Part of:
-
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-8
-
- Article
-
- You have access
- HTML
- Export citation
INEQUALITIES AND UNIFORM ASYMPTOTIC FORMULAE FOR SPT-CRANK OF PARTITIONS
- Part of:
-
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
MONOGENIC EVEN QUARTIC TRINOMIALS
- Part of:
-
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-6
-
- Article
-
- You have access
- HTML
- Export citation
ON A CONJECTURE ON SHIFTED PRIMES WITH LARGE PRIME FACTORS, II
- Part of:
-
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-8
-
- Article
-
- You have access
- HTML
- Export citation
ON A PROBLEM OF PONGSRIIAM ON THE SUM OF DIVISORS
- Part of:
-
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-6
-
- Article
-
- You have access
- HTML
- Export citation
RADIAL ASYMPTOTICS OF GENERATING FUNCTIONS OF k-REGULAR SEQUENCES
- Part of:
-
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-7
-
- Article
-
- You have access
- HTML
- Export citation
A q-SUPERCONGRUENCE ARISING FROM ANDREWS’
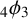 $_4\phi _3$ IDENTITY
$_4\phi _3$ IDENTITY
- Part of:
-
- Published online by Cambridge University Press:
- 29 August 2024, pp. 1-5
-
- Article
-
- You have access
- HTML
- Export citation
PhD Abstract
BAYESIAN METHODS AND POLYNOMIAL CHAOS: APPLICATION TO FINDING CARDIAC BIDOMAIN PARAMETERS
- Part of:
-
- Published online by Cambridge University Press:
- 27 August 2024, pp. 1-3
-
- Article
-
- You have access
- HTML
- Export citation
Research Article
ENUMERATION OF GROUPS IN SOME SPECIAL VARIETIES OF A-GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 27 August 2024, pp. 1-11
-
- Article
-
- You have access
- HTML
- Export citation
MULTIPLICATIVE FUNCTIONS k-ADDITIVE ON GENERALISED OCTAGONAL NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 27 August 2024, pp. 1-11
-
- Article
-
- You have access
- HTML
- Export citation
COMPUTING CENTRALISERS IN [FINITELY GENERATED FREE]-BY-CYCLIC GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 04 June 2024, pp. 1-10
-
- Article
-
- You have access
- HTML
- Export citation
ARITHMETIC PROPERTIES OF AN ANALOGUE OF t-CORE PARTITIONS
- Part of:
-
- Published online by Cambridge University Press:
- 03 June 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
CHARACTERISTIC POLYNOMIALS OF THE MATRICES WITH
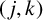 $(\,j,k)$-ENTRY
$(\,j,k)$-ENTRY 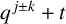 $q^{\,j\pm k}+t$
$q^{\,j\pm k}+t$
- Part of:
-
- Published online by Cambridge University Press:
- 03 June 2024, pp. 1-10
-
- Article
-
- You have access
- HTML
- Export citation
NOTES ON FERMAT-TYPE DIFFERENCE EQUATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 03 June 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
ON THE SET OF BETTI ELEMENTS OF A PUISEUX MONOID
- Part of:
-
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1-13
-
- Article
-
- You have access
- HTML
- Export citation
A TROPICAL ANALOGUE OF THE LEMMA ON THE LOGARITHMIC DERIVATIVE
- Part of:
-
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1-10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOME COUNTING FORMULAE FOR
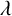 $\lambda $-QUIDDITIES OVER THE RINGS
$\lambda $-QUIDDITIES OVER THE RINGS  ${\mathbb {Z}}/2^{m}{\mathbb {Z}}$
${\mathbb {Z}}/2^{m}{\mathbb {Z}}$
- Part of:
-
- Published online by Cambridge University Press:
- 16 May 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation