Hostname: page-component-848d4c4894-4rdrl Total loading time: 0 Render date: 2024-06-20T18:15:34.008Z Has data issue: false hasContentIssue false
  • English
  • Français

CHARACTERISTIC POLYNOMIALS OF THE MATRICES WITH 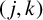$(\,j,k)$-ENTRY 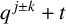$q^{\,j\pm k}+t$

Part of: Polynomials and matrices Special matrices Basic linear algebra Sequences and sets

Published online by Cambridge University Press:  03 June 2024

HAN WANG Open the ORCID record for HAN WANG [Opens in a new window]  and
ZHI-WEI SUN Open the ORCID record for ZHI-WEI SUN [Opens in a new window]
HAN WANG
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, PR China e-mail: hWang@smail.nju.edu.cn
ZHI-WEI SUN*
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, PR China
*
e-mail: zwsun@nju.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

We determine the characteristic polynomials of the matrices 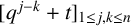$[q^{\,j-k}+t]_{1\le \,j,k\le n}$ and 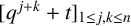$[q^{\,j+k}+t]_{1\le \,j,k\le n}$ for any complex number 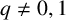$q\not =0,1$. As an application, for complex numbers 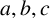$a,b,c$ with 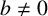$b\not =0$ and 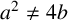$a^2\not =4b$, and the sequence 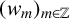$(w_m)_{m\in \mathbb Z}$ with 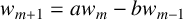$w_{m+1}=aw_m-bw_{m-1}$ for all 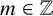$m\in \mathbb Z$, we determine the exact value of 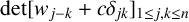$\det [w_{\,j-k}+c\delta _{jk}]_{1\le \,j,k\le n}$.

Keywords

characteristic polynomialdeterminanteigenvalueLucas sequence

MSC classification

Primary: 11C20: Matrices, determinants
Secondary: 11B39: Fibonacci and Lucas numbers and polynomials and generalizations 15A15: Determinants, permanents, other special matrix functions 15A18: Eigenvalues, singular values, and eigenvectors 15B05: Toeplitz, Cauchy, and related matrices
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 10
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Supported by the National Natural Science Foundation of China (grant no. 12371004).

References

Cloitre, B., ‘Sequence A079034’, OEIS (On-Line Encyclopedia of Integer Sequences). Available at https://oeis.org/A079034.Google Scholar
Krattenthaler, C., ‘Advanced determinant calculus: a complement’, Linear Algebra Appl. 411 (2005), 68–166.Google Scholar
Sun, Z.-W., New Conjectures in Number Theory and Combinatorics (Harbin Institute of Technology Press, Harbin, 2021) (in Chinese).Google Scholar
Sun, Z.-W., ‘Sequences A355175 and A355326’, OEIS (On-Line Encyclopedia of Integer Sequences). Available at https://oeis.org.Google Scholar
Sun, Z.-W., Fibonacci Numbers and Hilbert’s Tenth Problem (Harbin Institute of Technology Press, Harbin, 2024) (in Chinese).Google Scholar