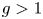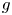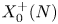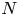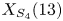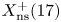1. Introduction
In this paper, we describe the current state of quadratic Chabauty-based algorithms for the resolution of Diophantine equations arising from modular curves. Here we consider the usual modular curves associated to congruence subgroups of ![]() $\mathrm {SL}_2(\mathbf {Z})$, as well as Atkin–Lehner quotients thereof.
$\mathrm {SL}_2(\mathbf {Z})$, as well as Atkin–Lehner quotients thereof.
Recall the motivating question of the subject. Let ![]() $E$ be an elliptic curve over a number field
$E$ be an elliptic curve over a number field ![]() $K$. What are the possible ways for the Galois group
$K$. What are the possible ways for the Galois group ![]() $\mathrm {Gal} (\overline {K}/K)$ to act on the group of torsion points of
$\mathrm {Gal} (\overline {K}/K)$ to act on the group of torsion points of ![]() $E$? Equivalently, what are the conjugacy classes of subgroups of
$E$? Equivalently, what are the conjugacy classes of subgroups of ![]() $\mathrm {GL} _2 (\mathbf {Z}/N\mathbf {Z})$ arising as images of the mod
$\mathrm {GL} _2 (\mathbf {Z}/N\mathbf {Z})$ arising as images of the mod ![]() $N$ Galois representation
$N$ Galois representation ![]() $\rho _{E,N}$?
$\rho _{E,N}$?
By a theorem of Serre [Reference SerreSer72], if ![]() $E$ is an elliptic curve without complex multiplication, then for all primes
$E$ is an elliptic curve without complex multiplication, then for all primes ![]() $N\gg 0$, the representation
$N\gg 0$, the representation ![]() $\rho _{E,N}$ is surjective. Serre's uniformity question [Reference SerreSer72] asks whether this can be made uniform over
$\rho _{E,N}$ is surjective. Serre's uniformity question [Reference SerreSer72] asks whether this can be made uniform over ![]() $\mathbf {Q}$: is there an
$\mathbf {Q}$: is there an ![]() $N_0$ such that, for all primes
$N_0$ such that, for all primes ![]() $N>N_0$, if
$N>N_0$, if ![]() $E/\mathbf {Q}$ is an elliptic curve without complex multiplication, then
$E/\mathbf {Q}$ is an elliptic curve without complex multiplication, then ![]() $\rho _{E,N}$ is surjective? By a classification of maximal subgroups of
$\rho _{E,N}$ is surjective? By a classification of maximal subgroups of ![]() $\mathrm {GL} _2 (\mathbf {Z}/N\mathbf {Z})$, this amounts to determining elliptic curves whose mod
$\mathrm {GL} _2 (\mathbf {Z}/N\mathbf {Z})$, this amounts to determining elliptic curves whose mod ![]() $N$ Galois representation is contained in a Borel subgroup, the normaliser of a split Cartan subgroup, the normaliser of a non-split Cartan subgroup, or an ‘exceptional’ subgroup (such that the projective image is
$N$ Galois representation is contained in a Borel subgroup, the normaliser of a split Cartan subgroup, the normaliser of a non-split Cartan subgroup, or an ‘exceptional’ subgroup (such that the projective image is ![]() $S_4$,
$S_4$, ![]() $A_4$, or
$A_4$, or ![]() $A_5$).
$A_5$).
Mazur's Program B [Reference MazurMaz77] asks for all of the possible Galois actions on torsion subgroups of elliptic curves without complex multiplication. This question includes Serre's uniformity question but is more general. From a Diophantine perspective, it roughly amounts to determining the rational points on all modular curves.
Rouse and Zureick-Brown [Reference Rouse and Zureick-BrownRZB15] settled this in the context of 2-primary torsion and very recently, with Sutherland [Reference Rouse, Sutherland and Zureick-BrownRSZB22], studied this in the context of ![]() $\ell$-primary torsion for other primes
$\ell$-primary torsion for other primes ![]() $\ell$. For each prime, this produces a finite number of curves, the determination of whose rational points would resolve the
$\ell$. For each prime, this produces a finite number of curves, the determination of whose rational points would resolve the ![]() $\ell$-primary part of Mazur's question. In §§ 5.1 and 5.3 we compute the rational points on four modular curves
$\ell$-primary part of Mazur's question. In §§ 5.1 and 5.3 we compute the rational points on four modular curves ![]() $X_{S_4}(13), X_{\scriptstyle \mathrm { ns}}^+(17), X_{11}$ and
$X_{S_4}(13), X_{\scriptstyle \mathrm { ns}}^+(17), X_{11}$ and ![]() $X_{15}$ arising in Mazur's Program B. In particular, we prove the following theorem.
$X_{15}$ arising in Mazur's Program B. In particular, we prove the following theorem.
Theorem 1.1 We have ![]() $\#X_{S_4}(13)(\mathbf {Q}) = 4$. One of these points is a complex multiplication (CM) point, corresponding to discriminant
$\#X_{S_4}(13)(\mathbf {Q}) = 4$. One of these points is a complex multiplication (CM) point, corresponding to discriminant ![]() $D=-3$. The other three are exceptional, with corresponding
$D=-3$. The other three are exceptional, with corresponding ![]() $j$-invariants listed in § 5.1.
$j$-invariants listed in § 5.1.
Here we call a non-cuspidal rational point exceptional if it does not correspond to an elliptic curve with complex multiplication. The curve ![]() $X_{S_4}(13)$ has genus 3. This completes the classification of elliptic curves
$X_{S_4}(13)$ has genus 3. This completes the classification of elliptic curves ![]() $E/\mathbf {Q}$ and prime level
$E/\mathbf {Q}$ and prime level ![]() $N>0$ such that
$N>0$ such that ![]() $\rho _{E,N}$ is contained in an exceptional subgroup.
$\rho _{E,N}$ is contained in an exceptional subgroup.
We also determine the rational points on ![]() $X_{\scriptstyle \mathrm { ns}}^+(17)$, the non-split Cartan modular curve of level 17, which is a genus 6 curve.
$X_{\scriptstyle \mathrm { ns}}^+(17)$, the non-split Cartan modular curve of level 17, which is a genus 6 curve.
Theorem 1.2 We have ![]() $\#X_{\scriptstyle \mathrm { ns}}^+(17)(\mathbf {Q}) = 7$ and all of these points are CM, corresponding to discriminants
$\#X_{\scriptstyle \mathrm { ns}}^+(17)(\mathbf {Q}) = 7$ and all of these points are CM, corresponding to discriminants ![]() $-3, -7, -11,$
$-3, -7, -11,$ ![]() $-12, -27, -28, -163$.
$-12, -27, -28, -163$.
Theorems 1.1 and 1.2 complete the classification of the possible 13-adic and 17-adic images of Galois.
Moving beyond torsion points of elliptic curves over ![]() $\mathbf {Q}$, another interesting problem in the Diophantine geometry of modular curves is the determination of the set of rational points on the Atkin–Lehner quotient
$\mathbf {Q}$, another interesting problem in the Diophantine geometry of modular curves is the determination of the set of rational points on the Atkin–Lehner quotient
of the modular curve ![]() $X_0 (N)$. In [Reference GalbraithGal02], Galbraith asks whether, for all primes
$X_0 (N)$. In [Reference GalbraithGal02], Galbraith asks whether, for all primes ![]() $N\gg 0$, the only rational points on
$N\gg 0$, the only rational points on ![]() $X_0 ^+ (N)$ are cusps or CM points. From a moduli perspective, this amounts to finding quadratic
$X_0 ^+ (N)$ are cusps or CM points. From a moduli perspective, this amounts to finding quadratic ![]() $\mathbf {Q}$-curves that are
$\mathbf {Q}$-curves that are ![]() $N$-isogenous to their conjugates. Dogra and Le Fourn [Reference Dogra and Le FournDLF21] proved that the quadratic Chabauty set
$N$-isogenous to their conjugates. Dogra and Le Fourn [Reference Dogra and Le FournDLF21] proved that the quadratic Chabauty set ![]() $X_0^+(N) (\mathbf {Q} _p )_2$ is finite whenever the genus of
$X_0^+(N) (\mathbf {Q} _p )_2$ is finite whenever the genus of ![]() $X_0^+(N)$ is greater than
$X_0^+(N)$ is greater than ![]() $1$. Hence, it is natural to ask whether the methods of this paper can be used to give an algorithm for computing
$1$. Hence, it is natural to ask whether the methods of this paper can be used to give an algorithm for computing ![]() $X_0^+(N) (\mathbf {Q} _p )_2$ for any
$X_0^+(N) (\mathbf {Q} _p )_2$ for any ![]() $N$. In fact, in the range of
$N$. In fact, in the range of ![]() $N$ we consider, finiteness of
$N$ we consider, finiteness of ![]() $X_0 ^+ (N)(\mathbf {Q} _p)_2$ follows from a criterion appearing in earlier work of Siksek [Reference SiksekSik17]. Our computations described in § 5.2 prove the following result.
$X_0 ^+ (N)(\mathbf {Q} _p)_2$ follows from a criterion appearing in earlier work of Siksek [Reference SiksekSik17]. Our computations described in § 5.2 prove the following result.
Theorem 1.3 The only prime values ![]() $N$ such that the curve
$N$ such that the curve ![]() $X_0^+(N)$ is of genus
$X_0^+(N)$ is of genus ![]() $2$ or
$2$ or ![]() $3$ and has an exceptional rational point are
$3$ and has an exceptional rational point are ![]() $N=73,\ 103,\ 191$. In particular, for prime
$N=73,\ 103,\ 191$. In particular, for prime ![]() $N$, there are no exceptional rational points on curves
$N$, there are no exceptional rational points on curves ![]() $X_0^+(N)$ of genus 3.
$X_0^+(N)$ of genus 3.
All rational points in Theorem 1.3 have already been found by Galbraith [Reference GalbraithGal99].
Remark 1.4 These computations were recently extended significantly by Adžaga, Arul, Beneish, Chen, Chidambaram, Keller and Wen [Reference Adžaga, Arul, Beneish, Chen, Chidambaram, Keller and WenAAB+21]. They use the quadratic Chabauty method described in this paper to determine the set of rational points on all curves ![]() $X_0 ^+ (N)$ of genus 4, 5 and 6 and prime level
$X_0 ^+ (N)$ of genus 4, 5 and 6 and prime level ![]() $N$. Arul and Müller [Reference Arul and MüllerAM23] also compute the rational points on
$N$. Arul and Müller [Reference Arul and MüllerAM23] also compute the rational points on ![]() $X_0^+(125)$ using the same method. Adžaga, Chidambaram, Keller and Padurariu [Reference Adžaga, Chidambaram, Keller and PadurariuACKP22] use several techniques, including quadratic Chabauty, to determine the set of rational points on the hyperelliptic Atkin–Lehner star quotient curves
$X_0^+(125)$ using the same method. Adžaga, Chidambaram, Keller and Padurariu [Reference Adžaga, Chidambaram, Keller and PadurariuACKP22] use several techniques, including quadratic Chabauty, to determine the set of rational points on the hyperelliptic Atkin–Lehner star quotient curves ![]() $X_0^*(N)$.
$X_0^*(N)$.
Going further, one may wonder what the potential applications of these algorithms are to non-modular curves. The main stumbling block in attempting such a generalisation is our running assumption on the Mordell–Weil rank and Picard number of the Jacobian (see § 2.1). Since a generic curve has Picard number ![]() $1$, it is not clear how often one should expect a genus
$1$, it is not clear how often one should expect a genus ![]() $g$ curve with Mordell–Weil rank
$g$ curve with Mordell–Weil rank ![]() $g$ to satisfy the quadratic Chabauty hypothesis. Nevertheless, there are other interesting curves where one would expect to get some mileage out of such algorithms. The most obvious examples are (Atkin–Lehner quotients of) Shimura curves. In particular, determining the set of rational points on the (infinitely many) curves
$g$ to satisfy the quadratic Chabauty hypothesis. Nevertheless, there are other interesting curves where one would expect to get some mileage out of such algorithms. The most obvious examples are (Atkin–Lehner quotients of) Shimura curves. In particular, determining the set of rational points on the (infinitely many) curves ![]() $X^D /\langle w_D\rangle$, in the notation of Parent and Yafaev [Reference Parent and YafaevPY07], would resolve a conjecture of Clark [Reference ClarkCla03] (Parent and Yafaev determine the rational points for an infinite family of Shimura curves whose Jacobian contains a rank zero isogeny factor).
$X^D /\langle w_D\rangle$, in the notation of Parent and Yafaev [Reference Parent and YafaevPY07], would resolve a conjecture of Clark [Reference ClarkCla03] (Parent and Yafaev determine the rational points for an infinite family of Shimura curves whose Jacobian contains a rank zero isogeny factor).
2. Quadratic Chabauty: theory
We give a brief overview of the quadratic Chabauty method. A more complete exposition can be found in [Reference Balakrishnan, Best, Bianchi, Lawrence, Müller, Triantafillou and VonkBBB+21], and we refer the reader to [Reference Balakrishnan and DograBD18, Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19] for more precise details and proofs. Our description is in terms of Galois representations and filtered ![]() $\phi$-modules, but we note that recently Edixhoven and Lido [Reference Edixhoven and LidoEL23] gave a geometric version of quadratic Chabauty, which they used to determine the set of rational points on the bielliptic modular curve
$\phi$-modules, but we note that recently Edixhoven and Lido [Reference Edixhoven and LidoEL23] gave a geometric version of quadratic Chabauty, which they used to determine the set of rational points on the bielliptic modular curve ![]() $X_0(129)/\langle w_3, w_{43} \rangle$ of genus 2. Duque-Rosero, Hashimoto and Spelier [Reference Duque-Rosero, Hashimoto and SpelierDRHS22] have related this approach to that presented here and used this to give algorithms for geometric quadratic Chabauty for hyperelliptic curves. Besser, Müller and Srinivasan [Reference Besser, Müller and SrinivasanBMS21] have also given an alternative approach to the quadratic Chabauty method based on a new construction of
$X_0(129)/\langle w_3, w_{43} \rangle$ of genus 2. Duque-Rosero, Hashimoto and Spelier [Reference Duque-Rosero, Hashimoto and SpelierDRHS22] have related this approach to that presented here and used this to give algorithms for geometric quadratic Chabauty for hyperelliptic curves. Besser, Müller and Srinivasan [Reference Besser, Müller and SrinivasanBMS21] have also given an alternative approach to the quadratic Chabauty method based on a new construction of ![]() $p$-adic heights on abelian varieties via
$p$-adic heights on abelian varieties via ![]() $p$-adic Arakelov theory.
$p$-adic Arakelov theory.
An early version of the method appeared in work of Kim [Reference KimKim10, Reference Balakrishnan, Kedlaya and KimBKK11], where Massey products were used to construct a locally analytic function, vanishing on the set of integral points of an elliptic curve of rank ![]() $1$. These functions were interpreted as height functions, extending the method, in Balakrishnan and Besser [Reference Balakrishnan and BesserBB15] and Balakrishnan, Besser and Müller [Reference Balakrishnan, Besser and MüllerBBM16]. It was extended to its current form in Balakrishnan and Dogra [Reference Balakrishnan and DograBD18], where a systematic use of Nekovář's theory of
$1$. These functions were interpreted as height functions, extending the method, in Balakrishnan and Besser [Reference Balakrishnan and BesserBB15] and Balakrishnan, Besser and Müller [Reference Balakrishnan, Besser and MüllerBBM16]. It was extended to its current form in Balakrishnan and Dogra [Reference Balakrishnan and DograBD18], where a systematic use of Nekovář's theory of ![]() $p$-adic heights suggested a streamlined approach towards a very general class of curves allowing an abundance of geometric correspondences. It was carried out to determine the set of rational points on
$p$-adic heights suggested a streamlined approach towards a very general class of curves allowing an abundance of geometric correspondences. It was carried out to determine the set of rational points on ![]() $X_{\rm s}^+(13)$, the split Cartan curve of level 13, in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19].
$X_{\rm s}^+(13)$, the split Cartan curve of level 13, in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19].
Remark This method fits into the vastly more general framework developed by Kim [Reference KimKim05, Reference KimKim09], elaborating on the idea of studying rational points on curves through path torsors of the étale fundamental group, suggested by Grothendieck's section conjecture. The approach discussed here represents an effective way to make this theory computable and applicable to a variety of examples. It is, however, important to note that different quotients of the fundamental group have been successfully used for this purpose (see, for instance, [Reference Balakrishnan and DograBD21]). Finally, although we restrict our attention to the base field ![]() $\mathbf {Q}$, suitable versions exist over number fields (see [Reference Balakrishnan and DograBD18, Reference Balakrishnan and DograBD21, Reference Balakrishnan, Besser, Bianchi and MüllerBBBM21]).
$\mathbf {Q}$, suitable versions exist over number fields (see [Reference Balakrishnan and DograBD18, Reference Balakrishnan and DograBD21, Reference Balakrishnan, Besser, Bianchi and MüllerBBBM21]).
2.1 Rational points and global heights
Consider a smooth projective curve ![]() $X_{\mathbf {Q}}$ of genus
$X_{\mathbf {Q}}$ of genus ![]() $g \geq 2$ whose Jacobian
$g \geq 2$ whose Jacobian ![]() $J$ has rank
$J$ has rank ![]() $r=g$. We also assume that the abelian logarithm induces an isomorphism
$r=g$. We also assume that the abelian logarithm induces an isomorphism
and that ![]() $X(\mathbf {Q})$ is non-empty, so we may choose a base point
$X(\mathbf {Q})$ is non-empty, so we may choose a base point ![]() $b$ in
$b$ in ![]() $X(\mathbf {Q})$. Suppose that the Néron–Severi rank
$X(\mathbf {Q})$. Suppose that the Néron–Severi rank ![]() $\mathrm {rk}_{\mathbf {Z}} \mathrm {NS}(J)$ is at least
$\mathrm {rk}_{\mathbf {Z}} \mathrm {NS}(J)$ is at least ![]() $2$, so that there exists a non-trivial class
$2$, so that there exists a non-trivial class
As explained in Balakrishnan and Dogra [Reference Balakrishnan and DograBD18, Lemma 3.2], we can attach to any such choice of ![]() $Z$ a suitable quotient
$Z$ a suitable quotient ![]() $U_Z$ of the
$U_Z$ of the ![]() $\mathbf {Q}_p$-pro-unipotent fundamental group of
$\mathbf {Q}_p$-pro-unipotent fundamental group of ![]() $X_{\bar {\mathbf {Q}}}$, which, via a twisting construction by path torsors, gives rise to a certain family of Galois representations,
$X_{\bar {\mathbf {Q}}}$, which, via a twisting construction by path torsors, gives rise to a certain family of Galois representations,
where ![]() $K \in \{ \mathbf {Q}, \mathbf {Q}_p \}$ and
$K \in \{ \mathbf {Q}, \mathbf {Q}_p \}$ and ![]() $G_K$ is the absolute Galois group of
$G_K$ is the absolute Galois group of ![]() $K$. We refer the reader to [Reference Balakrishnan and DograBD18, § 5.1] for the details of this construction (in particular, for the equivalence relation), and merely recall here that with respect to a suitable choice of basis, the representation
$K$. We refer the reader to [Reference Balakrishnan and DograBD18, § 5.1] for the details of this construction (in particular, for the equivalence relation), and merely recall here that with respect to a suitable choice of basis, the representation ![]() $\mathrm {A}(x)$ is lower triangular, of the form
$\mathrm {A}(x)$ is lower triangular, of the form
 \begin{equation} g \in G_K \longmapsto \left( \begin{matrix} 1 & & \\ \alpha(g) & \rho_V(g) & \\ \gamma(g) & \beta(g) & \chi_p(g) \end{matrix} \right), \end{equation}
\begin{equation} g \in G_K \longmapsto \left( \begin{matrix} 1 & & \\ \alpha(g) & \rho_V(g) & \\ \gamma(g) & \beta(g) & \chi_p(g) \end{matrix} \right), \end{equation}where
is a frame for the Galois action on the ![]() $p$-adic étale homology
$p$-adic étale homology ![]() $V = \mathrm {H}^1_{\scriptstyle \mathrm {\acute {e}t}}(X_{\overline {K}}, \mathbf {Q}_p)^{\vee }$, and
$V = \mathrm {H}^1_{\scriptstyle \mathrm {\acute {e}t}}(X_{\overline {K}}, \mathbf {Q}_p)^{\vee }$, and ![]() $\chi _p\colon G_K \to \mathbf {Q}_p^{\times }$ is the
$\chi _p\colon G_K \to \mathbf {Q}_p^{\times }$ is the ![]() $p$-adic cyclotomic character. Representations of this form, which admit a
$p$-adic cyclotomic character. Representations of this form, which admit a ![]() $G_K$-stable filtration with graded pieces
$G_K$-stable filtration with graded pieces ![]() $\mathbf {Q}_p(1), V, \mathbf {Q}_p$, are referred to as mixed extensions (see [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 3.1]).
$\mathbf {Q}_p(1), V, \mathbf {Q}_p$, are referred to as mixed extensions (see [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 3.1]).
The theory of ![]() $p$-adic heights due to Nekovář [Reference NekovářNek93, § 2] attaches to any mixed extension
$p$-adic heights due to Nekovář [Reference NekovářNek93, § 2] attaches to any mixed extension ![]() $M$ a
$M$ a ![]() $p$-adic height
$p$-adic height ![]() $h(M)$. When applied to the family of mixed extensions
$h(M)$. When applied to the family of mixed extensions ![]() $\mathrm {A}(x)$, this results in a map
$\mathrm {A}(x)$, this results in a map
The algebraic properties of this map lie at the heart of the quadratic Chabauty method. Most notably, the method relies on the following two facts.
− The
 $p$-adic height is a bilinear function of the pair of cohomology classes
$p$-adic height is a bilinear function of the pair of cohomology classes  $([\alpha ], [\beta ])$ associated to the vectors appearing in (2.2).
$([\alpha ], [\beta ])$ associated to the vectors appearing in (2.2).− It decomposes as a sum of local height functions
 $h_v$ defined locally at every finite place
$h_v$ defined locally at every finite place  $v$.
$v$.
2.2 Local decomposition
We now discuss in more detail the decomposition of the global ![]() $p$-adic height
$p$-adic height ![]() $h$ described above, as a sum of local height functions
$h$ described above, as a sum of local height functions
The nature of these local height functions is as follows.
(i) The case
 $v \neq p$. It follows from Kim and Tamagawa [Reference Kim and TamagawaKT08, Corollary 0.2] that the function
$v \neq p$. It follows from Kim and Tamagawa [Reference Kim and TamagawaKT08, Corollary 0.2] that the function  $h_v$ has finite image, in the sense that there exists a finite set
$h_v$ has finite image, in the sense that there exists a finite set  $\Upsilon _v$ such that
$\Upsilon _v$ such that
 \[ h_v \colon X(\mathbf{Q}_v) \longrightarrow \Upsilon_v \subset \mathbf{Q}_p. \]
\[ h_v \colon X(\mathbf{Q}_v) \longrightarrow \Upsilon_v \subset \mathbf{Q}_p. \]
(ii) The case
 $v=p$. The map
$v=p$. The map  $h_p$ is locally analytic and has a simple description in terms of linear algebra data of the filtered
$h_p$ is locally analytic and has a simple description in terms of linear algebra data of the filtered  $\phi$-module
where
$\phi$-module
where \[ M(x) := \big( \mathrm{A}(x) \otimes_{\mathbf{Q}_p} \mathrm{B}_{\scriptstyle \mathrm{ crys}}\big)^{G_{\mathbf{Q}_p}}, \]
\[ M(x) := \big( \mathrm{A}(x) \otimes_{\mathbf{Q}_p} \mathrm{B}_{\scriptstyle \mathrm{ crys}}\big)^{G_{\mathbf{Q}_p}}, \]
 $\mathrm {B}_{\scriptstyle \mathrm { crys}}$ is Fontaine's crystalline period ring. A crucial point in the method of quadratic Chabauty is that the definition of the family of Galois representations
$\mathrm {B}_{\scriptstyle \mathrm { crys}}$ is Fontaine's crystalline period ring. A crucial point in the method of quadratic Chabauty is that the definition of the family of Galois representations  $\mathrm {A}(x)$ comes from a motivic quotient of the fundamental group of
$\mathrm {A}(x)$ comes from a motivic quotient of the fundamental group of  $X$, and non-abelian
$X$, and non-abelian  $p$-adic Hodge theory yields an analogous de Rham realisation in the form of a filtered connection
$p$-adic Hodge theory yields an analogous de Rham realisation in the form of a filtered connection  $(\mathscr {M},\nabla )$ on
$(\mathscr {M},\nabla )$ on  $X$ with a Frobenius structure, together with an isomorphism of filtered
$X$ with a Frobenius structure, together with an isomorphism of filtered  $\phi$-modules
(see [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 5]). We have a pair of elements
$\phi$-modules
(see [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 5]). We have a pair of elements \[ x^* \mathscr{M} \simeq M(x) \]
\[ x^* \mathscr{M} \simeq M(x) \]
 $\pi _1 (M(x))$ and
$\pi _1 (M(x))$ and  $\pi _2 (M(x))^\vee (1)$ of
$\pi _2 (M(x))^\vee (1)$ of  $\mathrm {H}^0 (X_{\mathbf {Q} _p },\Omega )^\vee$ associated to the filtered
$\mathrm {H}^0 (X_{\mathbf {Q} _p },\Omega )^\vee$ associated to the filtered  $\phi$-module
$\phi$-module  $M(x)$, via the isomorphism
$M(x)$, via the isomorphism
 \[ \mathrm{Ext} ^1 _{\scriptstyle \mathrm{ Fil} ,\phi }(\mathbf{Q} _p ,\mathrm{H} ^1 _{\scriptstyle \mathrm{dR}}(X_{\mathbf{Q} _p })^\vee )\simeq \mathrm{H} ^0 (X_{\mathbf{Q} _p },\Omega )^\vee . \]
\[ \mathrm{Ext} ^1 _{\scriptstyle \mathrm{ Fil} ,\phi }(\mathbf{Q} _p ,\mathrm{H} ^1 _{\scriptstyle \mathrm{dR}}(X_{\mathbf{Q} _p })^\vee )\simeq \mathrm{H} ^0 (X_{\mathbf{Q} _p },\Omega )^\vee . \]
2.3 Finiteness
The decomposition ![]() $h = \sum _v h_v$ can be used to leverage the bilinear nature of
$h = \sum _v h_v$ can be used to leverage the bilinear nature of ![]() $h$ against the properties of the functions
$h$ against the properties of the functions ![]() $h_v$. By (1) in § 2.2, we know that there exists a finite set
$h_v$. By (1) in § 2.2, we know that there exists a finite set ![]() $\Upsilon = \Upsilon _Z \subset \mathbf {Q}_p$ such that
$\Upsilon = \Upsilon _Z \subset \mathbf {Q}_p$ such that
for any ![]() $x$ in
$x$ in ![]() $X(\mathbf {Q})$. In § 3, we describe how the terms in this equation may be computed explicitly.
$X(\mathbf {Q})$. In § 3, we describe how the terms in this equation may be computed explicitly.
− The set
 $\Upsilon$ is given by
$\Upsilon$ is given by  $\{\sum _v \epsilon _v :\epsilon _v \in \Upsilon _v \}$, where the sum is over primes of bad reduction, and
$\{\sum _v \epsilon _v :\epsilon _v \in \Upsilon _v \}$, where the sum is over primes of bad reduction, and  $\Upsilon _v$ is the set of values of
$\Upsilon _v$ is the set of values of  $h_v (x)$ for
$h_v (x)$ for  $x\in X(\mathbf {Q} _v ).$ For
$x\in X(\mathbf {Q} _v ).$ For  $v\ne p$, the map
$v\ne p$, the map  $h_v$ is made more explicit in § 3.1 using the results of Betts and Dogra [Reference Betts and DograBD19] to compute
$h_v$ is made more explicit in § 3.1 using the results of Betts and Dogra [Reference Betts and DograBD19] to compute  $\Upsilon _v$ when a regular semi-stable model
$\Upsilon _v$ when a regular semi-stable model  $\mathcal {X}$ is known. The map
$\mathcal {X}$ is known. The map  $h_v$ factors through the reduction map to the irreducible components of the special fibre of
$h_v$ factors through the reduction map to the irreducible components of the special fibre of  $\mathcal {X}$.
$\mathcal {X}$.− The map
 $h_p$ may be computed using [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, §§ 4,5], where it is explained how the universal properties of the bundle
$h_p$ may be computed using [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, §§ 4,5], where it is explained how the universal properties of the bundle  $\mathscr {M}$ rigidify the (known) structures on the graded pieces, enough to allow us to compute them explicitly (see § 3.2).
$\mathscr {M}$ rigidify the (known) structures on the graded pieces, enough to allow us to compute them explicitly (see § 3.2).− Using the isomorphism (2.1), we may view the global height as a pairing
Using global information, such as an abundance of global points \[ h \colon \mathrm{H}^0(X_{\mathbf{Q}_p},\Omega^1)^{\vee} \otimes \mathrm{H}^0(X_{\mathbf{Q}_p},\Omega^1)^{\vee} \longrightarrow \mathbf{Q}_p. \]
\[ h \colon \mathrm{H}^0(X_{\mathbf{Q}_p},\Omega^1)^{\vee} \otimes \mathrm{H}^0(X_{\mathbf{Q}_p},\Omega^1)^{\vee} \longrightarrow \mathbf{Q}_p. \]
 $x \in X(\mathbf {Q})$ if available, we can solve for the height pairing. This is discussed in § 3.3, where we also explain what to do when too few rational points are available.
$x \in X(\mathbf {Q})$ if available, we can solve for the height pairing. This is discussed in § 3.3, where we also explain what to do when too few rational points are available.
Via the above, the map ![]() $h$ may be extended to a bilinear map
$h$ may be extended to a bilinear map
The resulting map
is known to be Zariski dense on every residue disk. We call ![]() $\rho$ a quadratic Chabauty function, and we write
$\rho$ a quadratic Chabauty function, and we write ![]() $\rho _Z$ if we want to emphasise the dependence on
$\rho _Z$ if we want to emphasise the dependence on ![]() $Z$. Hence (2.3) implies that
$Z$. Hence (2.3) implies that ![]() $X(\mathbf {Q})$ is finite. Moreover, the computable nature of the quantities involved in (2.3), discussed at length in the next section, allows us to explicitly determine a
$X(\mathbf {Q})$ is finite. Moreover, the computable nature of the quantities involved in (2.3), discussed at length in the next section, allows us to explicitly determine a ![]() $p$-adic approximation of the finite set
$p$-adic approximation of the finite set
As explained in [Reference Balakrishnan and DograBD18, Proposition 5.5], this finite set contains the Chabauty–Kim set ![]() $X(\mathbf {Q} _p )_2$. In particular, a proof that this set equals
$X(\mathbf {Q} _p )_2$. In particular, a proof that this set equals ![]() $X(\mathbf {Q} )$ gives a verification of Kim's conjecture [Reference Balakrishnan, Dan-Cohen, Kim and WewersBDCKW18, Conjecture 3.1] for the curve
$X(\mathbf {Q} )$ gives a verification of Kim's conjecture [Reference Balakrishnan, Dan-Cohen, Kim and WewersBDCKW18, Conjecture 3.1] for the curve ![]() $X$ (we refer the reader to [Reference Balakrishnan, Dan-Cohen, Kim and WewersBDCKW18, Definition 2.7] for the definitions of the set
$X$ (we refer the reader to [Reference Balakrishnan, Dan-Cohen, Kim and WewersBDCKW18, Definition 2.7] for the definitions of the set ![]() $X(\mathbf {Q} _p )_2$).
$X(\mathbf {Q} _p )_2$).
3. Quadratic Chabauty: algorithms
In this section, we discuss the computation of the three ingredients outlined above:
(i) the local height function
 $h_v$ for
$h_v$ for  $v$ away from
$v$ away from  $p$, which is described in § 3.1 using the techniques in Betts and Dogra [Reference Betts and DograBD19], given a regular semi-stable model at
$p$, which is described in § 3.1 using the techniques in Betts and Dogra [Reference Betts and DograBD19], given a regular semi-stable model at  $v$;
$v$;(ii) the height function
 $h_p$, whose computation using the techniques of [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19] is described in § 3.2;
$h_p$, whose computation using the techniques of [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19] is described in § 3.2;(iii) the determination of the global height pairing
 $h$, described in § 3.3 using rational divisors as input in the absence of a supply of rational points on the curve.
$h$, described in § 3.3 using rational divisors as input in the absence of a supply of rational points on the curve.
Our contribution in this paper lies mainly in (i) and (iii), which reflect general features of the method of quadratic Chabauty that were not needed for the curve ![]() $X_{\rm s}^+(13)$ treated in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19]. In addition, we discuss some computational techniques to further automate the method of quadratic Chabauty to work for a wide class of modular curves. This includes the Mordell–Weil sieve, which is used to attempt to further refine the finite set of local points in the output to the true set of rational points
$X_{\rm s}^+(13)$ treated in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19]. In addition, we discuss some computational techniques to further automate the method of quadratic Chabauty to work for a wide class of modular curves. This includes the Mordell–Weil sieve, which is used to attempt to further refine the finite set of local points in the output to the true set of rational points ![]() $X(\mathbf {Q})$.
$X(\mathbf {Q})$.
Remark 3.1 The global height depends on the choice (which we henceforth fix) of
− a non-trivial continuous idèle class character
 $\chi \colon \mathbf {A}_{\mathbf {Q}}^\times / \mathbf {Q}^{\times } \longrightarrow \mathbf {Q}_p$ ramified at
$\chi \colon \mathbf {A}_{\mathbf {Q}}^\times / \mathbf {Q}^{\times } \longrightarrow \mathbf {Q}_p$ ramified at  $p$;
$p$;− a splitting
 $s\colon V_{\scriptstyle \mathrm {dR}}/\mathrm {Fil}^0 V_{\scriptstyle \mathrm {dR}} \longrightarrow V_{\scriptstyle \mathrm {dR}}$ of the Hodge filtration, where
$s\colon V_{\scriptstyle \mathrm {dR}}/\mathrm {Fil}^0 V_{\scriptstyle \mathrm {dR}} \longrightarrow V_{\scriptstyle \mathrm {dR}}$ of the Hodge filtration, where
 \[ V_{\scriptstyle \mathrm{dR}} = \mathrm{D}_{\scriptstyle \mathrm{ crys}}(V) = \mathrm{H}^1_{\scriptstyle \mathrm{dR}}(X_{\mathbf{Q}_p})^{\vee}. \]
\[ V_{\scriptstyle \mathrm{dR}} = \mathrm{D}_{\scriptstyle \mathrm{ crys}}(V) = \mathrm{H}^1_{\scriptstyle \mathrm{dR}}(X_{\mathbf{Q}_p})^{\vee}. \]
We also fix differentials ![]() $\omega _{0},\ldots,\omega _{2g-1}$ of the second kind whose classes form a symplectic basis of
$\omega _{0},\ldots,\omega _{2g-1}$ of the second kind whose classes form a symplectic basis of ![]() $\mathrm {H}^1_{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q}_p})$ with respect to the cup product, such that
$\mathrm {H}^1_{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q}_p})$ with respect to the cup product, such that ![]() $\omega _{0},\ldots,\omega _{g-1}$ generate
$\omega _{0},\ldots,\omega _{g-1}$ generate ![]() $\mathrm {H}^0(X_{\mathbf {Q}_p},\Omega ^1)$.
$\mathrm {H}^0(X_{\mathbf {Q}_p},\Omega ^1)$.
3.1 Local heights away from  $p$
$p$
Let ![]() $\ell \neq p$ and let
$\ell \neq p$ and let ![]() $F$ be an endomorphism of
$F$ be an endomorphism of ![]() $J$ whose class
$J$ whose class ![]() $Z$ lies in
$Z$ lies in ![]() $\mathrm {Ker}\big (\mathrm {NS}(J) \to \mathrm {NS}(X) \big )$. In [Reference Betts and DograBD19], a description of the map
$\mathrm {Ker}\big (\mathrm {NS}(J) \to \mathrm {NS}(X) \big )$. In [Reference Betts and DograBD19], a description of the map
associated to ![]() $F$ and
$F$ and ![]() $\chi$ is given, in terms of harmonic analysis on the reduction graph in the sense of Zhang [Reference ZhangZha93].
$\chi$ is given, in terms of harmonic analysis on the reduction graph in the sense of Zhang [Reference ZhangZha93].
To explain the result, we introduce some notation. Over some finite extension ![]() $K/\mathbf {Q} _{\ell }$, the curve
$K/\mathbf {Q} _{\ell }$, the curve ![]() $X$ admits a regular semi-stable model
$X$ admits a regular semi-stable model ![]() $\mathcal {X}_{\mathrm {reg}}/\mathcal {O}_K$, and a stable model
$\mathcal {X}_{\mathrm {reg}}/\mathcal {O}_K$, and a stable model ![]() $\mathcal {X}_{\mathrm {st}}/\mathcal {O}_K$. Let
$\mathcal {X}_{\mathrm {st}}/\mathcal {O}_K$. Let ![]() $\Gamma _{\mathrm {reg}}$ and
$\Gamma _{\mathrm {reg}}$ and ![]() $\Gamma _{\mathrm {st}}$ denote the dual graphs of the special fibres of these models. Recall that the dual graph of the special fibre is by definition the graphFootnote 1 whose vertices are the irreducible components of the special fibre, and whose edges are the singular points of the special fibre. The endpoints of an edge
$\Gamma _{\mathrm {st}}$ denote the dual graphs of the special fibres of these models. Recall that the dual graph of the special fibre is by definition the graphFootnote 1 whose vertices are the irreducible components of the special fibre, and whose edges are the singular points of the special fibre. The endpoints of an edge ![]() $e$ are defined to be the irreducible components containing the point (by semi-stability, a singular point
$e$ are defined to be the irreducible components containing the point (by semi-stability, a singular point ![]() $e$ lies on at most two irreducible components). By regularity, we have a reduction map
$e$ lies on at most two irreducible components). By regularity, we have a reduction map
from ![]() $X(\mathbf {Q} _{\ell })$ to the vertices of the dual graph
$X(\mathbf {Q} _{\ell })$ to the vertices of the dual graph ![]() $\Gamma _{\mathrm {reg}}$.
$\Gamma _{\mathrm {reg}}$.
The definition is the natural one: given ![]() $x\in X(\mathbf {Q} _{\ell })$, there is a unique extension to an
$x\in X(\mathbf {Q} _{\ell })$, there is a unique extension to an ![]() $\mathcal {O}_K$-section
$\mathcal {O}_K$-section ![]() $x\in \mathcal {X}_{\mathrm {reg}}(\mathcal {O}_K )$. Let
$x\in \mathcal {X}_{\mathrm {reg}}(\mathcal {O}_K )$. Let ![]() $k$ be the residue field of
$k$ be the residue field of ![]() $\mathcal {O}_K$. By regularity, the specialisation of
$\mathcal {O}_K$. By regularity, the specialisation of ![]() $x$ to
$x$ to ![]() $k$ lies on a unique irreducible component of
$k$ lies on a unique irreducible component of ![]() $\mathcal {X}_{\mathrm {reg},k}$.
$\mathcal {X}_{\mathrm {reg},k}$.
We may give ![]() $\Gamma _{\mathrm {reg}}$ and
$\Gamma _{\mathrm {reg}}$ and ![]() $\Gamma _{\mathrm {st}}$ the structure of rationally metrised graphs (i.e. graphs whose edges
$\Gamma _{\mathrm {st}}$ the structure of rationally metrised graphs (i.e. graphs whose edges ![]() $e$ have associated lengths
$e$ have associated lengths ![]() $\ell (e)\in \mathbb {\mathbf {Q} }_{>0}$) by defining the length of an edge
$\ell (e)\in \mathbb {\mathbf {Q} }_{>0}$) by defining the length of an edge ![]() $e$ to be
$e$ to be ![]() $i(e)/r$, where
$i(e)/r$, where ![]() $i$ is the intersection multiplicity of the corresponding singular point and
$i$ is the intersection multiplicity of the corresponding singular point and ![]() $r$ is the ramification degree of
$r$ is the ramification degree of ![]() $K/\mathbf {Q} _{\ell }$.
$K/\mathbf {Q} _{\ell }$.
Choose an orientation of the edges of ![]() $\Gamma := \Gamma _{\mathrm {st}}$, so that each
$\Gamma := \Gamma _{\mathrm {st}}$, so that each ![]() $e\in E(\Gamma )$ has a source
$e\in E(\Gamma )$ has a source ![]() $s(e)$ and target
$s(e)$ and target ![]() $t(e)$ in
$t(e)$ in ![]() $V(\Gamma )$. We define the (rational) homology of
$V(\Gamma )$. We define the (rational) homology of ![]() $\Gamma$,
$\Gamma$, ![]() $H_1 (\Gamma )\subset \mathbf {Q} E(\Gamma )$, to be the kernel of the map
$H_1 (\Gamma )\subset \mathbf {Q} E(\Gamma )$, to be the kernel of the map
where ![]() $\mathbf {Q} E(\Gamma )$ and
$\mathbf {Q} E(\Gamma )$ and ![]() $\mathbf {Q} V(\Gamma )$ are the free
$\mathbf {Q} V(\Gamma )$ are the free ![]() $\mathbf {Q}$-vector spaces generated by
$\mathbf {Q}$-vector spaces generated by ![]() $E(\Gamma )$ and
$E(\Gamma )$ and ![]() $V(\Gamma )$, respectively.
$V(\Gamma )$, respectively.
Define ![]() $\Gamma _{\mathbf {Q} }$ to be the set of points on
$\Gamma _{\mathbf {Q} }$ to be the set of points on ![]() $\Gamma$ whose distance from a vertex is rational. Formally,
$\Gamma$ whose distance from a vertex is rational. Formally,
where the equivalence relation is that ![]() $(e_1 ,1 )\sim (e_2 ,0)$ whenever
$(e_1 ,1 )\sim (e_2 ,0)$ whenever ![]() $t(e_1 )=s(e_2 )$. Since
$t(e_1 )=s(e_2 )$. Since ![]() $\mathcal {X}_{\mathrm {reg}}$ is obtained from
$\mathcal {X}_{\mathrm {reg}}$ is obtained from ![]() $\mathcal {X}_{\scriptstyle \mathrm {st}}$ by taking each singular point (corresponding to an edge
$\mathcal {X}_{\scriptstyle \mathrm {st}}$ by taking each singular point (corresponding to an edge ![]() $e$) and blowing up
$e$) and blowing up ![]() $i(e)$ times, we have an inclusion
$i(e)$ times, we have an inclusion ![]() $V(\Gamma _{\mathrm {reg}})\subset \Gamma _{\mathbf {Q} }$ (in the terminology of [Reference Betts and DograBD19, 3.7.1], we may view
$V(\Gamma _{\mathrm {reg}})\subset \Gamma _{\mathbf {Q} }$ (in the terminology of [Reference Betts and DograBD19, 3.7.1], we may view ![]() $\Gamma _{\mathrm {reg}}$ as a rational subdivision of
$\Gamma _{\mathrm {reg}}$ as a rational subdivision of ![]() $\Gamma _{\scriptstyle \mathrm {st} }$). In this way we can think of the reduction map,
$\Gamma _{\scriptstyle \mathrm {st} }$). In this way we can think of the reduction map, ![]() $\mathrm {red}$, as a map from
$\mathrm {red}$, as a map from ![]() $X(K)$ to
$X(K)$ to ![]() $\Gamma _{\mathbf {Q} }$ (see [Reference Betts and DograBD19, Definition 1.3.1]). The rationally metrised graph we obtain is independent of the choice of extension over which
$\Gamma _{\mathbf {Q} }$ (see [Reference Betts and DograBD19, Definition 1.3.1]). The rationally metrised graph we obtain is independent of the choice of extension over which ![]() $X$ acquires stable reduction [Reference Chinburg and RumelyCR91, Proposition 2.6], and in fact there is an equivalent definition of
$X$ acquires stable reduction [Reference Chinburg and RumelyCR91, Proposition 2.6], and in fact there is an equivalent definition of ![]() $\Gamma _{\mathbf {Q} }$ as the limit of the dual graphs of special fibres of regular semi-stable models of
$\Gamma _{\mathbf {Q} }$ as the limit of the dual graphs of special fibres of regular semi-stable models of ![]() $X_L$ over all finite extensions
$X_L$ over all finite extensions ![]() $L$ of
$L$ of ![]() $K$ (see [Reference Chinburg and RumelyCR93, § 2]).
$K$ (see [Reference Chinburg and RumelyCR93, § 2]).
In [Reference Betts and DograBD19, Lemma 12.1.1], a map
is defined such that ![]() $h_\ell =c\cdot j_{\Gamma }\circ \mathrm {red}$, where
$h_\ell =c\cdot j_{\Gamma }\circ \mathrm {red}$, where ![]() $c$ is a constant. The map
$c$ is a constant. The map ![]() $j_{\Gamma }$ is defined in terms of the Laplacian operator associated to
$j_{\Gamma }$ is defined in terms of the Laplacian operator associated to ![]() $\Gamma _{\mathrm {st}}$, which we now define. We say a function
$\Gamma _{\mathrm {st}}$, which we now define. We say a function
is piecewise polynomial if on each edge it is the restriction of a polynomial function ![]() $\mathbf {Q} \to \mathbf {Q} _p$. As in [Reference Betts and DograBD19, Definition 7.2.2], we define the Laplacian
$\mathbf {Q} \to \mathbf {Q} _p$. As in [Reference Betts and DograBD19, Definition 7.2.2], we define the Laplacian ![]() $\nabla ^2 (g)$ of a piecewise polynomial function
$\nabla ^2 (g)$ of a piecewise polynomial function ![]() $g\colon \Gamma _{\mathbf {Q} }\to \mathbf {Q} _p$ to be the formal sum
$g\colon \Gamma _{\mathbf {Q} }\to \mathbf {Q} _p$ to be the formal sum
 \[ -\sum _{e\in E(\Gamma )} g '' (x_e )\cdot e +\sum _{v\in V(\Gamma )}\biggl(\sum _{s(e)=v}g'(0)-\sum _{t(e)=v}g'(1)\biggr)\cdot v. \]
\[ -\sum _{e\in E(\Gamma )} g '' (x_e )\cdot e +\sum _{v\in V(\Gamma )}\biggl(\sum _{s(e)=v}g'(0)-\sum _{t(e)=v}g'(1)\biggr)\cdot v. \]
Here we write the function ![]() $g$ restricted to the edge
$g$ restricted to the edge ![]() $e$ as a polynomial in
$e$ as a polynomial in ![]() $\mathbf {Q} _p [x_e ]$ for notational simplicity, where
$\mathbf {Q} _p [x_e ]$ for notational simplicity, where ![]() $x_e$ is the inclusion from the edge
$x_e$ is the inclusion from the edge ![]() $e$, thought of as a line segment
$e$, thought of as a line segment ![]() $[0,\ell (e)]\cap \mathbf {Q}$, into
$[0,\ell (e)]\cap \mathbf {Q}$, into ![]() $\mathbf {Q}$. Hence, we have
$\mathbf {Q}$. Hence, we have
The Laplacian is linear on piecewise polynomial functions, and its kernel consists of constant functions. Thus ![]() $g$ is uniquely determined by
$g$ is uniquely determined by ![]() $\nabla ^2(g)$ and its value at one point.
$\nabla ^2(g)$ and its value at one point.
In [Reference Betts and DograBD19], an explicit construction is given of a piecewise polynomial function that corresponds, via ![]() $\mathrm {red}$, to the local height function we wish to compute. Recall that
$\mathrm {red}$, to the local height function we wish to compute. Recall that ![]() $F$ is an element of
$F$ is an element of ![]() $\mathrm {End} (J)\otimes \mathbf {Q} _p$ whose image in
$\mathrm {End} (J)\otimes \mathbf {Q} _p$ whose image in ![]() $\mathrm {NS} (J)$ lies in the kernel of
$\mathrm {NS} (J)$ lies in the kernel of ![]() $\mathrm {NS} (J)\to \mathrm {NS} (X)$, and
$\mathrm {NS} (J)\to \mathrm {NS} (X)$, and ![]() $b\in X(\mathbf {Q} )$ is a rational point.
$b\in X(\mathbf {Q} )$ is a rational point.
Theorem 3.2 [Reference Betts and DograBD19, Theorem 1.1.2, Lemma 12.1.1 and Corollary 12.1.3]
Let ![]() $\Gamma$ be the dual graph of
$\Gamma$ be the dual graph of ![]() $X$ corresponding to a regular semi-stable model of
$X$ corresponding to a regular semi-stable model of ![]() $X$ over
$X$ over ![]() $\mathcal {O}_K$, where
$\mathcal {O}_K$, where ![]() $K/\mathbf {Q} _{\ell }$ is a finite extension. Let
$K/\mathbf {Q} _{\ell }$ is a finite extension. Let ![]() $\mathrm {red} \colon X(\mathbf {Q} _{\ell } )\to V(\Gamma )$ be the reduction map. For an irreducible component
$\mathrm {red} \colon X(\mathbf {Q} _{\ell } )\to V(\Gamma )$ be the reduction map. For an irreducible component ![]() $X_w$ of the special fibre of the regular semi-stable model, let
$X_w$ of the special fibre of the regular semi-stable model, let ![]() $V_p (X_w )$ denote the
$V_p (X_w )$ denote the ![]() $\mathbf {Q} _p$-Tate module of its Jacobian. The morphism
$\mathbf {Q} _p$-Tate module of its Jacobian. The morphism ![]() $j_{\Gamma }$ is the unique piecewise polynomial function
$j_{\Gamma }$ is the unique piecewise polynomial function
satisfying ![]() $j_{\Gamma }(\mathrm {red} (b))=0$ and
$j_{\Gamma }(\mathrm {red} (b))=0$ and ![]() $\nabla ^2 (j_{\Gamma })=\mu _F$, where
$\nabla ^2 (j_{\Gamma })=\mu _F$, where
 \[ \mu _F := \sum _{e\in E(\Gamma )}\frac{1}{\ell (e)} e^* F(\pi (e)) \cdot e+\frac{1}{2}\sum _{w\in V(\Gamma )}\mathrm{Tr} (F|V_p (X_w ))\cdot w . \]
\[ \mu _F := \sum _{e\in E(\Gamma )}\frac{1}{\ell (e)} e^* F(\pi (e)) \cdot e+\frac{1}{2}\sum _{w\in V(\Gamma )}\mathrm{Tr} (F|V_p (X_w ))\cdot w . \]
Here, the morphism ![]() $\pi$ is by definition the orthogonal projection
$\pi$ is by definition the orthogonal projection
with respect to the pairing ![]() $e\cdot e'=\delta _{ee'}$ on
$e\cdot e'=\delta _{ee'}$ on ![]() $\mathbf {Q} E(\Gamma )$, and
$\mathbf {Q} E(\Gamma )$, and ![]() $e^*$ is the functional
$e^*$ is the functional ![]() $\mathbf {Q} E(\Gamma )\to \mathbf {Q}$ projecting onto the
$\mathbf {Q} E(\Gamma )\to \mathbf {Q}$ projecting onto the ![]() $e$ component. Recall (e.g. [Reference GrothendieckSGA7, 12.3.7]) that
$e$ component. Recall (e.g. [Reference GrothendieckSGA7, 12.3.7]) that ![]() $V_p (X)$ admits a
$V_p (X)$ admits a ![]() $G_K$-stable filtration
$G_K$-stable filtration
and we have isomorphisms of ![]() $G_K$-representations
$G_K$-representations
 \begin{align*} \mathrm{gr}^W _0 V_p (X) & \simeq H_1 (\Gamma )\otimes \mathbf{Q} _p , \\ \mathrm{gr}^W _1 V_p (X) & \simeq \bigoplus _{w\in V(\Gamma )}V_p (X_w ), \\ \mathrm{gr}^W _2 V_p (X) & \simeq H_1 (\Gamma )^* \otimes \mathbf{Q} _p (1). \end{align*}
\begin{align*} \mathrm{gr}^W _0 V_p (X) & \simeq H_1 (\Gamma )\otimes \mathbf{Q} _p , \\ \mathrm{gr}^W _1 V_p (X) & \simeq \bigoplus _{w\in V(\Gamma )}V_p (X_w ), \\ \mathrm{gr}^W _2 V_p (X) & \simeq H_1 (\Gamma )^* \otimes \mathbf{Q} _p (1). \end{align*}
The action of ![]() $F$ on
$F$ on ![]() $V_p (X)$ preserves this filtration since it is a morphism of Galois representations, and hence induces an action of
$V_p (X)$ preserves this filtration since it is a morphism of Galois representations, and hence induces an action of ![]() $F$ on the weight
$F$ on the weight ![]() $-1$ part of
$-1$ part of ![]() $V_p (X)$, which is isomorphic to
$V_p (X)$, which is isomorphic to ![]() $\bigoplus _w V_p (X_w )$. Although the action of
$\bigoplus _w V_p (X_w )$. Although the action of ![]() $F$ need not respect the direct sum decomposition, the decomposition
$F$ need not respect the direct sum decomposition, the decomposition
implies that we can define ![]() $\mathrm {Tr} (F|V_p (X_w ))$ as the trace of the
$\mathrm {Tr} (F|V_p (X_w ))$ as the trace of the ![]() $\mathrm {End} (V_p (X_w ))$-component of
$\mathrm {End} (V_p (X_w ))$-component of ![]() $F$.
$F$.
To determine the possible local heights, it suffices to compute the action of ![]() $F$ on
$F$ on ![]() $\mathrm {H}_1 (\Gamma )$ and on
$\mathrm {H}_1 (\Gamma )$ and on ![]() $V_p (X_v )$. In this paper, we do not discuss methods for the algorithmic computation of the action of
$V_p (X_v )$. In this paper, we do not discuss methods for the algorithmic computation of the action of ![]() $F$ on
$F$ on ![]() $\mathrm {H}_1 (\Gamma )$, but algorithms for these computations in the case when the curve
$\mathrm {H}_1 (\Gamma )$, but algorithms for these computations in the case when the curve ![]() $X$ is hyperelliptic will be discussed in forthcoming joint work of the first, second and fifth authors with David Corwin, Sachi Hashimoto, Benjamin Matschke, Oana Padurariu, Ciaran Schembri and Tian Wang.
$X$ is hyperelliptic will be discussed in forthcoming joint work of the first, second and fifth authors with David Corwin, Sachi Hashimoto, Benjamin Matschke, Oana Padurariu, Ciaran Schembri and Tian Wang.
As we explain in § 5.4, one can sometimes use partial information deduced from Theorem 3.2 to determine the possible local heights without computing the action of ![]() $F$ on
$F$ on ![]() $\mathrm {H}_1 (\Gamma )$ (e.g. if one has enough rational points on
$\mathrm {H}_1 (\Gamma )$ (e.g. if one has enough rational points on ![]() $X$ that are suitably independent in
$X$ that are suitably independent in ![]() $J(\mathbf {Q})$ and
$J(\mathbf {Q})$ and ![]() $\Gamma _{\mathbf {Q} }$).
$\Gamma _{\mathbf {Q} }$).
Example 3.3 One example for which this strategy succeeds is the curve ![]() $C_{188}/\mathbf {Q}$ defined by the equation
$C_{188}/\mathbf {Q}$ defined by the equation ![]() $y^2 = x^5 - x^4 + x^3 + x^2 - 2x + 1$, as described in Example 5.18. This curve does not have semi-stable reduction over
$y^2 = x^5 - x^4 + x^3 + x^2 - 2x + 1$, as described in Example 5.18. This curve does not have semi-stable reduction over ![]() $\mathbf {Q}_2$. Over
$\mathbf {Q}_2$. Over ![]() $K=\mathbf {Q}_2[\sqrt [3]{2}]$, we find a regular semi-stable model
$K=\mathbf {Q}_2[\sqrt [3]{2}]$, we find a regular semi-stable model ![]() $\mathcal {X}_{\mathrm {reg}}$ whose special fibre consists of two genus 1 curves that do not intersect and a genus zero curve intersecting both of them transversely, each at a unique point. We did not manage to obtain this information using any of the existing software packages for computing regular or semi-stable models, such as Magma's RegularModel or the SageMath package MCLF.Footnote 2) Therefore we computed this model by hand, using a standard (but tedious) sequence of blow-ups.
$\mathcal {X}_{\mathrm {reg}}$ whose special fibre consists of two genus 1 curves that do not intersect and a genus zero curve intersecting both of them transversely, each at a unique point. We did not manage to obtain this information using any of the existing software packages for computing regular or semi-stable models, such as Magma's RegularModel or the SageMath package MCLF.Footnote 2) Therefore we computed this model by hand, using a standard (but tedious) sequence of blow-ups.
Hence, the metric graph ![]() $\Gamma _{\mathrm {reg}}$ is a line segment and the image of
$\Gamma _{\mathrm {reg}}$ is a line segment and the image of ![]() $C_{188}(\mathbf {Q} _2 )$ in
$C_{188}(\mathbf {Q} _2 )$ in ![]() $\Gamma _{\mathbf {Q} }$ consists of three points on this line. The two edges of
$\Gamma _{\mathbf {Q} }$ consists of three points on this line. The two edges of ![]() $\Gamma _{\mathrm {reg}}$ both have length
$\Gamma _{\mathrm {reg}}$ both have length ![]() $1/3$. In this case, since
$1/3$. In this case, since ![]() $\Gamma$ has trivial homology, the function
$\Gamma$ has trivial homology, the function ![]() $j_{\Gamma }$ is affine linear, so it is uniquely determined by evaluating it at two distinct points. We use this to compute the rational points on
$j_{\Gamma }$ is affine linear, so it is uniquely determined by evaluating it at two distinct points. We use this to compute the rational points on ![]() $C_{188}$ in Example 5.18.
$C_{188}$ in Example 5.18.
3.2 Local heights at  $p$
$p$
We discuss the local height component
which appeared in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 5]. Recall that ![]() $h_p$ is a locally analytic function, described in terms of the filtered
$h_p$ is a locally analytic function, described in terms of the filtered ![]() $\phi$-module
$\phi$-module ![]() $M(x)$ discussed in § 2.2. Concretely, we may find two unipotent isomorphisms
$M(x)$ discussed in § 2.2. Concretely, we may find two unipotent isomorphisms
where ![]() $\lambda ^{\phi }$ respects the Frobenius action and
$\lambda ^{\phi }$ respects the Frobenius action and ![]() $\lambda ^{\mathrm {Fil}}$ respects the Hodge filtration, which with respect to a suitable basis for
$\lambda ^{\mathrm {Fil}}$ respects the Hodge filtration, which with respect to a suitable basis for ![]() $M(x)$ may be represented in (
$M(x)$ may be represented in (![]() $1+2g+1$)-block matrix form as
$1+2g+1$)-block matrix form as
 \begin{equation} \lambda^\phi(x) =\left(
\begin{array}{@{}ccc@{}} 1 & 0 & 0 \\ \boldsymbol{\alpha }_{\phi}
& 1 & 0 \\ \gamma_{\phi} & \boldsymbol{\beta
}^{\intercal}_{\phi} & 1 \\ \end{array} \right), \quad
\lambda^{\mathrm{Fil}}(x) = \left( \begin{array}{@{}ccc@{}} 1 & 0
& 0 \\ \boldsymbol{\alpha }_{\mathrm{Fil}} & 1 & 0 \\
\gamma_{\mathrm{Fil}} & \boldsymbol{\beta
}^{\intercal}_{\mathrm{Fil}} & 1 \\ \end{array} \right)
\end{equation}
\begin{equation} \lambda^\phi(x) =\left(
\begin{array}{@{}ccc@{}} 1 & 0 & 0 \\ \boldsymbol{\alpha }_{\phi}
& 1 & 0 \\ \gamma_{\phi} & \boldsymbol{\beta
}^{\intercal}_{\phi} & 1 \\ \end{array} \right), \quad
\lambda^{\mathrm{Fil}}(x) = \left( \begin{array}{@{}ccc@{}} 1 & 0
& 0 \\ \boldsymbol{\alpha }_{\mathrm{Fil}} & 1 & 0 \\
\gamma_{\mathrm{Fil}} & \boldsymbol{\beta
}^{\intercal}_{\mathrm{Fil}} & 1 \\ \end{array} \right)
\end{equation}
(see [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 5.3] and [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 4.5], respectively). The isomorphism ![]() $\lambda ^\phi$ is uniquely determined, whereas
$\lambda ^\phi$ is uniquely determined, whereas ![]() $\lambda ^{\mathrm {Fil}}$ is only well defined up to the stabiliser of the Hodge filtration
$\lambda ^{\mathrm {Fil}}$ is only well defined up to the stabiliser of the Hodge filtration ![]() $\mathrm {Fil}^0$. A suitable choice gives
$\mathrm {Fil}^0$. A suitable choice gives ![]() $\boldsymbol {\alpha }_{\mathrm {Fil}} =0$.
$\boldsymbol {\alpha }_{\mathrm {Fil}} =0$.
The splitting ![]() $s$ of the Hodge filtration (see Remark 3.1) defines idempotents
$s$ of the Hodge filtration (see Remark 3.1) defines idempotents ![]() $s_1,s_2$ on
$s_1,s_2$ on ![]() $V_{\scriptstyle \mathrm {dR}}$ with images
$V_{\scriptstyle \mathrm {dR}}$ with images ![]() $s(V_{\scriptstyle \mathrm {dR}}/\mathrm {Fil}^0 V_{\scriptstyle \mathrm {dR}})$ and
$s(V_{\scriptstyle \mathrm {dR}}/\mathrm {Fil}^0 V_{\scriptstyle \mathrm {dR}})$ and ![]() $\mathrm {Fil}^0 V_{\scriptstyle \mathrm {dR}}$ respectively, with respect to which the local height at
$\mathrm {Fil}^0 V_{\scriptstyle \mathrm {dR}}$ respectively, with respect to which the local height at ![]() $p$ is
$p$ is
by [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, Equation (17)].
In [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19] we outline a method to compute these quantities explicitly as functions of the local point ![]() $x$ in
$x$ in ![]() $X(\mathbf {Q}_p)$, which exploits the existence of the connection
$X(\mathbf {Q}_p)$, which exploits the existence of the connection ![]() $(\mathscr {M},\nabla )$ discussed in § 2.2. The Hodge filtration and Frobenius structures of this bundle are characterised by suitable universal properties, discussed at length in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, §§ 4 and 5]. We have made the algorithms for the computation of
$(\mathscr {M},\nabla )$ discussed in § 2.2. The Hodge filtration and Frobenius structures of this bundle are characterised by suitable universal properties, discussed at length in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, §§ 4 and 5]. We have made the algorithms for the computation of ![]() $h_p$ more general and streamlined and have added a precision analysis in § 4 but have not made further contributions to this part of the method beyond what is already contained in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19].
$h_p$ more general and streamlined and have added a precision analysis in § 4 but have not made further contributions to this part of the method beyond what is already contained in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19].
3.3 The global height pairing
One key step in the construction of a quadratic Chabauty function is to write the global height pairing ![]() $h$ in terms of a basis of the space of bilinear pairings on
$h$ in terms of a basis of the space of bilinear pairings on ![]() $\mathrm {H}^0(X_{\mathbf {Q}_p}, \Omega ^1)^{\vee }$. In [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19], we had as a working hypothesis that our curve
$\mathrm {H}^0(X_{\mathbf {Q}_p}, \Omega ^1)^{\vee }$. In [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19], we had as a working hypothesis that our curve ![]() $X$ had sufficiently many rational points, in the following sense. For
$X$ had sufficiently many rational points, in the following sense. For ![]() $x\in X(\mathbf {Q}_p)$, the Galois representation
$x\in X(\mathbf {Q}_p)$, the Galois representation ![]() $\mathrm {A}(x)$ can be projected onto
$\mathrm {A}(x)$ can be projected onto ![]() $\mathrm {H}^1_f(G_T, V)$ (respectively,
$\mathrm {H}^1_f(G_T, V)$ (respectively, ![]() $\mathrm {H}^1_f(G_T, V^*(1))$), where
$\mathrm {H}^1_f(G_T, V^*(1))$), where ![]() $G_T$ is the maximal quotient of
$G_T$ is the maximal quotient of ![]() $G_{\mathbf {Q}}$ unramified outside
$G_{\mathbf {Q}}$ unramified outside ![]() $T =\{p\}\cup \{$bad primes for
$T =\{p\}\cup \{$bad primes for ![]() $X\}$. With respect to the dual basis
$X\}$. With respect to the dual basis ![]() $\omega ^\ast _0,\ldots,\omega ^\ast _{g-1},$ the image is the vector
$\omega ^\ast _0,\ldots,\omega ^\ast _{g-1},$ the image is the vector ![]() $\alpha$ (respectively,
$\alpha$ (respectively, ![]() $\beta )$ in (2.2). Both of these cohomology groups are isomorphic, under our running assumptions, to
$\beta )$ in (2.2). Both of these cohomology groups are isomorphic, under our running assumptions, to ![]() $\mathrm {H}^0(X_{\mathbf {Q}_p}, \Omega ^1)^{\vee }$, so we obtain
$\mathrm {H}^0(X_{\mathbf {Q}_p}, \Omega ^1)^{\vee }$, so we obtain
Suppose that we can find a basis of ![]() $\mathrm {H}^0(X_{\mathbf {Q}_p}, \Omega ^1)^{\vee } \otimes \mathrm {H}^0(X_{\mathbf {Q}_p}, \Omega ^1)^{\vee }$ consisting of elements of the form
$\mathrm {H}^0(X_{\mathbf {Q}_p}, \Omega ^1)^{\vee } \otimes \mathrm {H}^0(X_{\mathbf {Q}_p}, \Omega ^1)^{\vee }$ consisting of elements of the form ![]() $\pi (\mathrm {A}_Z(b,x))$, where the
$\pi (\mathrm {A}_Z(b,x))$, where the ![]() $Z$ are cycles on
$Z$ are cycles on ![]() $J$ pulling back to degree 0 cycles on
$J$ pulling back to degree 0 cycles on ![]() $X$, and the
$X$, and the ![]() $x$ are rational points on
$x$ are rational points on ![]() $X$. Then we can compute the coefficients of
$X$. Then we can compute the coefficients of ![]() $h$ in terms of the dual basis by evaluating
$h$ in terms of the dual basis by evaluating ![]() $h_p(\mathrm {A}_Z(b,x))$ (and, if necessary,
$h_p(\mathrm {A}_Z(b,x))$ (and, if necessary, ![]() $h_{\ell }(\mathrm {A}_Z(b,x))$ for primes
$h_{\ell }(\mathrm {A}_Z(b,x))$ for primes ![]() $\ell \ne p$). With this choice of basis, the extension of
$\ell \ne p$). With this choice of basis, the extension of ![]() $h$ to a locally analytic function
$h$ to a locally analytic function ![]() $h\colon X(\mathbf {Q}_p)\to \mathbf {Q}_p$ is immediate.
$h\colon X(\mathbf {Q}_p)\to \mathbf {Q}_p$ is immediate.
The number of rational points required can be reduced by working with symmetric heights that are ![]() $\mathrm {End}(J)$-equivariant. By the latter we mean that
$\mathrm {End}(J)$-equivariant. By the latter we mean that ![]() $h(f(x), y) = h(x, f(y))$ for all
$h(f(x), y) = h(x, f(y))$ for all ![]() $f\in \mathrm {End}(J)$, using (2.1). This holds if the splitting
$f\in \mathrm {End}(J)$, using (2.1). This holds if the splitting ![]() $s$ of the Hodge filtration on
$s$ of the Hodge filtration on ![]() $V_{\scriptstyle \mathrm {dR}}$ commutes with
$V_{\scriptstyle \mathrm {dR}}$ commutes with ![]() $\mathrm {End}(J)$ and has the property that
$\mathrm {End}(J)$ and has the property that ![]() $\ker (s)$ is isotropic with respect to the cup product (see [Reference NekovářNek93, § 4.11] and [Reference Balakrishnan and DograBD21, § 4.1]). For instance, if
$\ker (s)$ is isotropic with respect to the cup product (see [Reference NekovářNek93, § 4.11] and [Reference Balakrishnan and DograBD21, § 4.1]). For instance, if ![]() $p$ is a prime of ordinary reduction for the Jacobian, then the height associated to the unit root splitting (see Remark 3.15) is symmetric and
$p$ is a prime of ordinary reduction for the Jacobian, then the height associated to the unit root splitting (see Remark 3.15) is symmetric and ![]() $\mathrm {End}(J)$-equivariant. Henceforth we shall assume that
$\mathrm {End}(J)$-equivariant. Henceforth we shall assume that ![]() $s$ satisfies these assumptions, and we say that
$s$ satisfies these assumptions, and we say that ![]() $X$ has sufficiently many rational points if the approach outlined above succeeds.
$X$ has sufficiently many rational points if the approach outlined above succeeds.
3.3.1 Heights on the Jacobian
If our curve does not have sufficiently many rational points in the above sense, then, in light of (2.1), it is natural to solve for the height pairing using rational points on the Jacobian. In this case, we do not have an algorithm at our disposal to compute ![]() $h$ using Nekovář's construction, but we can use the equivalence between this construction and that of Coleman and Gross [Reference Coleman and GrossCG89], proved by Besser [Reference BesserBes04]. In the case when the curve is hyperelliptic and given by an odd-degree model over
$h$ using Nekovář's construction, but we can use the equivalence between this construction and that of Coleman and Gross [Reference Coleman and GrossCG89], proved by Besser [Reference BesserBes04]. In the case when the curve is hyperelliptic and given by an odd-degree model over ![]() $\mathbf {Q}_p$ (but see Remark 3.7), we can further use the algorithm of Balakrishnan and Besser [Reference Balakrishnan and BesserBB12, Reference Balakrishnan and BesserBB21]. In the discussion that follows, we will assume that we are in this situation. We will also assume that we know
$\mathbf {Q}_p$ (but see Remark 3.7), we can further use the algorithm of Balakrishnan and Besser [Reference Balakrishnan and BesserBB12, Reference Balakrishnan and BesserBB21]. In the discussion that follows, we will assume that we are in this situation. We will also assume that we know ![]() $g$ independent points on the Jacobian.
$g$ independent points on the Jacobian.
Recall from Remark 3.1 that we have fixed a continuous idèle class character ![]() $\chi \colon \mathbf {A}_{\mathbf {Q}}^\times / \mathbf {Q}^{\times } \longrightarrow \mathbf {Q}_p$ ramified at
$\chi \colon \mathbf {A}_{\mathbf {Q}}^\times / \mathbf {Q}^{\times } \longrightarrow \mathbf {Q}_p$ ramified at ![]() $p$ and a splitting
$p$ and a splitting ![]() $s\colon V_{\scriptstyle \mathrm {dR}}/\mathrm {Fil}^0 V_{\scriptstyle \mathrm {dR}} \longrightarrow V_{\scriptstyle \mathrm {dR}}$ of the Hodge filtration on
$s\colon V_{\scriptstyle \mathrm {dR}}/\mathrm {Fil}^0 V_{\scriptstyle \mathrm {dR}} \longrightarrow V_{\scriptstyle \mathrm {dR}}$ of the Hodge filtration on ![]() $V_{\scriptstyle \mathrm {dR}} = \mathrm {H}^1_{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q}_p})^{\vee }\,.$ The latter corresponds to a subspace
$V_{\scriptstyle \mathrm {dR}} = \mathrm {H}^1_{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q}_p})^{\vee }\,.$ The latter corresponds to a subspace ![]() $W\subset H^1_{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q}_p})$, complementary to the image of
$W\subset H^1_{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q}_p})$, complementary to the image of ![]() $\mathrm {H}^0(X_{\mathbf {Q}_p},\Omega ^1)$. With respect to these choices, Coleman and Gross define the local
$\mathrm {H}^0(X_{\mathbf {Q}_p},\Omega ^1)$. With respect to these choices, Coleman and Gross define the local ![]() $p$-adic height pairing
$p$-adic height pairing ![]() $h_v(D_1,D_2) \in \mathbf {Q}_p$ at a finite prime
$h_v(D_1,D_2) \in \mathbf {Q}_p$ at a finite prime ![]() $v$ for divisors
$v$ for divisors ![]() $D_1,D_2\in \mathrm {Div}^0(X_{\mathbf {Q}_v})$ with disjoint support. The local pairing is bi-additive, and we have
$D_1,D_2\in \mathrm {Div}^0(X_{\mathbf {Q}_v})$ with disjoint support. The local pairing is bi-additive, and we have ![]() $h_v(D_1,D_2) = \chi _v(f(D_2))$ if
$h_v(D_1,D_2) = \chi _v(f(D_2))$ if ![]() $D_2 = \operatorname {div}(f)$ is principal. For
$D_2 = \operatorname {div}(f)$ is principal. For ![]() $v\ne p$, the pairing
$v\ne p$, the pairing ![]() $h_v$ is also symmetric;
$h_v$ is also symmetric; ![]() $h_p$ is symmetric if and only if
$h_p$ is symmetric if and only if ![]() $W$ is isotropic with respect to the cup product pairing, which we will assume from now on. Moreover, for
$W$ is isotropic with respect to the cup product pairing, which we will assume from now on. Moreover, for ![]() $D_1,D_2\in \mathrm {Div}^0(X)$ with disjoint support, only finitely many
$D_1,D_2\in \mathrm {Div}^0(X)$ with disjoint support, only finitely many ![]() $h_v(D_1,D_2):= h_v(D_1\otimes \mathbf {Q}_v ,D_2\otimes \mathbf {Q}_v)$ are non-zero. Therefore
$h_v(D_1,D_2):= h_v(D_1\otimes \mathbf {Q}_v ,D_2\otimes \mathbf {Q}_v)$ are non-zero. Therefore ![]() $h:= \sum _v h_v$ defines a symmetric bilinear pairing
$h:= \sum _v h_v$ defines a symmetric bilinear pairing ![]() $h\colon J(\mathbf {Q})\times J(\mathbf {Q})\to \mathbf {Q}_p$ (see [Reference Coleman and GrossCG89, § 6]).
$h\colon J(\mathbf {Q})\times J(\mathbf {Q})\to \mathbf {Q}_p$ (see [Reference Coleman and GrossCG89, § 6]).
If we have algorithms to compute the local height pairings, we can solve for the global height pairing in terms of the basis of symmetric bilinear pairings on ![]() $J(\mathbf {Q})\otimes \mathbf {Q}_p$ defined by
$J(\mathbf {Q})\otimes \mathbf {Q}_p$ defined by
Since we can express ![]() $\pi _1(\mathrm {A}(x))$ and
$\pi _1(\mathrm {A}(x))$ and ![]() $\pi _2(\mathrm {A}(x))$ in terms of the dual basis
$\pi _2(\mathrm {A}(x))$ in terms of the dual basis ![]() $\{\omega _i^*\}$, we can compute
$\{\omega _i^*\}$, we can compute ![]() $g_{ij}(\pi (\mathrm {A}(x)))$ for
$g_{ij}(\pi (\mathrm {A}(x)))$ for ![]() $x\in X(\mathbf {Q}_p)$ (with the obvious abuse of notation) and extend
$x\in X(\mathbf {Q}_p)$ (with the obvious abuse of notation) and extend ![]() $h$ to a locally analytic function
$h$ to a locally analytic function ![]() $h\colon X(\mathbf {Q}_p)\to \mathbf {Q}_p$.
$h\colon X(\mathbf {Q}_p)\to \mathbf {Q}_p$.
It remains to discuss the computation of the local heights. For ![]() $D_1,D_2\in \mathrm {Div}^0(X_{\mathbf {Q}_p})$ with disjoint support, the local height is the Coleman integral certain differential with residue divisor
$D_1,D_2\in \mathrm {Div}^0(X_{\mathbf {Q}_p})$ with disjoint support, the local height is the Coleman integral certain differential with residue divisor ![]() $\mathrm {Res}(\omega _{D_1})=D_1$, and
$\mathrm {Res}(\omega _{D_1})=D_1$, and ![]() $c_p$ is a constant so that
$c_p$ is a constant so that ![]() $c_p^{-1}\chi _p$ extends to a branch
$c_p^{-1}\chi _p$ extends to a branch ![]() $\mathbf {Q}_p^\times \to \mathbf {Q}_p$ of the
$\mathbf {Q}_p^\times \to \mathbf {Q}_p$ of the ![]() $p$-adic logarithm; the Coleman integral is taken with respect to this branch. The differential
$p$-adic logarithm; the Coleman integral is taken with respect to this branch. The differential ![]() $\omega _{D_1}$ is normalised with respect to the splitting
$\omega _{D_1}$ is normalised with respect to the splitting ![]() $s$ using a homomorphism
$s$ using a homomorphism
from ![]() $T(\mathbf {Q}_p)$, the group of differentials of the third kind with integer residues on
$T(\mathbf {Q}_p)$, the group of differentials of the third kind with integer residues on ![]() $X$, quotiented by
$X$, quotiented by ![]() $T_l(\mathbf {Q}_p)$, the group of logarithmic differentials
$T_l(\mathbf {Q}_p)$, the group of logarithmic differentials ![]() $\frac {df}{f}$ with
$\frac {df}{f}$ with ![]() $f\in \mathbf {Q}_p(X)^*$, as in the algorithm below. We restrict to degree zero divisors of the form
$f\in \mathbf {Q}_p(X)^*$, as in the algorithm below. We restrict to degree zero divisors of the form ![]() $P-Q$ where
$P-Q$ where ![]() $P,Q$ are non-Weierstrass points in
$P,Q$ are non-Weierstrass points in ![]() $X(\mathbf {Q}_p)$ that do not reduce to a Weierstrass point in
$X(\mathbf {Q}_p)$ that do not reduce to a Weierstrass point in ![]() $X(\mathbf {F}_p)$ since we will need to compute Coleman integrals between
$X(\mathbf {F}_p)$ since we will need to compute Coleman integrals between ![]() $P,Q$, and our implementation assumes that these points are in non-Weierstrass disks and defined over
$P,Q$, and our implementation assumes that these points are in non-Weierstrass disks and defined over ![]() $\mathbf {Q}_p$.
$\mathbf {Q}_p$.
Algorithm 3.4 The local height  $h_p(D_1,D_2)$ at
$h_p(D_1,D_2)$ at  $p$ of the global
$p$ of the global  $p$-adic height [Reference Balakrishnan and BesserBB12]
$p$-adic height [Reference Balakrishnan and BesserBB12]
Input:
− Hyperelliptic curve
 $X/\mathbf {Q}_p$, given by an affine model
$X/\mathbf {Q}_p$, given by an affine model  $y^2=f(x)$, where
$y^2=f(x)$, where  $f\in \mathbf {Z}_p[x]$ is square-free of degree
$f\in \mathbf {Z}_p[x]$ is square-free of degree  $2g+1>2$.
$2g+1>2$.− Prime
 $p>2g-1$ of good reduction.
$p>2g-1$ of good reduction.− Choice of isotropic subspace
 $W$ of
$W$ of  $H^1_{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q}_p})$, complementary to the subspace of regular 1-forms
$H^1_{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q}_p})$, complementary to the subspace of regular 1-forms  $\mathrm {H}^0(X_{\mathbf {Q}_p},\Omega ^1)$.
$\mathrm {H}^0(X_{\mathbf {Q}_p},\Omega ^1)$.− Divisors
 $D_1 = P-Q, D_2 = R-S$, where
$D_1 = P-Q, D_2 = R-S$, where  $P,Q,R,S$ are non-Weierstrass points in
$P,Q,R,S$ are non-Weierstrass points in  $X(\mathbf {Q}_p)$ that do not reduce to a Weierstrass point in
$X(\mathbf {Q}_p)$ that do not reduce to a Weierstrass point in  $X(\mathbf {F}_p)$, and
$X(\mathbf {F}_p)$, and  $R,S$ do not lie in the residue disks of
$R,S$ do not lie in the residue disks of  $P,Q$.
$P,Q$.
Output: The local height ![]() $h_p(D_1,D_2)$ at
$h_p(D_1,D_2)$ at ![]() $p$ of the Coleman–Gross global
$p$ of the Coleman–Gross global ![]() $p$-adic height
$p$-adic height
(i) Choose
 $\omega$ a differential in
$\omega$ a differential in  $T(\mathbf {Q}_p)$ with
$T(\mathbf {Q}_p)$ with  $\text {Res}(\omega )=D_1$.
$\text {Res}(\omega )=D_1$.(ii) Solve for the coefficients
 $b_i$ of
$b_i$ of  $\Psi (\omega )=\sum _{i=0}^{2g-1}b_i\omega _i\in \mathrm {H}_{\scriptstyle \mathrm {dR}}^1(X)$ by computing residues, as in [Reference Balakrishnan and BesserBB12, § 5.2]. Then
$\Psi (\omega )=\sum _{i=0}^{2g-1}b_i\omega _i\in \mathrm {H}_{\scriptstyle \mathrm {dR}}^1(X)$ by computing residues, as in [Reference Balakrishnan and BesserBB12, § 5.2]. Then  $\Psi (\omega )-\sum _{i=0}^{g-1}b_i\omega _i\in W$. Let
$\Psi (\omega )-\sum _{i=0}^{g-1}b_i\omega _i\in W$. Let
 \[ \omega_{D_1}:= \omega-\sum_{i=0}^{g-1}b_i\omega_i. \]
\[ \omega_{D_1}:= \omega-\sum_{i=0}^{g-1}b_i\omega_i. \]
(iii) Set
 $\alpha := \phi ^*(\omega )-p(\omega )$. Use Frobenius equivariance of the map
$\alpha := \phi ^*(\omega )-p(\omega )$. Use Frobenius equivariance of the map  $\Psi$ (and the matrix of Frobenius computed with respect to the basis
$\Psi$ (and the matrix of Frobenius computed with respect to the basis  $\{\omega _i\}$ of
$\{\omega _i\}$ of  $\mathrm {H}_{\scriptstyle \mathrm {dR}}^1(X)$) to compute
$\mathrm {H}_{\scriptstyle \mathrm {dR}}^1(X)$) to compute
 \[ \Psi(\alpha)=\phi^*\Psi(\omega)-p\Psi(\omega). \]
\[ \Psi(\alpha)=\phi^*\Psi(\omega)-p\Psi(\omega). \]
(iv) Let
 $\beta$ be a
$\beta$ be a  $1$-form with
$1$-form with  $\mathrm {Res}(\beta )=(R)-(S)$. Compute
$\mathrm {Res}(\beta )=(R)-(S)$. Compute  $\Psi (\beta )$.
$\Psi (\beta )$.(v) Compute
where \[ h_p(D_1,D_2):= \int_{D_2}\omega_{D_1} = \int_{S}^R \biggl(\omega - \sum_{i=0}^{g-1}b_i\omega_i\bigr), \]
(see [Reference Balakrishnan and BesserBB12, Remark 4.9]).
\[ h_p(D_1,D_2):= \int_{D_2}\omega_{D_1} = \int_{S}^R \biggl(\omega - \sum_{i=0}^{g-1}b_i\omega_i\bigr), \]
(see [Reference Balakrishnan and BesserBB12, Remark 4.9]). \[ \int_{S}^{R}\omega=\frac{1}{1-p}\biggl(\Psi(\alpha)\cup\Psi(\beta)+\sum_{A \in X(\mathbf{C}_p)}{\rm Res}_{A}\biggl(\alpha\int\beta\biggr)-
\int_{\phi(S)}^{S}\omega-\int_{R}^{\phi(R)}\omega\biggr) \]
\[ \int_{S}^{R}\omega=\frac{1}{1-p}\biggl(\Psi(\alpha)\cup\Psi(\beta)+\sum_{A \in X(\mathbf{C}_p)}{\rm Res}_{A}\biggl(\alpha\int\beta\biggr)-
\int_{\phi(S)}^{S}\omega-\int_{R}^{\phi(R)}\omega\biggr) \]
Remark 3.5 Note that in the last step above, ![]() $\int _{\phi (S)}^S\omega$ and
$\int _{\phi (S)}^S\omega$ and ![]() $\int _{R}^{\phi (R)}\omega$ are tiny integrals, that is, Coleman integrals between points in the same residue disk. Such integrals may be computed merely using a uniformising parameter at any point in the residue disk. The computation
$\int _{R}^{\phi (R)}\omega$ are tiny integrals, that is, Coleman integrals between points in the same residue disk. Such integrals may be computed merely using a uniformising parameter at any point in the residue disk. The computation ![]() $\sum _{A \in X(\mathbf {C}_p)}\mathrm {Res}_{A}\big (\alpha \int \beta \big )$ will, in most cases, require working over various extension of
$\sum _{A \in X(\mathbf {C}_p)}\mathrm {Res}_{A}\big (\alpha \int \beta \big )$ will, in most cases, require working over various extension of ![]() $\mathbf {Q}_p$ to pick up all contributions at all poles (see [Reference Balakrishnan and BesserBB12, Remark 4.10]).
$\mathbf {Q}_p$ to pick up all contributions at all poles (see [Reference Balakrishnan and BesserBB12, Remark 4.10]).
Remark 3.6 If our hyperelliptic curve ![]() $X$ does not admit an odd-degree model over
$X$ does not admit an odd-degree model over ![]() $\mathbf {Q}$, we may choose our prime
$\mathbf {Q}$, we may choose our prime ![]() $p$ such that
$p$ such that ![]() $X$ has an odd-degree model over
$X$ has an odd-degree model over ![]() $\mathbf {Q}_p$ and compute local heights at
$\mathbf {Q}_p$ and compute local heights at ![]() $p$ on this model. This follows from the fact that
$p$ on this model. This follows from the fact that ![]() $\Psi (\varphi ^*\omega ) = \varphi ^*(\Psi (\omega ))$ for
$\Psi (\varphi ^*\omega ) = \varphi ^*(\Psi (\omega ))$ for ![]() $\varphi$ an isomorphism of curves and
$\varphi$ an isomorphism of curves and ![]() $\omega$ a differential of the third kind.
$\omega$ a differential of the third kind.
Remark 3.7 In his thesis [Reference GajovićGaj22], Gajović has improved Algorithm 3.4 and extended it to even-degree models of hyperelliptic curves.
The local height at a prime ![]() $\ell \ne p$ is defined in terms of intersection theory. We can extend
$\ell \ne p$ is defined in terms of intersection theory. We can extend ![]() $D_1$ and
$D_1$ and ![]() $D_2$ to divisors
$D_2$ to divisors ![]() $\mathcal {D}_1$ and
$\mathcal {D}_1$ and ![]() $\mathcal {D}_2$ on a regular model of
$\mathcal {D}_2$ on a regular model of ![]() $X_{\mathbf {Q}_\ell }$ so that both
$X_{\mathbf {Q}_\ell }$ so that both ![]() $\mathcal {D}_i$ have trivial intersection multiplicity with all vertical divisors; then by [Reference Coleman and GrossCG89, Proposition 1.2], we have
$\mathcal {D}_i$ have trivial intersection multiplicity with all vertical divisors; then by [Reference Coleman and GrossCG89, Proposition 1.2], we have
3.4 Mordell–Weil sieving
The idea of the Mordell–Weil sieve, originally due to Scharaschkin [Reference ScharaschkinSch99], is to deduce information on rational points on ![]() $X$ via the intersection of the images of
$X$ via the intersection of the images of ![]() $X(\mathbf {F}_v)$ and
$X(\mathbf {F}_v)$ and ![]() $J(\mathbf {Q})$ in
$J(\mathbf {Q})$ in ![]() $J(\mathbf {F}_v)$ (or suitable quotients) for several primes
$J(\mathbf {F}_v)$ (or suitable quotients) for several primes ![]() $v$ of good reduction. It is often applied to verify that
$v$ of good reduction. It is often applied to verify that ![]() $X(\mathbf {Q})=\varnothing$, but it can also be combined with
$X(\mathbf {Q})=\varnothing$, but it can also be combined with ![]() $p$-adic techniques to compute
$p$-adic techniques to compute ![]() $X(\mathbf {Q})$ when there are rational points.
$X(\mathbf {Q})$ when there are rational points.
We review the basic idea, which is straightforward. Making the sieve perform well in practice is a different matter (see [Reference Bruin and StollBS10] for an elaborate discussion of the issues one encounters and detailed strategies). For ease of exposition, we assume that ![]() $J(\mathbf {Q})$ is torsion-free and that we have generators
$J(\mathbf {Q})$ is torsion-free and that we have generators ![]() $P_1,\ldots,P_r$ of
$P_1,\ldots,P_r$ of ![]() $J(\mathbf {Q})$. Let
$J(\mathbf {Q})$. Let ![]() $M>1$ be an integer and let
$M>1$ be an integer and let ![]() $S$ be a finite set of primes of good reduction for
$S$ be a finite set of primes of good reduction for ![]() $X$. Then the diagram
$X$. Then the diagram

is commutative. In the situation of interest to us, the horizontal maps are induced by our choice of base point ![]() $b \in X(\mathbf {Q})$.
$b \in X(\mathbf {Q})$.
In our work, we use the Mordell–Weil sieve in two ways. On the one hand, we apply it to show that for a fixed prime ![]() $p$, a given residue disk in
$p$, a given residue disk in ![]() $X(\mathbf {Q}_p)$ does not contain a rational point. To this end, we set
$X(\mathbf {Q}_p)$ does not contain a rational point. To this end, we set ![]() $M = M'\cdot p$ for some suitable auxiliary integer
$M = M'\cdot p$ for some suitable auxiliary integer ![]() $M'$, and we choose
$M'$, and we choose ![]() $S$ to consist of primes
$S$ to consist of primes ![]() $\ell$ so that
$\ell$ so that ![]() $\gcd (\#J(\mathbf {F}_{\ell }), \#J(\mathbf {F}_q))$ is large for some prime divisors
$\gcd (\#J(\mathbf {F}_{\ell }), \#J(\mathbf {F}_q))$ is large for some prime divisors ![]() $q\mid pM'$. We can then hope that the image of the reduction of the disk under
$q\mid pM'$. We can then hope that the image of the reduction of the disk under ![]() $\prod \beta _{S,M}$ does not meet the image of the map
$\prod \beta _{S,M}$ does not meet the image of the map ![]() $\prod \alpha _{S,M}$.
$\prod \alpha _{S,M}$.
On the other hand, we use the sieve to show for fixed ![]() $M>1$ that a given coset of
$M>1$ that a given coset of ![]() $MJ(\mathbf {Q})$ does not contain the image of a point in
$MJ(\mathbf {Q})$ does not contain the image of a point in ![]() $X(\mathbf {Q})$ under the Abel–Jacobi map
$X(\mathbf {Q})$ under the Abel–Jacobi map ![]() $P\mapsto [P-b]$. Suppose a point
$P\mapsto [P-b]$. Suppose a point ![]() $P\in X(\mathbf {Q}_p)$ is given to finite precision
$P\in X(\mathbf {Q}_p)$ is given to finite precision ![]() $p^N$. If
$p^N$. If ![]() $P$ is rational, then there are integers
$P$ is rational, then there are integers ![]() $a_1,\ldots,a_g$ such that
$a_1,\ldots,a_g$ such that
Via the abelian logarithm, we compute a tuple ![]() $(\tilde {a}_1,\ldots,\tilde {a}_g) \in \mathbf {Z}/p^N\mathbf {Z}$ satisfying
$(\tilde {a}_1,\ldots,\tilde {a}_g) \in \mathbf {Z}/p^N\mathbf {Z}$ satisfying ![]() $a_i \equiv \tilde {a}_i \pmod {p^N}$ for all
$a_i \equiv \tilde {a}_i \pmod {p^N}$ for all ![]() $i\in \{1,\ldots,g\}$. To show that
$i\in \{1,\ldots,g\}$. To show that ![]() $P$ is not rational, it suffices to show that the corresponding coset of
$P$ is not rational, it suffices to show that the corresponding coset of ![]() $p^NJ(\mathbf {Q})$ does not contain the image of such a point.
$p^NJ(\mathbf {Q})$ does not contain the image of such a point.
In our implementation, we have not tried to optimise the interplay between quadratic Chabauty and the Mordell–Weil sieve. Such an optimisation is discussed in [Reference Balakrishnan, Besser and MüllerBBM17, § 7]. Let us only note here that we may combine quadratic Chabauty information coming from several primes, and that we can enhance that information using an auxiliary integer ![]() $M'$ similar to the above. Another account of combining quadratic Chabauty with the Mordell–Weil sieve can be found in [Reference Balakrishnan, Best, Bianchi, Lawrence, Müller, Triantafillou and VonkBBB+21, § 6.7].
$M'$ similar to the above. Another account of combining quadratic Chabauty with the Mordell–Weil sieve can be found in [Reference Balakrishnan, Best, Bianchi, Lawrence, Müller, Triantafillou and VonkBBB+21, § 6.7].
Remark 3.8 All examples in this paper satisfy ![]() $r=g=\mathrm {rk}_{\mathbf {Z}}\mathrm {NS}(J)$, resulting in at least two independent locally analytic functions vanishing in
$r=g=\mathrm {rk}_{\mathbf {Z}}\mathrm {NS}(J)$, resulting in at least two independent locally analytic functions vanishing in ![]() $X(\mathbf {Q})$ for the
$X(\mathbf {Q})$ for the ![]() $g>2$ examples. Since we expect that their common zero set is precisely
$g>2$ examples. Since we expect that their common zero set is precisely ![]() $X(\mathbf {Q})$ (or that there is a geometric reason for the appearance of any additional
$X(\mathbf {Q})$ (or that there is a geometric reason for the appearance of any additional ![]() $p$-adic solutions), we do not expect to require the sieve. Indeed, we only had to apply the sieve for curves of genus 2. For these examples, we always required only one prime for the quadratic Chabauty computation; we chose this prime in such a way as to simplify the sieving.
$p$-adic solutions), we do not expect to require the sieve. Indeed, we only had to apply the sieve for curves of genus 2. For these examples, we always required only one prime for the quadratic Chabauty computation; we chose this prime in such a way as to simplify the sieving.
3.5 Implementation and scope
We have implemented the algorithms described in this section in the computer algebra system Magma [Reference Bosma, Cannon and PlayoustBCP97]. Our code is freely available at [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+]. It extends the code used for ![]() $X_{\mathrm {s}}^+(13)$ in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19] and can be used to recover that example. It is applied to new examples, as discussed in § 5.
$X_{\mathrm {s}}^+(13)$ in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19] and can be used to recover that example. It is applied to new examples, as discussed in § 5.
We begin by summarising our discussion so far and describe the general procedure to determine the finite set ![]() $X(\mathbf {Q}_p)_2$ as it would apply to the modular curve
$X(\mathbf {Q}_p)_2$ as it would apply to the modular curve ![]() $X$ attached to a general congruence subgroup, and Atkin–Lehner quotients thereof. In this generality, several steps cannot be easily automated, so we discuss the extent to which our implementation has automated the procedure, and point out which steps require additional action from the user. See Example 5.3 for a fairly detailed worked example.
$X$ attached to a general congruence subgroup, and Atkin–Lehner quotients thereof. In this generality, several steps cannot be easily automated, so we discuss the extent to which our implementation has automated the procedure, and point out which steps require additional action from the user. See Example 5.3 for a fairly detailed worked example.
Our techniques are built on prior work of Tuitman on computing the action of Frobenius on rigid cohomology [Reference TuitmanTui17]. We recall some of the underlying structures present in Tuitman's work and a set of assumptions on these auxiliary structures.
Suppose our modular curve ![]() $X/\mathbf {Q}$ is given by a (possibly singular) plane model
$X/\mathbf {Q}$ is given by a (possibly singular) plane model ![]() $Q=0$ with
$Q=0$ with ![]() $Q(x,y) \in \mathbf {Z}[x,y]$ a polynomial that is irreducible and monic in
$Q(x,y) \in \mathbf {Z}[x,y]$ a polynomial that is irreducible and monic in ![]() $y$. Let
$y$. Let ![]() $d_x$ and
$d_x$ and ![]() $d_y$ denote the degrees of the morphisms
$d_y$ denote the degrees of the morphisms ![]() $x$ and
$x$ and ![]() $y$, respectively, from
$y$, respectively, from ![]() $X$ to the projective line. Let
$X$ to the projective line. Let ![]() $\Delta (x) \in \mathbf {Z}[x]$ denote the discriminant of
$\Delta (x) \in \mathbf {Z}[x]$ denote the discriminant of ![]() $Q$ with respect to the variable
$Q$ with respect to the variable ![]() $y$. Moreover, define
$y$. Moreover, define ![]() $r(x) \in \mathbf {Z}[x]$ to be the square-free polynomial with the same zeros as
$r(x) \in \mathbf {Z}[x]$ to be the square-free polynomial with the same zeros as ![]() $\Delta (x)$, in other words,
$\Delta (x)$, in other words, ![]() $r=\Delta /(\gcd (\Delta,{d\Delta }/{{d} x}))$.
$r=\Delta /(\gcd (\Delta,{d\Delta }/{{d} x}))$.
Definition 3.9 Let ![]() $W^0 \in \mathrm {GL}_{d_x}(\mathbf {Q}[x,1/r])$ and
$W^0 \in \mathrm {GL}_{d_x}(\mathbf {Q}[x,1/r])$ and ![]() $W^{\infty } \in \mathrm {GL}_{d_x}(\mathbf {Q}[x,1/x,1/r])$ denote matrices such that, if we denote
$W^{\infty } \in \mathrm {GL}_{d_x}(\mathbf {Q}[x,1/x,1/r])$ denote matrices such that, if we denote
 \[ b^0_j = \sum_{i=0}^{d_x-1} W^0_{i+1,j+1} y^i \quad \text{and} \quad b^{\infty}_j = \sum_{i=0}^{d_x-1} W^{\infty}_{i+1,j+1} y^i \]
\[ b^0_j = \sum_{i=0}^{d_x-1} W^0_{i+1,j+1} y^i \quad \text{and} \quad b^{\infty}_j = \sum_{i=0}^{d_x-1} W^{\infty}_{i+1,j+1} y^i \]
for all ![]() $0 \leq j \leq d_x-1$, then
$0 \leq j \leq d_x-1$, then
(i)
 $[b^{0 \;}_0,\ldots,b^{0 \;}_{d_x-1}]$ is an integral basis for
$[b^{0 \;}_0,\ldots,b^{0 \;}_{d_x-1}]$ is an integral basis for  $\mathbf {Q}(X)$ over
$\mathbf {Q}(X)$ over  $\mathbf {Q}[x]$,
$\mathbf {Q}[x]$,(ii)
 $[b^{\infty }_0,\ldots,b^{\infty }_{d_x-1}]$ is an integral basis for
$[b^{\infty }_0,\ldots,b^{\infty }_{d_x-1}]$ is an integral basis for  $\mathbf {Q}(X)$ over
$\mathbf {Q}(X)$ over  $\mathbf {Q}[1/x]$,
$\mathbf {Q}[1/x]$,
where ![]() $\mathbf {Q}(X)$ denotes the function field of
$\mathbf {Q}(X)$ denotes the function field of ![]() $X$. Moreover, let
$X$. Moreover, let ![]() $W \in \mathrm {GL}_{d_x}(\mathbf {Q}[x,1/x])$ denote the change-of-basis matrix
$W \in \mathrm {GL}_{d_x}(\mathbf {Q}[x,1/x])$ denote the change-of-basis matrix ![]() $W=(W^0)^{-1} W^{\infty }$.
$W=(W^0)^{-1} W^{\infty }$.
Assumption 3.10 [Reference TuitmanTui17, Assumption 1]
(i) The discriminant of
 $r(x)$ is contained in
$r(x)$ is contained in  $\mathbf {Z}_p^{\times }$.
$\mathbf {Z}_p^{\times }$.(ii) If we denote
 $b^0_j = \sum _{i=0}^{d_x-1} W^0_{i+1,j+1} y^i$ and
$b^0_j = \sum _{i=0}^{d_x-1} W^0_{i+1,j+1} y^i$ and  $b^{\infty }_j = \sum _{i=0}^{d_x-1} W^{\infty }_{i+1,j+1} y^i$ for all
$b^{\infty }_j = \sum _{i=0}^{d_x-1} W^{\infty }_{i+1,j+1} y^i$ for all  $0 \leq j \leq d_x-1$, and if we let
$0 \leq j \leq d_x-1$, and if we let  $\mathbf {F}_p(x,y)$ be the field of fractions of
$\mathbf {F}_p(x,y)$ be the field of fractions of  $\mathbf {F}_p[x,y]/(Q)$, then:
$\mathbf {F}_p[x,y]/(Q)$, then:
(a) the reduction modulo
 $p$ of
$p$ of  $[b^{0 \;}_0,\ldots,b^{0 \;}_{d_x-1}]$ is an integral basis for
$[b^{0 \;}_0,\ldots,b^{0 \;}_{d_x-1}]$ is an integral basis for  $\mathbf {F}_p(x,y)$ over
$\mathbf {F}_p(x,y)$ over  $\mathbf {F}_p[x]$;
$\mathbf {F}_p[x]$;(b) the reduction modulo
 $p$ of
$p$ of  $[b^{\infty }_0,\ldots,b^{\infty }_{d_x-1}]$ is an integral basis for
$[b^{\infty }_0,\ldots,b^{\infty }_{d_x-1}]$ is an integral basis for  $\mathbf {F}_p(x,y)$ over
$\mathbf {F}_p(x,y)$ over  $\mathbf {F}_p[1/x]$.
$\mathbf {F}_p[1/x]$.
(iii)
 $W^0 \in \mathrm {GL}_{d_x}(\mathbf {Z}_p[x,1/r])$ and
$W^0 \in \mathrm {GL}_{d_x}(\mathbf {Z}_p[x,1/r])$ and  $W^{\infty } \in \mathrm {GL}_{d_x}(\mathbf {Z}_p[x,1/x,1/r])$.
$W^{\infty } \in \mathrm {GL}_{d_x}(\mathbf {Z}_p[x,1/x,1/r])$.(iv) Denote
For a ring \begin{align*} \mathcal{R}^0 &= \mathbf{Z}_p[x]b^{0}_0 +\cdots+\mathbf{Z}_p[x]b^{0}_{d_x-1}, \\ \mathcal{R}^{\infty} &= \mathbf{Z}_p[1/x]b^{\infty}_0+\cdots+\mathbf{Z}_p[1/x]b^{\infty}_{d_x-1}. \end{align*}
\begin{align*} \mathcal{R}^0 &= \mathbf{Z}_p[x]b^{0}_0 +\cdots+\mathbf{Z}_p[x]b^{0}_{d_x-1}, \\ \mathcal{R}^{\infty} &= \mathbf{Z}_p[1/x]b^{\infty}_0+\cdots+\mathbf{Z}_p[1/x]b^{\infty}_{d_x-1}. \end{align*}
 $R$, let
$R$, let  $R_{\textrm {red}}$ denote the reduced ring obtained by quotienting out by the nilradical. Then the discriminants of the finite
$R_{\textrm {red}}$ denote the reduced ring obtained by quotienting out by the nilradical. Then the discriminants of the finite  $\mathbf {Z}_p$-algebras
$\mathbf {Z}_p$-algebras  $(\mathcal {R}^0/(r(x)))_{\textrm {red}}$ and
$(\mathcal {R}^0/(r(x)))_{\textrm {red}}$ and  $(\mathcal {R}^{\infty }/(1/x))_{\textrm {red}}$ are contained in
$(\mathcal {R}^{\infty }/(1/x))_{\textrm {red}}$ are contained in  $\mathbf {Z}_p^{\times }$.
$\mathbf {Z}_p^{\times }$.
Remark 3.11 These conditions imply that the curve ![]() $X$ has good reduction at
$X$ has good reduction at ![]() $p$.
$p$.
Algorithm 3.12 Quadratic Chabauty for modular curves
Input:
− A modular curve
 $X/\mathbf {Q}$ with Mordell–Weil rank
$X/\mathbf {Q}$ with Mordell–Weil rank  $r=g$ and
$r=g$ and  $\mathrm {rk}_{\mathbf {Z}}\mathrm {NS}(J)>1$, and for which the image of
$\mathrm {rk}_{\mathbf {Z}}\mathrm {NS}(J)>1$, and for which the image of  $J(\mathbf {Q} )$ in
$J(\mathbf {Q} )$ in  $\mathrm {H}^0 (X_{\mathbf {Q} _p },\Omega ^1 )^\vee$ has rank
$\mathrm {H}^0 (X_{\mathbf {Q} _p },\Omega ^1 )^\vee$ has rank  $g$
$g$− A covering of
 $X$ by affine opens that are birational to a planar curve cut out by an equation that is monic in one variable, has
$X$ by affine opens that are birational to a planar curve cut out by an equation that is monic in one variable, has  $p$-integral coefficients and satisfies Assumption 3.10 (see § 3.5.1)
$p$-integral coefficients and satisfies Assumption 3.10 (see § 3.5.1)− A prime
 $p$ of good reduction such that the Hecke operator
$p$ of good reduction such that the Hecke operator  $T_p$ generates
$T_p$ generates  $\mathrm {End} ^0 (J)$
$\mathrm {End} ^0 (J)$− For all primes
 $\ell$ that are not of potentially good reduction, the local height functions
$\ell$ that are not of potentially good reduction, the local height functions  $X(\mathbf {Q} _{\ell })\to \mathrm {Ker} (\mathrm {NS} (J)\to \mathrm {NS} (X))_{\mathbf {Q} _p }^*$, computed using Theorem 3.2 (see § 3.5.3)
$X(\mathbf {Q} _{\ell })\to \mathrm {Ker} (\mathrm {NS} (J)\to \mathrm {NS} (X))_{\mathbf {Q} _p }^*$, computed using Theorem 3.2 (see § 3.5.3)− A starting precision
 $n$
$n$− A height bound
 $B$
$B$
Output: An approximation to a finite set containing the set of points ![]() $X(\mathbf {Q}_p)_2$, computed to precision
$X(\mathbf {Q}_p)_2$, computed to precision ![]() $n' \leq n$ or FAIL
$n' \leq n$ or FAIL
(i) Compute the set
 $X(\mathbf {Q})_{\mathrm {known}}$ of points in
$X(\mathbf {Q})_{\mathrm {known}}$ of points in  $X(\mathbf {Q})$ with height bounded by
$X(\mathbf {Q})$ with height bounded by  $B$.
$B$.(ii) Compute an integral symplectic basis for
 $\mathrm {H}^1_{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q}})$ or return FAIL.
$\mathrm {H}^1_{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q}})$ or return FAIL.(iii) Compute the action of Frobenius on
 $\mathrm {H}^1_{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q}_{p}})$ using Tuitman's algorithm [Reference TuitmanTui16, Reference TuitmanTui17]. Use the Eichler–Shimura relation to compute the matrix of the action of the Hecke operator
$\mathrm {H}^1_{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q}_{p}})$ using Tuitman's algorithm [Reference TuitmanTui16, Reference TuitmanTui17]. Use the Eichler–Shimura relation to compute the matrix of the action of the Hecke operator  $T_{p}$ on
$T_{p}$ on  $\mathrm {H}^1_{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q}_{{p}}})$.
$\mathrm {H}^1_{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q}_{{p}}})$.(iv) Compute a splitting of the Hodge filtration that is equivariant for the action of
 $\mathrm {End}(J)$ in the sense of § 3.3.
$\mathrm {End}(J)$ in the sense of § 3.3.(v) Compute the matrices of a basis
 $Z_1, \ldots, Z_{\mathrm {rk}\mathrm {NS}(J) - 1}$ of
$Z_1, \ldots, Z_{\mathrm {rk}\mathrm {NS}(J) - 1}$ of  $\mathrm {Ker}\big (\mathrm {NS}(J) \to \mathrm {NS}(X)\big )$ acting on
$\mathrm {Ker}\big (\mathrm {NS}(J) \to \mathrm {NS}(X)\big )$ acting on  $\mathrm {H}^1_{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q}_{p}})$ (see § 3.5.2).
$\mathrm {H}^1_{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q}_{p}})$ (see § 3.5.2).(vi) Let
 $A:= \varnothing$. For each
$A:= \varnothing$. For each  $Z_i$, compute the associated heights:
$Z_i$, compute the associated heights:
(a) For each affine patch, do the following:
(i) Compute the functions
 $\lambda ^{\mathrm {Fil} }$ from (3.1) using [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 4].
$\lambda ^{\mathrm {Fil} }$ from (3.1) using [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 4].(ii) Compute the functions
 $\lambda ^{\phi }$ from (3.1) using [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 5].
$\lambda ^{\phi }$ from (3.1) using [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 5].
(b) Solve for the height pairing, either using a large enough supply of known rational points
 $P_1, \ldots, P_n$ on
$P_1, \ldots, P_n$ on  $X$, if possible, or by computing the Coleman–Gross height pairing on
$X$, if possible, or by computing the Coleman–Gross height pairing on  $r$ independent points in
$r$ independent points in  $J(\mathbf {Q})$ (see § 3.5.4). If this is unsuccessful, return FAIL.
$J(\mathbf {Q})$ (see § 3.5.4). If this is unsuccessful, return FAIL.(c) Compute solutions of the function(s) coming from
 $Z_i$ or return FAIL if there has been too much precision loss to determine these solutions.
$Z_i$ or return FAIL if there has been too much precision loss to determine these solutions.(d) Check that the solutions are simple. If there is a non-simple solution corresponding to a point in
 $X(\mathbf {Q})_{\mathrm {known}}$, return FAIL. Else, add to the set
$X(\mathbf {Q})_{\mathrm {known}}$, return FAIL. Else, add to the set  $A$ the solutions that (simultaneously) satisfy the(se) function(s).
$A$ the solutions that (simultaneously) satisfy the(se) function(s).
(vii) Return
 $A$.
$A$.
Remark 3.13 We assume that we know a priori that the Mordell–Weil rank of the Jacobian is equal to the genus of the curve. For modular curves, by Gross, Zagier, Kolyvagin and Logachev this amounts to checking that the associated eigenforms have analytic rank ![]() $1$ (see, for example, [Reference Dogra and Le FournDLF21, § 7]). For hyperelliptic curves, it is sometimes simpler to carry out a
$1$ (see, for example, [Reference Dogra and Le FournDLF21, § 7]). For hyperelliptic curves, it is sometimes simpler to carry out a ![]() $2$-descent.
$2$-descent.
Remark 3.14 Note that if the algorithm fails due to a loss of precision, it may be possible to remedy this by increasing the starting precision. One place where increasing precision may not work is if the ![]() $p$-adic logarithm does not induce an isomorphism
$p$-adic logarithm does not induce an isomorphism ![]() $J(\mathbf {Q} )\otimes \mathbf {Q} _p \simeq \mathrm {H}^0 (X_{\mathbf {Q} _p },\Omega ^1 )^\vee$, even though the rank of
$J(\mathbf {Q} )\otimes \mathbf {Q} _p \simeq \mathrm {H}^0 (X_{\mathbf {Q} _p },\Omega ^1 )^\vee$, even though the rank of ![]() $J(\mathbf {Q})$ is
$J(\mathbf {Q})$ is ![]() $g$. For the Atkin–Lehner quotients
$g$. For the Atkin–Lehner quotients ![]() $X_0 ^+ (N)$, the weak Birch–Swinnerton-Dyer conjecture implies that
$X_0 ^+ (N)$, the weak Birch–Swinnerton-Dyer conjecture implies that ![]() $J(\mathbf {Q} )$ always generates
$J(\mathbf {Q} )$ always generates ![]() $\mathrm {H}^0 (X_{\mathbf {Q} _p },\Omega ^1 )^\vee$ (see [Reference Dogra and Le FournDLF21, Lemma 7]). In general, if
$\mathrm {H}^0 (X_{\mathbf {Q} _p },\Omega ^1 )^\vee$ (see [Reference Dogra and Le FournDLF21, Lemma 7]). In general, if ![]() $r=g$ and the Zariski closure of
$r=g$ and the Zariski closure of ![]() $J(\mathbf {Q} )$ is
$J(\mathbf {Q} )$ is ![]() $J$, then a conjecture of Waldschmidt [Reference WaldschmidtWal11, Conjecture 1] (an analogue of the Leopoldt conjecture for abelian varieties) implies that the
$J$, then a conjecture of Waldschmidt [Reference WaldschmidtWal11, Conjecture 1] (an analogue of the Leopoldt conjecture for abelian varieties) implies that the ![]() $p$-adic logarithm is always an isomorphism. In theory, if one knew that
$p$-adic logarithm is always an isomorphism. In theory, if one knew that ![]() $J$ gave a counterexample to Waldschmidt's conjecture, and
$J$ gave a counterexample to Waldschmidt's conjecture, and ![]() $r=g$, then one could simply apply the Chabauty–Coleman method. However, a priori it could happen that
$r=g$, then one could simply apply the Chabauty–Coleman method. However, a priori it could happen that ![]() $J$ gave a counterexample but there was no way of verifying this by a computation to finite
$J$ gave a counterexample but there was no way of verifying this by a computation to finite ![]() $p$-adic precision. Another place where increasing precision will not help is if there are multiple roots in step (vi)(c). However, we only expect this to happen for geometric reasons.
$p$-adic precision. Another place where increasing precision will not help is if there are multiple roots in step (vi)(c). However, we only expect this to happen for geometric reasons.
One can have ![]() $r>g$ for the curves
$r>g$ for the curves ![]() $X_0 ^+ (N)$ with
$X_0 ^+ (N)$ with ![]() $N$ prime, even though
$N$ prime, even though ![]() $X_0 ^+ (N)(\mathbf {Q} _p )_2$ is always finite when the genus is greater than
$X_0 ^+ (N)(\mathbf {Q} _p )_2$ is always finite when the genus is greater than ![]() $1$ [Reference Dogra and Le FournDLF21]. However, the smallest genus for which this happens is
$1$ [Reference Dogra and Le FournDLF21]. However, the smallest genus for which this happens is ![]() $g=206$ (with
$g=206$ (with ![]() $N=5077$), so the
$N=5077$), so the ![]() $r=g$ hypothesis is not the main restriction to the scope of our algorithms for this family of curves.
$r=g$ hypothesis is not the main restriction to the scope of our algorithms for this family of curves.
Remark 3.15 In the case when ![]() $p$ is a prime of ordinary reduction for the Jacobian, one may take the splitting of the Hodge filtration given by the unit root subspace, that is, the unit root eigenspace of Frobenius
$p$ is a prime of ordinary reduction for the Jacobian, one may take the splitting of the Hodge filtration given by the unit root subspace, that is, the unit root eigenspace of Frobenius ![]() $\phi$ acting on
$\phi$ acting on ![]() $\mathrm {H}^1(X_{\mathbf {Q}_p})$. Given a basis
$\mathrm {H}^1(X_{\mathbf {Q}_p})$. Given a basis ![]() $\{\eta _1, \ldots, \eta _{2g}\}$ of
$\{\eta _1, \ldots, \eta _{2g}\}$ of ![]() $\mathrm {H}^1(X_{\mathbf {Q}_p})$, where
$\mathrm {H}^1(X_{\mathbf {Q}_p})$, where ![]() $\eta _1, \ldots, \eta _g$ are holomorphic, a basis for the unit root eigenspace mod
$\eta _1, \ldots, \eta _g$ are holomorphic, a basis for the unit root eigenspace mod ![]() $p^n$ is given by
$p^n$ is given by ![]() $\{(\phi ^*)^n\eta _{g+1},\ldots, (\phi ^*)^n\eta _{2g}\}.$
$\{(\phi ^*)^n\eta _{g+1},\ldots, (\phi ^*)^n\eta _{2g}\}.$
Remark 3.16 In this paper, we do not discuss algorithms for computing the input of the local height functions as maps from ![]() $\mathbf {Q} _\ell$-points to
$\mathbf {Q} _\ell$-points to ![]() $\mathbf {Q}_p$-linear functionals on
$\mathbf {Q}_p$-linear functionals on ![]() $\mathrm {Ker} (\mathrm {NS} (J) \to \mathrm {NS} (X))$. In § 5 we give examples where this function can be non-trivial, and where
$\mathrm {Ker} (\mathrm {NS} (J) \to \mathrm {NS} (X))$. In § 5 we give examples where this function can be non-trivial, and where ![]() $X(\mathbf {Q} )$ can still be determined using quadratic Chabauty. There are two procedures we illustrate for doing this. In § 5.4 we calculate regular semi-stable models at bad primes and have a sufficient supply of rational points (and sufficiently simple dual graphs) to reconstruct the functions
$X(\mathbf {Q} )$ can still be determined using quadratic Chabauty. There are two procedures we illustrate for doing this. In § 5.4 we calculate regular semi-stable models at bad primes and have a sufficient supply of rational points (and sufficiently simple dual graphs) to reconstruct the functions ![]() $j_\ell$ from Theorem 3.2 using evaluation of
$j_\ell$ from Theorem 3.2 using evaluation of ![]() $p$-adic local heights at known rational points. In § 5.5, although we know a regular semi-stable model ‘abstractly’, we do not know the relation between the stable model (at the bad prime 17) and the model we use for
$p$-adic local heights at known rational points. In § 5.5, although we know a regular semi-stable model ‘abstractly’, we do not know the relation between the stable model (at the bad prime 17) and the model we use for ![]() $p$-adic calculations. This, together with the relative paucity of known rational points, makes it infeasible to apply the first procedure. Instead, we use extra information about the action of inertia on the stable model, together with Theorem 3.2, to identify a subspace of line bundles in
$p$-adic calculations. This, together with the relative paucity of known rational points, makes it infeasible to apply the first procedure. Instead, we use extra information about the action of inertia on the stable model, together with Theorem 3.2, to identify a subspace of line bundles in ![]() $\mathrm {Ker} (\mathrm {NS} (J)\to \mathrm {NS} (X))$ for which the associated local heights vanish.
$\mathrm {Ker} (\mathrm {NS} (J)\to \mathrm {NS} (X))$ for which the associated local heights vanish.
To further determine the subset of rational points ![]() $X(\mathbf {Q})$ from the finite set of points produced by our algorithm, we carry out the Mordell–Weil sieve. In practice it may happen (see below) that
$X(\mathbf {Q})$ from the finite set of points produced by our algorithm, we carry out the Mordell–Weil sieve. In practice it may happen (see below) that ![]() $X(\mathbf {Q})$ is returned by the algorithm, but this is typically not the case when
$X(\mathbf {Q})$ is returned by the algorithm, but this is typically not the case when ![]() $X$ has genus
$X$ has genus ![]() $2$.
$2$.
3.5.1 Affine patches
Most of the examples discussed in § 5 are either hyperelliptic curves or smooth plane quartics. As demonstrated in § 5.5, our code is sometimes able to treat more general examples. Our implementation was designed to take as input a plane affine patch ![]() $Y\colon Q(x,y)=0$ of a modular curve
$Y\colon Q(x,y)=0$ of a modular curve ![]() $X/\mathbf {Q}$ satisfying the requirements in § 2.1 and a prime
$X/\mathbf {Q}$ satisfying the requirements in § 2.1 and a prime ![]() $p$ of good reduction. It returns all rational points on
$p$ of good reduction. It returns all rational points on ![]() $X$ in affine residue disks where the lift of Frobenius constructed in [Reference TuitmanTui16, Reference TuitmanTui17] is defined. Note that we do not require
$X$ in affine residue disks where the lift of Frobenius constructed in [Reference TuitmanTui16, Reference TuitmanTui17] is defined. Note that we do not require ![]() $Y$ to be smooth, but we need
$Y$ to be smooth, but we need ![]() $Q$ to be monic with
$Q$ to be monic with ![]() $p$-integral coefficients.
$p$-integral coefficients.
We can sometimes find an affine patch ![]() $Y$ having the convenient property that all rational points on
$Y$ having the convenient property that all rational points on ![]() $X$ must be among the points returned by running our algorithm on
$X$ must be among the points returned by running our algorithm on ![]() $Y$. If no such
$Y$. If no such ![]() $Y$ is found, then we need to find two suitable affine patches such that every rational point on
$Y$ is found, then we need to find two suitable affine patches such that every rational point on ![]() $X$ is contained in at least one patch. For smooth plane quartics, our implementation includes an algorithm that automates this process for the convenience of the user. For other curves, this step is left to the user.
$X$ is contained in at least one patch. For smooth plane quartics, our implementation includes an algorithm that automates this process for the convenience of the user. For other curves, this step is left to the user.
3.5.2 The Néron–Severi classes  $Z_i$
$Z_i$
Under the assumption that ![]() $T_p$ generates the endomorphism ring of the Jacobian, which we made for convenience above, one may proceed precisely as in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 6.4] to determine a non-trivial class
$T_p$ generates the endomorphism ring of the Jacobian, which we made for convenience above, one may proceed precisely as in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 6.4] to determine a non-trivial class
Indeed, the matrix ![]() $A_p$ of the Hecke operator
$A_p$ of the Hecke operator ![]() $T_p$ acting on
$T_p$ acting on ![]() $\mathrm {H}^1_{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q}_p})$ is easily determined from the matrix of Frobenius
$\mathrm {H}^1_{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q}_p})$ is easily determined from the matrix of Frobenius ![]() $F_p$ (which is already a byproduct of the algorithms for the local height at
$F_p$ (which is already a byproduct of the algorithms for the local height at ![]() $p$), by the Eichler–Shimura relation:
$p$), by the Eichler–Shimura relation:
Under our assumption, the matrices of the classes ![]() $Z_i$ acting on
$Z_i$ acting on ![]() $\mathrm {H}^1_{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q}_p})$ may then be computed as linear combinations of powers of
$\mathrm {H}^1_{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q}_p})$ may then be computed as linear combinations of powers of ![]() $A_p$.
$A_p$.
Remark 3.17 This is the only part of our algorithm specific to modular curves, since it relies on the Eichler–Shimura relation. It should, however, be noted that this is mainly a matter of convenience adopted for the purpose of automation. More generally, for a smooth projective curve ![]() $X/\mathbf {Q}$ satisfying the assumptions of § 2.1, one could find
$X/\mathbf {Q}$ satisfying the assumptions of § 2.1, one could find ![]() $p$-adic approximations of the action of the non-trivial classes
$p$-adic approximations of the action of the non-trivial classes ![]() $Z_i$ on
$Z_i$ on ![]() $\mathrm {H}^1_{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q}_p})$ using just
$\mathrm {H}^1_{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q}_p})$ using just ![]() $p$-adic linear algebra. Indeed, the space of correspondences which are symmetric under the Rosati involution and induce endomorphisms of trace zero on the Tate module maps under the cycle class into the intersection of the
$p$-adic linear algebra. Indeed, the space of correspondences which are symmetric under the Rosati involution and induce endomorphisms of trace zero on the Tate module maps under the cycle class into the intersection of the ![]() $\mathrm {Fil} ^{1}$ and
$\mathrm {Fil} ^{1}$ and ![]() $\phi =p$ subspaces of
$\phi =p$ subspaces of
In fact, by the Tate conjecture, the rank of the space of (crystalline) cohomology classes of such correspondences over ![]() $\mathbf {F} _p$ is equal to the dimension of the
$\mathbf {F} _p$ is equal to the dimension of the ![]() $\phi =p$ subspace of (3.4), and by the
$\phi =p$ subspace of (3.4), and by the ![]() $p$-adic Lefschetz-
$p$-adic Lefschetz-![]() $(1,1)$ theorem of Berthelot and Ogus [Reference Berthelot and OgusBO83, § 3.8] such a correspondence over
$(1,1)$ theorem of Berthelot and Ogus [Reference Berthelot and OgusBO83, § 3.8] such a correspondence over ![]() $\mathbf {F} _p$ lifts to
$\mathbf {F} _p$ lifts to ![]() $\mathbf {Q} _p$ if and only if its cycle class lies in
$\mathbf {Q} _p$ if and only if its cycle class lies in ![]() $\mathrm {Fil} ^{1}$. Note that the dimension of the space of correspondences symmetric under the Rosati involution need not equal the dimension of
$\mathrm {Fil} ^{1}$. Note that the dimension of the space of correspondences symmetric under the Rosati involution need not equal the dimension of ![]() $\wedge ^2 \mathrm {H} ^1 _{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q} _p })^{\phi =p}\cap \mathrm {Fil} ^1$, as was erroneously claimed in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, Lemma 4.5], since the rank of the intersection of a
$\wedge ^2 \mathrm {H} ^1 _{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q} _p })^{\phi =p}\cap \mathrm {Fil} ^1$, as was erroneously claimed in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, Lemma 4.5], since the rank of the intersection of a ![]() $\mathbf {Z}$-lattice with a
$\mathbf {Z}$-lattice with a ![]() $\mathbf {Q} _p$-subspace may be less than the dimension of the intersection with the
$\mathbf {Q} _p$-subspace may be less than the dimension of the intersection with the ![]() $\mathbf {Q} _p$-subspace it spans. However, if one knows a set of generators of a finite index subgroup of
$\mathbf {Q} _p$-subspace it spans. However, if one knows a set of generators of a finite index subgroup of ![]() $\mathrm {End} (J)$ in advance (e.g. using algorithms for rigorous computation of the endomorphism algebra of the Jacobian [Reference Costa, Mascot, Sijsling and VoightCMSV19])) then one can use this to compute the classes of generators in cohomology.
$\mathrm {End} (J)$ in advance (e.g. using algorithms for rigorous computation of the endomorphism algebra of the Jacobian [Reference Costa, Mascot, Sijsling and VoightCMSV19])) then one can use this to compute the classes of generators in cohomology.
Therefore the assumption that ![]() $T_p$ generates the endomorphism algebra could be circumvented in this step with a little work, although it is used in the computation of the local heights away from
$T_p$ generates the endomorphism algebra could be circumvented in this step with a little work, although it is used in the computation of the local heights away from ![]() $p$ (see below). When the assumption is not satisfied, our implementation throws an error, urging the user to try a different choice of prime
$p$ (see below). When the assumption is not satisfied, our implementation throws an error, urging the user to try a different choice of prime ![]() $p$.
$p$.
3.5.3 The local heights away from  $p$
$p$
This step requires an explicit knowledge of a semi-stable model of the modular curve ![]() $X$, as well as a description of the action of
$X$, as well as a description of the action of ![]() $Z_i$ on the concomitant cohomological structures in order to be able to apply Theorem 3.2. It is clear that a full automation of this step, starting from a set of defining equations for
$Z_i$ on the concomitant cohomological structures in order to be able to apply Theorem 3.2. It is clear that a full automation of this step, starting from a set of defining equations for ![]() $X$, falls outside the scope of our implementation.
$X$, falls outside the scope of our implementation.
Semi-stable models for modular curves are known in many cases (see, for instance, the recent work of Edixhoven and Parent [Reference Edixhoven and ParentEP21]). In practice, one can also often use the SageMath toolbox MCLFFootnote 3 due to Rüth and Wewers to compute such models. The main advantage of having computed the ![]() $Z_i$ in § 3.5.2 as combinations of powers of
$Z_i$ in § 3.5.2 as combinations of powers of ![]() $T_p$ is that this makes it easier to compute the quantities appearing in Theorem 3.2. Even though we see no way to fully automate this step, we hope to convince the reader of its practicality by working it out for the genus 2 curves
$T_p$ is that this makes it easier to compute the quantities appearing in Theorem 3.2. Even though we see no way to fully automate this step, we hope to convince the reader of its practicality by working it out for the genus 2 curves ![]() $C_{188}$ and
$C_{188}$ and ![]() $C_{161}$ in Examples 5.18 and 5.19.
$C_{161}$ in Examples 5.18 and 5.19.
3.5.4 The global height pairing
If there are not sufficiently many rational points on the curve to solve for the height pairing, we instead compute the local heights ![]() $h_v$ in the sense of Coleman and Gross (see § 3.3.1). For hyperelliptic curves
$h_v$ in the sense of Coleman and Gross (see § 3.3.1). For hyperelliptic curves ![]() $X/\mathbf {Q}_p$ of odd degree,
$X/\mathbf {Q}_p$ of odd degree, ![]() $h_p(D_1,D_2)$ can be computed using an algorithm due to Balakrishnan and Besser [Reference Balakrishnan and BesserBB12, Reference Balakrishnan and BesserBB21]. Based on earlier SageMath code due to Balakrishnan, we have implemented this in Magma for divisors
$h_p(D_1,D_2)$ can be computed using an algorithm due to Balakrishnan and Besser [Reference Balakrishnan and BesserBB12, Reference Balakrishnan and BesserBB21]. Based on earlier SageMath code due to Balakrishnan, we have implemented this in Magma for divisors ![]() $D_1$ and
$D_1$ and ![]() $D_2$ that split over
$D_2$ that split over ![]() $\mathbf {Q}_p$, have support contained in disjoint residue disks, and for which no points in the support reduce to Weierstrass points mod
$\mathbf {Q}_p$, have support contained in disjoint residue disks, and for which no points in the support reduce to Weierstrass points mod ![]() $p$. To compute the local heights
$p$. To compute the local heights ![]() $h_\ell$ for
$h_\ell$ for ![]() $\ell \ne p$, we rely on Magma's implementation of an algorithm for local canonical heights on hyperelliptic curves described by Holmes and Müller [Reference HolmesHol12, Reference MüllerMül14]. An algorithm for general curves was given by van Bommel, Holmes and Müller [Reference van Bommel, Holmes and MüllervBHM20].
$\ell \ne p$, we rely on Magma's implementation of an algorithm for local canonical heights on hyperelliptic curves described by Holmes and Müller [Reference HolmesHol12, Reference MüllerMül14]. An algorithm for general curves was given by van Bommel, Holmes and Müller [Reference van Bommel, Holmes and MüllervBHM20].
To solve for the height pairing, we need to find representatives for ![]() $r$ independent points in
$r$ independent points in ![]() $J(\mathbf {Q})$ that satisfy the assumptions mentioned above. Our implementation is currently restricted to genus 2 curves, since this step was only necessary for such curves, but a generalisation to higher-genus hyperelliptic curves would be straightforward.
$J(\mathbf {Q})$ that satisfy the assumptions mentioned above. Our implementation is currently restricted to genus 2 curves, since this step was only necessary for such curves, but a generalisation to higher-genus hyperelliptic curves would be straightforward.
Remark 3.18 The code is currently restricted to the base field ![]() $K=\mathbf {Q}$. To extend it to more general number fields, one would need to combine these algorithms with those used in [Reference Balakrishnan and DograBD18] for imaginary quadratic fields in certain cases, or with those in [Reference Balakrishnan, Besser, Bianchi and MüllerBBBM21] for general number fields.
$K=\mathbf {Q}$. To extend it to more general number fields, one would need to combine these algorithms with those used in [Reference Balakrishnan and DograBD18] for imaginary quadratic fields in certain cases, or with those in [Reference Balakrishnan, Besser, Bianchi and MüllerBBBM21] for general number fields.
4. Precision analysis
In this section we bound the loss of absolute ![]() $p$-adic precision that may occur in our computations by bounding the valuations of the error terms. We also estimate the valuations of the power series expansion of the quadratic Chabauty function
$p$-adic precision that may occur in our computations by bounding the valuations of the error terms. We also estimate the valuations of the power series expansion of the quadratic Chabauty function ![]() $\rho$ and use this to bound the precision of its roots.
$\rho$ and use this to bound the precision of its roots.
We retain the notation used in the previous sections. Recall from (2.5) that ![]() $\rho = h-h_p$, where:
$\rho = h-h_p$, where:
−
 $h$ is the global
$h$ is the global  $p$-adic height defined in (2.4);
$p$-adic height defined in (2.4);−
 $h_p$ is the local component of
$h_p$ is the local component of  $h$, discussed in § 2.2.
$h$, discussed in § 2.2.
By (3.2), the local height ![]() $h_p$ satisfies
$h_p$ satisfies
where the Hodge filtration of the filtered ![]() $\phi$-module
$\phi$-module ![]() $M(x) := \big ( \mathrm {A}_Z(b,x) \otimes _{\mathbf {Q}_p} \mathrm {B}_{\scriptstyle \mathrm { crys}}\big )^{G_{\mathbf {Q}_p}}$ discussed in § 2.2 is encoded by
$M(x) := \big ( \mathrm {A}_Z(b,x) \otimes _{\mathbf {Q}_p} \mathrm {B}_{\scriptstyle \mathrm { crys}}\big )^{G_{\mathbf {Q}_p}}$ discussed in § 2.2 is encoded by ![]() $\boldsymbol {\beta }_{\mathrm {Fil}}$ and
$\boldsymbol {\beta }_{\mathrm {Fil}}$ and ![]() $\gamma _{\mathrm {Fil}}$. and
$\gamma _{\mathrm {Fil}}$. and ![]() $\boldsymbol {\alpha }_{\phi }, \boldsymbol {\beta }_{\phi }$ and
$\boldsymbol {\alpha }_{\phi }, \boldsymbol {\beta }_{\phi }$ and ![]() ${\gamma }_{\phi }$ encode the Frobenius structure of
${\gamma }_{\phi }$ encode the Frobenius structure of ![]() $M(x)$.
$M(x)$.
We will bound the loss of precision in the computation of the Hodge filtration in § 4.1, and we do the same for the Frobenius structure in § 4.2. In § 4.3 we bound the precision loss for the global height computation. In the final part of this section, § 4.4, we bound the valuation of the coefficients of the expansion of ![]() $\rho$ in a residue disk, and we discuss how this may be used to provably determine the roots of
$\rho$ in a residue disk, and we discuss how this may be used to provably determine the roots of ![]() $\rho$ to a certain precision. This section relies heavily on [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, §§ 4 and 5].
$\rho$ to a certain precision. This section relies heavily on [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, §§ 4 and 5].
4.1 Hodge filtration
We first bound the loss of precision in steps (ii)–(v) of Algorithm 3.12. For simplicity, we restrict to one class ![]() $Z$; the extension to
$Z$; the extension to ![]() $\mathrm {rk}\mathrm {NS}(J) - 1$ such classes is immediate. Let
$\mathrm {rk}\mathrm {NS}(J) - 1$ such classes is immediate. Let ![]() $Y/\mathbf {Q}$ be an affine open subset of
$Y/\mathbf {Q}$ be an affine open subset of ![]() $X$, birational to a curve given by an equation that satisfies Assumption 3.10. We may compute an integral, symplectic basis
$X$, birational to a curve given by an equation that satisfies Assumption 3.10. We may compute an integral, symplectic basis ![]() $\boldsymbol {\omega }=(\omega _0 ,\ldots,\omega _{2g-1})$ of de Rham cohomology over
$\boldsymbol {\omega }=(\omega _0 ,\ldots,\omega _{2g-1})$ of de Rham cohomology over ![]() $\mathbf {Q}$ exactly, and extend this to an integral basis of
$\mathbf {Q}$ exactly, and extend this to an integral basis of ![]() $H^1 _{\scriptstyle \mathrm {dR}}(Y)$ via differentials
$H^1 _{\scriptstyle \mathrm {dR}}(Y)$ via differentials ![]() $(\omega _{2g},\ldots,\omega _{2g+d-2})$ of the third kind. Using such a basis, we may compute the action of the Frobenius operator
$(\omega _{2g},\ldots,\omega _{2g+d-2})$ of the third kind. Using such a basis, we may compute the action of the Frobenius operator ![]() $F$ on
$F$ on ![]() $\mathrm {H} ^1 _{\scriptstyle \mathrm {dR}}(X/\mathbf {Q} _p )$ to any desired
$\mathrm {H} ^1 _{\scriptstyle \mathrm {dR}}(X/\mathbf {Q} _p )$ to any desired ![]() $p$-adic precision using Tuitman's algorithm [Reference TuitmanTui16, Reference TuitmanTui17], from which we obtain the action of the Hecke operator
$p$-adic precision using Tuitman's algorithm [Reference TuitmanTui16, Reference TuitmanTui17], from which we obtain the action of the Hecke operator ![]() $T_p = F + pF^{-1}$ on
$T_p = F + pF^{-1}$ on ![]() $\mathrm {H}^1 _{\scriptstyle \mathrm {dR}}(X/\mathbf {Q} _p)$ by the Eichler–Shimura relation. The inversion of
$\mathrm {H}^1 _{\scriptstyle \mathrm {dR}}(X/\mathbf {Q} _p)$ by the Eichler–Shimura relation. The inversion of ![]() $F$ results in a finite and computable loss of precision, which the code takes into account. This results in an algorithm that returns the action of the correspondence
$F$ results in a finite and computable loss of precision, which the code takes into account. This results in an algorithm that returns the action of the correspondence ![]() $Z$ correctly modulo
$Z$ correctly modulo ![]() $p^n$ for some
$p^n$ for some ![]() $n\geq 1$ that is returned by the algorithm.
$n\geq 1$ that is returned by the algorithm.
Using this, we may compute a matrix ![]() $\Lambda$ with entries in
$\Lambda$ with entries in ![]() $H^0 (Y,\Omega _{Y_{\mathbf {Q}}})$, of the form
$H^0 (Y,\Omega _{Y_{\mathbf {Q}}})$, of the form
 \[ \Lambda := -\left(
\begin{array}{@{}ccc@{}} 0 & 0 & 0 \\ \boldsymbol{\omega} & 0 & 0
\\ \eta & \boldsymbol{\omega}^{\intercal}Z & 0 \\
\end{array} \right) \]
\[ \Lambda := -\left(
\begin{array}{@{}ccc@{}} 0 & 0 & 0 \\ \boldsymbol{\omega} & 0 & 0
\\ \eta & \boldsymbol{\omega}^{\intercal}Z & 0 \\
\end{array} \right) \]
such that ![]() $d+\Lambda$ extends to a flat connection on
$d+\Lambda$ extends to a flat connection on ![]() $X$. From this, we may compute
$X$. From this, we may compute ![]() $\gamma _{\mathrm {Fil} }$ and
$\gamma _{\mathrm {Fil} }$ and ![]() $\boldsymbol {\beta }_{\mathrm {Fil} }$ from (3.1). We recall from [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 4] that the defining properties of
$\boldsymbol {\beta }_{\mathrm {Fil} }$ from (3.1). We recall from [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 4] that the defining properties of ![]() $\eta$, the
$\eta$, the ![]() $\boldsymbol {\beta }_{\mathrm {Fil} }$ and
$\boldsymbol {\beta }_{\mathrm {Fil} }$ and ![]() $\gamma _{\mathrm {Fil}}$ are as enumerated below. For
$\gamma _{\mathrm {Fil}}$ are as enumerated below. For ![]() $x\in (X-Y)(\overline {\mathbf {Q} })$, we let
$x\in (X-Y)(\overline {\mathbf {Q} })$, we let ![]() $t_x$ denote a parameter, and
$t_x$ denote a parameter, and ![]() $\boldsymbol {\Omega }_x$ denote the vector of formal integrals of the basis differentials
$\boldsymbol {\Omega }_x$ denote the vector of formal integrals of the basis differentials ![]() $\omega _i$:
$\omega _i$:
(i) The first
 $g$ entries of
$g$ entries of  $\boldsymbol {\beta }_{\mathrm {Fil} }$ are zero, and the last
$\boldsymbol {\beta }_{\mathrm {Fil} }$ are zero, and the last  $g$ are given by a vector
$g$ are given by a vector  $\mathbf {b}_{\mathrm {Fil} }$ of constants specified below.
$\mathbf {b}_{\mathrm {Fil} }$ of constants specified below.(ii)
 $\eta$ is a linear combination of
$\eta$ is a linear combination of  $\omega _{2g},\ldots,\omega _{2g+d-2}$, unique by [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, Lemma 4.10], such that
(4.1)has vanishing residues at all
$\omega _{2g},\ldots,\omega _{2g+d-2}$, unique by [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, Lemma 4.10], such that
(4.1)has vanishing residues at all \begin{equation} d\boldsymbol{\Omega }_x^{\intercal }Z \boldsymbol{\Omega }_x -\eta \end{equation}
\begin{equation} d\boldsymbol{\Omega }_x^{\intercal }Z \boldsymbol{\Omega }_x -\eta \end{equation} $x\in (X-Y)(\overline {\mathbf {Q} })$.
$x\in (X-Y)(\overline {\mathbf {Q} })$.(iii)
 $\mathbf {b}_{\mathrm {Fil} }$ and
$\mathbf {b}_{\mathrm {Fil} }$ and  $\gamma _{\mathrm {Fil} } \in \mathcal {O}(Y)$ are the unique solutions to the equation
$\gamma _{\mathrm {Fil} } \in \mathcal {O}(Y)$ are the unique solutions to the equation  $\gamma _{\mathrm {Fil} }(b)=0$ and
(4.2)for all
$\gamma _{\mathrm {Fil} }(b)=0$ and
(4.2)for all \begin{equation} g_x +\gamma _{\mathrm{Fil}}-\mathbf{b}_{\mathrm{Fil} }^\intercal N^\intercal \boldsymbol{\Omega }_x -\boldsymbol{\Omega }_x ^\intercal Z N N^\intercal \boldsymbol{\Omega }_x \in L[\! [t_x ]\! ] \end{equation}
\begin{equation} g_x +\gamma _{\mathrm{Fil}}-\mathbf{b}_{\mathrm{Fil} }^\intercal N^\intercal \boldsymbol{\Omega }_x -\boldsymbol{\Omega }_x ^\intercal Z N N^\intercal \boldsymbol{\Omega }_x \in L[\! [t_x ]\! ] \end{equation} $x\in (X-Y)(\overline {\mathbf {Q} })$, where
$x\in (X-Y)(\overline {\mathbf {Q} })$, where  $g_x \in \overline {\mathbf {Q} }[\! [t_x ]\! ]$ is defined to be the formal integral of
$g_x \in \overline {\mathbf {Q} }[\! [t_x ]\! ]$ is defined to be the formal integral of  $d\boldsymbol {\Omega }_x ^\intercal Zd\boldsymbol {\Omega }_x -\eta$ and
$d\boldsymbol {\Omega }_x ^\intercal Zd\boldsymbol {\Omega }_x -\eta$ and  $N$ is the block
$N$ is the block  $2g \times g$ matrix with top block zero and lower block a
$2g \times g$ matrix with top block zero and lower block a  $g \times g$ identity matrix.
$g \times g$ identity matrix.
Given our basis ![]() $\boldsymbol {\omega }$, we may calculate
$\boldsymbol {\omega }$, we may calculate ![]() $\boldsymbol {\Omega }_x$ to any given
$\boldsymbol {\Omega }_x$ to any given ![]() $t_x$-adic precision. Note that to solve (4.1), we only need to know
$t_x$-adic precision. Note that to solve (4.1), we only need to know ![]() $\boldsymbol {\Omega }_x$ modulo
$\boldsymbol {\Omega }_x$ modulo ![]() $t_x ^{m_x}$, where
$t_x ^{m_x}$, where ![]() $m_x$ is the maximum of the order of the poles of the entries of
$m_x$ is the maximum of the order of the poles of the entries of ![]() $\boldsymbol {\Omega }_x$. Similarly, to solve for
$\boldsymbol {\Omega }_x$. Similarly, to solve for ![]() $\gamma _{\mathrm {Fil}}$ and
$\gamma _{\mathrm {Fil}}$ and ![]() $\mathbf {b}_{\mathrm {Fil}}$ in (4.2), we need only compute the principal parts of
$\mathbf {b}_{\mathrm {Fil}}$ in (4.2), we need only compute the principal parts of ![]() $\boldsymbol {\Omega }_x$ and
$\boldsymbol {\Omega }_x$ and ![]() $\boldsymbol {\Omega }_x ^\intercal Z N N^\intercal \boldsymbol {\Omega }_x$. Hence, given the above, we may calculate
$\boldsymbol {\Omega }_x ^\intercal Z N N^\intercal \boldsymbol {\Omega }_x$. Hence, given the above, we may calculate ![]() $\eta,\gamma _{\mathrm {Fil} }$ and
$\eta,\gamma _{\mathrm {Fil} }$ and ![]() $\mathbf {b}_{\mathrm {Fil} }$ to precision
$\mathbf {b}_{\mathrm {Fil} }$ to precision ![]() $p^{n-2\nu }$, where
$p^{n-2\nu }$, where ![]() $\nu$ is minus the minimum of the valuations of the
$\nu$ is minus the minimum of the valuations of the ![]() $t_x^i$ coefficients of the entries of
$t_x^i$ coefficients of the entries of ![]() $\boldsymbol {\Omega }_x$, for
$\boldsymbol {\Omega }_x$, for ![]() $i\leq m_x$.
$i\leq m_x$.
4.2 Frobenius-equivariant splitting
We now bound the loss of precision in the computation of the Frobenius-equivariant splitting
 \[ \lambda^\phi(x) =\left(
\begin{array}{@{}ccc@{}} 1 & 0 & 0 \\ \boldsymbol{\alpha
}_{\phi}(b,x) & 1 & 0 \\ \gamma_{\phi}(b,x) &
\boldsymbol{\beta }^{\intercal}_{\phi}(b,x) & 1 \\
\end{array} \right) \]
\[ \lambda^\phi(x) =\left(
\begin{array}{@{}ccc@{}} 1 & 0 & 0 \\ \boldsymbol{\alpha
}_{\phi}(b,x) & 1 & 0 \\ \gamma_{\phi}(b,x) &
\boldsymbol{\beta }^{\intercal}_{\phi}(b,x) & 1 \\
\end{array} \right) \]
from (3.1) for ![]() $x \in X(\mathbf {Q}_p)\cap ]\mathcal {U}[$, where
$x \in X(\mathbf {Q}_p)\cap ]\mathcal {U}[$, where ![]() $\mathcal {U}$ is an open of
$\mathcal {U}$ is an open of ![]() $Y_{\mathbf {F} _p }$ on which we have an overconvergent lift of Frobenius. This computation is the content of [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 5].
$Y_{\mathbf {F} _p }$ on which we have an overconvergent lift of Frobenius. This computation is the content of [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 5].
The first step is to find the Frobenius structure on the filtered ![]() $\phi$-module
$\phi$-module ![]() $M(b)$. By [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 5.3.2], the inverse of the Frobenius structure is given by a matrix
$M(b)$. By [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 5.3.2], the inverse of the Frobenius structure is given by a matrix
such that
where ![]() $j^{\dagger} \mathcal {O}_Y$ is the overconvergent structure sheaf on the tube
$j^{\dagger} \mathcal {O}_Y$ is the overconvergent structure sheaf on the tube ![]() $]Y[$.
$]Y[$.
Compared to [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 5.3.2], we give a slightly more detailed account of the algorithm to find ![]() $G$. We first apply the algorithms in [Reference TuitmanTui16, Reference TuitmanTui17] (see [Reference Balakrishnan and TuitmanBT20, Algorithm 2.18]) to compute the action of Frobenius on
$G$. We first apply the algorithms in [Reference TuitmanTui16, Reference TuitmanTui17] (see [Reference Balakrishnan and TuitmanBT20, Algorithm 2.18]) to compute the action of Frobenius on ![]() $\mathrm {H}^1_{\scriptstyle \mathrm {{rig}}}(X\otimes \mathbf {Q}_p)$ as
$\mathrm {H}^1_{\scriptstyle \mathrm {{rig}}}(X\otimes \mathbf {Q}_p)$ as
for a matrix ![]() $F \in M_{2g}(\mathbf {Q}_p)$ and a column vector
$F \in M_{2g}(\mathbf {Q}_p)$ and a column vector ![]() $\mathbf {f}$ with entries in
$\mathbf {f}$ with entries in ![]() $\mathrm {H}^0(\,]Y[\,,j^{\dagger} \mathcal {O}_Y)$, uniquely determined by the condition that
$\mathrm {H}^0(\,]Y[\,,j^{\dagger} \mathcal {O}_Y)$, uniquely determined by the condition that ![]() $\mathbf {f}(b_0 ) = \mathbf {0}$, where
$\mathbf {f}(b_0 ) = \mathbf {0}$, where ![]() $b_0$ is the Teichmüller point in the disk of
$b_0$ is the Teichmüller point in the disk of ![]() $b$.
$b$.
Next, we define a vector of functions ![]() $\mathbf {g}_0 := -F^{\intercal}Z \mathbf {f}$. Then the differential
$\mathbf {g}_0 := -F^{\intercal}Z \mathbf {f}$. Then the differential
is of the second kind, and therefore the reduction algorithms in ![]() $\mathrm {H}^1_{\mathrm {rig}}(Y)$ from [Reference TuitmanTui16, Reference TuitmanTui17] can be applied to compute a vector of constants
$\mathrm {H}^1_{\mathrm {rig}}(Y)$ from [Reference TuitmanTui16, Reference TuitmanTui17] can be applied to compute a vector of constants ![]() $\mathbf {c} \in \mathbf {Q}_p^{2g}$ and a function
$\mathbf {c} \in \mathbf {Q}_p^{2g}$ and a function ![]() $H$Footnote 4
$H$Footnote 4 ![]() $\in \mathrm {H}^0(\,]Y[\,,j^{\dagger} \mathcal {O}_Y)$ such that
$\in \mathrm {H}^0(\,]Y[\,,j^{\dagger} \mathcal {O}_Y)$ such that
Hence, the function ![]() $\mathbf {g}:= \mathbf {g}_0 +\mathbf {c}$ satisfies
$\mathbf {g}:= \mathbf {g}_0 +\mathbf {c}$ satisfies
and we normalise ![]() $H$ by requiring that
$H$ by requiring that ![]() $H(b_0)=0$. The matrix
$H(b_0)=0$. The matrix
 \begin{equation} G = \left( \begin{array}{@{}ccc@{}} 1 & 0 & 0 \\ \mathbf{f} & F & 0\\ H & \mathbf{g}^\intercal & p \\ \end{array} \right) \end{equation}
\begin{equation} G = \left( \begin{array}{@{}ccc@{}} 1 & 0 & 0 \\ \mathbf{f} & F & 0\\ H & \mathbf{g}^\intercal & p \\ \end{array} \right) \end{equation}then satisfies (4.3).
4.2.1 Frobenius-equivariant splitting for Teichmüller points
Suppose that ![]() $x_0\in X(\mathbf {Q}_p)\cap ]\mathcal {U}[$ is a Teichmüller point. As described in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 5.3.2], the Frobenius-equivariant splitting of
$x_0\in X(\mathbf {Q}_p)\cap ]\mathcal {U}[$ is a Teichmüller point. As described in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 5.3.2], the Frobenius-equivariant splitting of ![]() $M(x_0)$ is given by
$M(x_0)$ is given by
 \begin{equation} \lambda^\phi(x_0) = \left( \begin{array}{@{}ccc@{}} 1 & 0 & 0 \\ (I-F)^{-1}\mathbf{f} & 1 & 0\\ \dfrac{1}{1-p}\big(\mathbf{g}^{\intercal}(I-F)^{-1}\mathbf{f} +H\big) & \mathbf{g}^{\intercal}(F-p)^{-1} & 1 \\ \end{array} \right)(x_0). \end{equation}
\begin{equation} \lambda^\phi(x_0) = \left( \begin{array}{@{}ccc@{}} 1 & 0 & 0 \\ (I-F)^{-1}\mathbf{f} & 1 & 0\\ \dfrac{1}{1-p}\big(\mathbf{g}^{\intercal}(I-F)^{-1}\mathbf{f} +H\big) & \mathbf{g}^{\intercal}(F-p)^{-1} & 1 \\ \end{array} \right)(x_0). \end{equation}
The loss of precision in the computation of ![]() $\mathbf {f}$ and
$\mathbf {f}$ and ![]() $F$ is estimated in [Reference TuitmanTui17]. Hence, it is easy to bound the precision loss in the computation of
$F$ is estimated in [Reference TuitmanTui17]. Hence, it is easy to bound the precision loss in the computation of ![]() $\lambda ^\phi (x_0)$ using the following result.
$\lambda ^\phi (x_0)$ using the following result.
Proposition 4.1 Suppose that the entries of the matrix ![]() $G$ and a point
$G$ and a point ![]() $P\in X(\mathbf {Q}_p)\cap ]\mathcal {U}[$ are accurate to
$P\in X(\mathbf {Q}_p)\cap ]\mathcal {U}[$ are accurate to ![]() $n$ digits of precision. Then
$n$ digits of precision. Then ![]() $G(P)$ is also accurate to
$G(P)$ is also accurate to ![]() $n$ digits of precision.
$n$ digits of precision.
Our proof of Proposition 4.1 is somewhat similar to but more involved than the proofs in [Reference Balakrishnan and TuitmanBT20, § 4], where the loss of precision in the evaluation of ![]() $\mathbf {f}$ and of single Coleman integrals is estimated. We may expand
$\mathbf {f}$ and of single Coleman integrals is estimated. We may expand
 \begin{equation} \xi = \sum_{j \in \mathbf{Z}}\biggl(\sum_{k=0}^{d_x - 1} \frac{w_{j,k}(x)}{r(x)^j} b_k^0\biggr)\frac{{d} x}{r}. \end{equation}
\begin{equation} \xi = \sum_{j \in \mathbf{Z}}\biggl(\sum_{k=0}^{d_x - 1} \frac{w_{j,k}(x)}{r(x)^j} b_k^0\biggr)\frac{{d} x}{r}. \end{equation}
The hardest part of the proof of Proposition 4.1 is to find lower bounds on the valuation of the coefficients ![]() $w_{j,k}$, which we now describe. Let
$w_{j,k}$, which we now describe. Let ![]() $e_0$ (respectively,
$e_0$ (respectively, ![]() $e_\infty$) be the maximum of the ramification indices of the map
$e_\infty$) be the maximum of the ramification indices of the map ![]() $x\colon X\to \mathbf {P}^1$ with respect to our chosen model at points lying in affine (resp., infinite) disks.
$x\colon X\to \mathbf {P}^1$ with respect to our chosen model at points lying in affine (resp., infinite) disks.
Lemma 4.2 There is a constant ![]() $\kappa$ such that for all
$\kappa$ such that for all ![]() $j,k$ we have
$j,k$ we have
 \begin{equation} \mathrm{ord}_p(w_{jk}) \geq \begin{cases} \left\lfloor\dfrac{j}{p}\right\rfloor + 1 - \log_p(je_0) +\kappa , & j \neq 0,\\ \kappa, & j = 0. \end{cases} \end{equation}
\begin{equation} \mathrm{ord}_p(w_{jk}) \geq \begin{cases} \left\lfloor\dfrac{j}{p}\right\rfloor + 1 - \log_p(je_0) +\kappa , & j \neq 0,\\ \kappa, & j = 0. \end{cases} \end{equation}Proof. Looking at the constituent parts of (4.5), we start with ![]() $(\phi ^*\boldsymbol {\omega }^{\intercal})Z\mathbf {f}$. We write
$(\phi ^*\boldsymbol {\omega }^{\intercal})Z\mathbf {f}$. We write
 \[ (\phi^*\boldsymbol{\omega}^{\intercal})_i = \sum_{j_1 \in \mathbf{Z}} \biggl(\sum_{k_1 = 0}^{d_x - 1} \frac{d_{j_1, k_1}^{(i)}(x)}{r^{j_1}} b_{k_1}^0\biggr) \frac{{d} x}{r}. \]
\[ (\phi^*\boldsymbol{\omega}^{\intercal})_i = \sum_{j_1 \in \mathbf{Z}} \biggl(\sum_{k_1 = 0}^{d_x - 1} \frac{d_{j_1, k_1}^{(i)}(x)}{r^{j_1}} b_{k_1}^0\biggr) \frac{{d} x}{r}. \]
Then ![]() $\mathrm {ord}_p(d_{j_1, k_1}^{(i)}) \geq \lfloor {j_1}/{p} \rfloor + 1$ by [Reference TuitmanTui17, Proof of Proposition 4.9]. We have
$\mathrm {ord}_p(d_{j_1, k_1}^{(i)}) \geq \lfloor {j_1}/{p} \rfloor + 1$ by [Reference TuitmanTui17, Proof of Proposition 4.9]. We have
where ![]() $f_{i,0}, f_{i,\infty }$ and
$f_{i,0}, f_{i,\infty }$ and ![]() $f_{i,\mathrm {end}}$ correspond to the three reduction steps (2), (3) and (4) in the reduction algorithm from [Reference TuitmanTui17], summarised in [Reference Balakrishnan and TuitmanBT20, Algorithm 2.18]. By (1), (3) and (4) of [Reference Balakrishnan and TuitmanBT20], there are
$f_{i,\mathrm {end}}$ correspond to the three reduction steps (2), (3) and (4) in the reduction algorithm from [Reference TuitmanTui17], summarised in [Reference Balakrishnan and TuitmanBT20, Algorithm 2.18]. By (1), (3) and (4) of [Reference Balakrishnan and TuitmanBT20], there are ![]() $\mu _1, \lambda _1\ge 0$ such that
$\mu _1, \lambda _1\ge 0$ such that
 \begin{gather*} f_{i,0} = \sum_{j_2 = 1}^{\infty}
\biggl(\sum_{k_2 = 0}^{d_x -1} \frac{c_{j_2, k_2}^{(i)}(x)}{r^{j_2}}b_{k_2}^0\biggr),\\ f_{i, \infty} = \sum_{k_3 = 0}^{d_x-1}
\sum_{l = 0}^{\mu_1} e_{k_3, l}^{(i)} x^l b_{k_3}^0, \quad f_{i,\mathrm{end}} = \sum_{k_4 = 0}^{d_x-1}\sum_{m=0}^{\lambda_1}
u_{k_4, m}^{(i)}x^m b_{k_4}^0. \end{gather*}
\begin{gather*} f_{i,0} = \sum_{j_2 = 1}^{\infty}
\biggl(\sum_{k_2 = 0}^{d_x -1} \frac{c_{j_2, k_2}^{(i)}(x)}{r^{j_2}}b_{k_2}^0\biggr),\\ f_{i, \infty} = \sum_{k_3 = 0}^{d_x-1}
\sum_{l = 0}^{\mu_1} e_{k_3, l}^{(i)} x^l b_{k_3}^0, \quad f_{i,\mathrm{end}} = \sum_{k_4 = 0}^{d_x-1}\sum_{m=0}^{\lambda_1}
u_{k_4, m}^{(i)}x^m b_{k_4}^0. \end{gather*}
Equation (2) of [Reference Balakrishnan and TuitmanBT20] implies the lower bound ![]() $\mathrm {ord}_p(c_{j_2, k_2}^{(i)}) \geq \left \lfloor {j_2}/{p} \right \rfloor + 1 - \log _p \lfloor j_2 e_0\rfloor.$ Let
$\mathrm {ord}_p(c_{j_2, k_2}^{(i)}) \geq \left \lfloor {j_2}/{p} \right \rfloor + 1 - \log _p \lfloor j_2 e_0\rfloor.$ Let
Without loss of generality, the matrix ![]() $Z$ has
$Z$ has ![]() $p$-integral entries. Hence, every
$p$-integral entries. Hence, every ![]() $(Z\mathbf {f})_i$ is of the form
$(Z\mathbf {f})_i$ is of the form
 \begin{equation} (Z\mathbf{f})_i = \sum_{j_2 = 0}^{\infty} \sum_{k_2 = 0}^{d_x -1} \frac{g^{(i)}_{j_2,k_2}(x)}{r^{j_2}}b_{k_2}^0 \end{equation}
\begin{equation} (Z\mathbf{f})_i = \sum_{j_2 = 0}^{\infty} \sum_{k_2 = 0}^{d_x -1} \frac{g^{(i)}_{j_2,k_2}(x)}{r^{j_2}}b_{k_2}^0 \end{equation}
where, for all ![]() $k_2$, we have
$k_2$, we have
 \begin{equation} \mathrm{ord}_p(g^{(i)}_{j_2,k_2}) \geq \begin{cases} \left\lfloor\dfrac{j_2}{p}\right\rfloor + 1 - \log_p\lfloor j_2 e_0\rfloor, & \text{if}\ j_2>0,\\ \kappa_1, & \text{if}\ j_2=0.\\ \end{cases} \end{equation}
\begin{equation} \mathrm{ord}_p(g^{(i)}_{j_2,k_2}) \geq \begin{cases} \left\lfloor\dfrac{j_2}{p}\right\rfloor + 1 - \log_p\lfloor j_2 e_0\rfloor, & \text{if}\ j_2>0,\\ \kappa_1, & \text{if}\ j_2=0.\\ \end{cases} \end{equation} Let us now consider, for each ![]() $i$,
$i$,
 \begin{align*}
\big(\phi^*\boldsymbol{\omega}^{\intercal}\big)_i \big(Z\mathbf{f}\big)_i &= \sum_{j_1 \in \mathbf{Z}}
\biggl(\sum_{k_1 = 0}^{d_x-1} \frac{d_{j_1,k_1}^{(i)}}{r^{j_1}}b_{k_1}^0\biggr) \biggl(\sum_{j_2 = 0}^{\infty}\sum_{k_2 = 0}^{d_x-1}
\frac{g^{(i)}_{j_2,k_2}}{r^{j_2}}b_{k_2}^0\biggr)\frac{{d} x}{r}\\ &=\sum_{j = j_1 + j_2 \in \mathbf{Z}, j_1 \in \mathbf{Z}, j_2 \geq 0}
\frac{1}{r^j}\biggl(\sum_{k = k_1 + k_2, k_i \in \{0,\ldots,d_x-1\}} \big(d^{(i)}_{j_1,k_1} g^{(i)}_{j_2,k_2}\big)b_k^0\biggr)\frac{{d} x}{r}\\
&=:\sum_{j\in \mathbf{Z}}\biggl(\frac{1}{r^j}\sum^{d_x-1}_{k=1} \tau_{jk}b_k^0\biggr) \frac{{d} x}{r}. \end{align*}
\begin{align*}
\big(\phi^*\boldsymbol{\omega}^{\intercal}\big)_i \big(Z\mathbf{f}\big)_i &= \sum_{j_1 \in \mathbf{Z}}
\biggl(\sum_{k_1 = 0}^{d_x-1} \frac{d_{j_1,k_1}^{(i)}}{r^{j_1}}b_{k_1}^0\biggr) \biggl(\sum_{j_2 = 0}^{\infty}\sum_{k_2 = 0}^{d_x-1}
\frac{g^{(i)}_{j_2,k_2}}{r^{j_2}}b_{k_2}^0\biggr)\frac{{d} x}{r}\\ &=\sum_{j = j_1 + j_2 \in \mathbf{Z}, j_1 \in \mathbf{Z}, j_2 \geq 0}
\frac{1}{r^j}\biggl(\sum_{k = k_1 + k_2, k_i \in \{0,\ldots,d_x-1\}} \big(d^{(i)}_{j_1,k_1} g^{(i)}_{j_2,k_2}\big)b_k^0\biggr)\frac{{d} x}{r}\\
&=:\sum_{j\in \mathbf{Z}}\biggl(\frac{1}{r^j}\sum^{d_x-1}_{k=1} \tau_{jk}b_k^0\biggr) \frac{{d} x}{r}. \end{align*}
We distinguish two cases. If ![]() $j_2 > 0$ then
$j_2 > 0$ then
If ![]() $j_2 = 0$, then
$j_2 = 0$, then ![]() $\mathrm {ord}_p(d^{(i)}_{j_1,k_1}g^{(i)}_{j_2,k_2})\geq \left \lfloor {j_1}/{p}\right \rfloor + 1 + \kappa _1$. Together, these yield
$\mathrm {ord}_p(d^{(i)}_{j_1,k_1}g^{(i)}_{j_2,k_2})\geq \left \lfloor {j_1}/{p}\right \rfloor + 1 + \kappa _1$. Together, these yield
The next term to consider in (4.5) is ![]() $\phi ^* \eta - p \eta$, where
$\phi ^* \eta - p \eta$, where ![]() $\eta$ is constructed in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 4]. Let
$\eta$ is constructed in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 4]. Let ![]() $\kappa _2$ denote the
$\kappa _2$ denote the ![]() $p$-adic valuation of the vector of coefficients of
$p$-adic valuation of the vector of coefficients of ![]() $\eta$ in terms of the basis differentials
$\eta$ in terms of the basis differentials ![]() $\omega _{2g},\ldots,\omega _{2g+2-d}$ (see [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 4.1]). Write
$\omega _{2g},\ldots,\omega _{2g+2-d}$ (see [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 4.1]). Write
 \[ \phi^*\eta - p\eta = \sum_{j \in \mathbf{Z}}\biggl(\sum_{k = 0}^{d_x-1} \frac{s_{jk}(x)}{r^j} b_k^0\biggr) \frac{{d} x}{r}. \]
\[ \phi^*\eta - p\eta = \sum_{j \in \mathbf{Z}}\biggl(\sum_{k = 0}^{d_x-1} \frac{s_{jk}(x)}{r^j} b_k^0\biggr) \frac{{d} x}{r}. \]
Then the ![]() $s_{jk}$ satisfy
$s_{jk}$ satisfy ![]() $\mathrm {ord}_p(s_{jk}) \geq \kappa _2 + \left \lfloor {j}/{p} \right \rfloor + 1$ if
$\mathrm {ord}_p(s_{jk}) \geq \kappa _2 + \left \lfloor {j}/{p} \right \rfloor + 1$ if ![]() $j\neq 0$ and
$j\neq 0$ and ![]() $\mathrm {ord}_p(s_{0k}) \geq \kappa _2 +1$, so
$\mathrm {ord}_p(s_{0k}) \geq \kappa _2 +1$, so
For the final summand ![]() $\mathbf {g}_0 ^{\intercal}\boldsymbol {\omega }$ in (4.5) note that since
$\mathbf {g}_0 ^{\intercal}\boldsymbol {\omega }$ in (4.5) note that since ![]() $F$ has
$F$ has ![]() $p$-integral entries, every
$p$-integral entries, every ![]() $(F^{\intercal}Z \mathbf {f})_i$ has an expansion as in (4.12). Because
$(F^{\intercal}Z \mathbf {f})_i$ has an expansion as in (4.12). Because ![]() $\omega _i$ is integral for all
$\omega _i$ is integral for all ![]() $i$, the lower bounds in (4.13) remain valid for
$i$, the lower bounds in (4.13) remain valid for ![]() $\mathbf {g}_0 ^{\intercal}\boldsymbol {\omega }$. The proof of Lemma 4.2 follows from this and from (4.14) and (4.15) upon setting
$\mathbf {g}_0 ^{\intercal}\boldsymbol {\omega }$. The proof of Lemma 4.2 follows from this and from (4.14) and (4.15) upon setting ![]() $\kappa = \min \{\kappa _1,\kappa _2\}$.
$\kappa = \min \{\kappa _1,\kappa _2\}$.
We now estimate the precision loss that can occur during the application of the reduction algorithm from [Reference TuitmanTui17] to the differential ![]() $\xi$. Our proof is similar to the proof of [Reference TuitmanTui17, Prop 4.9], which estimates the precision loss in the reduction of
$\xi$. Our proof is similar to the proof of [Reference TuitmanTui17, Prop 4.9], which estimates the precision loss in the reduction of ![]() $F^*(\omega _i)$. Suppose that
$F^*(\omega _i)$. Suppose that ![]() $\xi$ is correct to
$\xi$ is correct to ![]() $n$ digits of
$n$ digits of ![]() $p$-adic precision. First consider terms in (4.9) with
$p$-adic precision. First consider terms in (4.9) with ![]() $j>0$. It follows from (4.10) that
$j>0$. It follows from (4.10) that ![]() $j - p\log _p(je_0) \leq pm - p\kappa$ (note that
$j - p\log _p(je_0) \leq pm - p\kappa$ (note that ![]() $\kappa \le 0$). By [Reference TuitmanTui17, Proposition 3.7], the precision loss at pole order
$\kappa \le 0$). By [Reference TuitmanTui17, Proposition 3.7], the precision loss at pole order ![]() $j$ during the reduction at finite points is at most
$j$ during the reduction at finite points is at most ![]() $\lfloor \log _p(j_{\max }e_0)\rfloor,$ where
$\lfloor \log _p(j_{\max }e_0)\rfloor,$ where ![]() $j_{\max }$ is the largest integer
$j_{\max }$ is the largest integer ![]() $j$ such that
$j$ such that ![]() $j - p\log _p(je_0) \leq pn - p\kappa.$ As in the proof of [Reference TuitmanTui17, Proposition 4.9], this might introduce small poles above
$j - p\log _p(je_0) \leq pn - p\kappa.$ As in the proof of [Reference TuitmanTui17, Proposition 4.9], this might introduce small poles above ![]() $\infty$, but by the same reasoning as in [Reference TuitmanTui17], the reduction of these poles leads to a loss of precision bounded by
$\infty$, but by the same reasoning as in [Reference TuitmanTui17], the reduction of these poles leads to a loss of precision bounded by ![]() $\lfloor \log _p(-(\mathrm {ord}_\infty W^{-1})+1)e_{\infty }\rfloor$. We set
$\lfloor \log _p(-(\mathrm {ord}_\infty W^{-1})+1)e_{\infty }\rfloor$. We set
If we write
 \[ \xi = \biggl(\sum_{i=0}^{d_x-1} \alpha_i(x,x^{-1})b_i^{\infty}\biggr)\frac{{d} x}{r}\quad\text{and}\quad m_\infty= -\min_i \{\mathrm{ord}_\infty\alpha_i-\deg(r) + 1\}, \]
\[ \xi = \biggl(\sum_{i=0}^{d_x-1} \alpha_i(x,x^{-1})b_i^{\infty}\biggr)\frac{{d} x}{r}\quad\text{and}\quad m_\infty= -\min_i \{\mathrm{ord}_\infty\alpha_i-\deg(r) + 1\}, \]
then the loss of precision during the reductions above infinity (where ![]() $j\leq 0$) is bounded by
$j\leq 0$) is bounded by ![]() $g_2:= \lfloor \log _p(m_\infty e_\infty )\rfloor.$
$g_2:= \lfloor \log _p(m_\infty e_\infty )\rfloor.$
Hence, we have established the following lemma.
Lemma 4.3 Suppose that ![]() $\xi$ is correct to
$\xi$ is correct to ![]() $n$ digits of precision. Then
$n$ digits of precision. Then ![]() $\mathbf {c}$ and
$\mathbf {c}$ and ![]() $H$ are correct to
$H$ are correct to ![]() $n-\max \{g_1(n), g_2\}$ digits of precision.
$n-\max \{g_1(n), g_2\}$ digits of precision.
Proof of Proposition 4.1 Similar to the ![]() $f_i$, we may decompose
$f_i$, we may decompose ![]() $H$ as
$H$ as ![]() $H = H_0 + H_{\infty } + H_{\mathrm {end}}$, corresponding to steps (2), (3) and (4), respectively, in [Reference Balakrishnan and TuitmanBT20, Algorithm 2.18]. By the above, the reduction above finite points introduces a denominator of valuation at most
$H = H_0 + H_{\infty } + H_{\mathrm {end}}$, corresponding to steps (2), (3) and (4), respectively, in [Reference Balakrishnan and TuitmanBT20, Algorithm 2.18]. By the above, the reduction above finite points introduces a denominator of valuation at most ![]() $\log _p(je_0)$ for pole order
$\log _p(je_0)$ for pole order ![]() $j$, therefore we have
$j$, therefore we have
 \begin{equation} H_0 = \sum_{j \geq 1}\sum_{k = 0}^{d_x - 1} \frac{c_{jk}(x)}{r^j} b_k^0,\quad\text{where}\ \mathrm{ord}_p(c_{jk}) \geq \left\lfloor \frac{j}{p} \right\rfloor - 2\log_p(je_0) + \kappa. \end{equation}
\begin{equation} H_0 = \sum_{j \geq 1}\sum_{k = 0}^{d_x - 1} \frac{c_{jk}(x)}{r^j} b_k^0,\quad\text{where}\ \mathrm{ord}_p(c_{jk}) \geq \left\lfloor \frac{j}{p} \right\rfloor - 2\log_p(je_0) + \kappa. \end{equation} Recall that the matrix ![]() $G$ is defined in (4.7). There is no loss of precision when evaluating
$G$ is defined in (4.7). There is no loss of precision when evaluating ![]() $\mathbf {f}(P)$ by [Reference Balakrishnan and TuitmanBT20, Proposition 4.5]. By our assumption that
$\mathbf {f}(P)$ by [Reference Balakrishnan and TuitmanBT20, Proposition 4.5]. By our assumption that ![]() $F$ and
$F$ and ![]() $Z$ are
$Z$ are ![]() $p$-integral, there is no precision loss when evaluating
$p$-integral, there is no precision loss when evaluating ![]() $\mathbf {g_0}(P)$. Using the bounds (4.17), the proof of [Reference Balakrishnan and TuitmanBT20, Proposition 4.5] shows that
$\mathbf {g_0}(P)$. Using the bounds (4.17), the proof of [Reference Balakrishnan and TuitmanBT20, Proposition 4.5] shows that ![]() $H(P)$ is accurate to
$H(P)$ is accurate to ![]() $n$ digits of precision as well. Since
$n$ digits of precision as well. Since ![]() $\mathbf {g} = \mathbf {g_0} + \mathbf {c}$, the proposition follows.
$\mathbf {g} = \mathbf {g_0} + \mathbf {c}$, the proposition follows.
4.2.2 Frobenius-equivariant splitting for general points
For ![]() $x\in X(\mathbf {Q}_p)\cap ]\mathcal {U}[$, not necessarily Teichmüller, the Frobenius-equivariant splitting
$x\in X(\mathbf {Q}_p)\cap ]\mathcal {U}[$, not necessarily Teichmüller, the Frobenius-equivariant splitting ![]() $\lambda ^\phi (x)$ of
$\lambda ^\phi (x)$ of ![]() $M(x)$ is given by
$M(x)$ is given by
 \begin{equation} \begin{pmatrix} 1 & 0 &
0 \\ \int_{x}^{x_0} \boldsymbol{\omega} & 1 & 0 \\
\int_{x}^{x_0} \eta+\int ^x _{x_0 }\boldsymbol{\omega
}^{\intercal }Z \boldsymbol{\omega } & \int_{x}^{x_0}
\boldsymbol{\omega}^{\intercal}Z & 1 \\ \end{pmatrix}\cdot
\begin{pmatrix} 1 & 0 & 0 \\ \int_{b_0}^b
\boldsymbol{\omega} & 1 & 0 \\ \int_{b_0}^b \eta +\int ^b
_{b_0 }\boldsymbol{\omega }^{\intercal }Z
\boldsymbol{\omega } & -\int_{b_0}^b
\boldsymbol{\omega}^{\intercal}Z & 1 \\ \end{pmatrix}\cdot
\lambda^\phi(x_0), \end{equation}
\begin{equation} \begin{pmatrix} 1 & 0 &
0 \\ \int_{x}^{x_0} \boldsymbol{\omega} & 1 & 0 \\
\int_{x}^{x_0} \eta+\int ^x _{x_0 }\boldsymbol{\omega
}^{\intercal }Z \boldsymbol{\omega } & \int_{x}^{x_0}
\boldsymbol{\omega}^{\intercal}Z & 1 \\ \end{pmatrix}\cdot
\begin{pmatrix} 1 & 0 & 0 \\ \int_{b_0}^b
\boldsymbol{\omega} & 1 & 0 \\ \int_{b_0}^b \eta +\int ^b
_{b_0 }\boldsymbol{\omega }^{\intercal }Z
\boldsymbol{\omega } & -\int_{b_0}^b
\boldsymbol{\omega}^{\intercal}Z & 1 \\ \end{pmatrix}\cdot
\lambda^\phi(x_0), \end{equation}
where ![]() $x_0$ is the Teichmüller point in the disk of
$x_0$ is the Teichmüller point in the disk of ![]() $x$. The first two matrices in (4.18) correspond to parallel transport of
$x$. The first two matrices in (4.18) correspond to parallel transport of ![]() $\Lambda$ from
$\Lambda$ from ![]() $x$ to
$x$ to ![]() $x_0$ and from
$x_0$ and from ![]() $b_0$ to
$b_0$ to ![]() $b$, respectively.
$b$, respectively.
For the local height ![]() $h_p(A(x))$, we need the Frobenius-equivariant splitting
$h_p(A(x))$, we need the Frobenius-equivariant splitting ![]() $\lambda ^\phi (x)$ both for fixed
$\lambda ^\phi (x)$ both for fixed ![]() $x$ and for
$x$ and for ![]() $x$ varying inside a residue disk. We start by bounding the valuations of the coefficients of power series expansions of the differentials in the parallel transport matrices of
$x$ varying inside a residue disk. We start by bounding the valuations of the coefficients of power series expansions of the differentials in the parallel transport matrices of ![]() $\Lambda$ in terms of a local coordinate
$\Lambda$ in terms of a local coordinate ![]() $t$ at a fixed affine point
$t$ at a fixed affine point ![]() $y_0 \in X(\mathbf {Q}_p)\cap ]\mathcal {U}[$. By assumption, the entries of the expansions of
$y_0 \in X(\mathbf {Q}_p)\cap ]\mathcal {U}[$. By assumption, the entries of the expansions of ![]() $\boldsymbol {\omega }$ and
$\boldsymbol {\omega }$ and ![]() $\boldsymbol {\omega }^{\intercal }Z$ all have integral coefficients, so their integrals have entries whose
$\boldsymbol {\omega }^{\intercal }Z$ all have integral coefficients, so their integrals have entries whose ![]() $i$th coefficient has valuation
$i$th coefficient has valuation ![]() $-\geq \mathrm {ord}_p(i)$. Therefore, we have
$-\geq \mathrm {ord}_p(i)$. Therefore, we have
 \begin{equation} \boldsymbol{\omega}(t)^{\intercal}Z\int \boldsymbol{\omega}(t) = \sum_{i\ge 1} a_it^i,\quad\text{where}\ \mathrm{ord}_p(a_i)\ge -\lfloor \log_p(i)\rfloor. \end{equation}
\begin{equation} \boldsymbol{\omega}(t)^{\intercal}Z\int \boldsymbol{\omega}(t) = \sum_{i\ge 1} a_it^i,\quad\text{where}\ \mathrm{ord}_p(a_i)\ge -\lfloor \log_p(i)\rfloor. \end{equation}It follows that
 \begin{equation} \int\biggl(\boldsymbol{\omega}(t)^{\intercal}Z\int \boldsymbol{\omega}(t)\biggr) = \sum_{i\ge 1} b_it^i,\quad\text{where}\ \mathrm{ord}_p(b_i)\ge -2\lfloor \log_p(i)\rfloor. \end{equation}
\begin{equation} \int\biggl(\boldsymbol{\omega}(t)^{\intercal}Z\int \boldsymbol{\omega}(t)\biggr) = \sum_{i\ge 1} b_it^i,\quad\text{where}\ \mathrm{ord}_p(b_i)\ge -2\lfloor \log_p(i)\rfloor. \end{equation} By construction, the coefficients of ![]() $\eta$ in terms of
$\eta$ in terms of ![]() $\omega _{2g},\ldots,\omega _{2g+d-2}$ are polynomials in
$\omega _{2g},\ldots,\omega _{2g+d-2}$ are polynomials in ![]() $x$. Define
$x$. Define ![]() $d_i(\eta )$ to be the valuation of the
$d_i(\eta )$ to be the valuation of the ![]() $i$th coefficient if
$i$th coefficient if ![]() $i$ is smaller than the maximum of the degrees of these coefficients and 0 otherwise. Then the
$i$ is smaller than the maximum of the degrees of these coefficients and 0 otherwise. Then the ![]() $i$th coefficient of the integral of
$i$th coefficient of the integral of ![]() $\eta$ has valuation at least
$\eta$ has valuation at least ![]() $-\mathrm {ord}_p(i)-d_i(\eta )$. Hence, the
$-\mathrm {ord}_p(i)-d_i(\eta )$. Hence, the ![]() $i$th coefficient of every expansion of the parallel transport matrix in
$i$th coefficient of every expansion of the parallel transport matrix in ![]() $t$ has valuation at least
$t$ has valuation at least
For definite parallel transport from ![]() $y_0$ to another
$y_0$ to another ![]() $\mathbf {Q}_p$-point
$\mathbf {Q}_p$-point ![]() $y_1$ in the same residue disk, we need to evaluate the integrals above. Suppose that
$y_1$ in the same residue disk, we need to evaluate the integrals above. Suppose that ![]() $y_0,y_1$, and the coefficients of the expansions of
$y_0,y_1$, and the coefficients of the expansions of ![]() $\boldsymbol {\omega }$ and
$\boldsymbol {\omega }$ and ![]() $\eta$ are correct to
$\eta$ are correct to ![]() $n$ digits of
$n$ digits of ![]() $p$-adic precision, and suppose that the expansions are truncated modulo
$p$-adic precision, and suppose that the expansions are truncated modulo ![]() $t^l$. Let
$t^l$. Let
Then ![]() $\int _{y_0}^{y_1}\omega _j$ and
$\int _{y_0}^{y_1}\omega _j$ and ![]() $\int _{y_0}^{y_1}(Z\boldsymbol {\omega })_j$ are correct to
$\int _{y_0}^{y_1}(Z\boldsymbol {\omega })_j$ are correct to ![]() $\min \{\nu _1,\nu _2\}$ digits by [Reference Balakrishnan and TuitmanBT20, Proposition 4.1]. The proof of [Reference Balakrishnan and TuitmanBT20, Proposition 4.1] requires that the differential we integrate has integral coefficients. A modification of this proof yields that the integral
$\min \{\nu _1,\nu _2\}$ digits by [Reference Balakrishnan and TuitmanBT20, Proposition 4.1]. The proof of [Reference Balakrishnan and TuitmanBT20, Proposition 4.1] requires that the differential we integrate has integral coefficients. A modification of this proof yields that the integral ![]() $\int _{y_0}^{y_1}\eta$ is correct to
$\int _{y_0}^{y_1}\eta$ is correct to ![]() $\min \{\nu _1', \nu _2\}$ digits, where
$\min \{\nu _1', \nu _2\}$ digits, where ![]() $\nu '_1=1+\min _{i\ge l}\{i-\lfloor \log _p(i+1)\rfloor -d_i(\eta )\}.$ A similar modification shows that the double integral
$\nu '_1=1+\min _{i\ge l}\{i-\lfloor \log _p(i+1)\rfloor -d_i(\eta )\}.$ A similar modification shows that the double integral ![]() $\int ^{y_1} _{{y_0}}\boldsymbol {\omega }^{\intercal }Z \boldsymbol {\omega }$ is correct to
$\int ^{y_1} _{{y_0}}\boldsymbol {\omega }^{\intercal }Z \boldsymbol {\omega }$ is correct to ![]() $\min \{\nu _1'', \nu _2'\}$ digits, where
$\min \{\nu _1'', \nu _2'\}$ digits, where ![]() $\nu _1''= 1+\min _{i\ge l}\{i-2\lfloor \log _p(i+1)\rfloor \}$ and
$\nu _1''= 1+\min _{i\ge l}\{i-2\lfloor \log _p(i+1)\rfloor \}$ and
Hence, we obtain the following lemma.
Lemma 4.4 The parallel transport matrix from ![]() ${y_0}$ to
${y_0}$ to ![]() ${y_1}$ is correct to
${y_1}$ is correct to ![]() $\min \{\nu _1',\nu ''_2, \nu _2'\}$ digits of precision.
$\min \{\nu _1',\nu ''_2, \nu _2'\}$ digits of precision.
Using (4.18), we can finally bound the loss of precision in the computation of ![]() $\lambda ^\phi (x)$ for fixed points
$\lambda ^\phi (x)$ for fixed points ![]() $x\in X(\mathbf {Q}_p)\cap ]\mathcal {U}[$ by combining Lemma 4.4 and Proposition 4.1.
$x\in X(\mathbf {Q}_p)\cap ]\mathcal {U}[$ by combining Lemma 4.4 and Proposition 4.1.
4.3 Global heights
We now discuss the possible precision loss in the computation of the global height ![]() $h$. In step (vi(b)) of Algorithm 3.12 we solve for
$h$. In step (vi(b)) of Algorithm 3.12 we solve for ![]() $d_1,\ldots,d_g$ such that
$d_1,\ldots,d_g$ such that
in terms of a basis ![]() $\{\Psi _i\}$ of bilinear pairings on
$\{\Psi _i\}$ of bilinear pairings on ![]() $\mathrm {H}^0(X_{\mathbf {Q}_p}, \Omega ^1)^{\vee }$ by evaluating
$\mathrm {H}^0(X_{\mathbf {Q}_p}, \Omega ^1)^{\vee }$ by evaluating ![]() $h$ and the
$h$ and the ![]() $\Psi _i$. Recall that our method for determining the coefficients depends on whether there are sufficiently many rational points on
$\Psi _i$. Recall that our method for determining the coefficients depends on whether there are sufficiently many rational points on ![]() $X$ in the sense of § 3.3. If this is the case, meaning that we can use a basis consisting of
$X$ in the sense of § 3.3. If this is the case, meaning that we can use a basis consisting of ![]() $\pi (\mathrm {A}_Z(b,x))$ for rational points
$\pi (\mathrm {A}_Z(b,x))$ for rational points ![]() $x\in X(\mathbf {Q})\cap ]\mathcal {U}[$, then we need to compute
$x\in X(\mathbf {Q})\cap ]\mathcal {U}[$, then we need to compute ![]() $h_p(\mathrm {A}_Z(b,z)$ and
$h_p(\mathrm {A}_Z(b,z)$ and ![]() $\pi (\mathrm {A}_Z(b,x))$, and then apply simple linear algebra. The precision loss in the computation
$\pi (\mathrm {A}_Z(b,x))$, and then apply simple linear algebra. The precision loss in the computation ![]() $h_p(\mathrm {A}_Z(b,x))$ has already been bounded and
$h_p(\mathrm {A}_Z(b,x))$ has already been bounded and ![]() $\pi (\mathrm {A}_Z(b,x))$ can be obtained directly from the same data (see [Reference Balakrishnan, Best, Bianchi, Lawrence, Müller, Triantafillou and VonkBBB+21, Equation (41)]). The loss of precision in the linear algebra computations is easy to detect in practice, so we do not bound it explicitly here.
$\pi (\mathrm {A}_Z(b,x))$ can be obtained directly from the same data (see [Reference Balakrishnan, Best, Bianchi, Lawrence, Müller, Triantafillou and VonkBBB+21, Equation (41)]). The loss of precision in the linear algebra computations is easy to detect in practice, so we do not bound it explicitly here.
In the other case, the basis ![]() $\Psi _i$ is given in terms of products of abelian integrals. As mentioned above, the loss of precision in their computation is estimated in [Reference Balakrishnan and TuitmanBT20]. It remains to discuss precision loss in the computation of Coleman–Gross local heights
$\Psi _i$ is given in terms of products of abelian integrals. As mentioned above, the loss of precision in their computation is estimated in [Reference Balakrishnan and TuitmanBT20]. It remains to discuss precision loss in the computation of Coleman–Gross local heights ![]() $h_p(D_1,D_2)$, where
$h_p(D_1,D_2)$, where ![]() $D_1, D_2$ are divisors in
$D_1, D_2$ are divisors in ![]() $\mathrm {Div}^0(X)(\mathbf {Q}_p)$ for
$\mathrm {Div}^0(X)(\mathbf {Q}_p)$ for ![]() $X$ a hyperelliptic curve subject to the hypotheses of Algorithm 3.4 (see [Reference Balakrishnan and BesserBB12, § 6.2] for further details). Choosing
$X$ a hyperelliptic curve subject to the hypotheses of Algorithm 3.4 (see [Reference Balakrishnan and BesserBB12, § 6.2] for further details). Choosing ![]() $\omega$ in step (1) can be done up to the precision of the points in the support of the divisor
$\omega$ in step (1) can be done up to the precision of the points in the support of the divisor ![]() $D_1.$ To compute
$D_1.$ To compute ![]() $\Psi (\omega )$ and
$\Psi (\omega )$ and ![]() $\omega _{D_1}$ to
$\omega _{D_1}$ to ![]() $O(p^n)$ in step (2) (see § 5.2 and § 6.2.3 of [Reference Balakrishnan and BesserBB12]): one needs to compute the local coordinates
$O(p^n)$ in step (2) (see § 5.2 and § 6.2.3 of [Reference Balakrishnan and BesserBB12]): one needs to compute the local coordinates ![]() $(x(t),y(t))$ at infinity, with
$(x(t),y(t))$ at infinity, with ![]() $x(t)$ to precision
$x(t)$ to precision ![]() $t^{2(2g-1)}$ and
$t^{2(2g-1)}$ and ![]() $y(t)$ to precision
$y(t)$ to precision ![]() $t^{2g-1}$, where these
$t^{2g-1}$, where these ![]() $t$-adic estimates are made based on the maximal pole order in the basis of
$t$-adic estimates are made based on the maximal pole order in the basis of ![]() $H^1_{\scriptstyle \mathrm {dR}}(X)$. Step (4) proceeds similarly to this step as well.
$H^1_{\scriptstyle \mathrm {dR}}(X)$. Step (4) proceeds similarly to this step as well.
In step (5), the tiny integrals are computed as in [Reference Balakrishnan and BesserBB12, § 6]. In previous steps, we wrote ![]() $\Psi (\alpha )$ and
$\Psi (\alpha )$ and ![]() $\Psi (\beta )$ as
$\Psi (\beta )$ as ![]() $\mathbf {Q}_p$-linear combinations of the basis elements of
$\mathbf {Q}_p$-linear combinations of the basis elements of ![]() $H_{\scriptstyle \mathrm {dR}}^1(X)$, up to precision
$H_{\scriptstyle \mathrm {dR}}^1(X)$, up to precision ![]() $O(p^n)$. Note that the hypothesis that
$O(p^n)$. Note that the hypothesis that ![]() $p> 2g-1$ is to ensure that the cup product matrix has entries that are
$p> 2g-1$ is to ensure that the cup product matrix has entries that are ![]() $p$-integral, so no precision loss comes from the cup product matrix.
$p$-integral, so no precision loss comes from the cup product matrix.
Finally, for ![]() $\sum _{A \in X(\mathbf {C}_p)}\mathrm {Res}_{A}\big (\alpha \int \beta \big )$, we consider the cases of
$\sum _{A \in X(\mathbf {C}_p)}\mathrm {Res}_{A}\big (\alpha \int \beta \big )$, we consider the cases of ![]() $A$ a non-Weierstrass point (where we describe the computation in the annulus of
$A$ a non-Weierstrass point (where we describe the computation in the annulus of ![]() $A$) versus
$A$) versus ![]() $A$ Weierstrass (where we have just one contribution, at the Weierstrass point). If
$A$ Weierstrass (where we have just one contribution, at the Weierstrass point). If ![]() $A \neq (0,0)$ is a Weierstrass point, we compute the local coordinate
$A \neq (0,0)$ is a Weierstrass point, we compute the local coordinate ![]() $(x(t),y(t))$ at
$(x(t),y(t))$ at ![]() $A$ to precision
$A$ to precision ![]() $t^{2pn-p-1}$ (see the corrected Proposition 6.5 in [Reference Balakrishnan and BesserBB21]) so that
$t^{2pn-p-1}$ (see the corrected Proposition 6.5 in [Reference Balakrishnan and BesserBB21]) so that ![]() $\mathrm {Res}_A(\alpha \int \beta )$ is computed to
$\mathrm {Res}_A(\alpha \int \beta )$ is computed to ![]() $n$ digits of
$n$ digits of ![]() $p$-adic precision.
$p$-adic precision.
Now we consider the non-Weierstrass poles of ![]() $\alpha$. For the annulus of a non-Weierstrass pole
$\alpha$. For the annulus of a non-Weierstrass pole ![]() $A$, the generic situation is handled by [Reference Balakrishnan and BesserBB12, Corollary 6.4]. By [Reference Balakrishnan and BesserBB12, Remark 4.10], we consider all
$A$, the generic situation is handled by [Reference Balakrishnan and BesserBB12, Corollary 6.4]. By [Reference Balakrishnan and BesserBB12, Remark 4.10], we consider all ![]() $A \in \{P_i, Q_j\}_{i,j}$ where
$A \in \{P_i, Q_j\}_{i,j}$ where ![]() $x(P_i)$ corresponds to a root of an irreducible factor of
$x(P_i)$ corresponds to a root of an irreducible factor of ![]() $x^p - x(P)$ (and similarly where
$x^p - x(P)$ (and similarly where ![]() $x(Q_j)$ corresponds to a root of an irreducible factor of
$x(Q_j)$ corresponds to a root of an irreducible factor of ![]() $x^p - x(Q)$). For these
$x^p - x(Q)$). For these ![]() $i,j$, we compute
$i,j$, we compute ![]() $\int _P^{P_i}\beta$ and
$\int _P^{P_i}\beta$ and ![]() $\int _Q^{Q_j} \beta$ and trace down to
$\int _Q^{Q_j} \beta$ and trace down to ![]() $\mathbf {Q}_p$. We suppose
$\mathbf {Q}_p$. We suppose ![]() $P \in X(\mathbf {Q}_p)$ has precision
$P \in X(\mathbf {Q}_p)$ has precision ![]() $O(p^n)$. Fix
$O(p^n)$. Fix ![]() $m$ and suppose
$m$ and suppose ![]() $\beta$ is computed to
$\beta$ is computed to ![]() $t^{d_i m}$ at
$t^{d_i m}$ at ![]() $P_i$, where
$P_i$, where ![]() $d_i = [\mathbf {Q}_p(P_i): \mathbf {Q}_p]$. Let
$d_i = [\mathbf {Q}_p(P_i): \mathbf {Q}_p]$. Let ![]() $\pi _i$ be a uniformiser of
$\pi _i$ be a uniformiser of ![]() $\mathbf {Q}_p(P_i)$. Note that
$\mathbf {Q}_p(P_i)$. Note that ![]() $P$ is known to
$P$ is known to ![]() $d_i n$
$d_i n$ ![]() $\pi _i$-adic digits, and suppose that
$\pi _i$-adic digits, and suppose that ![]() $P_i$ is known to
$P_i$ is known to ![]() $n_i$
$n_i$ ![]() $\pi _i$-adic digits. Then the
$\pi _i$-adic digits. Then the ![]() $\pi _i$-adic precision of
$\pi _i$-adic precision of ![]() $\int _P^{P_i} \beta$ is at least
$\int _P^{P_i} \beta$ is at least ![]() $\min \{n_i, d_i n, \lfloor d_i m + 1\rfloor - \log _p(d_i m + 1)\}.$ We similarly repeat this for
$\min \{n_i, d_i n, \lfloor d_i m + 1\rfloor - \log _p(d_i m + 1)\}.$ We similarly repeat this for ![]() $Q$ and the corresponding
$Q$ and the corresponding ![]() $Q_j$. Hence,
$Q_j$. Hence, ![]() $\sum _A\mathrm {Res}_A(\alpha \int \beta )$, where the sum is over all non-Weierstrass poles
$\sum _A\mathrm {Res}_A(\alpha \int \beta )$, where the sum is over all non-Weierstrass poles ![]() $A$ of
$A$ of ![]() $\alpha$, is correct to
$\alpha$, is correct to ![]() $p$-adic precision
$p$-adic precision
where we consider the corresponding ![]() $i,j$ for all
$i,j$ for all ![]() $P_i$ and all
$P_i$ and all ![]() $Q_j$.
$Q_j$.
4.4 Coefficients of the quadratic Chabauty function and root finding
The previous results of this section bound the loss of precision in the computation of the quadratic Chabauty function ![]() $\rho = h-h_p$. Let
$\rho = h-h_p$. Let ![]() $D\subset X(\mathbf {Q}_p)\cap ]\mathcal {U}[$ be a residue disk and let
$D\subset X(\mathbf {Q}_p)\cap ]\mathcal {U}[$ be a residue disk and let ![]() $x_0$ be the Teichmüller point in
$x_0$ be the Teichmüller point in ![]() $D$. We now bound the valuations of the coefficients of the expansion of
$D$. We now bound the valuations of the coefficients of the expansion of ![]() $\rho$ in
$\rho$ in ![]() $D$ and show how to provably compute its roots to desired precision.
$D$ and show how to provably compute its roots to desired precision.
In our algorithm, we fix a point ![]() $x_1\in D$, and we compute the Frobenius-equivariant splitting
$x_1\in D$, and we compute the Frobenius-equivariant splitting ![]() $\lambda ^\phi (x)$ on
$\lambda ^\phi (x)$ on ![]() $D$ as a power series in a local coordinate
$D$ as a power series in a local coordinate ![]() $t$ in
$t$ in ![]() $x_1$ by first computing
$x_1$ by first computing ![]() $\lambda ^\phi (x_1)$ from
$\lambda ^\phi (x_1)$ from ![]() $\lambda ^\phi (x_0)$ and then multiplying this by the parallel transport matrix from
$\lambda ^\phi (x_0)$ and then multiplying this by the parallel transport matrix from ![]() $x_1$ to
$x_1$ to ![]() $x$. To bound the valuations of the coefficients of the entries of
$x$. To bound the valuations of the coefficients of the entries of ![]() $\lambda ^\phi (x)$, we first compute
$\lambda ^\phi (x)$, we first compute
using Lemma 4.4. By the above, we find that the ![]() $i$th coefficient of every entry of the expansion of
$i$th coefficient of every entry of the expansion of ![]() $\lambda ^\phi (x)$ has valuation at least
$\lambda ^\phi (x)$ has valuation at least ![]() $\varphi (i) + c_1$. We use this to bound the valuations of the coefficients of the local height
$\varphi (i) + c_1$. We use this to bound the valuations of the coefficients of the local height ![]() $h_p$. Recall from § 3.3 that we use a height with respect to an
$h_p$. Recall from § 3.3 that we use a height with respect to an ![]() $\mathrm {End}(J)$-equivariant splitting of the Hodge filtration; let
$\mathrm {End}(J)$-equivariant splitting of the Hodge filtration; let ![]() $v_{\mathrm {spl}}$ be the smallest valuation of the coefficients of this splitting in terms of our basis
$v_{\mathrm {spl}}$ be the smallest valuation of the coefficients of this splitting in terms of our basis ![]() $\boldsymbol {\omega }$. We denote by
$\boldsymbol {\omega }$. We denote by ![]() $\mathrm {ord}_p(\gamma _{\mathrm {Fil}})$ the smallest valuation in the coefficients of the rational function
$\mathrm {ord}_p(\gamma _{\mathrm {Fil}})$ the smallest valuation in the coefficients of the rational function ![]() $\gamma _{\mathrm {Fil}}$, and we set
$\gamma _{\mathrm {Fil}}$, and we set
Lemma 4.5 Let
be the expansion of ![]() $h_p$ on the residue disk
$h_p$ on the residue disk ![]() $D$ in the local parameter
$D$ in the local parameter ![]() $t$. Then we have
$t$. Then we have
Proof. This follows from the discussion above and from (3.2), which expresses ![]() $h_p(x)$ in terms of
$h_p(x)$ in terms of ![]() $\lambda ^{\mathrm {Fil}}(x)$ and
$\lambda ^{\mathrm {Fil}}(x)$ and ![]() $\lambda ^\phi (x)$.
$\lambda ^\phi (x)$.
We set ![]() $c_3:= \min _i\{\mathrm {ord}_p(d_i)\}$, where the
$c_3:= \min _i\{\mathrm {ord}_p(d_i)\}$, where the ![]() $d_i$ are the coefficients in (4.22). Let
$d_i$ are the coefficients in (4.22). Let ![]() $i_0\ge 0$ be such that
$i_0\ge 0$ be such that
for all ![]() $i\ge i_0$. Then we have
$i\ge i_0$. Then we have ![]() $\varphi (i) = -2\lfloor \log _p(i)\rfloor $ for all
$\varphi (i) = -2\lfloor \log _p(i)\rfloor $ for all ![]() $i\ge i_0$. This proves the following proposition.
$i\ge i_0$. This proves the following proposition.
Proposition 4.6 Let
be the expansion of the quadratic Chabauty function ![]() $\rho =h-h_p$ on
$\rho =h-h_p$ on ![]() $D$. If
$D$. If ![]() $i\ge i_0$, then we have
$i\ge i_0$, then we have
Together with Proposition 4.6, the following result allows us to provably determine the roots of ![]() $\rho$ to any desired precision.
$\rho$ to any desired precision.
Lemma 4.7 Suppose ![]() $F(x)=\sum _{i\geq 0}F_i x^i \in \mathbf {Q} _p [\! [x]\! ]$ is such that there are integers
$F(x)=\sum _{i\geq 0}F_i x^i \in \mathbf {Q} _p [\! [x]\! ]$ is such that there are integers ![]() $k,m,n$ satisfying
$k,m,n$ satisfying
and
and furthermore that ![]() $F$ has at most
$F$ has at most ![]() $d$ roots in the closed disk
$d$ roots in the closed disk ![]() $\{ \mathrm {ord}_p (x)\geq 1\}$. Then the roots of
$\{ \mathrm {ord}_p (x)\geq 1\}$. Then the roots of ![]() $F$ in the ball
$F$ in the ball ![]() $\{\mathrm {ord}_p (x)\geq 1\}$ can be determined, with multiplicity, to precision
$\{\mathrm {ord}_p (x)\geq 1\}$ can be determined, with multiplicity, to precision ![]() $(n-k)/d$, by computing
$(n-k)/d$, by computing ![]() $F_0 ,\ldots,F_{m-1}$ modulo
$F_0 ,\ldots,F_{m-1}$ modulo ![]() $p^n$.
$p^n$.
Proof. By our assumptions, ![]() $F(px)$ lies in
$F(px)$ lies in ![]() $p^k \mathbf {Z}_p [\! [x]\! ]-p^{k+1}\mathbf {Z}_p [\! [x]\! ]$. Hence, the power series
$p^k \mathbf {Z}_p [\! [x]\! ]-p^{k+1}\mathbf {Z}_p [\! [x]\! ]$. Hence, the power series ![]() $G(x):= p^{-k}F(px)$ lies in
$G(x):= p^{-k}F(px)$ lies in ![]() $\mathbf {Z}_p [\! [x]\! ]-p\mathbf {Z}_p [\! [x]\! ]$. Furthermore, by our assumptions, for any
$\mathbf {Z}_p [\! [x]\! ]-p\mathbf {Z}_p [\! [x]\! ]$. Furthermore, by our assumptions, for any ![]() $\alpha \in \mathbf {Z}_p$, the positive slopes of the Newton polygon of
$\alpha \in \mathbf {Z}_p$, the positive slopes of the Newton polygon of ![]() $G(x+\alpha )$ are uniquely determined by the first
$G(x+\alpha )$ are uniquely determined by the first ![]() $m$ coefficients. If
$m$ coefficients. If ![]() $G(x)$ is congruent modulo
$G(x)$ is congruent modulo ![]() $p^{n-k}$ to a polynomial
$p^{n-k}$ to a polynomial ![]() $H$ in
$H$ in ![]() $\mathbf {Z}_p [x]$ with a root
$\mathbf {Z}_p [x]$ with a root ![]() $\alpha \in \overline {\mathbf {Z}}_p$ of multiplicity
$\alpha \in \overline {\mathbf {Z}}_p$ of multiplicity ![]() $e$, then the valuation of the first
$e$, then the valuation of the first ![]() $e$ coefficients of
$e$ coefficients of ![]() $G(x+\alpha )$ must be at least
$G(x+\alpha )$ must be at least ![]() $n-k$. Since
$n-k$. Since ![]() $G(x+\alpha )$ has degree
$G(x+\alpha )$ has degree ![]() $\leq m$ mod
$\leq m$ mod ![]() $p^{n-k}$ and has at least one coefficient of valuation zero, we deduce that the Newton polygon of
$p^{n-k}$ and has at least one coefficient of valuation zero, we deduce that the Newton polygon of ![]() $G(x+\alpha )$ must contain a segment of slope at least
$G(x+\alpha )$ must contain a segment of slope at least ![]() $(n-k)/d$ of length at least
$(n-k)/d$ of length at least ![]() $e$.
$e$.
Remark 4.8 In practice, we usually apply this with ![]() $d=1$, by recentring and rescaling our power series so that there is only one root in the ball
$d=1$, by recentring and rescaling our power series so that there is only one root in the ball ![]() $\{ \mathrm {ord}_p (x) \geq 1\}$ (and because in practice the power series do not typically have repeated roots). Hence, most loss of precision occurs from
$\{ \mathrm {ord}_p (x) \geq 1\}$ (and because in practice the power series do not typically have repeated roots). Hence, most loss of precision occurs from ![]() $k$ being large, rather than
$k$ being large, rather than ![]() $d$.
$d$.
5. Examples
In this section, we apply our techniques to compute the rational points on:
− the exceptional modular curve
 $X_{S_4}(13)$ (see § 5.1);
$X_{S_4}(13)$ (see § 5.1);− all curves
 $X_0^+(N)$ of genus 2 and 3 for which
$X_0^+(N)$ of genus 2 and 3 for which  $N$ is prime and the rational points were not previously known (see § 5.2);
$N$ is prime and the rational points were not previously known (see § 5.2);− two genus 2 curves of interest in Mazur's Program B (see § 5.3);
− two genus 2 curves with Jacobian of
 $\mathrm {GL}_2$-type that have non-trivial local height contributions away from
$\mathrm {GL}_2$-type that have non-trivial local height contributions away from  $p$ (see § 5.4);
$p$ (see § 5.4);− the non-split Cartan curve
 $X_{\scriptstyle \mathrm { ns}}^+(17)$ (see § 5.5).
$X_{\scriptstyle \mathrm { ns}}^+(17)$ (see § 5.5).
For the computations, we used our Magma implementation. The code used for the examples, along with log files, can be found in the Examples folder at [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+].
5.1 The exceptional curve  $X_{S_4}(13)$
$X_{S_4}(13)$
Recall that for a prime ![]() $\ell \geq 5$, any proper subgroup of
$\ell \geq 5$, any proper subgroup of ![]() $\mathrm {GL}_2(\mathbf {F}_{\ell })$ is conjugate to a subgroup of a Borel subgroup, the normaliser of a Cartan subgroup, or an ‘exceptional’ subgroup with projective image isomorphic to
$\mathrm {GL}_2(\mathbf {F}_{\ell })$ is conjugate to a subgroup of a Borel subgroup, the normaliser of a Cartan subgroup, or an ‘exceptional’ subgroup with projective image isomorphic to ![]() $S_4, A_4$, or
$S_4, A_4$, or ![]() $A_5$. The field of definition of the modular curves attached to the exceptional subgroups is the unique quadratic subfield
$A_5$. The field of definition of the modular curves attached to the exceptional subgroups is the unique quadratic subfield ![]() $\mathbf {Q}(\sqrt {\pm \ell })$ of the cyclotomic field
$\mathbf {Q}(\sqrt {\pm \ell })$ of the cyclotomic field ![]() $\mathbf {Q}(\zeta _{\ell })$, with the exception of the curves
$\mathbf {Q}(\zeta _{\ell })$, with the exception of the curves ![]() $X_{S_4}(\ell )$ for
$X_{S_4}(\ell )$ for ![]() $\ell \equiv \pm 3 \pmod {8}$, which are defined over
$\ell \equiv \pm 3 \pmod {8}$, which are defined over ![]() $\mathbf {Q}$. For such values of
$\mathbf {Q}$. For such values of ![]() $\ell$, we would therefore like to determine
$\ell$, we would therefore like to determine ![]() $X_{S_4}(\ell )(\mathbf {Q})$.
$X_{S_4}(\ell )(\mathbf {Q})$.
Serre [Reference SerreSer72] shows by a monodromy argument that such tetrahedral modular curves have no points defined over ![]() $\mathbf {Q}_{\ell }$ when
$\mathbf {Q}_{\ell }$ when ![]() $\ell$ is large enough, and in particular he obtains
$\ell$ is large enough, and in particular he obtains
The curves ![]() $X_{S_4}(3)$ and
$X_{S_4}(3)$ and ![]() $X_{S_4}(5)$ are both of genus zero, and contain a unique rational cusp. Ligozat [Reference LigozatLig77] showed that
$X_{S_4}(5)$ are both of genus zero, and contain a unique rational cusp. Ligozat [Reference LigozatLig77] showed that ![]() $X_{S_4}(11)$ is an elliptic curve of conductor
$X_{S_4}(11)$ is an elliptic curve of conductor ![]() $11^2$ whose Mordell–Weil group is trivial, where the unique rational point is CM, corresponding to discriminant
$11^2$ whose Mordell–Weil group is trivial, where the unique rational point is CM, corresponding to discriminant ![]() $D=-3$. This leaves only the curve
$D=-3$. This leaves only the curve ![]() $X_{S_4}(13)$, which has genus
$X_{S_4}(13)$, which has genus ![]() $3$. In fact, this curve is the last remaining modular curve of level
$3$. In fact, this curve is the last remaining modular curve of level ![]() $13^n$ whose rational points have not been determined.
$13^n$ whose rational points have not been determined.
Using modular symbols algorithms, Banwait and Cremona [Reference Banwait and CremonaBC14] show that the curve ![]() $X_{S_4}(13)$ is a smooth plane quartic whose canonical model is given by
$X_{S_4}(13)$ is a smooth plane quartic whose canonical model is given by
 \begin{align*} &4x^3y - 3x^2y^2 + 3xy^3 - x^3z + 16x^2yz - 11xy^2z \\ &\quad +5y^3z + 3x^2z^2 + 9xyz^2 + y^2z^2 + xz^3 + 2yz^3 = 0. \end{align*}
\begin{align*} &4x^3y - 3x^2y^2 + 3xy^3 - x^3z + 16x^2yz - 11xy^2z \\ &\quad +5y^3z + 3x^2z^2 + 9xyz^2 + y^2z^2 + xz^3 + 2yz^3 = 0. \end{align*}
Furthermore, they exhibit the four rational points
where the rational point ![]() $(0 : 0 : 1)$ corresponds to an elliptic curve with CM by the order of discriminant
$(0 : 0 : 1)$ corresponds to an elliptic curve with CM by the order of discriminant ![]() $D = -3$, and the three other rational points correspond to non-CM elliptic curves over
$D = -3$, and the three other rational points correspond to non-CM elliptic curves over ![]() $\mathbf {Q}$ with projective mod
$\mathbf {Q}$ with projective mod ![]() $13$ image equal to
$13$ image equal to ![]() $S_4$, whose
$S_4$, whose ![]() $j$-invariants are given by
$j$-invariants are given by
 \begin{gather*} j = \frac{2^4\cdot 5 \cdot 13^4 \cdot 17^3}{3^{13}}, \quad j = - \frac{2^{12}\cdot 5^3 \cdot 11 \cdot 13^4}{3^{13}}, \\ j = \frac{2^{18}\cdot 3^3 \cdot 13^4\cdot 127^3 \cdot 139^3 \cdot 157^3 \cdot 283^3 \cdot 929}{5^{13} \cdot 61^{13}}. \end{gather*}
\begin{gather*} j = \frac{2^4\cdot 5 \cdot 13^4 \cdot 17^3}{3^{13}}, \quad j = - \frac{2^{12}\cdot 5^3 \cdot 11 \cdot 13^4}{3^{13}}, \\ j = \frac{2^{18}\cdot 3^3 \cdot 13^4\cdot 127^3 \cdot 139^3 \cdot 157^3 \cdot 283^3 \cdot 929}{5^{13} \cdot 61^{13}}. \end{gather*}
The Jacobian of ![]() $X_{S_4}(13)$ is isogenous to that of
$X_{S_4}(13)$ is isogenous to that of ![]() $X_{\rm s}^+(13)$, so it is absolutely simple and has Mordell–Weil rank 3 over
$X_{\rm s}^+(13)$, so it is absolutely simple and has Mordell–Weil rank 3 over ![]() $\mathbf {Q}$ by the results of [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 6]. The curve has potential good reduction at
$\mathbf {Q}$ by the results of [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 6]. The curve has potential good reduction at ![]() $p = 13$, as can be seen, for instance, using the Sage toolbox MCLF.
$p = 13$, as can be seen, for instance, using the Sage toolbox MCLF.
We determine the set of rational points on the curve ![]() $X_{S_4}(13)$ using quadratic Chabauty with
$X_{S_4}(13)$ using quadratic Chabauty with ![]() $p=11$ for the affine patches
$p=11$ for the affine patches
and
The computation is analogous to the computation of ![]() $X^+_{\rm s}(13)(\mathbf {Q})$ in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19]. The Hecke operator
$X^+_{\rm s}(13)(\mathbf {Q})$ in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19]. The Hecke operator ![]() $T_{11}$ generates the Hecke algebra, as can be verified, for instance, by checking the analogous statement for
$T_{11}$ generates the Hecke algebra, as can be verified, for instance, by checking the analogous statement for ![]() $X^+_{\rm s}(13)$. Hence, we may construct suitable cycles
$X^+_{\rm s}(13)$. Hence, we may construct suitable cycles ![]() $Z_1, Z_2$ from
$Z_1, Z_2$ from ![]() $T_{11}$ and its square, respectively. The set of common zeros of the resulting quadratic Chabauty functions consists precisely of the known rational points, so we obtain Theorem 1.1.
$T_{11}$ and its square, respectively. The set of common zeros of the resulting quadratic Chabauty functions consists precisely of the known rational points, so we obtain Theorem 1.1.
In order to solve for the height pairing, we use the four known rational points and the cycle ![]() $Z_1$, so the resulting function automatically vanishes there. However, since the cycles
$Z_1$, so the resulting function automatically vanishes there. However, since the cycles ![]() $Z_1$ and
$Z_1$ and ![]() $Z_2$ are independent, and
$Z_2$ are independent, and ![]() $Z_2$ is not used to solve for the height, the vanishing of the resulting function in the rational points provides a check for the correctness of our code.
$Z_2$ is not used to solve for the height, the vanishing of the resulting function in the rational points provides a check for the correctness of our code.
Remark 5.1 Since the Jacobian of ![]() $X_{S_4}(13)$ is isogenous to that of
$X_{S_4}(13)$ is isogenous to that of ![]() $X^+_{\mathrm {s}}(13)$, even if there were not enough rational points on
$X^+_{\mathrm {s}}(13)$, even if there were not enough rational points on ![]() $X_{S_4}(13)$ to solve for the height pairing, one could instead solve for it using
$X_{S_4}(13)$ to solve for the height pairing, one could instead solve for it using ![]() $X^+_{\mathrm {s}}(13)$.
$X^+_{\mathrm {s}}(13)$.
5.2 The Atkin–Lehner quotients  $X_0^+(N)$
$X_0^+(N)$
For a positive integer ![]() $N$, consider the Atkin–Lehner involution
$N$, consider the Atkin–Lehner involution ![]() $w_N$ acting on the modular curve
$w_N$ acting on the modular curve ![]() $X_0(N)$. Then the quotient
$X_0(N)$. Then the quotient
is a smooth projective curve defined over ![]() $\mathbf {Q}$ whose non-cuspidal points classify unordered pairs
$\mathbf {Q}$ whose non-cuspidal points classify unordered pairs ![]() $\{E_1,E_2\}$ of elliptic curves admitting an
$\{E_1,E_2\}$ of elliptic curves admitting an ![]() $N$-isogeny between them. The study of rational points on these curves is also important in an ongoing research programme aiming to compute quadratic points on the modular curves
$N$-isogeny between them. The study of rational points on these curves is also important in an ongoing research programme aiming to compute quadratic points on the modular curves ![]() $X_0(N)$ (see, for instance, recent work of Box [Reference BoxBox21]). Among the rational points, we distinguish between cusps, CM points and exceptional points, those which are neither cusps nor CM points. The exceptional points correspond to quadratic
$X_0(N)$ (see, for instance, recent work of Box [Reference BoxBox21]). Among the rational points, we distinguish between cusps, CM points and exceptional points, those which are neither cusps nor CM points. The exceptional points correspond to quadratic ![]() $\mathbf {Q}$-curves without CM.
$\mathbf {Q}$-curves without CM.
In this subsection we restrict to prime values ![]() $N$ such that
$N$ such that ![]() $X_0^+(N)$ has genus 2 or 3. Galbraith [Reference GalbraithGal96] has computed models for all these curves (and many more) by finding relations in the vector space spanned by the newforms of level
$X_0^+(N)$ has genus 2 or 3. Galbraith [Reference GalbraithGal96] has computed models for all these curves (and many more) by finding relations in the vector space spanned by the newforms of level ![]() $N$ and weight
$N$ and weight ![]() $2$ that are invariant under
$2$ that are invariant under ![]() $w_N$. Up to conjugation, there is a unique such newform.
$w_N$. Up to conjugation, there is a unique such newform.
By work of Ogg, for prime level ![]() $N$, the curve
$N$, the curve ![]() $X_0^+(N)$ has genus 2 if and only if
$X_0^+(N)$ has genus 2 if and only if
It has genus 3 if and only if
Models for all these curves were communicated to us by Elkies; one can also find such models in Galbraith's thesis [Reference GalbraithGal96] or by using the Magma command X0NQuotient.
Via a search for small rational points, Galbraith [Reference GalbraithGal99] found exceptional rational points on ![]() $X_0^+(N)$ for
$X_0^+(N)$ for ![]() $N=73,\ 91,\ 103,\ 191$ (genus 2) and
$N=73,\ 91,\ 103,\ 191$ (genus 2) and ![]() $N=137,\ 311$ (genus 4). The latter examples disproved an earlier conjecture of Elkies that there are no exceptional rational points on non-hyperelliptic
$N=137,\ 311$ (genus 4). The latter examples disproved an earlier conjecture of Elkies that there are no exceptional rational points on non-hyperelliptic ![]() $X_0^+(N)$ for prime level
$X_0^+(N)$ for prime level ![]() $N$. In [Reference GalbraithGal02], Galbraith also finds an exceptional point on
$N$. In [Reference GalbraithGal02], Galbraith also finds an exceptional point on ![]() $X_0^+(125)$ and conjectures that there are no further exceptional points on modular curves
$X_0^+(125)$ and conjectures that there are no further exceptional points on modular curves ![]() $X^+_0(N)$ of genus
$X^+_0(N)$ of genus ![]() $2\le g\le 5$.
$2\le g\le 5$.
Together with [Reference Balakrishnan, Best, Bianchi, Lawrence, Müller, Triantafillou and VonkBBB+21] and [Reference GalbraithGal96], our computations described below prove Theorem 1.3. We first check that for level ![]() $N$ as in (5.1) and (5.2) the curves
$N$ as in (5.1) and (5.2) the curves ![]() $X_0^+(N)$ satisfy the requirements to apply our algorithm. The Jacobian
$X_0^+(N)$ satisfy the requirements to apply our algorithm. The Jacobian ![]() $J_0^+(N)$ of
$J_0^+(N)$ of ![]() $X_0^+(N)$ has real multiplication over
$X_0^+(N)$ has real multiplication over ![]() $\mathbf {Q}$, so the Picard number is at least
$\mathbf {Q}$, so the Picard number is at least ![]() $g$. Using Magma, we computed the
$g$. Using Magma, we computed the ![]() $L$-function of the corresponding newforms to show that the analytic rank is
$L$-function of the corresponding newforms to show that the analytic rank is ![]() $g$, so the work of Gross and Zagier and of Kolyvagin and Logachev proves that the rank of
$g$, so the work of Gross and Zagier and of Kolyvagin and Logachev proves that the rank of ![]() $J(\mathbf {Q})$ is exactly
$J(\mathbf {Q})$ is exactly ![]() $g$. For the genus 2 examples, we also applied
$g$. For the genus 2 examples, we also applied ![]() $2$-descent on
$2$-descent on ![]() $J_0^+(N)$, as implemented in Magma, as an independent check.
$J_0^+(N)$, as implemented in Magma, as an independent check.
The curves ![]() $X_0^+(N)$ have good reduction away from
$X_0^+(N)$ have good reduction away from ![]() $N$, but, in contrast to
$N$, but, in contrast to ![]() $X^+_{\rm ns}(13)$ and
$X^+_{\rm ns}(13)$ and ![]() $X_{S_4}(13)$, they do not have potentially good reduction at
$X_{S_4}(13)$, they do not have potentially good reduction at ![]() $N$. Nevertheless, the following result implies that when applying quadratic Chabauty, there are no non-trivial contributions to the height away from
$N$. Nevertheless, the following result implies that when applying quadratic Chabauty, there are no non-trivial contributions to the height away from ![]() $p$.
$p$.
Lemma 5.2 There is a regular semi-stable model ![]() $\mathcal {X}_0^+(N)$ of
$\mathcal {X}_0^+(N)$ of ![]() $X_0^+(N)$ over
$X_0^+(N)$ over ![]() $\mathbf {Z}_N$ whose special fibre has a unique irreducible component. In particular, the local height
$\mathbf {Z}_N$ whose special fibre has a unique irreducible component. In particular, the local height ![]() $h_N$ is trivial on
$h_N$ is trivial on ![]() $X_0^+(\mathbf {Q}_N)$.
$X_0^+(\mathbf {Q}_N)$.
Proof. If ![]() $N=2,3$ the result is readily checked. When
$N=2,3$ the result is readily checked. When ![]() $N > 3$ the Atkin–Lehner quotient of the model
$N > 3$ the Atkin–Lehner quotient of the model ![]() $\mathcal {X}_0(N)$ for
$\mathcal {X}_0(N)$ for ![]() $X_0(N)$ over
$X_0(N)$ over ![]() $\mathrm {Spec} \mathbf {Z}$ constructed by Deligne and Rapoport [Reference Deligne and RapoportDR73] is shown by Xue [Reference XueXue09] to be regular and semi-stable. Its special fibre at
$\mathrm {Spec} \mathbf {Z}$ constructed by Deligne and Rapoport [Reference Deligne and RapoportDR73] is shown by Xue [Reference XueXue09] to be regular and semi-stable. Its special fibre at ![]() $N$ is a projective line, with an ordinary double point for every conjugate pair of supersingular
$N$ is a projective line, with an ordinary double point for every conjugate pair of supersingular ![]() $j$-invariants in
$j$-invariants in ![]() $\mathbf {F}_{N^2} \backslash \mathbf {F}_{N}$. It follows from Theorem 3.2 that
$\mathbf {F}_{N^2} \backslash \mathbf {F}_{N}$. It follows from Theorem 3.2 that ![]() $h_N$ is trivial.
$h_N$ is trivial.
Finally, we checked for all ![]() $N$ in (5.1) and in (5.2) that the Jacobian is absolutely simple by finding a prime
$N$ in (5.1) and in (5.2) that the Jacobian is absolutely simple by finding a prime ![]() $q$ of good reduction such that
$q$ of good reduction such that ![]() $J_{ \mathbf {F}_q}$ is absolutely simple, using the criterion of Howe and Zhu [Reference Howe and ZhuHZ02, Proposition 3].
$J_{ \mathbf {F}_q}$ is absolutely simple, using the criterion of Howe and Zhu [Reference Howe and ZhuHZ02, Proposition 3].
5.2.1 Genus 2
In [Reference Balakrishnan, Best, Bianchi, Lawrence, Müller, Triantafillou and VonkBBB+21], the rational points on ![]() $X_0^+(N)$ for
$X_0^+(N)$ for ![]() $N=67,\ 73,\ 103$ were computed. Using a combination of quadratic Chabauty and the Mordell–Weil sieve, it is shown there that
$N=67,\ 73,\ 103$ were computed. Using a combination of quadratic Chabauty and the Mordell–Weil sieve, it is shown there that ![]() $X_0^+(67)(\mathbf {Q})$ contains no exceptional points and that the sets
$X_0^+(67)(\mathbf {Q})$ contains no exceptional points and that the sets ![]() $X_0^+(73)(\mathbf {Q})$ and
$X_0^+(73)(\mathbf {Q})$ and ![]() $X_0^+(103)(\mathbf {Q})$ both contain one pair of exceptional points each, with respective
$X_0^+(103)(\mathbf {Q})$ both contain one pair of exceptional points each, with respective ![]() $j$-invariants (see [Reference GalbraithGal99, Table 1])
$j$-invariants (see [Reference GalbraithGal99, Table 1])
 \begin{align*} j&=
(81450017206599109708140525\pm
14758692270140155157349165\cdot\sqrt{- 127})/ 2^{74}, \\ j
&= (35982263935929364331785036841779200 \pm
669908635472124980731701532753920\\ &\quad
\cdot\sqrt{5\cdot577}). \end{align*}
\begin{align*} j&=
(81450017206599109708140525\pm
14758692270140155157349165\cdot\sqrt{- 127})/ 2^{74}, \\ j
&= (35982263935929364331785036841779200 \pm
669908635472124980731701532753920\\ &\quad
\cdot\sqrt{5\cdot577}). \end{align*}
The remaining prime level genus 2 curves ![]() $X_0^+(107)$,
$X_0^+(107)$, ![]() $X_0^+(167)$ and
$X_0^+(167)$ and ![]() $X_0^+(191)$ are more challenging, because they do not have sufficiently many rational points in the sense of § 3.3 to solve for the height pairing, so we need to compute heights between divisors. In all cases, the quadratic Chabauty function
$X_0^+(191)$ are more challenging, because they do not have sufficiently many rational points in the sense of § 3.3 to solve for the height pairing, so we need to compute heights between divisors. In all cases, the quadratic Chabauty function ![]() $\rho =h-h_p$ has
$\rho =h-h_p$ has ![]() $p$-adic zeros that do not come from a rational point; to verify this, we apply the Mordell–Weil sieve.
$p$-adic zeros that do not come from a rational point; to verify this, we apply the Mordell–Weil sieve.
Example 5.3 We discuss our computations for the example ![]() $X:= X_0^+(107)$ in some detail.
$X:= X_0^+(107)$ in some detail.
We look for a prime ![]() $p$ of good reduction such that
$p$ of good reduction such that
− there is a unique
 $\mathbf {Q}_p$-rational Weierstrass disk, and it does not contain known rational points,
$\mathbf {Q}_p$-rational Weierstrass disk, and it does not contain known rational points,− the Hecke operator
 $T_p$ generates the Hecke algebra, and
$T_p$ generates the Hecke algebra, and−
 $p$ is suitable for the Mordell–Weil sieve.
$p$ is suitable for the Mordell–Weil sieve.
For ![]() $p=61$, the first two conditions are satisfied; moreover, we have
$p=61$, the first two conditions are satisfied; moreover, we have
and since ![]() $J(\mathbf {F}_{61})\simeq \mathbf {Z}/(31\cdot 151)\mathbf {Z}$ has quite smooth order,
$J(\mathbf {F}_{61})\simeq \mathbf {Z}/(31\cdot 151)\mathbf {Z}$ has quite smooth order, ![]() $61$ is a suitable prime. We now go through the steps in Algorithm 3.12, applied to
$61$ is a suitable prime. We now go through the steps in Algorithm 3.12, applied to ![]() $X$.
$X$.
Step (i). The model
of ![]() $X$ has six small rational points of exponential height at most 1000, given by
$X$ has six small rational points of exponential height at most 1000, given by ![]() $\{(0,\pm 1), (\pm 1, \pm 1) \}$. It also has no
$\{(0,\pm 1), (\pm 1, \pm 1) \}$. It also has no ![]() $\mathbf {Q}_{61}$-adic points at infinity, so that we only need to run our algorithm for one affine patch. We fix the base point
$\mathbf {Q}_{61}$-adic points at infinity, so that we only need to run our algorithm for one affine patch. We fix the base point ![]() $b=(0,-1)$.
$b=(0,-1)$.
Steps (ii) and (iii). These are exactly as in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19].
Step (iv). We may use the unit root splitting, since ![]() $p=61$ is ordinary (see Remark 3.15).
$p=61$ is ordinary (see Remark 3.15).
Step (v). Using step (iii), we find for
 \begin{equation} Z=Z_1=
(\mathrm{Tr}(T_{{61}})\cdot I_{4}- 4T_{{61}})C^{-1} =
\left( \begin{array}{@{}cccc@{}} 0 & 2/3 & -2 & 4\\ -2/3 & 0 & 4
& 2\\ 2 & -4 & 0 & 0\\ -4 & -2 & 0 & 0\\ \end{array}
\right), \end{equation}
\begin{equation} Z=Z_1=
(\mathrm{Tr}(T_{{61}})\cdot I_{4}- 4T_{{61}})C^{-1} =
\left( \begin{array}{@{}cccc@{}} 0 & 2/3 & -2 & 4\\ -2/3 & 0 & 4
& 2\\ 2 & -4 & 0 & 0\\ -4 & -2 & 0 & 0\\ \end{array}
\right), \end{equation}
that
corresponds to a non-trivial cycle ![]() $Z \in \ker (\mathrm {NS}(J)\longrightarrow \mathrm {NS}(X))$ where
$Z \in \ker (\mathrm {NS}(J)\longrightarrow \mathrm {NS}(X))$ where ![]() $C$ is the standard symplectic matrix of dimension
$C$ is the standard symplectic matrix of dimension ![]() $2g$ and
$2g$ and ![]() $\boldsymbol {\omega }$ is the basis found in step (ii).
$\boldsymbol {\omega }$ is the basis found in step (ii).
Step (vi)(a). The Hodge filtration for ![]() $Z$ is given by
$Z$ is given by ![]() $\gamma _{\mathrm {Fil}}=-4x-4$ and
$\gamma _{\mathrm {Fil}}=-4x-4$ and ![]() $\beta _{\mathrm {Fil}}=0$. After computing the Frobenius structure, we obtain a power series expansion of the function
$\beta _{\mathrm {Fil}}=0$. After computing the Frobenius structure, we obtain a power series expansion of the function ![]() $x\mapsto h_{61}(\mathrm {A}(x))$ on all residue disks of
$x\mapsto h_{61}(\mathrm {A}(x))$ on all residue disks of ![]() $X(\mathbf {Q}_{61})$, except for the disks at infinity and the unique Weierstrass disk containing points that reduce to
$X(\mathbf {Q}_{61})$, except for the disks at infinity and the unique Weierstrass disk containing points that reduce to ![]() $(31,0)$.
$(31,0)$.
Step (vi)(b). The points ![]() $P, Q\in J(\mathbf {Q})$ with respective Mumford representations
$P, Q\in J(\mathbf {Q})$ with respective Mumford representations ![]() $(x^2 + x ,1)$ and
$(x^2 + x ,1)$ and ![]() $(x^2+1, 2x-1)$ generate a subgroup of
$(x^2+1, 2x-1)$ generate a subgroup of ![]() $J(\mathbf {Q})$ of index 2. To solve for the height pairing via § 3.3.1, we need divisor representatives with support in distinct non-Weierstrass residue disks. Let
$J(\mathbf {Q})$ of index 2. To solve for the height pairing via § 3.3.1, we need divisor representatives with support in distinct non-Weierstrass residue disks. Let ![]() $E$ be the degree 2 divisor on
$E$ be the degree 2 divisor on ![]() $X$ cut out by the functions
$X$ cut out by the functions ![]() $x^2+1$ and
$x^2+1$ and ![]() $2x-1$ and let
$2x-1$ and let ![]() $E'$ be its image under the hyperelliptic involution. We set
$E'$ be its image under the hyperelliptic involution. We set
Then we have ![]() $h(P,Q) = \sum _v h_v(D_1, D_2)$ and
$h(P,Q) = \sum _v h_v(D_1, D_2)$ and
The divisors above all split over ![]() $\mathbf {Q}_{61}$, so we can compute the height pairings
$\mathbf {Q}_{61}$, so we can compute the height pairings ![]() $h_{61}(D_1, D_2)$,
$h_{61}(D_1, D_2)$, ![]() $h_{61}(D_1, D'_1)$ and
$h_{61}(D_1, D'_1)$ and ![]() $h_{61}(D_2, D'_2)$, working on a monic odd-degree model over
$h_{61}(D_2, D'_2)$, working on a monic odd-degree model over ![]() $\mathbf {Q}_{61}$. Using Magma's implementation of the algorithm described in [Reference MüllerMül14], we also find
$\mathbf {Q}_{61}$. Using Magma's implementation of the algorithm described in [Reference MüllerMül14], we also find
 \begin{align*} \sum_{\ell\ne {61}} h_{\ell}(D_1, D'_1) &= -2\log_{61} 2+2\log_{61} 3-\log_{61} 7,\\ \sum_{\ell\ne {61}} h_{\ell}(D_1, D_2) &= 2\log_{61} 2-2\log_{61} 3 + \log_{61} 7,\\ \sum_{\ell\ne {61}} h_{\ell}(D_2, D'_2)& = 3\log_{61} 2-\log_{61} 5, \end{align*}
\begin{align*} \sum_{\ell\ne {61}} h_{\ell}(D_1, D'_1) &= -2\log_{61} 2+2\log_{61} 3-\log_{61} 7,\\ \sum_{\ell\ne {61}} h_{\ell}(D_1, D_2) &= 2\log_{61} 2-2\log_{61} 3 + \log_{61} 7,\\ \sum_{\ell\ne {61}} h_{\ell}(D_2, D'_2)& = 3\log_{61} 2-\log_{61} 5, \end{align*}
and we conclude that
where
 \begin{align*} \alpha_{00} &=58\cdot 61^{-1} + 19 + 2\cdot 61 + 43\cdot 61^2 + O(61^3),\\ \alpha_{01} &= 43\cdot 61^{-1} + 48 + 44\cdot 61 + 41\cdot 61^2 + O(61^3),\\ \alpha_{11} &=49\cdot 61^{-1} + 13 + 55\cdot 61 + 2\cdot 61^2 + O(61^3), \end{align*}
\begin{align*} \alpha_{00} &=58\cdot 61^{-1} + 19 + 2\cdot 61 + 43\cdot 61^2 + O(61^3),\\ \alpha_{01} &= 43\cdot 61^{-1} + 48 + 44\cdot 61 + 41\cdot 61^2 + O(61^3),\\ \alpha_{11} &=49\cdot 61^{-1} + 13 + 55\cdot 61 + 2\cdot 61^2 + O(61^3), \end{align*}
and the ![]() $g_{ij}$ are defined in (3.3).
$g_{ij}$ are defined in (3.3).
Steps (vi)(c)–(vii). Combining the functions resulting from steps (vi)(a) and (vi)(b), we find a power series expansion of the quadratic Chabauty function
in all affine non-Weierstrass disks. By Lemma 5.2, the local heights ![]() $h_{\ell }(\mathrm {A}(x))$ are trivial for
$h_{\ell }(\mathrm {A}(x))$ are trivial for ![]() $\ell \ne {61}$, so
$\ell \ne {61}$, so ![]() $\Upsilon =\{0\}$ and all rational points are zeros of
$\Upsilon =\{0\}$ and all rational points are zeros of ![]() $\rho$. We find that
$\rho$. We find that ![]() $\rho$ indeed vanishes on the known rational points, and that these are simple zeros of
$\rho$ indeed vanishes on the known rational points, and that these are simple zeros of ![]() $\rho$.
$\rho$.
In addition, ![]() $\rho$ vanishes to multiplicity 1 on 82 points in
$\rho$ vanishes to multiplicity 1 on 82 points in ![]() $X(\mathbf {Q}_{61})$ that do not appear to be rational. As described in § 3.4, these yield cosets of
$X(\mathbf {Q}_{61})$ that do not appear to be rational. As described in § 3.4, these yield cosets of ![]() $61^2J(\mathbf {Q})$, and our implementation of the Mordell–Weil sieve shows that the image of these cosets does not intersect the image of
$61^2J(\mathbf {Q})$, and our implementation of the Mordell–Weil sieve shows that the image of these cosets does not intersect the image of ![]() $X(\mathbf {F}_{229})$ inside
$X(\mathbf {F}_{229})$ inside ![]() $J(\mathbf {F}_{229})/61^2J(\mathbf {F}_{229})$. Hence, these additional zeros do not come from a rational point.
$J(\mathbf {F}_{229})/61^2J(\mathbf {F}_{229})$. Hence, these additional zeros do not come from a rational point.
Recall that there are no ![]() $\mathbf {Q}_{61}$-rational points at infinity, so it only remains to show that there are no rational points in the Weierstrass disk. To this end, we show that for
$\mathbf {Q}_{61}$-rational points at infinity, so it only remains to show that there are no rational points in the Weierstrass disk. To this end, we show that for
the image of the reduction of this disk does not intersect
where ![]() $M = 2\#J(\mathbf {F}_{61})$ and
$M = 2\#J(\mathbf {F}_{61})$ and ![]() $\beta _{2,61}\colon \prod _{v\in S}X(\mathbf {F}_v)\to \prod _{v\in S} J(\mathbf {F}_v)/MJ(\mathbf {F}_v)$ is induced by the Abel–Jacobi map with respect to
$\beta _{2,61}\colon \prod _{v\in S}X(\mathbf {F}_v)\to \prod _{v\in S} J(\mathbf {F}_v)/MJ(\mathbf {F}_v)$ is induced by the Abel–Jacobi map with respect to ![]() $b$ and the canonical surjections.
$b$ and the canonical surjections.
This completes the proof that ![]() $\#X(\mathbf {Q})=6$. According to Galbraith [Reference GalbraithGal96], these points are all cusps or CM points.
$\#X(\mathbf {Q})=6$. According to Galbraith [Reference GalbraithGal96], these points are all cusps or CM points.
Example 5.4 We were able to prove that the curve
only contains the four obvious rational points ![]() $\{ (- 1, \pm 1), \infty _{\pm }\}\,;$ these are all cusps or CM by Galbraith [Reference GalbraithGal96]. In our computation, we use our quadratic Chabauty algorithm for
$\{ (- 1, \pm 1), \infty _{\pm }\}\,;$ these are all cusps or CM by Galbraith [Reference GalbraithGal96]. In our computation, we use our quadratic Chabauty algorithm for ![]() $p=7$ and the Mordell–Weil sieve, following the same strategy as in Example 5.3. The verification that the additional solutions of the resulting
$p=7$ and the Mordell–Weil sieve, following the same strategy as in Example 5.3. The verification that the additional solutions of the resulting ![]() $p$-adic functions are not rational was the most challenging Mordell–Weil sieve computation we encountered in our work; it required the auxiliary integer
$p$-adic functions are not rational was the most challenging Mordell–Weil sieve computation we encountered in our work; it required the auxiliary integer ![]() $5\cdot 11\cdot 19$ and the set of good primes
$5\cdot 11\cdot 19$ and the set of good primes
Example 5.5 A model for ![]() $X_0^+(191)$ is given by
$X_0^+(191)$ is given by
We use quadratic Chabauty for ![]() $p=31$ together with the Mordell–Weil sieve exactly as above to show that
$p=31$ together with the Mordell–Weil sieve exactly as above to show that ![]() $X_0^+(191)(\mathbf {Q}) = \{ (0,\pm 1), (2, \pm 11), \infty _{\pm }\}.$ Galbraith (see [Reference GalbraithGal99, Table 1]) has shown that
$X_0^+(191)(\mathbf {Q}) = \{ (0,\pm 1), (2, \pm 11), \infty _{\pm }\}.$ Galbraith (see [Reference GalbraithGal99, Table 1]) has shown that ![]() $(2, -11)$ is exceptional, with corresponding
$(2, -11)$ is exceptional, with corresponding ![]() $j$-invariant
$j$-invariant
5.2.2 Genus 3
We apply our algorithm to show that the rational points on the curves ![]() $X_0^+(N)$ for
$X_0^+(N)$ for ![]() $N$ as in (5.2) are precisely the ones already found by Galbraith. All curves in our list are non-hyperelliptic and they have the convenient feature that they have sufficiently many rational points, so no heights on divisors need to be computed. We always find two independent cycles in
$N$ as in (5.2) are precisely the ones already found by Galbraith. All curves in our list are non-hyperelliptic and they have the convenient feature that they have sufficiently many rational points, so no heights on divisors need to be computed. We always find two independent cycles in ![]() $\ker (\mathrm {NS}(J)\longrightarrow \mathrm {NS}(X))$, and, as expected, the common zero set of the corresponding functions consists precisely of the rational points found by Galbraith.
$\ker (\mathrm {NS}(J)\longrightarrow \mathrm {NS}(X))$, and, as expected, the common zero set of the corresponding functions consists precisely of the rational points found by Galbraith.
Theorem 5.6 Let ![]() $N$ be a prime such that
$N$ be a prime such that ![]() $X_0^+(N)$ has genus
$X_0^+(N)$ has genus ![]() $3$. Then the rational points on
$3$. Then the rational points on ![]() $X_0^+(N)$ are as below. In particular, all rational points are either cusps or CM points, with discriminant
$X_0^+(N)$ are as below. In particular, all rational points are either cusps or CM points, with discriminant ![]() $\Delta$.
$\Delta$.
Example 5.7 A model for ![]() $X_0^+(97)$ is given by
$X_0^+(97)$ is given by
Using our algorithm for ![]() $p=5$, we find that the rational points are as follows:
$p=5$, we find that the rational points are as follows:
Example 5.8 A model for ![]() $X_0^+(109)$ is given by
$X_0^+(109)$ is given by
Using our algorithm for ![]() $p=29$, we find that the rational points are as follows:
$p=29$, we find that the rational points are as follows:
Example 5.9 A model for ![]() $X_0^+(113)$ is given by
$X_0^+(113)$ is given by
Using our algorithm for ![]() $p=17$, we find that the rational points are as follows:
$p=17$, we find that the rational points are as follows:
Example 5.10 A model for ![]() $X_0^+(127)$ is given by
$X_0^+(127)$ is given by
Using our algorithm for ![]() $p=11$, we find that the rational points are as follows:
$p=11$, we find that the rational points are as follows:
Example 5.11 A model for ![]() $X_0^+(139)$ is given by
$X_0^+(139)$ is given by
Using our algorithm for ![]() $p=19$, we find that the rational points are as follows:
$p=19$, we find that the rational points are as follows:
Example 5.12 A model for ![]() $X_0^+(149)$ is given by
$X_0^+(149)$ is given by
Using our algorithm for ![]() $p=11$, we find that the rational points are as follows:
$p=11$, we find that the rational points are as follows:
Example 5.13 A model for ![]() $X_0^+(151)$ is given by
$X_0^+(151)$ is given by
Using our algorithm for ![]() $p=19$, we find that the rational points are as follows:
$p=19$, we find that the rational points are as follows:
Example 5.14 A model for ![]() $X_0^+(179)$ is given by
$X_0^+(179)$ is given by
Using our algorithm for ![]() $p=17$, we find that the rational points are as follows:
$p=17$, we find that the rational points are as follows:
Example 5.15 A model for ![]() $X_0^+(239)$ is given by
$X_0^+(239)$ is given by
Using our algorithm for ![]() $p=13$, we find that the rational points are as follows:
$p=13$, we find that the rational points are as follows:
5.3 Genus 2 curves in Mazur's Program B
In this section, we determine the rational points on two genus 2 curves that were communicated to us by David Zureick-Brown. They arise in the work of Rouse, Sutherland and Zureick-Brown [Reference Rouse, Sutherland and Zureick-BrownRSZB22] on Mazur's Program B as modular curves ![]() $X_H = X(25)/H$, where
$X_H = X(25)/H$, where ![]() $\Gamma (25)\subset H\subset \mathrm {GL}_2(\mathbf {Z}_5)$. Both curves have the following properties:
$\Gamma (25)\subset H\subset \mathrm {GL}_2(\mathbf {Z}_5)$. Both curves have the following properties:
− They each have two rational points of exponential height at most 1000, good reduction away from 5, and potentially good reduction at 5.
− Their Jacobians have real multiplication, no rational torsion and Mordell–Weil rank 2; they are both absolutely simple.
− The Galois action on the 2-torsion field is
 $A_5$, which is too large for an elliptic curve Chabauty computation.
$A_5$, which is too large for an elliptic curve Chabauty computation.
We prove that ![]() $\#X_H(\mathbf {Q})=2$ for each curve
$\#X_H(\mathbf {Q})=2$ for each curve ![]() $X_H$ using quadratic Chabauty and the Mordell–Weil sieve, similar to the computation of
$X_H$ using quadratic Chabauty and the Mordell–Weil sieve, similar to the computation of ![]() $X^+_0(107)(\mathbf {Q})$ described in detail in Example 5.3.
$X^+_0(107)(\mathbf {Q})$ described in detail in Example 5.3.
Example 5.16 A suitable affine model of the curve ![]() $X_{11}$ is given by
$X_{11}$ is given by
As in Example 5.3, we found the rather large prime ![]() $p=61$ to be the most convenient one for our computations. We determine the height pairing on the Jacobian using divisors as in § 3.3.1. The quadratic Chabauty function
$p=61$ to be the most convenient one for our computations. We determine the height pairing on the Jacobian using divisors as in § 3.3.1. The quadratic Chabauty function ![]() $\rho$ has 62 solutions in addition to the rational ones. Applying the Mordell–Weil sieve with the primes 7, 29, 257 and 3457, we show that these are in fact not rational; to prove non-existence of rational points in the unique Weierstrass disk, we sieve with the primes 31, 61 and 191. This shows that
$\rho$ has 62 solutions in addition to the rational ones. Applying the Mordell–Weil sieve with the primes 7, 29, 257 and 3457, we show that these are in fact not rational; to prove non-existence of rational points in the unique Weierstrass disk, we sieve with the primes 31, 61 and 191. This shows that ![]() $X_{11}(\mathbf {Q}) = \{(1, \pm 5)\}$.
$X_{11}(\mathbf {Q}) = \{(1, \pm 5)\}$.
Example 5.17 We use the model
with small rational points ![]() $(0,\pm 5)$. Again we run quadratic Chabauty for a fairly large prime, namely
$(0,\pm 5)$. Again we run quadratic Chabauty for a fairly large prime, namely ![]() $p=71$, resulting in 78 additional zeros in
$p=71$, resulting in 78 additional zeros in ![]() $X(\mathbf {Q}_{71})$ which we show to be non-rational by sieving with the primes
$X(\mathbf {Q}_{71})$ which we show to be non-rational by sieving with the primes ![]() $7$,
$7$, ![]() $43$,
$43$, ![]() $83$,
$83$, ![]() $101$ and
$101$ and ![]() $1399$. There is an additional final sieving to show there are no rational points in the Weierstrass disk. We conclude that
$1399$. There is an additional final sieving to show there are no rational points in the Weierstrass disk. We conclude that ![]() $X_{15}(\mathbf {Q})=\{(0,\pm 5)\}$.
$X_{15}(\mathbf {Q})=\{(0,\pm 5)\}$.
5.4 Two curves with non-trivial local heights away from  $p$
$p$
We compute the rational points on two genus 2 curves ![]() $C_{188}$ and
$C_{188}$ and ![]() $C_{161}$ considered in [Reference Flynn, Leprévost, Schaefer, Stein, Stoll and WetherellFLS+01]. In both cases, the Jacobian of
$C_{161}$ considered in [Reference Flynn, Leprévost, Schaefer, Stein, Stoll and WetherellFLS+01]. In both cases, the Jacobian of ![]() $C_N$ is an optimal quotient of
$C_N$ is an optimal quotient of ![]() $J_0(N)$, so it has real multiplication and Picard number 2. The Mordell–Weil ranks are both 2 as well, and the rational torsion subgroup is trivial. In [Reference Flynn, Leprévost, Schaefer, Stein, Stoll and WetherellFLS+01] empirical evidence was presented that the full conjecture of Birch and Swinnerton-Dyer holds for both Jacobians. The curves themselves have good reduction away from
$J_0(N)$, so it has real multiplication and Picard number 2. The Mordell–Weil ranks are both 2 as well, and the rational torsion subgroup is trivial. In [Reference Flynn, Leprévost, Schaefer, Stein, Stoll and WetherellFLS+01] empirical evidence was presented that the full conjecture of Birch and Swinnerton-Dyer holds for both Jacobians. The curves themselves have good reduction away from ![]() $N$.
$N$.
So far, all curves whose rational points were computed via quadratic Chabauty had trivial contributions away from ![]() $p$, except for the bielliptic examples in [Reference Balakrishnan and DograBD18, Reference Balakrishnan and DograBD21]. However, for those examples it was possible to find the local contributions away from
$p$, except for the bielliptic examples in [Reference Balakrishnan and DograBD18, Reference Balakrishnan and DograBD21]. However, for those examples it was possible to find the local contributions away from ![]() $p$ by relating them to local heights on the elliptic quotients. In the examples presented here, we compute these contributions using Theorem 3.2. As discussed in § 3.1, we do not have a general algorithm for the action induced by an endomorphism on étale cohomology. Nevertheless, we show below that we can sometimes derive sufficient information from Theorem 3.2 to pin down the local contributions precisely, by computing the local heights at
$p$ by relating them to local heights on the elliptic quotients. In the examples presented here, we compute these contributions using Theorem 3.2. As discussed in § 3.1, we do not have a general algorithm for the action induced by an endomorphism on étale cohomology. Nevertheless, we show below that we can sometimes derive sufficient information from Theorem 3.2 to pin down the local contributions precisely, by computing the local heights at ![]() $p=3$ for the known rational points and by exploiting the bilinearity of the global height pairing.
$p=3$ for the known rational points and by exploiting the bilinearity of the global height pairing.
We include these examples to illustrate the practicality of our algorithms. However, we note that the rational points on both curves can be computed by combining covering collections with elliptic curve Chabauty. For ![]() $C_{188}$ this was pointed out to us by Nils Bruin, and for
$C_{188}$ this was pointed out to us by Nils Bruin, and for ![]() $C_{161}$ this computation is due to Bars, González and Xarles [Reference Bars, González and XarlesBGX21].
$C_{161}$ this computation is due to Bars, González and Xarles [Reference Bars, González and XarlesBGX21].
Example 5.18 We first consider the genus 2 curve
Over ![]() $\mathbf {Z}_{47}$, it has a regular semi-stable model whose special fibre is a curve of genus 1 with a node, so
$\mathbf {Z}_{47}$, it has a regular semi-stable model whose special fibre is a curve of genus 1 with a node, so ![]() $h_{47}$ is trivial by Theorem 3.2. However, as we shall see, there are non-trivial contributions to the local height at 2.
$h_{47}$ is trivial by Theorem 3.2. However, as we shall see, there are non-trivial contributions to the local height at 2.
The integral points on ![]() $C_{188}$ over
$C_{188}$ over ![]() $\mathbf {Q}(\sqrt {-3})$ were computed in [Reference Balakrishnan, Besser, Bianchi and MüllerBBBM21, Example 6.5]. In the present work, we show that
$\mathbf {Q}(\sqrt {-3})$ were computed in [Reference Balakrishnan, Besser, Bianchi and MüllerBBBM21, Example 6.5]. In the present work, we show that
For our computations, we use the good ordinary prime ![]() $p=3$, the base point
$p=3$, the base point ![]() $b=(1,1)$, and a cycle
$b=(1,1)$, and a cycle ![]() $Z$ constructed from the Hecke operator
$Z$ constructed from the Hecke operator ![]() $T_3$ as in (5.3).
$T_3$ as in (5.3).
Recall from Example 3.3 that there is a regular semi-stable model over ![]() $K=\mathbf {Q}_2(\sqrt [3]{2})$ and that the corresponding metric graph
$K=\mathbf {Q}_2(\sqrt [3]{2})$ and that the corresponding metric graph ![]() $\Gamma _{\mathrm {reg}}$ is a line segment. The two genus
$\Gamma _{\mathrm {reg}}$ is a line segment. The two genus ![]() $1$ vertices
$1$ vertices ![]() $w_0$ and
$w_0$ and ![]() $w_1$ have pre-images
$w_1$ have pre-images
respectively. The set ![]() $\mathcal {U}_2 := \{P\in C_{188}(\mathbf {Q} _2 ):\mathrm {ord}_2 (x(P))<0 \}$ maps to the midpoint
$\mathcal {U}_2 := \{P\in C_{188}(\mathbf {Q} _2 ):\mathrm {ord}_2 (x(P))<0 \}$ maps to the midpoint ![]() $w_2$ of the line segment.
$w_2$ of the line segment.
Since the function ![]() $j_{\Gamma }$ from Theorem 3.2 is affine linear and vanishes at
$j_{\Gamma }$ from Theorem 3.2 is affine linear and vanishes at ![]() $w_1$, there is a constant
$w_1$, there is a constant ![]() $\kappa$ such that for all
$\kappa$ such that for all ![]() $x\in C_{188}(\mathbf {Q}_2)$ we have
$x\in C_{188}(\mathbf {Q}_2)$ we have
where
 \[ m(P)= \begin{cases} 2, & \text{when }x(P)\text{ is divisible by 2},\\ 0, & \text{when }x(P)\text{ is a 2-adic unit},\\ 1, & \text{when }x(P)\text{ is non-integral}. \end{cases} \]
\[ m(P)= \begin{cases} 2, & \text{when }x(P)\text{ is divisible by 2},\\ 0, & \text{when }x(P)\text{ is a 2-adic unit},\\ 1, & \text{when }x(P)\text{ is non-integral}. \end{cases} \]
One could determine ![]() $\kappa$ by further computing the trace of
$\kappa$ by further computing the trace of ![]() $Z$ acting on the cohomology of the two genus
$Z$ acting on the cohomology of the two genus ![]() $1$ curves in the special fibre of the regular model described in Example 3.3. In this example, we can determine
$1$ curves in the special fibre of the regular model described in Example 3.3. In this example, we can determine ![]() $\kappa$ by computing local heights at
$\kappa$ by computing local heights at ![]() $p$, as there is a unique choice of
$p$, as there is a unique choice of ![]() $\kappa$ such that
$\kappa$ such that
satisfies the bilinearity properties of a global height. We can reduce the determination of ![]() $\kappa$ to linear algebra by computing
$\kappa$ to linear algebra by computing ![]() $h_3(\mathrm {A}(P))$ and the values of a basis of the space of
$h_3(\mathrm {A}(P))$ and the values of a basis of the space of ![]() $\mathrm {End}_0(J)$-equivariant bilinear pairings for
$\mathrm {End}_0(J)$-equivariant bilinear pairings for ![]() $3=g+1$ rational points
$3=g+1$ rational points ![]() $P\in X(\mathbf {Q})$. We find
$P\in X(\mathbf {Q})$. We find ![]() $\kappa =\tfrac {4}{3}\log _{p} (2)$.
$\kappa =\tfrac {4}{3}\log _{p} (2)$.
To finish the computation of the rational points, we first solve for the zeros of the quadratic Chabauty function ![]() $\rho$ on the affine patch (5.4). In order to deal with the Weierstrass disk at infinity, we move the point at infinity to
$\rho$ on the affine patch (5.4). In order to deal with the Weierstrass disk at infinity, we move the point at infinity to ![]() $(0,0)$ and repeat the computation for the resulting affine patch. We then apply the trick described in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 5.5], changing the base point and reducing the computation of the Frobenius structure to the computation of Coleman integrals.
$(0,0)$ and repeat the computation for the resulting affine patch. We then apply the trick described in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 5.5], changing the base point and reducing the computation of the Frobenius structure to the computation of Coleman integrals.
We find that ![]() $\rho$ vanishes on the known rational points and that it vanishes on 13 additional
$\rho$ vanishes on the known rational points and that it vanishes on 13 additional ![]() $\mathbf {Q}_3$-points to precision
$\mathbf {Q}_3$-points to precision ![]() $3^5$. Upon noticing that
$3^5$. Upon noticing that ![]() $J(\mathbf {F}_{43})\simeq (\mathbf {Z}/54\mathbf {Z})^2$, we show that the reductions of the corresponding cosets of
$J(\mathbf {F}_{43})\simeq (\mathbf {Z}/54\mathbf {Z})^2$, we show that the reductions of the corresponding cosets of ![]() $27J(\mathbf {Q})$ do not meet the image of
$27J(\mathbf {Q})$ do not meet the image of ![]() $C_{188}(\mathbf {F}_{43})$ in
$C_{188}(\mathbf {F}_{43})$ in ![]() $J(\mathbf {F}_{43})/27J(\mathbf {F}_{43})$. This suffices to prove (5.5).
$J(\mathbf {F}_{43})/27J(\mathbf {F}_{43})$. This suffices to prove (5.5).
Example 5.19 The curve ![]() $C_{161}$ has an affine equation
$C_{161}$ has an affine equation
As discussed in [Reference Bars, González and XarlesBGX21], this is in fact a model for the modular curve ![]() $X_0^*(161) = X_0(161)/\langle w_7, w_{23}\rangle$. The curve has ten small rational points
$X_0^*(161) = X_0(161)/\langle w_7, w_{23}\rangle$. The curve has ten small rational points
Anticipating the need to use the Mordell–Weil sieve, we choose the prime ![]() $p=29$ and the cycle
$p=29$ and the cycle ![]() $Z$ corresponding to the endomorphism
$Z$ corresponding to the endomorphism ![]() $4T_{29}-\mathrm {Tr}(T_{29})I_4$.
$4T_{29}-\mathrm {Tr}(T_{29})I_4$.
The bad primes are ![]() $7$ and
$7$ and ![]() $23$. At both of these primes, the stable model has special fibre a genus zero curve with two double points. One can show this, for instance, using the program genus2reduction due to Qing Liu, now contained in Pari/GP or Sage. This (or Magma's RegularModel package) also shows that the model over
$23$. At both of these primes, the stable model has special fibre a genus zero curve with two double points. One can show this, for instance, using the program genus2reduction due to Qing Liu, now contained in Pari/GP or Sage. This (or Magma's RegularModel package) also shows that the model over ![]() $\mathbf {Z}_{23}$ defined by the given equation is regular. Indeed, the 23-adic valuation of the discriminant is 2; therefore both singular points
$\mathbf {Z}_{23}$ defined by the given equation is regular. Indeed, the 23-adic valuation of the discriminant is 2; therefore both singular points ![]() $(2,0)$ and
$(2,0)$ and ![]() $(11,0)$ on the reduction modulo 23 define regular points on this model. Hence, the given equation defines a regular semi-stable model over
$(11,0)$ on the reduction modulo 23 define regular points on this model. Hence, the given equation defines a regular semi-stable model over ![]() $\mathbf {Z}_{23}$, and all of the
$\mathbf {Z}_{23}$, and all of the ![]() $\mathbf {Q} _{23}$ points lie on a common irreducible component of a minimal regular model over
$\mathbf {Q} _{23}$ points lie on a common irreducible component of a minimal regular model over ![]() $\mathbf {Z}_{23}$, so the height contribution at this prime is zero by Theorem 3.2.
$\mathbf {Z}_{23}$, so the height contribution at this prime is zero by Theorem 3.2.
At 7, the discriminant has valuation 4, so the model defined by the given equation is not regular. The singular points on the special fibre are ![]() $(1,0)$ and
$(1,0)$ and ![]() $(4,0)$. Blowing up once in both of these yields a semi-stable regular model whose special fiber consists of two genus zero curves
$(4,0)$. Blowing up once in both of these yields a semi-stable regular model whose special fiber consists of two genus zero curves ![]() $w_1$ and
$w_1$ and ![]() $w_2$ that do not intersect and another genus zero curve
$w_2$ that do not intersect and another genus zero curve ![]() $w_0$ which reduces to the smooth locus of the stable model and which intersects
$w_0$ which reduces to the smooth locus of the stable model and which intersects ![]() $w_1$ and
$w_1$ and ![]() $w_2$ transversely in two points each,
$w_2$ transversely in two points each, ![]() $e_1$ and
$e_1$ and ![]() $e_2$ and
$e_2$ and ![]() $e_3$ and
$e_3$ and ![]() $e_4$, respectively. This information can also be obtained from genus2reduction or RegularModel.
$e_4$, respectively. This information can also be obtained from genus2reduction or RegularModel.
The corresponding dual graph is shown in Figure 1. We choose an orientation by designating ![]() $w_0$ as the source of
$w_0$ as the source of ![]() $e_1$ and
$e_1$ and ![]() $e_3$ and as the target of
$e_3$ and as the target of ![]() $e_2$ and
$e_2$ and ![]() $e_4$. The points
$e_4$. The points ![]() $(\tfrac {1}{4},\pm \tfrac {209}{64}),(-1,\pm 1), \infty _{\pm }$ listed in (5.6) reduce to the component
$(\tfrac {1}{4},\pm \tfrac {209}{64}),(-1,\pm 1), \infty _{\pm }$ listed in (5.6) reduce to the component ![]() $w_0$. The points
$w_0$. The points ![]() $(1,\pm 7)$ reduce to
$(1,\pm 7)$ reduce to ![]() $w_1$ and the points
$w_1$ and the points ![]() $(\tfrac {1}{2},\pm \tfrac {35}{8})$ reduce to
$(\tfrac {1}{2},\pm \tfrac {35}{8})$ reduce to ![]() $w_2$. We may again use Theorem 3.2 to determine the possible values of
$w_2$. We may again use Theorem 3.2 to determine the possible values of ![]() $h_7 (P)$, without computing the action of our chosen correspondence on
$h_7 (P)$, without computing the action of our chosen correspondence on ![]() $\mathrm {H}^1 (\Gamma )$. Note that in this case, the homology
$\mathrm {H}^1 (\Gamma )$. Note that in this case, the homology ![]() $\mathrm {H}_1 (\Gamma )$ is generated by
$\mathrm {H}_1 (\Gamma )$ is generated by ![]() $\gamma _1 =e_2 + e_1$ and
$\gamma _1 =e_2 + e_1$ and ![]() $\gamma _2 =e_3 +e_4$, respectively. Since
$\gamma _2 =e_3 +e_4$, respectively. Since ![]() $Z$ is trace
$Z$ is trace ![]() $0$ on
$0$ on ![]() $\mathrm {H}_1 (\Gamma )$, with respect to this basis, the corresponding endomorphism must be of the form
$\mathrm {H}_1 (\Gamma )$, with respect to this basis, the corresponding endomorphism must be of the form ![]() $\big (\begin {smallmatrix} a & b \\ c & -a \end {smallmatrix}\big ).$ Then, by Theorem 3.2, the measure
$\big (\begin {smallmatrix} a & b \\ c & -a \end {smallmatrix}\big ).$ Then, by Theorem 3.2, the measure ![]() $\mu _Z$ is simply given by
$\mu _Z$ is simply given by ![]() $({a}/{2})(\gamma _1 -\gamma _2 )$, since both edges have length 2. The image of
$({a}/{2})(\gamma _1 -\gamma _2 )$, since both edges have length 2. The image of ![]() $X(\mathbf {Q} _7 )$ in
$X(\mathbf {Q} _7 )$ in ![]() $\Gamma$ consists of the three vertices
$\Gamma$ consists of the three vertices ![]() $w_0, w_1,$ and
$w_0, w_1,$ and ![]() $w_2$ and hence if we take the basepoint
$w_2$ and hence if we take the basepoint ![]() $(\tfrac {1}{4},\tfrac {209}{64})$ reducing to
$(\tfrac {1}{4},\tfrac {209}{64})$ reducing to ![]() $w_0$, the values of
$w_0$, the values of ![]() $j_{\Gamma }$ are simply
$j_{\Gamma }$ are simply ![]() $a,0,-a$. We solve for
$a,0,-a$. We solve for ![]() $a$ using a 29-adic computation similar to the previous example, and we find that
$a$ using a 29-adic computation similar to the previous example, and we find that ![]() $a=-4$. Finally, we apply the Mordell–Weil sieve with
$a=-4$. Finally, we apply the Mordell–Weil sieve with ![]() $M=4\cdot 29^3$ and primes
$M=4\cdot 29^3$ and primes ![]() $199,373,463$ to show that the only 29-adic points in the zero set of
$199,373,463$ to show that the only 29-adic points in the zero set of ![]() $\rho$ modulo
$\rho$ modulo ![]() $29^3$ are the rational points listed in (5.6). This proves that these are indeed the only rational points on
$29^3$ are the rational points listed in (5.6). This proves that these are indeed the only rational points on ![]() $C_{161}$.
$C_{161}$.

Figure 1. Dual graph of the minimal regular model of ![]() $C_{161}$ at
$C_{161}$ at ![]() $\ell =7$.
$\ell =7$.
5.5 The non-split Cartan modular curve  $X_{\scriptstyle \mathrm { ns}} ^+ (17)$
$X_{\scriptstyle \mathrm { ns}} ^+ (17)$
The modular curve
attached to the normaliser of the non-split Cartan subgroup of level ![]() $17$ has genus
$17$ has genus ![]() $6$. By [Reference Dogra and Le FournDLF21, § 5.3], the rank of
$6$. By [Reference Dogra and Le FournDLF21, § 5.3], the rank of ![]() $J_{\rm ns}^+(17)(\mathbf {Q})$ is also 6. The set of rational points
$J_{\rm ns}^+(17)(\mathbf {Q})$ is also 6. The set of rational points ![]() $X(\mathbf {Q} )$ can be determined without computing local heights at the bad prime
$X(\mathbf {Q} )$ can be determined without computing local heights at the bad prime ![]() $17$, even though these contribute non-trivially when determining
$17$, even though these contribute non-trivially when determining ![]() $X(\mathbf {Q}_p)_2$, by carefully choosing the correspondence
$X(\mathbf {Q}_p)_2$, by carefully choosing the correspondence ![]() $Z$.
$Z$.
The curve ![]() $X$ has a semi-stable model
$X$ has a semi-stable model ![]() $\mathcal {X}$ over
$\mathcal {X}$ over ![]() $W(\overline {\mathbf {F}}_{17})[\varpi ]$ with
$W(\overline {\mathbf {F}}_{17})[\varpi ]$ with ![]() $\varpi = (1+\zeta _{17})^{1/9}$, where
$\varpi = (1+\zeta _{17})^{1/9}$, where ![]() $W(\overline {\mathbf {F}}_{17})$ is the ring of Witt vectors of
$W(\overline {\mathbf {F}}_{17})$ is the ring of Witt vectors of ![]() $\overline {\mathbf {F}}_{17}$, described by Edixhoven and Parent [Reference Edixhoven and ParentEP21]. Its special fibre has two irreducible components
$\overline {\mathbf {F}}_{17}$, described by Edixhoven and Parent [Reference Edixhoven and ParentEP21]. Its special fibre has two irreducible components
 \begin{align*} &C_1 : y^2 = x(x^9 +a), \quad a \in \overline{\mathbf{F}}_{17}^{\times}, \\ &C_2 : z^2 = w(w^3 +b), \quad b \in \overline{\mathbf{F}}_{17}^{\times}, \end{align*}
\begin{align*} &C_1 : y^2 = x(x^9 +a), \quad a \in \overline{\mathbf{F}}_{17}^{\times}, \\ &C_2 : z^2 = w(w^3 +b), \quad b \in \overline{\mathbf{F}}_{17}^{\times}, \end{align*}
which have genus ![]() $4$ and
$4$ and ![]() $1$, respectively. They are smooth and intersect transversely at two points, so that the Jacobian has toric rank
$1$, respectively. They are smooth and intersect transversely at two points, so that the Jacobian has toric rank ![]() $1$. The inertia subgroup
$1$. The inertia subgroup ![]() $I \subset G_{\mathbf {Q}_{17}}$ acts via automorphisms on the special fibre of this model, and the stabiliser of the set of irreducible components is contained in
$I \subset G_{\mathbf {Q}_{17}}$ acts via automorphisms on the special fibre of this model, and the stabiliser of the set of irreducible components is contained in ![]() $\mu _{18}(\overline {\mathbf {F}}_{17^2}) = \langle \zeta \rangle$, where the root of unity
$\mu _{18}(\overline {\mathbf {F}}_{17^2}) = \langle \zeta \rangle$, where the root of unity ![]() $\zeta ^{18}=1$ acts on the components by
$\zeta ^{18}=1$ acts on the components by
 \begin{align*} \zeta : (x,y) & \longmapsto (\zeta^4x,\zeta^2y), \\ \zeta : (z,w) & \longmapsto (\zeta^{12}z,\zeta^{6}w). \end{align*}
\begin{align*} \zeta : (x,y) & \longmapsto (\zeta^4x,\zeta^2y), \\ \zeta : (z,w) & \longmapsto (\zeta^{12}z,\zeta^{6}w). \end{align*}
The resulting operator ![]() $[\zeta ]$ on the cohomology of these curves has characteristic polynomial
$[\zeta ]$ on the cohomology of these curves has characteristic polynomial
 \begin{align*} \det\big(1 - t [\zeta] : \mathrm{H}^1(C_1,\mathbf{Q}_p) \big) &= (t^2+t+1)(t^6+t^3+1), \\ \det\big(1 - t [\zeta] : \mathrm{H}^1(C_2,\mathbf{Q}_p) \big) &= (t^2+t+1). \end{align*}
\begin{align*} \det\big(1 - t [\zeta] : \mathrm{H}^1(C_1,\mathbf{Q}_p) \big) &= (t^2+t+1)(t^6+t^3+1), \\ \det\big(1 - t [\zeta] : \mathrm{H}^1(C_2,\mathbf{Q}_p) \big) &= (t^2+t+1). \end{align*}
Since the Hecke action on the cohomology of ![]() $X$ is defined over
$X$ is defined over ![]() $\mathbf {Q}$, it must commute with the action of inertia, and therefore the irreducible Hecke modules of the Jacobian up to isogeny must be contained in the submodules coming from the toric part (dimension
$\mathbf {Q}$, it must commute with the action of inertia, and therefore the irreducible Hecke modules of the Jacobian up to isogeny must be contained in the submodules coming from the toric part (dimension ![]() $1$) and the parts where the operator
$1$) and the parts where the operator ![]() $[\zeta ]$ is of order
$[\zeta ]$ is of order ![]() $3$ (dimension
$3$ (dimension ![]() $2$) and of order
$2$) and of order ![]() $9$ (dimension
$9$ (dimension ![]() $3$). By the work of Chen and of Edixhoven and de Smit [Reference ChenChe00, Reference Edixhoven and de SmitEdS00] the Jacobian of
$3$). By the work of Chen and of Edixhoven and de Smit [Reference ChenChe00, Reference Edixhoven and de SmitEdS00] the Jacobian of ![]() $X$ admits an isogeny to the new part of the Jacobian of
$X$ admits an isogeny to the new part of the Jacobian of ![]() $X_0^+(17^2)$ equivariant for the anaemic Hecke algebra. The new part of the Jacobian of
$X_0^+(17^2)$ equivariant for the anaemic Hecke algebra. The new part of the Jacobian of ![]() $X_0^+(17^2)$ decomposes up to isogeny into irreducible factors
$X_0^+(17^2)$ decomposes up to isogeny into irreducible factors ![]() $M_1 \times M_2 \times M_3$ of dimensions
$M_1 \times M_2 \times M_3$ of dimensions ![]() $1,2,3$ respectively, where
$1,2,3$ respectively, where ![]() $M_1,M_2,M_3$ are killed by the Hecke operators
$M_1,M_2,M_3$ are killed by the Hecke operators
 \begin{align*} M_1 & : (T_{2} + 1) = 0, \\ M_2 & : (T^2_{2} +T_2 - 3) = 0,\\ M_3 & : (T_{2}^3 -3T_{2} + 1) = 0. \end{align*}
\begin{align*} M_1 & : (T_{2} + 1) = 0, \\ M_2 & : (T^2_{2} +T_2 - 3) = 0,\\ M_3 & : (T_{2}^3 -3T_{2} + 1) = 0. \end{align*}
If we set ![]() $M = (T_{2} +1)(T^2_{2} +T_2 - 3)$, we find that
$M = (T_{2} +1)(T^2_{2} +T_2 - 3)$, we find that ![]() $Z=M$ and
$Z=M$ and ![]() $Z=2M^3 + 3M^2$ are non-trivial trace zero correspondences that induce the zero endomorphisms on
$Z=2M^3 + 3M^2$ are non-trivial trace zero correspondences that induce the zero endomorphisms on ![]() $H_1 (\Gamma,\mathbf {Q} )$ and the cohomology of
$H_1 (\Gamma,\mathbf {Q} )$ and the cohomology of ![]() $C_2$, so that Theorem 3.2 implies that
$C_2$, so that Theorem 3.2 implies that ![]() $\mu _F = 0$, and hence the
$\mu _F = 0$, and hence the ![]() $17$-adic height vanishes:
$17$-adic height vanishes:
In fact, starting from any generator ![]() $T$ of the Hecke algebra (like
$T$ of the Hecke algebra (like ![]() $T=T_2$ above), one easily computes two linearly independent trace zero correspondences
$T=T_2$ above), one easily computes two linearly independent trace zero correspondences ![]() $Z \in \mathbf {Z}[T]$ that act trivially on the dual graph and the cohomology of
$Z \in \mathbf {Z}[T]$ that act trivially on the dual graph and the cohomology of ![]() $C_2$, which therefore likewise ensures the triviality of the associated
$C_2$, which therefore likewise ensures the triviality of the associated ![]() $17$-adic height.
$17$-adic height.
To put these observations into action, we choose ![]() $p=31$ and use the model of
$p=31$ and use the model of ![]() $X$ found by Mercuri and Schoof [Reference Mercuri and SchoofMS20, § 6] as an intersection of six quadrics in
$X$ found by Mercuri and Schoof [Reference Mercuri and SchoofMS20, § 6] as an intersection of six quadrics in ![]() $\mathbf {P}^5$. Our strategy for finding a suitable singular plane curve model largely follows [Reference Adžaga, Arul, Beneish, Chen, Chidambaram, Keller and WenAAB+21]. To find a model with small coefficients, we use the Magma function Genus6PlaneCurveModel, and then apply an automorphism of
$\mathbf {P}^5$. Our strategy for finding a suitable singular plane curve model largely follows [Reference Adžaga, Arul, Beneish, Chen, Chidambaram, Keller and WenAAB+21]. To find a model with small coefficients, we use the Magma function Genus6PlaneCurveModel, and then apply an automorphism of ![]() $\mathbf {P}^2$ to ensure that there are two rational points at infinity (this speeds up the computation of the Hodge filtration (see [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 4]) where one passes to a number field over which the divisor at infinity splits completely). We obtain a singular plane curve model
$\mathbf {P}^2$ to ensure that there are two rational points at infinity (this speeds up the computation of the Hodge filtration (see [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, § 4]) where one passes to a number field over which the divisor at infinity splits completely). We obtain a singular plane curve model ![]() $Q(x,y)=0$, where
$Q(x,y)=0$, where
 \begin{align*} 5\cdot Q(x,y)&=5y^6 +
\big(24x + 12\big)y^5 + \big(\!-495x^2 - 543x -153 \big)y^4
\\ &\quad+ \big(\!-1472x^3 - 2814x^2 - 1719x - 337 \big)y^3
\\ &\quad+ \big(\!-1686x^4 - 4875x^3 - 4761x^2 - 1902x -
263\big)y^2 \\ &\quad +\big(\!-540x^5 - 2082x^4 - 2952x^3 -
1875x^2 - 535x - 56 \big)y \\ &\quad +188x^6 + 534x^5 +
567x^4 + 284 x^3 + 70x^2 + 7x. \end{align*}
\begin{align*} 5\cdot Q(x,y)&=5y^6 +
\big(24x + 12\big)y^5 + \big(\!-495x^2 - 543x -153 \big)y^4
\\ &\quad+ \big(\!-1472x^3 - 2814x^2 - 1719x - 337 \big)y^3
\\ &\quad+ \big(\!-1686x^4 - 4875x^3 - 4761x^2 - 1902x -
263\big)y^2 \\ &\quad +\big(\!-540x^5 - 2082x^4 - 2952x^3 -
1875x^2 - 535x - 56 \big)y \\ &\quad +188x^6 + 534x^5 +
567x^4 + 284 x^3 + 70x^2 + 7x. \end{align*}
The fact that ![]() $T_{31}$ generates the Hecke algebra can be checked from the LMFDB page for newforms of weight
$T_{31}$ generates the Hecke algebra can be checked from the LMFDB page for newforms of weight ![]() $2$, level 289, trivial character and Atkin–Lehner eigenvalue
$2$, level 289, trivial character and Atkin–Lehner eigenvalue ![]() $1$ [LMFDB21]. We compute two correspondences
$1$ [LMFDB21]. We compute two correspondences ![]() $Z \in \mathbf {Z}[T_{31}]$ as above, and obtain a pair of power series in each residue disk, whose common zeros to precision
$Z \in \mathbf {Z}[T_{31}]$ as above, and obtain a pair of power series in each residue disk, whose common zeros to precision ![]() $O(31^{20})$ correspond to the rational points
$O(31^{20})$ correspond to the rational points
where ![]() $\infty _1$ and
$\infty _1$ and ![]() $\infty _2$ are the points
$\infty _2$ are the points ![]() $(1:-1:0)$ and
$(1:-1:0)$ and ![]() $(1:-\frac {1}{5}:0)$. Therefore, this must be the full set of rational points
$(1:-\frac {1}{5}:0)$. Therefore, this must be the full set of rational points ![]() $X(\mathbf {Q})$. These were already found by Mercuri and Schoof [Reference Mercuri and SchoofMS20, § 6]; they are all CM points and the corresponding discriminants are
$X(\mathbf {Q})$. These were already found by Mercuri and Schoof [Reference Mercuri and SchoofMS20, § 6]; they are all CM points and the corresponding discriminants are ![]() $-3, -7, -11, -12, -27, -28, -163$. This proves Theorem 1.2.
$-3, -7, -11, -12, -27, -28, -163$. This proves Theorem 1.2.
Remark 5.20 It would be interesting to use the techniques of this paper to compute the rational points on ![]() $X_{\scriptstyle \mathrm { ns}} ^+ (19)$. Mercuri and Schoof [Reference Mercuri and SchoofMS20, § 7] found a model for this curve as well. Nevertheless, we were unable to find a plane affine equation for this curve and a prime
$X_{\scriptstyle \mathrm { ns}} ^+ (19)$. Mercuri and Schoof [Reference Mercuri and SchoofMS20, § 7] found a model for this curve as well. Nevertheless, we were unable to find a plane affine equation for this curve and a prime ![]() $p$, satisfying Assumption 3.10, such that it is feasible to carry out Algorithm 3.12. Difficulties arose in computing a basis of
$p$, satisfying Assumption 3.10, such that it is feasible to carry out Algorithm 3.12. Difficulties arose in computing a basis of ![]() $\mathrm {H} ^1 _{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q} _p })$ due to the large degrees of the field extensions we encountered when applying the algorithms in [Reference TuitmanTui17, § 3].
$\mathrm {H} ^1 _{\scriptstyle \mathrm {dR}}(X_{\mathbf {Q} _p })$ due to the large degrees of the field extensions we encountered when applying the algorithms in [Reference TuitmanTui17, § 3].
Acknowledgements
We are deeply indebted to B. Edixhoven for his numerous generous insights on this subject. It is a pleasure to thank N. Elkies, B. Mazur, J. Rouse, A. Sutherland and D. Zureick-Brown for suggesting several modular curves of interest, as well as many helpful discussions, which provided the impetus for this work. We are grateful for the contributions of N. Adz̆aga, V. Arul, L. Beneish, A. Best, F. Bianchi, M. Chen, S. Chidambaram, T. Keller, N. Triantafillou and B. Wen in finding a number of bugs in earlier versions of our code. We would also like to thank M. Stoll for kindly providing an implementation of the Mordell–Weil sieve, on which ours is based and N. Bruin for sharing another approach to determining ![]() $C_{188}(\mathbf {Q})$. We are grateful to F. Bianchi, D. Holmes, T. Keller and M. Stoll for helpful comments on an earlier version of this paper. We thank the referee for a helpful and entertaining report.
$C_{188}(\mathbf {Q})$. We are grateful to F. Bianchi, D. Holmes, T. Keller and M. Stoll for helpful comments on an earlier version of this paper. We thank the referee for a helpful and entertaining report.