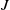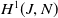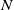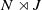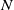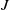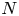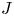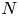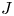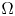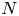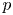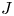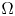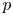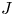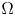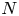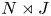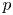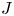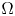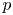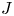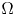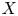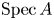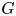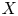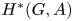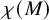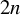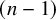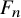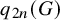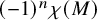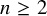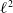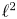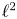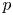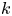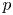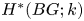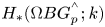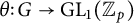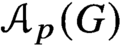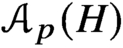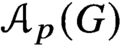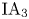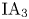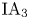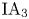62 results in 20Jxx
Ample Groupoids, Topological Full groups, Algebraic K-theory Spectra and Infinite Loop Spaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 February 2025, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Actions of nilpotent groups on nilpotent groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 16 January 2025, pp. 228-231
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Classifying spaces for families of abelian subgroups of braid groups, RAAGs and graphs of abelian groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 290-307
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Higher dimensional algebraic fiberings for pro-p groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 22 December 2023, pp. 300-323
- Print publication:
- February 2025
-
- Article
- Export citation
FAITHFULNESS OF THE 2-BRAID GROUP VIA ZIGZAG ALGEBRA IN TYPE B
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 27 October 2023, pp. 67-84
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
On subdirect products of type FPn of limit groups over Droms RAAGs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 11 October 2023, pp. 417-440
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
Fixed point conditions for non-coprime actions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 September 2023, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on virtual duality and automorphism groups of right-angled Artin groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 19 June 2023, pp. 573-581
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Balmer spectrum of certain Deligne–Mumford stacks
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 24 May 2023, pp. 1314-1346
- Print publication:
- June 2023
-
- Article
- Export citation
Minimal Euler characteristics for even-dimensional manifolds with finite fundamental group
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 31 March 2023, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized Bockstein maps and Massey products
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 23 January 2023, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Hanna Neumann conjecture for surface groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 12 October 2022, pp. 1850-1877
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COHOMOLOGICAL MACKEY 2-FUNCTORS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 18 August 2022, pp. 279-309
- Print publication:
- January 2024
-
- Article
-
- You have access
- HTML
- Export citation
A note on the rational homological dimension of lattices in positive characteristic
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 10 June 2022, pp. 138-140
- Print publication:
- January 2023
-
- Article
- Export citation
The first $\ell ^{2}$
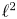 -betti number and groups acting on trees
-betti number and groups acting on trees
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 25 October 2021, pp. 916-923
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Massey products in the homology of the loop space of a p-completed classifying space: finite groups with cyclic Sylow p-subgroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 30 September 2021, pp. 908-915
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Galois-theoretic features for 1-smooth pro-p groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 29 June 2021, pp. 525-541
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An approach to Quillen’s conjecture via centralisers of simple groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 June 2021, e48
-
- Article
-
- You have access
- Open access
- Export citation
On the low-dimensional cohomology groups of the IA-automorphism group of the free group of rank three
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 05 May 2021, pp. 338-363
-
- Article
-
- You have access
- Open access
- Export citation
Higher horospherical limit sets for G-modules over CAT(0)-spaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 1 / July 2021
- Published online by Cambridge University Press:
- 12 March 2021, pp. 133-163
- Print publication:
- July 2021
-
- Article
- Export citation