No CrossRef data available.
Article contents
Higher dimensional algebraic fiberings for pro-p groups
Published online by Cambridge University Press: 22 December 2023
Abstract
We prove some conditions for higher-dimensional algebraic fibering of pro-p group extensions, and we establish corollaries about incoherence of pro-p groups. In particular, if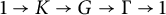 
$1 \to K \to G \to \Gamma \to 1$ is a short exact sequence of pro-p groups, such that 
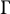$\Gamma $ contains a finitely generated, non-abelian, free pro-p subgroup, K a finitely presented pro-p group with N a normal pro-p subgroup of K such that 
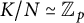$K/ N \simeq \mathbb {Z}_p$ and N not finitely generated as a pro-p group, then G is incoherent (in the category of pro-p groups). Furthermore, we show that if K is a finitely generated, free pro-p group with 
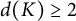$d(K) \geq 2$, then either 
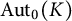$\mathrm{Aut}_0(K)$ is incoherent (in the category of pro-p groups) or there is a finitely presented pro-p group, without non-procyclic free pro-p subgroups, that has a metabelian pro-p quotient that is not finitely presented, i.e., a pro-p version of a result of Bieri–Strebel does not hold.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
The author was partially supported by Bolsa de produtividade em pesquisa CNPq 305457/2021-7 and Projeto temático FAPESP 2018/23690-6.
References
Barnea, Y. and Larsen, M.,
A non-abelian free pro-p group is not linear over a local field
. J. Algebra 214(1999), no. 1, 338–341.CrossRefGoogle Scholar
Ben-Ezra, D. E.-C. and Zelmanov, E.,
On pro-2 identities of 2
$\times$
2 linear groups
. Trans. Amer. Math. Soc. 374(2021), no. 6, 4093–4128.CrossRefGoogle Scholar
$\times$
2 linear groups
. Trans. Amer. Math. Soc. 374(2021), no. 6, 4093–4128.CrossRefGoogle ScholarBestvina, M. and Brady, N.,
Morse theory and finiteness properties of groups
. Invent. Math. 129(1997), 445–470.CrossRefGoogle Scholar
Bieri, R. and Strebel, R.,
Valuations and finitely presented metabelian groups
. Proc. Lond. Math. Soc. 41(1980), 439–464.CrossRefGoogle Scholar
Demushkin, S.,
On the maximal p-extension of a local field
. Izv. Akad. Nauk, USSR Math. Ser. 25, (1961), 329—346.Google Scholar
Dixon, J., Du Sautoy, M. P. F., Mann, A., and Segal, D., Analytic pro-p groups, London Mathematical Society Lecture Note Series, 157, Cambridge University Press, Cambridge, 1991.Google Scholar
Feign, M. and Handel, M.,
Mapping tori of free group automorphisms are coherent
. Ann. Math. 149(1999), 1061–1077.CrossRefGoogle Scholar
Gordon, C. McA.,
Artin groups, 3-manifolds and coherence
. Bol. Soc. Mat. Mexicana (3) 10 (2004), 193—198.Google Scholar
King, J. D.,
Homological finiteness conditions for pro-p groups
. Comm. Algebra 27(1999), no. 10, 4969–4991.CrossRefGoogle Scholar
King, J. D.,
A geometric invariant for metabelian pro-p groups
. J. Lond. Math. Soc. (2) 60(1999), no. 1, 83–94.CrossRefGoogle Scholar
Kochloukova, D. H. and Lima, F. F.,
Homological finiteness properties of fibre products
. Q. J. Math. 69(2018), no. 3, 835–854.CrossRefGoogle Scholar
Kochloukova, D. H. and Vidussi, S.,
Higher dimensional algebraic fiberings of group extensions
. J. Lond. Math. Soc. (2) 108(2023), no. 3, 978–1003.CrossRefGoogle Scholar
Kochloukova, D. H. and Zalesskii, P. A.,
On pro-
$p$
analogues of limit groups via extensions of centralizers
. Math. Z. 267(2011), nos. 1–2, 109–128.CrossRefGoogle Scholar
$p$
analogues of limit groups via extensions of centralizers
. Math. Z. 267(2011), nos. 1–2, 109–128.CrossRefGoogle ScholarKropholler, R. and Walsh, G.,
Incoherence and fibering of many free-by-free groups
. Ann. Inst. Fourier (Grenoble) 72(2022), no. 6, 2385–2397.CrossRefGoogle Scholar
Kuckuck, B.,
Subdirect products of groups and the
$n-\left(n+1\right)-\left(n+2\right)$
conjecture
. Q. J. Math. 65(2014), 1293–1318.CrossRefGoogle Scholar
$n-\left(n+1\right)-\left(n+2\right)$
conjecture
. Q. J. Math. 65(2014), 1293–1318.CrossRefGoogle ScholarLabute, J. P.,
Classification of Demushkin groups
. Canad. J. Math. 19(1967), 106–132.CrossRefGoogle Scholar
Lubotzky, A.,
Combinatorial group theory for pro-p-groups
. J. Pure Appl. Algebra 25(1982), 311–325.CrossRefGoogle Scholar
Ribes, L. and Zalesskii, P.,
Pro-p trees and applications
. In: New horizons in pro-p groups, Progress in Mathematics, 184, Birkhauser, Boston, MA, 2000, pp. 75–119.CrossRefGoogle Scholar
Ribes, L. and Zalesskii, P., Profinite groups, 2nd ed., Springer, Berlin, 2010.CrossRefGoogle Scholar
Romankov, V. A.,
Generators for the automorphism groups of free metabelian pro-
$p$
groups
. Sibirsk. Mat. Zh. 33(1992), no. 5, 145–158.Google Scholar
$p$
groups
. Sibirsk. Mat. Zh. 33(1992), no. 5, 145–158.Google ScholarRomankov, V. A.,
Infinite generation of groups of automorphisms of free pro-p-groups
. Sibirsk. Mat. Zh. 34(1993), no. 4, 153—159.Google Scholar
Serre, J.-P.,
Structure de certains pro-p-groupes
. Seminaire Bourbaki 1962/63(1971), no. 252, 357—364.Google Scholar
Wilson, J. S., Profinite groups, London Mathematical Society Monographs. New Series, 19, The Clarendon Press and Oxford University Press, New York, 1998.CrossRefGoogle Scholar
Wilton, H.,
Hall’s theorem for limit groups
. Geom. Funct. Anal. 18(2008), no. 1, 271–303.CrossRefGoogle Scholar
Wise, D. T.,
An invitation to coherent groups
. In: What’s next?—the mathematical legacy of William P. Thurston, Annals of Mathematics Studies, 205, Princeton University Press, Princeton, NJ, 2020, pp. 326–414.CrossRefGoogle Scholar
Zalesskii, P. and Zapata, T.,
Profinite extensions of centralizers and the profinite completion of limit groups
. Rev. Mat. Iberoam. 36(2020), no. 1, 61–78.CrossRefGoogle Scholar
Zubkov, A. N., Nonrepresentability of a free nonabelian pro-p-group by second-order matrices. Sibirsk. Mat. Zh. 28(1987), no. 5, 64–69.Google Scholar