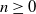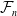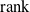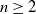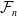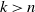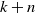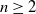1. Introduction
Given a group
![]() $G$
, we say that a collection
$G$
, we say that a collection
![]() $\mathcal F$
of subgroups of
$\mathcal F$
of subgroups of
![]() $G$
is a family if it is nonempty and closed under conjugation and taking subgroups. We fix a group
$G$
is a family if it is nonempty and closed under conjugation and taking subgroups. We fix a group
![]() $G$
and a family
$G$
and a family
![]() $\mathcal F$
of subgroups of
$\mathcal F$
of subgroups of
![]() $G$
. We say that a
$G$
. We say that a
![]() $G$
-CW-complex
$G$
-CW-complex
![]() $X$
is a model for the classifying space
$X$
is a model for the classifying space
![]() $E_{{\mathcal F}}G$
if all of its isotropy groups belong to
$E_{{\mathcal F}}G$
if all of its isotropy groups belong to
![]() $\mathcal F$
and if
$\mathcal F$
and if
![]() $Y$
is a
$Y$
is a
![]() $G$
-CW-complex with isotropy groups belonging to
$G$
-CW-complex with isotropy groups belonging to
![]() $\mathcal F$
, there is precisely one
$\mathcal F$
, there is precisely one
![]() $G$
-map
$G$
-map
![]() $Y\to X$
up to
$Y\to X$
up to
![]() $G$
-homotopy. It can be shown that a model for the classifying space
$G$
-homotopy. It can be shown that a model for the classifying space
![]() $E_{{\mathcal F}}G$
always exists and it is unique up to
$E_{{\mathcal F}}G$
always exists and it is unique up to
![]() $G$
-homotopy equivalence. We define the
$G$
-homotopy equivalence. We define the
![]() $\mathcal F$
-geometric dimension of
$\mathcal F$
-geometric dimension of
![]() $G$
as
$G$
as
The
![]() $\mathcal F$
-geometric dimension has its algebraic counterpart, the
$\mathcal F$
-geometric dimension has its algebraic counterpart, the
![]() $\mathcal F$
-cohomological dimension
$\mathcal F$
-cohomological dimension
![]() $\textrm{cd}_{{\mathcal F}}(G)$
, which can be defined in terms of Bredon cohomology (see Section 2). The
$\textrm{cd}_{{\mathcal F}}(G)$
, which can be defined in terms of Bredon cohomology (see Section 2). The
![]() $\mathcal F$
-geometric dimension and the
$\mathcal F$
-geometric dimension and the
![]() $\mathcal F$
-cohomological dimension satisfy the following inequality (see [Reference Lück and Meintrup17, Theorem 0.1]):
$\mathcal F$
-cohomological dimension satisfy the following inequality (see [Reference Lück and Meintrup17, Theorem 0.1]):
It follows that if
![]() $\textrm{cd}_{{\mathcal F}}(G)\geq 3$
then
$\textrm{cd}_{{\mathcal F}}(G)\geq 3$
then
![]() $\textrm{cd}_{{\mathcal F}}(G)=\textrm{gd}_{{\mathcal F}}(G)$
. It is not generally true that
$\textrm{cd}_{{\mathcal F}}(G)=\textrm{gd}_{{\mathcal F}}(G)$
. It is not generally true that
![]() $\textrm{cd}_{{\mathcal F}}(G)=\textrm{gd}_{{\mathcal F}}(G)$
. For example, for the family of finite subgroups
$\textrm{cd}_{{\mathcal F}}(G)=\textrm{gd}_{{\mathcal F}}(G)$
. For example, for the family of finite subgroups
![]() ${\mathcal F}_0$
, in [Reference Brady, Leary and Nucinkis3] it was proved that there is a right-angled Coxeter group
${\mathcal F}_0$
, in [Reference Brady, Leary and Nucinkis3] it was proved that there is a right-angled Coxeter group
![]() $W$
such that
$W$
such that
![]() $\textrm{cd}_{{\mathcal F}_0}(W)=2$
and
$\textrm{cd}_{{\mathcal F}_0}(W)=2$
and
![]() $\textrm{gd}_{{\mathcal F}_0}(W)=3$
. For other examples see [Reference Serre25].
$\textrm{gd}_{{\mathcal F}_0}(W)=3$
. For other examples see [Reference Serre25].
Let
![]() $n\geq 0$
be an integer. A group is said to be virtually
$n\geq 0$
be an integer. A group is said to be virtually
![]() $\mathbb{Z}^n$
if it contains a subgroup of finite index isomorphic to
$\mathbb{Z}^n$
if it contains a subgroup of finite index isomorphic to
![]() $\mathbb{Z}^n$
. Define the family
$\mathbb{Z}^n$
. Define the family
The families
![]() ${\mathcal F}_0$
and
${\mathcal F}_0$
and
![]() ${\mathcal F}_1$
are relevant due to their connection with the Farrell–Jones and Baum-Connes isomorphism conjectures; see for example [Reference Lück and Reich18]. The Farrell–Jones conjecture has been proved for braid groups in [Reference Aravinda, Farrell and Roushon1, Reference Flores and González-Meneses12, Reference Álvarez and Saldaña15] and for some even Artin groups in [Reference Wu27].
${\mathcal F}_1$
are relevant due to their connection with the Farrell–Jones and Baum-Connes isomorphism conjectures; see for example [Reference Lück and Reich18]. The Farrell–Jones conjecture has been proved for braid groups in [Reference Aravinda, Farrell and Roushon1, Reference Flores and González-Meneses12, Reference Álvarez and Saldaña15] and for some even Artin groups in [Reference Wu27].
For
![]() $n\geq 2$
, the families
$n\geq 2$
, the families
![]() ${\mathcal F}_n$
have been recently studied by several people; see for example [Reference Huang and Prytuła13, Reference Juan-Pineda and Saldaña14, Reference Lück16, Reference Rolland, Álvarez and Saldaña23, Reference Serre25]. For a virtually
${\mathcal F}_n$
have been recently studied by several people; see for example [Reference Huang and Prytuła13, Reference Juan-Pineda and Saldaña14, Reference Lück16, Reference Rolland, Álvarez and Saldaña23, Reference Serre25]. For a virtually
![]() $\mathbb{Z}^n$
group
$\mathbb{Z}^n$
group
![]() $G$
, it was proved in [Reference Rolland, Álvarez and Saldaña23] that
$G$
, it was proved in [Reference Rolland, Álvarez and Saldaña23] that
![]() $\textrm{gd}_{{\mathcal F}_k}(G)\leq n+k$
for all
$\textrm{gd}_{{\mathcal F}_k}(G)\leq n+k$
for all
![]() $0\leq k\lt n$
. For a free abelian group, this upper bound was also obtained by Corob Cook, Moreno, Nucinkis, and Pasini in [Reference Charney4], and they asked whether this upper bound was sharp:
$0\leq k\lt n$
. For a free abelian group, this upper bound was also obtained by Corob Cook, Moreno, Nucinkis, and Pasini in [Reference Charney4], and they asked whether this upper bound was sharp:
Question 1 ([Reference Charney4], Question 2.7). For
![]() $0\leq k\lt n$
, is
$0\leq k\lt n$
, is
![]() $\textrm{gd}_{{\mathcal F}_k}(\mathbb{Z}^n)=n+k$
?
$\textrm{gd}_{{\mathcal F}_k}(\mathbb{Z}^n)=n+k$
?
We answer this question affirmatively in Theorem 1.1. For
![]() $k=1$
, this was proved in [Reference Mislin and Valette20, Theorem 5.13] and for
$k=1$
, this was proved in [Reference Mislin and Valette20, Theorem 5.13] and for
![]() $k=2$
in [Reference Prytuła22, Proposition A.]. As an application, we provide lower bounds for the
$k=2$
in [Reference Prytuła22, Proposition A.]. As an application, we provide lower bounds for the
![]() ${\mathcal F}_k$
-geometric dimension of virtually abelian groups, braid groups, and right-angled Artin groups (RAAGs). Combining these lower bounds with previously known results in the literature, we show that they are sharp. We also prove that the
${\mathcal F}_k$
-geometric dimension of virtually abelian groups, braid groups, and right-angled Artin groups (RAAGs). Combining these lower bounds with previously known results in the literature, we show that they are sharp. We also prove that the
![]() ${\mathcal F}_k$
-geometric dimension is equal to the
${\mathcal F}_k$
-geometric dimension is equal to the
![]() ${\mathcal F}_k$
-cohomological dimension in all these cases. On the other hand, inspired by [Reference Lück16], we use Bass–Serre theory to explicitly calculate, for all
${\mathcal F}_k$
-cohomological dimension in all these cases. On the other hand, inspired by [Reference Lück16], we use Bass–Serre theory to explicitly calculate, for all
![]() $k\geq 1$
, the
$k\geq 1$
, the
![]() ${\mathcal F}_k$
-geometric dimension of graphs of groups whose vertex groups are infinite finitely generated virtually abelian groups.
${\mathcal F}_k$
-geometric dimension of graphs of groups whose vertex groups are infinite finitely generated virtually abelian groups.
There are few explicit calculations of the
![]() ${\mathcal F}_n$
-geometric dimension for
${\mathcal F}_n$
-geometric dimension for
![]() $n\geq 2$
. For example, the
$n\geq 2$
. For example, the
![]() ${\mathcal F}_n$
-geometric dimension for orientable
${\mathcal F}_n$
-geometric dimension for orientable
![]() $3$
-manifold groups was explicitly calculated in [Reference Lück16] for all
$3$
-manifold groups was explicitly calculated in [Reference Lück16] for all
![]() $n\geq 2$
. In [Reference Prytuła22, Proposition A.], it was shown that
$n\geq 2$
. In [Reference Prytuła22, Proposition A.], it was shown that
![]() $\textrm{gd}_{{\mathcal F}_2}(\mathbb{Z}^k)=k+2$
for all
$\textrm{gd}_{{\mathcal F}_2}(\mathbb{Z}^k)=k+2$
for all
![]() $k\geq 3$
. With our results we add braid groups, RAAGs, and graphs of groups whose vertex groups are infinite finitely generated virtually abelian groups to this list. In what follows, we present more precisely these results.
$k\geq 3$
. With our results we add braid groups, RAAGs, and graphs of groups whose vertex groups are infinite finitely generated virtually abelian groups to this list. In what follows, we present more precisely these results.
The
 ${\mathcal F}_n$
-dimension of virtually abelian groups
${\mathcal F}_n$
-dimension of virtually abelian groups
Let
![]() $G$
be a virtually
$G$
be a virtually
![]() $\mathbb{Z}^n$
group. In [Reference Rolland, Álvarez and Saldaña23, Proposition 1.3], it was proved that
$\mathbb{Z}^n$
group. In [Reference Rolland, Álvarez and Saldaña23, Proposition 1.3], it was proved that
![]() $\textrm{gd}_{{\mathcal F}_k}(G)\leq n+k$
for
$\textrm{gd}_{{\mathcal F}_k}(G)\leq n+k$
for
![]() $0\leq k\lt n$
. For a free abelian group, this upper bound has also been proved in [Reference Charney4]. In this article, we prove that this upper bound is sharp.
$0\leq k\lt n$
. For a free abelian group, this upper bound has also been proved in [Reference Charney4]. In this article, we prove that this upper bound is sharp.
Theorem 1.1.
Let
![]() $k,n\in \mathbb{N}$
such that
$k,n\in \mathbb{N}$
such that
![]() $0\leq k\lt n$
. Let
$0\leq k\lt n$
. Let
![]() $G$
be a virtually
$G$
be a virtually
![]() $\mathbb{Z}^n$
group. Then
$\mathbb{Z}^n$
group. Then
![]() $\textrm{gd}_{{\mathcal F}_k}(G)=\textrm{cd}_{{\mathcal F}_k}(G)=n+k$
.
$\textrm{gd}_{{\mathcal F}_k}(G)=\textrm{cd}_{{\mathcal F}_k}(G)=n+k$
.
For
![]() $k=1$
, the Theorem 1.1 was proved in [Reference Mislin and Valette20, Theorem 5.13]. For
$k=1$
, the Theorem 1.1 was proved in [Reference Mislin and Valette20, Theorem 5.13]. For
![]() $k=2$
, a particular case was proved in [Reference Prytuła22, Proposition A.], specifically
$k=2$
, a particular case was proved in [Reference Prytuła22, Proposition A.], specifically
![]() $\textrm{gd}_{{\mathcal F}_2}(\mathbb{Z}^k)=k+2$
for all
$\textrm{gd}_{{\mathcal F}_2}(\mathbb{Z}^k)=k+2$
for all
![]() $k\geq 3$
. As a corollary of Theorem 1.1, we have
$k\geq 3$
. As a corollary of Theorem 1.1, we have
Corollary 1.2.
Let
![]() $n\geq 1$
and let
$n\geq 1$
and let
![]() $G$
be a group that has a virtually
$G$
be a group that has a virtually
![]() $\mathbb{Z}^n$
subgroup. Then for
$\mathbb{Z}^n$
subgroup. Then for
![]() $0\leq k\lt n$
we have
$0\leq k\lt n$
we have
![]() $\textrm{gd}_{{\mathcal F}_k}(G)\geq n+k$
and
$\textrm{gd}_{{\mathcal F}_k}(G)\geq n+k$
and
![]() $\textrm{cd}_{{\mathcal F}_k}(G)\geq n+k$
.
$\textrm{cd}_{{\mathcal F}_k}(G)\geq n+k$
.
The
 ${\mathcal F}_n$
-dimension of braid groups
${\mathcal F}_n$
-dimension of braid groups
There are various ways to define the (full) braid group
![]() $B_n$
on
$B_n$
on
![]() $n$
strands. For our purposes, the following definition is convenient. Let
$n$
strands. For our purposes, the following definition is convenient. Let
![]() $D_n$
be the closed disc with
$D_n$
be the closed disc with
![]() $n$
punctures. We define the braid group
$n$
punctures. We define the braid group
![]() $B_n$
on
$B_n$
on
![]() $n$
strands as the isotopy classes of orientation preserving diffeomorphisms of
$n$
strands as the isotopy classes of orientation preserving diffeomorphisms of
![]() $D_n$
that restrict to the identity on the boundary
$D_n$
that restrict to the identity on the boundary
![]() $\partial D_n$
. In the literature, this group is known as the mapping class group of
$\partial D_n$
. In the literature, this group is known as the mapping class group of
![]() $D_n$
. It is well known that
$D_n$
. It is well known that
![]() $\textrm{gd}_{{\mathcal F}_0}(B_n)=n-1$
see for example [Reference Arnold2, Section 3]. In [Reference Juan-Pineda and Saldaña14, Theorem 1.4], it was proved that
$\textrm{gd}_{{\mathcal F}_0}(B_n)=n-1$
see for example [Reference Arnold2, Section 3]. In [Reference Juan-Pineda and Saldaña14, Theorem 1.4], it was proved that
![]() $\textrm{gd}_{{\mathcal F}_k}(B_n)\leq n+k-1$
for all
$\textrm{gd}_{{\mathcal F}_k}(B_n)\leq n+k-1$
for all
![]() $k\in \mathbb{N}$
. Using Corollary 1.2 and [Reference Farrell and Roushon11, Proposition 3.7] we prove that this upper bound is sharp.
$k\in \mathbb{N}$
. Using Corollary 1.2 and [Reference Farrell and Roushon11, Proposition 3.7] we prove that this upper bound is sharp.
Theorem 1.3.
Let
![]() $k,n \in \mathbb{N}$
such that
$k,n \in \mathbb{N}$
such that
![]() $0\leq k\lt n-1$
and
$0\leq k\lt n-1$
and
![]() $G$
be either the full braid group
$G$
be either the full braid group
![]() $B_n$
or the pure braid group
$B_n$
or the pure braid group
![]() $P_n$
. Then
$P_n$
. Then
![]() $\textrm{gd}_{{\mathcal F}_k}(G)=\textrm{cd}_{{\mathcal F}_k}(G)=\textrm{vcd}(G)+k= n+k-1.$
$\textrm{gd}_{{\mathcal F}_k}(G)=\textrm{cd}_{{\mathcal F}_k}(G)=\textrm{vcd}(G)+k= n+k-1.$
The
 ${\mathcal F}_n$
-dimension of right-angled Artin groups
${\mathcal F}_n$
-dimension of right-angled Artin groups
Let
![]() $\Gamma$
be a finite simple graph, that is, a finite graph without loops or multiple edges between vertices. We define the right-angled Artin group (RAAG)
$\Gamma$
be a finite simple graph, that is, a finite graph without loops or multiple edges between vertices. We define the right-angled Artin group (RAAG)
![]() $A_{\Gamma }$
as the group generated by the vertices of
$A_{\Gamma }$
as the group generated by the vertices of
![]() $\Gamma$
with all the relations of the form
$\Gamma$
with all the relations of the form
![]() $vw=wv$
whenever
$vw=wv$
whenever
![]() $v$
and
$v$
and
![]() $w$
are joined by an edge.
$w$
are joined by an edge.
Let
![]() $A_\Gamma$
be a RAAG. It is well-known
$A_\Gamma$
be a RAAG. It is well-known
![]() $A_\Gamma$
is a
$A_\Gamma$
is a
![]() $\textrm{CAT}(0)$
group, in fact
$\textrm{CAT}(0)$
group, in fact
![]() $A_\Gamma$
acts on the universal cover
$A_\Gamma$
acts on the universal cover
![]() $\tilde{S}_\Gamma$
of its Salvetti CW-complex
$\tilde{S}_\Gamma$
of its Salvetti CW-complex
![]() $S_\Gamma$
, see Section 4.2. In [Reference Rolland, Álvarez and Saldaña23], it was proved that
$S_\Gamma$
, see Section 4.2. In [Reference Rolland, Álvarez and Saldaña23], it was proved that
![]() $\textrm{cd}_{{\mathcal F}_k}(A_\Gamma ) \leq \dim (S_{\Gamma })+k+1$
. Following the proof of [Reference Rolland, Álvarez and Saldaña23], Proof of Theorem 3.1] and using [Reference Huang and Prytuła13, Proposition 7.3], we can actually show that
$\textrm{cd}_{{\mathcal F}_k}(A_\Gamma ) \leq \dim (S_{\Gamma })+k+1$
. Following the proof of [Reference Rolland, Álvarez and Saldaña23], Proof of Theorem 3.1] and using [Reference Huang and Prytuła13, Proposition 7.3], we can actually show that
![]() $\textrm{cd}_{{\mathcal F}_k}(A_\Gamma ) \leq \dim (S_{\Gamma })+k$
in Theorem 4.6. Moreover, by using Corollary 1.2 and Remark 4.2, we can prove that this upper bound is sharp.
$\textrm{cd}_{{\mathcal F}_k}(A_\Gamma ) \leq \dim (S_{\Gamma })+k$
in Theorem 4.6. Moreover, by using Corollary 1.2 and Remark 4.2, we can prove that this upper bound is sharp.
Theorem 1.4.
Let
![]() $A_\Gamma$
be a right-angled Artin group. Then for
$A_\Gamma$
be a right-angled Artin group. Then for
![]() $0 \leq k \lt \textrm{cd}(A_\Gamma )$
we have
$0 \leq k \lt \textrm{cd}(A_\Gamma )$
we have
![]() $ \textrm{gd}_{{\mathcal F}_k}(A_\Gamma )= \textrm{cd}_{{\mathcal F}_k}(A_\Gamma )=\dim (S_{\Gamma })+k=\textrm{cd}(A_\Gamma )+k$
.
$ \textrm{gd}_{{\mathcal F}_k}(A_\Gamma )= \textrm{cd}_{{\mathcal F}_k}(A_\Gamma )=\dim (S_{\Gamma })+k=\textrm{cd}(A_\Gamma )+k$
.
This calculation of the
![]() ${\mathcal F}_k$
-geometric dimension of a RAAG
${\mathcal F}_k$
-geometric dimension of a RAAG
![]() $A_\Gamma$
is explicit because the dimension of the Salvetti CW-complex
$A_\Gamma$
is explicit because the dimension of the Salvetti CW-complex
![]() $S_{\Gamma }$
is the maximum of all natural numbers
$S_{\Gamma }$
is the maximum of all natural numbers
![]() $n$
such that there is a complete subgraph
$n$
such that there is a complete subgraph
![]() $\Gamma '$
of
$\Gamma '$
of
![]() $\Gamma$
with
$\Gamma$
with
![]() $|V(\Gamma ')| = n$
(see Lemma 4.5).
$|V(\Gamma ')| = n$
(see Lemma 4.5).
Using Corollary 1.2, we can give a lower bound for the
![]() ${\mathcal F}_k$
-geometric dimension of the outer automorphism group
${\mathcal F}_k$
-geometric dimension of the outer automorphism group
![]() $\textrm{Out}(A_\Gamma )$
of some RAAGs
$\textrm{Out}(A_\Gamma )$
of some RAAGs
![]() $A_\Gamma$
.
$A_\Gamma$
.
Proposition 1.5.
Let
![]() $n\geq 2$
. Let
$n\geq 2$
. Let
![]() $F_n$
be the free group in
$F_n$
be the free group in
![]() $n$
generators. Then for all
$n$
generators. Then for all
![]() $0\leq k\lt 2n-3$
we have
$0\leq k\lt 2n-3$
we have
Proposition 1.6.
Let
![]() $A_d$
be the right-angled Artin group given by a string of
$A_d$
be the right-angled Artin group given by a string of
![]() $d$
diamonds. Then
$d$
diamonds. Then
![]() $\textrm{gd}_{{\mathcal F}_k}(\textrm{Out}(A_d))\geq \textrm{vcd}(\textrm{Out}(A_d))+k\geq 4d +k-1$
for all
$\textrm{gd}_{{\mathcal F}_k}(\textrm{Out}(A_d))\geq \textrm{vcd}(\textrm{Out}(A_d))+k\geq 4d +k-1$
for all
![]() $0\leq k\lt 4d-1$
.
$0\leq k\lt 4d-1$
.
Question 2.
Given Theorems
1.3
and
4.7
, it is natural to ask whether it is true that in Proposition
1.5
we can have
![]() $\textrm{gd}_{{\mathcal F}_k}(\textrm{Out}(F_n)) \leq \textrm{vcd}(\textrm{Out}(F_n)) + k \leq 2n + k - 3$
for all
$\textrm{gd}_{{\mathcal F}_k}(\textrm{Out}(F_n)) \leq \textrm{vcd}(\textrm{Out}(F_n)) + k \leq 2n + k - 3$
for all
![]() $0 \leq k \lt 2n - 3$
. Similarly, if it is true that in Proposition
1.6
, we can have
$0 \leq k \lt 2n - 3$
. Similarly, if it is true that in Proposition
1.6
, we can have
![]() $\textrm{gd}_{{\mathcal F}_k}(\textrm{Out}(A_d)) \leq \textrm{vcd}(\textrm{Out}(A_d)) + k \leq 4d + k - 1$
for all
$\textrm{gd}_{{\mathcal F}_k}(\textrm{Out}(A_d)) \leq \textrm{vcd}(\textrm{Out}(A_d)) + k \leq 4d + k - 1$
for all
![]() $0 \leq k \lt 4d - 1$
.
$0 \leq k \lt 4d - 1$
.
The
 ${\mathcal F}_n$
-geometric dimension for graphs of groups of finitely generated virtually abelian groups
${\mathcal F}_n$
-geometric dimension for graphs of groups of finitely generated virtually abelian groups
Inspired by [Reference Lück16], we use Bass–Serre theory, Theorem 1.1 and Corollary 1.2 to compute the
![]() ${\mathcal F}_n$
-geometric dimension of graphs of groups whose vertex groups are finitely generated virtually abelian groups.
${\mathcal F}_n$
-geometric dimension of graphs of groups whose vertex groups are finitely generated virtually abelian groups.
Theorem 1.7.
Let
![]() $Y$
be a finite graph of groups such that for each
$Y$
be a finite graph of groups such that for each
![]() $v\in V(Y)$
the group
$v\in V(Y)$
the group
![]() $G_v$
is infinite finitely generated virtually abelian, with
$G_v$
is infinite finitely generated virtually abelian, with
![]() $\textrm{rank}(G_e)\lt \textrm{rank}(G_v)$
. Suppose that the splitting of
$\textrm{rank}(G_e)\lt \textrm{rank}(G_v)$
. Suppose that the splitting of
![]() $G=\pi _1(Y)$
is acylindrical. Let
$G=\pi _1(Y)$
is acylindrical. Let
![]() $m=\max \{\textrm{rank}(G_v)| v\in V(Y) \}$
. Then for
$m=\max \{\textrm{rank}(G_v)| v\in V(Y) \}$
. Then for
![]() $1\leq k\lt m$
we have
$1\leq k\lt m$
we have
![]() $\textrm{gd}_{{\mathcal F}_k}(G)=m+k.$
$\textrm{gd}_{{\mathcal F}_k}(G)=m+k.$
Corollary 1.8.
Let
![]() $Y$
be a finite graph of groups such that for each
$Y$
be a finite graph of groups such that for each
![]() $v\in V(Y)$
the group
$v\in V(Y)$
the group
![]() $G_v$
is infinite finitely generated virtually abelian and for each
$G_v$
is infinite finitely generated virtually abelian and for each
![]() $e\in E(Y)$
the group
$e\in E(Y)$
the group
![]() $G_e$
is a finite group. Let
$G_e$
is a finite group. Let
![]() $m=\max \{\textrm{rank}(G_v)| v\in V(Y) \}$
. Then for
$m=\max \{\textrm{rank}(G_v)| v\in V(Y) \}$
. Then for
![]() $1\leq k\lt m$
we have
$1\leq k\lt m$
we have
![]() $\textrm{gd}_{{\mathcal F}_k}(G)=m+k.$
$\textrm{gd}_{{\mathcal F}_k}(G)=m+k.$
Outline of the paper
In Section 2, we introduce the Lück–Weiermann construction, which enables us to build models inductively for the classifying space of
![]() $E_{{\mathcal F}_n\cap H}\mathbb{Z}^n$
. Later in the same section, we define Bredon cohomology and present the Mayer–Vietoris sequence, which is as a crucial tool in proving Theorem 3.6. In Section 3, we prove Theorem 1.1. In Section 4, we present some applications of Corollary 1.2, for instance, we explicitly calculate the
$E_{{\mathcal F}_n\cap H}\mathbb{Z}^n$
. Later in the same section, we define Bredon cohomology and present the Mayer–Vietoris sequence, which is as a crucial tool in proving Theorem 3.6. In Section 3, we prove Theorem 1.1. In Section 4, we present some applications of Corollary 1.2, for instance, we explicitly calculate the
![]() ${\mathcal F}_k$
-geometric dimension of braid groups and RAAGs. Furthermore, we provide a lower bound for the
${\mathcal F}_k$
-geometric dimension of braid groups and RAAGs. Furthermore, we provide a lower bound for the
![]() ${\mathcal F}_k$
-geometric dimension of the outer automorphism group of certain RAAGs. Finally, we use Bass–Serre theory to prove Theorem 1.7.
${\mathcal F}_k$
-geometric dimension of the outer automorphism group of certain RAAGs. Finally, we use Bass–Serre theory to prove Theorem 1.7.
2. Preliminaries
The Lück–Weiermann construction
In this subsection, we give a particular construction of Lück–Weiermann [Reference Mislin and Valette20, Theorem 2.3] that we will use later.
Definition 2.1.
Let
![]() ${\mathcal F}\subset{\mathcal G}$
be two families of subgroups of
${\mathcal F}\subset{\mathcal G}$
be two families of subgroups of
![]() $G$
. Let
$G$
. Let
![]() $\sim$
be an equivalence relation in
$\sim$
be an equivalence relation in
![]() ${\mathcal G}-{\mathcal F}$
. We say that
${\mathcal G}-{\mathcal F}$
. We say that
![]() $\sim$
is strong if the following is satisfied
$\sim$
is strong if the following is satisfied
-
(a) If
 $H, K \in{\mathcal G}-{\mathcal F}$
with
$H, K \in{\mathcal G}-{\mathcal F}$
with
 $H\subseteq K$
, then
$H\subseteq K$
, then
 $H\sim K$
;
$H\sim K$
; -
(b) If
 $H, K \in{\mathcal G}-{\mathcal F}$
and
$H, K \in{\mathcal G}-{\mathcal F}$
and
 $g\in G$
, then
$g\in G$
, then
 $H\sim K$
if and only if
$H\sim K$
if and only if
 $gHg^{-1} \sim gKg^{-1}$
.
$gHg^{-1} \sim gKg^{-1}$
.
Definition 2.2.
Let
![]() $G$
be a group and
$G$
be a group and
![]() $L, K$
be subgroups of
$L, K$
be subgroups of
![]() $G$
. We say that
$G$
. We say that
![]() $L$
and
$L$
and
![]() $K$
are commensurable if
$K$
are commensurable if
![]() $L\cap K$
has finite index in both
$L\cap K$
has finite index in both
![]() $L$
and
$L$
and
![]() $K$
.
$K$
.
Definition 2.3.
Let
![]() $G$
be a group and let
$G$
be a group and let
![]() $H$
be a subgroup of
$H$
be a subgroup of
![]() $G$
. We define the commensurator of
$G$
. We define the commensurator of
![]() $H$
in
$H$
in
![]() $G$
as
$G$
as
Definition 2.4.
Let
![]() $G$
be a group, let
$G$
be a group, let
![]() $H$
be a subgroup of
$H$
be a subgroup of
![]() $G$
, and
$G$
, and
![]() $\mathcal F$
a family of subgroups of
$\mathcal F$
a family of subgroups of
![]() $G$
. We define the family
$G$
. We define the family
![]() ${\mathcal F}\cap H$
of
${\mathcal F}\cap H$
of
![]() $H$
as all the subgroups of
$H$
as all the subgroups of
![]() $H$
that belong to
$H$
that belong to
![]() $\mathcal F$
. We can complete the family
$\mathcal F$
. We can complete the family
![]() ${\mathcal F}\cap H$
in order to get a family
${\mathcal F}\cap H$
in order to get a family
![]() $\overline{{\mathcal F}\cap H}$
of
$\overline{{\mathcal F}\cap H}$
of
![]() $G$
.
$G$
.
Remark 2.5. Following the notation of Definition 2.4 note that:
-
• If
 $H=G$
then
$H=G$
then
 $\overline{{\mathcal F}\cap H}={\mathcal F}$
.
$\overline{{\mathcal F}\cap H}={\mathcal F}$
. -
• If
 $H$
is normal subgroup of
$H$
is normal subgroup of
 $G$
, then
$G$
, then
 $\overline{{\mathcal F}\cap H}={\mathcal F}\cap H$
.
$\overline{{\mathcal F}\cap H}={\mathcal F}\cap H$
.
Let
![]() $G$
be a group,
$G$
be a group,
![]() $H$
a subgroup of
$H$
a subgroup of
![]() $G$
and
$G$
and
![]() $n\geq 0$
. Consider the following nested families of
$n\geq 0$
. Consider the following nested families of
![]() $G$
,
$G$
,
![]() $\overline{{\mathcal F}_n\cap H}\subseteq \overline{{\mathcal F}_{n+1}\cap H}$
, let
$\overline{{\mathcal F}_n\cap H}\subseteq \overline{{\mathcal F}_{n+1}\cap H}$
, let
![]() $\sim$
the equivalence relation in
$\sim$
the equivalence relation in
![]() $\overline{{\mathcal F}_{n+1}\cap H}-\overline{{\mathcal F}_n\cap H}$
given by commensurability. It is easy to check that this is a strong equivalence relation.
$\overline{{\mathcal F}_{n+1}\cap H}-\overline{{\mathcal F}_n\cap H}$
given by commensurability. It is easy to check that this is a strong equivalence relation.
We introduce the following notation:
-
• We denote by
 $(\overline{{\mathcal F}_{n+1}\cap H}-\overline{{\mathcal F}_n\cap H})/\sim$
the equivalence classes in
$(\overline{{\mathcal F}_{n+1}\cap H}-\overline{{\mathcal F}_n\cap H})/\sim$
the equivalence classes in
 $\overline{{\mathcal F}_{n+1}\cap H}-\overline{{\mathcal F}_n\cap H}$
. Given
$\overline{{\mathcal F}_{n+1}\cap H}-\overline{{\mathcal F}_n\cap H}$
. Given
 $L\in (\overline{{\mathcal F}_{n+1}\cap H}-\overline{{\mathcal F}_n\cap H})$
we denote by
$L\in (\overline{{\mathcal F}_{n+1}\cap H}-\overline{{\mathcal F}_n\cap H})$
we denote by
 $[L]$
its equivalence class.
$[L]$
its equivalence class. -
• Given
 $[L]\in (\overline{{\mathcal F}_{n+1}\cap H}-\overline{{\mathcal F}_n\cap H})/\sim$
, we define the next family of subgroups of
$[L]\in (\overline{{\mathcal F}_{n+1}\cap H}-\overline{{\mathcal F}_n\cap H})/\sim$
, we define the next family of subgroups of
 $N_{G}[L]$
$N_{G}[L]$
 \begin{equation*}(\overline {{\mathcal F}_{n+1}\cap H})[L]\;:\!=\;\{K\leq N_G[L]| K\in (\overline {{\mathcal F}_{n+1}\cap H}-\overline {{\mathcal F}_n\cap H}), [K]=[L]\}\cup (\overline {{\mathcal F}_n\cap H}\cap N_G[L]).\end{equation*}
\begin{equation*}(\overline {{\mathcal F}_{n+1}\cap H})[L]\;:\!=\;\{K\leq N_G[L]| K\in (\overline {{\mathcal F}_{n+1}\cap H}-\overline {{\mathcal F}_n\cap H}), [K]=[L]\}\cup (\overline {{\mathcal F}_n\cap H}\cap N_G[L]).\end{equation*}
Theorem 2.6 ([Reference Mislin and Valette20], Theorem 2.3). Let
![]() $G$
be a group, let
$G$
be a group, let
![]() $H$
be a subgroup of
$H$
be a subgroup of
![]() $G$
and
$G$
and
![]() $n\geq 0$
. Consider the following nested families of
$n\geq 0$
. Consider the following nested families of
![]() $G$
,
$G$
,
![]() $\overline{{\mathcal F}_n\cap H}\subseteq \overline{{\mathcal F}_{n+1}\cap H}$
, let
$\overline{{\mathcal F}_n\cap H}\subseteq \overline{{\mathcal F}_{n+1}\cap H}$
, let
![]() $\sim$
be the equivalence relation given by commensurability in
$\sim$
be the equivalence relation given by commensurability in
![]() $\overline{{\mathcal F}_{n+1}\cap H}-\overline{{\mathcal F}_n\cap H}$
. Let
$\overline{{\mathcal F}_{n+1}\cap H}-\overline{{\mathcal F}_n\cap H}$
. Let
![]() $I$
be a complete set of representatives of conjugation classes in
$I$
be a complete set of representatives of conjugation classes in
![]() $(\overline{{\mathcal F}_{n+1}\cap H}-\overline{{\mathcal F}_n\cap H})/\sim$
. Choose arbitrary
$(\overline{{\mathcal F}_{n+1}\cap H}-\overline{{\mathcal F}_n\cap H})/\sim$
. Choose arbitrary
![]() $N_G[L]$
-CW-models for
$N_G[L]$
-CW-models for
![]() $E_{(\overline{{\mathcal F}_n\cap H})\cap N_{G}[L]}N_{G}[L]$
and
$E_{(\overline{{\mathcal F}_n\cap H})\cap N_{G}[L]}N_{G}[L]$
and
![]() $E_{ (\overline{{\mathcal F}_{n+1}\cap H})[L]}N_{G}[L]$
and an arbitrary model for
$E_{ (\overline{{\mathcal F}_{n+1}\cap H})[L]}N_{G}[L]$
and an arbitrary model for
![]() $E_{\overline{{\mathcal F}_n\cap H}}G$
. Consider the following
$E_{\overline{{\mathcal F}_n\cap H}}G$
. Consider the following
![]() $G$
-push-out
$G$
-push-out

such that
![]() $f_{[L]}$
is a cellular
$f_{[L]}$
is a cellular
![]() $G$
-map for every
$G$
-map for every
![]() $[L]\in I$
and either (1)
$[L]\in I$
and either (1)
![]() $i$
is an inclusion of
$i$
is an inclusion of
![]() $G$
-CW-complexes or (2) such that every map
$G$
-CW-complexes or (2) such that every map
![]() $f_{[L]}$
is an inclusion of
$f_{[L]}$
is an inclusion of
![]() $G$
-CW-complexes for every
$G$
-CW-complexes for every
![]() $[L]\in I$
and
$[L]\in I$
and
![]() $i$
is a cellular
$i$
is a cellular
![]() $G$
-map. Then
$G$
-map. Then
![]() $X$
is a model for
$X$
is a model for
![]() $E_{\overline{{\mathcal F}_{n+1}\cap H}}G$
.
$E_{\overline{{\mathcal F}_{n+1}\cap H}}G$
.
Remark 2.7.
The conditions in Theorem
2.6
are not restrictive. For instance, to satisfy the condition
![]() $(2)$
, we can use the equivariant cellular approximation theorem to assume that the maps
$(2)$
, we can use the equivariant cellular approximation theorem to assume that the maps
![]() $i$
and
$i$
and
![]() $f_{[L]}$
are cellular maps for all
$f_{[L]}$
are cellular maps for all
![]() $[L]\in I$
and to make the function
$[L]\in I$
and to make the function
![]() $f_{[L]}$
an inclusion for every
$f_{[L]}$
an inclusion for every
![]() $[L]\in I$
, we can replace the spaces by the mapping cylinders. See [
Reference Mislin and Valette20, Remark 2.5].
$[L]\in I$
, we can replace the spaces by the mapping cylinders. See [
Reference Mislin and Valette20, Remark 2.5].
Following the notation from Theorem 2.6 we have
Corollary 2.8.
![]() $\textrm{gd}_{\overline{{\mathcal F}_{n+1}\cap H}}(G)\leq \max \{ \textrm{gd}_{ \overline{{\mathcal F}_{n}\cap H}}(G)+1, \textrm{gd}_{ (\overline{{\mathcal F}_{n+1}\cap H})[L]}(N_{G}[L])| L\in I\}.$
$\textrm{gd}_{\overline{{\mathcal F}_{n+1}\cap H}}(G)\leq \max \{ \textrm{gd}_{ \overline{{\mathcal F}_{n}\cap H}}(G)+1, \textrm{gd}_{ (\overline{{\mathcal F}_{n+1}\cap H})[L]}(N_{G}[L])| L\in I\}.$
The push-out of a union of families
The following lemma will be also useful.
Lemma 2.9 ([Reference Day, Sale and Wade8], Lemma 4.4). Let
![]() $G$
be a group and
$G$
be a group and
![]() ${\mathcal F},\,{\mathcal G}$
be two families of subgroups of
${\mathcal F},\,{\mathcal G}$
be two families of subgroups of
![]() $G$
. Choose arbitrary
$G$
. Choose arbitrary
![]() $G$
-
$G$
-
![]() $CW$
-models for
$CW$
-models for
![]() $E_{{\mathcal F}} G$
,
$E_{{\mathcal F}} G$
,
![]() $E_{{\mathcal G}}G$
and
$E_{{\mathcal G}}G$
and
![]() $E_{{\mathcal F}\cap{\mathcal G}} G$
. Then, the
$E_{{\mathcal F}\cap{\mathcal G}} G$
. Then, the
![]() $G$
-
$G$
-
![]() $CW$
-complex
$CW$
-complex
![]() $X$
given by the cellular homotopy
$X$
given by the cellular homotopy
![]() $G$
-push-out
$G$
-push-out

is a model for
![]() $E_{{\mathcal F}\cup{\mathcal G}}G$
.
$E_{{\mathcal F}\cup{\mathcal G}}G$
.
With the notation Lemma 2.9 we have the following
Corollary 2.10.
![]() $\textrm{gd}_{{\mathcal G}\cup{\mathcal F}}(G)\leq \max \{\textrm{gd}_{{\mathcal F}}(G), \textrm{gd}_{{\mathcal G}}(G), \textrm{gd}_{{\mathcal G}\cap{\mathcal F}}(G)+1\}.$
$\textrm{gd}_{{\mathcal G}\cup{\mathcal F}}(G)\leq \max \{\textrm{gd}_{{\mathcal F}}(G), \textrm{gd}_{{\mathcal G}}(G), \textrm{gd}_{{\mathcal G}\cap{\mathcal F}}(G)+1\}.$
Nested families
Given a group
![]() $G$
and two nested families
$G$
and two nested families
![]() ${\mathcal F}\subseteq{\mathcal G}$
of
${\mathcal F}\subseteq{\mathcal G}$
of
![]() $G$
, we will use the following propositions to bound the geometric dimension
$G$
, we will use the following propositions to bound the geometric dimension
![]() $\textrm{gd}_{{\mathcal F}}(G)$
using the geometric dimension
$\textrm{gd}_{{\mathcal F}}(G)$
using the geometric dimension
![]() $\textrm{gd}_{{\mathcal G}}(G)$
.
$\textrm{gd}_{{\mathcal G}}(G)$
.
Proposition 2.11 ([Reference Mislin and Valette20], Proposition 5.1 (i)). Let
![]() $G$
be a group and let
$G$
be a group and let
![]() $\mathcal F$
and
$\mathcal F$
and
![]() $\mathcal G$
be two families of subgroups such that
$\mathcal G$
be two families of subgroups such that
![]() ${\mathcal F}\subseteq{\mathcal G}$
. Suppose for every
${\mathcal F}\subseteq{\mathcal G}$
. Suppose for every
![]() $H\in{\mathcal G}$
we have
$H\in{\mathcal G}$
we have
![]() $\textrm{gd}_{{\mathcal F}\cap H}(H)\leq d$
. Then
$\textrm{gd}_{{\mathcal F}\cap H}(H)\leq d$
. Then
![]() $\textrm{gd}_{{\mathcal F}}(G)\leq \textrm{gd}_{{\mathcal G}}(G)+d.$
$\textrm{gd}_{{\mathcal F}}(G)\leq \textrm{gd}_{{\mathcal G}}(G)+d.$
The proof of the following proposition is implicit in [Reference Lück and Weiermann19, Proof of Theorem 3.1] and [Reference Mislin and Valette20, Proposition 5.1].
Proposition 2.12.
Let
![]() $G$
be a group. Let
$G$
be a group. Let
![]() $\mathcal F$
and
$\mathcal F$
and
![]() $\mathcal G$
be families of subgroups of
$\mathcal G$
be families of subgroups of
![]() $G$
such that
$G$
such that
![]() ${\mathcal F}\subseteq{\mathcal G}$
. If
${\mathcal F}\subseteq{\mathcal G}$
. If
![]() $X$
is a model for
$X$
is a model for
![]() $E_{\mathcal G} G$
, then
$E_{\mathcal G} G$
, then
Bredon cohomology
In this subsection, we recall the definition of Bredon cohomology, the cohomological dimension for families and its connection with the geometric dimension for families. For further details see [Reference Onorio21].
Fix a group
![]() $G$
and
$G$
and
![]() $\mathcal F$
a family of subgroups of
$\mathcal F$
a family of subgroups of
![]() $G$
. The orbit category
$G$
. The orbit category
![]() $\mathcal{O}_{{\mathcal F}}G$
is the category whose objects are
$\mathcal{O}_{{\mathcal F}}G$
is the category whose objects are
![]() $G$
-homogeneous spaces
$G$
-homogeneous spaces
![]() $G/H$
with
$G/H$
with
![]() $H\in{\mathcal F}$
and morphisms are
$H\in{\mathcal F}$
and morphisms are
![]() $G$
-functions. The category of Bredon modules is the category whose objects are contravariant functors
$G$
-functions. The category of Bredon modules is the category whose objects are contravariant functors
![]() $M\colon \mathcal{O}_{{\mathcal F}}G \to Ab$
from the orbit category to the category of abelian groups, and morphisms are natural transformations
$M\colon \mathcal{O}_{{\mathcal F}}G \to Ab$
from the orbit category to the category of abelian groups, and morphisms are natural transformations
![]() $f\colon M\to N$
. This is an abelian category with enough projectives. The constant Bredon module
$f\colon M\to N$
. This is an abelian category with enough projectives. The constant Bredon module
![]() $\underline{\mathbb{Z}}\colon \mathcal{O}_{{\mathcal F}}G \to Ab$
is defined in objects by
$\underline{\mathbb{Z}}\colon \mathcal{O}_{{\mathcal F}}G \to Ab$
is defined in objects by
![]() $\underline{\mathbb{Z}}(G/H)=\mathbb{Z}$
and in morphisms by
$\underline{\mathbb{Z}}(G/H)=\mathbb{Z}$
and in morphisms by
![]() $\underline{\mathbb{Z}}(\varphi )=id_{\mathbb{Z}}$
. Let
$\underline{\mathbb{Z}}(\varphi )=id_{\mathbb{Z}}$
. Let
![]() $P_{\bullet }$
be a projective resolution of the Bredon module
$P_{\bullet }$
be a projective resolution of the Bredon module
![]() $\underline{\mathbb{Z}}$
, and
$\underline{\mathbb{Z}}$
, and
![]() $M$
be a Bredon module. We define the Bredon cohomology of
$M$
be a Bredon module. We define the Bredon cohomology of
![]() $G$
with coefficients in
$G$
with coefficients in
![]() $M$
as
$M$
as
We define the
![]() $\mathcal F$
-cohomological dimension of
$\mathcal F$
-cohomological dimension of
![]() $G$
as
$G$
as
We have the following Eilenberg–Ganea type theorem that relates the
![]() $\mathcal F$
-cohomological dimension and the
$\mathcal F$
-cohomological dimension and the
![]() $\mathcal F$
-geometric dimension.
$\mathcal F$
-geometric dimension.
Theorem 2.13 ([Reference Lück and Meintrup17], Theorem 0.1). Let
![]() $G$
be a group and
$G$
be a group and
![]() $\mathcal F$
be a family of subgroups of
$\mathcal F$
be a family of subgroups of
![]() $G$
. Then
$G$
. Then
This Theorem 2.13 together with the following Mayer–Vietoris sequence will be used to give lower bounds for the
![]() $\mathcal F$
-geometric dimension
$\mathcal F$
-geometric dimension
![]() $\textrm{gd}_{{\mathcal F}}(G)$
.
$\textrm{gd}_{{\mathcal F}}(G)$
.
Mayer–Vietoris sequence
Following the notation of Theorem 2.6, by [Reference Davis, Quinn and Reich7, Proposition 7.1] [Reference Mislin and Valette20] we have the next long exact sequence
 \begin{align*} \begin{split} \cdots \to H^{n}( X/G)\to \left (\prod _{L\in I}H^{n}(E_{ (\overline{{\mathcal F}_{n+1}\cap H})[L]}N_{G}[L]/N_G[H])\right )\oplus H^n( E_{\overline{{\mathcal F}_n\cap H}}G/G)\to & \\ \prod _{L\in I}H^{n}( E_{(\overline{{\mathcal F}_n\cap H})\cap N_{G}[L]}N_{G}[L]/N_G[L])\to H^{n+1}(X/G)\to \cdots & \end{split} \end{align*}
\begin{align*} \begin{split} \cdots \to H^{n}( X/G)\to \left (\prod _{L\in I}H^{n}(E_{ (\overline{{\mathcal F}_{n+1}\cap H})[L]}N_{G}[L]/N_G[H])\right )\oplus H^n( E_{\overline{{\mathcal F}_n\cap H}}G/G)\to & \\ \prod _{L\in I}H^{n}( E_{(\overline{{\mathcal F}_n\cap H})\cap N_{G}[L]}N_{G}[L]/N_G[L])\to H^{n+1}(X/G)\to \cdots & \end{split} \end{align*}
Remark 2.14.
The results presented in Corollaries
2.8
,
2.10
, and Proposition
2.11
have cohomological counterparts. Specifically, if we replace
![]() $\textrm{gd}_{{\mathcal F}}$
with
$\textrm{gd}_{{\mathcal F}}$
with
![]() $\textrm{cd}_{{\mathcal F}}$
, all the results hold true, see for instance [
Reference Rolland, Álvarez and Saldaña23, Remark 2.9].
$\textrm{cd}_{{\mathcal F}}$
, all the results hold true, see for instance [
Reference Rolland, Álvarez and Saldaña23, Remark 2.9].
3. The
 ${\mathcal F}_k$
-dimension of a virtually
${\mathcal F}_k$
-dimension of a virtually
 $\mathbb{Z}^n$
group
$\mathbb{Z}^n$
group
The objective of this section is to prove Theorem 1.1. Let
![]() $G$
be a virtually
$G$
be a virtually
![]() $\mathbb{Z}^n$
group. By [Reference Rolland, Álvarez and Saldaña23, Proposition 1.3], Theorem 2.13 and since the
$\mathbb{Z}^n$
group. By [Reference Rolland, Álvarez and Saldaña23, Proposition 1.3], Theorem 2.13 and since the
![]() $\mathcal F$
-cohomological dimension is monotone, we have for all
$\mathcal F$
-cohomological dimension is monotone, we have for all
![]() $0\leq k\lt n$
the following inequalities
$0\leq k\lt n$
the following inequalities
Therefore, to prove Theorem 1.1, it is enough to show that
![]() $\textrm{cd}_{{\mathcal F}_k\cap \mathbb{Z}^n}(\mathbb{Z}^n)\geq n+k$
for
$\textrm{cd}_{{\mathcal F}_k\cap \mathbb{Z}^n}(\mathbb{Z}^n)\geq n+k$
for
![]() $0\leq k\lt n$
. In Theorem 3.6, we prove this inequality. In order to prove Theorem 3.6 we need Lemma 3.1, Mayer–Vietoris sequence, Lemma 3.5, and Corollary 3.3.
$0\leq k\lt n$
. In Theorem 3.6, we prove this inequality. In order to prove Theorem 3.6 we need Lemma 3.1, Mayer–Vietoris sequence, Lemma 3.5, and Corollary 3.3.
Lemma 3.1.
Let
![]() $k,t,n \in \mathbb{N}$
such that
$k,t,n \in \mathbb{N}$
such that
![]() $0\leq k\lt t\leq n$
. Let
$0\leq k\lt t\leq n$
. Let
![]() $H$
be a subgroup of
$H$
be a subgroup of
![]() $\mathbb{Z}^n$
of
$\mathbb{Z}^n$
of
![]() $\textrm{rank}$
$\textrm{rank}$
![]() $t$
, then
$t$
, then
![]() $\textrm{gd}_{{\mathcal F}_k\cap H}(\mathbb{Z}^n)\leq n+k$
.
$\textrm{gd}_{{\mathcal F}_k\cap H}(\mathbb{Z}^n)\leq n+k$
.
Proof. The proof is by induction on
![]() $k$
. Let
$k$
. Let
![]() $G=\mathbb{Z}^n$
. For
$G=\mathbb{Z}^n$
. For
![]() $k=0$
, we have
$k=0$
, we have
![]() $\textrm{gd}_{{\mathcal F}_0\cap H}(G)=\textrm{gd}_{}(G)=n.$
Suppose that the inequality is true for all
$\textrm{gd}_{{\mathcal F}_0\cap H}(G)=\textrm{gd}_{}(G)=n.$
Suppose that the inequality is true for all
![]() $k\lt m$
. We prove that the inequality is true for
$k\lt m$
. We prove that the inequality is true for
![]() $k=m$
. Let
$k=m$
. Let
![]() $\sim$
be the equivalence relation on
$\sim$
be the equivalence relation on
![]() ${\mathcal F}_m\cap H-{\mathcal F}_{m-1}\cap H$
defined by commensurability, and let
${\mathcal F}_m\cap H-{\mathcal F}_{m-1}\cap H$
defined by commensurability, and let
![]() $I$
a complete set of representatives classes in
$I$
a complete set of representatives classes in
![]() $({\mathcal F}_m\cap H-{\mathcal F}_{m-1}\cap H)/\sim$
. By Corollary 2.8 and Remark 2.5, we have
$({\mathcal F}_m\cap H-{\mathcal F}_{m-1}\cap H)/\sim$
. By Corollary 2.8 and Remark 2.5, we have
then to prove that
![]() $\textrm{gd}_{{\mathcal F}_m\cap H}(G)\leq n+m$
it is enough to prove that
$\textrm{gd}_{{\mathcal F}_m\cap H}(G)\leq n+m$
it is enough to prove that
![]() $\textrm{gd}_{({\mathcal F}_m\cap H)[L]}(G)\leq n+m$
for all
$\textrm{gd}_{({\mathcal F}_m\cap H)[L]}(G)\leq n+m$
for all
![]() $L\in I$
. Let
$L\in I$
. Let
![]() $L\in I$
. We can write the family
$L\in I$
. We can write the family
as the union of two families
![]() $ ({\mathcal F}_m\cap H)[L]={\mathcal G} \cup ({\mathcal F}_{m-1}\cap H)$
where
$ ({\mathcal F}_m\cap H)[L]={\mathcal G} \cup ({\mathcal F}_{m-1}\cap H)$
where
![]() $\mathcal G$
is the family generated by
$\mathcal G$
is the family generated by
![]() $\{ K\leq G|K\in{\mathcal F}_m\cap H-{\mathcal F}_{m-1}\cap H, [K]=[L]\}$
. By Corollary 2.10, we have
$\{ K\leq G|K\in{\mathcal F}_m\cap H-{\mathcal F}_{m-1}\cap H, [K]=[L]\}$
. By Corollary 2.10, we have
We prove the following inequalities
-
(i)
 $\textrm{gd}_{{\mathcal G}}(G)\leq n-m$
,
$\textrm{gd}_{{\mathcal G}}(G)\leq n-m$
, -
(ii)
 $\textrm{gd}_{{\mathcal G} \cap ({\mathcal F}_{m-1}\cap H)}(G)\leq n+m-1$
$\textrm{gd}_{{\mathcal G} \cap ({\mathcal F}_{m-1}\cap H)}(G)\leq n+m-1$
and as a consequence we will have
![]() $\textrm{gd}_{{\mathcal F}_m\cap H[L]}(G)\leq n+m$
. First, we prove item (i). Note that a model for
$\textrm{gd}_{{\mathcal F}_m\cap H[L]}(G)\leq n+m$
. First, we prove item (i). Note that a model for
![]() $E_{{\mathcal F}_0}(G/L)$
is a model for
$E_{{\mathcal F}_0}(G/L)$
is a model for
![]() $E_{\mathcal G} G$
via the action given by the projection
$E_{\mathcal G} G$
via the action given by the projection
![]() $G\to G/L$
. Since
$G\to G/L$
. Since
![]() $ G/L$
is virtually
$ G/L$
is virtually
![]() $\mathbb{Z}^{n-m}$
by [Reference Rolland, Álvarez and Saldaña23, Proposition 1.3] we have
$\mathbb{Z}^{n-m}$
by [Reference Rolland, Álvarez and Saldaña23, Proposition 1.3] we have
![]() $\textrm{gd}_{{\mathcal F}_0}(G/L)\leq n-m$
.
$\textrm{gd}_{{\mathcal F}_0}(G/L)\leq n-m$
.
Now we prove item (ii). Applying Proposition 2.11 to the inclusion of families
![]() ${\mathcal G}\cap ({\mathcal F}_{m-1}\cap H) \subset{\mathcal G}$
, we get
${\mathcal G}\cap ({\mathcal F}_{m-1}\cap H) \subset{\mathcal G}$
, we get
for some
![]() $d$
such that for any
$d$
such that for any
![]() $K\in{\mathcal G}$
we have
$K\in{\mathcal G}$
we have
![]() $\textrm{gd}_{{\mathcal G}\cap ({\mathcal F}_{m-1}\cap H)\cap K}(K)\leq d$
. Since we already proved
$\textrm{gd}_{{\mathcal G}\cap ({\mathcal F}_{m-1}\cap H)\cap K}(K)\leq d$
. Since we already proved
![]() $\textrm{gd}_{{\mathcal G}}(G)\leq n-m$
, our next task is to show that
$\textrm{gd}_{{\mathcal G}}(G)\leq n-m$
, our next task is to show that
![]() $d$
can be chosen to be equal to
$d$
can be chosen to be equal to
![]() $2m-1$
.
$2m-1$
.
Recall that any
![]() $K\in{\mathcal G}$
is virtually
$K\in{\mathcal G}$
is virtually
![]() $\mathbb{Z}^t$
for some
$\mathbb{Z}^t$
for some
![]() $0\leq t \leq m$
. We split our proof into two cases. First assume that
$0\leq t \leq m$
. We split our proof into two cases. First assume that
![]() $K\in{\mathcal G}$
is virtually
$K\in{\mathcal G}$
is virtually
![]() $\mathbb{Z}^t$
for some
$\mathbb{Z}^t$
for some
![]() $0\leq t \leq m-1$
. Hence,
$0\leq t \leq m-1$
. Hence,
![]() $K$
belongs to
$K$
belongs to
![]() ${\mathcal F}_{m-1}\cap H$
, it follows that
${\mathcal F}_{m-1}\cap H$
, it follows that
![]() $K$
belongs to
$K$
belongs to
![]() ${\mathcal G} \cap ({\mathcal F}_{m-1}\cap H)$
and we conclude
${\mathcal G} \cap ({\mathcal F}_{m-1}\cap H)$
and we conclude
![]() $\textrm{gd}_{({\mathcal G} \cap ({\mathcal F}_{m-1}\cap H))\cap K}(K)=0$
. Now assume
$\textrm{gd}_{({\mathcal G} \cap ({\mathcal F}_{m-1}\cap H))\cap K}(K)=0$
. Now assume
![]() $K\in{\mathcal G}$
is virtually
$K\in{\mathcal G}$
is virtually
![]() $\mathbb{Z}^{m}$
. We claim that
$\mathbb{Z}^{m}$
. We claim that
![]() $({\mathcal G} \cap ({\mathcal F}_{m-1}\cap H))\cap K={\mathcal F}_{m-1}\cap K$
. The inclusion
$({\mathcal G} \cap ({\mathcal F}_{m-1}\cap H))\cap K={\mathcal F}_{m-1}\cap K$
. The inclusion
![]() $({\mathcal G} \cap ({\mathcal F}_{m-1}\cap H))\cap K \subset{\mathcal F}_{m-1}\cap K$
is clear since
$({\mathcal G} \cap ({\mathcal F}_{m-1}\cap H))\cap K \subset{\mathcal F}_{m-1}\cap K$
is clear since
![]() ${\mathcal F}_{m-1}\cap H\subset{\mathcal F}_{m-1}$
. For the other inclusion let
${\mathcal F}_{m-1}\cap H\subset{\mathcal F}_{m-1}$
. For the other inclusion let
![]() $M\in{\mathcal F}_{m-1}\cap K$
. Since
$M\in{\mathcal F}_{m-1}\cap K$
. Since
![]() $K\leq H$
we get
$K\leq H$
we get
![]() ${\mathcal F}_{m-1}\cap K \subseteq{\mathcal F}_{m-1}\cap H$
and as a consequence
${\mathcal F}_{m-1}\cap K \subseteq{\mathcal F}_{m-1}\cap H$
and as a consequence
![]() $M\in{\mathcal F}_{m-1}\cap H$
, on the other hand
$M\in{\mathcal F}_{m-1}\cap H$
, on the other hand
![]() $M\leq K\in{\mathcal G}$
, therefore
$M\leq K\in{\mathcal G}$
, therefore
![]() $M\in ({\mathcal G} \cap ({\mathcal F}_{m-1}\cap H))\cap K$
. This establishes the claim. We conclude that
$M\in ({\mathcal G} \cap ({\mathcal F}_{m-1}\cap H))\cap K$
. This establishes the claim. We conclude that
where the inequality follows from [Reference Rolland, Álvarez and Saldaña23, Proposition 1.3].
The following proposition is a mild generalization of [Reference Charney4, Lemma 2.3].
Proposition 3.2.
Let
![]() $H$
be a subgroup of
$H$
be a subgroup of
![]() $\mathbb{Z}^n$
that is maximal in
$\mathbb{Z}^n$
that is maximal in
![]() ${\mathcal F}_t-{\mathcal F}_{t-1}$
. Then, for all
${\mathcal F}_t-{\mathcal F}_{t-1}$
. Then, for all
![]() $0\le k\le t$
, each
$0\le k\le t$
, each
![]() $L\in ({\mathcal F}_k\cap H-{\mathcal F}_{k-1}\cap H)$
is contained in a unique maximal element
$L\in ({\mathcal F}_k\cap H-{\mathcal F}_{k-1}\cap H)$
is contained in a unique maximal element
![]() $M\in ({\mathcal F}_k-{\mathcal F}_{k-1})$
and
$M\in ({\mathcal F}_k-{\mathcal F}_{k-1})$
and
![]() $M$
is a subgroup of
$M$
is a subgroup of
![]() $H$
.
$H$
.
Proof. We have two cases
![]() $\textrm{rank}(H)=n$
or
$\textrm{rank}(H)=n$
or
![]() $\textrm{rank}(H)\lt n$
. In the first case, by the maximality of
$\textrm{rank}(H)\lt n$
. In the first case, by the maximality of
![]() $H$
we have that
$H$
we have that
![]() $H=\mathbb{Z}^n$
and
$H=\mathbb{Z}^n$
and
![]() ${\mathcal F}_{k}\cap H={\mathcal F}_k$
. Let
${\mathcal F}_{k}\cap H={\mathcal F}_k$
. Let
![]() $L\in ({\mathcal F}_k-{\mathcal F}_{k-1})$
, we consider the following short exact sequence:
$L\in ({\mathcal F}_k-{\mathcal F}_{k-1})$
, we consider the following short exact sequence:
Since
![]() $\operatorname{rank}(\mathbb{Z}^n) = \operatorname{rank}(L) + \operatorname{rank}(\mathbb{Z}^n/ L)$
and by the classification theorem of finitely generated abelian groups, we have that
$\operatorname{rank}(\mathbb{Z}^n) = \operatorname{rank}(L) + \operatorname{rank}(\mathbb{Z}^n/ L)$
and by the classification theorem of finitely generated abelian groups, we have that
![]() $\mathbb{Z}^n/ L$
is isomorphic to
$\mathbb{Z}^n/ L$
is isomorphic to
![]() $\mathbb{Z}^{n-k} \oplus F$
where
$\mathbb{Z}^{n-k} \oplus F$
where
![]() $F$
is the torsion part. Therefore, it is clear that
$F$
is the torsion part. Therefore, it is clear that
![]() $p^{-1}(F)$
is the unique maximal subgroup of
$p^{-1}(F)$
is the unique maximal subgroup of
![]() $\mathbb{Z}^n$
of rank
$\mathbb{Z}^n$
of rank
![]() $k$
that contains
$k$
that contains
![]() $L$
.
$L$
.
Suppose that
![]() $\textrm{rank}(H)=t\lt n$
. Let
$\textrm{rank}(H)=t\lt n$
. Let
![]() $L\in{\mathcal F}_{k}\cap H-{\mathcal F}_{k-1}\cap H$
, in particular
$L\in{\mathcal F}_{k}\cap H-{\mathcal F}_{k-1}\cap H$
, in particular
![]() $L\in{\mathcal F}_k$
then by the first case
$L\in{\mathcal F}_k$
then by the first case
![]() $L$
is contained in a unique maximal
$L$
is contained in a unique maximal
![]() $M\in{\mathcal F}_{k}-{\mathcal F}_{k-1}$
. We claim that
$M\in{\mathcal F}_{k}-{\mathcal F}_{k-1}$
. We claim that
![]() $M\leq H$
. Note that
$M\leq H$
. Note that
![]() $MH$
is virtually
$MH$
is virtually
![]() $\mathbb{Z}^t$
because
$\mathbb{Z}^t$
because
it follows that
![]() $MH\in{\mathcal F}_t$
, and then the maximality of
$MH\in{\mathcal F}_t$
, and then the maximality of
![]() $H$
implies
$H$
implies
![]() $H=MH$
. This finishes the proof of claim. Now it is easy to see that
$H=MH$
. This finishes the proof of claim. Now it is easy to see that
![]() $M\in{\mathcal F}_{k}\cap H-{\mathcal F}_{k-1}\cap H$
is the unique maximal in
$M\in{\mathcal F}_{k}\cap H-{\mathcal F}_{k-1}\cap H$
is the unique maximal in
![]() ${\mathcal F}_{k}\cap H-{\mathcal F}_{k-1}\cap H$
containing
${\mathcal F}_{k}\cap H-{\mathcal F}_{k-1}\cap H$
containing
![]() $L$
. In fact, suppose that there is another
$L$
. In fact, suppose that there is another
![]() $N\in{\mathcal F}_{k}\cap H-{\mathcal F}_{k-1}\cap H$
that is maximal and contains
$N\in{\mathcal F}_{k}\cap H-{\mathcal F}_{k-1}\cap H$
that is maximal and contains
![]() $L$
. Then we have
$L$
. Then we have
which implies
![]() $NM\in{\mathcal F}_k\cap H$
. This contradicts the maximality of
$NM\in{\mathcal F}_k\cap H$
. This contradicts the maximality of
![]() $N$
.
$N$
.
Corollary 3.3.
Let
![]() $H$
be a subgroup of
$H$
be a subgroup of
![]() $\mathbb{Z}^n$
that is maximal in
$\mathbb{Z}^n$
that is maximal in
![]() ${\mathcal F}_t-{\mathcal F}_{t-1}$
. Then, for all
${\mathcal F}_t-{\mathcal F}_{t-1}$
. Then, for all
![]() $0\le k\le t$
the following statements hold
$0\le k\le t$
the following statements hold
-
(a) Each
 $L\in ({\mathcal F}_k\cap H-{\mathcal F}_{k-1}\cap H)$
is contained in a unique maximal element
$L\in ({\mathcal F}_k\cap H-{\mathcal F}_{k-1}\cap H)$
is contained in a unique maximal element
 $M\in ({\mathcal F}_k\cap H-{\mathcal F}_{k-1}\cap H)$
.
$M\in ({\mathcal F}_k\cap H-{\mathcal F}_{k-1}\cap H)$
. -
(b) Let
 $S\in ({\mathcal F}_{k}\cap H-{\mathcal F}_{k-1}\cap H)$
be a maximal element, then
$S\in ({\mathcal F}_{k}\cap H-{\mathcal F}_{k-1}\cap H)$
be a maximal element, then
 $S$
is maximal in
$S$
is maximal in
 ${\mathcal F}_k-{\mathcal F}_{k-1}$
.
${\mathcal F}_k-{\mathcal F}_{k-1}$
.
Lemma 3.4.
Let
![]() $n, t\in \mathbb{N}$
such that
$n, t\in \mathbb{N}$
such that
![]() $0\leq t\lt n$
. Let
$0\leq t\lt n$
. Let
![]() $L$
be a subgroup of
$L$
be a subgroup of
![]() $\mathbb{Z}^n$
that is maximal in
$\mathbb{Z}^n$
that is maximal in
![]() ${\mathcal F}_t-{\mathcal F}_{t-1}$
. Let
${\mathcal F}_t-{\mathcal F}_{t-1}$
. Let
![]() $SUB(L)$
be the family of all the subgroups of
$SUB(L)$
be the family of all the subgroups of
![]() $L$
. Then
$L$
. Then
![]() $\textrm{gd}_{SUB(L)}(\mathbb{Z}^n)\leq n-t$
.
$\textrm{gd}_{SUB(L)}(\mathbb{Z}^n)\leq n-t$
.
Proof. A model for
![]() $E_{{\mathcal F}_0}(\mathbb{Z}^n/L)$
is a model for
$E_{{\mathcal F}_0}(\mathbb{Z}^n/L)$
is a model for
![]() $E_{SUB(L)}\mathbb{Z}^n$
via the action given by the projection
$E_{SUB(L)}\mathbb{Z}^n$
via the action given by the projection
![]() $\mathbb{Z}^n\to \mathbb{Z}^n/L$
. Since
$\mathbb{Z}^n\to \mathbb{Z}^n/L$
. Since
![]() $\mathbb{Z}^n/L=\mathbb{Z}^{n-t}$
, a model for
$\mathbb{Z}^n/L=\mathbb{Z}^{n-t}$
, a model for
![]() $E_{{\mathcal F}_0}(\mathbb{Z}^n/L)$
is
$E_{{\mathcal F}_0}(\mathbb{Z}^n/L)$
is
![]() $\mathbb{R}^{n-t}$
with the action given by translation.
$\mathbb{R}^{n-t}$
with the action given by translation.
Lemma 3.5.
Let
![]() $p,t,n\in \mathbb{N}$
such that
$p,t,n\in \mathbb{N}$
such that
![]() $0\leq k\leq p\lt t\leq n$
. Let
$0\leq k\leq p\lt t\leq n$
. Let
![]() $H$
be a subgroup of
$H$
be a subgroup of
![]() $\mathbb{Z}^n$
that is maximal in
$\mathbb{Z}^n$
that is maximal in
![]() ${\mathcal F}_t-{\mathcal F}_{t-1}$
, and let
${\mathcal F}_t-{\mathcal F}_{t-1}$
, and let
![]() $S$
be maximal in
$S$
be maximal in
![]() ${\mathcal F}_{p}\cap H-{\mathcal F}_{p-1}\cap H$
(note that
${\mathcal F}_{p}\cap H-{\mathcal F}_{p-1}\cap H$
(note that
![]() $S$
is a subgroup of
$S$
is a subgroup of
![]() $H$
). Then, we can choose a model
$H$
). Then, we can choose a model
![]() $X$
of
$X$
of
![]() $E_{{\mathcal F}_k\cap S}\mathbb{Z}^n$
with
$E_{{\mathcal F}_k\cap S}\mathbb{Z}^n$
with
![]() $\dim (X)\leq n+k$
, and a model
$\dim (X)\leq n+k$
, and a model
![]() $Y$
of
$Y$
of
![]() $E_{{\mathcal F}_k\cap H}\mathbb{Z}^n$
with
$E_{{\mathcal F}_k\cap H}\mathbb{Z}^n$
with
![]() $\dim (Y)\leq n+k$
such that we have an inclusion
$\dim (Y)\leq n+k$
such that we have an inclusion
![]() $X\hookrightarrow Y$
.
$X\hookrightarrow Y$
.
Proof. The proof is by induction on
![]() $k$
. Let
$k$
. Let
![]() $G=\mathbb{Z}^n$
. For
$G=\mathbb{Z}^n$
. For
![]() $k=0$
, we have
$k=0$
, we have
![]() $E_{{\mathcal F}_0\cap S}G=EG$
and
$E_{{\mathcal F}_0\cap S}G=EG$
and
![]() $E_{{\mathcal F}_0\cap H}G=EG$
. A model for
$E_{{\mathcal F}_0\cap H}G=EG$
. A model for
![]() $EG$
is
$EG$
is
![]() $\mathbb{R}^n$
and the claim follows. Assuming the claim holds for all
$\mathbb{R}^n$
and the claim follows. Assuming the claim holds for all
![]() $k \lt m$
, we prove that it holds for
$k \lt m$
, we prove that it holds for
![]() $k = m$
, that is, we show that there is a model
$k = m$
, that is, we show that there is a model
![]() $X$
of
$X$
of
![]() $E_{{\mathcal F}_m\cap S}G$
with
$E_{{\mathcal F}_m\cap S}G$
with
![]() $\dim (X)\leq n+m$
, and a model
$\dim (X)\leq n+m$
, and a model
![]() $Y$
of
$Y$
of
![]() $E_{{\mathcal F}_m\cap H}G$
with
$E_{{\mathcal F}_m\cap H}G$
with
![]() $\dim (Y)\leq n+m$
such that we have a inclusion
$\dim (Y)\leq n+m$
such that we have a inclusion
![]() $X\hookrightarrow Y$
. Let
$X\hookrightarrow Y$
. Let
![]() $\sim$
be the equivalence relation on
$\sim$
be the equivalence relation on
![]() ${\mathcal F}_m\cap H-{\mathcal F}_{m-1}\cap H$
defined by commensurability. Let
${\mathcal F}_m\cap H-{\mathcal F}_{m-1}\cap H$
defined by commensurability. Let
![]() $I_1$
be a complete set of representatives of classes of subgroups in
$I_1$
be a complete set of representatives of classes of subgroups in
![]() $ ({\mathcal F}_m\cap H -{\mathcal F}_{m-1}\cap H)/\sim$
. By Corollary 3.3, these representatives can be chosen to be maximal within their class. Applying Theorem 2.6 and Remark 2.5, the following homotopy
$ ({\mathcal F}_m\cap H -{\mathcal F}_{m-1}\cap H)/\sim$
. By Corollary 3.3, these representatives can be chosen to be maximal within their class. Applying Theorem 2.6 and Remark 2.5, the following homotopy
![]() $G$
-push-out gives us a model
$G$
-push-out gives us a model
![]() $X_1$
for
$X_1$
for
![]() $E_{{\mathcal F}_m\cap H}G$
$E_{{\mathcal F}_m\cap H}G$

For
![]() $L\in I_1$
, by maximality of
$L\in I_1$
, by maximality of
![]() $L$
in its commensuration class we can write the family
$L$
in its commensuration class we can write the family
as the union of two families
where
![]() $SUB(L)$
is the family of all the subgroups of
$SUB(L)$
is the family of all the subgroups of
![]() $L$
.
$L$
.
On the other hand, let
![]() $\sim$
be the equivalence relation on
$\sim$
be the equivalence relation on
![]() ${\mathcal F}_m\cap S-{\mathcal F}_{m-1}\cap S$
defined by commensurability. Let
${\mathcal F}_m\cap S-{\mathcal F}_{m-1}\cap S$
defined by commensurability. Let
![]() $I_2$
be a complete set of representatives of classes of subgroups in
$I_2$
be a complete set of representatives of classes of subgroups in
![]() $ ({\mathcal F}_m\cap S -{\mathcal F}_{m-1}\cap S)/\sim$
. By Corollary 3.3, these representatives can be chosen to be maximal within their class. Applying Theorem 2.6, we obtain a homotopy
$ ({\mathcal F}_m\cap S -{\mathcal F}_{m-1}\cap S)/\sim$
. By Corollary 3.3, these representatives can be chosen to be maximal within their class. Applying Theorem 2.6, we obtain a homotopy
![]() $G$
-push-out that gives us a model
$G$
-push-out that gives us a model
![]() $X_2$
for
$X_2$
for
![]() $E_{{\mathcal F}_m\cap S}G$
$E_{{\mathcal F}_m\cap S}G$

Let
![]() $T \in I_2$
. We claim that a model for
$T \in I_2$
. We claim that a model for
![]() $E_{SUB(T) \cup ({\mathcal F}_{m-1} \cap H)}G$
is also a model for
$E_{SUB(T) \cup ({\mathcal F}_{m-1} \cap H)}G$
is also a model for
![]() $E_{SUB(L) \cup ({\mathcal F}_{m-1} \cap H)}G$
for every
$E_{SUB(L) \cup ({\mathcal F}_{m-1} \cap H)}G$
for every
![]() $L \in I_1$
. Let
$L \in I_1$
. Let
![]() $L \in I_1$
. Note that
$L \in I_1$
. Note that
![]() $T$
and
$T$
and
![]() $L$
are maximal subgroups of
$L$
are maximal subgroups of
![]() $H$
, thus
$H$
, thus
![]() $H = L \oplus N_1$
and
$H = L \oplus N_1$
and
![]() $H = T \oplus N_2$
. We can construct an automorphism of
$H = T \oplus N_2$
. We can construct an automorphism of
![]() $H$
,
$H$
,
![]() $\sigma \colon L \oplus N_1 \to T \oplus N_2$
, that maps
$\sigma \colon L \oplus N_1 \to T \oplus N_2$
, that maps
![]() $L$
to
$L$
to
![]() $T$
isomorphically. Since
$T$
isomorphically. Since
![]() $H$
is maximal in
$H$
is maximal in
![]() $G$
, we can split
$G$
, we can split
![]() $G$
as
$G$
as
![]() $G = H \oplus R$
. Therefore, we can extend the automorphism
$G = H \oplus R$
. Therefore, we can extend the automorphism
![]() $\sigma$
to an automorphism of
$\sigma$
to an automorphism of
![]() $G$
,
$G$
,
![]() $\hat{\sigma }\colon L \oplus N_1 \oplus R \to T \oplus N_2 \oplus R$
, that maps
$\hat{\sigma }\colon L \oplus N_1 \oplus R \to T \oplus N_2 \oplus R$
, that maps
![]() $L$
to
$L$
to
![]() $T$
isomorphically and preserves the subgroup
$T$
isomorphically and preserves the subgroup
![]() $H$
. It follows that
$H$
. It follows that
![]() $E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}G$
is a model for
$E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}G$
is a model for
![]() $E_{SUB(L)\cup ({\mathcal F}_{m-1}\cap H)}G$
via the action given by the automorphism
$E_{SUB(L)\cup ({\mathcal F}_{m-1}\cap H)}G$
via the action given by the automorphism
![]() $\hat{\sigma }$
. From Corollary 3.3 it follows that
$\hat{\sigma }$
. From Corollary 3.3 it follows that
![]() $I_1=I_2\sqcup (I_1-I_2)$
. Therefore, we can replace the homotopy
$I_1=I_2\sqcup (I_1-I_2)$
. Therefore, we can replace the homotopy
![]() $G$
-push-outs in equations (3.1) and (3.2) with the following homotopy
$G$
-push-outs in equations (3.1) and (3.2) with the following homotopy
![]() $G$
-push-outs.
$G$
-push-outs.


By induction hypothesis there is a model
![]() $X$
of
$X$
of
![]() $E_{{\mathcal F}_{m-1}\cap S}G$
with
$E_{{\mathcal F}_{m-1}\cap S}G$
with
![]() $\dim (X)\leq n+m-1$
, and a model
$\dim (X)\leq n+m-1$
, and a model
![]() $Y$
of
$Y$
of
![]() $E_{{\mathcal F}_{m-1}\cap H}G$
with
$E_{{\mathcal F}_{m-1}\cap H}G$
with
![]() $\dim (Y)\leq n+m-1$
, such that we have a inclusion
$\dim (Y)\leq n+m-1$
, such that we have a inclusion
![]() $X\hookrightarrow Y$
. By the
$X\hookrightarrow Y$
. By the
![]() $G$
-push-outs in equations (3.3) and (3.4), to prove that there is a inclusion
$G$
-push-outs in equations (3.3) and (3.4), to prove that there is a inclusion
![]() $E_{{\mathcal F}_{m}\cap S}\hookrightarrow E_{{\mathcal F}_{m}\cap H}$
it is enough to prove that there is a inclusion
$E_{{\mathcal F}_{m}\cap S}\hookrightarrow E_{{\mathcal F}_{m}\cap H}$
it is enough to prove that there is a inclusion
![]() $E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap S) }G \hookrightarrow E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}G$
. By Lemma 2.9, the following
$E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap S) }G \hookrightarrow E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}G$
. By Lemma 2.9, the following
![]() $G$
-push-outs gives us a model for
$G$
-push-outs gives us a model for
![]() $E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap S) }G$
and
$E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap S) }G$
and
![]() $E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H) }G$
, respectively.
$E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H) }G$
, respectively.

Note that
![]() $SUB(T)\cap ({\mathcal F}_{m-1}\cap S)={\mathcal F}_{m-1}\cap T= SUB(T)\cap ({\mathcal F}_{m-1}\cap H)$
. It follows from these
$SUB(T)\cap ({\mathcal F}_{m-1}\cap S)={\mathcal F}_{m-1}\cap T= SUB(T)\cap ({\mathcal F}_{m-1}\cap H)$
. It follows from these
![]() $G$
-push-outs that we have a inclusion
$G$
-push-outs that we have a inclusion
![]() $E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap S) }G \hookrightarrow E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}G$
.
$E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap S) }G \hookrightarrow E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}G$
.
Finally, we prove that
![]() $\dim (X_1)\leq n+m$
and
$\dim (X_1)\leq n+m$
and
![]() $\dim (X_2)\leq n+m$
. From equation (3.3) it follows
$\dim (X_2)\leq n+m$
. From equation (3.3) it follows
Then to prove that
![]() $\dim (X_1)\leq n+m$
it is enough to prove
$\dim (X_1)\leq n+m$
it is enough to prove
![]() $\textrm{gd}_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}(G)\leq n+m$
. By equation (3.5) and since
$\textrm{gd}_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}(G)\leq n+m$
. By equation (3.5) and since
![]() $SUB(T) \cap ({\mathcal F}_{m-1}\cap H)={\mathcal F}_{m-1}\cap T$
we have
$SUB(T) \cap ({\mathcal F}_{m-1}\cap H)={\mathcal F}_{m-1}\cap T$
we have
 \begin{align*} \begin{split} \textrm{gd}_{ SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}(G) &\leq \dim (Y_1)\\ &\leq \max \{\textrm{gd}_{{\mathcal F}_{m-1}\cap H}(G), \textrm{gd}_{SUB(T) \cap ({\mathcal F}_{m-1}\cap H)}(G)+1, \textrm{gd}_{SUB(T)}(G)\}\\ &=\max \{\textrm{gd}_{{\mathcal F}_{m-1}\cap H}(G), \textrm{gd}_{{\mathcal F}_{m-1}\cap T}(G)+1, \textrm{gd}_{SUB(T)}(G)\}\\ &\leq \max \{n+m-1, n+m, n-m\}\text{, By Lemma 3.1 and Lemma 3.4}\\ &=n+m. \end{split} \end{align*}
\begin{align*} \begin{split} \textrm{gd}_{ SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}(G) &\leq \dim (Y_1)\\ &\leq \max \{\textrm{gd}_{{\mathcal F}_{m-1}\cap H}(G), \textrm{gd}_{SUB(T) \cap ({\mathcal F}_{m-1}\cap H)}(G)+1, \textrm{gd}_{SUB(T)}(G)\}\\ &=\max \{\textrm{gd}_{{\mathcal F}_{m-1}\cap H}(G), \textrm{gd}_{{\mathcal F}_{m-1}\cap T}(G)+1, \textrm{gd}_{SUB(T)}(G)\}\\ &\leq \max \{n+m-1, n+m, n-m\}\text{, By Lemma 3.1 and Lemma 3.4}\\ &=n+m. \end{split} \end{align*}
Theorem 3.6 (The lower bound). Let
![]() $m,t,n\in \mathbb{N}$
such that
$m,t,n\in \mathbb{N}$
such that
![]() $0\leq m\lt t\leq n$
. Let
$0\leq m\lt t\leq n$
. Let
![]() $H$
be a subgroup of
$H$
be a subgroup of
![]() $\mathbb{Z}^n$
that is maximal in
$\mathbb{Z}^n$
that is maximal in
![]() ${\mathcal F}_t-{\mathcal F}_{t-1}$
, then
${\mathcal F}_t-{\mathcal F}_{t-1}$
, then
![]() $H_{{\mathcal F}_m\cap H}^{n+m}(\mathbb{Z}^n;\;\underline{\mathbb{Z}})\neq 0$
.
$H_{{\mathcal F}_m\cap H}^{n+m}(\mathbb{Z}^n;\;\underline{\mathbb{Z}})\neq 0$
.
Proof. Let
![]() $G=\mathbb{Z}^n$
. The proof is by double induction on
$G=\mathbb{Z}^n$
. The proof is by double induction on
![]() $(t,m)$
. The claim is true for all
$(t,m)$
. The claim is true for all
![]() $(t,0)\in \mathbb{N}\times \{0\}$
. Let
$(t,0)\in \mathbb{N}\times \{0\}$
. Let
![]() $H$
be a subgroup of
$H$
be a subgroup of
![]() $G$
that is maximal in
$G$
that is maximal in
![]() ${\mathcal F}_t-{\mathcal F}_{t-1}$
, then
${\mathcal F}_t-{\mathcal F}_{t-1}$
, then
Suppose that the claim is true for all
![]() $(t,s)\in \mathbb{N}\times \{0,1,\dots, m-1\}$
, we prove that the claim is true for
$(t,s)\in \mathbb{N}\times \{0,1,\dots, m-1\}$
, we prove that the claim is true for
![]() $(t,m)$
, i.e.
$(t,m)$
, i.e.
![]() $H_{{\mathcal F}_m\cap H}^{n+m}(G;\;\underline{\mathbb{Z}})\neq 0$
.
$H_{{\mathcal F}_m\cap H}^{n+m}(G;\;\underline{\mathbb{Z}})\neq 0$
.
Applying Mayer–Vietoris to the
![]() $G$
-push-out in equation (3.3) and Lemma 3.1, we have the following long exact sequence
$G$
-push-out in equation (3.3) and Lemma 3.1, we have the following long exact sequence
 \begin{equation} \begin{split} \cdots \to \left (\prod _{L\in{I}_1}H^{n+m-1}(E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}G/G)\right )\oplus H^{n+m-1}(E_{{\mathcal F}_{m-1}\cap H}G/G)\xrightarrow []{\varphi }& \\ \prod _{L\in I_1}H^{n+m-1}(E_{{\mathcal F}_{m-1}\cap H}G/G)\to H^{n+m}(X_1/G) \to \prod _{L\in{I}_1}H^{n+m}(E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}G/G)& \to 0 \end{split} \end{equation}
\begin{equation} \begin{split} \cdots \to \left (\prod _{L\in{I}_1}H^{n+m-1}(E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}G/G)\right )\oplus H^{n+m-1}(E_{{\mathcal F}_{m-1}\cap H}G/G)\xrightarrow []{\varphi }& \\ \prod _{L\in I_1}H^{n+m-1}(E_{{\mathcal F}_{m-1}\cap H}G/G)\to H^{n+m}(X_1/G) \to \prod _{L\in{I}_1}H^{n+m}(E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}G/G)& \to 0 \end{split} \end{equation}
We now show that
![]() $\prod _{L\in{I}_1}H^{n+m}(E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}G/G)=0$
. It is enough to show that
$\prod _{L\in{I}_1}H^{n+m}(E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}G/G)=0$
. It is enough to show that
![]() $\textrm{gd}_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}(G)\leq n+m-1$
. By Lemma 2.9 the following homotopy
$\textrm{gd}_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}(G)\leq n+m-1$
. By Lemma 2.9 the following homotopy
![]() $G$
-push-out gives us a model
$G$
-push-out gives us a model
![]() $Y$
for
$Y$
for
![]() $E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}G$
.
$E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}G$
.

Note that
![]() $SUB(T)\cap ({\mathcal F}_{m-1}\cap H)={\mathcal F}_{m-1}\cap T$
. By Lemma 3.5, the map
$SUB(T)\cap ({\mathcal F}_{m-1}\cap H)={\mathcal F}_{m-1}\cap T$
. By Lemma 3.5, the map
![]() $g$
can be taken as an inclusion, then by [Reference Waner26, Theorem 1.1] the homotopy
$g$
can be taken as an inclusion, then by [Reference Waner26, Theorem 1.1] the homotopy
![]() $G$
-push-out can be taken as a
$G$
-push-out can be taken as a
![]() $G$
-push-out. It follows that
$G$
-push-out. It follows that
 \begin{equation} \begin{split} \textrm{gd}_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}(G)& \leq \dim (Y)\\ &=\max \{\textrm{gd}_{SUB(T)}(G), \textrm{gd}_{{\mathcal F}_{m-1}\cap T}(G), \textrm{gd}_{{\mathcal F}_{m-1}\cap H}(G)\}\\ &\leq \max \{n-m,n+m-1,n+m-1\}\text{, by Lemma 3.1 and Lemma 3.4}\\ &=n+m-1 \end{split} \end{equation}
\begin{equation} \begin{split} \textrm{gd}_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}(G)& \leq \dim (Y)\\ &=\max \{\textrm{gd}_{SUB(T)}(G), \textrm{gd}_{{\mathcal F}_{m-1}\cap T}(G), \textrm{gd}_{{\mathcal F}_{m-1}\cap H}(G)\}\\ &\leq \max \{n-m,n+m-1,n+m-1\}\text{, by Lemma 3.1 and Lemma 3.4}\\ &=n+m-1 \end{split} \end{equation}
Then the sequence equation (3.6) reduce to
 \begin{align*} \begin{split} \cdots \to \left (\prod _{L\in{I}_1}H^{n+m-1}(E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}G/G)\right )\oplus H^{n+m-1}(E_{{\mathcal F}_{m-1}\cap H}G/G)\xrightarrow []{\varphi }& \\ \prod _{L\in I_1}H^{n+m-1}(E_{{\mathcal F}_{m-1}\cap H}G/G)\to H^{n+m}(X_1/G) \to & 0 \end{split} \end{align*}
\begin{align*} \begin{split} \cdots \to \left (\prod _{L\in{I}_1}H^{n+m-1}(E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}G/G)\right )\oplus H^{n+m-1}(E_{{\mathcal F}_{m-1}\cap H}G/G)\xrightarrow []{\varphi }& \\ \prod _{L\in I_1}H^{n+m-1}(E_{{\mathcal F}_{m-1}\cap H}G/G)\to H^{n+m}(X_1/G) \to & 0 \end{split} \end{align*}
Then to prove that
![]() $H_{{\mathcal F}_k\cap H}^{n+m}(G;\;\underline{\mathbb{Z}})=H^{n+m}(X_1/G)\neq 0$
is enough to prove that
$H_{{\mathcal F}_k\cap H}^{n+m}(G;\;\underline{\mathbb{Z}})=H^{n+m}(X_1/G)\neq 0$
is enough to prove that
![]() $\varphi$
is not surjective. By equation (3.3) we have
$\varphi$
is not surjective. By equation (3.3) we have
![]() $\varphi = (\prod _{L\in I_1}f_{T}^{*})-\Delta$
, where
$\varphi = (\prod _{L\in I_1}f_{T}^{*})-\Delta$
, where
![]() $\Delta$
is the diagonal embedding. First, we prove that
$\Delta$
is the diagonal embedding. First, we prove that
![]() $f_{T}^{*}$
is not surjective.
$f_{T}^{*}$
is not surjective.
Applying Mayer–Vietoris to the
![]() $G$
-push-out in equation (3.7) we have the following long exact sequence
$G$
-push-out in equation (3.7) we have the following long exact sequence
Since
![]() $\textrm{gd}_{SUB(T)}(G)\leq n-m$
and since there is precisely one
$\textrm{gd}_{SUB(T)}(G)\leq n-m$
and since there is precisely one
![]() $G$
-map
$G$
-map
![]() $E_{{\mathcal F}_{m-1}\cap H}G\to E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}G$
up to
$E_{{\mathcal F}_{m-1}\cap H}G\to E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}G$
up to
![]() $G$
-homotopy we can reduce the sequence to
$G$
-homotopy we can reduce the sequence to
By hypothesis
![]() $T$
is maximal in
$T$
is maximal in
![]() ${\mathcal F}_m\cap H-{\mathcal F}_{m-1}\cap H$
, then by Corollary 3.3 (b) we have that
${\mathcal F}_m\cap H-{\mathcal F}_{m-1}\cap H$
, then by Corollary 3.3 (b) we have that
![]() $T$
is maximal in
$T$
is maximal in
![]() ${\mathcal F}_m-{\mathcal F}_{m-1}$
, by induction hypothesis we have that
${\mathcal F}_m-{\mathcal F}_{m-1}$
, by induction hypothesis we have that
![]() $H^{n+m-1}(E_{{\mathcal F}_{m-1}\cap T}G/G)\neq 0$
, thus
$H^{n+m-1}(E_{{\mathcal F}_{m-1}\cap T}G/G)\neq 0$
, thus
![]() $f_T^{*}$
is not surjective.
$f_T^{*}$
is not surjective.
Finally, we see that
![]() $\varphi$
is not surjective. In fact, let
$\varphi$
is not surjective. In fact, let
![]() $b_K\notin \textrm{Im}(f_{T}^{*})$
, for some
$b_K\notin \textrm{Im}(f_{T}^{*})$
, for some
![]() $K\in I_1$
, then
$K\in I_1$
, then
![]() $(0,0, \cdots, b_K,\cdots,0)\notin \textrm{Im}(\varphi )$
. Suppose that is not the case, that is, there is
$(0,0, \cdots, b_K,\cdots,0)\notin \textrm{Im}(\varphi )$
. Suppose that is not the case, that is, there is
 \begin{equation*}\left(\prod _{L\in {I}_1}a_L,c\right)\in \left (\prod _{L\in {I}_1}H^{n+m-1}(E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}G/G)\right )\oplus H^{n+m-1}(E_{{\mathcal F}_{m-1}\cap H}G/G)\end{equation*}
\begin{equation*}\left(\prod _{L\in {I}_1}a_L,c\right)\in \left (\prod _{L\in {I}_1}H^{n+m-1}(E_{SUB(T)\cup ({\mathcal F}_{m-1}\cap H)}G/G)\right )\oplus H^{n+m-1}(E_{{\mathcal F}_{m-1}\cap H}G/G)\end{equation*}
such that
![]() $(0,0, \cdots, b_K,\cdots,0)=\varphi ((\prod _{L\in{I}_1}a_L,c))=\prod _{L\in{I}_1}f_{T}^{*}(a_L)-\Delta (c)=(f_{T}^{*}(a_L)-c)_{L\in I_1}.$
Then
$(0,0, \cdots, b_K,\cdots,0)=\varphi ((\prod _{L\in{I}_1}a_L,c))=\prod _{L\in{I}_1}f_{T}^{*}(a_L)-\Delta (c)=(f_{T}^{*}(a_L)-c)_{L\in I_1}.$
Then
![]() $f_{T}^{*}(a_L)=c$
for
$f_{T}^{*}(a_L)=c$
for
![]() $L\neq K$
and
$L\neq K$
and
![]() $f_{T}^{*}(a_K)-c=b_K$
, it follows that
$f_{T}^{*}(a_K)-c=b_K$
, it follows that
then
![]() $b_K\in \textrm{Im}(f_{T}^{*})$
and this is a contradiction.
$b_K\in \textrm{Im}(f_{T}^{*})$
and this is a contradiction.
Proposition 3.7.
Let
![]() $k,t,n\in \mathbb{N}$
such that
$k,t,n\in \mathbb{N}$
such that
![]() $0\leq k\lt t\leq n$
. Let
$0\leq k\lt t\leq n$
. Let
![]() $H$
be a subgroup of
$H$
be a subgroup of
![]() $\mathbb{Z}^n$
that is maximal in
$\mathbb{Z}^n$
that is maximal in
![]() ${\mathcal F}_t-{\mathcal F}_{t-1}$
. Let
${\mathcal F}_t-{\mathcal F}_{t-1}$
. Let
![]() ${\mathcal F}_k\cap H$
be the family that consists of all the subgroups of
${\mathcal F}_k\cap H$
be the family that consists of all the subgroups of
![]() $H$
that belong to
$H$
that belong to
![]() ${\mathcal F}_k$
. Then
${\mathcal F}_k$
. Then
![]() $\textrm{cd}_{{\mathcal F}_k\cap H}(\mathbb{Z}^n)=\textrm{gd}_{{\mathcal F}_k\cap H}(\mathbb{Z}^n)=n+k$
.
$\textrm{cd}_{{\mathcal F}_k\cap H}(\mathbb{Z}^n)=\textrm{gd}_{{\mathcal F}_k\cap H}(\mathbb{Z}^n)=n+k$
.
4. Some applications of Corollary 1.2
4.1. The
 ${\mathcal F}_k$
-dimension of braid groups
${\mathcal F}_k$
-dimension of braid groups
In this subsection, we compute the
![]() ${\mathcal F}_n$
-dimension of full and pure braid groups. For our purposes, it is convenient to define the braid group as follows: let
${\mathcal F}_n$
-dimension of full and pure braid groups. For our purposes, it is convenient to define the braid group as follows: let
![]() $D_n$
the closed disc with
$D_n$
the closed disc with
![]() $n$
punctures, we define the braid group
$n$
punctures, we define the braid group
![]() $B_n$
on
$B_n$
on
![]() $n$
strands, as the isotopy classes of orientation preserving diffeomorphisms of
$n$
strands, as the isotopy classes of orientation preserving diffeomorphisms of
![]() $D_n$
that restrict to the identity on the boundary
$D_n$
that restrict to the identity on the boundary
![]() $\partial D_n$
. We define the pure braid group,
$\partial D_n$
. We define the pure braid group,
![]() $P_n$
, as the finite index subgroup of
$P_n$
, as the finite index subgroup of
![]() $B_n$
consisting of elements that fixe point-wise the punctures.
$B_n$
consisting of elements that fixe point-wise the punctures.
Theorem 4.1.
Let
![]() $k,n \in \mathbb{N}$
such that
$k,n \in \mathbb{N}$
such that
![]() $0\leq k\lt n-1$
and let
$0\leq k\lt n-1$
and let
![]() $G$
be either the braid group
$G$
be either the braid group
![]() $B_n$
or the pure braid group
$B_n$
or the pure braid group
![]() $P_n$
. Then
$P_n$
. Then
![]() $\textrm{gd}_{{\mathcal F}_k}(G)=\textrm{cd}_{{\mathcal F}_k}(G)=n+k-1$
.
$\textrm{gd}_{{\mathcal F}_k}(G)=\textrm{cd}_{{\mathcal F}_k}(G)=n+k-1$
.
Proof. It is enough to prove the following inequalities
In [Reference Juan-Pineda and Saldaña14, Theorem 1.4] was proved that
![]() $\textrm{gd}_{{\mathcal F}_k}(B_n)\leq \textrm{vcd}(B_n)+k$
for all
$\textrm{gd}_{{\mathcal F}_k}(B_n)\leq \textrm{vcd}(B_n)+k$
for all
![]() $0\leq k\lt n-1$
. Since
$0\leq k\lt n-1$
. Since
![]() $P_n$
has finite index in
$P_n$
has finite index in
![]() $B_n$
also we have
$B_n$
also we have
![]() $\textrm{gd}_{{\mathcal F}_k}(P_n)\leq \textrm{vcd}(P_n)+k$
for all
$\textrm{gd}_{{\mathcal F}_k}(P_n)\leq \textrm{vcd}(P_n)+k$
for all
![]() $0\leq k\lt n-1$
. On the other hand, it is well known that
$0\leq k\lt n-1$
. On the other hand, it is well known that
![]() $\textrm{vcd}(B_n)=n-1$
see for example [Reference Arnold2, Section 3]. This proves the first inequality. The second inequality is by Theorem 2.13. In [Reference Farrell and Roushon11, Proposition 3.7] it is shown that
$\textrm{vcd}(B_n)=n-1$
see for example [Reference Arnold2, Section 3]. This proves the first inequality. The second inequality is by Theorem 2.13. In [Reference Farrell and Roushon11, Proposition 3.7] it is shown that
![]() $P_n$
has a subgroup isomorphic to
$P_n$
has a subgroup isomorphic to
![]() $\mathbb{Z}^{n-1}$
. Therefore, by monotonicity of the
$\mathbb{Z}^{n-1}$
. Therefore, by monotonicity of the
![]() ${\mathcal F}_k$
-geometric dimension and Corollary 1.2, we have
${\mathcal F}_k$
-geometric dimension and Corollary 1.2, we have
![]() $\textrm{cd}_{{\mathcal F}_k}(B_n)\geq \textrm{cd}_{{\mathcal F}_k}(P_n)\geq n+k-1$
for all
$\textrm{cd}_{{\mathcal F}_k}(B_n)\geq \textrm{cd}_{{\mathcal F}_k}(P_n)\geq n+k-1$
for all
![]() $0\leq k\lt n-1$
. This proves the last inequality.
$0\leq k\lt n-1$
. This proves the last inequality.
For
![]() $k=1$
, this theorem has been proved in [Reference Farrell and Roushon11].
$k=1$
, this theorem has been proved in [Reference Farrell and Roushon11].
4.2. The
 ${\mathcal F}_k$
-dimension of RAAGs and their outer automorphism groups
${\mathcal F}_k$
-dimension of RAAGs and their outer automorphism groups
In this subsection, we compute the
![]() ${\mathcal F}_n$
-dimension of RAAGs and we give a lower bound for the
${\mathcal F}_n$
-dimension of RAAGs and we give a lower bound for the
![]() ${\mathcal F}_n$
-geometric dimension of the outer automorphism group of some RAAGs.
${\mathcal F}_n$
-geometric dimension of the outer automorphism group of some RAAGs.
We recall some basic notions about RAAGs, for further details see for instance [Reference Cook, Moreno, Nucinkis and Pasini5]. Let
![]() $\Gamma$
be a finite simple graph, that is, a finite graph without loops or multiple edges between vertices. We define the right-angled Artin group (RAAG)
$\Gamma$
be a finite simple graph, that is, a finite graph without loops or multiple edges between vertices. We define the right-angled Artin group (RAAG)
![]() $A_{\Gamma }$
as the group generated by the vertices of
$A_{\Gamma }$
as the group generated by the vertices of
![]() $\Gamma$
with all the relations of the form
$\Gamma$
with all the relations of the form
![]() $vw=wv$
whenever
$vw=wv$
whenever
![]() $v$
and
$v$
and
![]() $w$
are joined by an edge.
$w$
are joined by an edge.
The Salvetti complex
For the construction of the Salvetti complex we follow [Reference Cook, Moreno, Nucinkis and Pasini5, Subsection 3.6]. Let
![]() $A_\Gamma$
be a RAAG, its Salvetti complex
$A_\Gamma$
be a RAAG, its Salvetti complex
![]() $S_\Gamma$
is a CW-complex that can be constructed as follows:
$S_\Gamma$
is a CW-complex that can be constructed as follows:
-
• The
 $S_\Gamma ^{(1)}$
skeleton is constructed as follows: we take a point
$S_\Gamma ^{(1)}$
skeleton is constructed as follows: we take a point
 $x_0$
, and for each
$x_0$
, and for each
 $v\in V(\Gamma )$
, we attach a
$v\in V(\Gamma )$
, we attach a
 $1$
-cell
$1$
-cell
 $I=[0,1]$
that identifies the endpoints of
$I=[0,1]$
that identifies the endpoints of
 $I$
to
$I$
to
 $x_0$
. Then, the
$x_0$
. Then, the
 $S_\Gamma ^{(1)}$
skeleton is a wedge of circles.
$S_\Gamma ^{(1)}$
skeleton is a wedge of circles. -
• The
 $S_\Gamma ^{(2)}$
skeleton is constructed as follows. For each edge of
$S_\Gamma ^{(2)}$
skeleton is constructed as follows. For each edge of
 $\Gamma$
we attach a
$\Gamma$
we attach a
 $2$
-cell
$2$
-cell
 $I\times I$
to
$I\times I$
to
 $S_\Gamma ^{(1)}$
by the boundary
$S_\Gamma ^{(1)}$
by the boundary
 $\partial (I\times I)$
as
$\partial (I\times I)$
as
 $s_vs_w s_{v}^{-1}s_{w}^{-1}$
.
$s_vs_w s_{v}^{-1}s_{w}^{-1}$
. -
• In general the
 $S_\Gamma ^{(n)}$
skeleton is constructed as follows. For each complete subgraph
$S_\Gamma ^{(n)}$
skeleton is constructed as follows. For each complete subgraph
 $\Gamma '$
of
$\Gamma '$
of
 $\Gamma$
with
$\Gamma$
with
 $|V(\Gamma ')|=n$
, we attach a
$|V(\Gamma ')|=n$
, we attach a
 $n$
-cell
$n$
-cell
 $I^n$
to the
$I^n$
to the
 $S_\Gamma ^{(n-1)}$
skeleton using the generators
$S_\Gamma ^{(n-1)}$
skeleton using the generators
 $V(\Gamma ')$
.
$V(\Gamma ')$
.
Remark 4.2.
Note that, by the construction of the Salvetti complex
![]() $S_\Gamma$
, its fundamental group is
$S_\Gamma$
, its fundamental group is
![]() $A_\Gamma$
. Additionally,
$A_\Gamma$
. Additionally,
![]() $S_\Gamma$
has a
$S_\Gamma$
has a
![]() $\dim (S_\Gamma )$
-dimensional torus embedded in it, which follows from its construction. Therefore, the fundamental group
$\dim (S_\Gamma )$
-dimensional torus embedded in it, which follows from its construction. Therefore, the fundamental group
![]() $\pi _1(S_\Gamma,x_0)=A_\Gamma$
has a subgroup that is isomorphic to
$\pi _1(S_\Gamma,x_0)=A_\Gamma$
has a subgroup that is isomorphic to
![]() $\mathbb{Z}^{\dim (S_\Gamma )}$
.
$\mathbb{Z}^{\dim (S_\Gamma )}$
.
Theorem 4.3 ([Reference Cook, Moreno, Nucinkis and Pasini5], Theorem 3.6). The universal cover of the Salvetti complex,
![]() $\tilde{S_\Gamma }$
, is a
$\tilde{S_\Gamma }$
, is a
![]() $\textrm{CAT}(0)$
cube complex. In particular,
$\textrm{CAT}(0)$
cube complex. In particular,
![]() $S_\Gamma$
is a
$S_\Gamma$
is a
![]() $K(A_\Gamma, 1)$
space.
$K(A_\Gamma, 1)$
space.
Corollary 4.4.
Let
![]() $G$
be a RAAG. Then
$G$
be a RAAG. Then
![]() $G$
is torsion-free.
$G$
is torsion-free.
Lemma 4.5.
Let
![]() $A_\Gamma$
be a RAAG then
$A_\Gamma$
be a RAAG then
![]() $\textrm{gd}(A_\Gamma )=\textrm{cd}(A_\Gamma )=\dim (S_\Gamma )$
. Moreover,
$\textrm{gd}(A_\Gamma )=\textrm{cd}(A_\Gamma )=\dim (S_\Gamma )$
. Moreover,
Proof. It is enough to prove the following inequalities
The first inequality follows from Theorem 4.3. The second inequality follows from Theorem 2.13. By [Reference Cook, Moreno, Nucinkis and Pasini5, Subsection 3.7]
![]() $H^{\dim (S_\Gamma )}(S_\Gamma )=H^{\dim (S_\Gamma )}(A_\Gamma )$
is a free abelian generated by each
$H^{\dim (S_\Gamma )}(S_\Gamma )=H^{\dim (S_\Gamma )}(A_\Gamma )$
is a free abelian generated by each
![]() $\dim (S_\Gamma )$
-cell. The third inequality follows.
$\dim (S_\Gamma )$
-cell. The third inequality follows.
By construction of the Salvetti complex
![]() $S_\Gamma$
, we have that
$S_\Gamma$
, we have that
Since
![]() $\textrm{cd}(A_\Gamma )= \dim (S_\Gamma )$
the claim follows.
$\textrm{cd}(A_\Gamma )= \dim (S_\Gamma )$
the claim follows.
Let
![]() $G$
be a right-angled Artin group. In [Reference Rolland, Álvarez and Saldaña23, Corollary 1.2], it was proved that
$G$
be a right-angled Artin group. In [Reference Rolland, Álvarez and Saldaña23, Corollary 1.2], it was proved that
![]() $\textrm{cd}_{{\mathcal F}_k}(G)\leq \textrm{cd}(G)+k+1$
for all
$\textrm{cd}_{{\mathcal F}_k}(G)\leq \textrm{cd}(G)+k+1$
for all
![]() $0\leq k\lt \textrm{cd}(G)$
. However, by following their proof in [Reference Rolland, Álvarez and Saldaña23, Proof of Theorem 3.1] and using [Reference Huang and Prytuła13, Proposition 7.3], we can actually prove that
$0\leq k\lt \textrm{cd}(G)$
. However, by following their proof in [Reference Rolland, Álvarez and Saldaña23, Proof of Theorem 3.1] and using [Reference Huang and Prytuła13, Proposition 7.3], we can actually prove that
![]() $\textrm{cd}_{{\mathcal F}_k}(G)\leq \textrm{cd}(G)+k$
for all
$\textrm{cd}_{{\mathcal F}_k}(G)\leq \textrm{cd}(G)+k$
for all
![]() $0\leq k\lt \textrm{cd}(G)$
. In [Reference Rolland, Álvarez and Saldaña23] and [Reference Huang and Prytuła13, Proposition 7.3], they work with the
$0\leq k\lt \textrm{cd}(G)$
. In [Reference Rolland, Álvarez and Saldaña23] and [Reference Huang and Prytuła13, Proposition 7.3], they work with the
![]() ${\mathcal F}_k$
-cohomological dimension instead of
${\mathcal F}_k$
-cohomological dimension instead of
![]() ${\mathcal F}_k$
-geometric dimension, that is the reason the following Theorem 4.6 is stated in terms of
${\mathcal F}_k$
-geometric dimension, that is the reason the following Theorem 4.6 is stated in terms of
![]() ${\mathcal F}_k$
-cohomological dimension.
${\mathcal F}_k$
-cohomological dimension.
Theorem 4.6.
Let
![]() $G$
be a RAAG. Then
$G$
be a RAAG. Then
![]() $\textrm{cd}_{{\mathcal F}_k}(G)\leq \textrm{cd}(G)+k$
for
$\textrm{cd}_{{\mathcal F}_k}(G)\leq \textrm{cd}(G)+k$
for
![]() $k\in \mathbb{N}$
.
$k\in \mathbb{N}$
.
Proof. The proof is by induction on
![]() $k$
. For
$k$
. For
![]() $k=0$
it follows from Lemma 4.5. Suppose that the inequality is true for all
$k=0$
it follows from Lemma 4.5. Suppose that the inequality is true for all
![]() $k\lt m$
. We prove the inequality for
$k\lt m$
. We prove the inequality for
![]() $k=m$
. Let
$k=m$
. Let
![]() $\sim$
be the equivalence relation on
$\sim$
be the equivalence relation on
![]() ${\mathcal F}_m-{\mathcal F}_{m-1}$
defined by commensurability, and let
${\mathcal F}_m-{\mathcal F}_{m-1}$
defined by commensurability, and let
![]() $I$
be a complete set of representatives of conjugacy classes in
$I$
be a complete set of representatives of conjugacy classes in
![]() $({\mathcal F}_m-{\mathcal F}_{m-1})/\sim$
. Then by the cohomological version of Corollary 2.8 (see Remark 2.14) we have
$({\mathcal F}_m-{\mathcal F}_{m-1})/\sim$
. Then by the cohomological version of Corollary 2.8 (see Remark 2.14) we have
Then to prove that
![]() $\textrm{cd}_{{\mathcal F}_{m}}(G)\leq \textrm{cd}(G)+m$
it is enough to prove that
$\textrm{cd}_{{\mathcal F}_{m}}(G)\leq \textrm{cd}(G)+m$
it is enough to prove that
![]() $\textrm{cd}_{{\mathcal F}_{m}[L]}(N_{G}[L])\leq \textrm{cd}(G)+m$
for all
$\textrm{cd}_{{\mathcal F}_{m}[L]}(N_{G}[L])\leq \textrm{cd}(G)+m$
for all
![]() $L\in I$
. Let
$L\in I$
. Let
![]() $L\in I$
, we can write the family
$L\in I$
, we can write the family
as the union of two families
![]() ${\mathcal F}_m[L]={\mathcal G} \cup ({\mathcal F}_{m-1}\cap N_{G}[L])$
where
${\mathcal F}_m[L]={\mathcal G} \cup ({\mathcal F}_{m-1}\cap N_{G}[L])$
where
![]() $\mathcal G$
is the family generated by
$\mathcal G$
is the family generated by
![]() $\{ K\leq N_G[L]|K\in{\mathcal F}_m-{\mathcal F}_{m-1}, K\sim L\}$
. By the cohomological version of Corollary 2.10 (see Remark 2.14) we have
$\{ K\leq N_G[L]|K\in{\mathcal F}_m-{\mathcal F}_{m-1}, K\sim L\}$
. By the cohomological version of Corollary 2.10 (see Remark 2.14) we have
We prove that
-
1.
 $\textrm{cd}_{{\mathcal G}}(N_{G}[L])\leq \textrm{cd}(G)-m$
$\textrm{cd}_{{\mathcal G}}(N_{G}[L])\leq \textrm{cd}(G)-m$
-
2.
 $\textrm{cd}_{{\mathcal G}\cap{\mathcal F}_{m-1}}(N_{G}[L])\leq \textrm{cd}(G)+m-1$
$\textrm{cd}_{{\mathcal G}\cap{\mathcal F}_{m-1}}(N_{G}[L])\leq \textrm{cd}(G)+m-1$
As a consequence we will have
![]() $\textrm{cd}_{{\mathcal F}_m[L]}(N_{G}[L])\leq \textrm{cd}(G)+m$
. First, we prove item
$\textrm{cd}_{{\mathcal F}_m[L]}(N_{G}[L])\leq \textrm{cd}(G)+m$
. First, we prove item
![]() $(1)$
. We define the family
$(1)$
. We define the family
![]() ${\mathcal F}=\{K\leq N_{G}[L] \mid [K\;:\;K\cap L]\lt \infty \}$
. We claim that
${\mathcal F}=\{K\leq N_{G}[L] \mid [K\;:\;K\cap L]\lt \infty \}$
. We claim that
![]() ${\mathcal F} ={\mathcal G}$
. To show that
${\mathcal F} ={\mathcal G}$
. To show that
![]() ${\mathcal G} \subseteq{\mathcal F}$
, note that
${\mathcal G} \subseteq{\mathcal F}$
, note that
since, by definition,
![]() $\mathcal G$
is the smallest family that contains
$\mathcal G$
is the smallest family that contains
![]() $\{ K \leq N_G[L] \mid K \in{\mathcal F}_m -{\mathcal F}_{m-1}, K \sim L \}$
, it follows that
$\{ K \leq N_G[L] \mid K \in{\mathcal F}_m -{\mathcal F}_{m-1}, K \sim L \}$
, it follows that
![]() ${\mathcal G} \subseteq{\mathcal F}$
. Now let’s prove the other inclusion
${\mathcal G} \subseteq{\mathcal F}$
. Now let’s prove the other inclusion
![]() ${\mathcal F} \subseteq{\mathcal G}$
. Let
${\mathcal F} \subseteq{\mathcal G}$
. Let
![]() $S \in{\mathcal F}$
, then
$S \in{\mathcal F}$
, then
![]() $[S \;:\; S \cap L] \lt \infty$
. Note that
$[S \;:\; S \cap L] \lt \infty$
. Note that
![]() $[LS \;:\; L] = [S \;:\; S \cap L] \lt \infty$
, it follows that
$[LS \;:\; L] = [S \;:\; S \cap L] \lt \infty$
, it follows that
![]() $LS$
is commensurable with
$LS$
is commensurable with
![]() $L$
, and as a consequence
$L$
, and as a consequence
![]() $S \leq LS \in{\mathcal G}$
, in particular it follows that
$S \leq LS \in{\mathcal G}$
, in particular it follows that
![]() $S \in{\mathcal G}$
. This proves the claim. Since
$S \in{\mathcal G}$
. This proves the claim. Since
![]() ${\mathcal G}={\mathcal F}$
we have by [Reference Huang and Prytuła13, Proposition 7.3 and Definition 7.2] that
${\mathcal G}={\mathcal F}$
we have by [Reference Huang and Prytuła13, Proposition 7.3 and Definition 7.2] that
![]() $\textrm{cd}_{{\mathcal G}}(N_{G}[L])\leq \textrm{cd}(G)-m$
.
$\textrm{cd}_{{\mathcal G}}(N_{G}[L])\leq \textrm{cd}(G)-m$
.
We now prove the item
![]() $(2)$
. Applying the cohomological version of Proposition 2.11 (see Remark 2.14) to the inclusion of families
$(2)$
. Applying the cohomological version of Proposition 2.11 (see Remark 2.14) to the inclusion of families
![]() $({\mathcal G}\cap{\mathcal F}_{m-1}) \subset{\mathcal G}$
we get
$({\mathcal G}\cap{\mathcal F}_{m-1}) \subset{\mathcal G}$
we get
for some
![]() $d$
such that for any
$d$
such that for any
![]() $K\in{\mathcal G}$
we have
$K\in{\mathcal G}$
we have
![]() $\textrm{cd}_{({\mathcal G}\cap{\mathcal F}_{m-1})\cap K}(K)\leq d$
. Since we already proved
$\textrm{cd}_{({\mathcal G}\cap{\mathcal F}_{m-1})\cap K}(K)\leq d$
. Since we already proved
![]() $\textrm{cd}_{{\mathcal G}}(N_{G}[L])\leq \textrm{cd}(G)-m$
, our next task is to show that
$\textrm{cd}_{{\mathcal G}}(N_{G}[L])\leq \textrm{cd}(G)-m$
, our next task is to show that
![]() $d$
can be chosen to be equal to
$d$
can be chosen to be equal to
![]() $2m-1$
.
$2m-1$
.
Recall that any
![]() $K\in{\mathcal G}$
is virtually
$K\in{\mathcal G}$
is virtually
![]() $\mathbb{Z}^t$
for some
$\mathbb{Z}^t$
for some
![]() $0\leq t \leq m$
. We split our proof into two cases. First assume that
$0\leq t \leq m$
. We split our proof into two cases. First assume that
![]() $K\in{\mathcal G}$
is virtually
$K\in{\mathcal G}$
is virtually
![]() $\mathbb{Z}^t$
for some
$\mathbb{Z}^t$
for some
![]() $0\leq t \leq m-1$
. Hence
$0\leq t \leq m-1$
. Hence
![]() $K$
belongs to
$K$
belongs to
![]() ${\mathcal F}_{m-1}$
, it follows that
${\mathcal F}_{m-1}$
, it follows that
![]() $K$
belongs to
$K$
belongs to
![]() ${\mathcal G} \cap{\mathcal F}_{m-1}$
and we conclude
${\mathcal G} \cap{\mathcal F}_{m-1}$
and we conclude
![]() $\textrm{cd}_{{\mathcal G} \cap{\mathcal F}_{m-1}\cap K}(K)=0$
. Now assume
$\textrm{cd}_{{\mathcal G} \cap{\mathcal F}_{m-1}\cap K}(K)=0$
. Now assume
![]() $K\in{\mathcal G}$
is virtually
$K\in{\mathcal G}$
is virtually
![]() $\mathbb{Z}^{m}$
. We claim that
$\mathbb{Z}^{m}$
. We claim that
![]() $({\mathcal G} \cap{\mathcal F}_{m-1})\cap K={\mathcal F}_{m-1}\cap K$
. The inclusion
$({\mathcal G} \cap{\mathcal F}_{m-1})\cap K={\mathcal F}_{m-1}\cap K$
. The inclusion
![]() $({\mathcal G} \cap{\mathcal F}_{m-1})\cap K \subset{\mathcal F}_{m-1}\cap K$
is clear. For the other inclusion let
$({\mathcal G} \cap{\mathcal F}_{m-1})\cap K \subset{\mathcal F}_{m-1}\cap K$
is clear. For the other inclusion let
![]() $M\in{\mathcal F}_{m-1}\cap K$
. Since
$M\in{\mathcal F}_{m-1}\cap K$
. Since
![]() $M\leq K\in{\mathcal G}$
, therefore
$M\leq K\in{\mathcal G}$
, therefore
![]() $M\in ({\mathcal G} \cap{\mathcal F}_{m-1})\cap K$
. This establishes the claim. We conclude that
$M\in ({\mathcal G} \cap{\mathcal F}_{m-1})\cap K$
. This establishes the claim. We conclude that
where the inequality follows from [Reference Rolland, Álvarez and Saldaña23, Proposition 1.3].
Theorem 4.7.
Let
![]() $G$
be a right-angled Artin group. Then for
$G$
be a right-angled Artin group. Then for
![]() $0 \leq k \lt \textrm{cd}(G)$
we have
$0 \leq k \lt \textrm{cd}(G)$
we have
![]() $ \textrm{cd}_{{\mathcal F}_k}(G)=\textrm{cd}(G)+k$
.
$ \textrm{cd}_{{\mathcal F}_k}(G)=\textrm{cd}(G)+k$
.
Proof. By Theorem 4.6, we have
![]() $\textrm{cd}_{{\mathcal F}_k}(G)\leq \textrm{cd}(G)+k$
. On the other hand, by Lemma 4.5
$\textrm{cd}_{{\mathcal F}_k}(G)\leq \textrm{cd}(G)+k$
. On the other hand, by Lemma 4.5
![]() $G$
has a subgroup isomorphic to
$G$
has a subgroup isomorphic to
![]() $\mathbb{Z}^{\textrm{cd}(G)}$
, then the claim it follows from Corollary 1.2.
$\mathbb{Z}^{\textrm{cd}(G)}$
, then the claim it follows from Corollary 1.2.
Theorem 4.8.
Let
![]() $G$
be a right-angled Artin group. Then for
$G$
be a right-angled Artin group. Then for
![]() $0 \leq k \lt \textrm{cd}(G)$
we have
$0 \leq k \lt \textrm{cd}(G)$
we have
![]() $ \textrm{gd}_{{\mathcal F}_k}(G)= \textrm{cd}_{{\mathcal F}_k}(G)$
.
$ \textrm{gd}_{{\mathcal F}_k}(G)= \textrm{cd}_{{\mathcal F}_k}(G)$
.
Proof. If
![]() $k=0$
the claim follows from Lemma 4.5. Suppose that
$k=0$
the claim follows from Lemma 4.5. Suppose that
![]() $k\geq 1$
, hence by hypothesis,
$k\geq 1$
, hence by hypothesis,
![]() $\textrm{cd}(G)\geq 2$
. By Theorem 4.7, we have
$\textrm{cd}(G)\geq 2$
. By Theorem 4.7, we have
![]() $\textrm{cd}_{{\mathcal F}_k}(G)\geq 3$
, then by Theorem 2.13,
$\textrm{cd}_{{\mathcal F}_k}(G)\geq 3$
, then by Theorem 2.13,
![]() $\textrm{gd}_{{\mathcal F}_k}(G)= \textrm{cd}_{{\mathcal F}_k}(G)$
.
$\textrm{gd}_{{\mathcal F}_k}(G)= \textrm{cd}_{{\mathcal F}_k}(G)$
.
Given a fixed right-angled Artin group
![]() $A_{\Gamma }$
, we denote by
$A_{\Gamma }$
, we denote by
![]() ${\textrm{Aut}}(A_\Gamma )$
the group of automorphisms of
${\textrm{Aut}}(A_\Gamma )$
the group of automorphisms of
![]() $A_\Gamma$
and by
$A_\Gamma$
and by
![]() $\textrm{Inn}(A_\Gamma )$
the subgroup consisting of inner automorphisms. The outer automorphism group of
$\textrm{Inn}(A_\Gamma )$
the subgroup consisting of inner automorphisms. The outer automorphism group of
![]() $A_\Gamma$
is defined as the quotient
$A_\Gamma$
is defined as the quotient
![]() $\textrm{Out}(A_\Gamma )={\textrm{Aut}}(A_\Gamma )/\textrm{Inn}(A_\Gamma )$
. If
$\textrm{Out}(A_\Gamma )={\textrm{Aut}}(A_\Gamma )/\textrm{Inn}(A_\Gamma )$
. If
![]() $S\subseteq V(\Gamma )$
, then the subgroup
$S\subseteq V(\Gamma )$
, then the subgroup
![]() $H$
generated by
$H$
generated by
![]() $S$
is called a special subgroup of
$S$
is called a special subgroup of
![]() $A_\Gamma$
. It can be proven that, in fact,
$A_\Gamma$
. It can be proven that, in fact,
![]() $H$
is the right-angled Artin group
$H$
is the right-angled Artin group
![]() $A_S$
associated with the full subgraph induced by
$A_S$
associated with the full subgraph induced by
![]() $S$
in
$S$
in
![]() $\Gamma$
.
$\Gamma$
.
If
![]() $\Delta$
is a full subgraph of
$\Delta$
is a full subgraph of
![]() $\Gamma$
, we denote by
$\Gamma$
, we denote by
![]() $A_{\Delta }$
the special subgroup generated by the vertices contained in
$A_{\Delta }$
the special subgroup generated by the vertices contained in
![]() $\Delta$
. An outer automorphism
$\Delta$
. An outer automorphism
![]() $F$
of
$F$
of
![]() $A_\Gamma$
preserves
$A_\Gamma$
preserves
![]() $A_\Delta$
if there exists a representative
$A_\Delta$
if there exists a representative
![]() $f\in F$
that restricts to an automorphism of
$f\in F$
that restricts to an automorphism of
![]() $A_\Delta$
. An outer automorphism
$A_\Delta$
. An outer automorphism
![]() $F$
acts trivially on
$F$
acts trivially on
![]() $A_{\Delta }$
if there exists representative
$A_{\Delta }$
if there exists representative
![]() $f\in F$
that acts as the identity on
$f\in F$
that acts as the identity on
![]() $A_\Delta$
.
$A_\Delta$
.
Definition 4.9.
Let
![]() $\mathcal G$
,
$\mathcal G$
,
![]() $\mathcal H$
be two collections of special subgroups of
$\mathcal H$
be two collections of special subgroups of
![]() $A_\Gamma$
. The relative outer automorphism group
$A_\Gamma$
. The relative outer automorphism group
![]() $\textrm{Out}(A_{\Gamma };\;{\mathcal G},{\mathcal H}^t)$
consists of automorphisms that preserve each
$\textrm{Out}(A_{\Gamma };\;{\mathcal G},{\mathcal H}^t)$
consists of automorphisms that preserve each
![]() $A_\Delta \in{\mathcal G}$
and act trivially on each
$A_\Delta \in{\mathcal G}$
and act trivially on each
![]() $A_\Delta \in{\mathcal H}.$
$A_\Delta \in{\mathcal H}.$
Proposition 4.10.
Let
![]() $A_{\Gamma }=A_{\Delta _1}*A_{\Delta _1}*\cdots *A_{\Delta _k}*F_n$
be a free factor decomposition of a right-angled Artin group with
$A_{\Gamma }=A_{\Delta _1}*A_{\Delta _1}*\cdots *A_{\Delta _k}*F_n$
be a free factor decomposition of a right-angled Artin group with
![]() $k\geq 1$
. Then
$k\geq 1$
. Then
![]() $\textrm{gd}_{{\mathcal F}_k}(\textrm{Out}(A_{\Gamma };\; \{A_{\Delta _i}\}^{t}))\geq \textrm{vcd}(\textrm{Out}(A_{\Gamma };\; \{A_{\Delta _i}\}^{t}))+k$
for all
$\textrm{gd}_{{\mathcal F}_k}(\textrm{Out}(A_{\Gamma };\; \{A_{\Delta _i}\}^{t}))\geq \textrm{vcd}(\textrm{Out}(A_{\Gamma };\; \{A_{\Delta _i}\}^{t}))+k$
for all
![]() $0\leq k\lt \textrm{vcd}(\textrm{Out}(A_{\Gamma };\; \{A_{\Delta _i}\}^{t})).$
$0\leq k\lt \textrm{vcd}(\textrm{Out}(A_{\Gamma };\; \{A_{\Delta _i}\}^{t})).$
Proof. By [Reference Day and Wade9, Theorem A]
![]() $\textrm{Out}(A_{\Gamma };\; \{A_{\Delta _i}\}^{t})$
has a free abelian subgroup of
$\textrm{Out}(A_{\Gamma };\; \{A_{\Delta _i}\}^{t})$
has a free abelian subgroup of
![]() $\textrm{rank}$
equal to
$\textrm{rank}$
equal to
![]() $\textrm{vcd}(\textrm{Out}(A_{\Gamma };\; \{A_{\Delta _i}\}^{t}))$
. The inequality follows from Corollary 1.2.
$\textrm{vcd}(\textrm{Out}(A_{\Gamma };\; \{A_{\Delta _i}\}^{t}))$
. The inequality follows from Corollary 1.2.
Let
![]() $F_n$
be the free group in
$F_n$
be the free group in
![]() $n$
generators. The group
$n$
generators. The group
![]() $F_n$
can be seen as the RAAG associated with the graph that has
$F_n$
can be seen as the RAAG associated with the graph that has
![]() $n$
vertices and no edges. In [Reference Culler and Vogtmann6] was proved that
$n$
vertices and no edges. In [Reference Culler and Vogtmann6] was proved that
![]() $\textrm{vcd}(\textrm{Out}(F_n))=2n-3$
for
$\textrm{vcd}(\textrm{Out}(F_n))=2n-3$
for
![]() $n\geq 2$
and that
$n\geq 2$
and that
![]() $\textrm{Out}(F_n)$
has a subgroup ismorphic to
$\textrm{Out}(F_n)$
has a subgroup ismorphic to
![]() $\mathbb{Z}^{\textrm{vcd}(\textrm{Out}(F_n))}$
. From Corollary 1.2, we get the following
$\mathbb{Z}^{\textrm{vcd}(\textrm{Out}(F_n))}$
. From Corollary 1.2, we get the following
Proposition 4.11.
Let
![]() $n\geq 2$
. Let
$n\geq 2$
. Let
![]() $F_n$
be the free group in
$F_n$
be the free group in
![]() $n$
generators. Then
$n$
generators. Then
![]() $\textrm{gd}_{{\mathcal F}_k}(\textrm{Out}(F_n))\geq 2n+k-3$
for all
$\textrm{gd}_{{\mathcal F}_k}(\textrm{Out}(F_n))\geq 2n+k-3$
for all
![]() $0\leq k\lt 2n-3$
.
$0\leq k\lt 2n-3$
.
Let
![]() $A_d$
be the right-angled Artin group given by a string of
$A_d$
be the right-angled Artin group given by a string of
![]() $d$
diamonds. In [Reference Degrijse and Petrosyan10, Proposition 6.5] was proved that
$d$
diamonds. In [Reference Degrijse and Petrosyan10, Proposition 6.5] was proved that
![]() $\textrm{vcd}(Out(A_d))=4d-1$
and
$\textrm{vcd}(Out(A_d))=4d-1$
and
![]() $Out(A_d)$
has a subgroup isomorphic to
$Out(A_d)$
has a subgroup isomorphic to
![]() $\mathbb{Z}^{\textrm{vcd}(\textrm{Out}(A_d))}$
, from Corollary 1.2 we have
$\mathbb{Z}^{\textrm{vcd}(\textrm{Out}(A_d))}$
, from Corollary 1.2 we have
Proposition 4.12.
Let
![]() $A_d$
be the right-angled Artin group given by a string of
$A_d$
be the right-angled Artin group given by a string of
![]() $d$
diamonds. Then
$d$
diamonds. Then
![]() $\textrm{gd}_{{\mathcal F}_k}(\textrm{Out}(A_d))\geq 4d +k-1$
for all
$\textrm{gd}_{{\mathcal F}_k}(\textrm{Out}(A_d))\geq 4d +k-1$
for all
![]() $0\leq k\lt 4d-1$
.
$0\leq k\lt 4d-1$
.
4.3. The
 ${\mathcal F}_k$
-geometric dimension for graphs of groups of finitely generated virtually abelian groups
${\mathcal F}_k$
-geometric dimension for graphs of groups of finitely generated virtually abelian groups
The objective of this section is to explicitly calculate the
![]() ${\mathcal F}_n$
-geometric dimension of the fundamental group of a graph of groups whose vertex groups are finitely generated virtually abelian groups, and whose edge groups are finite groups.
${\mathcal F}_n$
-geometric dimension of the fundamental group of a graph of groups whose vertex groups are finitely generated virtually abelian groups, and whose edge groups are finite groups.
Bass–Serre theory
We recall some basic notions about Bass–Serre theory, for further details see [Reference Saldaña24]. A graph of groups
![]() $\mathbf{Y}$
consists of a graph
$\mathbf{Y}$
consists of a graph
![]() $Y$
, a group
$Y$
, a group
![]() $Y_v$
for each
$Y_v$
for each
![]() $v\in V(Y)$
, and a group
$v\in V(Y)$
, and a group
![]() $Y_e$
for each
$Y_e$
for each
![]() $e=\{v,w\}\in E(Y)$
, together with monomorphisms
$e=\{v,w\}\in E(Y)$
, together with monomorphisms
![]() $\varphi \colon Y_e \to Y_{i}$
$\varphi \colon Y_e \to Y_{i}$
![]() $i=v,w$
.
$i=v,w$
.
Given a graph of groups
![]() $\mathbf{Y}$
, one of the classic theorems of Bass–Serre theory provides the existence of a group
$\mathbf{Y}$
, one of the classic theorems of Bass–Serre theory provides the existence of a group
![]() $G=\pi _1(\mathbf{Y})$
, called the fundamental group of the graph of groups
$G=\pi _1(\mathbf{Y})$
, called the fundamental group of the graph of groups
![]() $\mathbf{Y}$
and the tree
$\mathbf{Y}$
and the tree
![]() $T$
(a graph with no cycles), called the Bass–Serre tree of
$T$
(a graph with no cycles), called the Bass–Serre tree of
![]() $\mathbf{Y}$
, such that
$\mathbf{Y}$
, such that
![]() $G$
acts on
$G$
acts on
![]() $T$
without inversions, and the induced graph of groups is isomorphic to
$T$
without inversions, and the induced graph of groups is isomorphic to
![]() $\mathbf{Y}$
. The identification
$\mathbf{Y}$
. The identification
![]() $G=\pi _1(\mathbf{Y})$
is called a splitting of
$G=\pi _1(\mathbf{Y})$
is called a splitting of
![]() $G$
.
$G$
.
Definition 4.13.
Let
![]() $Y$
be a graph of groups with fundamental group
$Y$
be a graph of groups with fundamental group
![]() $G$
. The splitting
$G$
. The splitting
![]() $G=\pi _1(Y)$
is acylindrical if there is an integer
$G=\pi _1(Y)$
is acylindrical if there is an integer
![]() $k$
such that, for every path
$k$
such that, for every path
![]() $\gamma$
of length
$\gamma$
of length
![]() $k$
in the Bass–Serre tree
$k$
in the Bass–Serre tree
![]() $T$
of
$T$
of
![]() $Y$
, the stabilizer of
$Y$
, the stabilizer of
![]() $\gamma$
is finite.
$\gamma$
is finite.
Recall a geodesic line of a simplicial tree
![]() $T$
, is a simplicial embedding of
$T$
, is a simplicial embedding of
![]() $\mathbb{R}$
in
$\mathbb{R}$
in
![]() $T$
, where
$T$
, where
![]() $\mathbb{R}$
has as vertex set
$\mathbb{R}$
has as vertex set
![]() $\mathbb{Z}$
and an edge joining any two consecutive integers.
$\mathbb{Z}$
and an edge joining any two consecutive integers.
Theorem 4.14 ([Reference Lück16], Theorem 6.3). Let
![]() $Y$
be a graph of groups with finitely generated fundamental group
$Y$
be a graph of groups with finitely generated fundamental group
![]() $G$
and Bass–Serre tree
$G$
and Bass–Serre tree
![]() $T$
. Consider the collection
$T$
. Consider the collection
![]() $\mathcal{A}$
of all the geodesics of
$\mathcal{A}$
of all the geodesics of
![]() $T$
that admit a co-compact action of an infinite virtually cyclic subgroup of
$T$
that admit a co-compact action of an infinite virtually cyclic subgroup of
![]() $G$
. Then the space
$G$
. Then the space
![]() $\widetilde{T}$
given by the following homotopy
$\widetilde{T}$
given by the following homotopy
![]() $G$
-push-out
$G$
-push-out

is a model
![]() $\widetilde{T}$
for
$\widetilde{T}$
for
![]() $E_{\textrm{Iso}_{G}(\widetilde{T})}G$
where
$E_{\textrm{Iso}_{G}(\widetilde{T})}G$
where
![]() $\textrm{Iso}_{G}(\widetilde{T})$
is the family generated by the isotropy groups of
$\textrm{Iso}_{G}(\widetilde{T})$
is the family generated by the isotropy groups of
![]() $\widetilde{T}$
, i.e., by coning-off on
$\widetilde{T}$
, i.e., by coning-off on
![]() $T$
the geodesics in
$T$
the geodesics in
![]() $\mathcal{A}$
we obtain a model for
$\mathcal{A}$
we obtain a model for
![]() $E_{\textrm{Iso}_{G}(\widetilde{T})}G$
. Moreover, if the splitting
$E_{\textrm{Iso}_{G}(\widetilde{T})}G$
. Moreover, if the splitting
![]() $G=\pi _1(Y)$
is acylindrical, then the family
$G=\pi _1(Y)$
is acylindrical, then the family
![]() $\textrm{Iso}_{G}(\widetilde{T})$
contains the family
$\textrm{Iso}_{G}(\widetilde{T})$
contains the family
![]() ${\mathcal F}_n$
of
${\mathcal F}_n$
of
![]() $G$
for all
$G$
for all
![]() $n\ge 0$
.
$n\ge 0$
.
The following theorem is mild generalization of [Reference Lück16, Proposition 7.4]. We include a proof for the sake of completeness.

Figure 1. Promoting
![]() $T$
to
$T$
to
![]() $\tilde{T}$
.
$\tilde{T}$
.
Theorem 4.15.
Let
![]() $Y$
be a graph of groups with finitely generated fundamental group
$Y$
be a graph of groups with finitely generated fundamental group
![]() $G$
and Bass–Serre tree
$G$
and Bass–Serre tree
![]() $T$
. Suppose that the splitting of
$T$
. Suppose that the splitting of
![]() $G$
is acylindrical. Then for all
$G$
is acylindrical. Then for all
![]() $k\geq 1$
we have
$k\geq 1$
we have
and
Proof. For each
![]() $s\in V(Y)\cup E(Y)$
we have that
$s\in V(Y)\cup E(Y)$
we have that
![]() $G_s$
is a subgroup of
$G_s$
is a subgroup of
![]() $G$
, then the first inequality follows. Now we prove the second inequality. The splitting of
$G$
, then the first inequality follows. Now we prove the second inequality. The splitting of
![]() $G$
is acylindrical, then we can use Theorem 4.14 to obtain a 2-dimensional space
$G$
is acylindrical, then we can use Theorem 4.14 to obtain a 2-dimensional space
![]() $\widetilde{T}$
that is obtained from
$\widetilde{T}$
that is obtained from
![]() $T$
coning-off some geodesics of
$T$
coning-off some geodesics of
![]() $T$
, see Figure 1, the space
$T$
, see Figure 1, the space
![]() $\widetilde{T}$
is a model for
$\widetilde{T}$
is a model for
![]() $E_{\textrm{Iso}_{G}(\widetilde{T})}G$
and
$E_{\textrm{Iso}_{G}(\widetilde{T})}G$
and
![]() ${\mathcal F}_k\subseteq \textrm{Iso}_{G}(\widetilde{T})$
. By Proposition 2.12, we have
${\mathcal F}_k\subseteq \textrm{Iso}_{G}(\widetilde{T})$
. By Proposition 2.12, we have
Let
![]() $\sigma$
be a cell of
$\sigma$
be a cell of
![]() $\widetilde{T}$
, we compute
$\widetilde{T}$
, we compute
![]() $\textrm{gd}_{{\mathcal F}_k\cap G_\sigma }(G_{\sigma })+\dim (\sigma )$
.
$\textrm{gd}_{{\mathcal F}_k\cap G_\sigma }(G_{\sigma })+\dim (\sigma )$
.
-
• If
 $\sigma$
is 0-cell, we have two cases
$\sigma$
is 0-cell, we have two cases
 $\sigma \in T$
or
$\sigma \in T$
or
 $\sigma \in \widetilde{T}-T$
, in the first case we have
$\sigma \in \widetilde{T}-T$
, in the first case we have
 $G_\sigma =G_v$
for some
$G_\sigma =G_v$
for some
 $v\in V(Y)$
, in the other case we have
$v\in V(Y)$
, in the other case we have
 $G_\sigma$
is virtually cyclic, then
$G_\sigma$
is virtually cyclic, then
 $\textrm{gd}_{{\mathcal F}_k\cap G_\sigma }(G_{\sigma })+\dim (\sigma )= \textrm{gd}_{{\mathcal F}_k\cap G_v}(G_v)$
or
$\textrm{gd}_{{\mathcal F}_k\cap G_\sigma }(G_{\sigma })+\dim (\sigma )= \textrm{gd}_{{\mathcal F}_k\cap G_v}(G_v)$
or
 $0$
.
$0$
. -
• If
 $\sigma$
is 1-cell, we have two cases
$\sigma$
is 1-cell, we have two cases
 $\sigma \in T$
or
$\sigma \in T$
or
 $\sigma$
has a vertex in
$\sigma$
has a vertex in
 $\widetilde{T}-T$
, in the first case we have
$\widetilde{T}-T$
, in the first case we have
 $G_\sigma =G_e$
for some
$G_\sigma =G_e$
for some
 $e\in E(Y)$
, in the other case we have
$e\in E(Y)$
, in the other case we have
 $G_\sigma$
is virtually cyclic, then
$G_\sigma$
is virtually cyclic, then
 $\textrm{gd}_{{\mathcal F}_k\cap G_\sigma }(G_{\sigma })+\dim (\sigma )= \textrm{gd}_{{\mathcal F}_k\cap G_e}(G_e)+1$
or
$\textrm{gd}_{{\mathcal F}_k\cap G_\sigma }(G_{\sigma })+\dim (\sigma )= \textrm{gd}_{{\mathcal F}_k\cap G_e}(G_e)+1$
or
 $1$
.
$1$
. -
• If
 $\sigma$
is 2-cell, then
$\sigma$
is 2-cell, then
 $\sigma$
has a vertex in
$\sigma$
has a vertex in
 $\widetilde{T}-T$
, then
$\widetilde{T}-T$
, then
 $G_\sigma$
is virtually cyclic, it follows that
$G_\sigma$
is virtually cyclic, it follows that
 $\textrm{gd}_{{\mathcal F}_k\cap G_\sigma }(G_{\sigma })+\dim (\sigma )= 2$
.
$\textrm{gd}_{{\mathcal F}_k\cap G_\sigma }(G_{\sigma })+\dim (\sigma )= 2$
.
The inequality follows.
Proposition 4.16.
Let
![]() $Y$
be a finite graph of groups such that for each
$Y$
be a finite graph of groups such that for each
![]() $v\in V(Y)$
the group
$v\in V(Y)$
the group
![]() $G_v$
is infinite finitely generated virtually abelian, with
$G_v$
is infinite finitely generated virtually abelian, with
![]() $\textrm{rank}(G_e)\lt \textrm{rank}(G_v)$
. Suppose that the splitting of
$\textrm{rank}(G_e)\lt \textrm{rank}(G_v)$
. Suppose that the splitting of
![]() $G=\pi _1(Y)$
is acylindrical. Let
$G=\pi _1(Y)$
is acylindrical. Let
![]() $m=\max \{\textrm{rank}(G_v)| v\in V(Y) \}$
. Then for
$m=\max \{\textrm{rank}(G_v)| v\in V(Y) \}$
. Then for
![]() $1\leq k\lt m$
we have
$1\leq k\lt m$
we have
![]() $\textrm{gd}_{{\mathcal F}_k}(G)=m+k.$
$\textrm{gd}_{{\mathcal F}_k}(G)=m+k.$
Proof. First, we prove that
![]() $\textrm{gd}_{{\mathcal F}_k}(G)\geq m+k$
. The splitting of
$\textrm{gd}_{{\mathcal F}_k}(G)\geq m+k$
. The splitting of
![]() $G$
is acylindrical, then by Theorem 4.15 we have
$G$
is acylindrical, then by Theorem 4.15 we have
 \begin{align*} \begin{split} \textrm{gd}_{{\mathcal F}_k}(G) & \geq \max \{ \textrm{gd}_{{\mathcal F}_k\cap G_v}(G_v), \textrm{gd}_{{\mathcal F}_k\cap G_e}(G_e)| v\in V(Y), e\in E(Y)\}\\ & \geq \max \{ \textrm{rank}(G_v)+k, \textrm{rank}(G_e)+k| v\in V(Y), e\in E(Y)\}, \text{ from Corollary 1.2}\\ &= \max \{ \textrm{rank}(G_v)+k| v\in V(Y)\}, \textrm{rank}(G_e)\leq \textrm{rank}(G_v)\\ &=m+k. \end{split} \end{align*}
\begin{align*} \begin{split} \textrm{gd}_{{\mathcal F}_k}(G) & \geq \max \{ \textrm{gd}_{{\mathcal F}_k\cap G_v}(G_v), \textrm{gd}_{{\mathcal F}_k\cap G_e}(G_e)| v\in V(Y), e\in E(Y)\}\\ & \geq \max \{ \textrm{rank}(G_v)+k, \textrm{rank}(G_e)+k| v\in V(Y), e\in E(Y)\}, \text{ from Corollary 1.2}\\ &= \max \{ \textrm{rank}(G_v)+k| v\in V(Y)\}, \textrm{rank}(G_e)\leq \textrm{rank}(G_v)\\ &=m+k. \end{split} \end{align*}
Also by Theorem 4.15, we have
 \begin{align*} \begin{split} \textrm{gd}_{{\mathcal F}_k}(G)&\leq \max \{ 2, \textrm{gd}_{{\mathcal F}_k\cap G_v}(G_v), \textrm{gd}_{{\mathcal F}_k\cap G_e}(G_e)+1| v\in V(Y), e\in E(Y)\}\\ &= \max \{ 2, \textrm{rank}(G_v)+k, \textrm{rank}(G_e)+k+1 | v\in V(Y), e\in E(Y)\}, \text{ from Theorem 1.1}\\ &= \max \{ \textrm{rank}(G_v)+k | v\in V(Y)\}, \textrm{rank}(G_e)\lt \textrm{rank}(G_v)\ \textrm{and}\ k\geq 1\\ &=m+k. \end{split} \end{align*}
\begin{align*} \begin{split} \textrm{gd}_{{\mathcal F}_k}(G)&\leq \max \{ 2, \textrm{gd}_{{\mathcal F}_k\cap G_v}(G_v), \textrm{gd}_{{\mathcal F}_k\cap G_e}(G_e)+1| v\in V(Y), e\in E(Y)\}\\ &= \max \{ 2, \textrm{rank}(G_v)+k, \textrm{rank}(G_e)+k+1 | v\in V(Y), e\in E(Y)\}, \text{ from Theorem 1.1}\\ &= \max \{ \textrm{rank}(G_v)+k | v\in V(Y)\}, \textrm{rank}(G_e)\lt \textrm{rank}(G_v)\ \textrm{and}\ k\geq 1\\ &=m+k. \end{split} \end{align*}
Corollary 4.17.
Let
![]() $Y$
be a finite graph of groups such that for each
$Y$
be a finite graph of groups such that for each
![]() $v\in V(Y)$
the group
$v\in V(Y)$
the group
![]() $G_v$
is infinite finitely generated virtually abelian, and for each
$G_v$
is infinite finitely generated virtually abelian, and for each
![]() $e\in E(Y)$
the group
$e\in E(Y)$
the group
![]() $G_e$
is a finite group.
$G_e$
is a finite group.
Let
![]() $m=\max \{rank(G_v)| v\in V(Y) \}$
. Then for
$m=\max \{rank(G_v)| v\in V(Y) \}$
. Then for
![]() $1\leq k\lt m$
we have
$1\leq k\lt m$
we have
![]() $\textrm{gd}_{{\mathcal F}_k}(G)=m+k.$
$\textrm{gd}_{{\mathcal F}_k}(G)=m+k.$
Acknowledgements
I was supported by a doctoral scholarship of the Mexican Council of Humanities, Science and Technology (CONAHCyT). I would like to thank Luis Jorge Sánchez Saldaña for several useful discussions during the preparation of this article. I also thank Rita Jiménez Rolland for comments on a draft of the present article. I am grateful for the financial support of DGAPA-UNAM grant PAPIIT IA106923 and CONACyT grant CF 2019-217392. I thank the anonymous referee for corrections and comments that improved the exposition.