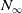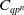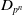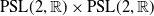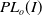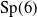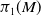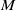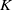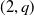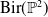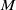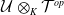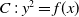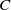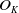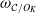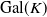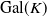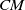FirstView articles
Research Article
On a weighted anisotropic eigenvalue problem
- Part of:
-
- Published online by Cambridge University Press:
- 17 October 2024, pp. 1-14
-
- Article
-
- You have access
- HTML
- Export citation
Classification of multiplication modules over multiplication rings with finitely many minimal primes
- Part of:
-
- Published online by Cambridge University Press:
- 03 October 2024, pp. 1-5
-
- Article
-
- You have access
- HTML
- Export citation
The combinatorics of
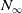 $N_\infty$ operads for
$N_\infty$ operads for 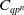 $C_{qp^n}$ and
$C_{qp^n}$ and 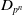 $D_{p^n}$
$D_{p^n}$
-
- Published online by Cambridge University Press:
- 03 October 2024, pp. 1-17
-
- Article
-
- You have access
- HTML
- Export citation
Volume and Euler classes in bounded cohomology of transformation groups
- Part of:
-
- Published online by Cambridge University Press:
- 02 October 2024, pp. 1-16
-
- Article
-
- You have access
- HTML
- Export citation
Weyl chamber length compactification of the
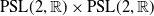 $\textrm{PSL}(2,{\mathbb{R}})\times \textrm{PSL}(2,{\mathbb{R}})$ maximal character variety
$\textrm{PSL}(2,{\mathbb{R}})\times \textrm{PSL}(2,{\mathbb{R}})$ maximal character variety
- Part of:
-
- Published online by Cambridge University Press:
- 27 September 2024, pp. 1-23
-
- Article
-
- You have access
- HTML
- Export citation
Stereographic compactification and affine bi-Lipschitz homeomorphisms
- Part of:
-
- Published online by Cambridge University Press:
- 16 May 2024, pp. 1-15
-
- Article
-
- You have access
- HTML
- Export citation
Girth Alternative for subgroups of
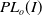 $PL_o(I)$
$PL_o(I)$
- Part of:
-
- Published online by Cambridge University Press:
- 09 May 2024, pp. 1-10
-
- Article
-
- You have access
- HTML
- Export citation
Thinness of some hypergeometric groups in
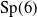 $\mathrm{Sp}(6)$
$\mathrm{Sp}(6)$
- Part of:
-
- Published online by Cambridge University Press:
- 02 May 2024, pp. 1-11
-
- Article
-
- You have access
- HTML
- Export citation
Simplicial volume of manifolds with amenable fundamental group at infinity
- Part of:
-
- Published online by Cambridge University Press:
- 22 April 2024, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximal subgroups of a family of iterated monodromy groups
- Part of:
-
- Published online by Cambridge University Press:
- 17 April 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Twisted Blanchfield pairings and twisted signatures III: Applications
- Part of:
-
- Published online by Cambridge University Press:
- 15 April 2024, pp. 1-40
-
- Article
-
- You have access
- HTML
- Export citation
A note on quantum K-theory of root constructions
- Part of:
-
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Galois points and Cremona transformations
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On almost quotient Yamabe solitons
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-15
-
- Article
-
- You have access
- HTML
- Export citation
Triangular matrix categories over quasi-hereditary categories
- Part of:
-
- Published online by Cambridge University Press:
- 21 March 2024, pp. 1-22
-
- Article
-
- You have access
- HTML
- Export citation
Models and integral differentials of hyperelliptic curves
- Part of:
-
- Published online by Cambridge University Press:
- 18 March 2024, pp. 1-58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Examples of hyperbolic spaces without the properties of quasi-ball or bounded eccentricity
- Part of:
-
- Published online by Cambridge University Press:
- 11 March 2024, pp. 1-9
-
- Article
-
- You have access
- HTML
- Export citation
On twisted group ring isomorphism problem for p-groups
- Part of:
-
- Published online by Cambridge University Press:
- 16 February 2024, pp. 1-14
-
- Article
-
- You have access
- HTML
- Export citation
Abelian absolute Galois groups: In Erinnerung an Wulf-Dieter Geyer (1939–2019)
- Part of:
-
- Published online by Cambridge University Press:
- 02 February 2024, pp. 1-9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kato’s main conjecture for potentially ordinary primes
- Part of:
-
- Published online by Cambridge University Press:
- 26 January 2024, pp. 1-21
-
- Article
-
- You have access
- HTML
- Export citation