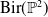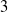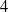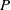1. Introduction
Let
![]() $k$
be an algebraically closed field. Let
$k$
be an algebraically closed field. Let
![]() $C$
be an irreducible plane curve in
$C$
be an irreducible plane curve in
![]() $\mathbb{P}^2$
. Giving a point
$\mathbb{P}^2$
. Giving a point
![]() $P\in \mathbb{P}^2$
, we consider the projection
$P\in \mathbb{P}^2$
, we consider the projection
![]() $\pi _P |_C\;:\; C\dashrightarrow \mathbb{P}^1$
, which is the restriction of the projection
$\pi _P |_C\;:\; C\dashrightarrow \mathbb{P}^1$
, which is the restriction of the projection
![]() $\pi _P\;:\;\mathbb{P}^2 \dashrightarrow \mathbb{P}^1$
with centre
$\pi _P\;:\;\mathbb{P}^2 \dashrightarrow \mathbb{P}^1$
with centre
![]() $P$
. Let
$P$
. Let
![]() $K_P = \pi ^*_P(k(\mathbb{P}^1))$
. If
$K_P = \pi ^*_P(k(\mathbb{P}^1))$
. If
![]() $P\in C$
$P\in C$
![]() $[$
resp.
$[$
resp.
![]() $P\notin C]$
, we say that
$P\notin C]$
, we say that
![]() $P$
is an inner [resp. outer] Galois point for
$P$
is an inner [resp. outer] Galois point for
![]() $C$
if
$C$
if
![]() $k(C)/K_{P}$
is Galois. In this case, we write
$k(C)/K_{P}$
is Galois. In this case, we write
![]() $G_{P}=\mathrm{Gal}(k(C)/K_P)$
and call it the Galois group at
$G_{P}=\mathrm{Gal}(k(C)/K_P)$
and call it the Galois group at
![]() $P$
. A de Jonquières map is a birational map
$P$
. A de Jonquières map is a birational map
![]() $\varphi$
for which there exist
$\varphi$
for which there exist
![]() $P\in \mathbb{P}^2$
such that
$P\in \mathbb{P}^2$
such that
![]() $\varphi$
preserves the pencil of lines passing through
$\varphi$
preserves the pencil of lines passing through
![]() $P$
. The group of a de Jonquières transformations preserving the pencil of lines passing through a given point
$P$
. The group of a de Jonquières transformations preserving the pencil of lines passing through a given point
![]() $P \in \mathbb{P}^2$
is denoted by
$P \in \mathbb{P}^2$
is denoted by
![]() $\mathrm{Jonq}_{P} \subset \mathrm{Bir}(\mathbb{P}^2)$
, this corresponding to ask that
$\mathrm{Jonq}_{P} \subset \mathrm{Bir}(\mathbb{P}^2)$
, this corresponding to ask that
![]() $\phi$
preserves a pencil of lines through the point
$\phi$
preserves a pencil of lines through the point
![]() $P$
. As in ref. [Reference Miura4], we are interested in the extension of elements of
$P$
. As in ref. [Reference Miura4], we are interested in the extension of elements of
![]() $G_P$
to
$G_P$
to
![]() $\mathrm{Bir}(\mathbb{P}^2)$
. There are two interesting questions:
$\mathrm{Bir}(\mathbb{P}^2)$
. There are two interesting questions:
Question 1.1.
If
![]() $P$
is Galois, does
$P$
is Galois, does
![]() $G_P$
extends to
$G_P$
extends to
![]() $\mathrm{Bir}(\mathbb{P}^2)$
?
$\mathrm{Bir}(\mathbb{P}^2)$
?
Question 1.2. [Reference Yoshihara8] If an element extends to
![]() $\mathrm{Bir}(\mathbb{P}^2)$
, does it extend to a de Jonquières map?
$\mathrm{Bir}(\mathbb{P}^2)$
, does it extend to a de Jonquières map?
![]() $i.e.$
to an element
$i.e.$
to an element
![]() $\varphi \in \mathrm{Bir}(\mathbb{P}^2)$
with
$\varphi \in \mathrm{Bir}(\mathbb{P}^2)$
with
![]() $\pi _{P}\circ \varphi =\pi _P$
?
$\pi _{P}\circ \varphi =\pi _P$
?
Consider a point
![]() $P\in \mathbb{P}^2$
with multiplicity
$P\in \mathbb{P}^2$
with multiplicity
![]() $m_{P}$
on an irreducible plane curve
$m_{P}$
on an irreducible plane curve
![]() $C$
in
$C$
in
![]() $\mathbb{P}^2$
of degree
$\mathbb{P}^2$
of degree
![]() $d$
, we will show later that the extension
$d$
, we will show later that the extension
![]() $[k(C)\;:\;K_{P}]$
has degree
$[k(C)\;:\;K_{P}]$
has degree
![]() $d-m_{P}$
. Our first main result is the following theorem, that considers the case of degree
$d-m_{P}$
. Our first main result is the following theorem, that considers the case of degree
![]() $3$
.
$3$
.
Theorem A.
Let
![]() $P\in \mathbb{P}^2$
, let
$P\in \mathbb{P}^2$
, let
![]() $C\subset \mathbb{P}^2$
be an irreducible curve. If the extension
$C\subset \mathbb{P}^2$
be an irreducible curve. If the extension
![]() $k(C)/K_{P}$
is Galois of degree at most
$k(C)/K_{P}$
is Galois of degree at most
![]() $3$
, then
$3$
, then
![]() $G_{P}$
always extends to a subgroup of
$G_{P}$
always extends to a subgroup of
![]() $ \mathrm{Jonq}_{P}\subseteq \mathrm{Bir}(\mathbb{P}^2)$
.
$ \mathrm{Jonq}_{P}\subseteq \mathrm{Bir}(\mathbb{P}^2)$
.
Theorem A resulted from Theorem 3.2, which provides more information on the Galois extensions of degree at most
![]() $3$
and the related Galois Groups at a point
$3$
and the related Galois Groups at a point
![]() $P$
. This encourages us to study higher-degree Galois extensions and determine if their Galois groups
$P$
. This encourages us to study higher-degree Galois extensions and determine if their Galois groups
![]() $G_P$
can always be extended to
$G_P$
can always be extended to
![]() $\mathrm{Bir}(\mathbb{P}^2)$
as well as to the group of de Jonquières map with respect to
$\mathrm{Bir}(\mathbb{P}^2)$
as well as to the group of de Jonquières map with respect to
![]() $P$
. The following theorem gives a negative answer to Question 1.2.
$P$
. The following theorem gives a negative answer to Question 1.2.
Theorem B.
Let
![]() $k$
be a field of characteristic
$k$
be a field of characteristic
![]() $char(k)\neq 2$
containing a primitive fourth root of unity, and let
$char(k)\neq 2$
containing a primitive fourth root of unity, and let
![]() $C$
be the irreducible curve defined by the equation
$C$
be the irreducible curve defined by the equation
![]() $X^{4}-4 Z Y X^{2}-Z Y^{3}+2 Z^{2} Y^{2}-Y Z^{3} =0$
, then the point
$X^{4}-4 Z Y X^{2}-Z Y^{3}+2 Z^{2} Y^{2}-Y Z^{3} =0$
, then the point
![]() $P=[1\;:\;0\;:\;0]$
is an outer Galois point of
$P=[1\;:\;0\;:\;0]$
is an outer Galois point of
![]() $C$
and the extension induced by the projection
$C$
and the extension induced by the projection
![]() $\pi _P\;:\; C\dashrightarrow \mathbb{P}^1$
is Galois of degree
$\pi _P\;:\; C\dashrightarrow \mathbb{P}^1$
is Galois of degree
![]() $4$
. The group
$4$
. The group
![]() $G_{P}$
extends to
$G_{P}$
extends to
![]() $\mathrm{Bir}(\mathbb{P}^2)$
but not to
$\mathrm{Bir}(\mathbb{P}^2)$
but not to
![]() $\mathrm{Jonq}_{P}$
.
$\mathrm{Jonq}_{P}$
.
The following result gives a negative answer to Question 1.1 (see also [Reference Yoshihara8, Example 5]); it follows from Lemma 5.2.
Theorem C.
Let
![]() $k$
be a field with
$k$
be a field with
![]() $char(k)\neq 5$
that contains a primitive
$char(k)\neq 5$
that contains a primitive
![]() $5$
th root of unity, and let
$5$
th root of unity, and let
![]() $\phi \;:\;\mathbb{P}^1 \rightarrow \mathbb{P}^2$
given by
$\phi \;:\;\mathbb{P}^1 \rightarrow \mathbb{P}^2$
given by
![]() $\phi \;:\;[u\;:\;v]\mapsto [u v^6-u^7\;:\;u^5(u^2+v^2)\;:\; v^5(u^2+v^2)]$
. We define
$\phi \;:\;[u\;:\;v]\mapsto [u v^6-u^7\;:\;u^5(u^2+v^2)\;:\; v^5(u^2+v^2)]$
. We define
![]() $C\;:\!=\;\overline{\phi (\mathbb{P}^1)}$
which is an irreducible curve of
$C\;:\!=\;\overline{\phi (\mathbb{P}^1)}$
which is an irreducible curve of
![]() $\mathbb{P}^2$
, then the point
$\mathbb{P}^2$
, then the point
![]() $P=[1\;:\;0\;:\;0]$
is an inner Galois point of
$P=[1\;:\;0\;:\;0]$
is an inner Galois point of
![]() $C$
and the extension induced by the projection
$C$
and the extension induced by the projection
![]() $\pi _P\;:\; C\dashrightarrow \mathbb{P}^1$
is Galois of degree
$\pi _P\;:\; C\dashrightarrow \mathbb{P}^1$
is Galois of degree
![]() $5$
. Moreover, the identity is the only element of the Galois group that extends to
$5$
. Moreover, the identity is the only element of the Galois group that extends to
![]() $\mathrm{Bir}(\mathbb{P}^2)$
.
$\mathrm{Bir}(\mathbb{P}^2)$
.
Remark 1.3.
After this article was uploaded to the ArXiv, [Reference Miura5] was uploaded. Theorem 1 in [Reference Miura5] corresponds to the case
![]() $k=\mathbb{C}$
of Theorem A.
$k=\mathbb{C}$
of Theorem A.
2. Preliminaries
The concept of Galois points for irreducible plane curve
![]() $C\subset \mathbb{P}^2$
was introduced by [Reference Miura and Yoshihara6], [Reference Yoshihara8], [Reference Fukasawa1]. In order to study the extension of an element in
$C\subset \mathbb{P}^2$
was introduced by [Reference Miura and Yoshihara6], [Reference Yoshihara8], [Reference Fukasawa1]. In order to study the extension of an element in
![]() $G_P$
to
$G_P$
to
![]() $\mathrm{Bir}(\mathbb{P}^2)$
, we need the following lemma.
$\mathrm{Bir}(\mathbb{P}^2)$
, we need the following lemma.
Lemma 2.1.
The field extension
![]() $ k(\mathbb{P}^1) \hookrightarrow k(C)$
induced by
$ k(\mathbb{P}^1) \hookrightarrow k(C)$
induced by
![]() $\pi _P$
has degree
$\pi _P$
has degree
![]() $d-m_P$
, where
$d-m_P$
, where
![]() $m_P$
is the multiplicity of
$m_P$
is the multiplicity of
![]() $C$
at
$C$
at
![]() $P$
, and
$P$
, and
![]() $d$
is the degree of
$d$
is the degree of
![]() $C$
.
$C$
.
Proof. Let
![]() $F(X, Y, Z) = 0$
be the defining equation of
$F(X, Y, Z) = 0$
be the defining equation of
![]() $C$
of degree
$C$
of degree
![]() $d$
. We may fix
$d$
. We may fix
![]() $P=[1\;:\;0\;:\;0]\in \mathbb{P}^2$
and choose that
$P=[1\;:\;0\;:\;0]\in \mathbb{P}^2$
and choose that
![]() $C$
is not the line
$C$
is not the line
![]() $Z=0$
. Since
$Z=0$
. Since
![]() $P$
has multiplicity
$P$
has multiplicity
![]() $m_P$
, then the equation of
$m_P$
, then the equation of
![]() $C$
is
$C$
is
![]() $F(X,Y,Z)=F_{m_p}(Y,Z)X^{d-m_p}+\ldots \ldots +F_{d-1}(Y,Z)X+F_{d}(Y,Z)$
, where
$F(X,Y,Z)=F_{m_p}(Y,Z)X^{d-m_p}+\ldots \ldots +F_{d-1}(Y,Z)X+F_{d}(Y,Z)$
, where
![]() $F_i(Y,Z)$
is a homogeneous polynomial of
$F_i(Y,Z)$
is a homogeneous polynomial of
![]() $Y$
and
$Y$
and
![]() $Z$
of degree
$Z$
of degree
![]() $i\,(m_P\leq i\leq d)$
and
$i\,(m_P\leq i\leq d)$
and
![]() $F_{m_P}(Y,Z)\neq 0$
. Since
$F_{m_P}(Y,Z)\neq 0$
. Since
![]() $F(X,Y,Z)$
is irreducible in
$F(X,Y,Z)$
is irreducible in
![]() $k[X,Y,Z]$
and not a multiple of
$k[X,Y,Z]$
and not a multiple of
![]() $Z$
, then
$Z$
, then
![]() $f=F(X,Y,1)\in k[X,Y]$
is also irreducible in
$f=F(X,Y,1)\in k[X,Y]$
is also irreducible in
![]() $k[X,Y]$
. We can see
$k[X,Y]$
. We can see
![]() $f$
as an irreducible polynomial in
$f$
as an irreducible polynomial in
![]() $\tilde{k}[X]$
with
$\tilde{k}[X]$
with
![]() $deg_{X}(f)=d-m_P$
where
$deg_{X}(f)=d-m_P$
where
![]() $\tilde{k}=k(Y)$
. Hence, the extension
$\tilde{k}=k(Y)$
. Hence, the extension
![]() $k(C)/K_{P}$
is isomorphic to
$k(C)/K_{P}$
is isomorphic to
![]() $(k(Y)[X]/(f))/(k(Y))$
, and thus, it has the same degree equal to the degree of the irreducible polynomial
$(k(Y)[X]/(f))/(k(Y))$
, and thus, it has the same degree equal to the degree of the irreducible polynomial
![]() $f\in \tilde{k}[X]$
, so
$f\in \tilde{k}[X]$
, so
![]() $[k(C)\;:\;\tilde{k}]=deg_{X}(f)=d-m_P$
.
$[k(C)\;:\;\tilde{k}]=deg_{X}(f)=d-m_P$
.
It is well known [Reference Hartshorne2, Ch. 1, Theorem 4.4] that for any two varieties
![]() $X$
and
$X$
and
![]() $Y$
, there is a bijection between the set of dominant rational maps
$Y$
, there is a bijection between the set of dominant rational maps
![]() $\varphi \;:\;X \dashrightarrow Y$
, and the set of field homomorphisms
$\varphi \;:\;X \dashrightarrow Y$
, and the set of field homomorphisms
![]() $\varphi ^{\star }\;:\;k(Y) \rightarrow k(X)$
. In particular, we obtain:
$\varphi ^{\star }\;:\;k(Y) \rightarrow k(X)$
. In particular, we obtain:
Lemma 2.2.
For each variety
![]() $X$
, we have a group isomorphism
$X$
, we have a group isomorphism
![]() $\mathrm{Bir}(X) \stackrel{\simeq }{\rightarrow }\mathrm{Aut}_{k}(k(X))$
which sends
$\mathrm{Bir}(X) \stackrel{\simeq }{\rightarrow }\mathrm{Aut}_{k}(k(X))$
which sends
![]() $\varphi$
to
$\varphi$
to
![]() $\varphi ^{*}$
.
$\varphi ^{*}$
.
Lemma 2.3.
For any field
![]() $k$
, we have
$k$
, we have
![]() $\mathrm{Aut}_k(k(x))=\{x\mapsto (a x+b)/(c x +d);\,a,b,c,d\in k, \,a d-b c\neq 0\}$
and
$\mathrm{Aut}_k(k(x))=\{x\mapsto (a x+b)/(c x +d);\,a,b,c,d\in k, \,a d-b c\neq 0\}$
and
![]() $\mathrm{Aut}_k(k(x))\cong \mathrm{Bir}(\mathbb{A}^1)\cong \mathrm{Bir}(\mathbb{P}^1)=\mathrm{Aut}(\mathbb{P}^1)$
.
$\mathrm{Aut}_k(k(x))\cong \mathrm{Bir}(\mathbb{A}^1)\cong \mathrm{Bir}(\mathbb{P}^1)=\mathrm{Aut}(\mathbb{P}^1)$
.
Definition 2.4.
Let
![]() $P\in \mathbb{P}^2$
, we write
$P\in \mathbb{P}^2$
, we write
![]() $\mathrm{Jonq}_{P}=\{\varphi \in \mathrm{Bir}(\mathbb{P}^2)|\exists \,\alpha \in \,\mathrm{Aut}(\mathbb{P}^1);\; \pi _P\circ \varphi =\alpha \circ \pi _P\}$
and call it the Jonquières group of
$\mathrm{Jonq}_{P}=\{\varphi \in \mathrm{Bir}(\mathbb{P}^2)|\exists \,\alpha \in \,\mathrm{Aut}(\mathbb{P}^1);\; \pi _P\circ \varphi =\alpha \circ \pi _P\}$
and call it the Jonquières group of
![]() $P$
.
$P$
.
Lemma 2.5.
Let
![]() $P=[1\;:\;0\;:\;0]$
, by taking an affine chart, a de Jonquières map with respect to
$P=[1\;:\;0\;:\;0]$
, by taking an affine chart, a de Jonquières map with respect to
![]() $P$
is a special case of a Cremona transformation, of the form
$P$
is a special case of a Cremona transformation, of the form
and
![]() $ \iota \;:\;\mathbb{A}^2 \hookrightarrow \mathbb{P}^2,\, (x,y) \longmapsto [x\;:\;y\;:\;1]$
, where
$ \iota \;:\;\mathbb{A}^2 \hookrightarrow \mathbb{P}^2,\, (x,y) \longmapsto [x\;:\;y\;:\;1]$
, where
![]() $a,b,c,d\in k$
with
$a,b,c,d\in k$
with
![]() $a d-b c\neq 0$
and
$a d-b c\neq 0$
and
![]() $r_1(x),r_4(x),r_2(x), r_3(x)\in k(x)$
with
$r_1(x),r_4(x),r_2(x), r_3(x)\in k(x)$
with
![]() $r_1(x) r_4(x)-r_2(x) r_3(x)\neq 0$
.
$r_1(x) r_4(x)-r_2(x) r_3(x)\neq 0$
.
Proof. We have the following commutative diagram

where
![]() $\iota \;:\;(x,y)\mapsto [x\;:\;y\;:\;1]$
and
$\iota \;:\;(x,y)\mapsto [x\;:\;y\;:\;1]$
and
![]() $\psi \;:\;x\mapsto [x\;:\;1]$
, which gives the equality
$\psi \;:\;x\mapsto [x\;:\;1]$
, which gives the equality
Let
![]() $f\in \iota ^{-1}\circ \mathrm{Jonq}_P\circ \iota$
given by
$f\in \iota ^{-1}\circ \mathrm{Jonq}_P\circ \iota$
given by
![]() $(x,y)\mapsto (f_1(x,y),f_2(x,y))$
, then
$(x,y)\mapsto (f_1(x,y),f_2(x,y))$
, then
![]() $\pi _x\circ f\;:\;(x,y)\mapsto f_1(x,y)$
. Since
$\pi _x\circ f\;:\;(x,y)\mapsto f_1(x,y)$
. Since
![]() $\alpha \circ \pi _x=\alpha (x)$
, it follows that
$\alpha \circ \pi _x=\alpha (x)$
, it follows that
![]() $f_1(x,y)$
depends only on
$f_1(x,y)$
depends only on
![]() $x$
and is of the form
$x$
and is of the form
![]() $f_1(x,y)=(a x+b)/(c x +d)$
where
$f_1(x,y)=(a x+b)/(c x +d)$
where
![]() $a,b,c,d\in k$
and
$a,b,c,d\in k$
and
![]() $a d-b c\neq 0$
by Lemma 2.3. From Lemma 2.2,
$a d-b c\neq 0$
by Lemma 2.3. From Lemma 2.2,
![]() $f^*$
is subjective, so
$f^*$
is subjective, so
![]() $k(x,y)= k((a x+b)/(c x +d),f_2(x,y))$
. To describe the second component
$k(x,y)= k((a x+b)/(c x +d),f_2(x,y))$
. To describe the second component
![]() $f_2(x,y)$
, let us define the birational map
$f_2(x,y)$
, let us define the birational map
![]() $\tau \;:\;(x,y)\mapsto ((d x-b)/(-c x +a),y)$
, hence
$\tau \;:\;(x,y)\mapsto ((d x-b)/(-c x +a),y)$
, hence
![]() $\tau \circ f\;:\;(x,y)\mapsto (x,f_2(x,y))$
is a birational map since both
$\tau \circ f\;:\;(x,y)\mapsto (x,f_2(x,y))$
is a birational map since both
![]() $f$
and
$f$
and
![]() $\tau$
are birationals. By Lemma 2.2,
$\tau$
are birationals. By Lemma 2.2,
![]() $k(x)(f_2(x,y))=k(x)(y)$
. Apply Lemma 2.3 over the field
$k(x)(f_2(x,y))=k(x)(y)$
. Apply Lemma 2.3 over the field
![]() $k(x)$
, then
$k(x)$
, then
![]() $f_2(x,y)=(r_1(x) y+ r_2(x))/(r_3(x) y+ r_4(x))$
.
$f_2(x,y)=(r_1(x) y+ r_2(x))/(r_3(x) y+ r_4(x))$
.
Lemma 2.6.
Let
![]() $P,Q\in \mathbb{P}^2$
and
$P,Q\in \mathbb{P}^2$
and
![]() $C,D\subset \mathbb{P}^2$
be two irreducible curves, if
$C,D\subset \mathbb{P}^2$
be two irreducible curves, if
![]() $\phi \in \mathrm{Bir}(\mathbb{P}^2)$
and
$\phi \in \mathrm{Bir}(\mathbb{P}^2)$
and
![]() $\phi |_{C}\;:\;C\dashrightarrow D$
is birational map, and there exists
$\phi |_{C}\;:\;C\dashrightarrow D$
is birational map, and there exists
![]() $\theta \in \mathrm{Aut}(\mathbb{P}^1)$
such that
$\theta \in \mathrm{Aut}(\mathbb{P}^1)$
such that
![]() $\pi _{Q}\circ \phi =\theta \circ \pi _P$
, then
$\pi _{Q}\circ \phi =\theta \circ \pi _P$
, then
![]() $P$
is a Galois point of
$P$
is a Galois point of
![]() $C$
if and only if
$C$
if and only if
![]() $Q$
is a Galois point of
$Q$
is a Galois point of
![]() $D$
. Moreover, if
$D$
. Moreover, if
![]() $P$
is Galois, an element of
$P$
is Galois, an element of
![]() $G_{P}$
extends an element of
$G_{P}$
extends an element of
![]() $\mathrm{Bir}(\mathbb{P}^2)$
(respectively
$\mathrm{Bir}(\mathbb{P}^2)$
(respectively
![]() $\mathrm{Jonq}_{P}$
) if and only if its image in
$\mathrm{Jonq}_{P}$
) if and only if its image in
![]() $G_{Q}$
extends an element of
$G_{Q}$
extends an element of
![]() $\mathrm{Bir}(\mathbb{P}^2)$
(respectively
$\mathrm{Bir}(\mathbb{P}^2)$
(respectively
![]() $\mathrm{Jonq}_{Q}$
)
$\mathrm{Jonq}_{Q}$
)

Proof. Since
![]() $\phi |_C$
is birational map from
$\phi |_C$
is birational map from
![]() $C$
to
$C$
to
![]() $D$
, then
$D$
, then
![]() $\phi ^{*}|_C \;:\;k(D)\rightarrow k(C)$
is an isomorphism. Moreover, as
$\phi ^{*}|_C \;:\;k(D)\rightarrow k(C)$
is an isomorphism. Moreover, as
![]() $\pi _Q\circ \phi =\theta \circ \pi _P$
, we have a commutative diagram
$\pi _Q\circ \phi =\theta \circ \pi _P$
, we have a commutative diagram

Therefore,
![]() $k(D)/\pi _{Q}^{*}(k(\mathbb{P}^1))$
is Galois if and only if
$k(D)/\pi _{Q}^{*}(k(\mathbb{P}^1))$
is Galois if and only if
![]() $k(C)/\pi _{P}^{*}(k(\mathbb{P}^1))$
is Galois. In addition,
$k(C)/\pi _{P}^{*}(k(\mathbb{P}^1))$
is Galois. In addition,
![]() $\phi$
conjugates
$\phi$
conjugates
![]() $\mathrm{Jonq}_{P}$
to
$\mathrm{Jonq}_{P}$
to
![]() $\mathrm{Jonq}_{Q}$
and sends any element of
$\mathrm{Jonq}_{Q}$
and sends any element of
![]() $\mathrm{Bir}(\mathbb{P}^2)$
that preserves
$\mathrm{Bir}(\mathbb{P}^2)$
that preserves
![]() $C$
onto element of
$C$
onto element of
![]() $\mathrm{Bir}(\mathbb{P}^2)$
that preserves
$\mathrm{Bir}(\mathbb{P}^2)$
that preserves
![]() $D$
.
$D$
.
Example 2.7.
Let
![]() $P=Q\in \{[1\;:\;0\;:\;0],[0\;:\;1\;:\;0],[0\;:\;0\;:\;1]\},\,\phi \;:\;[X\;:\;Y\;:\;Z] \mapsto [Y Z\;:\;X Z\;:\;X Y]$
and
$P=Q\in \{[1\;:\;0\;:\;0],[0\;:\;1\;:\;0],[0\;:\;0\;:\;1]\},\,\phi \;:\;[X\;:\;Y\;:\;Z] \mapsto [Y Z\;:\;X Z\;:\;X Y]$
and
![]() $\theta \;:\;[Y\;:\;Z] \mapsto [ Z\;:\;Y]$
, let
$\theta \;:\;[Y\;:\;Z] \mapsto [ Z\;:\;Y]$
, let
![]() $C\subset \mathbb{P}^2$
be an irreducible curve not equal to
$C\subset \mathbb{P}^2$
be an irreducible curve not equal to
![]() $x=0,\,y=0$
or
$x=0,\,y=0$
or
![]() $z=0$
and let
$z=0$
and let
![]() $D=\phi (C)$
, so we have the following diagram
$D=\phi (C)$
, so we have the following diagram

Thus, if
![]() $P$
is a Galois point for
$P$
is a Galois point for
![]() $C$
, then
$C$
, then
![]() $P$
becomes a Galois point for
$P$
becomes a Galois point for
![]() $D$
, this is a particular case of Lemma 2.6 corresponding to [Reference Miura3, Corollary 3].
$D$
, this is a particular case of Lemma 2.6 corresponding to [Reference Miura3, Corollary 3].
3. Extensions of degree at most three
Lemma 3.1.
Let
![]() $k$
be a field and let
$k$
be a field and let
![]() $L=k[x]/(x^3+a_2 x^2+a_1 x+a_0)$
where
$L=k[x]/(x^3+a_2 x^2+a_1 x+a_0)$
where
![]() $f=x^3+a_2 x^2+a_1 x+a_0$
is a separable irreducible polynomial in
$f=x^3+a_2 x^2+a_1 x+a_0$
is a separable irreducible polynomial in
![]() $k[x]$
, then the field extension
$k[x]$
, then the field extension
![]() $L/K$
is Galois if and only if there exists an element
$L/K$
is Galois if and only if there exists an element
![]() $\sigma \in \mathrm{Gal}(L/K)$
of order
$\sigma \in \mathrm{Gal}(L/K)$
of order
![]() $3$
such that,
$3$
such that,
Proof. As
![]() $f$
is a separable irreducible polynomial of degree 3, the extension
$f$
is a separable irreducible polynomial of degree 3, the extension
![]() $L/K$
is separable of degree 3. It is then Galois if and only if there exists
$L/K$
is separable of degree 3. It is then Galois if and only if there exists
![]() $\sigma \in \mathrm{Aut}(L/K)$
of order
$\sigma \in \mathrm{Aut}(L/K)$
of order
![]() $3$
, so it remains to prove that we can choose
$3$
, so it remains to prove that we can choose
![]() $\sigma$
with the right form. If
$\sigma$
with the right form. If
![]() $\sigma \in \mathrm{Aut}(L/K)$
where,
$\sigma \in \mathrm{Aut}(L/K)$
where,
![]() $\sigma \;:\;x\mapsto \nu _2 x^2+\nu _1 x+\nu _0$
and
$\sigma \;:\;x\mapsto \nu _2 x^2+\nu _1 x+\nu _0$
and
![]() $\nu _i\in k$
for
$\nu _i\in k$
for
![]() $i=0,1,2$
, so the question here is can we find
$i=0,1,2$
, so the question here is can we find
![]() $\{\alpha, \beta, \gamma,\delta \}\subset K$
with
$\{\alpha, \beta, \gamma,\delta \}\subset K$
with
![]() $\alpha \delta -\beta \gamma \neq 0$
such that the following equality holds?
$\alpha \delta -\beta \gamma \neq 0$
such that the following equality holds?
We can find a solution
![]() $\{\alpha = a_2 \nu _1 \nu _2 -a_1 \nu _2^2 + \nu _0 \nu _2 - \nu _1^2,\,\beta = a \nu _0 \nu _2 - a_0 \nu _2^2 - \nu _0\nu _2,\,\delta = a_2 \nu _2 - \nu _1,\,\gamma =\nu _2\}$
. We observe that
$\{\alpha = a_2 \nu _1 \nu _2 -a_1 \nu _2^2 + \nu _0 \nu _2 - \nu _1^2,\,\beta = a \nu _0 \nu _2 - a_0 \nu _2^2 - \nu _0\nu _2,\,\delta = a_2 \nu _2 - \nu _1,\,\gamma =\nu _2\}$
. We observe that
![]() $\alpha \delta -\beta \gamma \neq 0$
, otherwise we have
$\alpha \delta -\beta \gamma \neq 0$
, otherwise we have
![]() $\sigma (x)\in K$
and this gives a contradiction as
$\sigma (x)\in K$
and this gives a contradiction as
![]() $x\notin K$
.
$x\notin K$
.
Theorem 3.2.
Let
![]() $P\in \mathbb{P}^2$
, let
$P\in \mathbb{P}^2$
, let
![]() $C\subset \mathbb{P}^2$
be an irreducible curve of degree
$C\subset \mathbb{P}^2$
be an irreducible curve of degree
![]() $d$
: with multiplicity
$d$
: with multiplicity
![]() $m_{P}$
at
$m_{P}$
at
![]() $P$
. We have
$P$
. We have
![]() $[k(C)\;:\;K_{P}]=d-m_{P}$
.
$[k(C)\;:\;K_{P}]=d-m_{P}$
.
-
1. If
 $d-m_P=1$
, then
$d-m_P=1$
, then
 $\pi _P\;:\;C\dashrightarrow \mathbb{P}^1$
is a birational.
$\pi _P\;:\;C\dashrightarrow \mathbb{P}^1$
is a birational.
-
2. If
 $d-m_P=2$
,
$d-m_P=2$
,
 $P$
is Galois if and only if the extension is separable, and if this holds, then the non-trivial element
$P$
is Galois if and only if the extension is separable, and if this holds, then the non-trivial element
 $\sigma \in G_P$
of order
$\sigma \in G_P$
of order
 $2$
extends to a de Jonquières map with respect to
$2$
extends to a de Jonquières map with respect to
 $P$
.
$P$
. -
3. If
 $d-m_P=3$
and
$d-m_P=3$
and
 $P$
is Galois, then there is a de Jonquières map with respect to
$P$
is Galois, then there is a de Jonquières map with respect to
 $P$
extending the action.
$P$
extending the action.
Proof. The equality
![]() $[k(C)\;:\;K_{P}]=d-m_{P}$
follows from Lemma 2.1. We may assume
$[k(C)\;:\;K_{P}]=d-m_{P}$
follows from Lemma 2.1. We may assume
![]() $P=[1\;:\;0\;:\;0]$
. Let
$P=[1\;:\;0\;:\;0]$
. Let
![]() $x = X/Z$
and
$x = X/Z$
and
![]() $y = Y/Z$
be affine coordinates. Since the field extension
$y = Y/Z$
be affine coordinates. Since the field extension
![]() $k(C)/\pi _{P}^{*}(k(\mathbb{P}^1))$
is of degree
$k(C)/\pi _{P}^{*}(k(\mathbb{P}^1))$
is of degree
![]() $d-m_{P}$
, then
$d-m_{P}$
, then
![]() $k(C)=k(y)[x]/(f)$
, where
$k(C)=k(y)[x]/(f)$
, where
![]() $f\in k[x,y]$
is the equation of
$f\in k[x,y]$
is the equation of
![]() $C$
in these affine coordinates.
$C$
in these affine coordinates.
-
(1) If
 $d-m_p=1$
, then
$d-m_p=1$
, then
 $k(C)=\pi _{P}^{*}(k(\mathbb{P}^1))$
and therefore
$k(C)=\pi _{P}^{*}(k(\mathbb{P}^1))$
and therefore
 $\pi _{P}^{*}\;:\;k(\mathbb{P}^1)\rightarrow k(C)$
is an isomorphism. Hence
$\pi _{P}^{*}\;:\;k(\mathbb{P}^1)\rightarrow k(C)$
is an isomorphism. Hence
 $\pi _{P}\;:\;C\dashrightarrow \mathbb{P}^1$
is birational.
$\pi _{P}\;:\;C\dashrightarrow \mathbb{P}^1$
is birational. -
(2) If
 $d-m_p=2$
, then the extension
$d-m_p=2$
, then the extension
 $k(C)/\pi _{P}^{*}(k(\mathbb{P}^1))$
is of degree
$k(C)/\pi _{P}^{*}(k(\mathbb{P}^1))$
is of degree
 $2$
and it is thus Galois if and only if it is separable.
$2$
and it is thus Galois if and only if it is separable.
 $k(C)/\pi _{P}^{*}(k(\mathbb{P}^1))$
is Galois
$k(C)/\pi _{P}^{*}(k(\mathbb{P}^1))$
is Galois
 $\Leftrightarrow$
there exists an element
$\Leftrightarrow$
there exists an element
 $\sigma \in G_{P}$
of order
$\sigma \in G_{P}$
of order
 $2$
that permutes the roots of
$2$
that permutes the roots of
 $f\,\Leftrightarrow \,f$
is separable
$f\,\Leftrightarrow \,f$
is separable
 $\Leftrightarrow$
the extension is separable. Furthermore, the element
$\Leftrightarrow$
the extension is separable. Furthermore, the element
 $\sigma \in G_P$
of order
$\sigma \in G_P$
of order
 $2$
is given by
$2$
is given by
 $x\mapsto -x$
up to a suitable change of coordinates.
$x\mapsto -x$
up to a suitable change of coordinates. -
(3) If
 $d-m_{P}=3$
, the equation of the curve
$d-m_{P}=3$
, the equation of the curve
 $C$
is given by
$C$
is given by
 $f=F_{d-3}(y,1)x^3+F_{d-2}(y,1)x^2+F_{d-1}(y,1)x+F_{d}(y,1)$
. We apply Lemma 3.1, replacing
$f=F_{d-3}(y,1)x^3+F_{d-2}(y,1)x^2+F_{d-1}(y,1)x+F_{d}(y,1)$
. We apply Lemma 3.1, replacing
 $k$
by
$k$
by
 $k(y)$
.
$k(y)$
.
We now illustrate Theorem 3.2 in two examples.
Lemma 3.3.
Let
![]() $k$
be a field with
$k$
be a field with
![]() $char(k)\neq 3$
that contains a primitive third root of unity. Let
$char(k)\neq 3$
that contains a primitive third root of unity. Let
![]() $\phi \;:\;\mathbb{P}^1 \rightarrow \mathbb{P}^2$
given by
$\phi \;:\;\mathbb{P}^1 \rightarrow \mathbb{P}^2$
given by
![]() $\phi \;:\;[u\;:\;v]\mapsto [uv^2+u^2v\;:\;u^3\;:\; v^3]$
. We define
$\phi \;:\;[u\;:\;v]\mapsto [uv^2+u^2v\;:\;u^3\;:\; v^3]$
. We define
![]() $C\;:\!=\;\overline{\phi (\mathbb{P}^1)}$
is a curve of
$C\;:\!=\;\overline{\phi (\mathbb{P}^1)}$
is a curve of
![]() $\mathbb{P}^2$
, then the point
$\mathbb{P}^2$
, then the point
![]() $P=[1\;:\;0\;:\;0]$
is a Galois point of
$P=[1\;:\;0\;:\;0]$
is a Galois point of
![]() $C$
and the extension induced by the projection
$C$
and the extension induced by the projection
![]() $\pi _P\;:\; C\dashrightarrow \mathbb{P}^1$
is Galois of degree
$\pi _P\;:\; C\dashrightarrow \mathbb{P}^1$
is Galois of degree
![]() $3$
. The element of order
$3$
. The element of order
![]() $3$
extends to an element of
$3$
extends to an element of
![]() $\mathrm{Jonq}_{P}$
.
$\mathrm{Jonq}_{P}$
.
Proof. The curve
![]() $C$
is birational to
$C$
is birational to
![]() $\mathbb{P}^1$
via
$\mathbb{P}^1$
via
![]() $\phi$
, with inverse
$\phi$
, with inverse
![]() $[X\;:\;Y\;:\;Z]\mapsto [X +Y\;:\; X +Z]$
. Define the projection by
$[X\;:\;Y\;:\;Z]\mapsto [X +Y\;:\; X +Z]$
. Define the projection by
![]() $\pi _P\;:\;[X\;:\;Y\;:\;Z]\mapsto [Y\;:\;Z]$
. Let
$\pi _P\;:\;[X\;:\;Y\;:\;Z]\mapsto [Y\;:\;Z]$
. Let
![]() $\psi =\pi _{P}\circ \phi$
, then
$\psi =\pi _{P}\circ \phi$
, then
![]() $\psi \;:\;\mathbb{P}^1\rightarrow \mathbb{P}^1$
maps
$\psi \;:\;\mathbb{P}^1\rightarrow \mathbb{P}^1$
maps
![]() $[u\;:\;v]$
to
$[u\;:\;v]$
to
![]() $[u^3\;:\;v^3]$
, so the extension is Galois of degree
$[u^3\;:\;v^3]$
, so the extension is Galois of degree
![]() $3$
with Galois group
$3$
with Galois group
![]() $G_{P}$
generated by
$G_{P}$
generated by
![]() $\sigma \;:\;x\mapsto \omega \cdot x$
, where
$\sigma \;:\;x\mapsto \omega \cdot x$
, where
![]() $\omega$
is a primitive cubic root of unity. By Theorem 3.2, every element of order
$\omega$
is a primitive cubic root of unity. By Theorem 3.2, every element of order
![]() $3$
extends to an element of
$3$
extends to an element of
![]() $\mathrm{Jonq}_{P}$
. Explicitly,
$\mathrm{Jonq}_{P}$
. Explicitly,
![]() $\sigma$
extends to the map that is given by
$\sigma$
extends to the map that is given by
Lemma 3.4.
Let
![]() $k$
be a field with
$k$
be a field with
![]() $char(k)=3$
and
$char(k)=3$
and
![]() $C\subset \mathbb{P}^2$
given by the polynomial
$C\subset \mathbb{P}^2$
given by the polynomial
![]() $f= X^{3}- Y^{2} X+Z^{3}$
, then the point
$f= X^{3}- Y^{2} X+Z^{3}$
, then the point
![]() $P=[1\;:\;0\;:\;0]$
is Galois point of
$P=[1\;:\;0\;:\;0]$
is Galois point of
![]() $C$
and the extension induced by the projection
$C$
and the extension induced by the projection
![]() $\pi _P\;:\; C\dashrightarrow \mathbb{P}^1$
is Galois of degree
$\pi _P\;:\; C\dashrightarrow \mathbb{P}^1$
is Galois of degree
![]() $3$
.
$3$
.
Proof. Define the birational map
![]() $\phi \;:\;\mathbb{P}^1 \dashrightarrow C$
by
$\phi \;:\;\mathbb{P}^1 \dashrightarrow C$
by
![]() $ \phi \;:\;[u\;:\;v] \mapsto [v^{3}\;:\; u^{3} \;:\; u^{2} v- v^3]$
with inverse
$ \phi \;:\;[u\;:\;v] \mapsto [v^{3}\;:\; u^{3} \;:\; u^{2} v- v^3]$
with inverse
![]() $[X\;:\;Y\;:\;Z]\mapsto [Y\;:\;Z+X]$
. Define the projection by
$[X\;:\;Y\;:\;Z]\mapsto [Y\;:\;Z+X]$
. Define the projection by
![]() $\pi _P\;:\;[X\;:\;Y\;:\;Z]\mapsto [Y\;:\;Z]$
. Let
$\pi _P\;:\;[X\;:\;Y\;:\;Z]\mapsto [Y\;:\;Z]$
. Let
![]() $\psi =\pi _{P}\circ \phi$
, then
$\psi =\pi _{P}\circ \phi$
, then
![]() $\psi \;:\;\mathbb{P}^1\rightarrow \mathbb{P}^1$
maps
$\psi \;:\;\mathbb{P}^1\rightarrow \mathbb{P}^1$
maps
![]() $[u\;:\;v]$
to
$[u\;:\;v]$
to
![]() $[u^{3} \;:\; u^{2} v- v^3]$
, so the extension is Galois of degree
$[u^{3} \;:\; u^{2} v- v^3]$
, so the extension is Galois of degree
![]() $3$
with Galois group
$3$
with Galois group
![]() $G_{P}$
generated by
$G_{P}$
generated by
![]() $\sigma \;:\;[u\;:\;v]\mapsto [u\;:\;u+v]$
. By Theorem 3.2, we know that every element of order
$\sigma \;:\;[u\;:\;v]\mapsto [u\;:\;u+v]$
. By Theorem 3.2, we know that every element of order
![]() $3$
extends to an element of
$3$
extends to an element of
![]() $\mathrm{Jonq}_{P}$
. Explicitly
$\mathrm{Jonq}_{P}$
. Explicitly
![]() $\sigma$
extends to the map that is given by
$\sigma$
extends to the map that is given by
![]() $\sigma$
that is given by
$\sigma$
that is given by
![]() $[X\;:\;Y\;:\;Z]\mapsto [X +Y \;:\;Y\;:\;Z]$
.
$[X\;:\;Y\;:\;Z]\mapsto [X +Y \;:\;Y\;:\;Z]$
.
4. Curves that are Cremona equivalent to a line
Definition 4.1.
Let
![]() $X$
be a smooth projective variety and
$X$
be a smooth projective variety and
![]() $D$
a divisor in
$D$
a divisor in
![]() $X$
. Let
$X$
. Let
![]() $K_X$
denote a canonical divisor of
$K_X$
denote a canonical divisor of
![]() $X$
. We define the Kodaira dimension of
$X$
. We define the Kodaira dimension of
![]() $D\subset X$
, written
$D\subset X$
, written
![]() $\mathcal{K}(D,X)$
to be the dimension of the image of
$\mathcal{K}(D,X)$
to be the dimension of the image of
![]() $X \mapsto P(H^{0}(m(D+ K_X)))$
for
$X \mapsto P(H^{0}(m(D+ K_X)))$
for
![]() $m\gt \gt 0$
. By convention we say that the Kodaira dimension is
$m\gt \gt 0$
. By convention we say that the Kodaira dimension is
![]() $\mathcal{K}(D,X)= -\infty$
if
$\mathcal{K}(D,X)= -\infty$
if
![]() $|m(D+ K_X)|=\varnothing \,\forall \, m\gt 0$
.
$|m(D+ K_X)|=\varnothing \,\forall \, m\gt 0$
.
Definition 4.2. [Reference Mohan Kumar and Murthy7] Let
![]() $C\subset \mathbb{P}^2$
be an irreducible curve. If
$C\subset \mathbb{P}^2$
be an irreducible curve. If
![]() $C$
is a smooth curve, we define
$C$
is a smooth curve, we define
![]() $\bar{\mathcal{K}}(C,\mathbb{P}^2)$
to be
$\bar{\mathcal{K}}(C,\mathbb{P}^2)$
to be
![]() $\mathcal{K}(C,\mathbb{P}^2)$
. If
$\mathcal{K}(C,\mathbb{P}^2)$
. If
![]() $C$
is a singular curve, we take
$C$
is a singular curve, we take
![]() $X\rightarrow \mathbb{P}^2$
to be an embedded resolution of singularities of
$X\rightarrow \mathbb{P}^2$
to be an embedded resolution of singularities of
![]() $C$
in
$C$
in
![]() $\mathbb{P}^2$
where
$\mathbb{P}^2$
where
![]() $\tilde{C}$
is the strict transform of
$\tilde{C}$
is the strict transform of
![]() $C$
, then we define
$C$
, then we define
![]() $\bar{\mathcal{K}}(C,\mathbb{P}^2)$
to be
$\bar{\mathcal{K}}(C,\mathbb{P}^2)$
to be
![]() $\mathcal{K}(\tilde{C},X)$
. This does not depend on the choice of the resolution.
$\mathcal{K}(\tilde{C},X)$
. This does not depend on the choice of the resolution.
Definition 4.3.
Let
![]() $C$
be an irreducible smooth plane curve. The curve
$C$
be an irreducible smooth plane curve. The curve
![]() $C$
is said to be Cremona equivalent to a line if there is a birational map
$C$
is said to be Cremona equivalent to a line if there is a birational map
![]() $\varphi \;:\;\mathbb{P}^2\dashrightarrow \mathbb{P}^2$
that sends
$\varphi \;:\;\mathbb{P}^2\dashrightarrow \mathbb{P}^2$
that sends
![]() $C$
to a line.
$C$
to a line.
Theorem 4.4. (Coolidge) [Reference Mohan Kumar and Murthy7, Theorem 2.6] Let
![]() $C\hookrightarrow \mathbb{P}^2$
be an irreducible rational curve. Then, there exists a Cremona transformation
$C\hookrightarrow \mathbb{P}^2$
be an irreducible rational curve. Then, there exists a Cremona transformation
![]() $\sigma$
of
$\sigma$
of
![]() $\mathbb{P}^2$
such that
$\mathbb{P}^2$
such that
![]() $\sigma (C)$
is a line if and only if
$\sigma (C)$
is a line if and only if
![]() $\overline{\mathcal{K}}(C,\mathbb{P}^2)=-\infty$
.
$\overline{\mathcal{K}}(C,\mathbb{P}^2)=-\infty$
.
Lemma 4.5.
If
![]() $C\hookrightarrow \mathbb{P}^2$
is an irreducible rational curve of degree
$C\hookrightarrow \mathbb{P}^2$
is an irreducible rational curve of degree
![]() $d\lt 6$
, then
$d\lt 6$
, then
![]() $C$
is equivalent to a line.
$C$
is equivalent to a line.
Proof. Let
![]() $\pi _1\;:\;X_1 \rightarrow \mathbb{P}^2$
be the blow-up of
$\pi _1\;:\;X_1 \rightarrow \mathbb{P}^2$
be the blow-up of
![]() $\mathbb{P}^2$
at
$\mathbb{P}^2$
at
![]() $P_1$
, and let
$P_1$
, and let
![]() $\pi _i\;:\;X_{i} \rightarrow X_{i-1}$
the blow-up of
$\pi _i\;:\;X_{i} \rightarrow X_{i-1}$
the blow-up of
![]() $X_{i-1}$
at
$X_{i-1}$
at
![]() $P_i\in X_{i-1}$
for
$P_i\in X_{i-1}$
for
![]() $i\geq 2$
,
$i\geq 2$
,
![]() $\mathcal{E}_{i}=\pi _i^{-1}(P_i)$
is a
$\mathcal{E}_{i}=\pi _i^{-1}(P_i)$
is a
![]() $(-1)$
-curve, where
$(-1)$
-curve, where
![]() $\mathcal{E}_{i}^2=-1$
and
$\mathcal{E}_{i}^2=-1$
and
![]() $\mathcal{E}_{i}\cong \mathbb{P}^1$
. After blowing up
$\mathcal{E}_{i}\cong \mathbb{P}^1$
. After blowing up
![]() $n$
points, let
$n$
points, let
![]() $\pi \;:\; Y\mapsto \mathbb{P}^2$
be the composition of the blow-ups
$\pi \;:\; Y\mapsto \mathbb{P}^2$
be the composition of the blow-ups
![]() $\pi _i$
, where
$\pi _i$
, where
![]() $Y=X_n$
we choose enough points such that the strict transform of
$Y=X_n$
we choose enough points such that the strict transform of
![]() $C$
is smooth. By induction, we have
$C$
is smooth. By induction, we have
![]() $E_i=(\pi _{i+1}\circ \ldots ..\circ \pi _{n})^{*}(\mathcal{E}_i)$
,
$E_i=(\pi _{i+1}\circ \ldots ..\circ \pi _{n})^{*}(\mathcal{E}_i)$
,
![]() $Pic(Y)=\pi ^*(Pic(\mathbb{P}^2))\oplus \mathbb{Z}E_{1}\oplus \ldots \oplus \mathbb{Z}E_{n}$
, and
$Pic(Y)=\pi ^*(Pic(\mathbb{P}^2))\oplus \mathbb{Z}E_{1}\oplus \ldots \oplus \mathbb{Z}E_{n}$
, and
![]() $E_i^2=-1$
for every
$E_i^2=-1$
for every
![]() $i=1,\ldots,n,$
and
$i=1,\ldots,n,$
and
![]() $E_i\cdot E_j=0$
for every
$E_i\cdot E_j=0$
for every
![]() $i\neq j$
. Moreover,
$i\neq j$
. Moreover,
The strict transform
![]() $\tilde{C}\subset C$
is equivalent to
$\tilde{C}\subset C$
is equivalent to
![]() $\tilde{C}=d \cdot \pi ^*(L)-\Sigma _{i=1}^{n}m_{P_i}(C)E_{i}$
. Hence we have
$\tilde{C}=d \cdot \pi ^*(L)-\Sigma _{i=1}^{n}m_{P_i}(C)E_{i}$
. Hence we have
![]() $2 K_Y+\tilde{C}=(-6+d)\cdot \pi ^*(L)+\Sigma _{i=1}^{n}(2-m_{P_i}(C))E_{i}$
, so
$2 K_Y+\tilde{C}=(-6+d)\cdot \pi ^*(L)+\Sigma _{i=1}^{n}(2-m_{P_i}(C))E_{i}$
, so
![]() $\pi ^*(L)\cdot (2 K_{Y}+\tilde{C})=-6+d$
, thus
$\pi ^*(L)\cdot (2 K_{Y}+\tilde{C})=-6+d$
, thus
![]() $|2 K_{Y}+\tilde{C}|=\phi$
for every curve of degree
$|2 K_{Y}+\tilde{C}|=\phi$
for every curve of degree
![]() $d\lt 6$
. [Reference Mohan Kumar and Murthy7, Corollary
$d\lt 6$
. [Reference Mohan Kumar and Murthy7, Corollary
![]() $2.4$
] shows that
$2.4$
] shows that
![]() $|2 K_{Y}+\tilde{C}|=\varnothing$
is equivalent to
$|2 K_{Y}+\tilde{C}|=\varnothing$
is equivalent to
![]() $\bar{\mathcal{K}}(C,\mathbb{P}^2)=-\infty$
, so
$\bar{\mathcal{K}}(C,\mathbb{P}^2)=-\infty$
, so
![]() $C$
is equivalent to a line by Theorem 4.4.
$C$
is equivalent to a line by Theorem 4.4.
Lemma 4.6.
If
![]() $C$
is a Cremona equivalent to a line
$C$
is a Cremona equivalent to a line
![]() $L\subseteq \mathbb{P}^2$
and
$L\subseteq \mathbb{P}^2$
and
![]() $P$
is a Galois point, then every non-trivial element in
$P$
is a Galois point, then every non-trivial element in
![]() $G_{P}$
extends to an element in
$G_{P}$
extends to an element in
![]() $\mathrm{Bir}(\mathbb{P}^2)$
.
$\mathrm{Bir}(\mathbb{P}^2)$
.
Proof. Let
![]() $\varphi \in \mathrm{Bir}(\mathbb{P}^2)$
that sends
$\varphi \in \mathrm{Bir}(\mathbb{P}^2)$
that sends
![]() $C$
onto a line
$C$
onto a line
![]() $L$
. For each
$L$
. For each
![]() $g\in G_{P},\,\varphi |_{C}\;:\;C\dashrightarrow L$
conjugates
$g\in G_{P},\,\varphi |_{C}\;:\;C\dashrightarrow L$
conjugates
![]() $g$
to an element of
$g$
to an element of
![]() $\mathrm{Aut}(L)$
, that extends to
$\mathrm{Aut}(L)$
, that extends to
![]() $\hat{g}\in \mathrm{Aut}(\mathbb{P}^2)$
. Hence,
$\hat{g}\in \mathrm{Aut}(\mathbb{P}^2)$
. Hence,
![]() $g$
extends to
$g$
extends to
![]() $\varphi ^{-1}\hat{g}\varphi \in \mathrm{Bir}(\mathbb{P}^2)$
.
$\varphi ^{-1}\hat{g}\varphi \in \mathrm{Bir}(\mathbb{P}^2)$
.
Remark 4.7.
Let
![]() $C$
be the smooth conic given by
$C$
be the smooth conic given by
![]() $C= \{[X \;:\; Y \;:\; Z] | Y^2=XZ\}\subset \mathbb{P}^2$
, then the natural embedding of
$C= \{[X \;:\; Y \;:\; Z] | Y^2=XZ\}\subset \mathbb{P}^2$
, then the natural embedding of
![]() $\mathrm{Aut}(\mathbb{P}^2, C)=\{g\in \mathrm{Aut}(\mathbb{P}^2)|g(C)=C\}= \mathrm{PGL}_2$
in
$\mathrm{Aut}(\mathbb{P}^2, C)=\{g\in \mathrm{Aut}(\mathbb{P}^2)|g(C)=C\}= \mathrm{PGL}_2$
in
![]() $\mathrm{Aut}(\mathbb{P}^2) = \mathrm{PGL}_3$
is the one induced from the injective group homomorphism
$\mathrm{Aut}(\mathbb{P}^2) = \mathrm{PGL}_3$
is the one induced from the injective group homomorphism
 \begin{equation*} \mathrm {GL}_2(k)\rightarrow \mathrm {GL}_3(k),\, \left [\begin {array}{c@{\quad}c} a & b \\[5pt] c & d \end {array}\right ]\mapsto \frac {1}{ad-bc}\left [\begin {array}{c@{\quad}c@{\quad}c} a^2 & ab&b^2 \\[5pt] 2ac & ad+bc&2bd\\[5pt] c^2&cd&d^2 \end {array}\right ] \end{equation*}
\begin{equation*} \mathrm {GL}_2(k)\rightarrow \mathrm {GL}_3(k),\, \left [\begin {array}{c@{\quad}c} a & b \\[5pt] c & d \end {array}\right ]\mapsto \frac {1}{ad-bc}\left [\begin {array}{c@{\quad}c@{\quad}c} a^2 & ab&b^2 \\[5pt] 2ac & ad+bc&2bd\\[5pt] c^2&cd&d^2 \end {array}\right ] \end{equation*}
where
![]() $\rho \;:\;[u\;:\;v]\mapsto [u^2\;:\;uv\;:\;v^2]$
, and the following diagram commutes.
$\rho \;:\;[u\;:\;v]\mapsto [u^2\;:\;uv\;:\;v^2]$
, and the following diagram commutes.

Lemma 4.8.
Let
![]() $k$
be a field of characteristic
$k$
be a field of characteristic
![]() $char(k)\neq 2$
containing a primitive fourth root of unity, and let
$char(k)\neq 2$
containing a primitive fourth root of unity, and let
![]() $C$
be the irreducible curve defined by the equation
$C$
be the irreducible curve defined by the equation
then the point
![]() $P=[1\;:\;0\;:\;0]$
is an outer Galois point of
$P=[1\;:\;0\;:\;0]$
is an outer Galois point of
![]() $C$
and the extension induced by the projection
$C$
and the extension induced by the projection
![]() $\pi _P\;:\; C\dashrightarrow \mathbb{P}^1$
is Galois of degree
$\pi _P\;:\; C\dashrightarrow \mathbb{P}^1$
is Galois of degree
![]() $4$
. Furthermore, the group
$4$
. Furthermore, the group
![]() $G_{P}$
extends to
$G_{P}$
extends to
![]() $\mathrm{Bir}(\mathbb{P}^2)$
but not to
$\mathrm{Bir}(\mathbb{P}^2)$
but not to
![]() $\mathrm{Jonq}_{P}$
.
$\mathrm{Jonq}_{P}$
.
Proof. Define the birational map
![]() $\phi \;:\;\mathbb{A}^1 \dashrightarrow C$
by
$\phi \;:\;\mathbb{A}^1 \dashrightarrow C$
by
![]() $\phi \;:\;t\mapsto [t+t^3\;:\;t^4\;:\;1]$
with inverse
$\phi \;:\;t\mapsto [t+t^3\;:\;t^4\;:\;1]$
with inverse
![]() $[X\;:\;Y\;:\;Z]\mapsto \left (X \left (Y +Z \right )\right )/(X^{2}-Y Z +Z^{2})$
. Hence
$[X\;:\;Y\;:\;Z]\mapsto \left (X \left (Y +Z \right )\right )/(X^{2}-Y Z +Z^{2})$
. Hence
![]() $C$
is a rational irreducible curve of degree
$C$
is a rational irreducible curve of degree
![]() $4$
and therefore,
$4$
and therefore,
![]() $C$
is equivalent to a line by Lemma 4.5. Furthermore, every non-trivial element in
$C$
is equivalent to a line by Lemma 4.5. Furthermore, every non-trivial element in
![]() $G_{P}$
extends to an element in
$G_{P}$
extends to an element in
![]() $\mathrm{Bir}(\mathbb{P}^2)$
by Lemma 4.6. We will also prove it explicitly below. We have
$\mathrm{Bir}(\mathbb{P}^2)$
by Lemma 4.6. We will also prove it explicitly below. We have
![]() $K(C)=k(t)$
and define the projection by
$K(C)=k(t)$
and define the projection by
![]() $\pi _P\;:\;[X\;:\;Y\;:\;Z]\mapsto [Y\;:\;Z]$
. Let
$\pi _P\;:\;[X\;:\;Y\;:\;Z]\mapsto [Y\;:\;Z]$
. Let
![]() $x = X/Z$
and
$x = X/Z$
and
![]() $y = Y/Z$
be affine coordinates, so the affine equation
$y = Y/Z$
be affine coordinates, so the affine equation
![]() $x^{4}-4 y x^{2}- y^{3}+2 y^{2}-y =0$
is defining the extension field
$x^{4}-4 y x^{2}- y^{3}+2 y^{2}-y =0$
is defining the extension field
![]() $k(y)[x]/k(y)=k(t)/k(t^4)$
. Since
$k(y)[x]/k(y)=k(t)/k(t^4)$
. Since
![]() $k$
contains the
$k$
contains the
![]() $4th$
root of unity, the extension is Galois of degree
$4th$
root of unity, the extension is Galois of degree
![]() $4$
with basis
$4$
with basis
![]() $\{1,t, t^2,t^3\}$
, and we have the following diagram
$\{1,t, t^2,t^3\}$
, and we have the following diagram

where
![]() $\psi$
is given by
$\psi$
is given by
![]() $\psi \;:\;t\mapsto t^4$
. By contradiction, we prove that there is no de Jonquières map
$\psi \;:\;t\mapsto t^4$
. By contradiction, we prove that there is no de Jonquières map
![]() $f$
extending the action. Let us assume that there exists a de Jonquières map
$f$
extending the action. Let us assume that there exists a de Jonquières map
![]() $g$
that extends the action,
$g$
that extends the action,
![]() $i.e$
there exists
$i.e$
there exists
![]() $\tilde{\alpha },\tilde{\beta }, \tilde{\gamma },\tilde{\delta }\in k(y)$
with
$\tilde{\alpha },\tilde{\beta }, \tilde{\gamma },\tilde{\delta }\in k(y)$
with
![]() $\tilde{\alpha }\tilde{ \delta }-\tilde{\beta } \tilde{\gamma }\neq 0$
such that
$\tilde{\alpha }\tilde{ \delta }-\tilde{\beta } \tilde{\gamma }\neq 0$
such that
![]() $g\;:\;(x,y)\mapsto (\frac{\tilde{\alpha } x+\tilde{\beta }}{\tilde{\gamma } x+\tilde{\delta }},y)$
. Since
$g\;:\;(x,y)\mapsto (\frac{\tilde{\alpha } x+\tilde{\beta }}{\tilde{\gamma } x+\tilde{\delta }},y)$
. Since
![]() $g\circ \phi =\phi \circ \sigma$
, writing
$g\circ \phi =\phi \circ \sigma$
, writing
![]() $\alpha =\tilde{\alpha }(t^4),\beta =\tilde{\beta }(t^4), \gamma =\tilde{\gamma }(t^4)$
and
$\alpha =\tilde{\alpha }(t^4),\beta =\tilde{\beta }(t^4), \gamma =\tilde{\gamma }(t^4)$
and
![]() $\delta =\tilde{\delta }(t^4)$
where
$\delta =\tilde{\delta }(t^4)$
where
![]() $\alpha,\beta,\gamma, \delta \in k(t^4)$
. We obtain the equation
$\alpha,\beta,\gamma, \delta \in k(t^4)$
. We obtain the equation
This implies that
![]() $\beta = \beta (t)=-(\mathrm{i} t^{6}- \mathrm{i})\gamma t^{2}-(\mathrm{i} \delta +\alpha ) t^{3}+(\delta \mathrm{i}-\alpha )t\in k(t^4)$
and is then
$\beta = \beta (t)=-(\mathrm{i} t^{6}- \mathrm{i})\gamma t^{2}-(\mathrm{i} \delta +\alpha ) t^{3}+(\delta \mathrm{i}-\alpha )t\in k(t^4)$
and is then
![]() $(\mathrm{i} t^{4}- \mathrm{i})\gamma =0,$
$(\mathrm{i} t^{4}- \mathrm{i})\gamma =0,$
![]() $\mathrm{i} \delta +\alpha =0$
and
$\mathrm{i} \delta +\alpha =0$
and
![]() $\delta \mathrm{i}-\alpha =0$
. This gives
$\delta \mathrm{i}-\alpha =0$
. This gives
![]() $\alpha =0,\gamma =0$
which is a contradiction. Viewing
$\alpha =0,\gamma =0$
which is a contradiction. Viewing
![]() $C$
as an irreducible curve in
$C$
as an irreducible curve in
![]() $\mathbb{P}^2$
of degree
$\mathbb{P}^2$
of degree
![]() $4$
, there are three singular points on the curve
$4$
, there are three singular points on the curve
![]() $ [0\;:\; 1\;:\; 1], \left [\mathrm{i} \sqrt{2}\;:\;-1\;:\; 1\right ], \left [\mathrm{i} \sqrt{2}\;:\; 1\;:\; -1\right ]$
. After suitable change of coordinates,
$ [0\;:\; 1\;:\; 1], \left [\mathrm{i} \sqrt{2}\;:\;-1\;:\; 1\right ], \left [\mathrm{i} \sqrt{2}\;:\; 1\;:\; -1\right ]$
. After suitable change of coordinates,
![]() $\sigma \;:\;\mathbb{P}^2\rightarrow \mathbb{P}^2$
is given by
$\sigma \;:\;\mathbb{P}^2\rightarrow \mathbb{P}^2$
is given by
![]() $[X\;:\;Y\;:\;Z]\mapsto \left [-\mathrm{i} \sqrt{2} X-\mathrm{i} \sqrt{2} Z\;:\; 2 X+Y-Z \;:\; 2X-Y+Z \right ]$
, this map sends the curve
$[X\;:\;Y\;:\;Z]\mapsto \left [-\mathrm{i} \sqrt{2} X-\mathrm{i} \sqrt{2} Z\;:\; 2 X+Y-Z \;:\; 2X-Y+Z \right ]$
, this map sends the curve
![]() $C$
to
$C$
to
![]() $\tilde{C}$
, which is given by
$\tilde{C}$
, which is given by
![]() $\tilde{f}=X^{2} Y^{2}+6 X^{2} Y Z +X^{2} Z^{2}+4 Y^{2} Z^{2}=0$
and this new equation has
$\tilde{f}=X^{2} Y^{2}+6 X^{2} Y Z +X^{2} Z^{2}+4 Y^{2} Z^{2}=0$
and this new equation has
![]() $\{[1\;:\;0\;:\;0], [0\;:\;1\;:\;0],[0\;:\;0\;:\;1]\}$
as multiple points of order
$\{[1\;:\;0\;:\;0], [0\;:\;1\;:\;0],[0\;:\;0\;:\;1]\}$
as multiple points of order
![]() $2$
. After blowing up the three points
$2$
. After blowing up the three points
![]() $\{[1\;:\;0\;:\;0], [0\;:\;1\;:\;0],[0\;:\;0\;:\;1]\}$
in
$\{[1\;:\;0\;:\;0], [0\;:\;1\;:\;0],[0\;:\;0\;:\;1]\}$
in
![]() $\mathbb{P}^2$
and contract again, the strict transform curve is of degree
$\mathbb{P}^2$
and contract again, the strict transform curve is of degree
![]() $d'=2 \cdot d-m_1-m_2-m_3=2\cdot 4-2-2-2=2$
, so it is a conic given by the equation
$d'=2 \cdot d-m_1-m_2-m_3=2\cdot 4-2-2-2=2$
, so it is a conic given by the equation
![]() $F=4 X^{2}+Y^{2}+6 Y Z +Z^{2}=0$
. We change the coordinates using the following matrix
$F=4 X^{2}+Y^{2}+6 Y Z +Z^{2}=0$
. We change the coordinates using the following matrix
 \begin{equation*}\left [\begin {array}{c@{\quad}c@{\quad}c} 4\mathrm {I} & 0 & -\mathrm {I} \\[5pt] 0 & 2\sqrt {2} & 0 \\[5pt] 8 & -6 \sqrt {2} & 2 \end {array}\right ]\end{equation*}
\begin{equation*}\left [\begin {array}{c@{\quad}c@{\quad}c} 4\mathrm {I} & 0 & -\mathrm {I} \\[5pt] 0 & 2\sqrt {2} & 0 \\[5pt] 8 & -6 \sqrt {2} & 2 \end {array}\right ]\end{equation*}
to send the conic to
![]() $Y^2-XZ=0$
and we extend
$Y^2-XZ=0$
and we extend
![]() $G_{P}$
explicitly using Remark 4.7.
$G_{P}$
explicitly using Remark 4.7.
5. Example where
 $\boldsymbol{G}_{\boldsymbol{P}}$
cannot be extended to
$\boldsymbol{G}_{\boldsymbol{P}}$
cannot be extended to
 $\mathrm{Bir}(\mathbb{P}^2)$
$\mathrm{Bir}(\mathbb{P}^2)$
Lemma 5.1.
Let k be an algebraically closed field,
![]() $C\subset \mathbb{P}^2$
be an irreducible curve,
$C\subset \mathbb{P}^2$
be an irreducible curve,
![]() $f\;:\; \mathbb{P}^2\dashrightarrow \mathbb{P}^2$
be a birational map sends the curve
$f\;:\; \mathbb{P}^2\dashrightarrow \mathbb{P}^2$
be a birational map sends the curve
![]() $C$
to itself, and
$C$
to itself, and
![]() $X\rightarrow \mathbb{P}^2$
is an embedded resolution of singularities of
$X\rightarrow \mathbb{P}^2$
is an embedded resolution of singularities of
![]() $C$
in
$C$
in
![]() $\mathbb{P}^2$
where
$\mathbb{P}^2$
where
![]() $\tilde{C}$
is the strict transform of
$\tilde{C}$
is the strict transform of
![]() $C$
. If all singular points of
$C$
. If all singular points of
![]() $C$
have a multiplicity
$C$
have a multiplicity
![]() $m_P(C)\lt deg(C)/3$
, then
$m_P(C)\lt deg(C)/3$
, then
![]() $f$
is an automorphism of
$f$
is an automorphism of
![]() $\mathbb{P}^2$
.
$\mathbb{P}^2$
.
Proof. Let
![]() $deg(f)=d$
, and assume for contradiction that
$deg(f)=d$
, and assume for contradiction that
![]() $d\gt 1$
. We take a commutative diagram where
$d\gt 1$
. We take a commutative diagram where
![]() $\pi$
and
$\pi$
and
![]() $\eta$
are sequences of blow-ups
$\eta$
are sequences of blow-ups

and we can assume that the strict transform of
![]() $C$
is smooth. As in Lemma 4.5
$C$
is smooth. As in Lemma 4.5
![]() $\eta ^{*}(L)=d\cdot \pi ^{*}(L)-\Sigma m_iE_i,\,K_{X}=-3\pi ^{*}(L)+\Sigma E_i$
, and
$\eta ^{*}(L)=d\cdot \pi ^{*}(L)-\Sigma m_iE_i,\,K_{X}=-3\pi ^{*}(L)+\Sigma E_i$
, and
![]() $\eta ^{*}(C)=\tilde{C}=deg(C)\cdot \pi ^{*}(L)-\Sigma m_{P_{i}}(C)E_i$
. Since
$\eta ^{*}(C)=\tilde{C}=deg(C)\cdot \pi ^{*}(L)-\Sigma m_{P_{i}}(C)E_i$
. Since
![]() $deg(C)=C\cdot L=\eta ^{*}(C)\cdot \eta ^{*}(L)=d\cdot deg(C)-\Sigma m_i\cdot m_{P_{i}}(C)$
, then
$deg(C)=C\cdot L=\eta ^{*}(C)\cdot \eta ^{*}(L)=d\cdot deg(C)-\Sigma m_i\cdot m_{P_{i}}(C)$
, then
![]() $deg(C)(d-1)=\Sigma m_i\cdot m_{P_{i}}(C)\lt \Sigma m_i\cdot deg(C)/3$
and therefore
$deg(C)(d-1)=\Sigma m_i\cdot m_{P_{i}}(C)\lt \Sigma m_i\cdot deg(C)/3$
and therefore
![]() $3(d-1)\lt \Sigma m_i$
Noether equality, which is a contradiction as
$3(d-1)\lt \Sigma m_i$
Noether equality, which is a contradiction as
![]() $\Sigma m_i=3(d-1)$
: this equation follows from
$\Sigma m_i=3(d-1)$
: this equation follows from
![]() $\eta ^*(L)^2=L^2=1$
and from the adjunction formula
$\eta ^*(L)^2=L^2=1$
and from the adjunction formula
![]() $\eta ^*(L)\cdot (\eta ^*(L)+K_X)=-2$
, which gives
$\eta ^*(L)\cdot (\eta ^*(L)+K_X)=-2$
, which gives
![]() $\eta ^*(L)\cdot K_X=-3$
.
$\eta ^*(L)\cdot K_X=-3$
.
Lemma 5.2.
Let
![]() $k$
be a field with
$k$
be a field with
![]() $char(k)\neq 5$
that contains a primitive
$char(k)\neq 5$
that contains a primitive
![]() $5$
th root of unity, and let
$5$
th root of unity, and let
![]() $\phi \;:\;\mathbb{P}^1 \rightarrow \mathbb{P}^2$
given by
$\phi \;:\;\mathbb{P}^1 \rightarrow \mathbb{P}^2$
given by
![]() $\phi \;:\;[u\;:\;v]\mapsto [u v^6-u^7\;:\;u^5(u^2+v^2)\;:\; v^5(u^2+v^2)]$
. We define
$\phi \;:\;[u\;:\;v]\mapsto [u v^6-u^7\;:\;u^5(u^2+v^2)\;:\; v^5(u^2+v^2)]$
. We define
![]() $C\;:\!=\;\overline{\phi (\mathbb{P}^1)}$
, then the point
$C\;:\!=\;\overline{\phi (\mathbb{P}^1)}$
, then the point
![]() $P=[1\;:\;0\;:\;0]$
is an inner Galois point of
$P=[1\;:\;0\;:\;0]$
is an inner Galois point of
![]() $C$
and the extension induced by the projection
$C$
and the extension induced by the projection
![]() $\pi _P\;:\; C\dashrightarrow \mathbb{P}^1$
is Galois of degree
$\pi _P\;:\; C\dashrightarrow \mathbb{P}^1$
is Galois of degree
![]() $5$
. Moreover, there is no birational map
$5$
. Moreover, there is no birational map
![]() $f$
extending the action of the generator of the Galois group.
$f$
extending the action of the generator of the Galois group.
Proof. The curve
![]() $C$
is birational to
$C$
is birational to
![]() $\mathbb{P}^1$
via
$\mathbb{P}^1$
via
![]() $\phi$
, with inverse
$\phi$
, with inverse
![]() $[X\;:\;Y\;:\;Z]\mapsto [X^{4} Y +4 X^{3} Y^{2}-2 X^{3} Z^{2}+6 X^{2} Y^{3}-2 X^{2} YZ^{2}+4 X Y^{4}+X Z^{4}+Y^{5}\;:\;Z (X^{4}+2 X^{3} Y+X^{2} Y^{2}-3 X^{2} Z^{2} -3 X Y Z^{2}+Z^{4})]$
. Define the projection by
$[X\;:\;Y\;:\;Z]\mapsto [X^{4} Y +4 X^{3} Y^{2}-2 X^{3} Z^{2}+6 X^{2} Y^{3}-2 X^{2} YZ^{2}+4 X Y^{4}+X Z^{4}+Y^{5}\;:\;Z (X^{4}+2 X^{3} Y+X^{2} Y^{2}-3 X^{2} Z^{2} -3 X Y Z^{2}+Z^{4})]$
. Define the projection by
![]() $\pi _P\;:\;[X\;:\;Y\;:\;Z]\mapsto [Y\;:\;Z]$
. Let
$\pi _P\;:\;[X\;:\;Y\;:\;Z]\mapsto [Y\;:\;Z]$
. Let
![]() $\psi =\pi _P\circ \phi$
then
$\psi =\pi _P\circ \phi$
then
![]() $\psi \;:\;\mathbb{P}^1\rightarrow \mathbb{P}^1$
maps
$\psi \;:\;\mathbb{P}^1\rightarrow \mathbb{P}^1$
maps
![]() $[u\;:\;v]$
to
$[u\;:\;v]$
to
![]() $[u^5:v^5]$
, hence the extension is Galois of degree
$[u^5:v^5]$
, hence the extension is Galois of degree
![]() $5$
with Galois group
$5$
with Galois group
![]() $G_{P}$
generated by
$G_{P}$
generated by
![]() $\sigma \;:\;x\mapsto \zeta \cdot x$
, where
$\sigma \;:\;x\mapsto \zeta \cdot x$
, where
![]() $\zeta$
is the
$\zeta$
is the
![]() $5$
th root of unity. We now prove that the curve
$5$
th root of unity. We now prove that the curve
![]() $C$
does not have a point
$C$
does not have a point
![]() $P$
of multiplicity
$P$
of multiplicity
![]() $m_P(C)\geq 3$
. By contradiction, we take a point
$m_P(C)\geq 3$
. By contradiction, we take a point
![]() $P=[P_0\;:\;P_1\;:\;P_2]$
of multiplicity
$P=[P_0\;:\;P_1\;:\;P_2]$
of multiplicity
![]() $3$
, and then we take two distinct lines
$3$
, and then we take two distinct lines
![]() $a_{1}x+a_{2}y-a_{3}z=0$
and
$a_{1}x+a_{2}y-a_{3}z=0$
and
![]() $b_{2}y-b_{3}z=0$
passing through the point
$b_{2}y-b_{3}z=0$
passing through the point
![]() $P$
. We take the preimage in
$P$
. We take the preimage in
![]() $\mathbb{P}^1$
, so we get a common factor of degree at least
$\mathbb{P}^1$
, so we get a common factor of degree at least
![]() $3$
. Let
$3$
. Let
![]() $f_{1}(u,v) = a_{1} \left (-u^{7}+u \,v^{6}\right )+a_{2} u^{5} \left (u^{2}+v^{2}\right )+a_{3} v^{5} \left (u^{2}+v^{2}\right )$
and
$f_{1}(u,v) = a_{1} \left (-u^{7}+u \,v^{6}\right )+a_{2} u^{5} \left (u^{2}+v^{2}\right )+a_{3} v^{5} \left (u^{2}+v^{2}\right )$
and
![]() $f_{2}(u,v) =\left (u^{2}+v^{2}\right ) \left (b_{2} u^{5}+b_{3} v^{5}\right )$
. We check now that it is not possible for the polynomials
$f_{2}(u,v) =\left (u^{2}+v^{2}\right ) \left (b_{2} u^{5}+b_{3} v^{5}\right )$
. We check now that it is not possible for the polynomials
![]() $f_1$
and
$f_1$
and
![]() $f_2$
to have a factor of degree
$f_2$
to have a factor of degree
![]() $3$
in common. Assume first that
$3$
in common. Assume first that
![]() $u +\mathrm{i} v$
divides both polynomials, so we should have
$u +\mathrm{i} v$
divides both polynomials, so we should have
![]() $f_{1}(1,\mathrm{i})=f_{2}(1,\mathrm{i})=0$
implies to
$f_{1}(1,\mathrm{i})=f_{2}(1,\mathrm{i})=0$
implies to
![]() $a_{1}=0$
, hence
$a_{1}=0$
, hence
![]() $P=[1\;:\;0\;:\;0]$
is a smooth point and this gives a contradiction. If we assume that
$P=[1\;:\;0\;:\;0]$
is a smooth point and this gives a contradiction. If we assume that
![]() $u -\mathrm{i} v$
divides both polynomials, then we should have
$u -\mathrm{i} v$
divides both polynomials, then we should have
![]() $f_{1}(1,-\mathrm{i})=f_{2}(1,-\mathrm{i})=0$
, again we have
$f_{1}(1,-\mathrm{i})=f_{2}(1,-\mathrm{i})=0$
, again we have
![]() $a_{1}=0$
, so the factor of degree
$a_{1}=0$
, so the factor of degree
![]() $3$
must divide
$3$
must divide
![]() $b_{2} u^{5}+b_{3} v^{5}$
. If we assume that
$b_{2} u^{5}+b_{3} v^{5}$
. If we assume that
![]() $u$
divides the polynomial
$u$
divides the polynomial
![]() $f_{2}$
, then
$f_{2}$
, then
![]() $b_{3}=0$
and
$b_{3}=0$
and
![]() $u^3$
should divide
$u^3$
should divide
![]() $f_{1}$
, but this is not true as
$f_{1}$
, but this is not true as
![]() $f_{1}=-u(u^6 - v^6)$
. If we assume that
$f_{1}=-u(u^6 - v^6)$
. If we assume that
![]() $v$
divides the polynomial
$v$
divides the polynomial
![]() $f_{2}$
, then
$f_{2}$
, then
![]() $b_{2}=0$
and
$b_{2}=0$
and
![]() $v^3$
should divide
$v^3$
should divide
![]() $f_{1}$
, but this is not true as
$f_{1}$
, but this is not true as
![]() $f_{1}=uv^2(u^4 + v^4)$
. So the factor of degree
$f_{1}=uv^2(u^4 + v^4)$
. So the factor of degree
![]() $3$
must divide
$3$
must divide
![]() $b_{2} u^{5}+b_{3} v^{5}$
,
$b_{2} u^{5}+b_{3} v^{5}$
,
![]() $b_{2}\neq 0$
and
$b_{2}\neq 0$
and
![]() $b_{3}\neq 0$
. Hence we can assume that
$b_{3}\neq 0$
. Hence we can assume that
![]() $a_{1}=1$
and replace
$a_{1}=1$
and replace
![]() $f_{1}$
by
$f_{1}$
by
![]() $f_{1}-a_{3}f_{2}/b_{3}$
so we can put
$f_{1}-a_{3}f_{2}/b_{3}$
so we can put
![]() $a_{3}=0$
and up to multiple, we can assume that
$a_{3}=0$
and up to multiple, we can assume that
![]() $b_{3}=1, a_{1}=1$
and
$b_{3}=1, a_{1}=1$
and
![]() $b_{2}=-\xi ^{5}$
. So
$b_{2}=-\xi ^{5}$
. So
![]() $f_{2}=-u^{5} \xi ^{5}+v^{5}$
,
$f_{2}=-u^{5} \xi ^{5}+v^{5}$
,
![]() $f_{1}=\left (-u^{7}+u \,v^{6}\right )+a_{2} u^{5} \left (u^{2}+v^{2}\right )$
this implies that the roots of
$f_{1}=\left (-u^{7}+u \,v^{6}\right )+a_{2} u^{5} \left (u^{2}+v^{2}\right )$
this implies that the roots of
![]() $f_{2}$
are
$f_{2}$
are
![]() $(u, v)=(1,\xi \zeta ^i)$
, where
$(u, v)=(1,\xi \zeta ^i)$
, where
![]() $\zeta$
is a
$\zeta$
is a
![]() $5$
th root of unity. Since
$5$
th root of unity. Since
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
should have three roots in common, therefore let
$f_{2}$
should have three roots in common, therefore let
![]() $\{(1,\xi ),(1,\xi \zeta ),(1,\xi \rho )\}$
are the three roots in common where
$\{(1,\xi ),(1,\xi \zeta ),(1,\xi \rho )\}$
are the three roots in common where
![]() $\rho ^5=1$
and
$\rho ^5=1$
and
![]() $\zeta ^5=1$
, and
$\zeta ^5=1$
, and
![]() $\rho ^5\neq \zeta$
and they are not equal to
$\rho ^5\neq \zeta$
and they are not equal to
![]() $1$
, so
$1$
, so
![]() $f_{1}$
should vanish on these three roots. This gives three equations
$f_{1}$
should vanish on these three roots. This gives three equations
![]() $ q_{1}=\xi ^{6}-1+a_{2} \left (\xi ^{2}+1\right )=0,\,q_{2}=a_{2} \left (\xi ^{2} \zeta ^{2}+1\right )+\xi ^{6} \zeta -1=0,\,q_{3}=a_{2} \left (\rho ^{2} \xi ^{2}+1\right )+\rho \,\xi ^{6}-1=0$
, by solving this system in
$ q_{1}=\xi ^{6}-1+a_{2} \left (\xi ^{2}+1\right )=0,\,q_{2}=a_{2} \left (\xi ^{2} \zeta ^{2}+1\right )+\xi ^{6} \zeta -1=0,\,q_{3}=a_{2} \left (\rho ^{2} \xi ^{2}+1\right )+\rho \,\xi ^{6}-1=0$
, by solving this system in
![]() $a_{2}, \zeta$
and
$a_{2}, \zeta$
and
![]() $\rho$
, we found that
$\rho$
, we found that
![]() $\zeta =\rho =(\xi ^{4}+1)/(\xi ^{6}-1)$
, which is a contradiction as
$\zeta =\rho =(\xi ^{4}+1)/(\xi ^{6}-1)$
, which is a contradiction as
![]() $\zeta \neq \rho$
. Finally,
$\zeta \neq \rho$
. Finally,
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
cannot have a factor of degree
$f_{2}$
cannot have a factor of degree
![]() $d\geq 3$
. Since
$d\geq 3$
. Since
![]() $m_P(C)\lt 3$
for each
$m_P(C)\lt 3$
for each
![]() $P\in \mathbb{P}^2$
, let us assume that there exists a birational map
$P\in \mathbb{P}^2$
, let us assume that there exists a birational map
![]() $g$
that extends the generator of the Galois group, then by Lemma 5.1,
$g$
that extends the generator of the Galois group, then by Lemma 5.1,
![]() $g$
is a linear automorphism of
$g$
is a linear automorphism of
![]() $\mathbb{P}^2$
, so it is given by a matrix let us say
$\mathbb{P}^2$
, so it is given by a matrix let us say
![]() $A\in \mathrm{PGL}_{3}$
, Since
$A\in \mathrm{PGL}_{3}$
, Since
![]() $g\circ \phi =\phi \circ \sigma$
, so we have
$g\circ \phi =\phi \circ \sigma$
, so we have
 \begin{equation*}\left [\begin {array}{c}U V^6-U^7 \\[5pt] U^5(U^2+V^2)\\[5pt] V^5(U^2+V^2)\end {array}\right ]=A\cdot \left [\begin {array}{c}\zeta U V^6-\zeta ^2 U^7 \\[5pt] U^5(\zeta ^2 U^2+V^2)\\[5pt] V^5(\zeta ^2 U^2+V^2) \end {array}\right ]\end{equation*}
\begin{equation*}\left [\begin {array}{c}U V^6-U^7 \\[5pt] U^5(U^2+V^2)\\[5pt] V^5(U^2+V^2)\end {array}\right ]=A\cdot \left [\begin {array}{c}\zeta U V^6-\zeta ^2 U^7 \\[5pt] U^5(\zeta ^2 U^2+V^2)\\[5pt] V^5(\zeta ^2 U^2+V^2) \end {array}\right ]\end{equation*}
where
![]() $\zeta$
is the
$\zeta$
is the
![]() $5th$
root of unity. Since
$5th$
root of unity. Since
![]() $ U V^6, U^7, U^5 V^2,$
and
$ U V^6, U^7, U^5 V^2,$
and
![]() $V^7$
are linearly independent, after checking the calculation we found that
$V^7$
are linearly independent, after checking the calculation we found that
![]() $A$
should be diagonal, but
$A$
should be diagonal, but
![]() $U^5(\zeta ^2 U^2+V^2)$
is not a multiple of
$U^5(\zeta ^2 U^2+V^2)$
is not a multiple of
![]() $U^5(\zeta ^2 U^2+V^2)$
, then we have a contradiction.
$U^5(\zeta ^2 U^2+V^2)$
, then we have a contradiction.
Acknowledgements
I would like to thank my PhD advisor Jérémy Blanc for suggesting the question and for interesting discussions during the preparation of this text. I would also like to thank the Department of Mathematics and Computer Science at Basel for the hospitality. Thanks also to the referee Gavin Brown for his remarks that helped to improve the presentation of the article.
The author acknowledges support from the Federal Commission for Scholarships for Foreign Students of Switzerland.