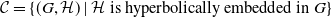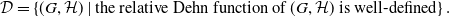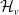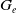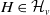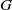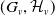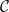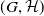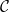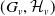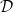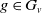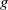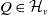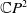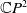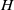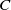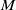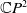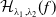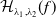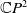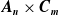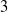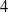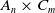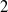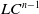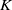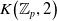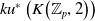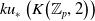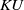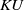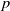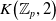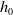Most read
This page lists the top ten most read articles for this journal based on the number of full text views and downloads recorded on Cambridge Core over the last 90 days. This list is updated on a daily basis.
Relative Dehn functions, hyperbolically embedded subgroups and combination theorems
- Part of:
-
- Published online by Cambridge University Press:
- 25 August 2023, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Null hypersurfaces in 4-manifolds endowed with a product structure
- Part of:
-
- Published online by Cambridge University Press:
- 28 September 2023, pp. 24-35
-
- Article
- Export citation
A Helfrich functional for compact surfaces in
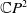 $\mathbb{C}P^{2}$
$\mathbb{C}P^{2}$
- Part of:
-
- Published online by Cambridge University Press:
- 04 October 2023, pp. 36-50
-
- Article
- Export citation
Autocorrelations of characteristic polynomials for the Alternative Circular Unitary Ensemble
- Part of:
-
- Published online by Cambridge University Press:
- 27 October 2023, pp. 51-64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tropical invariants for binary quintics and reduction types of Picard curves
- Part of:
-
- Published online by Cambridge University Press:
- 06 November 2023, pp. 65-87
-
- Article
- Export citation
Representatives of similarity classes of matrices over PIDs corresponding to ideal classes
- Part of:
-
- Published online by Cambridge University Press:
- 18 October 2023, pp. 88-103
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the reducing projective dimension over local rings
- Part of:
-
- Published online by Cambridge University Press:
- 31 October 2023, pp. 104-118
-
- Article
- Export citation
On
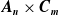 $\boldsymbol{A}_{\boldsymbol{n}} \times \boldsymbol{C}_{\boldsymbol{m}}$-unramified extensions over imaginary quadratic fields
$\boldsymbol{A}_{\boldsymbol{n}} \times \boldsymbol{C}_{\boldsymbol{m}}$-unramified extensions over imaginary quadratic fields
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2023, pp. 119-125
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Notes on hyperelliptic mapping class groups
- Part of:
-
- Published online by Cambridge University Press:
- 31 October 2023, pp. 126-161
-
- Article
- Export citation
A natural pseudometric on homotopy groups of metric spaces
- Part of:
-
- Published online by Cambridge University Press:
- 08 November 2023, pp. 162-174
-
- Article
- Export citation
A classification of some thick subcategories in locally noetherian Grothendieck categories
- Part of:
-
- Published online by Cambridge University Press:
- 23 November 2023, pp. 175-182
-
- Article
- Export citation
A note on almost Yamabe solitons
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2023, pp. 183-187
-
- Article
- Export citation
The connective
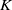 $K$-theory of the Eilenberg–MacLane space
$K$-theory of the Eilenberg–MacLane space 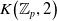 $K\!\left({\mathbb{Z}}_p,\textrm{2}\right)$
$K\!\left({\mathbb{Z}}_p,\textrm{2}\right)$
- Part of:
-
- Published online by Cambridge University Press:
- 11 December 2023, pp. 188-220
-
- Article
- Export citation
On a variant of the product replacement algorithm
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2024, pp. 221-228
-
- Article
- Export citation
GMJ volume 66 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 26 February 2024, pp. f1-f2
-
- Article
-
- You have access
- Export citation
GMJ volume 66 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 26 February 2024, pp. b1-b2
-
- Article
-
- You have access
- Export citation