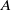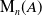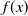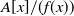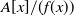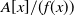1. Introduction
Latimer and MacDuffee [Reference Latimer and MacDuffee4] showed that there is a bijection between the similarity classes of matrices with integer entries (i.e. the orbits under the action of
![]() $\textrm{GL}_{n}({\mathbb{Z}})$
on
$\textrm{GL}_{n}({\mathbb{Z}})$
on
![]() $\textrm{M}_{n}({\mathbb{Z}})$
by conjugation) with irreducible characteristic polynomial
$\textrm{M}_{n}({\mathbb{Z}})$
by conjugation) with irreducible characteristic polynomial
![]() $f(x)\in{\mathbb{Z}}[x]$
and the ideal classes of the order
$f(x)\in{\mathbb{Z}}[x]$
and the ideal classes of the order
![]() ${\mathbb{Z}}[x]/(f(x))$
. Another proof of this was given by Taussky [Reference Taussky15]. Later, generalisations show that the correspondence also holds when
${\mathbb{Z}}[x]/(f(x))$
. Another proof of this was given by Taussky [Reference Taussky15]. Later, generalisations show that the correspondence also holds when
![]() $\mathbb{Z}$
is replaced by an arbitrary principal ideal domain (PID); see Section 3.
$\mathbb{Z}$
is replaced by an arbitrary principal ideal domain (PID); see Section 3.
In [Reference Ochoa10], Ochoa claimed that every similarity class with characteristic polynomial
![]() $f(x)$
contains a representative of the form
$f(x)$
contains a representative of the form

where
![]() $a,z\in{\mathbb{Z}}$
are such that
$a,z\in{\mathbb{Z}}$
are such that
![]() $a$
divides
$a$
divides
![]() $f(z)$
and the
$f(z)$
and the
![]() $u_i\in{\mathbb{Z}}$
are explicitly determined by
$u_i\in{\mathbb{Z}}$
are explicitly determined by
![]() $f(x)$
and
$f(x)$
and
![]() $z$
(see Lemma 5.1). For the case of
$z$
(see Lemma 5.1). For the case of
![]() $n=2$
,
$n=2$
,
 \begin{equation*} C_{f}(a,z)=\begin {pmatrix} u_1 & -f(z)a^{-1}\\[5pt] a & z \end {pmatrix} \end{equation*}
\begin{equation*} C_{f}(a,z)=\begin {pmatrix} u_1 & -f(z)a^{-1}\\[5pt] a & z \end {pmatrix} \end{equation*}
is a general
![]() $2\times 2$
matrix over
$2\times 2$
matrix over
![]() $\mathbb{Z}$
; that is, any
$\mathbb{Z}$
; that is, any
![]() $2\times 2$
matrix is already of the form
$2\times 2$
matrix is already of the form
![]() $C_{f}(a,z)$
for some
$C_{f}(a,z)$
for some
![]() $a,z\in{\mathbb{Z}}$
, so it is trivial that every similarity class contains such a representative. Note that since
$a,z\in{\mathbb{Z}}$
, so it is trivial that every similarity class contains such a representative. Note that since
![]() $f(x)$
is irreducible,
$f(x)$
is irreducible,
![]() $C_{f}(a,z)$
is
$C_{f}(a,z)$
is
![]() $\textrm{GL}_{n}({\mathbb{Q}})$
-similar to the companion matrix of
$\textrm{GL}_{n}({\mathbb{Q}})$
-similar to the companion matrix of
![]() $f(x)$
and that if
$f(x)$
and that if
![]() $f(z)a^{-1}=\pm 1$
, then
$f(z)a^{-1}=\pm 1$
, then
![]() $C_{f}(a,z)$
is
$C_{f}(a,z)$
is
![]() $\textrm{GL}_{n}({\mathbb{Z}})$
-similar to the companion matrix of
$\textrm{GL}_{n}({\mathbb{Z}})$
-similar to the companion matrix of
![]() $f(x)$
. In general, it is often of great value to have a normal form for matrices under similarity. Ochoa’s motivation was to give an explicit version of the Latimer–MacDuffee correspondence and transfer the structure of the ideal class monoid of
$f(x)$
. In general, it is often of great value to have a normal form for matrices under similarity. Ochoa’s motivation was to give an explicit version of the Latimer–MacDuffee correspondence and transfer the structure of the ideal class monoid of
![]() ${\mathbb{Z}}[x]/(f(x))$
to sets of matrices of the form
${\mathbb{Z}}[x]/(f(x))$
to sets of matrices of the form
![]() $C_{f}(a,z)$
, up to similarity. Unfortunately, [Reference Ochoa10] contains several mistakes (e.g. Theorem I-4 is not true) and while Ochoa’s follow-up paper [Reference Ochoa11] was an attempt to rectify some of these mistakes, this was ultimately inconclusive, as already the central Lemma I-1 in [Reference Ochoa11] has a counter-example (see Rehm’s review [Reference Rehm12] of [Reference Ochoa11]).
$C_{f}(a,z)$
, up to similarity. Unfortunately, [Reference Ochoa10] contains several mistakes (e.g. Theorem I-4 is not true) and while Ochoa’s follow-up paper [Reference Ochoa11] was an attempt to rectify some of these mistakes, this was ultimately inconclusive, as already the central Lemma I-1 in [Reference Ochoa11] has a counter-example (see Rehm’s review [Reference Rehm12] of [Reference Ochoa11]).
It seems that the approach in [Reference Ochoa10] and [Reference Ochoa11] is not salvageable. On the other hand, Rehm [Reference Rehm13] did establish Ochoa’s claim that every similarity class as above contains a representative of the form
![]() $C_{f}(a,z)$
under the (necessary) condition that
$C_{f}(a,z)$
under the (necessary) condition that
![]() ${\mathbb{Z}}[x]/(f(x))$
is the maximal order (i.e. the ring of integers) of the number field
${\mathbb{Z}}[x]/(f(x))$
is the maximal order (i.e. the ring of integers) of the number field
![]() ${\mathbb{Q}}[x]/(f(x))$
. (Note that Rehm used conventions that led to the transpose of
${\mathbb{Q}}[x]/(f(x))$
. (Note that Rehm used conventions that led to the transpose of
![]() $C_{f}(a,z)$
.)
$C_{f}(a,z)$
.)
The purpose of this paper is to generalise Rehm’s result to the case where
![]() $\mathbb{Z}$
is replaced by an arbitrary PID. Our main result is Theorem 5.2. The most serious obstacle to such a generalisation is Rehm’s use of the fact that every ideal class in the ring of integers of a number field contains a prime ideal of degree one. The classical proofs of this fact are rather non-trivial, based either on the Chebotarev density theorem or on analytic properties of the Dedekind zeta function, and it is not clear whether an analogous proof exists in the more algebraic setting of an arbitrary PID. Nevertheless, Rehm showed more generally (i.e. when
$\mathbb{Z}$
is replaced by an arbitrary PID. Our main result is Theorem 5.2. The most serious obstacle to such a generalisation is Rehm’s use of the fact that every ideal class in the ring of integers of a number field contains a prime ideal of degree one. The classical proofs of this fact are rather non-trivial, based either on the Chebotarev density theorem or on analytic properties of the Dedekind zeta function, and it is not clear whether an analogous proof exists in the more algebraic setting of an arbitrary PID. Nevertheless, Rehm showed more generally (i.e. when
![]() ${\mathbb{Z}}[x]/(f(x))$
is not necessarily maximal) that any similarity class corresponding to an ideal class containing an ideal of the form
${\mathbb{Z}}[x]/(f(x))$
is not necessarily maximal) that any similarity class corresponding to an ideal class containing an ideal of the form
![]() $\mathfrak{q}_{1}\cdots \mathfrak{q}_{r}$
, where
$\mathfrak{q}_{1}\cdots \mathfrak{q}_{r}$
, where
![]() $r\in{\mathbb{N}}$
, each
$r\in{\mathbb{N}}$
, each
![]() $\mathfrak{q}_{i}$
is a prime ideal of degree one and the
$\mathfrak{q}_{i}$
is a prime ideal of degree one and the
![]() $\mathfrak{q}_{i}$
lies over pairwise distinct primes, contains a matrix
$\mathfrak{q}_{i}$
lies over pairwise distinct primes, contains a matrix
![]() ${\mathcal{C}}_{f}(a,z)$
(see [Reference Rehm13, Theorem 2]; note again that Rehm used the transposed matrix). Rehm’s proof of this fact goes through without difficulty for the order
${\mathcal{C}}_{f}(a,z)$
(see [Reference Rehm13, Theorem 2]; note again that Rehm used the transposed matrix). Rehm’s proof of this fact goes through without difficulty for the order
![]() $A[x]/(f(x))$
, where
$A[x]/(f(x))$
, where
![]() $A$
is an arbitrary PID and
$A$
is an arbitrary PID and
![]() $f(x)\in A[x]$
is irreducible. It is however not clear (and perhaps not even true) that if
$f(x)\in A[x]$
is irreducible. It is however not clear (and perhaps not even true) that if
![]() $A[x]/(f(x))$
is assumed to be the maximal order, hence a Dedekind domain, then each of its ideal classes contains an ideal of the form
$A[x]/(f(x))$
is assumed to be the maximal order, hence a Dedekind domain, then each of its ideal classes contains an ideal of the form
![]() $\mathfrak{q}_{1}\cdots \mathfrak{q}_{r}$
, as above.
$\mathfrak{q}_{1}\cdots \mathfrak{q}_{r}$
, as above.
Generalising [Reference Rehm13, Theorem 2], we show that any similarity class in
![]() $\textrm{M}_{n}(A)$
corresponding to an ideal class of
$\textrm{M}_{n}(A)$
corresponding to an ideal class of
![]() $A[x]/(f(x))$
containing an ideal of the form
$A[x]/(f(x))$
containing an ideal of the form
where
![]() $r\in{\mathbb{N}}\cup \{0\}$
,
$r\in{\mathbb{N}}\cup \{0\}$
,
![]() $e_{i}\in{\mathbb{N}}$
, each
$e_{i}\in{\mathbb{N}}$
, each
![]() $\mathfrak{q}_{i}$
is a prime ideal of degree one and of ramification index one, and the
$\mathfrak{q}_{i}$
is a prime ideal of degree one and of ramification index one, and the
![]() $\mathfrak{q}_{i}$
lies over pairwise distinct primes, contains a matrix
$\mathfrak{q}_{i}$
lies over pairwise distinct primes, contains a matrix
![]() ${\mathcal{C}}_{f}(a,z)$
(note that when
${\mathcal{C}}_{f}(a,z)$
(note that when
![]() $r=0$
we have the empty product
$r=0$
we have the empty product
![]() $(1)$
, which lies in the trivial ideal class). The main point here is that, unlike Rehm, we allow higher powers of our prime ideals. We prove this by working with “ideals (not necessarily prime) of degree one”. If
$(1)$
, which lies in the trivial ideal class). The main point here is that, unlike Rehm, we allow higher powers of our prime ideals. We prove this by working with “ideals (not necessarily prime) of degree one”. If
![]() $A$
is a Dedekind domain with field of fractions
$A$
is a Dedekind domain with field of fractions
![]() $K$
,
$K$
,
![]() $L/K$
is a finite separable extension and
$L/K$
is a finite separable extension and
![]() $B$
is the integral closure of
$B$
is the integral closure of
![]() $A$
in
$A$
in
![]() $L$
, then it is standard to say that a prime ideal
$L$
, then it is standard to say that a prime ideal
![]() $\mathfrak{q}$
of
$\mathfrak{q}$
of
![]() $B$
is of degree one if
$B$
is of degree one if
![]() $[B/\mathfrak{q}:A/(A\cap \mathfrak{q})]=1$
. As a generalisation of this, we say that a proper ideal
$[B/\mathfrak{q}:A/(A\cap \mathfrak{q})]=1$
. As a generalisation of this, we say that a proper ideal
![]() $\mathfrak{b}$
of
$\mathfrak{b}$
of
![]() $B$
is of degree one if
$B$
is of degree one if
![]() $A+\mathfrak{b}=B$
, that is, if the inclusion of
$A+\mathfrak{b}=B$
, that is, if the inclusion of
![]() $A/(A\cap \mathfrak{b})$
in
$A/(A\cap \mathfrak{b})$
in
![]() $B/\mathfrak{b}$
is an isomorphism. It turns out that ideals of the form
$B/\mathfrak{b}$
is an isomorphism. It turns out that ideals of the form
![]() $\mathfrak{q}_{1}^{e_{1}}\cdots \mathfrak{q}_{r}^{e_{r}}$
, as above, are of degree one. In fact, we prove that any similarity class corresponding to an ideal class containing an ideal of degree one contains a matrix
$\mathfrak{q}_{1}^{e_{1}}\cdots \mathfrak{q}_{r}^{e_{r}}$
, as above, are of degree one. In fact, we prove that any similarity class corresponding to an ideal class containing an ideal of degree one contains a matrix
![]() $C_{f}(a,z)$
.
$C_{f}(a,z)$
.
To prove that every similarity class contains a matrix
![]() $C_{f}(a,z)$
when
$C_{f}(a,z)$
when
![]() $A[x]/(f(x))$
is the maximal order, it remains to show that in this case, every ideal class contains an ideal of the form
$A[x]/(f(x))$
is the maximal order, it remains to show that in this case, every ideal class contains an ideal of the form
![]() $\mathfrak{q}_{1}^{e_{1}}\cdots \mathfrak{q}_{r}^{e_{r}}$
, as above. This is achieved by a result of Lenstra (Theorem 2.7), which is a strengthening of a previous result of Lenstra–Stevenhagen [Reference Lenstra and Stevenhagen5, Theorem 1] with the extra condition that the prime ideals lie over pairwise distinct primes. The proof of Theorem 2.7 was previously unpublished and kindly communicated to us by Lenstra.
$\mathfrak{q}_{1}^{e_{1}}\cdots \mathfrak{q}_{r}^{e_{r}}$
, as above. This is achieved by a result of Lenstra (Theorem 2.7), which is a strengthening of a previous result of Lenstra–Stevenhagen [Reference Lenstra and Stevenhagen5, Theorem 1] with the extra condition that the prime ideals lie over pairwise distinct primes. The proof of Theorem 2.7 was previously unpublished and kindly communicated to us by Lenstra.
2. Ideals of degree one
Let
![]() $A$
be a Dedekind domain with field of fractions
$A$
be a Dedekind domain with field of fractions
![]() $K$
, let
$K$
, let
![]() $L/K$
be a finite separable field extension of degree
$L/K$
be a finite separable field extension of degree
![]() $n$
and let
$n$
and let
![]() $B$
be the integral closure of
$B$
be the integral closure of
![]() $A$
in
$A$
in
![]() $L$
. Then
$L$
. Then
![]() $B$
is a Dedekind domain (see [Reference Lorenzini6, I.6.2]). An
$B$
is a Dedekind domain (see [Reference Lorenzini6, I.6.2]). An
![]() $A$
-order in
$A$
-order in
![]() $L$
is a subring
$L$
is a subring
![]() $\mathcal{O}$
of
$\mathcal{O}$
of
![]() $L$
that is a finitely generated
$L$
that is a finitely generated
![]() $A$
-module such that
$A$
-module such that
![]() $K{\mathcal{O}}=L$
. In particular,
$K{\mathcal{O}}=L$
. In particular,
![]() $B$
is an
$B$
is an
![]() $A$
-order in
$A$
-order in
![]() $L$
([Reference Lorenzini6, I.4.7]). Moreover, every element of an
$L$
([Reference Lorenzini6, I.4.7]). Moreover, every element of an
![]() $A$
-order
$A$
-order
![]() $\mathcal{O}$
is integral over
$\mathcal{O}$
is integral over
![]() $A$
(see [Reference Reiner14, (8.6)]), so
$A$
(see [Reference Reiner14, (8.6)]), so
![]() ${\mathcal{O}}\subseteq B$
. Let
${\mathcal{O}}\subseteq B$
. Let
![]() $\theta \in B$
be such that
$\theta \in B$
be such that
![]() $L=K(\theta )$
; then
$L=K(\theta )$
; then
![]() $A[\theta ]$
is an
$A[\theta ]$
is an
![]() $A$
-order in
$A$
-order in
![]() $L$
.
$L$
.
Definition 2.1.
Let
![]() $\mathcal{O}$
be an
$\mathcal{O}$
be an
![]() $A$
-order in
$A$
-order in
![]() $L$
. A proper ideal
$L$
. A proper ideal
![]() $\mathfrak{b}$
of
$\mathfrak{b}$
of
![]() $\mathcal{O}$
is said to be of degree one (over
$\mathcal{O}$
is said to be of degree one (over
![]() $A$
) if
$A$
) if
![]() $A+\mathfrak{b}={\mathcal{O}}$
.
$A+\mathfrak{b}={\mathcal{O}}$
.
By the second isomorphism theorem,
![]() $(A+\mathfrak{b})/\mathfrak{b}\cong A/(A\cap \mathfrak{b})$
, so
$(A+\mathfrak{b})/\mathfrak{b}\cong A/(A\cap \mathfrak{b})$
, so
![]() $\mathfrak{b}$
is of degree one if and only if the map
$\mathfrak{b}$
is of degree one if and only if the map
![]() $A/(A\cap \mathfrak{b})\rightarrow{\mathcal{O}}/\mathfrak{b}$
induced by the embedding
$A/(A\cap \mathfrak{b})\rightarrow{\mathcal{O}}/\mathfrak{b}$
induced by the embedding
![]() $A\rightarrow{\mathcal{O}}$
is an isomorphism. Thus, the notion of an ideal of degree one generalises the standard notion of a prime ideal of degree one.
$A\rightarrow{\mathcal{O}}$
is an isomorphism. Thus, the notion of an ideal of degree one generalises the standard notion of a prime ideal of degree one.
Lemma 2.2.
Let
![]() $\mathfrak{b}$
be an ideal of
$\mathfrak{b}$
be an ideal of
![]() $A[\theta ]$
and
$A[\theta ]$
and
![]() $\mathfrak{a}=A\cap \mathfrak{b}$
. Suppose that there exists a
$\mathfrak{a}=A\cap \mathfrak{b}$
. Suppose that there exists a
![]() $z\in A$
such that
$z\in A$
such that
![]() $\theta -z\in \mathfrak{b}$
. Then, the embedding
$\theta -z\in \mathfrak{b}$
. Then, the embedding
![]() $A\rightarrow A[\theta ]$
induces an isomorphism
$A\rightarrow A[\theta ]$
induces an isomorphism
![]() $A/\mathfrak{a}\rightarrow A[\theta ]/(\theta -z,\mathfrak{a})$
and
$A/\mathfrak{a}\rightarrow A[\theta ]/(\theta -z,\mathfrak{a})$
and
![]() $\mathfrak{b}=(\theta -z,\mathfrak{a})$
.
$\mathfrak{b}=(\theta -z,\mathfrak{a})$
.
Proof. We have
![]() $\mathfrak{b}\supseteq (\theta -z,\mathfrak{a})$
, so
$\mathfrak{b}\supseteq (\theta -z,\mathfrak{a})$
, so
and thus
![]() $\mathfrak{a}=A\cap (\theta -z,\mathfrak{a})$
. This implies that the map
$\mathfrak{a}=A\cap (\theta -z,\mathfrak{a})$
. This implies that the map
![]() $A/\mathfrak{a}\rightarrow A[\theta ]/(\theta -z,\mathfrak{a})$
is injective. The map is also surjective, as for any
$A/\mathfrak{a}\rightarrow A[\theta ]/(\theta -z,\mathfrak{a})$
is injective. The map is also surjective, as for any
![]() $g(x)\in A[x]$
, we have
$g(x)\in A[x]$
, we have
![]() $g(\theta )-g(z)\in (\theta -z,\mathfrak{a})$
, so
$g(\theta )-g(z)\in (\theta -z,\mathfrak{a})$
, so
![]() $g(z)+\mathfrak{a}\in A/\mathfrak{a}$
maps to
$g(z)+\mathfrak{a}\in A/\mathfrak{a}$
maps to
![]() $g(\theta )+(\theta -z,\mathfrak{a})\in A[\theta ]/(\theta -z,\mathfrak{a})$
. We thus have a commutative diagram
$g(\theta )+(\theta -z,\mathfrak{a})\in A[\theta ]/(\theta -z,\mathfrak{a})$
. We thus have a commutative diagram
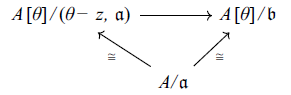
implying that the top surjective map must be an isomorphism, that is,
Lemma 2.3.
Let
![]() $\mathfrak{b}$
be a proper ideal of
$\mathfrak{b}$
be a proper ideal of
![]() $A[\theta ]$
and
$A[\theta ]$
and
![]() $\mathfrak{a}=A\cap \mathfrak{b}$
. Then,
$\mathfrak{a}=A\cap \mathfrak{b}$
. Then,
![]() $\mathfrak{b}$
is of degree one if and only if there exists a
$\mathfrak{b}$
is of degree one if and only if there exists a
![]() $z\in A$
such that
$z\in A$
such that
![]() $\mathfrak{b}=(\theta -z,\mathfrak{a})$
.
$\mathfrak{b}=(\theta -z,\mathfrak{a})$
.
Proof. Assume that
![]() $\mathfrak{b}$
is of degree one and choose
$\mathfrak{b}$
is of degree one and choose
![]() $z\in A$
such that
$z\in A$
such that
![]() $\theta \in z+\mathfrak{b}$
. Since
$\theta \in z+\mathfrak{b}$
. Since
![]() $\theta -z\in \mathfrak{b}$
, Lemma 2.2 implies that
$\theta -z\in \mathfrak{b}$
, Lemma 2.2 implies that
![]() $\mathfrak{b}=(\theta -z,\mathfrak{a}).$
$\mathfrak{b}=(\theta -z,\mathfrak{a}).$
Conversely, assume that there is a
![]() $z\in A$
such that
$z\in A$
such that
![]() $\mathfrak{b}=(\theta -z,\mathfrak{a})$
. By Lemma 2.2,
$\mathfrak{b}=(\theta -z,\mathfrak{a})$
. By Lemma 2.2,
![]() $A/\mathfrak{a}\rightarrow A[\theta ]/(\theta -z,\mathfrak{a})=A[\theta ]/\mathfrak{b}$
is an isomorphism. Thus,
$A/\mathfrak{a}\rightarrow A[\theta ]/(\theta -z,\mathfrak{a})=A[\theta ]/\mathfrak{b}$
is an isomorphism. Thus,
![]() $\mathfrak{b}$
is of degree one, as it is a proper ideal.
$\mathfrak{b}$
is of degree one, as it is a proper ideal.
Recall that a prime ideal
![]() $\mathfrak{q}$
of
$\mathfrak{q}$
of
![]() $B$
has ramification index one (over
$B$
has ramification index one (over
![]() $A)$
if it appears with exponent
$A)$
if it appears with exponent
![]() $1$
in the prime ideal decomposition of
$1$
in the prime ideal decomposition of
![]() $(A\cap \mathfrak{q})B$
, and it is called unramified if, in addition, the field extension
$(A\cap \mathfrak{q})B$
, and it is called unramified if, in addition, the field extension
![]() $(B/\mathfrak{q})/(A/(A\cap \mathfrak{q}))$
is separable (see [Reference Neukirch8, Chapter I, (8.3)]).
$(B/\mathfrak{q})/(A/(A\cap \mathfrak{q}))$
is separable (see [Reference Neukirch8, Chapter I, (8.3)]).
Proposition 2.4.
If
![]() $\mathfrak{b}$
is an ideal of
$\mathfrak{b}$
is an ideal of
![]() $B$
of degree one, then each of its prime ideal factors is of degree one. Moreover, if
$B$
of degree one, then each of its prime ideal factors is of degree one. Moreover, if
![]() $\mathfrak{q}_{1},\ldots,\mathfrak{q}_{r}$
are prime ideals of
$\mathfrak{q}_{1},\ldots,\mathfrak{q}_{r}$
are prime ideals of
![]() $B$
lying over distinct primes in
$B$
lying over distinct primes in
![]() $A$
(i.e.
$A$
(i.e.
![]() $A\cap \mathfrak{q}_{i}\neq A\cap \mathfrak{q}_{j}$
for
$A\cap \mathfrak{q}_{i}\neq A\cap \mathfrak{q}_{j}$
for
![]() $i\neq j$
), and each
$i\neq j$
), and each
![]() $\mathfrak{q}_{i}$
is of degree one and has ramification index one, then
$\mathfrak{q}_{i}$
is of degree one and has ramification index one, then
![]() $\mathfrak{q}_{1}^{e_{1}}\cdots \mathfrak{q}_{r}^{e_{r}}$
is of degree one for any
$\mathfrak{q}_{1}^{e_{1}}\cdots \mathfrak{q}_{r}^{e_{r}}$
is of degree one for any
![]() $e_{i}\in{\mathbb{N}}$
.
$e_{i}\in{\mathbb{N}}$
.
Proof. Assume that
![]() $\mathfrak{b}$
is of degree one, let
$\mathfrak{b}$
is of degree one, let
![]() $\mathfrak{q}$
be a prime ideal factor and write
$\mathfrak{q}$
be a prime ideal factor and write
![]() $\mathfrak{b}=\mathfrak{q}\mathfrak{b}'$
, for some ideal
$\mathfrak{b}=\mathfrak{q}\mathfrak{b}'$
, for some ideal
![]() $\mathfrak{b}'$
. Since
$\mathfrak{b}'$
. Since
![]() $\mathfrak{b}$
is of degree one, we have
$\mathfrak{b}$
is of degree one, we have
![]() $A+\mathfrak{q}\mathfrak{b}'=B$
and thus (as
$A+\mathfrak{q}\mathfrak{b}'=B$
and thus (as
![]() $\mathfrak{q}\mathfrak{b}'\subseteq \mathfrak{q}$
)
$\mathfrak{q}\mathfrak{b}'\subseteq \mathfrak{q}$
)
that is,
![]() $\mathfrak{q}$
is of degree one. This proves the first assertion.
$\mathfrak{q}$
is of degree one. This proves the first assertion.
For the second assertion, it is enough to prove the following two statements:
-
1. If
 $\mathfrak{q}$
is a prime ideal of
$\mathfrak{q}$
is a prime ideal of
 $B$
of degree one and ramification index one, then
$B$
of degree one and ramification index one, then
 $\mathfrak{q}^{e}$
is of degree one, for all
$\mathfrak{q}^{e}$
is of degree one, for all
 $e\in{\mathbb{N}}$
.
$e\in{\mathbb{N}}$
. -
2. If
 $\mathfrak{b}$
and
$\mathfrak{b}$
and
 $\mathfrak{c}$
are two ideals of
$\mathfrak{c}$
are two ideals of
 $B$
of degree one such that
$B$
of degree one such that
 $A\cap \mathfrak{b}$
is coprime to
$A\cap \mathfrak{b}$
is coprime to
 $A\cap \mathfrak{c}$
, then
$A\cap \mathfrak{c}$
, then
 $\mathfrak{b}\mathfrak{c}$
is of degree one.
$\mathfrak{b}\mathfrak{c}$
is of degree one.
To prove (1), let
![]() $\mathfrak{p}=A\cap \mathfrak{q}$
. Then,
$\mathfrak{p}=A\cap \mathfrak{q}$
. Then,
![]() $\mathfrak{p}^{e}\subseteq A\cap \mathfrak{q}^{e}$
, so
$\mathfrak{p}^{e}\subseteq A\cap \mathfrak{q}^{e}$
, so
![]() $A\cap \mathfrak{q}^{e}=\mathfrak{p}^{m}$
, for some
$A\cap \mathfrak{q}^{e}=\mathfrak{p}^{m}$
, for some
![]() $m\leq e$
. Further, we have
$m\leq e$
. Further, we have
and since
![]() $\mathfrak{q}$
has ramification index one, it appears with multiplicity
$\mathfrak{q}$
has ramification index one, it appears with multiplicity
![]() $m$
in
$m$
in
![]() $(\mathfrak{p} B)^{m}$
, hence
$(\mathfrak{p} B)^{m}$
, hence
![]() $e\leq m$
, forcing
$e\leq m$
, forcing
![]() $m=e$
, so that
$m=e$
, so that
In order to to prove that
![]() $\mathfrak{q}^{e}$
is of degree one, we thus need to show that
$\mathfrak{q}^{e}$
is of degree one, we thus need to show that
![]() $A/\mathfrak{p}^{e}\rightarrow B/\mathfrak{q}^{e}$
is surjective (i.e. an isomorphism). We do this by induction on
$A/\mathfrak{p}^{e}\rightarrow B/\mathfrak{q}^{e}$
is surjective (i.e. an isomorphism). We do this by induction on
![]() $e$
, the case
$e$
, the case
![]() $e=1$
holding because of the hypothesis that
$e=1$
holding because of the hypothesis that
![]() $\mathfrak{q}$
is of degree one. Assume that the map is surjective for some
$\mathfrak{q}$
is of degree one. Assume that the map is surjective for some
![]() $i\geq 1$
and consider the commutative diagram
$i\geq 1$
and consider the commutative diagram

If the leftmost vertical inclusion is surjective then the middle one is as well and we will be done. But
![]() $\mathfrak{p}^{i}/\mathfrak{p}^{i+1}$
is a vector space over
$\mathfrak{p}^{i}/\mathfrak{p}^{i+1}$
is a vector space over
![]() $A/\mathfrak{p}$
of dimension
$A/\mathfrak{p}$
of dimension
![]() $1$
(since
$1$
(since
![]() $A$
is of dimension
$A$
is of dimension
![]() $1$
), and similarly,
$1$
), and similarly,
![]() $\mathfrak{q}^{i}/\mathfrak{q}^{i+1}$
is a vector space over
$\mathfrak{q}^{i}/\mathfrak{q}^{i+1}$
is a vector space over
![]() $B/\mathfrak{q}$
of dimension
$B/\mathfrak{q}$
of dimension
![]() $1$
. But
$1$
. But
![]() $A/\mathfrak{p}\rightarrow B/\mathfrak{q}$
is an isomorphism, as
$A/\mathfrak{p}\rightarrow B/\mathfrak{q}$
is an isomorphism, as
![]() $\mathfrak{q}$
is of degree one, and this isomorphism is compatible with the leftmost vertical inclusion, which is therefore an injective linear map of
$\mathfrak{q}$
is of degree one, and this isomorphism is compatible with the leftmost vertical inclusion, which is therefore an injective linear map of
![]() $A/\mathfrak{p}$
-vector spaces of dimension
$A/\mathfrak{p}$
-vector spaces of dimension
![]() $1$
and is hence surjective. Thus,
$1$
and is hence surjective. Thus,
![]() $\mathfrak{q}^{e}$
has degree one for all
$\mathfrak{q}^{e}$
has degree one for all
![]() $e\in{\mathbb{N}}$
.
$e\in{\mathbb{N}}$
.
We now prove (2). Since
![]() $A\cap \mathfrak{b}$
is assumed to be coprime to
$A\cap \mathfrak{b}$
is assumed to be coprime to
![]() $A\cap \mathfrak{c}$
we have that
$A\cap \mathfrak{c}$
we have that
![]() $\mathfrak{b}$
is coprime to
$\mathfrak{b}$
is coprime to
![]() $\mathfrak{c}$
. By the Chinese Remainder Theorem, we thus have
$\mathfrak{c}$
. By the Chinese Remainder Theorem, we thus have
as well as the fact that products of coprime ideals are intersections, so that
and
We thus have a commutative diagram

where the rightmost inclusion is given by the inclusions in each component. This diagram immediately implies that
![]() $\mathfrak{b}\mathfrak{c}$
is of degree one, since
$\mathfrak{b}\mathfrak{c}$
is of degree one, since
![]() $\mathfrak{b}$
and
$\mathfrak{b}$
and
![]() $\mathfrak{c}$
are.
$\mathfrak{c}$
are.
Remark.
It is not true that every prime ideal factor of an ideal of
![]() $B$
of degree one has ramification index one. For example, any ramified prime ideal of a quadratic number field has degree one (over
$B$
of degree one has ramification index one. For example, any ramified prime ideal of a quadratic number field has degree one (over
![]() $\mathbb{Z}$
).
$\mathbb{Z}$
).
2.1. Every ideal class contains an ideal of degree one
This section contains a proof of the following result of Lenstra. Let
![]() $S$
be a finite set of prime ideals of
$S$
be a finite set of prime ideals of
![]() $B$
. Then, every ideal class of
$B$
. Then, every ideal class of
![]() $B$
contains an ideal of the form
$B$
contains an ideal of the form
where
![]() $r\in{\mathbb{N}}\cup \{0\}$
,
$r\in{\mathbb{N}}\cup \{0\}$
,
![]() $e_{i}\in{\mathbb{N}}$
, each
$e_{i}\in{\mathbb{N}}$
, each
![]() $\mathfrak{q}_{i}$
is a prime ideal of
$\mathfrak{q}_{i}$
is a prime ideal of
![]() $B$
of degree one such that
$B$
of degree one such that
![]() $\mathfrak{q}_{i}\not \in S$
and the
$\mathfrak{q}_{i}\not \in S$
and the
![]() $\mathfrak{q}_{i}$
lies over pairwise distinct prime ideals of
$\mathfrak{q}_{i}$
lies over pairwise distinct prime ideals of
![]() $A$
, that is,
$A$
, that is,
![]() $A\cap \mathfrak{q}_{i}\neq A\cap \mathfrak{q}_{j}$
unless
$A\cap \mathfrak{q}_{i}\neq A\cap \mathfrak{q}_{j}$
unless
![]() $i=j$
. Note that we allow the empty product
$i=j$
. Note that we allow the empty product
![]() $(1)=B$
when
$(1)=B$
when
![]() $r=0$
, so the trivial ideal class is covered. As is easily seen, this result is equivalent to Theorem 2.7, but in the proof it is more convenient to use the formulation of the latter. The proof builds on and strengthens a previous result of Lenstra and Stevenhagen [Reference Lenstra and Stevenhagen5, Theorem 1]. The following two lemmas on which Theorem 2.7 depends are also due to Lenstra.
$r=0$
, so the trivial ideal class is covered. As is easily seen, this result is equivalent to Theorem 2.7, but in the proof it is more convenient to use the formulation of the latter. The proof builds on and strengthens a previous result of Lenstra and Stevenhagen [Reference Lenstra and Stevenhagen5, Theorem 1]. The following two lemmas on which Theorem 2.7 depends are also due to Lenstra.
If
![]() $A$
is a field, then
$A$
is a field, then
![]() $B$
is as well so the class group of
$B$
is as well so the class group of
![]() $B$
is trivial and Theorem 2.7 likewise. Then to prove the theorem, it will be sufficient to assume for the rest of this subsection that
$B$
is trivial and Theorem 2.7 likewise. Then to prove the theorem, it will be sufficient to assume for the rest of this subsection that
![]() $A$
is not a field, in which case it is infinite.
$A$
is not a field, in which case it is infinite.
Note that we do not require
![]() $A/\mathfrak{p}$
to be finite in any of the statements below.
$A/\mathfrak{p}$
to be finite in any of the statements below.
Lemma 2.5.
For each positive integer
![]() $m$
, the number of primes
$m$
, the number of primes
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() $A$
for which
$A$
for which
![]() $|A/\mathfrak{p}|$
is at most
$|A/\mathfrak{p}|$
is at most
![]() $m$
is finite.
$m$
is finite.
Proof. Consider the polynomial
![]() $F=\prod _{q}(X^{q}-X)\in K[X]$
, with
$F=\prod _{q}(X^{q}-X)\in K[X]$
, with
![]() $q$
ranging over the set of prime powers (
$q$
ranging over the set of prime powers (
![]() $\gt 1$
) that are at most
$\gt 1$
) that are at most
![]() $m$
. Since
$m$
. Since
![]() $F$
is non-zero, it has only a finite number of zeros in
$F$
is non-zero, it has only a finite number of zeros in
![]() $A$
, so we can choose
$A$
, so we can choose
![]() $a\in A$
with
$a\in A$
with
![]() $F(a)$
non-zero. If
$F(a)$
non-zero. If
![]() $\mathfrak{p}$
is a prime of
$\mathfrak{p}$
is a prime of
![]() $A$
with
$A$
with
![]() $|A/\mathfrak{p}|$
at most
$|A/\mathfrak{p}|$
at most
![]() $m$
, then with
$m$
, then with
![]() $|A/\mathfrak{p}|=q$
we have
$|A/\mathfrak{p}|=q$
we have
![]() $a^{q}\equiv a\mod \mathfrak{p}$
, so
$a^{q}\equiv a\mod \mathfrak{p}$
, so
![]() $\mathfrak{p}$
divides
$\mathfrak{p}$
divides
![]() $F(a)$
. But
$F(a)$
. But
![]() $F(a)$
has only finitely many prime divisors, which proves the lemma.
$F(a)$
has only finitely many prime divisors, which proves the lemma.
In the following lemma, note that there is always a non-zero
![]() $d\in A$
such that
$d\in A$
such that
![]() $dB\subset A[\theta ]$
(i.e. the discriminant of the minimal polynomial of
$dB\subset A[\theta ]$
(i.e. the discriminant of the minimal polynomial of
![]() $\theta$
over
$\theta$
over
![]() $K$
).
$K$
).
Lemma 2.6.
Let
![]() $d$
be a non-zero element of
$d$
be a non-zero element of
![]() $A$
such that
$A$
such that
![]() $dB\subset A[\theta ]$
and such that every prime
$dB\subset A[\theta ]$
and such that every prime
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() $A$
for which
$A$
for which
![]() $|A/\mathfrak{p}|$
is at most
$|A/\mathfrak{p}|$
is at most
![]() $[L:K]$
divides
$[L:K]$
divides
![]() $dA$
. Let
$dA$
. Let
![]() $U$
be a finite set of primes of
$U$
be a finite set of primes of
![]() $B$
not dividing
$B$
not dividing
![]() $dB$
, and suppose that
$dB$
, and suppose that
![]() $\mathfrak{q}$
is a prime of degree one of
$\mathfrak{q}$
is a prime of degree one of
![]() $B$
that does not divide
$B$
that does not divide
![]() $dB$
. Then, there exists a non-zero element
$dB$
. Then, there exists a non-zero element
![]() $x\in B$
such that:
$x\in B$
such that:
-
1.
 $x\equiv 1\mod dB$
;
$x\equiv 1\mod dB$
; -
2. one has
with \begin{equation*} xB = \mathfrak{q}\prod _{i = 1}^t \mathfrak{q}_i^{e_i}, \end{equation*}
\begin{equation*} xB = \mathfrak{q}\prod _{i = 1}^t \mathfrak{q}_i^{e_i}, \end{equation*}
 $t\in{\mathbb{N}}\cup \{0\}$
,
$t\in{\mathbb{N}}\cup \{0\}$
,
 $e_i\in{\mathbb{N}}$
, where the
$e_i\in{\mathbb{N}}$
, where the
 $\mathfrak{q}_1,\ldots,\mathfrak{q}_t$
are primes of
$\mathfrak{q}_1,\ldots,\mathfrak{q}_t$
are primes of
 $B$
satisfying the following properties.
$B$
satisfying the following properties.
-
(i)
 $\mathfrak{q}_i \neq \mathfrak{q}$
and
$\mathfrak{q}_i \neq \mathfrak{q}$
and
 $\mathfrak{q}_i$
does not divide
$\mathfrak{q}_i$
does not divide
 $dB$
;
$dB$
; -
(ii)
 $\mathfrak{q}_i$
is of degree one and the primes
$\mathfrak{q}_i$
is of degree one and the primes
 $A \cap \mathfrak{q}_i$
and
$A \cap \mathfrak{q}_i$
and
 $A \cap \mathfrak{q}_j$
are different whenever
$A \cap \mathfrak{q}_j$
are different whenever
 $i\neq j$
;
$i\neq j$
; -
(iii)
 $\mathfrak{q}_i \not \in U$
.
$\mathfrak{q}_i \not \in U$
.
-
Proof. Let
![]() $\mathfrak{p}=A \cap \mathfrak{q}$
and
$\mathfrak{p}=A \cap \mathfrak{q}$
and
![]() $\beta =d\theta$
. Then,
$\beta =d\theta$
. Then,
![]() $B_{\mathfrak{p}}=A_{\mathfrak{p}}[\beta ]$
, and from Kummer–Dedekind’s theorem, we obtain
$B_{\mathfrak{p}}=A_{\mathfrak{p}}[\beta ]$
, and from Kummer–Dedekind’s theorem, we obtain
![]() $\mathfrak{q}=\mathfrak{p} B+(\beta +u)B$
for some
$\mathfrak{q}=\mathfrak{p} B+(\beta +u)B$
for some
![]() $u\in A$
. Moreover, we may assume that
$u\in A$
. Moreover, we may assume that
![]() $\beta +u\not \in \mathfrak{q}^2$
(if
$\beta +u\not \in \mathfrak{q}^2$
(if
![]() $\mathfrak{p}\subseteq \mathfrak{q}^2$
,
$\mathfrak{p}\subseteq \mathfrak{q}^2$
,
![]() $\beta +u\in \mathfrak{q}^2$
would lead to
$\beta +u\in \mathfrak{q}^2$
would lead to
![]() $\mathfrak{q} \subseteq \mathfrak{q}^2$
and if
$\mathfrak{q} \subseteq \mathfrak{q}^2$
and if
![]() $\mathfrak{p}\not \subseteq \mathfrak{q}^2$
and
$\mathfrak{p}\not \subseteq \mathfrak{q}^2$
and
![]() $\beta +u \in \mathfrak{q}^2$
, then
$\beta +u \in \mathfrak{q}^2$
, then
![]() $\beta +u+u'\not \in \mathfrak{q}^2$
for any
$\beta +u+u'\not \in \mathfrak{q}^2$
for any
![]() $u'\in \mathfrak{p}\setminus \mathfrak{q}^2$
).
$u'\in \mathfrak{p}\setminus \mathfrak{q}^2$
).
The idea is to replace
![]() $u$
by an element
$u$
by an element
![]() $v\in A$
satisfying the conditions (a)–(c) below and show that
$v\in A$
satisfying the conditions (a)–(c) below and show that
![]() $x=\beta +v$
satisfies the statements of the lemma. In order to state condition (c), we need to introduce a bit of notation. Let
$x=\beta +v$
satisfies the statements of the lemma. In order to state condition (c), we need to introduce a bit of notation. Let
![]() $\mathfrak{r}$
be a prime of
$\mathfrak{r}$
be a prime of
![]() $A$
lying below a prime in
$A$
lying below a prime in
![]() $U$
. Then
$U$
. Then
![]() $|A/\mathfrak{r}|\gt [L:K]$
by hypothesis. There are at most
$|A/\mathfrak{r}|\gt [L:K]$
by hypothesis. There are at most
![]() $[L:K]$
primes of
$[L:K]$
primes of
![]() $B$
of degree one over
$B$
of degree one over
![]() $\mathfrak{r}$
, so say
$\mathfrak{r}$
, so say
![]() $m$
such primes exist. By Kummer–Dedekind’s theorem, each prime
$m$
such primes exist. By Kummer–Dedekind’s theorem, each prime
![]() $\mathfrak{s}$
of
$\mathfrak{s}$
of
![]() $U$
above
$U$
above
![]() $\mathfrak{r}$
has the form
$\mathfrak{r}$
has the form
![]() $\mathfrak{r} B+(\beta +r_{\mathfrak{s}})B$
for some
$\mathfrak{r} B+(\beta +r_{\mathfrak{s}})B$
for some
![]() $r_{\mathfrak{s}}\in A$
that is uniquely determined modulo
$r_{\mathfrak{s}}\in A$
that is uniquely determined modulo
![]() $\mathfrak{r}$
. Since
$\mathfrak{r}$
. Since
![]() $|A/\mathfrak{r}|\gt [L:K]\geq m$
, we can choose
$|A/\mathfrak{r}|\gt [L:K]\geq m$
, we can choose
![]() $a_{\mathfrak{r}}\in A$
such that
$a_{\mathfrak{r}}\in A$
such that
![]() $a_{\mathfrak{r}}$
is not congruent to any of the
$a_{\mathfrak{r}}$
is not congruent to any of the
![]() $r_{\mathfrak{s}}$
modulo
$r_{\mathfrak{s}}$
modulo
![]() $\mathfrak{r}$
.
$\mathfrak{r}$
.
Let
![]() $U_A=\{A\cap \mathfrak{s} \mid \mathfrak{s} \in U\}$
and consider the following three conditions.
$U_A=\{A\cap \mathfrak{s} \mid \mathfrak{s} \in U\}$
and consider the following three conditions.
-
(a)
 $v\equiv 1 \mod dA$
,
$v\equiv 1 \mod dA$
, -
(b)
 $v\equiv u \mod \mathfrak{q}^2$
,
$v\equiv u \mod \mathfrak{q}^2$
, -
(c)
 $v\equiv a_{\mathfrak{r}} \mod \mathfrak{r}$
for all
$v\equiv a_{\mathfrak{r}} \mod \mathfrak{r}$
for all
 $\mathfrak{r} \in U_A\setminus \{\mathfrak{p}\}$
.
$\mathfrak{r} \in U_A\setminus \{\mathfrak{p}\}$
.
We claim that by the Chinese Remainder Theorem for the ring
![]() $A$
, there exists an element
$A$
, there exists an element
![]() $v\in A$
that satisfies the three conditions (a)–(c). For this, we only need to verify that the ideals appearing in the moduli in the three conditions are pairwise coprime. Indeed,
$v\in A$
that satisfies the three conditions (a)–(c). For this, we only need to verify that the ideals appearing in the moduli in the three conditions are pairwise coprime. Indeed,
![]() $u,v\in A$
so (b) is equivalent to
$u,v\in A$
so (b) is equivalent to
![]() $v\equiv u\mod A\cap \mathfrak{q}^2$
and
$v\equiv u\mod A\cap \mathfrak{q}^2$
and
![]() $dA$
and
$dA$
and
![]() $A\cap \mathfrak{q}^2$
are coprime since
$A\cap \mathfrak{q}^2$
are coprime since
![]() $A\cap \mathfrak{q}^2$
is a power of
$A\cap \mathfrak{q}^2$
is a power of
![]() $\mathfrak{p}$
and
$\mathfrak{p}$
and
![]() $\mathfrak{q}$
does not divide
$\mathfrak{q}$
does not divide
![]() $dB$
. Moreover, each
$dB$
. Moreover, each
![]() $\mathfrak{r}$
in (c) is different from
$\mathfrak{r}$
in (c) is different from
![]() $\mathfrak{p}$
and each
$\mathfrak{p}$
and each
![]() $\mathfrak{r}\in U_A$
is coprime to
$\mathfrak{r}\in U_A$
is coprime to
![]() $dA$
because this is so for
$dA$
because this is so for
![]() $A\cap \mathfrak{s}$
for any
$A\cap \mathfrak{s}$
for any
![]() $\mathfrak{s}\in U$
, by hypothesis.
$\mathfrak{s}\in U$
, by hypothesis.
Let
![]() $x:=\beta +v$
, for
$x:=\beta +v$
, for
![]() $v$
satisfying (a)–(c). Condition (b) ensures that
$v$
satisfying (a)–(c). Condition (b) ensures that
![]() $x$
is non-zero since we have chosen
$x$
is non-zero since we have chosen
![]() $u$
such that
$u$
such that
![]() $\beta +u\not \in \mathfrak{q}^2$
. Condition (a) ensures (1) since
$\beta +u\not \in \mathfrak{q}^2$
. Condition (a) ensures (1) since
![]() $\beta \in dB$
.
$\beta \in dB$
.
Furthermore, condition (b) ensures
![]() $x\in \mathfrak{q}\setminus \mathfrak{q}^2$
, so that
$x\in \mathfrak{q}\setminus \mathfrak{q}^2$
, so that
![]() $\mathfrak{q}$
occurs exactly once in the prime factorisation of
$\mathfrak{q}$
occurs exactly once in the prime factorisation of
![]() $xB$
. Thus, this prime factorisation has the form
$xB$
. Thus, this prime factorisation has the form
as in (2), for
![]() $\mathfrak{q}_i$
pairwise distinct primes of
$\mathfrak{q}_i$
pairwise distinct primes of
![]() $B$
and it follows from (1) that none of the
$B$
and it follows from (1) that none of the
![]() $\mathfrak{q}_i$
divide
$\mathfrak{q}_i$
divide
![]() $dB$
. This proves (2) (i).
$dB$
. This proves (2) (i).
Next, we prove (2) (ii). Write
![]() $\mathfrak{p}_i = A\cap \mathfrak{q}_i$
. From
$\mathfrak{p}_i = A\cap \mathfrak{q}_i$
. From
![]() $\mathfrak{p}_i$
not dividing
$\mathfrak{p}_i$
not dividing
![]() $d$
, it follows that
$d$
, it follows that
![]() $B_{\mathfrak{p}_i}=A_{\mathfrak{p}_i}[\beta ]$
so
$B_{\mathfrak{p}_i}=A_{\mathfrak{p}_i}[\beta ]$
so
![]() $B/(\mathfrak{p}_i B+(\beta +v)B) \hookrightarrow A_{\mathfrak{p}_i}/\mathfrak{p}_iA_{\mathfrak{p}_i}\cong A/\mathfrak{p}_i$
has
$B/(\mathfrak{p}_i B+(\beta +v)B) \hookrightarrow A_{\mathfrak{p}_i}/\mathfrak{p}_iA_{\mathfrak{p}_i}\cong A/\mathfrak{p}_i$
has
![]() $A/\mathfrak{p}_i$
-dimension at most 1. However,
$A/\mathfrak{p}_i$
-dimension at most 1. However,
![]() $\mathfrak{q}_i$
contains
$\mathfrak{q}_i$
contains
![]() $\mathfrak{p}_iB+(\beta +v)B$
and because of the
$\mathfrak{p}_iB+(\beta +v)B$
and because of the
![]() $A/\mathfrak{p}_i$
-surjection
$A/\mathfrak{p}_i$
-surjection
![]() $B/(\mathfrak{p}_i B+(\beta +v)B) \rightarrow B/\mathfrak{q}_i$
this dimension is at least
$B/(\mathfrak{p}_i B+(\beta +v)B) \rightarrow B/\mathfrak{q}_i$
this dimension is at least
![]() $[B/\mathfrak{q}_i: A/\mathfrak{p}_i]$
, so we obtain both that
$[B/\mathfrak{q}_i: A/\mathfrak{p}_i]$
, so we obtain both that
and
![]() $[B/\mathfrak{q}_i: A/\mathfrak{p}_i]=1$
. Therefore, each
$[B/\mathfrak{q}_i: A/\mathfrak{p}_i]=1$
. Therefore, each
![]() $\mathfrak{q}_i$
has degree one over
$\mathfrak{q}_i$
has degree one over
![]() $A$
, and
$A$
, and
![]() $\mathfrak{p}_i=\mathfrak{p}_j$
implies
$\mathfrak{p}_i=\mathfrak{p}_j$
implies
![]() $\mathfrak{q}_i=\mathfrak{q}_j$
, which implies
$\mathfrak{q}_i=\mathfrak{q}_j$
, which implies
![]() $i=j$
. Similarly, each
$i=j$
. Similarly, each
![]() $\mathfrak{p}_i$
is distinct from
$\mathfrak{p}_i$
is distinct from
![]() $\mathfrak{p}$
because if
$\mathfrak{p}$
because if
![]() $\mathfrak{p}_i = \mathfrak{p}$
, then
$\mathfrak{p}_i = \mathfrak{p}$
, then
![]() $\mathfrak{q}_i = \mathfrak{p} B+(\beta +v)B=\mathfrak{q}$
; contradiction.
$\mathfrak{q}_i = \mathfrak{p} B+(\beta +v)B=\mathfrak{q}$
; contradiction.
It remains to prove (2) (iii), that is, that none of the
![]() $\mathfrak{q}_i$
are in
$\mathfrak{q}_i$
are in
![]() $U$
. If
$U$
. If
![]() $\mathfrak{q}_i\in U$
, then
$\mathfrak{q}_i\in U$
, then
![]() $\mathfrak{p}_i \in U_A\setminus \{\mathfrak{p}\}$
(since we have shown that
$\mathfrak{p}_i \in U_A\setminus \{\mathfrak{p}\}$
(since we have shown that
![]() $\mathfrak{p}_i \neq \mathfrak{p}$
), so (c) implies that
$\mathfrak{p}_i \neq \mathfrak{p}$
), so (c) implies that
![]() $v\equiv a_{\mathfrak{p}_i} \mod \mathfrak{p}_i$
. Thus, as
$v\equiv a_{\mathfrak{p}_i} \mod \mathfrak{p}_i$
. Thus, as
![]() $x=\beta +v\in \mathfrak{q}_i$
, we obtain
$x=\beta +v\in \mathfrak{q}_i$
, we obtain
![]() $\beta +a_{\mathfrak{p}_i}\in \mathfrak{q}_i = \mathfrak{p}_i B+(\beta +r_{\mathfrak{q}_i})B$
. As
$\beta +a_{\mathfrak{p}_i}\in \mathfrak{q}_i = \mathfrak{p}_i B+(\beta +r_{\mathfrak{q}_i})B$
. As
![]() $\beta +r_{\mathfrak{q}_i} \in \mathfrak{q}_i$
, we get
$\beta +r_{\mathfrak{q}_i} \in \mathfrak{q}_i$
, we get
![]() $a_{\mathfrak{p}_i}-r_{\mathfrak{q}_i}\in \mathfrak{q}_i$
. But
$a_{\mathfrak{p}_i}-r_{\mathfrak{q}_i}\in \mathfrak{q}_i$
. But
![]() $a_{\mathfrak{p}_i},r_{\mathfrak{q}_i}\in A$
, so
$a_{\mathfrak{p}_i},r_{\mathfrak{q}_i}\in A$
, so
![]() $a_{\mathfrak{p}_i}-r_{\mathfrak{q}_i}\in A \cap \mathfrak{q}_i=\mathfrak{p}_i$
, contradicting
$a_{\mathfrak{p}_i}-r_{\mathfrak{q}_i}\in A \cap \mathfrak{q}_i=\mathfrak{p}_i$
, contradicting
![]() $a_{\mathfrak{p}_i}\not \equiv r_{\mathfrak{q}_i}\mod \mathfrak{p}_i$
.
$a_{\mathfrak{p}_i}\not \equiv r_{\mathfrak{q}_i}\mod \mathfrak{p}_i$
.
Theorem 2.7.
Let
![]() $S$
be a finite set of primes of
$S$
be a finite set of primes of
![]() $B$
. For every ideal class
$B$
. For every ideal class
![]() $c$
of
$c$
of
![]() $B$
, there exist a finite set
$B$
, there exist a finite set
![]() $T$
(possibly empty) of primes of degree one of
$T$
(possibly empty) of primes of degree one of
![]() $B$
and a function
$B$
and a function
![]() $e:T \to{\mathbb{N}}$
such that
$e:T \to{\mathbb{N}}$
such that
![]() $c$
contains an ideal of the form
$c$
contains an ideal of the form
![]() $\prod _{\mathfrak{q} \in T} \mathfrak{q}^{e(\mathfrak{q})}$
, where
$\prod _{\mathfrak{q} \in T} \mathfrak{q}^{e(\mathfrak{q})}$
, where
-
1.
 $T$
is disjoint from
$T$
is disjoint from
 $S$
,
$S$
, -
2. For any two distinct
 $\mathfrak{q}, \mathfrak{q}' \in T$
the primes
$\mathfrak{q}, \mathfrak{q}' \in T$
the primes
 $A \cap \mathfrak{q}$
and
$A \cap \mathfrak{q}$
and
 $A \cap \mathfrak{q}'$
are different.
$A \cap \mathfrak{q}'$
are different.
Note that in [Reference Lenstra and Stevenhagen5], the lemma is invoked for a prime
![]() $\mathfrak{q}$
, but the condition of the lemma that
$\mathfrak{q}$
, but the condition of the lemma that
![]() $\mathfrak{q}$
does not divide
$\mathfrak{q}$
does not divide
![]() $dB$
is disregarded. To repair this, one should introduce
$dB$
is disregarded. To repair this, one should introduce
![]() $d$
earlier and add its prime divisors to
$d$
earlier and add its prime divisors to
![]() $S$
, as we do below.
$S$
, as we do below.
Proof. First, we enlarge
![]() $S$
in two ways. By Lemma 2.5, for only finitely many primes
$S$
in two ways. By Lemma 2.5, for only finitely many primes
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() $A$
is
$A$
is
![]() $|A/\mathfrak{p}|$
at most
$|A/\mathfrak{p}|$
at most
![]() $[L:K]$
, and the finitely many primes of
$[L:K]$
, and the finitely many primes of
![]() $B$
lying over such
$B$
lying over such
![]() $\mathfrak{p}$
are adjoined to
$\mathfrak{p}$
are adjoined to
![]() $S$
. Secondly, choose
$S$
. Secondly, choose
![]() $d$
as in Lemma 2.6, but such that
$d$
as in Lemma 2.6, but such that
![]() $d$
is divisible by all primes in
$d$
is divisible by all primes in
![]() $S$
, and replace
$S$
, and replace
![]() $S$
by the set of prime divisors of
$S$
by the set of prime divisors of
![]() $dB$
in
$dB$
in
![]() $B$
. By [Reference Lenstra and Stevenhagen5, Theorem 1], the class group of
$B$
. By [Reference Lenstra and Stevenhagen5, Theorem 1], the class group of
![]() $B$
is generated by the primes of degree one that are not in
$B$
is generated by the primes of degree one that are not in
![]() $S$
. Hence, the ideal class
$S$
. Hence, the ideal class
![]() $c$
contains a fractional ideal of the form
$c$
contains a fractional ideal of the form
![]() $\prod _{\mathfrak{q} \in T} \mathfrak{q}^{e(\mathfrak{q})}$
, where
$\prod _{\mathfrak{q} \in T} \mathfrak{q}^{e(\mathfrak{q})}$
, where
![]() $T$
is a finite set of primes of degree one of
$T$
is a finite set of primes of degree one of
![]() $B$
, the set
$B$
, the set
![]() $T$
is disjoint from
$T$
is disjoint from
![]() $S$
, and
$S$
, and
![]() $e: T \to{\mathbb{Z}}\setminus \{0\}$
is a map.
$e: T \to{\mathbb{Z}}\setminus \{0\}$
is a map.
What remains to be done, is achieve (2), as well as to achieve that all
![]() $e(\mathfrak{q})$
are positive. We deal with these in order, first achieving (2), which requires that all
$e(\mathfrak{q})$
are positive. We deal with these in order, first achieving (2), which requires that all
![]() $A \cap \mathfrak{q}$
, with
$A \cap \mathfrak{q}$
, with
![]() $\mathfrak{q} \in T$
, are pairwise different. This we do by induction on the number of “coincidences” in the product, a coincidence being defined as a prime
$\mathfrak{q} \in T$
, are pairwise different. This we do by induction on the number of “coincidences” in the product, a coincidence being defined as a prime
![]() $\mathfrak{q} \in T$
for which there exists
$\mathfrak{q} \in T$
for which there exists
![]() $\mathfrak{q}' \in T$
,
$\mathfrak{q}' \in T$
,
![]() $\mathfrak{q}'\neq \mathfrak{q}$
, with
$\mathfrak{q}'\neq \mathfrak{q}$
, with
![]() $A \cap \mathfrak{q} = A \cap \mathfrak{q}'$
. If there are no such
$A \cap \mathfrak{q} = A \cap \mathfrak{q}'$
. If there are no such
![]() $\mathfrak{q}$
, then (2) is achieved. Next suppose that
$\mathfrak{q}$
, then (2) is achieved. Next suppose that
![]() $\mathfrak{q}^{*}$
is a coincidence. Apply Lemma 2.6 to
$\mathfrak{q}^{*}$
is a coincidence. Apply Lemma 2.6 to
![]() $\mathfrak{q} = \mathfrak{q}^{*}$
and
$\mathfrak{q} = \mathfrak{q}^{*}$
and
![]() $U$
equal to the set of primes of
$U$
equal to the set of primes of
![]() $B$
that lie over the same prime of
$B$
that lie over the same prime of
![]() $A$
as some prime in
$A$
as some prime in
![]() $T$
. Then we find, with the notation of the conclusion of Lemma 2.6, that
$T$
. Then we find, with the notation of the conclusion of Lemma 2.6, that
![]() $\mathfrak{q}^{*}$
is in the same ideal class as
$\mathfrak{q}^{*}$
is in the same ideal class as
![]() $\prod _{i = 1}^t \mathfrak{q}_i^{-e_i}$
for certain primes
$\prod _{i = 1}^t \mathfrak{q}_i^{-e_i}$
for certain primes
![]() $\mathfrak{q}_i$
of degree one of
$\mathfrak{q}_i$
of degree one of
![]() $B$
not in
$B$
not in
![]() $S$
nor in
$S$
nor in
![]() $U$
, with all
$U$
, with all
![]() $A \cap \mathfrak{q}_i$
pairwise different. Thus, one can replace the factor
$A \cap \mathfrak{q}_i$
pairwise different. Thus, one can replace the factor
![]() $(\mathfrak{q}^{*})^{e(\mathfrak{q}^{*})}$
in our product by
$(\mathfrak{q}^{*})^{e(\mathfrak{q}^{*})}$
in our product by
![]() $\prod _{i = 1}^t \mathfrak{q}_i^{-e_ie(\mathfrak{q}^{*})}$
. By the choice of
$\prod _{i = 1}^t \mathfrak{q}_i^{-e_ie(\mathfrak{q}^{*})}$
. By the choice of
![]() $U$
, this replacement does not introduce new coincidences, and it eliminates the coincidence
$U$
, this replacement does not introduce new coincidences, and it eliminates the coincidence
![]() $\mathfrak{q}^{*}$
. Hence in the new product, the number of coincidences is strictly smaller than in the old product.
$\mathfrak{q}^{*}$
. Hence in the new product, the number of coincidences is strictly smaller than in the old product.
We have now proved that every ideal class of
![]() $B$
contains a fractional ideal of the form
$B$
contains a fractional ideal of the form
![]() $\prod _{\mathfrak{q} \in T} \mathfrak{q}^{e(\mathfrak{q})}$
, where
$\prod _{\mathfrak{q} \in T} \mathfrak{q}^{e(\mathfrak{q})}$
, where
![]() $T$
is a finite set of primes of degree one of
$T$
is a finite set of primes of degree one of
![]() $B$
, the set
$B$
, the set
![]() $T$
is disjoint from
$T$
is disjoint from
![]() $S$
, all primes
$S$
, all primes
![]() $A \cap \mathfrak{q}$
of
$A \cap \mathfrak{q}$
of
![]() $A$
are pairwise different as
$A$
are pairwise different as
![]() $\mathfrak{q}$
ranges over
$\mathfrak{q}$
ranges over
![]() $T$
, and
$T$
, and
![]() $e: T \to{\mathbb{Z}}\setminus \{0\}$
is a map. It remains to change this product such that all
$e: T \to{\mathbb{Z}}\setminus \{0\}$
is a map. It remains to change this product such that all
![]() $e(\mathfrak{q})$
are positive. This we do by induction on the number of
$e(\mathfrak{q})$
are positive. This we do by induction on the number of
![]() $\mathfrak{q} \in T$
for which
$\mathfrak{q} \in T$
for which
![]() $e(\mathfrak{q}) \lt 0$
. If this number is 0, we are done. Suppose this number is positive, and let
$e(\mathfrak{q}) \lt 0$
. If this number is 0, we are done. Suppose this number is positive, and let
![]() $\mathfrak{q}^{*}\in T$
be such that
$\mathfrak{q}^{*}\in T$
be such that
![]() $e(\mathfrak{q}^{*}) \lt 0$
. We again apply Lemma 2.6 to the same choices of
$e(\mathfrak{q}^{*}) \lt 0$
. We again apply Lemma 2.6 to the same choices of
![]() $\mathfrak{q}$
and
$\mathfrak{q}$
and
![]() $U$
, which again enables us to replace the factor
$U$
, which again enables us to replace the factor
![]() $(\mathfrak{q}^{*})^{e(\mathfrak{q}^{*})}$
in our product by
$(\mathfrak{q}^{*})^{e(\mathfrak{q}^{*})}$
in our product by
![]() $\prod _{i = 1}^t \mathfrak{q}_i^{-e_ie(\mathfrak{q}^{*})}$
; note that all exponents
$\prod _{i = 1}^t \mathfrak{q}_i^{-e_ie(\mathfrak{q}^{*})}$
; note that all exponents
![]() $-e_ie(\mathfrak{q}^{*})$
are positive. By construction, this new product satisfies the same conditions as we listed for the original product, but the number of
$-e_ie(\mathfrak{q}^{*})$
are positive. By construction, this new product satisfies the same conditions as we listed for the original product, but the number of
![]() $\mathfrak{q} \in T$
for which
$\mathfrak{q} \in T$
for which
![]() $e(\mathfrak{q}) \lt 0$
has decreased by 1. Thus, the proof is now finished by induction.
$e(\mathfrak{q}) \lt 0$
has decreased by 1. Thus, the proof is now finished by induction.
Note that the difference between the above theorem and the results in [Reference Lenstra and Stevenhagen5] is the extra condition that the
![]() $\mathfrak{q}_{i}$
lie over distinct prime ideals of
$\mathfrak{q}_{i}$
lie over distinct prime ideals of
![]() $A$
. This is necessary for us because from this we can deduce:
$A$
. This is necessary for us because from this we can deduce:
Corollary 2.8.
Every ideal class of
![]() $B$
contains an ideal of degree one.
$B$
contains an ideal of degree one.
Proof. Let
![]() $S$
be the set of prime ideals of
$S$
be the set of prime ideals of
![]() $B$
that are not unramified. Then,
$B$
that are not unramified. Then,
![]() $S$
is finite (see [Reference Neukirch8, Chapter I, (8.4)]) so by Theorem 2.7, every ideal class of
$S$
is finite (see [Reference Neukirch8, Chapter I, (8.4)]) so by Theorem 2.7, every ideal class of
![]() $B$
contains an ideal
$B$
contains an ideal
![]() $\mathfrak{b}$
that is a product of unramified prime ideals of degree one lying above pairwise distinct prime ideals of
$\mathfrak{b}$
that is a product of unramified prime ideals of degree one lying above pairwise distinct prime ideals of
![]() $A$
. Since unramified primes have ramification index one, Proposition 2.4 implies that
$A$
. Since unramified primes have ramification index one, Proposition 2.4 implies that
![]() $\mathfrak{b}$
is of degree one.
$\mathfrak{b}$
is of degree one.
3. The Latimer–MacDuffee correspondence and ideal matrices
We keep the
![]() $A,K,B,L$
set-up from before, with
$A,K,B,L$
set-up from before, with
![]() $\theta \in B$
such that
$\theta \in B$
such that
![]() $L=K(\theta )$
and
$L=K(\theta )$
and
![]() $n=[L:K]$
. From now on and throughout the rest of the paper, we assume that
$n=[L:K]$
. From now on and throughout the rest of the paper, we assume that
![]() $A$
is PID. The following is a well-known fact that depends on this assumption on
$A$
is PID. The following is a well-known fact that depends on this assumption on
![]() $A$
.
$A$
.
Lemma 3.1.
Let
![]() $\mathcal{O}$
be an
$\mathcal{O}$
be an
![]() $A$
-order in
$A$
-order in
![]() $L$
and
$L$
and
![]() $\mathfrak{b}$
a non-zero ideal of
$\mathfrak{b}$
a non-zero ideal of
![]() $\mathcal{O}$
. Then,
$\mathcal{O}$
. Then,
![]() $\mathfrak{b}$
is free of rank
$\mathfrak{b}$
is free of rank
![]() $n$
over
$n$
over
![]() $A$
.
$A$
.
Let
be the regular embedding with respect to the basis
![]() $1,\theta,\ldots,\theta ^{n-1}$
, that is, for any
$1,\theta,\ldots,\theta ^{n-1}$
, that is, for any
![]() $x\in A[\theta ]$
,
$x\in A[\theta ]$
,
 \begin{equation*} T(x)\begin {pmatrix}1\\[5pt] \vdots \\[5pt] \theta ^{n-1} \end {pmatrix}=x\begin {pmatrix}1\\[5pt] \vdots \\[5pt] \theta ^{n-1} \end {pmatrix}. \end{equation*}
\begin{equation*} T(x)\begin {pmatrix}1\\[5pt] \vdots \\[5pt] \theta ^{n-1} \end {pmatrix}=x\begin {pmatrix}1\\[5pt] \vdots \\[5pt] \theta ^{n-1} \end {pmatrix}. \end{equation*}
In particular, if
denotes the minimal polynomial of
![]() $\theta$
over
$\theta$
over
![]() $K$
, then
$K$
, then

Let
![]() $I$
be the kernel of the surjective homomorphism
$I$
be the kernel of the surjective homomorphism
![]() $A[x]\rightarrow A[\theta ]$
,
$A[x]\rightarrow A[\theta ]$
,
![]() $x\mapsto \theta$
. Even though
$x\mapsto \theta$
. Even though
![]() $A[x]$
is not necessarily a PID, it is true that
$A[x]$
is not necessarily a PID, it is true that
![]() $I$
is principal. Indeed, let
$I$
is principal. Indeed, let
![]() $g(x)\in I$
be a non-zero element. Then, as
$g(x)\in I$
be a non-zero element. Then, as
![]() $f(x)$
is the minimal polynomial of
$f(x)$
is the minimal polynomial of
![]() $\theta$
over
$\theta$
over
![]() $K$
, we have
$K$
, we have
![]() $g(x)=f(x)h(x)$
, for some monic
$g(x)=f(x)h(x)$
, for some monic
![]() $h(x)\in K[x]$
. Since
$h(x)\in K[x]$
. Since
![]() $A$
is a PID, there is a
$A$
is a PID, there is a
![]() $d\in A$
such that
$d\in A$
such that
![]() $dh(x)\in A[x]$
and
$dh(x)\in A[x]$
and
![]() $c(dh)=(1)$
, where
$c(dh)=(1)$
, where
![]() $c(\cdot )$
denotes the content of a polynomial in
$c(\cdot )$
denotes the content of a polynomial in
![]() $A[x]$
. By Gauss’s lemma,
$A[x]$
. By Gauss’s lemma,
![]() $d\cdot c(g)=c(f)c(dh)=(1)$
, so
$d\cdot c(g)=c(f)c(dh)=(1)$
, so
![]() $d$
is a unit and
$d$
is a unit and
![]() $h(x)\in A[x]$
. Thus,
$h(x)\in A[x]$
. Thus,
![]() $I=(f(x))$
, and we have an isomorphism
$I=(f(x))$
, and we have an isomorphism
The Latimer–MacDuffee correspondence is a bijection between similarity classes of matrices in
![]() $\textrm{M}_{n}({\mathbb{Z}})$
with characteristic polynomial
$\textrm{M}_{n}({\mathbb{Z}})$
with characteristic polynomial
![]() $f(x)$
and ideal classes of the order
$f(x)$
and ideal classes of the order
![]() ${\mathbb{Z}}[\theta ]$
. It was first established by Latimer and MacDuffee [Reference Latimer and MacDuffee4] and later given a new simpler proof by Taussky (see [Reference Taussky15], [Reference Newman9, Chapter III, Section 16] and the last appendix of [Reference Cohn3]). As shown by Bender [Reference Bender1] and Buccino [Reference Buccino2], Taussky’s proof translates readily to the more general situation of similarity classes of matrices over an integral domain
${\mathbb{Z}}[\theta ]$
. It was first established by Latimer and MacDuffee [Reference Latimer and MacDuffee4] and later given a new simpler proof by Taussky (see [Reference Taussky15], [Reference Newman9, Chapter III, Section 16] and the last appendix of [Reference Cohn3]). As shown by Bender [Reference Bender1] and Buccino [Reference Buccino2], Taussky’s proof translates readily to the more general situation of similarity classes of matrices over an integral domain
![]() $R$
and classes of ideals that are free
$R$
and classes of ideals that are free
![]() $R$
-modules of rank
$R$
-modules of rank
![]() $n$
. More precisely, Lemma 3.1 together with [Reference Bender1, Theorem 1] imply:
$n$
. More precisely, Lemma 3.1 together with [Reference Bender1, Theorem 1] imply:
Theorem 3.2.
There is a canonical bijection between the similarity classes of matrices in
![]() $\textrm{M}_{n}(A)$
with characteristic polynomial
$\textrm{M}_{n}(A)$
with characteristic polynomial
![]() $f(x)$
and ideal classes in
$f(x)$
and ideal classes in
![]() $A[\theta ]$
.
$A[\theta ]$
.
The bijection is canonical in the following sense. Let
![]() $\alpha \in \textrm{M}_{n}(A)$
have characteristic polynomial
$\alpha \in \textrm{M}_{n}(A)$
have characteristic polynomial
![]() $f(x)$
. Then
$f(x)$
. Then
![]() $\theta$
is an eigenvalue of
$\theta$
is an eigenvalue of
![]() $\alpha$
and since
$\alpha$
and since
![]() $f(x)$
is irreducible and we have assumed that
$f(x)$
is irreducible and we have assumed that
![]() $L/K$
is separable, all the eigenvalues (in some algebraic closure
$L/K$
is separable, all the eigenvalues (in some algebraic closure
![]() $\mkern 1.5mu\overline{\mkern -1muK\mkern -1mu}\mkern 1.5mu$
of
$\mkern 1.5mu\overline{\mkern -1muK\mkern -1mu}\mkern 1.5mu$
of
![]() $K$
) are distinct so the eigenspaces have dimension
$K$
) are distinct so the eigenspaces have dimension
![]() $1$
over
$1$
over
![]() $\mkern 1.5mu\overline{\mkern -1muK\mkern -1mu}\mkern 1.5mu$
and thus two eigenvectors corresponding to the same eigenvalue
$\mkern 1.5mu\overline{\mkern -1muK\mkern -1mu}\mkern 1.5mu$
and thus two eigenvectors corresponding to the same eigenvalue
![]() $\theta$
must be proportional (by a factor in
$\theta$
must be proportional (by a factor in
![]() $\mkern 1.5mu\overline{\mkern -1muK\mkern -1mu}\mkern 1.5mu$
). Since
$\mkern 1.5mu\overline{\mkern -1muK\mkern -1mu}\mkern 1.5mu$
). Since
![]() $\alpha$
has an eigenvector in
$\alpha$
has an eigenvector in
![]() $K(\theta )^{n}$
corresponding to
$K(\theta )^{n}$
corresponding to
![]() $\theta$
, it also has an eigenvector
$\theta$
, it also has an eigenvector
 $v=\begin{pmatrix}v_{1}\\[5pt] \vdots \\[5pt] v_{n} \end{pmatrix}$
in
$v=\begin{pmatrix}v_{1}\\[5pt] \vdots \\[5pt] v_{n} \end{pmatrix}$
in
![]() $A[\theta ]^{n}$
(by clearing denominators). Let
$A[\theta ]^{n}$
(by clearing denominators). Let
![]() $I=Av_{1}+\ldots +Av_{n} \subseteq A[\theta ]$
. Then,
$I=Av_{1}+\ldots +Av_{n} \subseteq A[\theta ]$
. Then,
![]() $\alpha v=\theta v$
implies that
$\alpha v=\theta v$
implies that
![]() $\theta I\subseteq I$
, and thus,
$\theta I\subseteq I$
, and thus,
![]() $\theta ^{i}I\subseteq I$
for every
$\theta ^{i}I\subseteq I$
for every
![]() $i\geq 1$
, which implies that
$i\geq 1$
, which implies that
![]() $I$
is an ideal of
$I$
is an ideal of
![]() $A[\theta ]$
. It is then easy to see that any other choice of eigenvector
$A[\theta ]$
. It is then easy to see that any other choice of eigenvector
![]() $v$
leads to an ideal that is in the same ideal class as
$v$
leads to an ideal that is in the same ideal class as
![]() $I$
and that any other matrix in the similarity class of
$I$
and that any other matrix in the similarity class of
![]() $\alpha$
leads to the same ideal class (see [Reference Newman9, Chapter III, Section 16]).
$\alpha$
leads to the same ideal class (see [Reference Newman9, Chapter III, Section 16]).
Definition 3.3.
A matrix
![]() $\kappa \in \textrm{M}_{n}(A)$
is called an ideal matrix for an ideal
$\kappa \in \textrm{M}_{n}(A)$
is called an ideal matrix for an ideal
![]() $\mathfrak{b}$
of
$\mathfrak{b}$
of
![]() $A[\theta ]$
(with respect to the basis
$A[\theta ]$
(with respect to the basis
![]() $1,\theta,\ldots,\theta ^{n-1}$
of
$1,\theta,\ldots,\theta ^{n-1}$
of
![]() $A[\theta ]$
) if
$A[\theta ]$
) if
Such a
![]() $\kappa$
always exists because left ideals in
$\kappa$
always exists because left ideals in
![]() $\textrm{M}_{n}(A)$
are principal [
Reference Newman9, Theorem II.5].
$\textrm{M}_{n}(A)$
are principal [
Reference Newman9, Theorem II.5].
The following characterisation is taken as the definition of ideal matrix in [Reference Taussky16] and [Reference Cohn3]. The result is essentially a theorem of MacDuffee [Reference MacDuffee7], which we here translate into our notation.
Lemma 3.4.
Let
![]() $\mathfrak{b}$
be a non-zero ideal of
$\mathfrak{b}$
be a non-zero ideal of
![]() $A[\theta ]$
and
$A[\theta ]$
and
![]() $\kappa \in \textrm{M}_{n}(A)$
. Then, the following two conditions are equivalent.
$\kappa \in \textrm{M}_{n}(A)$
. Then, the following two conditions are equivalent.
-
1.
 $\kappa$
is an ideal matrix for
$\kappa$
is an ideal matrix for
 $\mathfrak{b}$
(with respect to the basis
$\mathfrak{b}$
(with respect to the basis
 $1,\theta,\ldots,\theta ^{n-1}$
of
$1,\theta,\ldots,\theta ^{n-1}$
of
 $A[\theta ]$
),
$A[\theta ]$
),
-
2. the entries of
form an \begin{equation*} \kappa \begin {pmatrix}1\\[5pt] \vdots \\[5pt] \theta ^{n-1} \end {pmatrix} \end{equation*}
\begin{equation*} \kappa \begin {pmatrix}1\\[5pt] \vdots \\[5pt] \theta ^{n-1} \end {pmatrix} \end{equation*}
 $A$
-basis for
$A$
-basis for
 $\mathfrak{b}$
.
$\mathfrak{b}$
.
Proof. Let
![]() $a_{1},\ldots,a_{n}$
be an
$a_{1},\ldots,a_{n}$
be an
![]() $A$
-basis for
$A$
-basis for
![]() $\mathfrak{b}$
. In [Reference MacDuffee7], the elements
$\mathfrak{b}$
. In [Reference MacDuffee7], the elements
![]() $\alpha _{1},\ldots,\alpha _{k}$
are arbitrary generators of the ideal. We may thus take
$\alpha _{1},\ldots,\alpha _{k}$
are arbitrary generators of the ideal. We may thus take
![]() $k=n$
and
$k=n$
and
![]() $\alpha _{i}=a_{i}$
. Recall that we have embedded
$\alpha _{i}=a_{i}$
. Recall that we have embedded
![]() $A[\theta ]$
in
$A[\theta ]$
in
![]() $\textrm{M}_{n}(A)$
via the regular embedding
$\textrm{M}_{n}(A)$
via the regular embedding
![]() $T$
.
$T$
.
Assume that the second condition holds and write
![]() $\kappa =(k_{ij})$
,
$\kappa =(k_{ij})$
,
![]() $k_{ij}\in A$
, so that
$k_{ij}\in A$
, so that
For any
![]() $1\leq i,j\leq n$
, write
$1\leq i,j\leq n$
, write
for some
![]() $c_{ijk}\in A$
. We then have, for each fixed
$c_{ijk}\in A$
. We then have, for each fixed
![]() $j$
,
$j$
,
(note that
![]() $(c_{ijk})_{ik}=M_{j}$
in the notation of [Reference MacDuffee7]). For any
$(c_{ijk})_{ik}=M_{j}$
in the notation of [Reference MacDuffee7]). For any
![]() $r,i=1,\ldots,n$
, we then have
$r,i=1,\ldots,n$
, we then have
On the other hand, since
![]() $a_{1},\ldots,a_{n}$
is a basis for
$a_{1},\ldots,a_{n}$
is a basis for
![]() $\mathfrak{b}$
, there exist uniquely determined elements
$\mathfrak{b}$
, there exist uniquely determined elements
![]() $q_{rij}\in A$
such that
$q_{rij}\in A$
such that
From this we conclude that for any
![]() $r,i,k=1,\ldots,n$
, we have
$r,i,k=1,\ldots,n$
, we have
Letting
![]() $Q_{i}=(q_{ris})_{rs}\in \textrm{M}_{n}(A)$
, for each
$Q_{i}=(q_{ris})_{rs}\in \textrm{M}_{n}(A)$
, for each
![]() $i$
, the relations (3.1) and (3.3) imply that (3.4) can be rewritten as
$i$
, the relations (3.1) and (3.3) imply that (3.4) can be rewritten as
Thus,
![]() $\kappa$
is a common right divisor of the matrices
$\kappa$
is a common right divisor of the matrices
![]() $T(a_{1}),\ldots,T(a_{n})$
.
$T(a_{1}),\ldots,T(a_{n})$
.
Moreover, writing
for any
![]() $r=1,\ldots,n$
(where
$r=1,\ldots,n$
(where
![]() $\delta _{ij}\in A$
is the Kronecker delta) and
$\delta _{ij}\in A$
is the Kronecker delta) and
with
![]() $p_{rj1}=\delta _{rj}$
and
$p_{rj1}=\delta _{rj}$
and
![]() $p_{rjh}=0$
if
$p_{rjh}=0$
if
![]() $h\gt 1$
, we get
$h\gt 1$
, we get
 \begin{align*} \sum _{s=1}^{n}k_{rs}\theta ^{s-1} & \overset{(3.1)}{{=}}a_{r}=\sum _{j=1}^{n}\Big (\sum _{h=1}^{n}p_{rjh}\theta ^{h-1}\Big )a_{j}=\sum _{j=1}^{n}\Big (\sum _{h=1}^{n}p_{rjh}\theta ^{h-1}\Big )\Big (\sum _{l=1}^{n}k_{jl}\theta ^{l-1}\Big )\\[5pt] & \overset{(3.2)}{=}\sum _{j,h,l=1}^{n}\sum _{s=1}^{n}p_{rjh}k_{jl}c_{hls}\theta ^{s-1}. \end{align*}
\begin{align*} \sum _{s=1}^{n}k_{rs}\theta ^{s-1} & \overset{(3.1)}{{=}}a_{r}=\sum _{j=1}^{n}\Big (\sum _{h=1}^{n}p_{rjh}\theta ^{h-1}\Big )a_{j}=\sum _{j=1}^{n}\Big (\sum _{h=1}^{n}p_{rjh}\theta ^{h-1}\Big )\Big (\sum _{l=1}^{n}k_{jl}\theta ^{l-1}\Big )\\[5pt] & \overset{(3.2)}{=}\sum _{j,h,l=1}^{n}\sum _{s=1}^{n}p_{rjh}k_{jl}c_{hls}\theta ^{s-1}. \end{align*}
This implies that for each
![]() $r$
and
$r$
and
![]() $s$
,
$s$
,
which, using (3.1) and (3.3), can be written
where
![]() $P_{j}=(p_{rjh})_{rh}$
(which equals the elementary matrix with a
$P_{j}=(p_{rjh})_{rh}$
(which equals the elementary matrix with a
![]() $1$
in the
$1$
in the
![]() $(j,1)$
-position and has
$(j,1)$
-position and has
![]() $0$
s everywhere else). Thus, any common right divisor of
$0$
s everywhere else). Thus, any common right divisor of
![]() $T(a_{1}),\ldots,T(a_{n})$
in
$T(a_{1}),\ldots,T(a_{n})$
in
![]() $\textrm{M}_n(A)$
is a right divisor of
$\textrm{M}_n(A)$
is a right divisor of
![]() $\kappa$
, so
$\kappa$
, so
![]() $\kappa$
is a greatest common right divisor and therefore
$\kappa$
is a greatest common right divisor and therefore
that is,
![]() $\kappa$
is an ideal matrix for
$\kappa$
is an ideal matrix for
![]() $\mathfrak{b}$
.
$\mathfrak{b}$
.
Conversely, assume that
![]() $\textrm{M}_{n}(A)T(\mathfrak{b})=\textrm{M}_{n}(A)\kappa$
, so that
$\textrm{M}_{n}(A)T(\mathfrak{b})=\textrm{M}_{n}(A)\kappa$
, so that
![]() $\kappa$
is a greatest common right divisor of
$\kappa$
is a greatest common right divisor of
![]() $T(a_{1}),\ldots,T(a_{n})$
. Note that
$T(a_{1}),\ldots,T(a_{n})$
. Note that
![]() $\textrm{det}(\kappa )\neq 0$
, or else we would have
$\textrm{det}(\kappa )\neq 0$
, or else we would have
![]() $\textrm{det}(T(\mathfrak{b}))=0$
, which implies that
$\textrm{det}(T(\mathfrak{b}))=0$
, which implies that
![]() $\mathfrak{b}=0$
. This follows from the commutative diagram
$\mathfrak{b}=0$
. This follows from the commutative diagram

where the top arrow is the regular embedding of
![]() $L$
with respect to the
$L$
with respect to the
![]() $K$
-basis
$K$
-basis
![]() $1,\ldots,\theta ^{n-1}$
; note that the image in
$1,\ldots,\theta ^{n-1}$
; note that the image in
![]() $\textrm{M}_{n}(K)$
of any non-zero element of
$\textrm{M}_{n}(K)$
of any non-zero element of
![]() $L$
is invertible.
$L$
is invertible.
Let
![]() $\kappa '\in \textrm{M}_{n}(A)$
be the (uniquely determined) matrix such that
$\kappa '\in \textrm{M}_{n}(A)$
be the (uniquely determined) matrix such that
 \begin{equation*} \kappa '\begin {pmatrix}1\\[5pt] \vdots \\[5pt] \theta ^{n-1} \end {pmatrix}=\begin {pmatrix}a_{1}\\[5pt] \vdots \\[5pt] a_{n} \end {pmatrix}. \end{equation*}
\begin{equation*} \kappa '\begin {pmatrix}1\\[5pt] \vdots \\[5pt] \theta ^{n-1} \end {pmatrix}=\begin {pmatrix}a_{1}\\[5pt] \vdots \\[5pt] a_{n} \end {pmatrix}. \end{equation*}
We have shown above that
![]() $\kappa '$
must be a greatest common right divisor of
$\kappa '$
must be a greatest common right divisor of
![]() $T(a_{1}),\ldots,T(a_{n})$
, so, as
$T(a_{1}),\ldots,T(a_{n})$
, so, as
![]() $\kappa$
is invertible in
$\kappa$
is invertible in
![]() $\textrm{M}_{n}(K)$
, there exists an invertible matrix
$\textrm{M}_{n}(K)$
, there exists an invertible matrix
![]() $\omega \in \textrm{GL}_{n}(A)$
such that
$\omega \in \textrm{GL}_{n}(A)$
such that
![]() $\kappa =\omega \kappa '$
. Thus, the entries of
$\kappa =\omega \kappa '$
. Thus, the entries of
 \begin{equation*} \kappa \begin {pmatrix}1\\[5pt] \vdots \\[5pt] \theta ^{n-1} \end {pmatrix}=\omega \begin {pmatrix}a_{1}\\[5pt] \vdots \\[5pt] a_{n} \end {pmatrix} \end{equation*}
\begin{equation*} \kappa \begin {pmatrix}1\\[5pt] \vdots \\[5pt] \theta ^{n-1} \end {pmatrix}=\omega \begin {pmatrix}a_{1}\\[5pt] \vdots \\[5pt] a_{n} \end {pmatrix} \end{equation*}
form an
![]() $A$
-basis for
$A$
-basis for
![]() $\mathfrak{b}$
.
$\mathfrak{b}$
.
Lemma 3.5.
Let
![]() $\mathfrak{b}$
be a non-zero ideal of
$\mathfrak{b}$
be a non-zero ideal of
![]() $A[\theta ]$
and
$A[\theta ]$
and
![]() $\kappa$
an ideal matrix for
$\kappa$
an ideal matrix for
![]() $\mathfrak{b}$
(with respect to the basis
$\mathfrak{b}$
(with respect to the basis
![]() $1,\theta,\ldots,\theta ^{n-1}$
of
$1,\theta,\ldots,\theta ^{n-1}$
of
![]() $A[\theta ]$
). The similarity class in
$A[\theta ]$
). The similarity class in
![]() $\textrm{M}_{n}(A)$
corresponding to the ideal class of
$\textrm{M}_{n}(A)$
corresponding to the ideal class of
![]() $\mathfrak{b}$
under the Latimer–MacDuffee correspondence contains
$\mathfrak{b}$
under the Latimer–MacDuffee correspondence contains
![]() $\kappa T(\theta )\kappa ^{-1}$
.
$\kappa T(\theta )\kappa ^{-1}$
.
Proof. Let
![]() $\alpha \in \textrm{M}_{n}(A)$
be a representative of the similarity class corresponding to the ideal class of
$\alpha \in \textrm{M}_{n}(A)$
be a representative of the similarity class corresponding to the ideal class of
![]() $\mathfrak{b}$
. Then,
$\mathfrak{b}$
. Then,
where the entries
![]() $v_{1},\ldots,v_{n}\in A[\theta ]$
of
$v_{1},\ldots,v_{n}\in A[\theta ]$
of
![]() $v$
span
$v$
span
![]() $\mathfrak{b}$
over
$\mathfrak{b}$
over
![]() $A$
. Since
$A$
. Since
![]() $\mathfrak{b}$
is free of rank
$\mathfrak{b}$
is free of rank
![]() $n$
over
$n$
over
![]() $A$
(Lemma 3.1), the elements
$A$
(Lemma 3.1), the elements
![]() $v_{1},\ldots,v_{n}$
must be linearly independent and thus form a basis for the ideal
$v_{1},\ldots,v_{n}$
must be linearly independent and thus form a basis for the ideal
![]() $\mathfrak{b}$
. By Lemma 3.4 there is an
$\mathfrak{b}$
. By Lemma 3.4 there is an
![]() $\omega \in \textrm{GL}_{n}(A)$
such that
$\omega \in \textrm{GL}_{n}(A)$
such that
 \begin{equation*} \omega \kappa \begin {pmatrix}1\\[5pt] \vdots \\[5pt] \theta ^{n-1} \end {pmatrix}=v, \end{equation*}
\begin{equation*} \omega \kappa \begin {pmatrix}1\\[5pt] \vdots \\[5pt] \theta ^{n-1} \end {pmatrix}=v, \end{equation*}
and therefore
 \begin{equation*} (\omega \kappa )^{-1}\alpha \omega \kappa \begin {pmatrix}1\\[5pt] \vdots \\[5pt] \theta ^{n-1} \end {pmatrix}=\theta \begin {pmatrix}1\\[5pt] \vdots \\[5pt] \theta ^{n-1} \end {pmatrix}. \end{equation*}
\begin{equation*} (\omega \kappa )^{-1}\alpha \omega \kappa \begin {pmatrix}1\\[5pt] \vdots \\[5pt] \theta ^{n-1} \end {pmatrix}=\theta \begin {pmatrix}1\\[5pt] \vdots \\[5pt] \theta ^{n-1} \end {pmatrix}. \end{equation*}
This means that
![]() $(\omega \kappa )^{-1}\alpha \omega \kappa =T(\theta )$
and thus
$(\omega \kappa )^{-1}\alpha \omega \kappa =T(\theta )$
and thus
which lies in the same similarity class as
![]() $\kappa T(\theta )\kappa ^{-1}$
.
$\kappa T(\theta )\kappa ^{-1}$
.
4. An ideal matrix for ideals of degree one
Lemma 4.1.
For any
![]() $z\in A$
, the matrix
$z\in A$
, the matrix

is an ideal matrix for
![]() $(\theta -z)$
, that is,
$(\theta -z)$
, that is,
![]() $\textrm{M}_{n}(A)T(\theta -z)=\textrm{M}_{n}(A)\lambda$
.
$\textrm{M}_{n}(A)T(\theta -z)=\textrm{M}_{n}(A)\lambda$
.
Proof. We may perform successive elementary row operations on
![]() $T(\theta -z)$
. The first operation consists of the row permutation
$T(\theta -z)$
. The first operation consists of the row permutation
![]() $(1,2,3,\ldots,n)$
:
$(1,2,3,\ldots,n)$
:

Next, starting from the second column, successively use each of the
![]() $1$
s on the diagonal to clear the entry just below it. This yields
$1$
s on the diagonal to clear the entry just below it. This yields

Finally, starting from the second column, successively use each of the
![]() $1$
s on the diagonal to clear the top row entry above it. The resulting matrix is
$1$
s on the diagonal to clear the top row entry above it. The resulting matrix is

for some polynomial
![]() $g(x)\in A[x]$
. But since
$g(x)\in A[x]$
. But since
the result follows.
For any
![]() $a,z\in A$
, define the matrix
$a,z\in A$
, define the matrix

Proposition 4.2.
Assume that
![]() $\mathfrak{b}$
is an ideal of
$\mathfrak{b}$
is an ideal of
![]() $A[\theta ]$
of degree one and let
$A[\theta ]$
of degree one and let
![]() $a$
be a generator of
$a$
be a generator of
![]() $A\cap \mathfrak{b}$
. Then, there exists a
$A\cap \mathfrak{b}$
. Then, there exists a
![]() $z\in A$
such that
$z\in A$
such that
![]() $f(z)\equiv 0\mod (a)$
and
$f(z)\equiv 0\mod (a)$
and
![]() $\kappa =\kappa (a,z)$
is an ideal matrix for
$\kappa =\kappa (a,z)$
is an ideal matrix for
![]() $\mathfrak{b}$
.
$\mathfrak{b}$
.
Proof. By Lemma 2.3, there exists a
![]() $z\in A$
such that
$z\in A$
such that
![]() $\mathfrak{b}=(\theta -z,a)$
. Then,
$\mathfrak{b}=(\theta -z,a)$
. Then,
![]() $\theta \equiv z\mod \mathfrak{b}$
, so
$\theta \equiv z\mod \mathfrak{b}$
, so
![]() $f(z)\equiv f(\theta )\equiv 0\mod \mathfrak{b}$
and hence
$f(z)\equiv f(\theta )\equiv 0\mod \mathfrak{b}$
and hence
![]() $f(z)\equiv 0\mod (a)$
, as
$f(z)\equiv 0\mod (a)$
, as
![]() $f(z)\in A$
. Thus,
$f(z)\in A$
. Thus,
with
![]() $\lambda$
as in Lemma 4.1. Let
$\lambda$
as in Lemma 4.1. Let
![]() $E_{ij}\in \textrm{M}_{n}(A)$
be the matrix defined by having
$E_{ij}\in \textrm{M}_{n}(A)$
be the matrix defined by having
![]() $(i,j)$
-entry equal to
$(i,j)$
-entry equal to
![]() $1$
and all other entries equal to
$1$
and all other entries equal to
![]() $0$
. Writing
$0$
. Writing
![]() $f(z)=am$
, for
$f(z)=am$
, for
![]() $m\in A$
, we then have
$m\in A$
, we then have
![]() $\kappa =\lambda +E_{11}(1-m)a$
and hence
$\kappa =\lambda +E_{11}(1-m)a$
and hence
On the other hand,
![]() $aI\in \textrm{M}_{n}(A)\kappa$
since the adjoint matrix
$aI\in \textrm{M}_{n}(A)\kappa$
since the adjoint matrix
![]() $\textrm{adj}(\kappa )\in \textrm{M}_{n}(A)$
satisfies
$\textrm{adj}(\kappa )\in \textrm{M}_{n}(A)$
satisfies
![]() $\textrm{adj}(\kappa )\kappa =\textrm{det}(\kappa )I=aI$
. Furthermore,
$\textrm{adj}(\kappa )\kappa =\textrm{det}(\kappa )I=aI$
. Furthermore,
![]() $\lambda \in \textrm{M}_{n}(A)\kappa$
since
$\lambda \in \textrm{M}_{n}(A)\kappa$
since
![]() $\lambda =\kappa -E_{11}(1-m)a=(I-(1-m)E_{11}\textrm{adj}(\kappa ))\kappa$
. Thus,
$\lambda =\kappa -E_{11}(1-m)a=(I-(1-m)E_{11}\textrm{adj}(\kappa ))\kappa$
. Thus,
![]() $\textrm{M}_{n}(A)\lambda +\textrm{M}_{n}(A)a\subseteq \textrm{M}_{n}(A)\kappa$
and so
$\textrm{M}_{n}(A)\lambda +\textrm{M}_{n}(A)a\subseteq \textrm{M}_{n}(A)\kappa$
and so
![]() $\textrm{M}_{n}(A)T(\mathfrak{b})=\textrm{M}_{n}(A)\lambda +\textrm{M}_{n}(A)a=\textrm{M}_{n}(A)\kappa$
.
$\textrm{M}_{n}(A)T(\mathfrak{b})=\textrm{M}_{n}(A)\lambda +\textrm{M}_{n}(A)a=\textrm{M}_{n}(A)\kappa$
.
5. Representatives of similarity classes
In the following lemma, note that
![]() $\kappa =\kappa (a,z)$
in (4.1) is not necessarily invertible in
$\kappa =\kappa (a,z)$
in (4.1) is not necessarily invertible in
![]() $\textrm{M}_n(A)$
and that it is therefore not true in general that
$\textrm{M}_n(A)$
and that it is therefore not true in general that
![]() $\theta$
is similar (i.e.
$\theta$
is similar (i.e.
![]() $\textrm{GL}_n(A)$
-conjugate) to
$\textrm{GL}_n(A)$
-conjugate) to
![]() $C_f(a,z)$
.
$C_f(a,z)$
.
Lemma 5.1.
Let
![]() $a\in A$
and assume that there exists a
$a\in A$
and assume that there exists a
![]() $z\in A$
such that
$z\in A$
such that
![]() $f(z)\equiv 0\mod (a)$
. Then, the matrix
$f(z)\equiv 0\mod (a)$
. Then, the matrix
![]() $\kappa T(\theta )\kappa ^{-1}\in \textrm{M}_{n}(A)$
is similar to
$\kappa T(\theta )\kappa ^{-1}\in \textrm{M}_{n}(A)$
is similar to

where
![]() $u_{i}=-(z^{i}+k_{n-1}z^{i-1}+k_{n-2}z^{i-2}+\ldots +k_{n-i+1}z+k_{n-i})$
, for
$u_{i}=-(z^{i}+k_{n-1}z^{i-1}+k_{n-2}z^{i-2}+\ldots +k_{n-i+1}z+k_{n-i})$
, for
![]() $i=1,\ldots,n-1$
with
$i=1,\ldots,n-1$
with
![]() $k_i$
the coefficients of
$k_i$
the coefficients of
![]() $f(x)$
; see Section
3
.
$f(x)$
; see Section
3
.
Proof. Define the following matrices in
![]() $\textrm{GL}_{n}(A)$
:
$\textrm{GL}_{n}(A)$
:

Then, direct computation shows that
Remark.
Matrices of the form
![]() $C_{f}(a,z)$
were first introduced by Ochoa (see [Reference Ochoa10] and [Reference Ochoa11]
) who called them “
$C_{f}(a,z)$
were first introduced by Ochoa (see [Reference Ochoa10] and [Reference Ochoa11]
) who called them “
![]() $A$
-matrices”, presumably because of the shape of their non-zero entries. The matrix
$A$
-matrices”, presumably because of the shape of their non-zero entries. The matrix
![]() $C_{f}(a,z)$
is similar to the matrix
$C_{f}(a,z)$
is similar to the matrix

considered by Rehm in [Reference Rehm13], associated with an ideal
![]() $\textbf{a}$
(which we have called
$\textbf{a}$
(which we have called
![]() $\mathfrak{b}$
). The difference is that we use a more standard form of the companion matrix
$\mathfrak{b}$
). The difference is that we use a more standard form of the companion matrix
![]() $T(\theta )$
and corresponding variants of
$T(\theta )$
and corresponding variants of
![]() $\lambda$
and
$\lambda$
and
![]() $\kappa$
, compared to Rehm, in order to obtain matrices
$\kappa$
, compared to Rehm, in order to obtain matrices
![]() $C_{f}(a,z)$
that agree with Ochoa’s
$C_{f}(a,z)$
that agree with Ochoa’s
![]() $A$
-matrices. To see that
$A$
-matrices. To see that
![]() $\hspace{1pt}{\vphantom{\theta }}^{\textbf{a}}\hspace{-1pt}{\theta }$
is similar to
$\hspace{1pt}{\vphantom{\theta }}^{\textbf{a}}\hspace{-1pt}{\theta }$
is similar to
![]() $C_{f}(a,z)$
, let
$C_{f}(a,z)$
, let

One then easily verifies that
We can now finish the proof of our main result which gives conditions for similarity classes to contain matrices of the form
![]() $C_f(a,z)$
from Lemma 5.1. Recall that from Section 3 onwards we assumed that
$C_f(a,z)$
from Lemma 5.1. Recall that from Section 3 onwards we assumed that
![]() $A$
is a PID. We have also assumed throughout that
$A$
is a PID. We have also assumed throughout that
![]() $f(x)$
is irreducible.
$f(x)$
is irreducible.
Theorem 5.2.
Let
![]() $\mathfrak{b}$
be an ideal of
$\mathfrak{b}$
be an ideal of
![]() $A[\theta ]$
of degree one. The similarity class in
$A[\theta ]$
of degree one. The similarity class in
![]() $\textrm{M}_{n}(A)$
that corresponds to the ideal class of
$\textrm{M}_{n}(A)$
that corresponds to the ideal class of
![]() $\mathfrak{b}$
under the Latimer–MacDuffee correspondence contains a matrix of the form
$\mathfrak{b}$
under the Latimer–MacDuffee correspondence contains a matrix of the form
![]() $C_{f}(a,z)$
, where
$C_{f}(a,z)$
, where
![]() $a,z\in A$
and
$a,z\in A$
and
![]() $f(z)\equiv 0\mod (a)$
. In particular, if
$f(z)\equiv 0\mod (a)$
. In particular, if
![]() $A[\theta ]=B$
is the maximal order, then every similarity class in
$A[\theta ]=B$
is the maximal order, then every similarity class in
![]() $\textrm{M}_{n}(A)$
contains a matrix of this form.
$\textrm{M}_{n}(A)$
contains a matrix of this form.
Proof. Let
![]() $\mathcal{C}$
be a similarity class in
$\mathcal{C}$
be a similarity class in
![]() $\textrm{M}_{n}(A)$
corresponding to the ideal class of
$\textrm{M}_{n}(A)$
corresponding to the ideal class of
![]() $\mathfrak{b}$
. By Lemma 3.5,
$\mathfrak{b}$
. By Lemma 3.5,
![]() $\mathcal{C}$
contains a matrix
$\mathcal{C}$
contains a matrix
![]() $\alpha T(\theta )\alpha ^{-1}$
, where
$\alpha T(\theta )\alpha ^{-1}$
, where
![]() $\alpha$
is an ideal matrix for
$\alpha$
is an ideal matrix for
![]() $\mathfrak{b}$
. By Proposition 4.2, there exists a
$\mathfrak{b}$
. By Proposition 4.2, there exists a
![]() $z\in A$
such that
$z\in A$
such that
![]() $f(z)\equiv 0\mod (a)$
, where
$f(z)\equiv 0\mod (a)$
, where
![]() $a$
is a generator of
$a$
is a generator of
![]() $A\cap \mathfrak{b}$
and
$A\cap \mathfrak{b}$
and
![]() $\kappa =\kappa (a,z)$
is an ideal matrix for
$\kappa =\kappa (a,z)$
is an ideal matrix for
![]() $\mathfrak{b}$
. Thus the similarity class of
$\mathfrak{b}$
. Thus the similarity class of
![]() $\mathcal{C}$
contains
$\mathcal{C}$
contains
![]() $\kappa T(\theta )\kappa ^{-1}$
, so by Lemma 5.1
$\kappa T(\theta )\kappa ^{-1}$
, so by Lemma 5.1
![]() $\mathcal{C}$
contains
$\mathcal{C}$
contains
![]() $C_{f}(a,z)$
.
$C_{f}(a,z)$
.
If
![]() $A[\theta ]=B$
, then by Corollary 2.8, every ideal class contains an ideal of degree one, so the argument above implies that every similarity class contains a matrix of the desired form.
$A[\theta ]=B$
, then by Corollary 2.8, every ideal class contains an ideal of degree one, so the argument above implies that every similarity class contains a matrix of the desired form.
6. Examples
Example 6.1.
Let
![]() $A={\mathbb{Z}}$
,
$A={\mathbb{Z}}$
,
![]() $K=\textrm{Frac}(A)={\mathbb{Q}}$
,
$K=\textrm{Frac}(A)={\mathbb{Q}}$
,
![]() $L={\mathbb{Q}}(\theta )$
be the number field with defining polynomial
$L={\mathbb{Q}}(\theta )$
be the number field with defining polynomial
(LMFDB [17] Number Field 3.1.283.1), and
![]() $B=\mathcal{O}_{L}={\mathbb{Z}}[\theta ]$
its ring of integers.
$B=\mathcal{O}_{L}={\mathbb{Z}}[\theta ]$
its ring of integers.
![]() ${\mathbb{Z}}[\theta ]$
has ideal class group of order 2, generated by the ideal class of
${\mathbb{Z}}[\theta ]$
has ideal class group of order 2, generated by the ideal class of
![]() $\mathfrak{b}=(3,\theta -2)$
. Let
$\mathfrak{b}=(3,\theta -2)$
. Let
![]() $T(\theta )$
be the companion matrix of
$T(\theta )$
be the companion matrix of
![]() $f(x)$
, and
$f(x)$
, and
![]() $v$
be as in the proof of Lemma 5.1:
$v$
be as in the proof of Lemma 5.1:
 \begin{equation*}T(\theta )=\begin {pmatrix} 0\;\;\;\; & 1\;\;\;\; & 0\\[5pt] 0\;\;\;\; & 0\;\;\;\; & 1\\[5pt] 1\;\;\;\; & -4\;\;\;\; & 0\end {pmatrix}, \quad v=\begin {pmatrix} 0 & 1 & 0\\[5pt] 0\;\;\;\; & 0\;\;\;\; & 1\\[5pt] 1\;\;\;\; & 0\;\;\;\; & 0 \end {pmatrix}.\end{equation*}
\begin{equation*}T(\theta )=\begin {pmatrix} 0\;\;\;\; & 1\;\;\;\; & 0\\[5pt] 0\;\;\;\; & 0\;\;\;\; & 1\\[5pt] 1\;\;\;\; & -4\;\;\;\; & 0\end {pmatrix}, \quad v=\begin {pmatrix} 0 & 1 & 0\\[5pt] 0\;\;\;\; & 0\;\;\;\; & 1\\[5pt] 1\;\;\;\; & 0\;\;\;\; & 0 \end {pmatrix}.\end{equation*}
-
1. For
 $[\mathfrak{b}]=[(3, \theta -2)]$
, we may take
$[\mathfrak{b}]=[(3, \theta -2)]$
, we may take
 $a=3, z=2$
to define
$a=3, z=2$
to define
 $\kappa (3,2)$
(as defined in (
4.1
)) as an ideal matrix for
$\kappa (3,2)$
(as defined in (
4.1
)) as an ideal matrix for
 $\mathfrak{b}$
, and
$\mathfrak{b}$
, and
 $\tau _1$
as in the proof of Lemma 5.1:By Lemma 3.5, the similarity class of
$\tau _1$
as in the proof of Lemma 5.1:By Lemma 3.5, the similarity class of \begin{equation*}\kappa _1=\kappa (3,2)=\begin {pmatrix} 3\;\;\;\; & 0\;\;\;\; & 0 \\[5pt] -2\;\;\;\; & 1\;\;\;\; & 0\\[5pt] -4\;\;\;\; & 0\;\;\;\; & 1 \end {pmatrix}, \quad \tau _1=\begin {pmatrix} 1\;\;\;\; & 0\;\;\;\; & 0\\[5pt] 0\;\;\;\; & 1\;\;\;\; & 0\\[5pt] 0\;\;\;\; & -2\;\;\;\; & 1 \end {pmatrix}.\end{equation*}
\begin{equation*}\kappa _1=\kappa (3,2)=\begin {pmatrix} 3\;\;\;\; & 0\;\;\;\; & 0 \\[5pt] -2\;\;\;\; & 1\;\;\;\; & 0\\[5pt] -4\;\;\;\; & 0\;\;\;\; & 1 \end {pmatrix}, \quad \tau _1=\begin {pmatrix} 1\;\;\;\; & 0\;\;\;\; & 0\\[5pt] 0\;\;\;\; & 1\;\;\;\; & 0\\[5pt] 0\;\;\;\; & -2\;\;\;\; & 1 \end {pmatrix}.\end{equation*}
 $\textrm{M}_n({\mathbb{Z}})$
corresponding to
$\textrm{M}_n({\mathbb{Z}})$
corresponding to
 $\mathfrak{b}$
under the Latimer–MacDuffee correspondence contains
$\mathfrak{b}$
under the Latimer–MacDuffee correspondence contains
 $\kappa _1 T(\theta ) \kappa _1^{-1}$
, and a representative for this similarity class of the form
$\kappa _1 T(\theta ) \kappa _1^{-1}$
, and a representative for this similarity class of the form
 $C_{f}(a,z)$
is given by:
$C_{f}(a,z)$
is given by:
 \begin{equation*}v\tau _1(\kappa _1 T(\theta )\kappa _1^{-1})\tau _1^{-1}v^{-1}=\begin {pmatrix} 0\;\;\;\; & 1\;\;\;\; & 0 \\[5pt] -8\;\;\;\; & -2\;\;\;\; & -5\\[5pt] 3\;\;\;\; & 0\;\;\;\; & 2 \end {pmatrix}=C_{f}(3,2)\end{equation*}
\begin{equation*}v\tau _1(\kappa _1 T(\theta )\kappa _1^{-1})\tau _1^{-1}v^{-1}=\begin {pmatrix} 0\;\;\;\; & 1\;\;\;\; & 0 \\[5pt] -8\;\;\;\; & -2\;\;\;\; & -5\\[5pt] 3\;\;\;\; & 0\;\;\;\; & 2 \end {pmatrix}=C_{f}(3,2)\end{equation*}
-
2. For
 $[1]=[(1, \theta )]$
, we may take
$[1]=[(1, \theta )]$
, we may take
 $a=1, z=0$
, so
$a=1, z=0$
, so
 $\kappa _2=\tau _2=I$
. The similarity class of
$\kappa _2=\tau _2=I$
. The similarity class of
 $\textrm{M}_n({\mathbb{Z}})$
corresponding to the trivial ideal class contains
$\textrm{M}_n({\mathbb{Z}})$
corresponding to the trivial ideal class contains
 $T(\theta )$
, and a representative for this similarity class of the form
$T(\theta )$
, and a representative for this similarity class of the form
 $C_f(a,z)$
is given by:
$C_f(a,z)$
is given by:
 \begin{equation*}v\tau _2(\kappa _2 T(\theta )\kappa _2^{-1})\tau _2^{-1}v^{-1}=vT(\theta )v^{-1}=\begin {pmatrix} 0\;\;\;\; & 1\;\;\;\; & 0\\[5pt] -4\;\;\;\; & 0\;\;\;\; & 1\\[5pt] 1\;\;\;\; & 0\;\;\;\; & 0 \end {pmatrix}=C_f(1,0)\end{equation*}
\begin{equation*}v\tau _2(\kappa _2 T(\theta )\kappa _2^{-1})\tau _2^{-1}v^{-1}=vT(\theta )v^{-1}=\begin {pmatrix} 0\;\;\;\; & 1\;\;\;\; & 0\\[5pt] -4\;\;\;\; & 0\;\;\;\; & 1\\[5pt] 1\;\;\;\; & 0\;\;\;\; & 0 \end {pmatrix}=C_f(1,0)\end{equation*}
Example 6.2.
Let
![]() $A={\mathbb{F}}_2[x], K={\mathbb{F}}_2(x)$
,
$A={\mathbb{F}}_2[x], K={\mathbb{F}}_2(x)$
,
![]() $L={\mathbb{F}}_2(x,y)/(f(x,y))$
and
$L={\mathbb{F}}_2(x,y)/(f(x,y))$
and
![]() $B={\mathbb{F}}_2[x,y]/(f(x,y))$
be the (affine) coordinate ring of the curve
$B={\mathbb{F}}_2[x,y]/(f(x,y))$
be the (affine) coordinate ring of the curve
over
![]() ${\mathbb{F}}_2$
. Note that
${\mathbb{F}}_2$
. Note that
![]() $f(x,y)$
is smooth, so
$f(x,y)$
is smooth, so
![]() $B$
is a Dedekind domain.
$B$
is a Dedekind domain.
![]() $B$
has ideal class group of order 3, generated by the ideal class of
$B$
has ideal class group of order 3, generated by the ideal class of
![]() $\mathfrak{b}=(x,y)$
. Let
$\mathfrak{b}=(x,y)$
. Let
![]() $T(y)$
be the companion matrix of
$T(y)$
be the companion matrix of
![]() $f(x,y)$
, and
$f(x,y)$
, and
![]() $v$
be as in the proof of Lemma 5.1:
$v$
be as in the proof of Lemma 5.1:
 \begin{equation*}T(y)=\begin {pmatrix} 0\;\;\;\; & 1\;\;\;\; & 0\\[5pt] 0\;\;\;\; & 0\;\;\;\; & 1\\[5pt] x^3+x^2+x\;\;\;\; & 0\;\;\;\; & 0 \end {pmatrix}, \quad v=\begin {pmatrix} 0\;\;\;\; & 1\;\;\;\; & 0\\[5pt] 0\;\;\;\; & 0\;\;\;\; & 1\\[5pt] 1\;\;\;\; & 0\;\;\;\; & 0 \end {pmatrix}.\end{equation*}
\begin{equation*}T(y)=\begin {pmatrix} 0\;\;\;\; & 1\;\;\;\; & 0\\[5pt] 0\;\;\;\; & 0\;\;\;\; & 1\\[5pt] x^3+x^2+x\;\;\;\; & 0\;\;\;\; & 0 \end {pmatrix}, \quad v=\begin {pmatrix} 0\;\;\;\; & 1\;\;\;\; & 0\\[5pt] 0\;\;\;\; & 0\;\;\;\; & 1\\[5pt] 1\;\;\;\; & 0\;\;\;\; & 0 \end {pmatrix}.\end{equation*}
-
1. For
 $[\mathfrak{b}]=[(x,y)]$
, we may take
$[\mathfrak{b}]=[(x,y)]$
, we may take
 $a=x, z=0$
to define
$a=x, z=0$
to define
 $\kappa (x,0)$
as an ideal matrix for
$\kappa (x,0)$
as an ideal matrix for
 $\mathfrak{b}$
, and define
$\mathfrak{b}$
, and define
 $\tau _1$
as in the proof of Lemma 5.1:The similarity class of
$\tau _1$
as in the proof of Lemma 5.1:The similarity class of \begin{equation*}\kappa _1=\kappa (x,0) =\begin {pmatrix} x\;\;\;\; & 0\;\;\;\; & 0 \\[5pt] 0\;\;\;\; & 1\;\;\;\; & 0\\[5pt] 0\;\;\;\; & 0\;\;\;\; & 1 \end {pmatrix}, \quad \tau _1=\begin {pmatrix} 1\;\;\;\; & 0\;\;\;\; & 0\\[5pt] 0\;\;\;\; & 1\;\;\;\; & 0\\[5pt] 0\;\;\;\; & 0\;\;\;\; & 1 \end {pmatrix}. \end{equation*}
\begin{equation*}\kappa _1=\kappa (x,0) =\begin {pmatrix} x\;\;\;\; & 0\;\;\;\; & 0 \\[5pt] 0\;\;\;\; & 1\;\;\;\; & 0\\[5pt] 0\;\;\;\; & 0\;\;\;\; & 1 \end {pmatrix}, \quad \tau _1=\begin {pmatrix} 1\;\;\;\; & 0\;\;\;\; & 0\\[5pt] 0\;\;\;\; & 1\;\;\;\; & 0\\[5pt] 0\;\;\;\; & 0\;\;\;\; & 1 \end {pmatrix}. \end{equation*}
 $\textrm{M}_n({\mathbb{F}}_2[x])$
corresponding to
$\textrm{M}_n({\mathbb{F}}_2[x])$
corresponding to
 $\mathfrak{p}$
under the Latimer–MacDuffee correspondence contains
$\mathfrak{p}$
under the Latimer–MacDuffee correspondence contains
 $\kappa _1 T(y) \kappa _1^{-1}$
, and a representative for this similarity class of the form
$\kappa _1 T(y) \kappa _1^{-1}$
, and a representative for this similarity class of the form
 $C_{f}(a,z)$
is given by:
$C_{f}(a,z)$
is given by:
 \begin{equation*}v\tau _1(\kappa _1 T(y) \kappa _1^{-1})\tau _1^{-1} v^{-1}=\begin {pmatrix} 0\;\;\;\; & 1\;\;\;\; & 0 \\[5pt] 0\;\;\;\; & 0\;\;\;\; & x^2+x+1\\[5pt] x\;\;\;\; & 0\;\;\;\; & 0\;\;\;\; \end {pmatrix} =C_f(x,0)\end{equation*}
\begin{equation*}v\tau _1(\kappa _1 T(y) \kappa _1^{-1})\tau _1^{-1} v^{-1}=\begin {pmatrix} 0\;\;\;\; & 1\;\;\;\; & 0 \\[5pt] 0\;\;\;\; & 0\;\;\;\; & x^2+x+1\\[5pt] x\;\;\;\; & 0\;\;\;\; & 0\;\;\;\; \end {pmatrix} =C_f(x,0)\end{equation*}
-
2. For
 $[\mathfrak{b}^2]=[(x+1,y+1)]$
, we may take
$[\mathfrak{b}^2]=[(x+1,y+1)]$
, we may take
 $a=x+1, z=1$
to define
$a=x+1, z=1$
to define
 $\kappa (x+1,1)$
and
$\kappa (x+1,1)$
and
 $\tau _2$
:A representative for the similarity class of
$\tau _2$
:A representative for the similarity class of \begin{equation*}\kappa _2=\kappa (x-1, 1) =\begin {pmatrix} x+1\;\;\;\; & 0\;\;\;\; & 0 \\[5pt] 1\;\;\;\; & 1\;\;\;\; & 0\\[5pt] 1\;\;\;\; & 0\;\;\;\; & 1 \end {pmatrix}, \quad \tau _2=\begin {pmatrix} 1\;\;\;\; & 0\;\;\;\; & 0\\[5pt] 0\;\;\;\; & 1\;\;\;\; & 0\\[5pt] 0\;\;\;\; & 1\;\;\;\; & 1 \end {pmatrix}. \end{equation*}
\begin{equation*}\kappa _2=\kappa (x-1, 1) =\begin {pmatrix} x+1\;\;\;\; & 0\;\;\;\; & 0 \\[5pt] 1\;\;\;\; & 1\;\;\;\; & 0\\[5pt] 1\;\;\;\; & 0\;\;\;\; & 1 \end {pmatrix}, \quad \tau _2=\begin {pmatrix} 1\;\;\;\; & 0\;\;\;\; & 0\\[5pt] 0\;\;\;\; & 1\;\;\;\; & 0\\[5pt] 0\;\;\;\; & 1\;\;\;\; & 1 \end {pmatrix}. \end{equation*}
 $\textrm{M}_n({\mathbb{F}}_2[x])$
containing
$\textrm{M}_n({\mathbb{F}}_2[x])$
containing
 $\kappa _2 T(y)\kappa _2^{-1}$
of the form
$\kappa _2 T(y)\kappa _2^{-1}$
of the form
 $C_{f}(a,z)$
is given by:
$C_{f}(a,z)$
is given by:
 \begin{equation*}v\tau _2(\kappa _2 T(y) \kappa _2^{-1})\tau _2^{-1} v^{-1}=\begin {pmatrix} 0\;\;\;\; & 1\;\;\;\; & 0\\[5pt] 1\;\;\;\; & 1\;\;\;\; & x^2+1\\[5pt] x+1\;\;\;\; & 0\;\;\;\; & 1 \end {pmatrix} =C_f(x+1,1) \end{equation*}
\begin{equation*}v\tau _2(\kappa _2 T(y) \kappa _2^{-1})\tau _2^{-1} v^{-1}=\begin {pmatrix} 0\;\;\;\; & 1\;\;\;\; & 0\\[5pt] 1\;\;\;\; & 1\;\;\;\; & x^2+1\\[5pt] x+1\;\;\;\; & 0\;\;\;\; & 1 \end {pmatrix} =C_f(x+1,1) \end{equation*}
-
3. For
 $[\mathfrak{b}^3]=[1]=[(1,y)]$
, we may take
$[\mathfrak{b}^3]=[1]=[(1,y)]$
, we may take
 $a=1,z=0$
so
$a=1,z=0$
so
 $\kappa _3=\kappa (1,0)=I$
and
$\kappa _3=\kappa (1,0)=I$
and
 $\tau _2=I$
. The similarity class of
$\tau _2=I$
. The similarity class of
 $\textrm{M}_n({\mathbb{F}}_2[x])$
corresponding to the trivial ideal class contains
$\textrm{M}_n({\mathbb{F}}_2[x])$
corresponding to the trivial ideal class contains
 $T(y)$
, and a representative for this similarity class of the form
$T(y)$
, and a representative for this similarity class of the form
 $C_{f}(a,z)$
is given by:
$C_{f}(a,z)$
is given by:
 \begin{equation*}v\tau _3(\kappa _3 T(y)\kappa _3^{-1})\tau _3^{-1} v^{-1}=v T(y)v^{-1}=\begin {pmatrix} 0\;\;\;\; & 1\;\;\;\; & 0\\[5pt] 0\;\;\;\; & 0\;\;\;\; & x^3+x^2+x\\[5pt] 1\;\;\;\; & 0\;\;\;\; & 0 \end {pmatrix}=C_f(1,0). \end{equation*}
\begin{equation*}v\tau _3(\kappa _3 T(y)\kappa _3^{-1})\tau _3^{-1} v^{-1}=v T(y)v^{-1}=\begin {pmatrix} 0\;\;\;\; & 1\;\;\;\; & 0\\[5pt] 0\;\;\;\; & 0\;\;\;\; & x^3+x^2+x\\[5pt] 1\;\;\;\; & 0\;\;\;\; & 0 \end {pmatrix}=C_f(1,0). \end{equation*}
Acknowledgement
We are deeply grateful to H. W. Lenstra for providing the proof of Theorem 2.7 and allowing us to include it here.