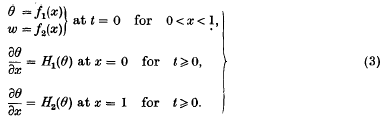Research Article
On the product of three non-homogeneous linear forms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 137-152
-
- Article
- Export citation
A note on the distribution of the different orderings of n objects
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-9
-
- Article
- Export citation
On the number of representations of an integer as the sum of three r-free integers
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 433-441
-
- Article
- Export citation
The Parseval formulae for monotonic functions. I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 289-306
-
- Article
- Export citation
On a class of linear integro-differential equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 153-163
-
- Article
- Export citation
Some remarks on Schottky's theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 442-454
-
- Article
- Export citation
Notes on Fourier series (IV): Summability (R2)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 10-25
-
- Article
- Export citation
The theory of surfaces in a geometry based on the notion of area
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 307-313
-
- Article
- Export citation
The gravitational field of a rotating cohesive system
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 164-177
-
- Article
- Export citation
A ring in graph theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 26-40
-
- Article
- Export citation
On a new analytical representation of curves in space
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 455-458
-
- Article
- Export citation
On homotopy and deformation retracts
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 314-320
-
- Article
- Export citation
Note on the velocity of propagation of gravitation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 178-182
-
- Article
- Export citation
Functions of a statistical variate with given means, with special reference to Laplacian distributions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 41-49
-
- Article
- Export citation
Random associations on a lattice
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 321-328
-
- Article
- Export citation
A family of cubical graphs
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 459-474
-
- Article
- Export citation
A note on relativistic second quantization
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 183-195
-
- Article
- Export citation
Combinants of a pencil of quadric surfaces. I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 475-487
-
- Article
- Export citation
The problem of random intervals on a line
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 329-341
-
- Article
- Export citation
A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 50-67
-
- Article
- Export citation

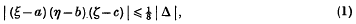
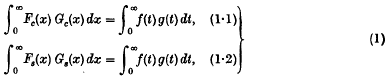
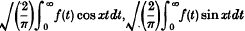 respectively; and
respectively; and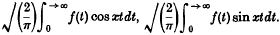 .
.
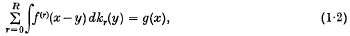
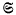 the class of all functions regular in |
the class of all functions regular in |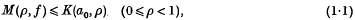


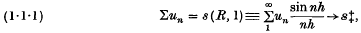
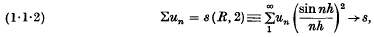
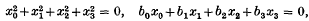
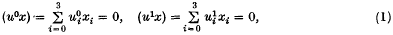
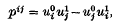
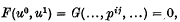
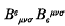 at a point in a plane containing a rotating cohesive system such as a rod is calculated for a point at great distances from the system. It is found that the invariant has a stationary value when the rod is
at a point in a plane containing a rotating cohesive system such as a rod is calculated for a point at great distances from the system. It is found that the invariant has a stationary value when the rod is 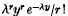 (see e.g. (1)). Consider the case when each event consists of an interval of length α (an event being characterized by its first point). What is the probability that the covered portion of the interval [0,
(see e.g. (1)). Consider the case when each event consists of an interval of length α (an event being characterized by its first point). What is the probability that the covered portion of the interval [0,