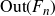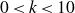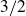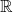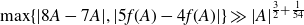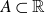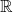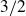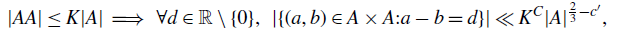FirstView articles
Research Article
Centralisers of linear growth automorphisms of free groups
- Part of:
-
- Published online by Cambridge University Press:
- 20 September 2024, pp. 1-22
-
- Article
-
- You have access
- HTML
- Export citation
Linked orbits of homeomorphisms of the plane and Gambaudo–Kolev Theorem
- Part of:
-
- Published online by Cambridge University Press:
- 20 September 2024, pp. 1-6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Domination inequalities and dominating graphs
- Part of:
-
- Published online by Cambridge University Press:
- 19 September 2024, pp. 1-18
-
- Article
-
- You have access
- HTML
- Export citation
The Failure of Galois Descent for p-Selmer Groups of Elliptic Curves
- Part of:
-
- Published online by Cambridge University Press:
- 19 September 2024, pp. 1-34
-
- Article
-
- You have access
- HTML
- Export citation
Generalised knotoids
-
- Published online by Cambridge University Press:
- 19 September 2024, pp. 1-36
-
- Article
-
- You have access
- HTML
- Export citation
Multiplicative dependence of rational values modulo approximate finitely generated groups
- Part of:
-
- Published online by Cambridge University Press:
- 19 September 2024, pp. 1-17
-
- Article
-
- You have access
- HTML
- Export citation
Tropical curves in abelian surfaces I: enumeration of curves passing through points
- Part of:
-
- Published online by Cambridge University Press:
- 19 September 2024, pp. 1-40
-
- Article
-
- You have access
- HTML
- Export citation
Differential forms on universal K3 surfaces
- Part of:
-
- Published online by Cambridge University Press:
- 12 July 2024, pp. 1-9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A better than
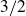 $3/2$ exponent for iterated sums and products over
$3/2$ exponent for iterated sums and products over 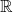 $\mathbb R$
$\mathbb R$
- Part of:
-
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
The Ulam–Hammersley problem for multiset permutations
- Part of:
-
- Published online by Cambridge University Press:
- 09 May 2024, pp. 1-26
-
- Article
-
- You have access
- HTML
- Export citation
Non-invertible planar self-affine sets
- Part of:
-
- Published online by Cambridge University Press:
- 08 May 2024, pp. 1-17
-
- Article
-
- You have access
- HTML
- Export citation