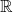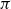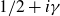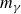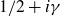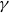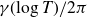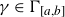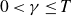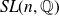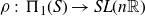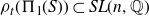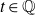Most read
This page lists the top ten most read articles for this journal based on the number of full text views and downloads recorded on Cambridge Core over the last 90 days. This list is updated on a daily basis.
A bound of the number of weighted blow-ups to compute the minimal log discrepancy for smooth 3-folds
- Part of:
-
- Published online by Cambridge University Press:
- 08 March 2024, pp. 495-515
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The sup-norm problem beyond the newform
- Part of:
-
- Published online by Cambridge University Press:
- 12 March 2024, pp. 517-545
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Log Calabi–Yau surfaces and Jeffrey–Kirwan residues
- Part of:
-
- Published online by Cambridge University Press:
- 04 March 2024, pp. 547-592
-
- Article
- Export citation
The uniform distribution modulo one of certain subsequences of ordinates of zeros of the zeta function
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2024, pp. 593-608
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
How to solve a binary cubic equation in integers
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2024, pp. 609-624
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on Hodge–Tate spectral sequences
- Part of:
-
- Published online by Cambridge University Press:
- 22 March 2024, pp. 625-642
-
- Article
-
- You have access
- HTML
- Export citation
Zariski dense surface subgroups in
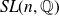 $SL(n,\mathbb{Q})$ with odd
$SL(n,\mathbb{Q})$ with odd  $n$
$n$
- Part of:
-
- Published online by Cambridge University Press:
- 26 March 2024, pp. 643-653
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PSP volume 176 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 April 2024, pp. f1-f2
-
- Article
-
- You have access
- Export citation
PSP volume 176 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 12 April 2024, pp. b1-b5
-
- Article
-
- You have access
- Export citation