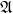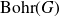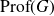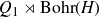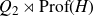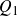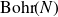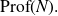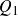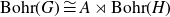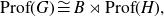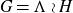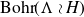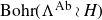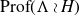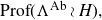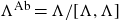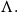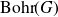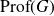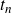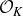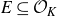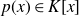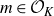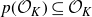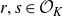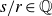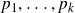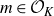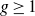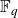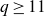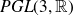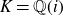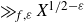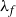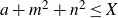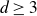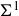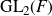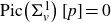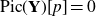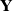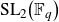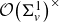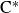Open access
Research Article
Zariski dense surface subgroups in
 $SL(n,\mathbb{Q})$ with odd
$SL(n,\mathbb{Q})$ with odd  $n$
$n$
- Part of:
-
- Published online by Cambridge University Press:
- 26 March 2024, pp. 643-653
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The sup-norm problem beyond the newform
- Part of:
-
- Published online by Cambridge University Press:
- 12 March 2024, pp. 517-545
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
How to solve a binary cubic equation in integers
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2024, pp. 609-624
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Abelian tropical covers
- Part of:
-
- Published online by Cambridge University Press:
- 10 October 2023, pp. 395-416
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Bohr compactifications and profinite completions of group extensions
- Part of:
-
- Published online by Cambridge University Press:
- 09 October 2023, pp. 373-393
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonvarying, affine and extremal geometry of strata of differentials
- Part of:
-
- Published online by Cambridge University Press:
- 06 October 2023, pp. 361-371
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A problem of Erdős–Graham–Granville–Selfridge on integral points on hyperelliptic curves
- Part of:
-
- Published online by Cambridge University Press:
- 05 October 2023, pp. 309-323
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiple recurrence and popular differences for polynomial patterns in rings of integers
- Part of:
-
- Published online by Cambridge University Press:
- 02 October 2023, pp. 239-278
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lower bounds on the maximal number of rational points on curves over finite fields
- Part of:
-
- Published online by Cambridge University Press:
- 28 September 2023, pp. 213-238
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Galois groups and prime divisors in random quadratic sequences
- Part of:
-
- Published online by Cambridge University Press:
- 07 September 2023, pp. 95-122
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equidistribution of exponential sums indexed by a subgroup of fixed cardinality
- Part of:
-
- Published online by Cambridge University Press:
- 24 August 2023, pp. 65-94
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the values taken by slice torus invariants
-
- Published online by Cambridge University Press:
- 23 August 2023, pp. 55-63
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Projection theorems for linear-fractional families of projections
- Part of:
-
- Published online by Cambridge University Press:
- 08 August 2023, pp. 625-647
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prime divisors and the number of conjugacy classes of finite groups
- Part of:
-
- Published online by Cambridge University Press:
- 10 July 2023, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sign changes of fourier coefficients of holomorphic cusp forms at norm form arguments
- Part of:
-
- Published online by Cambridge University Press:
- 23 May 2023, pp. 539-567
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Positive lower density for prime divisors of generic linear recurrences
- Part of:
-
- Published online by Cambridge University Press:
- 24 April 2023, pp. 467-478
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relatively hyperbolic groups with strongly shortcut parabolics are strongly shortcut
- Part of:
-
- Published online by Cambridge University Press:
- 17 April 2023, pp. 367-380
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Picard group of vertex affinoids in the first Drinfeld covering
- Part of:
-
- Published online by Cambridge University Press:
- 13 April 2023, pp. 423-432
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random amenable C*-algebras
- Part of:
-
- Published online by Cambridge University Press:
- 12 April 2023, pp. 345-366
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Intermediate-scale statistics for real-valued lacunary sequences
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2023, pp. 303-318
-
- Article
-
- You have access
- Open access
- HTML
- Export citation