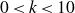1. Introduction
Let
![]() ${{\mathcal{F}_{g,n}}}$
be the moduli space of n-pointed K3 surfaces of genus
${{\mathcal{F}_{g,n}}}$
be the moduli space of n-pointed K3 surfaces of genus
![]() $g>2$
, i.e., primitively polarised of degree
$g>2$
, i.e., primitively polarised of degree
![]() $2g-2$
. It is a quasi-projective variety of dimension
$2g-2$
. It is a quasi-projective variety of dimension
![]() $19+2n$
with a natural morphism
$19+2n$
with a natural morphism
![]() ${{\mathcal{F}_{g,n}}}\to {{\mathcal{F}_{g}}}$
to the moduli space
${{\mathcal{F}_{g,n}}}\to {{\mathcal{F}_{g}}}$
to the moduli space
![]() ${{\mathcal{F}_{g}}}$
of K3 surfaces of genus g, which is generically a
${{\mathcal{F}_{g}}}$
of K3 surfaces of genus g, which is generically a
![]() $K3^{n}$
-fibration. In this paper we study holomorphic differential k-forms on a smooth projective model of
$K3^{n}$
-fibration. In this paper we study holomorphic differential k-forms on a smooth projective model of
![]() ${{\mathcal{F}_{g,n}}}$
. They do not depend on the choice of a smooth projective model, and thus are fundamental birational invariants of
${{\mathcal{F}_{g,n}}}$
. They do not depend on the choice of a smooth projective model, and thus are fundamental birational invariants of
![]() ${{\mathcal{F}_{g,n}}}$
. We prove a vanishing result for about half of the values of the degree k, and for the remaining degrees give a correspondence with modular forms on the period domain.
${{\mathcal{F}_{g,n}}}$
. We prove a vanishing result for about half of the values of the degree k, and for the remaining degrees give a correspondence with modular forms on the period domain.
Our main result is stated as follows.
Theorem 1·1. Let
![]() ${{\bar{\mathcal{F}}_{g,n}}}$
be a smooth projective model of
${{\bar{\mathcal{F}}_{g,n}}}$
be a smooth projective model of
![]() ${{\mathcal{F}_{g,n}}}$
with
${{\mathcal{F}_{g,n}}}$
with
![]() $g>2$
. Then we have a natural isomorphism:
$g>2$
. Then we have a natural isomorphism:
 \begin{equation} H^{0}({{\bar{\mathcal{F}}_{g,n}}}, \Omega^{k}) \simeq\begin{cases}0 & \: \: 0<k\leq 9 \\ M_{\wedge^{k},k}({{\Gamma_{g}}}) & \: \: 10 \leq k \leq 18 \\ 0 & \: \: k>19, \: k\in 2{{\mathbb{Z}}} \\ S_{19+m}({{\Gamma_{g}}}, \det)\otimes {{\mathbb{C}}}\mathcal{S}_{n,m} & \: \: k=19+2m, \: 0\leq m \leq n\end{cases}. \end{equation}
\begin{equation} H^{0}({{\bar{\mathcal{F}}_{g,n}}}, \Omega^{k}) \simeq\begin{cases}0 & \: \: 0<k\leq 9 \\ M_{\wedge^{k},k}({{\Gamma_{g}}}) & \: \: 10 \leq k \leq 18 \\ 0 & \: \: k>19, \: k\in 2{{\mathbb{Z}}} \\ S_{19+m}({{\Gamma_{g}}}, \det)\otimes {{\mathbb{C}}}\mathcal{S}_{n,m} & \: \: k=19+2m, \: 0\leq m \leq n\end{cases}. \end{equation}
Here
![]() ${{\Gamma_{g}}}$
is the modular group for K3 surfaces of genus g, which is defined as the kernel of
${{\Gamma_{g}}}$
is the modular group for K3 surfaces of genus g, which is defined as the kernel of
![]() $\mathrm{O}^{+}(L_{g})\to \mathrm{O}(L_{g}^{\vee}/L_{g})$
where
$\mathrm{O}^{+}(L_{g})\to \mathrm{O}(L_{g}^{\vee}/L_{g})$
where
![]() $L_{g}=2U\oplus 2E_{8}\oplus \langle 2-2g \rangle$
is the period lattice of K3 surfaces of genus g. In the second case,
$L_{g}=2U\oplus 2E_{8}\oplus \langle 2-2g \rangle$
is the period lattice of K3 surfaces of genus g. In the second case,
![]() $M_{\wedge^{k},k}({{\Gamma_{g}}})$
stands for the space of vector-valued modular forms of weight
$M_{\wedge^{k},k}({{\Gamma_{g}}})$
stands for the space of vector-valued modular forms of weight
![]() $(\wedge^{k},k)$
for
$(\wedge^{k},k)$
for
![]() ${{\Gamma_{g}}}$
(see [
Reference Ma4
]). In the last case,
${{\Gamma_{g}}}$
(see [
Reference Ma4
]). In the last case,
![]() $S_{19+m}({{\Gamma_{g}}}, \det)$
stands for the space of scalar-valued cusp forms of weight
$S_{19+m}({{\Gamma_{g}}}, \det)$
stands for the space of scalar-valued cusp forms of weight
![]() $19+m$
and determinant character for
$19+m$
and determinant character for
![]() ${{\Gamma_{g}}}$
, and
${{\Gamma_{g}}}$
, and
![]() $\mathcal{S}_{n,m}$
stands for the right quotient
$\mathcal{S}_{n,m}$
stands for the right quotient
![]() $\mathfrak{S}_{n}/(\mathfrak{S}_{m}\times \mathfrak{S}_{n-m})$
, which is a left
$\mathfrak{S}_{n}/(\mathfrak{S}_{m}\times \mathfrak{S}_{n-m})$
, which is a left
![]() $\mathfrak{S}_{n}$
-set. Theorem 1·1 is actually formulated and proved in the generality of lattice-polarisation (Theorem 2·6).
$\mathfrak{S}_{n}$
-set. Theorem 1·1 is actually formulated and proved in the generality of lattice-polarisation (Theorem 2·6).
In the case of the top degree
![]() $k=19+2n$
, namely for canonical forms, the isomorphism (1·1) is proved in [
Reference Ma2
]. Theorem 1·1 is the extension of this result to all degrees
$k=19+2n$
, namely for canonical forms, the isomorphism (1·1) is proved in [
Reference Ma2
]. Theorem 1·1 is the extension of this result to all degrees
![]() $k<19+2n$
. The spaces in the right-hand side of (1·1) can also be geometrically explained as follows. In the case
$k<19+2n$
. The spaces in the right-hand side of (1·1) can also be geometrically explained as follows. In the case
![]() $k\leq 18$
,
$k\leq 18$
,
![]() $M_{\wedge^{k},k}({{\Gamma_{g}}})$
is identified with the space of holomorphic k-forms on a smooth projective model of
$M_{\wedge^{k},k}({{\Gamma_{g}}})$
is identified with the space of holomorphic k-forms on a smooth projective model of
![]() ${{\mathcal{F}_{g}}}$
, pulled back by
${{\mathcal{F}_{g}}}$
, pulled back by
![]() ${{\mathcal{F}_{g,n}}}\to {{\mathcal{F}_{g}}}$
. In the case
${{\mathcal{F}_{g,n}}}\to {{\mathcal{F}_{g}}}$
. In the case
![]() $k=19+2m$
,
$k=19+2m$
,
![]() $S_{19+m}({{\Gamma_{g}}}, \det)$
is identified with the space of canonical forms on
$S_{19+m}({{\Gamma_{g}}}, \det)$
is identified with the space of canonical forms on
![]() $\bar{\mathcal{F}}_{g,m}$
, and the tensor product
$\bar{\mathcal{F}}_{g,m}$
, and the tensor product
![]() $S_{19+m}({{\Gamma_{g}}}, \det)\otimes {{\mathbb{C}}}\mathcal{S}_{n,m}$
is the direct sum of pullback of such canonical forms by various projections
$S_{19+m}({{\Gamma_{g}}}, \det)\otimes {{\mathbb{C}}}\mathcal{S}_{n,m}$
is the direct sum of pullback of such canonical forms by various projections
![]() ${{\mathcal{F}_{g,n}}}\to \mathcal{F}_{g,m}$
. Therefore Theorem 1·1 can be understood as a kind of classification result which says that except for canonical forms, there are essentially no new differential forms on the tower
${{\mathcal{F}_{g,n}}}\to \mathcal{F}_{g,m}$
. Therefore Theorem 1·1 can be understood as a kind of classification result which says that except for canonical forms, there are essentially no new differential forms on the tower
![]() $({{\mathcal{F}_{g,n}}})_{n}$
of moduli spaces. In fact, this is how the proof proceeds.
$({{\mathcal{F}_{g,n}}})_{n}$
of moduli spaces. In fact, this is how the proof proceeds.
The space
![]() $S_{l}({{\Gamma_{g}}}, \det)$
is nonzero for every sufficiently large l, so the space
$S_{l}({{\Gamma_{g}}}, \det)$
is nonzero for every sufficiently large l, so the space
![]() $H^{0}({{\bar{\mathcal{F}}_{g,n}}}, \Omega^{k})$
for odd
$H^{0}({{\bar{\mathcal{F}}_{g,n}}}, \Omega^{k})$
for odd
![]() $k\geq 19$
is typically nonzero (at least when k is large). On the other hand, it is not clear at present whether
$k\geq 19$
is typically nonzero (at least when k is large). On the other hand, it is not clear at present whether
![]() $M_{\wedge^{k},k}({{\Gamma_{g}}})\ne 0$
or not in the range
$M_{\wedge^{k},k}({{\Gamma_{g}}})\ne 0$
or not in the range
![]() $10\leq k \leq 18$
. This is a subject of study in the theory of vector-valued orthogonal modular forms.
$10\leq k \leq 18$
. This is a subject of study in the theory of vector-valued orthogonal modular forms.
The isomorphism (1·1) in the case
![]() $k=19+2m$
is an
$k=19+2m$
is an
![]() $\mathfrak{S}_{n}$
-equivariant isomorphism, where
$\mathfrak{S}_{n}$
-equivariant isomorphism, where
![]() $\mathfrak{S}_{n}$
acts on
$\mathfrak{S}_{n}$
acts on
![]() $H^{0}({{\bar{\mathcal{F}}_{g,n}}}, \Omega^{k})$
by its permutation action on
$H^{0}({{\bar{\mathcal{F}}_{g,n}}}, \Omega^{k})$
by its permutation action on
![]() ${{\mathcal{F}_{g,n}}}$
, while it acts on
${{\mathcal{F}_{g,n}}}$
, while it acts on
![]() $S_{19+m}({{\Gamma_{g}}}, \det)\otimes {{\mathbb{C}}}\mathcal{S}_{n,m}$
by its natural left action on
$S_{19+m}({{\Gamma_{g}}}, \det)\otimes {{\mathbb{C}}}\mathcal{S}_{n,m}$
by its natural left action on
![]() $\mathcal{S}_{n,m}$
. Therefore, taking the
$\mathcal{S}_{n,m}$
. Therefore, taking the
![]() $\mathfrak{S}_{n}$
-invariant part, we obtain the following simpler result for the unordered pointed moduli space
$\mathfrak{S}_{n}$
-invariant part, we obtain the following simpler result for the unordered pointed moduli space
![]() ${{\mathcal{F}_{g,n}}}/\mathfrak{S}_{n}$
, which is birationally a
${{\mathcal{F}_{g,n}}}/\mathfrak{S}_{n}$
, which is birationally a
![]() $K3^{[n]}$
-fibration over
$K3^{[n]}$
-fibration over
![]() ${{\mathcal{F}_{g}}}$
.
${{\mathcal{F}_{g}}}$
.
Corollary 1·2. Let
![]() $\overline{{{\mathcal{F}_{g,n}}}/\mathfrak{S}_{n}}$
be a smooth projective model of
$\overline{{{\mathcal{F}_{g,n}}}/\mathfrak{S}_{n}}$
be a smooth projective model of
![]() ${{\mathcal{F}_{g,n}}}/\mathfrak{S}_{n}$
. Then we have a natural isomorphism:
${{\mathcal{F}_{g,n}}}/\mathfrak{S}_{n}$
. Then we have a natural isomorphism:
 \begin{equation*}H^{0}(\overline{{{\mathcal{F}_{g,n}}}/\mathfrak{S}_{n}}, \Omega^{k}) \simeq\begin{cases}0 & \: \: 0<k\leq 9 \\ M_{\wedge^{k},k}({{\Gamma_{g}}}) & \: \: 10\leq k \leq 18 \\ 0 & \: \: k>19, \: k\in 2{{\mathbb{Z}}} \\ S_{19+m}({{\Gamma_{g}}}, \det) & \: \: k=19+2m, \: 0 \leq m \leq n\end{cases}.\end{equation*}
\begin{equation*}H^{0}(\overline{{{\mathcal{F}_{g,n}}}/\mathfrak{S}_{n}}, \Omega^{k}) \simeq\begin{cases}0 & \: \: 0<k\leq 9 \\ M_{\wedge^{k},k}({{\Gamma_{g}}}) & \: \: 10\leq k \leq 18 \\ 0 & \: \: k>19, \: k\in 2{{\mathbb{Z}}} \\ S_{19+m}({{\Gamma_{g}}}, \det) & \: \: k=19+2m, \: 0 \leq m \leq n\end{cases}.\end{equation*}
The universal K3 surface
![]() $\mathcal{F}_{g,1}$
is an analogue of elliptic modular surfaces ([
Reference Shioda6
]), and the moduli spaces
$\mathcal{F}_{g,1}$
is an analogue of elliptic modular surfaces ([
Reference Shioda6
]), and the moduli spaces
![]() ${{\mathcal{F}_{g,n}}}$
for general n are analogues of the so-called Kuga varieties over modular curves ([
Reference Shokurov7
]). Starting with the case of elliptic modular surfaces [
Reference Shioda6
], holomorphic differential forms on the Kuga varieties have been described in terms of elliptic modular forms: [
Reference Shokurov7
] for canonical forms, and [
Reference Gordon1
] for the case of lower degrees (somewhat implicitly). Theorem 1·1 can be regarded as a K3 version of these results.
${{\mathcal{F}_{g,n}}}$
for general n are analogues of the so-called Kuga varieties over modular curves ([
Reference Shokurov7
]). Starting with the case of elliptic modular surfaces [
Reference Shioda6
], holomorphic differential forms on the Kuga varieties have been described in terms of elliptic modular forms: [
Reference Shokurov7
] for canonical forms, and [
Reference Gordon1
] for the case of lower degrees (somewhat implicitly). Theorem 1·1 can be regarded as a K3 version of these results.
As a final remark, in view of the analogy between universal K3 surfaces and elliptic modular surfaces, invoking the classical fact that elliptic modular surfaces have maximal Picard number ([
Reference Shioda6
]) now raises the question if
![]() $H^{k,0}({{\bar{\mathcal{F}}_{g,n}}})\oplus H^{0,k}({{\bar{\mathcal{F}}_{g,n}}})$
is a sub
$H^{k,0}({{\bar{\mathcal{F}}_{g,n}}})\oplus H^{0,k}({{\bar{\mathcal{F}}_{g,n}}})$
is a sub
![]() ${{\mathbb{Q}}}$
-Hodge structure of
${{\mathbb{Q}}}$
-Hodge structure of
![]() $H^{k}({{\bar{\mathcal{F}}_{g,n}}}, {{\mathbb{C}}})$
. This is independent of the choice of a smooth projective model
$H^{k}({{\bar{\mathcal{F}}_{g,n}}}, {{\mathbb{C}}})$
. This is independent of the choice of a smooth projective model
![]() ${{\bar{\mathcal{F}}_{g,n}}}$
.
${{\bar{\mathcal{F}}_{g,n}}}$
.
The rest of this paper is devoted to the proof of Theorem 1·1. In Section 2·1 we compute a part of the holomorphic Leray spectral sequence associated to a certain type of
![]() $K3^{n}$
-fibration. This is the main step of the proof. In Section 2·2 we study differential forms on a compactification of such a fibration. In Section 2·3 we deduce (a generalised version of) Theorem 1·1 by combining the result of Section 2·2 with some results from [
Reference Ma2–Reference Pommerening5
]. Sometimes we drop the subscript X from the notation
$K3^{n}$
-fibration. This is the main step of the proof. In Section 2·2 we study differential forms on a compactification of such a fibration. In Section 2·3 we deduce (a generalised version of) Theorem 1·1 by combining the result of Section 2·2 with some results from [
Reference Ma2–Reference Pommerening5
]. Sometimes we drop the subscript X from the notation
![]() $\Omega_{X}^{k}$
when the variety X is clear from the context.
$\Omega_{X}^{k}$
when the variety X is clear from the context.
2. Proof
2·1. Holomorphic Leray spectral sequence
Let
![]() $\pi\colon X\to B$
be a smooth family of K3 surfaces over a smooth connected base B. In this subsection X and B may be analytic. We put the following assumption:
$\pi\colon X\to B$
be a smooth family of K3 surfaces over a smooth connected base B. In this subsection X and B may be analytic. We put the following assumption:
Condition 2·1. In a neighbourhood of every point of B, the period map is an embedding.
This is equivalent to the condition that the differential of the period map
is injective for every
![]() $b\in B$
, where
$b\in B$
, where
![]() $X_{b}$
is the fiber of
$X_{b}$
is the fiber of
![]() $\pi$
over b.
$\pi$
over b.
For a natural number
![]() $n>0$
we denote by
$n>0$
we denote by
![]() $X_{n}=X\times_{B}\cdots \times_{B}X$
the n-fold fiber product of X over B, and let
$X_{n}=X\times_{B}\cdots \times_{B}X$
the n-fold fiber product of X over B, and let
![]() $\pi_{n}\colon X_{n}\to B$
be the projection. We denote by
$\pi_{n}\colon X_{n}\to B$
be the projection. We denote by
![]() $\Omega_{\pi_{n}}$
the relative cotangent bundle of
$\Omega_{\pi_{n}}$
the relative cotangent bundle of
![]() $\pi_{n}$
, and
$\pi_{n}$
, and
![]() $\Omega_{\pi_{n}}^{p}=\wedge^{p}\Omega_{\pi_{n}}$
for
$\Omega_{\pi_{n}}^{p}=\wedge^{p}\Omega_{\pi_{n}}$
for
![]() $p\geq 0$
as usual.
$p\geq 0$
as usual.
Proposition 2·2. Let
![]() $\pi\colon X\to B$
be a K3 fibration satisfying Condition 2·1. Then we have a natural isomorphism:
$\pi\colon X\to B$
be a K3 fibration satisfying Condition 2·1. Then we have a natural isomorphism:
 \begin{equation*}(\pi_{n})_{\ast}\Omega_{X_{n}}^{k} \simeq\begin{cases}\Omega_{B}^{k} & \; \; k\leq \dim B \\ 0 & \; \; k>\dim B, \: \: k\not \equiv \dim B \: \: \mathrm{mod} \; 2 \\ K_{B}\otimes (\pi_{n})_{\ast}\Omega_{\pi_{n}}^{2m} & \; \; k=\dim B+2m, \: 0\leq m \leq n\end{cases}.\end{equation*}
\begin{equation*}(\pi_{n})_{\ast}\Omega_{X_{n}}^{k} \simeq\begin{cases}\Omega_{B}^{k} & \; \; k\leq \dim B \\ 0 & \; \; k>\dim B, \: \: k\not \equiv \dim B \: \: \mathrm{mod} \; 2 \\ K_{B}\otimes (\pi_{n})_{\ast}\Omega_{\pi_{n}}^{2m} & \; \; k=\dim B+2m, \: 0\leq m \leq n\end{cases}.\end{equation*}
This assertion amounts to a partial degeneration of the holomorphic Leray spectral sequence. Recall ([
Reference Voisin8
, section 5·2]) that
![]() $\Omega_{X_{n}}^k$
has the holomorphic Leray filtration
$\Omega_{X_{n}}^k$
has the holomorphic Leray filtration
![]() $L^{\bullet}\Omega_{X_{n}}^k$
defined by
$L^{\bullet}\Omega_{X_{n}}^k$
defined by
whose graded quotients are naturally isomorphic to
This filtration induces the holomorphic Leray spectral sequence
which converges to the filtration
By [
Reference Voisin8
, proposition 5·9], the
![]() $E_{1}$
page coincides with the collection of the Koszul complexes associated to the variation of Hodge structures for
$E_{1}$
page coincides with the collection of the Koszul complexes associated to the variation of Hodge structures for
![]() $\pi_{n}$
:
$\pi_{n}$
:
Here
![]() $\mathcal{H}^{\ast, \ast}$
are the Hodge bundles associated to the fibration
$\mathcal{H}^{\ast, \ast}$
are the Hodge bundles associated to the fibration
![]() $\pi_{n}\colon X_{n}\to B$
, and
$\pi_{n}\colon X_{n}\to B$
, and
are the differentials in the Koszul complexes (see [
Reference Voisin8
, section 5·1·3]). For degree reasons, the range of (l, q) in the
![]() $E_{1}$
page satisfies the inequalities
$E_{1}$
page satisfies the inequalities
The first two can be unified:
We calculate the
![]() $E_{1}$
to
$E_{1}$
to
![]() $E_{2}$
pages on the edge line
$E_{2}$
pages on the edge line
![]() $l+q=0$
.
$l+q=0$
.
Lemma 2·3. The following holds:
-
(1)
 $E_{1}^{l,-l}=0$
when
$E_{1}^{l,-l}=0$
when
 $l\leq \min\!(\!\dim B, k)$
with
$l\leq \min\!(\!\dim B, k)$
with
 $l\not\equiv k$
mod 2;
$l\not\equiv k$
mod 2; -
(2)
 $E_{2}^{l,-l}=0$
when
$E_{2}^{l,-l}=0$
when
 $l< \min\!(\!\dim B, k)$
;
$l< \min\!(\!\dim B, k)$
; -
(3) For
 $l_{0} = \min\!(\!\dim B, k)$
we have
$l_{0} = \min\!(\!\dim B, k)$
we have
 $E_{1}^{l_{0},-l_{0}}=E_{2}^{l_{0},-l_{0}}= \cdots = E_{\infty}^{l_{0},-l_{0}}$
.
$E_{1}^{l_{0},-l_{0}}=E_{2}^{l_{0},-l_{0}}= \cdots = E_{\infty}^{l_{0},-l_{0}}$
.
Proof. By (2·1), we have
![]() $E_{1}^{l,-l}=\mathcal{H}^{k-l,0}\otimes \Omega_{B}^{l}$
. By the Künneth formula, the fiber of
$E_{1}^{l,-l}=\mathcal{H}^{k-l,0}\otimes \Omega_{B}^{l}$
. By the Künneth formula, the fiber of
![]() $\mathcal{H}^{k-l,0}$
over a point
$\mathcal{H}^{k-l,0}$
over a point
![]() $b\in B$
is identified with
$b\in B$
is identified with
where
![]() $(p_{1}, \cdots, p_{n})$
ranges over all indices with
$(p_{1}, \cdots, p_{n})$
ranges over all indices with
![]() $\sum_{i}p_{i}=k-l$
and
$\sum_{i}p_{i}=k-l$
and
![]() $0\leq p_{i} \leq 2$
.
$0\leq p_{i} \leq 2$
.
(1) When
![]() $k-l$
is odd, every index
$k-l$
is odd, every index
![]() $(p_{1}, \cdots, p_{n})$
in (2·3) must contain a component
$(p_{1}, \cdots, p_{n})$
in (2·3) must contain a component
![]() $p_{i}=1$
. Since
$p_{i}=1$
. Since
![]() $H^{1,0}(X_b)=0$
, we see that
$H^{1,0}(X_b)=0$
, we see that
![]() $H^{k-l,0}(X_{b}^{n})=0$
. Therefore
$H^{k-l,0}(X_{b}^{n})=0$
. Therefore
![]() $\mathcal{H}^{k-l,0}=0$
when
$\mathcal{H}^{k-l,0}=0$
when
![]() $k-l$
is odd.
$k-l$
is odd.
(3) Let
![]() $l_{0} = \min\!(\!\dim B, k)$
. By the range (2·2) of (l, q), we see that for every
$l_{0} = \min\!(\!\dim B, k)$
. By the range (2·2) of (l, q), we see that for every
![]() $r\geq 1$
the source of
$r\geq 1$
the source of
![]() $d_{r}$
that hits
$d_{r}$
that hits
![]() $E_{r}^{l_{0}, -l_{0}}$
is zero, and the target of
$E_{r}^{l_{0}, -l_{0}}$
is zero, and the target of
![]() $d_{r}$
that starts from
$d_{r}$
that starts from
![]() $E_{r}^{l_{0}, -l_{0}}$
is also zero. This proves our assertion.
$E_{r}^{l_{0}, -l_{0}}$
is also zero. This proves our assertion.
(2) Let
![]() $l < \min\!(\!\dim B, k)$
. In view of (1), we may assume that
$l < \min\!(\!\dim B, k)$
. In view of (1), we may assume that
![]() $l=k-2m$
for some
$l=k-2m$
for some
![]() $m>0$
. By (2·2), the source of
$m>0$
. By (2·2), the source of
![]() $d_{1}$
that hits
$d_{1}$
that hits
![]() $E_{1}^{l,-l}$
is zero. We shall show that
$E_{1}^{l,-l}$
is zero. We shall show that
![]() $d_{1}\colon E_{1}^{l,-l}\to E_{1}^{l+1,-l}$
is injective. By (2·1), this morphism is identified with
$d_{1}\colon E_{1}^{l,-l}\to E_{1}^{l+1,-l}$
is injective. By (2·1), this morphism is identified with
By the Künneth formula as in (2·3), the fibers of the Hodge bundles
![]() $\mathcal{H}^{2m,0}$
,
$\mathcal{H}^{2m,0}$
,
![]() $\mathcal{H}^{2m-1,1}$
over
$\mathcal{H}^{2m-1,1}$
over
![]() $b\in B$
are respectively identified with
$b\in B$
are respectively identified with
 \begin{eqnarray}H^{2m-1,1}(X_{b}^{n})& = & \bigoplus_{|\sigma'|=m-1} \bigoplus_{i\not\in \sigma'} H^{2,0}(X_{b})^{\otimes \sigma'}\otimes H^{1,1}(X_{b}) \\ & = & \bigoplus_{|\sigma|=m} \bigoplus_{i\in \sigma} H^{2,0}(X_{b})^{\otimes \sigma-\{ i \}}\otimes H^{1,1}(X_{b}). \nonumber\end{eqnarray}
\begin{eqnarray}H^{2m-1,1}(X_{b}^{n})& = & \bigoplus_{|\sigma'|=m-1} \bigoplus_{i\not\in \sigma'} H^{2,0}(X_{b})^{\otimes \sigma'}\otimes H^{1,1}(X_{b}) \\ & = & \bigoplus_{|\sigma|=m} \bigoplus_{i\in \sigma} H^{2,0}(X_{b})^{\otimes \sigma-\{ i \}}\otimes H^{1,1}(X_{b}). \nonumber\end{eqnarray}
In (2·5),
![]() $\sigma$
ranges over all subsets of
$\sigma$
ranges over all subsets of
![]() $\{ 1, \cdots, n\}$
consisting of m elements, and
$\{ 1, \cdots, n\}$
consisting of m elements, and
![]() $H^{2,0}(X_{b})^{\otimes \sigma}$
stands for the tensor product of
$H^{2,0}(X_{b})^{\otimes \sigma}$
stands for the tensor product of
![]() $H^{2,0}(X_{b})$
for the jth factors
$H^{2,0}(X_{b})$
for the jth factors
![]() $X_{b}$
of
$X_{b}$
of
![]() $X_{b}^{n}$
over all
$X_{b}^{n}$
over all
![]() $j\in \sigma$
. The notations
$j\in \sigma$
. The notations
![]() $\sigma', \sigma$
in (2·6) are similar, and
$\sigma', \sigma$
in (2·6) are similar, and
![]() $H^{1,1}(X_{b})$
in (2·6) is the
$H^{1,1}(X_{b})$
in (2·6) is the
![]() $H^{1,1}$
of the ith factor
$H^{1,1}$
of the ith factor
![]() $X_{b}$
of
$X_{b}$
of
![]() $X_{b}^{n}$
.
$X_{b}^{n}$
.
Let us write
![]() $V=H^{2,0}(X_{b})$
and
$V=H^{2,0}(X_{b})$
and
![]() $W=(T_{b}B)^{\vee}$
for simplicity. The homomorphism (2·4) over
$W=(T_{b}B)^{\vee}$
for simplicity. The homomorphism (2·4) over
![]() $b\in B$
is written as
$b\in B$
is written as
 \begin{equation}\bigoplus_{|\sigma|=m} \left( V^{\otimes \sigma}\otimes \wedge^{l}W \to\bigoplus_{i\in \sigma} V^{\otimes \sigma - \{ i\}}\otimes H^{1,1}(X_{b})\otimes \wedge^{l+1}W \right).\end{equation}
\begin{equation}\bigoplus_{|\sigma|=m} \left( V^{\otimes \sigma}\otimes \wedge^{l}W \to\bigoplus_{i\in \sigma} V^{\otimes \sigma - \{ i\}}\otimes H^{1,1}(X_{b})\otimes \wedge^{l+1}W \right).\end{equation}
By [
Reference Voisin8
, lemma 5·8], the
![]() $(\sigma, i)$
-component
$(\sigma, i)$
-component
factorises as
where the first map is induced by the adjunction
![]() $V\to H^{1,1}(X_b)\otimes W$
of the differential of the period map for the ith factor
$V\to H^{1,1}(X_b)\otimes W$
of the differential of the period map for the ith factor
![]() $X_{b}$
, and the second map is induced by the wedge product
$X_{b}$
, and the second map is induced by the wedge product
![]() $W \otimes \wedge^{l}W \to \wedge^{l+1}W$
. By linear algebra, this composition can also be decomposed as
$W \otimes \wedge^{l}W \to \wedge^{l+1}W$
. By linear algebra, this composition can also be decomposed as
where the first map is induced by the adjunction
![]() $\wedge^{l}W \to W^{\vee} \otimes \wedge^{l+1}W$
of the wedge product, and the second map is induced by the adjunction
$\wedge^{l}W \to W^{\vee} \otimes \wedge^{l+1}W$
of the wedge product, and the second map is induced by the adjunction
![]() $V\otimes W^{\vee}\to H^{1,1}(X_{b})$
of the differential of the period map. By our initial Condition 2·1, the second map of (2·9) is injective. Moreover, since
$V\otimes W^{\vee}\to H^{1,1}(X_{b})$
of the differential of the period map. By our initial Condition 2·1, the second map of (2·9) is injective. Moreover, since
![]() $l+1\leq \dim W$
by our assumption, the wedge product
$l+1\leq \dim W$
by our assumption, the wedge product
![]() $\wedge^{l}W\times W \to \wedge^{l+1}W$
is nondegenerate, so its adjunction
$\wedge^{l}W\times W \to \wedge^{l+1}W$
is nondegenerate, so its adjunction
![]() $\wedge^{l}W \to W^{\vee} \otimes \wedge^{l+1}W$
is injective. Thus the first map of (2·9) is also injective. It follows that (2·8) is injective. Since the map (2·7) is the direct sum of its
$\wedge^{l}W \to W^{\vee} \otimes \wedge^{l+1}W$
is injective. Thus the first map of (2·9) is also injective. It follows that (2·8) is injective. Since the map (2·7) is the direct sum of its
![]() $(\sigma, i)$
-components, it is injective. This finishes the proof of Lemma 2·3.
$(\sigma, i)$
-components, it is injective. This finishes the proof of Lemma 2·3.
We can now complete the proof of Proposition 2·2.
Proof of Proposition
2·2. By Lemma 2·3 (2), we have
![]() $E_{\infty}^{l,-l}=0$
when
$E_{\infty}^{l,-l}=0$
when
![]() $l<l_{0}=\min\!(\!\dim B, k)$
. Together with Lemma 2·3 (3), we obtain
$l<l_{0}=\min\!(\!\dim B, k)$
. Together with Lemma 2·3 (3), we obtain
When
![]() $k\leq \dim B$
, we have
$k\leq \dim B$
, we have
![]() $l_{0}=k$
, and
$l_{0}=k$
, and
![]() $E_{1}^{l_{0}, -l_{0}}=\Omega_{B}^{k}$
by (2·1). When
$E_{1}^{l_{0}, -l_{0}}=\Omega_{B}^{k}$
by (2·1). When
![]() $k> \dim B$
, we have
$k> \dim B$
, we have
![]() $l_{0}= \dim B$
, and
$l_{0}= \dim B$
, and
![]() $E_{1}^{l_{0}, -l_{0}}=\mathcal{H}^{k-\dim B, 0}\otimes K_{B}$
by (2·1). When
$E_{1}^{l_{0}, -l_{0}}=\mathcal{H}^{k-\dim B, 0}\otimes K_{B}$
by (2·1). When
![]() $k-\dim B$
is odd, this vanishes by Lemma 2·3 (1).
$k-\dim B$
is odd, this vanishes by Lemma 2·3 (1).
In the case
![]() $k=\dim B + 2m$
, the vector bundle
$k=\dim B + 2m$
, the vector bundle
![]() $\mathcal{H}^{2m,0}\otimes K_{B}=(\pi_{n})_{\ast}\Omega_{\pi_{n}}^{2m}\otimes K_{B}$
can be written more specifically as follows. For a subset
$\mathcal{H}^{2m,0}\otimes K_{B}=(\pi_{n})_{\ast}\Omega_{\pi_{n}}^{2m}\otimes K_{B}$
can be written more specifically as follows. For a subset
![]() $\sigma$
of
$\sigma$
of
![]() $\{ 1, \cdots, n \}$
with cardinality
$\{ 1, \cdots, n \}$
with cardinality
![]() $| \sigma |=m$
, we denote by
$| \sigma |=m$
, we denote by
![]() $X_{\sigma}\simeq X_{m}$
the fiber product of the ith factors
$X_{\sigma}\simeq X_{m}$
the fiber product of the ith factors
![]() $X\to B$
of
$X\to B$
of
![]() $X_{n}\to B$
over all
$X_{n}\to B$
over all
![]() $i\in \sigma$
. We denote by
$i\in \sigma$
. We denote by
the natural projections. The Künneth formula (2·5) says that
Combining this with the isomorphism
for each
![]() $X_{\sigma}$
, we can rewrite the isomorphism in the last case of Proposition 2·2 as
$X_{\sigma}$
, we can rewrite the isomorphism in the last case of Proposition 2·2 as
2·2. Extension over compactification
Let
![]() $\pi\colon X\to B$
be a K3 fibration as in Section 2·1. We now assume that X, B are quasi-projective and
$\pi\colon X\to B$
be a K3 fibration as in Section 2·1. We now assume that X, B are quasi-projective and
![]() $\pi$
is a morphism of algebraic varieties. We take smooth projective compactifications of
$\pi$
is a morphism of algebraic varieties. We take smooth projective compactifications of
![]() $X_{n}, X_{\sigma}, B$
and denote them by
$X_{n}, X_{\sigma}, B$
and denote them by
![]() $\bar{X}_{n}, \bar{X}_{\sigma}, \bar{B}$
respectively.
$\bar{X}_{n}, \bar{X}_{\sigma}, \bar{B}$
respectively.
Proposition 2·4. We have
 \begin{equation*}H^{0}(\bar{X}_{n}, \Omega^{k}) \simeq\begin{cases}H^{0}(\bar{B}, \Omega^{k}) & \: \: k\leq \dim B \\ 0 & \: \: k>\dim B, \: \: k\not\equiv \dim B \: \: \mathrm{mod} \; 2 \\ \oplus_{\sigma}H^{0}(\bar{X}_{\sigma}, K_{\bar{X}_{\sigma}}) & \: \: k=\dim B+2m, \: 0\leq m \leq n\end{cases}\end{equation*}
\begin{equation*}H^{0}(\bar{X}_{n}, \Omega^{k}) \simeq\begin{cases}H^{0}(\bar{B}, \Omega^{k}) & \: \: k\leq \dim B \\ 0 & \: \: k>\dim B, \: \: k\not\equiv \dim B \: \: \mathrm{mod} \; 2 \\ \oplus_{\sigma}H^{0}(\bar{X}_{\sigma}, K_{\bar{X}_{\sigma}}) & \: \: k=\dim B+2m, \: 0\leq m \leq n\end{cases}\end{equation*}
In the last case,
![]() $\sigma$
ranges over all subsets of
$\sigma$
ranges over all subsets of
![]() $\{ 1, \cdots, n \}$
with
$\{ 1, \cdots, n \}$
with
![]() $|\sigma|=m$
. The isomorphism in the first case is given by the pullback by
$|\sigma|=m$
. The isomorphism in the first case is given by the pullback by
![]() $\pi_{n}\colon X_{n}\to B$
, and the isomorphism in the last case is given by the direct sum of the pullbacks by
$\pi_{n}\colon X_{n}\to B$
, and the isomorphism in the last case is given by the direct sum of the pullbacks by
![]() $\pi_{\sigma}\colon X_{n}\to X_{\sigma}$
for all
$\pi_{\sigma}\colon X_{n}\to X_{\sigma}$
for all
![]() $\sigma$
.
$\sigma$
.
Proof. The assertion in the case
![]() $k>\dim B$
with
$k>\dim B$
with
![]() $k\not\equiv \dim B$
mod 2 follows directly from the second case of Proposition 2·2. Next we consider the case
$k\not\equiv \dim B$
mod 2 follows directly from the second case of Proposition 2·2. Next we consider the case
![]() $k\leq \dim B$
. We may assume that
$k\leq \dim B$
. We may assume that
![]() $\pi_{n}\colon X_{n}\to B$
extends to a surjective morphism
$\pi_{n}\colon X_{n}\to B$
extends to a surjective morphism
![]() $\bar{X}_{n}\to \bar{B}$
. Let
$\bar{X}_{n}\to \bar{B}$
. Let
![]() $\omega$
be a holomorphic k-form on
$\omega$
be a holomorphic k-form on
![]() $\bar{X}_{n}$
. By the first case of Proposition 2·2, we have
$\bar{X}_{n}$
. By the first case of Proposition 2·2, we have
![]() $\omega|_{X_{n}}=\pi_{n}^{\ast}\omega_{B}$
for a holomorphic k-form
$\omega|_{X_{n}}=\pi_{n}^{\ast}\omega_{B}$
for a holomorphic k-form
![]() $\omega_{B}$
on B. Since
$\omega_{B}$
on B. Since
![]() $\omega$
is holomorphic over
$\omega$
is holomorphic over
![]() $\bar{X}_{n}$
,
$\bar{X}_{n}$
,
![]() $\omega_{B}$
is holomorphic over
$\omega_{B}$
is holomorphic over
![]() $\bar{B}$
as well by a standard property of holomorphic differential forms. (Otherwise
$\bar{B}$
as well by a standard property of holomorphic differential forms. (Otherwise
![]() $\omega$
must have pole at the divisors of
$\omega$
must have pole at the divisors of
![]() $\bar{X}_{n}$
dominating the divisors of
$\bar{X}_{n}$
dominating the divisors of
![]() $\bar{B}$
where
$\bar{B}$
where
![]() $\omega_{B}$
has pole.) Therefore the pullback
$\omega_{B}$
has pole.) Therefore the pullback
![]() $H^{0}(\bar{B}, \Omega^{k})\to H^{0}(\bar{X}_{n}, \Omega^{k})$
is surjective.
$H^{0}(\bar{B}, \Omega^{k})\to H^{0}(\bar{X}_{n}, \Omega^{k})$
is surjective.
Finally, we consider the case
![]() $k=\dim B+2m$
,
$k=\dim B+2m$
,
![]() $0\leq m \leq n$
. Let
$0\leq m \leq n$
. Let
![]() $\omega$
be a holomorphic k-form on
$\omega$
be a holomorphic k-form on
![]() $\bar{X}_{n}$
. By (2·11), we can uniquely write
$\bar{X}_{n}$
. By (2·11), we can uniquely write
![]() $\omega|_{X_{n}}=\sum_{\sigma}\pi_{\sigma}^{\ast}\omega_{\sigma}$
for some canonical forms
$\omega|_{X_{n}}=\sum_{\sigma}\pi_{\sigma}^{\ast}\omega_{\sigma}$
for some canonical forms
![]() $\omega_{\sigma}$
on
$\omega_{\sigma}$
on
![]() $X_{\sigma}$
.
$X_{\sigma}$
.
Claim 2.5. For each
![]() $\sigma$
,
$\sigma$
,
![]() $\omega_{\sigma}$
is holomorphic over
$\omega_{\sigma}$
is holomorphic over
![]() $\bar{X}_{\sigma}$
.
$\bar{X}_{\sigma}$
.
Proof. We identify
![]() $X_{n}$
with the fiber product
$X_{n}$
with the fiber product
![]() $X_{\sigma}\times_{B}X_{\tau}$
where
$X_{\sigma}\times_{B}X_{\tau}$
where
![]() $\tau=\{ 1, \cdots, n\} - \sigma$
is the complement of
$\tau=\{ 1, \cdots, n\} - \sigma$
is the complement of
![]() $\sigma$
. We may assume that this fiber product diagram extends to a commutative diagram of surjective morphisms
$\sigma$
. We may assume that this fiber product diagram extends to a commutative diagram of surjective morphisms
![]()
between smooth projective models. We take an irreducible subvariety
![]() $\tilde{B}\subset \bar{X}_{\tau}$
such that
$\tilde{B}\subset \bar{X}_{\tau}$
such that
![]() $\tilde{B}\to \bar{B}$
is surjective and generically finite. Then
$\tilde{B}\to \bar{B}$
is surjective and generically finite. Then
![]() $\pi_{\tau}^{-1}(\tilde{B})\subset \bar{X}_{n}$
has a unique irreducible component dominating
$\pi_{\tau}^{-1}(\tilde{B})\subset \bar{X}_{n}$
has a unique irreducible component dominating
![]() $\tilde{B}$
. We take its desingularisation and denote it by Y. By construction
$\tilde{B}$
. We take its desingularisation and denote it by Y. By construction
![]() $\pi_{\sigma}|_{Y} \colon Y\to \bar{X}_{\sigma}$
is dominant (and so surjective) and generically finite. On the other hand, for any
$\pi_{\sigma}|_{Y} \colon Y\to \bar{X}_{\sigma}$
is dominant (and so surjective) and generically finite. On the other hand, for any
![]() $\sigma'\ne \sigma$
with
$\sigma'\ne \sigma$
with
![]() $|\sigma'|=m$
, the projection
$|\sigma'|=m$
, the projection
![]() $\pi_{\sigma'}|_{Y} \colon Y\dashrightarrow X_{\sigma'}$
is not dominant. Indeed, such
$\pi_{\sigma'}|_{Y} \colon Y\dashrightarrow X_{\sigma'}$
is not dominant. Indeed, such
![]() $\sigma'$
contains at least one component
$\sigma'$
contains at least one component
![]() $i\in \tau$
, so if
$i\in \tau$
, so if
![]() $Y\dashrightarrow X_{\sigma'}$
was dominant, then the ith projection
$Y\dashrightarrow X_{\sigma'}$
was dominant, then the ith projection
![]() $Y\dashrightarrow X$
would be also dominant, which is absurd because it factorises as
$Y\dashrightarrow X$
would be also dominant, which is absurd because it factorises as
![]() $Y\to \tilde{B}\subset \bar{X}_{\tau}\dashrightarrow X$
.
$Y\to \tilde{B}\subset \bar{X}_{\tau}\dashrightarrow X$
.
We pullback the differential form
![]() $\omega=\pi_{\sigma}^{\ast}\omega_{\sigma}+\sum_{\sigma'\ne \sigma}\pi_{\sigma'}^{\ast}\omega_{\sigma'}$
to Y and denote it by
$\omega=\pi_{\sigma}^{\ast}\omega_{\sigma}+\sum_{\sigma'\ne \sigma}\pi_{\sigma'}^{\ast}\omega_{\sigma'}$
to Y and denote it by
![]() $\omega|_{Y}$
. Since
$\omega|_{Y}$
. Since
![]() $\omega$
is holomorphic over
$\omega$
is holomorphic over
![]() $\bar{X}_{n}$
,
$\bar{X}_{n}$
,
![]() $\omega|_{Y}$
is holomorphic over Y. Since
$\omega|_{Y}$
is holomorphic over Y. Since
![]() $\pi_{\sigma'}^{\ast}\omega_{\sigma'}|_{Y}$
is the pullback of the canonical form
$\pi_{\sigma'}^{\ast}\omega_{\sigma'}|_{Y}$
is the pullback of the canonical form
![]() $\omega_{\sigma'}$
on
$\omega_{\sigma'}$
on
![]() $X_{\sigma'}$
by the non-dominant map
$X_{\sigma'}$
by the non-dominant map
![]() $Y \dashrightarrow X_{\sigma'}$
, it vanishes identically. Hence
$Y \dashrightarrow X_{\sigma'}$
, it vanishes identically. Hence
![]() $\pi_{\sigma}^{\ast}\omega_{\sigma}|_{Y}=\omega|_{Y}$
is holomorphic over Y. Since
$\pi_{\sigma}^{\ast}\omega_{\sigma}|_{Y}=\omega|_{Y}$
is holomorphic over Y. Since
![]() $\pi_{\sigma}|_{Y}\colon Y \to \bar{X}_{\sigma}$
is surjective, this implies that
$\pi_{\sigma}|_{Y}\colon Y \to \bar{X}_{\sigma}$
is surjective, this implies that
![]() $\omega_{\sigma}$
is holomorphic over
$\omega_{\sigma}$
is holomorphic over
![]() $\bar{X}_{\sigma}$
as before.
$\bar{X}_{\sigma}$
as before.
The above argument will be clear if we consider over the generic point
![]() $\eta$
of B: we restrict
$\eta$
of B: we restrict
![]() $\omega$
to the fiber of
$\omega$
to the fiber of
![]() $(X_{\eta})^{n}\to (X_{\eta})^{\tau}$
over the geometric point
$(X_{\eta})^{n}\to (X_{\eta})^{\tau}$
over the geometric point
![]() $\tilde{B}$
of
$\tilde{B}$
of
![]() $(X_{\eta})^{\tau}$
over
$(X_{\eta})^{\tau}$
over
![]() $\eta$
.
$\eta$
.
By Claim 2.5, the pullback
is surjective. It is also injective as implied by (2·11). This proves Proposition 2·4.
2·3. Universal K3 surface
Now we prove Theorem 1·1, in the generality of lattice-polarisation. Let L be an even lattice of signature (2, d) which can be embedded as a primitive sublattice of the K3 lattice
![]() $3U\oplus 2E_{8}$
. We denote by
$3U\oplus 2E_{8}$
. We denote by
the Hermitian symmetric domain associated to L, where
![]() $+$
means a connected component.
$+$
means a connected component.
Let
![]() $\pi\colon X\to B$
be a smooth projective family of K3 surfaces over a smooth quasi-projective connected base B. We say ([
Reference Ma3
]) that the family
$\pi\colon X\to B$
be a smooth projective family of K3 surfaces over a smooth quasi-projective connected base B. We say ([
Reference Ma3
]) that the family
![]() $\pi\colon X\to B$
is lattice-polarised with period lattice L if there exists a sub local system
$\pi\colon X\to B$
is lattice-polarised with period lattice L if there exists a sub local system
![]() $\Lambda$
of
$\Lambda$
of
![]() $R^{2}\pi_{\ast}{{\mathbb{Z}}}$
such that each fiber
$R^{2}\pi_{\ast}{{\mathbb{Z}}}$
such that each fiber
![]() $\Lambda_{b}$
is a hyperbolic sublattice of the Néron-Severi lattice
$\Lambda_{b}$
is a hyperbolic sublattice of the Néron-Severi lattice
![]() $NS(X_{b})$
and the fibers of the orthogonal complement
$NS(X_{b})$
and the fibers of the orthogonal complement
![]() $\Lambda^{\perp}$
are isometric to L. Then we have a period map
$\Lambda^{\perp}$
are isometric to L. Then we have a period map
for some finite-index subgroup
![]() ${{\Gamma}}$
of
${{\Gamma}}$
of
![]() $\mathrm{O}^{+}(L)$
. By Borel’s extension theorem,
$\mathrm{O}^{+}(L)$
. By Borel’s extension theorem,
![]() $\mathcal{P}$
is a morphism of algebraic varieties.
$\mathcal{P}$
is a morphism of algebraic varieties.
Let us put the assumption
For such a family
![]() $\pi\colon X\to B$
, if we shrink B as necessary, then
$\pi\colon X\to B$
, if we shrink B as necessary, then
![]() $\mathcal{P}$
is an open immersion and Condition 2·1 is satisfied. For example, the universal K3 surface
$\mathcal{P}$
is an open immersion and Condition 2·1 is satisfied. For example, the universal K3 surface
![]() $\mathcal{F}_{g,1}\to {{\mathcal{F}_{g}}}$
for
$\mathcal{F}_{g,1}\to {{\mathcal{F}_{g}}}$
for
![]() $g>2$
restricted over a Zariski open set of
$g>2$
restricted over a Zariski open set of
![]() ${{\mathcal{F}_{g}}}$
satisfies this assumption with
${{\mathcal{F}_{g}}}$
satisfies this assumption with
![]() $L=L_{g}$
and
$L=L_{g}$
and
![]() ${{\Gamma}}={{\Gamma_{g}}}$
(see Section 1 for these notations).
${{\Gamma}}={{\Gamma_{g}}}$
(see Section 1 for these notations).
As in Section 1, we denote by
![]() $M_{\wedge^{k},k}({{\Gamma}})$
the space of vector-valued modular forms of weight
$M_{\wedge^{k},k}({{\Gamma}})$
the space of vector-valued modular forms of weight
![]() $(\wedge^{k},k)$
for
$(\wedge^{k},k)$
for
![]() ${{\Gamma}}$
,
${{\Gamma}}$
,
![]() $S_{l}({{\Gamma}}, \det)$
the space of scalar-valued cusp forms of weight l and character
$S_{l}({{\Gamma}}, \det)$
the space of scalar-valued cusp forms of weight l and character
![]() $\det$
for
$\det$
for
![]() ${{\Gamma}}$
, and
${{\Gamma}}$
, and
![]() $\mathcal{S}_{n,m}=\mathfrak{S}_{n}/(\mathfrak{S}_{m}\times \mathfrak{S}_{n-m})$
.
$\mathcal{S}_{n,m}=\mathfrak{S}_{n}/(\mathfrak{S}_{m}\times \mathfrak{S}_{n-m})$
.
Theorem 2·6. Let
![]() $\pi\colon X\to B$
be a lattice-polarised K3 family with period lattice L of signature (2, d) with
$\pi\colon X\to B$
be a lattice-polarised K3 family with period lattice L of signature (2, d) with
![]() $d\geq 3$
and monodromy group
$d\geq 3$
and monodromy group
![]() ${{\Gamma}}$
satisfying (2·12). Then we have an
${{\Gamma}}$
satisfying (2·12). Then we have an
![]() $\mathfrak{S}_{n}$
-equivariant isomorphism
$\mathfrak{S}_{n}$
-equivariant isomorphism
 \begin{equation*}H^{0}(\bar{X}_{n}, \Omega^{k}) \simeq\begin{cases}0 & \: \: 0<k< d/2 \\ M_{\wedge^{k},k}({{\Gamma}}) & \: \: d/2 \leq k < d \\ 0 & \: \: k>d, \: k-d\not\in 2{{\mathbb{Z}}} \\ S_{d+m}({{\Gamma}}, \det)\otimes {{\mathbb{C}}}\mathcal{S}_{n,m} & \: \: k=d+2m, \: 0\leq m \leq n\end{cases}.\end{equation*}
\begin{equation*}H^{0}(\bar{X}_{n}, \Omega^{k}) \simeq\begin{cases}0 & \: \: 0<k< d/2 \\ M_{\wedge^{k},k}({{\Gamma}}) & \: \: d/2 \leq k < d \\ 0 & \: \: k>d, \: k-d\not\in 2{{\mathbb{Z}}} \\ S_{d+m}({{\Gamma}}, \det)\otimes {{\mathbb{C}}}\mathcal{S}_{n,m} & \: \: k=d+2m, \: 0\leq m \leq n\end{cases}.\end{equation*}
Proof. When
![]() $k\leq d$
, we have
$k\leq d$
, we have
![]() $H^{0}(\bar{X}_{n}, \Omega^{k}) \simeq H^{0}(\bar{B}, \Omega^{k})$
by Proposition 2·4. Then
$H^{0}(\bar{X}_{n}, \Omega^{k}) \simeq H^{0}(\bar{B}, \Omega^{k})$
by Proposition 2·4. Then
![]() $\bar{B}$
is a smooth projective model of the modular variety
$\bar{B}$
is a smooth projective model of the modular variety
![]() ${{\Gamma}}\backslash \mathcal{D}$
. By a theorem of Pommerening [
Reference Pommerening5
], the space
${{\Gamma}}\backslash \mathcal{D}$
. By a theorem of Pommerening [
Reference Pommerening5
], the space
![]() $H^{0}(\bar{B}, \Omega^{k})$
for
$H^{0}(\bar{B}, \Omega^{k})$
for
![]() $k<d$
is isomorphic to the space of
$k<d$
is isomorphic to the space of
![]() ${{\Gamma}}$
-invariant holomorphic k-forms on
${{\Gamma}}$
-invariant holomorphic k-forms on
![]() $\mathcal{D}$
, which in turn is identified with the space
$\mathcal{D}$
, which in turn is identified with the space
![]() $M_{\wedge^{k},k}({{\Gamma}})$
of vector-valued modular forms of weight
$M_{\wedge^{k},k}({{\Gamma}})$
of vector-valued modular forms of weight
![]() $(\wedge^{k},k)$
for
$(\wedge^{k},k)$
for
![]() ${{\Gamma}}$
(see [
Reference Ma4
]). The vanishing of this space in
${{\Gamma}}$
(see [
Reference Ma4
]). The vanishing of this space in
![]() $0<k<d/2$
is proved in [
Reference Ma4
, theorem 1·2] in the case when L has Witt index 2, and in [
Reference Ma4
, theorem 1·5 (1)] in the case when L has Witt index
$0<k<d/2$
is proved in [
Reference Ma4
, theorem 1·2] in the case when L has Witt index 2, and in [
Reference Ma4
, theorem 1·5 (1)] in the case when L has Witt index
![]() $\leq 1$
.
$\leq 1$
.
The vanishing in the case
![]() $k>d$
with
$k>d$
with
![]() $k\not\equiv d$
mod 2 follows from Proposition 2·4. Finally, we consider the case
$k\not\equiv d$
mod 2 follows from Proposition 2·4. Finally, we consider the case
![]() $k=d+2m$
,
$k=d+2m$
,
![]() $0\leq m \leq n$
. By Proposition 2·4, we have a natural
$0\leq m \leq n$
. By Proposition 2·4, we have a natural
![]() $\mathfrak{S}_{n}$
-equivariant isomorphism
$\mathfrak{S}_{n}$
-equivariant isomorphism
where
![]() $\mathfrak{S}_{n}$
permutes the subsets
$\mathfrak{S}_{n}$
permutes the subsets
![]() $\sigma$
of
$\sigma$
of
![]() $\{ 1, \cdots, n \}$
. Here note that the stabiliser of each
$\{ 1, \cdots, n \}$
. Here note that the stabiliser of each
![]() $\sigma$
acts on
$\sigma$
acts on
![]() $H^{0}(\bar{X}_{\sigma}, K_{\bar{X}_{\sigma}})$
trivially by (2·10). Therefore, as an
$H^{0}(\bar{X}_{\sigma}, K_{\bar{X}_{\sigma}})$
trivially by (2·10). Therefore, as an
![]() $\mathfrak{S}_{n}$
-representation, the right-hand side can be written as
$\mathfrak{S}_{n}$
-representation, the right-hand side can be written as
 \begin{equation*}H^{0}(\bar{X}_{m}, K_{\bar{X}_{m}}) \otimes \left( \bigoplus_{|\sigma|=m}{{\mathbb{C}}}\sigma \right)\simeq H^{0}(\bar{X}_{m}, K_{\bar{X}_{m}}) \otimes {{\mathbb{C}}}\mathcal{S}_{n,m}.\end{equation*}
\begin{equation*}H^{0}(\bar{X}_{m}, K_{\bar{X}_{m}}) \otimes \left( \bigoplus_{|\sigma|=m}{{\mathbb{C}}}\sigma \right)\simeq H^{0}(\bar{X}_{m}, K_{\bar{X}_{m}}) \otimes {{\mathbb{C}}}\mathcal{S}_{n,m}.\end{equation*}
Finally, we have
![]() $H^{0}(\bar{X}_{m}, K_{\bar{X}_{m}})\simeq S_{d+m}({{\Gamma}}, \det)$
by [
Reference Ma3
, theorem 3·1].
$H^{0}(\bar{X}_{m}, K_{\bar{X}_{m}})\simeq S_{d+m}({{\Gamma}}, \det)$
by [
Reference Ma3
, theorem 3·1].
Remark 2·7. The case
![]() $k\geq d$
of Theorem 2·6 holds also when
$k\geq d$
of Theorem 2·6 holds also when
![]() $d=1, 2$
. We put the assumption
$d=1, 2$
. We put the assumption
![]() $d\geq 3$
for the requirement of the Koecher principle from [
Reference Pommerening5
]. Therefore, in fact, only the case
$d\geq 3$
for the requirement of the Koecher principle from [
Reference Pommerening5
]. Therefore, in fact, only the case
![]() $(d, k)=(2, 1)$
with Witt index 2 is not covered.
$(d, k)=(2, 1)$
with Witt index 2 is not covered.