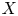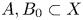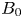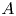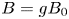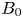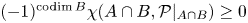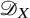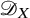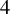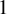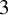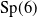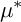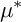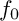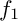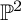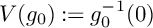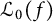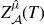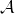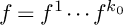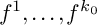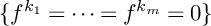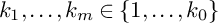92 results in 32Sxx
A new generic vanishing theorem on homogeneous varieties and the positivity conjecture for triple intersections of Schubert cells
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 1-12
- Print publication:
- January 2025
-
- Article
- Export citation
On the gluing of germs of complex analytic spaces, Betti numbers, and their structure
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 20 December 2024, pp. 1-16
-
- Article
-
- You have access
- HTML
- Export citation
Hyperplane Arrangements Satisfy (Un)Twisted Logarithmic Comparison Theorems, Applications to
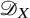 $\mathscr {D}_{X}$-modules
$\mathscr {D}_{X}$-modules
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 November 2024, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the embedded Nash problem
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 16 October 2024, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strict positivity of Kähler–Einstein currents
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 27 May 2024, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deformations of Calabi–Yau varieties with k-liminal singularities
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 May 2024, e59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Thinness of some hypergeometric groups in
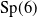 $\mathrm{Sp}(6)$
$\mathrm{Sp}(6)$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 02 May 2024, pp. 571-581
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
The analytic classification of plane curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 19 March 2024, pp. 915-944
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
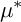 $\mu ^*$-ZARISKI PAIRS OF SURFACE SINGULARITIES
$\mu ^*$-ZARISKI PAIRS OF SURFACE SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 05 December 2023, pp. 488-497
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
CODIMENSION ONE FOLIATIONS IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 1705-1750
- Print publication:
- July 2024
-
- Article
-
- You have access
- HTML
- Export citation
Perverse sheaves on Riemann surfaces as Milnor sheaves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 06 October 2023, e92
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deformations of corank 1 frontals
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 26 June 2023, pp. 1204-1234
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Łojasiewicz exponent of nondegenerate surface singularities
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 26 June 2023, pp. 1391-1410
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weighted Hodge ideals of reduced divisors
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 16 June 2023, e51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relative regular Riemann–Hilbert correspondence II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 15 June 2023, pp. 1413-1465
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON A BERNSTEIN–SATO POLYNOMIAL OF A MEROMORPHIC FUNCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 251 / September 2023
- Published online by Cambridge University Press:
- 06 June 2023, pp. 715-733
- Print publication:
- September 2023
-
- Article
- Export citation
Foliated affine and projective structures
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1153-1187
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Motivic zeta functions of hyperplane arrangements
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 1 / July 2023
- Published online by Cambridge University Press:
- 07 March 2023, pp. 187-215
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE MILNOR FIBRATION OF CERTAIN NEWTON DEGENERATE FUNCTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 01 December 2022, pp. 410-433
- Print publication:
- June 2023
-
- Article
- Export citation
Non-abelian Mellin transformations and applications
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 16 November 2022, e100
-
- Article
-
- You have access
- Open access
- HTML
- Export citation