Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-05-01T09:13:12.425Z Has data issue: false hasContentIssue false
  • English
  • Français

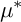$\mu ^*$-ZARISKI PAIRS OF SURFACE SINGULARITIES

Part of: Surfaces and higher-dimensional varieties Local theory Singularities Special varieties

Published online by Cambridge University Press:  05 December 2023

CHRISTOPHE EYRAL Open the ORCID record for CHRISTOPHE EYRAL [Opens in a new window]  and
MUTSUO OKA Open the ORCID record for MUTSUO OKA [Opens in a new window]
CHRISTOPHE EYRAL*
Affiliation:
Institute of Mathematics Polish Academy of Sciences ul. Śniadeckich 8 00-656 Warsaw Poland
MUTSUO OKA
Affiliation:
Professor Emeritus of Tokyo Institute of Technology 3-19-8 Nakaochiai Shinjuku-ku Tokyo 161-0032 Japan okamutsuo@gmail.com
*
cheyral@impan.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 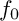$f_0$ and 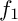$f_1$ be two homogeneous polynomials of degree d in three complex variables 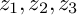$z_1,z_2,z_3$. We show that the Lê–Yomdin surface singularities defined by 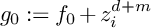$g_0:=f_0+z_i^{d+m}$ and 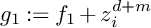$g_1:=f_1+z_i^{d+m}$ have the same abstract topology, the same monodromy zeta-function, the same 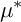$\mu ^*$-invariant, but lie in distinct path-connected components of the 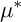$\mu ^*$-constant stratum if their projective tangent cones (defined by 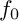$f_0$ and 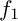$f_1$, respectively) make a Zariski pair of curves in 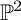$\mathbb {P}^2$, the singularities of which are Newton non-degenerate. In this case, we say that 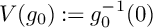$V(g_0):=g_0^{-1}(0)$ and 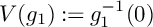$V(g_1):=g_1^{-1}(0)$ make a 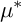$\mu ^*$-Zariski pair of surface singularities. Being such a pair is a necessary condition for the germs 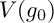$V(g_0)$ and 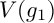$V(g_1)$ to have distinct embedded topologies.

Keywords

link of isolated surface singularitiesLê–Yomdin singularitiesmonodromy zeta-functionμ*-constant stratumabstract and embedded topology

MSC classification

Primary: 14M25: Toric varieties, Newton polyhedra 14B05: Singularities 14J17: Singularities 32S55: Milnor fibration; relations with knot theory 32S05: Local singularities
Type
Article
Information
Nagoya Mathematical Journal , First View , pp. 1 - 10
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

A’Campo, N., La fonction zêta d’une monodromie , Comment. Math. Helv. 50 (1975), 233–248.CrossRefGoogle Scholar
Arnol’d, V. I., Normal forms of functions near degenerate critical points, the Weyl groups ${A}_k$ , ${D}_k$ , ${E}_k$ and Lagrangian singularities , Funkcional. Anal. i Priložen. 6 (1972), no. 4, 3–25.Google Scholar
Artal-Bartolo, E., Sur la monodromie des singularités superisolées , C. R. Acad. Sci. 312 (1991), no. 8, 601–604.Google Scholar
Artal-Bartolo, E., Forme de Jordan de la monodromie des singularités superisolées de surfaces, Memoirs of the American Mathematical Society, Vol. 109 (525), American Mathematical Society, Providence, RI, 1994.Google Scholar
Artal-Bartolo, E., Sur les couples de Zariski , J. Algebraic Geom. 3 (1994), 223–247.Google Scholar
Artal-Bartolo, E., Cogolludo, J. I. and Tokunaga, H., “A survey on Zariski pairs” in Algebraic geometry in East Asia–Hanoi 2005, Advanced Studies in Pure Mathematics, Vol. 50, Mathematical Society of Japan, Tokyo, 2008, 1–100.Google Scholar
Artal-Bartolo, E., Cogolludo-Agustín, J. I. and Martín-Morales, J., “Cremona transformations of weighted projective planes, Zariski pairs, and rational cuspidal curves” in Singularities and their interaction with geometry and low dimensional topology—In honor of András Némethi, Trends in Mathematics, Birkhäuser/Springer, Cham, 2021, 117–157.CrossRefGoogle Scholar
Clemens, C. H. Jr., Picard–Lefschetz theorem for families of nonsingular algebraic varieties acquiring ordinary singularities , Trans. Amer. Math. Soc. 136 (1969), 93–108.CrossRefGoogle Scholar
Dimca, A., Singularities and topology of hypersurfaces, Universitext, Springer, New York, 1992.CrossRefGoogle Scholar
Eyral, C. and Oka, M., On paths in the $\mu$ -constant and ${\mu}^{\ast }$ -constant strata, to appear in Hiroshima Math. J. 54, no. 2.Google Scholar
Gusein-Zade, S. M., Luengo, I. and Melle-Hernández, A., Partial resolutions and the zeta-function of a singularity , Comment. Math. Helv. 72 (1997), no. 2, 244–256.CrossRefGoogle Scholar
Haş Bey, C., Sur l’irréductibilité de la monodromie locale; application à l’équisingularité , C. R. Acad. Sci. Paris Sér. A–B. 275 (1972), A105–A107.Google Scholar
Iomdin, I. N., Complex surfaces with a one-dimensional set of singularities , Sibirsk. Mat. Ž. 15 (1974), 1061–1082, 1181 (in Russian). English translation: Siberian Math. J. 15 (1974), no. 5, 748–762 (1975).Google Scholar
Kouchnirenko, A. G., Polyèdres de Newton et nombres de Milnor , Invent. Math. 32 (1976), 1–31.CrossRefGoogle Scholar
Lazzeri, F., “A theorem on the monodromy of isolated singularities” in Singularités à Cargèse (Rencontre Singularités Géom. Anal., Inst. Études Sci. de Cargèse, 1972), Astérisque, Vols. 7–8, Société Mathématique de France, Paris, 1973, 269–275.Google Scholar
Lê, D. T., Sur un critère d’équisingularité, C. R. Acad. Sci. Paris Sér. A–B. 272 (1971), A138–A140.Google Scholar
Lê, D. T., Une application d’un théorème d’A’Campo à l’équisingularité, Nederl. Akad. Wetensch. Proc. Ser. A. 76 (= Indag. Math. 35) (1973), 403–409.CrossRefGoogle Scholar
Lê, D. T., “Topologie des singularités des hypersurfaces complexes” in Singularités à Cargèse (Rencontre Singularités Géom. Anal., Inst. Études Sci., Cargèse, 1972), Astérisque, Vols. 7–8, Société Mathématique de France, Paris, 1973, 171–182.Google Scholar
Lê, D. T., “Ensembles analytiques complexes avec lieu singulier de dimension un (d’après I. N. Iomdine)” in Seminar on singularities (Paris, 1976/1977), Publications Mathématiques de l’Université Paris VII, Vol. 7, Université Paris VII, Paris, 1980, 87–95.Google Scholar
Luengo, I., The $\mu$ -constant stratum is not smooth , Invent. Math. 90 (1987), no. 1, 139–152.CrossRefGoogle Scholar
Luengo, I. and Melle, A., A formula for the Milnor number , C. R. Acad. Sci. 321 (1995), no. 11, 1473–1478.Google Scholar
Mather, J., Notes on topological stability , Bull. Amer. Math. Soc. (N.S.). 49 (2012), no. 4, 475–506.CrossRefGoogle Scholar
Milnor, J., Singular points of complex hypersurfaces, Annals of Mathematics Studies, Vol. 61, Princeton University Press, Princeton, NJ; University of Tokyo Press, Tokyo, 1968.Google Scholar
Oka, M., Non-degenerate complete intersection singularity, Hermann, Paris, 1997.Google Scholar
Oka, M., “A survey on Alexander polynomials of plane curves” in Singularités Franco-Japonaises, Séminaire et Congrès, Vol. 10, Société Mathématique de France, Paris, 2005, 209–232.Google Scholar
Oka, M., “Almost non-degenerate functions and a Zariski pair of links” in Essays in geometry, dedicated to N. A’Campo, edited by Papadopoulos, A., IRMA Lectures in Mathematics and Theoretical Physics, Vol. 34, European Mathematical Society, Zürich, 2023, 601–628.CrossRefGoogle Scholar
Oka, M., On $\mu$ -Zariski pairs of links , J. Math. Soc. Japan. 75 (2023), no. 4, 1227–1259.CrossRefGoogle Scholar
Saeki, O., Topological types of complex isolated hypersurface singularities , Kodai Math. J. 12 (1989), no. 1, 23–29.CrossRefGoogle Scholar
Siersma, D., The monodromy of a series of hypersurface singularities , Comment. Math. Helv. 65 (1990), no. 2, 181–197.CrossRefGoogle Scholar
Siersma, D., “The vanishing topology of non-isolated singularities” in New developments in singularity theory (Cambridge, 2000), NATO Science Series II: Mathematics, Physics and Chemistry, Vol. 21, Kluwer Academic Publishers, Dordrecht, 2001, 447–472.CrossRefGoogle Scholar
Stevens, J., On the $\mu$ -constant stratum and the $V$ -filtration: An example , Math. Z. 201 (1989), no. 1, 139–144.CrossRefGoogle Scholar
Teissier, B., “Cycles évanescents, sections planes et conditions de Whitney” in Singularités à Cargèse (Rencontre Singularités Géom. Anal., Inst. Études Sci., Cargèse, 1972), Astérisque, Vols. 7–8, Société Mathématique de France, Paris, 1973, 285–362.Google Scholar
Teissier, B., “Déformations à type topologique constant” in Quelques problèmes de modules (Sém. de Géométrie Analytique, École Norm. Sup., Paris, 1971–1972), Astérisque, Vol. 16, Société Mathématique de France, Paris, 1974, 215–249.Google Scholar
Varchenko, A. N., Zeta-function of monodromy and Newton’s diagram , Invent. Math. 37 (1976), no. 3, 253–262.CrossRefGoogle Scholar
Wall, C. T. C., Singular points of plane curves, London Mathematical Society Student Texts, Vol. 63, Cambridge University Press, Cambridge, 2004.CrossRefGoogle Scholar
Zariski, O., On the problem of existence of algebraic functions of two variables possessing a given branched curve , Amer. J. Math. 51 (1929), no. 2, 305–328.CrossRefGoogle Scholar