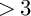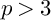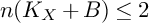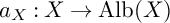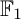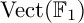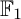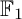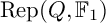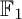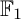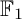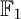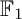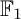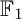FirstView articles
Article
CONSTANCY OF THE HILBERT–SAMUEL FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1-15
-
- Article
- Export citation
A REMARK ON THE N-INVARIANT GEOMETRY OF BOUNDED HOMOGENEOUS DOMAINS
- Part of:
-
- Published online by Cambridge University Press:
- 23 May 2024, pp. 1-10
-
- Article
- Export citation
WHEN IS THE SILTING-DISCRETENESS INHERITED?
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-23
-
- Article
-
- You have access
- HTML
- Export citation
SUBCOMPLEXES OF CERTAIN FREE RESOLUTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 25 March 2024, pp. 1-19
-
- Article
-
- You have access
- HTML
- Export citation
TILTING COMPLEXES AND CODIMENSION FUNCTIONS OVER COMMUTATIVE NOETHERIAN RINGS
- Part of:
-
- Published online by Cambridge University Press:
- 15 March 2024, pp. 1-76
-
- Article
- Export citation
NOTE ON THE THREE-DIMENSIONAL LOG CANONICAL ABUNDANCE IN CHARACTERISTIC
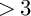 $>3$
$>3$
- Part of:
-
- Published online by Cambridge University Press:
- 28 February 2024, pp. 1-30
-
- Article
- Export citation
COUNTING GEOMETRIC BRANCHES VIA THE FROBENIUS MAP AND F-NILPOTENT SINGULARITIES
- Part of:
-
- Published online by Cambridge University Press:
- 27 February 2024, pp. 1-18
-
- Article
- Export citation
A CALCULATION OF THE PERFECTOIDIZATION OF SEMIPERFECTOID RINGS
- Part of:
-
- Published online by Cambridge University Press:
- 23 February 2024, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A HOMOMORPHISM BETWEEN BOTT–SAMELSON BIMODULES
- Part of:
-
- Published online by Cambridge University Press:
- 22 January 2024, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TOPICS SURROUNDING THE COMBINATORIAL ANABELIAN GEOMETRY OF HYPERBOLIC CURVES IV: DISCRETENESS AND SECTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 18 January 2024, pp. 1-101
-
- Article
- Export citation
COEFFICIENT QUIVERS,
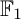 ${\mathbb {F}}_1$-REPRESENTATIONS, AND EULER CHARACTERISTICS OF QUIVER GRASSMANNIANS
${\mathbb {F}}_1$-REPRESENTATIONS, AND EULER CHARACTERISTICS OF QUIVER GRASSMANNIANS
- Part of:
-
- Published online by Cambridge University Press:
- 13 December 2023, pp. 1-57
-
- Article
- Export citation
HOW TO EXTEND CLOSURE AND INTERIOR OPERATIONS TO MORE MODULES
- Part of:
-
- Published online by Cambridge University Press:
- 01 December 2023, pp. 1-48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation