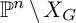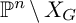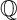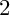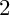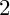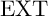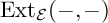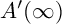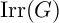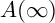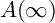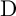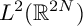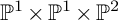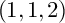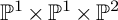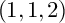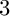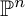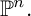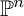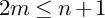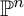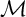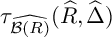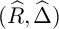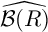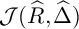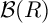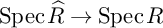Open access
Article
A CALCULATION OF THE PERFECTOIDIZATION OF SEMIPERFECTOID RINGS
- Part of:
-
- Published online by Cambridge University Press:
- 23 February 2024, pp. 742-759
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A HOMOMORPHISM BETWEEN BOTT–SAMELSON BIMODULES
- Part of:
-
- Published online by Cambridge University Press:
- 22 January 2024, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LOCAL SECTIONS OF ARITHMETIC FUNDAMENTAL GROUPS OF p-ADIC CURVES
- Part of:
-
- Published online by Cambridge University Press:
- 20 December 2023, pp. 462-487
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HOW TO EXTEND CLOSURE AND INTERIOR OPERATIONS TO MORE MODULES
- Part of:
-
- Published online by Cambridge University Press:
- 01 December 2023, pp. 513-560
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON A COMPARISON BETWEEN DWORK AND RIGID COHOMOLOGIES OF PROJECTIVE COMPLEMENTS
- Part of:
-
- Published online by Cambridge University Press:
- 01 December 2023, pp. 420-461
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENUS
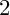 $2$ CURVES WITH BAD REDUCTION AT ONE ODD PRIME
$2$ CURVES WITH BAD REDUCTION AT ONE ODD PRIME
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2023, pp. 498-512
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NON-ISOMORPHIC SMOOTH COMPACTIFICATIONS OF THE MODULI SPACE OF CUBIC SURFACES
- Part of:
-
- Published online by Cambridge University Press:
- 03 October 2023, pp. 315-365
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXACT SUBCATEGORIES, SUBFUNCTORS OF
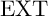 ${\operatorname{EXT}}$, AND SOME APPLICATIONS
${\operatorname{EXT}}$, AND SOME APPLICATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 27 September 2023, pp. 379-419
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DISTRIBUTION OF IWASAWA INVARIANTS ASSOCIATED TO MULTIGRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 08 September 2023, pp. 48-90
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTENSIONS OF CHARACTERS IN TYPE D AND THE INDUCTIVE MCKAY CONDITION, I
- Part of:
-
- Published online by Cambridge University Press:
- 08 September 2023, pp. 906-958
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A VARIANT OF PERFECTOID ABHYANKAR’S LEMMA AND ALMOST COHEN–MACAULAY ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2023, pp. 164-215
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE ESSENTIAL TORSION FINITENESS OF ABELIAN VARIETIES OVER TORSION FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 24 August 2023, pp. 91-127
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWISTED SHIFT-INVARIANT SYSTEM IN
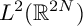 $L^2(\mathbb {R}^{2N})$
$L^2(\mathbb {R}^{2N})$
- Part of:
-
- Published online by Cambridge University Press:
- 05 June 2023, pp. 734-767
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
K-STABLE DIVISORS IN
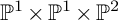 $\mathbb {P}^1\times \mathbb {P}^1\times \mathbb {P}^2$ OF DEGREE
$\mathbb {P}^1\times \mathbb {P}^1\times \mathbb {P}^2$ OF DEGREE 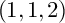 $(1,1,2)$
$(1,1,2)$
- Part of:
-
- Published online by Cambridge University Press:
- 28 April 2023, pp. 686-714
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CATEGORIFICATION OF ACYCLIC PRINCIPAL COEFFICIENT CLUSTER ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 22 February 2023, pp. 769-809
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
K-THEORY OF NON-ARCHIMEDEAN RINGS II
- Part of:
-
- Published online by Cambridge University Press:
- 21 February 2023, pp. 669-685
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONSTRUCTING MAXIMAL COFINITARY GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 30 January 2023, pp. 622-651
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERIC LINES IN PROJECTIVE SPACE AND THE KOSZUL PROPERTY
- Part of:
-
- Published online by Cambridge University Press:
- 06 January 2023, pp. 576-605
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXACT SOLUTIONS FOR THE SINGULARLY PERTURBED RICCATI EQUATION AND EXACT WKB ANALYSIS
- Part of:
-
- Published online by Cambridge University Press:
- 08 December 2022, pp. 434-469
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIG COHEN–MACAULAY TEST IDEALS IN EQUAL CHARACTERISTIC ZERO VIA ULTRAPRODUCTS
- Part of:
-
- Published online by Cambridge University Press:
- 07 December 2022, pp. 549-575
-
- Article
-
- You have access
- Open access
- HTML
- Export citation