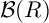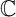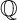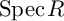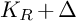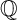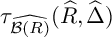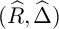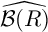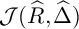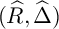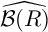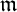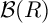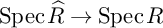1 Introduction
A (balanced) big Cohen–Macaulay (BCM) algebra over a Noetherian local ring
![]() $(R,\mathfrak {m})$
is an R-algebra B such that every system of parameters is a regular sequence on B. Its existence implies many fundamental homological conjectures including the direct summand conjecture (now a theorem). Hochster and Huneke [Reference Hochster and Huneke14], [Reference Hochster and Huneke15] proved the existence of a BCM algebra in equal characteristic, and André [Reference André1] settled the mixed characteristic case. Recently, using BCM algebras, Ma and Schwede [Reference Ma and Schwede18], [Reference Ma and Schwede19] introduced the notion of BCM test ideals as an analog of test ideals in tight closure theory.
$(R,\mathfrak {m})$
is an R-algebra B such that every system of parameters is a regular sequence on B. Its existence implies many fundamental homological conjectures including the direct summand conjecture (now a theorem). Hochster and Huneke [Reference Hochster and Huneke14], [Reference Hochster and Huneke15] proved the existence of a BCM algebra in equal characteristic, and André [Reference André1] settled the mixed characteristic case. Recently, using BCM algebras, Ma and Schwede [Reference Ma and Schwede18], [Reference Ma and Schwede19] introduced the notion of BCM test ideals as an analog of test ideals in tight closure theory.
The test ideal
![]() $\tau (R)$
of a Noetherian local ring R of positive characteristic was originally defined as the annihilator ideal of all tight closure relations of R. Since it turned out that
$\tau (R)$
of a Noetherian local ring R of positive characteristic was originally defined as the annihilator ideal of all tight closure relations of R. Since it turned out that
![]() $\tau (R)$
was related to multiplier ideals via reduction to characteristic p, the definition of
$\tau (R)$
was related to multiplier ideals via reduction to characteristic p, the definition of
![]() $\tau (R)$
was generalized in [Reference Hara and Yoshida11], [Reference Takagi29] to involve effective
$\tau (R)$
was generalized in [Reference Hara and Yoshida11], [Reference Takagi29] to involve effective
![]() $\mathbb {Q}$
-Weil divisors
$\mathbb {Q}$
-Weil divisors
![]() $\Delta $
on
$\Delta $
on
![]() $\operatorname {Spec} R$
and ideals
$\operatorname {Spec} R$
and ideals
![]() $\mathfrak {a}\subseteq R$
with real exponent
$\mathfrak {a}\subseteq R$
with real exponent
![]() $t>0$
. In these papers, it was shown that multiplier ideals coincide, after reduction to characteristic
$t>0$
. In these papers, it was shown that multiplier ideals coincide, after reduction to characteristic
![]() $p \gg 0$
, with such generalized test ideals
$p \gg 0$
, with such generalized test ideals
![]() $\tau (R,\Delta ,\mathfrak {a}^t)$
. In positive characteristic, Ma-Schwede’s BCM test ideals are the same as the generalized test ideals. In this paper, we study BCM test ideals in equal characteristic zero.
$\tau (R,\Delta ,\mathfrak {a}^t)$
. In positive characteristic, Ma-Schwede’s BCM test ideals are the same as the generalized test ideals. In this paper, we study BCM test ideals in equal characteristic zero.
Using ultraproducts, Schoutens [Reference Schoutens24] gave a characterization of log-terminal singularities, an important class of singularities in the minimal model program. He also gave an explicit construction of a BCM algebra
![]() $\mathcal {B}(R)$
in equal characteristic zero:
$\mathcal {B}(R)$
in equal characteristic zero:
![]() $\mathcal {B}(R)$
is described as the ultraproduct of the absolute integral closures of Noetherian local domains of positive characteristic. He defined a closure operation associated with
$\mathcal {B}(R)$
is described as the ultraproduct of the absolute integral closures of Noetherian local domains of positive characteristic. He defined a closure operation associated with
![]() $\mathcal {B}(R)$
to introduce the notions of
$\mathcal {B}(R)$
to introduce the notions of
![]() $\mathcal {B}$
-rationality and
$\mathcal {B}$
-rationality and
![]() $\mathcal {B}$
-regularity, which are closely related to BCM rationality and BCM regularity defined in [Reference Ma and Schwede19], and proved that
$\mathcal {B}$
-regularity, which are closely related to BCM rationality and BCM regularity defined in [Reference Ma and Schwede19], and proved that
![]() $\mathcal {B}$
-rationality is equivalent to being rational singularities. The aim of this paper is to give a geometric characterization of BCM test ideals associated with
$\mathcal {B}$
-rationality is equivalent to being rational singularities. The aim of this paper is to give a geometric characterization of BCM test ideals associated with
![]() $\mathcal {B}(R)$
. Our main result is stated as follows:
$\mathcal {B}(R)$
. Our main result is stated as follows:
Theorem 1.1 (Theorem 6.4).
Let R be a normal local domain essentially of finite type over
![]() $\mathbb {C}$
. Let
$\mathbb {C}$
. Let
![]() $\Delta $
be an effective
$\Delta $
be an effective
![]() $\mathbb {Q}$
-Weil divisor on
$\mathbb {Q}$
-Weil divisor on
![]() $\operatorname {Spec} R$
such that
$\operatorname {Spec} R$
such that
![]() $K_R+\Delta $
is
$K_R+\Delta $
is
![]() $\mathbb {Q}$
-Cartier, where
$\mathbb {Q}$
-Cartier, where
![]() $K_R$
is a canonical divisor on
$K_R$
is a canonical divisor on
![]() $\operatorname {Spec} R$
. Suppose that
$\operatorname {Spec} R$
. Suppose that
![]() $\widehat {R}$
and
$\widehat {R}$
and
![]() $\widehat {\mathcal {B}(R)}$
are the
$\widehat {\mathcal {B}(R)}$
are the
![]() $\mathfrak {m}$
-adic completions of R and
$\mathfrak {m}$
-adic completions of R and
![]() $\mathcal {B}(R)$
, and
$\mathcal {B}(R)$
, and
![]() $\widehat {\Delta }$
is the flat pullback of
$\widehat {\Delta }$
is the flat pullback of
![]() $\Delta $
by the canonical morphism
$\Delta $
by the canonical morphism
![]() $\operatorname {Spec} \widehat {R}\to \operatorname {Spec} R$
. Then we have
$\operatorname {Spec} \widehat {R}\to \operatorname {Spec} R$
. Then we have
where
![]() $\tau _{\widehat {\mathcal {B}(R)}}(\widehat {R},\widehat {\Delta })$
is the BCM test ideal of
$\tau _{\widehat {\mathcal {B}(R)}}(\widehat {R},\widehat {\Delta })$
is the BCM test ideal of
![]() $(\widehat {R},\widehat {\Delta })$
with respect to
$(\widehat {R},\widehat {\Delta })$
with respect to
![]() $\widehat {\mathcal {B}(R)}$
and
$\widehat {\mathcal {B}(R)}$
and
![]() $\mathcal {J}(\widehat {R},\widehat {\Delta })$
is the multiplier ideal of
$\mathcal {J}(\widehat {R},\widehat {\Delta })$
is the multiplier ideal of
![]() $(\widehat {R},\widehat {\Delta })$
.
$(\widehat {R},\widehat {\Delta })$
.
The inclusion
![]() $\mathcal {J}(\widehat {R},\widehat {\Delta }) \subseteq \tau _{\widehat {\mathcal {B}(R)}}(\widehat {R},\widehat {\Delta })$
is obtained by comparing reductions of the multiplier ideal modulo
$\mathcal {J}(\widehat {R},\widehat {\Delta }) \subseteq \tau _{\widehat {\mathcal {B}(R)}}(\widehat {R},\widehat {\Delta })$
is obtained by comparing reductions of the multiplier ideal modulo
![]() $p\gg 0$
to its approximations. We prove the opposite inclusion by combining an argument similar to that in [Reference Schoutens25] with the description of multiplier ideals as the kernel of a map between local cohomology modules in [Reference Takagi29]. As an application of Theorem 1.1, we show the next result about a behavior of multiplier ideals under pure ring extensions, which is a generalization of [Reference Yamaguchi31, Cor. 5.30].
$p\gg 0$
to its approximations. We prove the opposite inclusion by combining an argument similar to that in [Reference Schoutens25] with the description of multiplier ideals as the kernel of a map between local cohomology modules in [Reference Takagi29]. As an application of Theorem 1.1, we show the next result about a behavior of multiplier ideals under pure ring extensions, which is a generalization of [Reference Yamaguchi31, Cor. 5.30].
Theorem 1.2 (Corollary 7.11).
Let
![]() $R\hookrightarrow S$
be a pure local homomorphism of normal local domains essentially of finite type over
$R\hookrightarrow S$
be a pure local homomorphism of normal local domains essentially of finite type over
![]() $\mathbb {C}$
. Suppose that R is
$\mathbb {C}$
. Suppose that R is
![]() $\mathbb {Q}$
-Gorenstein. Let
$\mathbb {Q}$
-Gorenstein. Let
![]() $\Delta _S$
be an effective
$\Delta _S$
be an effective
![]() $\mathbb {Q}$
-Weil divisor such that
$\mathbb {Q}$
-Weil divisor such that
![]() $K_S+\Delta _S$
is
$K_S+\Delta _S$
is
![]() $\mathbb {Q}$
-Cartier, where
$\mathbb {Q}$
-Cartier, where
![]() $K_S$
is a canonical divisor on
$K_S$
is a canonical divisor on
![]() $\operatorname {Spec} S$
. Let
$\operatorname {Spec} S$
. Let
![]() $\mathfrak {a}\subseteq R$
be a nonzero ideal, and let
$\mathfrak {a}\subseteq R$
be a nonzero ideal, and let
![]() $t>0$
be a positive rational number. Then we have
$t>0$
be a positive rational number. Then we have
In [Reference Yamaguchi31], we defined ultra-test ideals, a variant of test ideals in equal characteristic zero, to generalize the notion of ultra-F-regularity introduced by Schoutens [Reference Schoutens24]. Theorem 1.2 was proved by using ultra-test ideals under the assumption that
![]() $\mathfrak {a}$
is a principal ideal. The description of multiplier ideals as BCM test ideals associated with
$\mathfrak {a}$
is a principal ideal. The description of multiplier ideals as BCM test ideals associated with
![]() $\mathcal {B}(R)$
(Theorem 1.1) and a generalization of module closures in [Reference Pérez and Rebecca20] enables us to show Theorem 1.2 without any assumptions.
$\mathcal {B}(R)$
(Theorem 1.1) and a generalization of module closures in [Reference Pérez and Rebecca20] enables us to show Theorem 1.2 without any assumptions.
As another application of Theorem 1.1, we give an affirmative answer to one of the conjectures proposed by Schoutens [Reference Schoutens24, Rem. 3.10], which says that
![]() $\mathcal {B}$
-regularity is equivalent to being log-terminal singularities (see Theorem 8.2).
$\mathcal {B}$
-regularity is equivalent to being log-terminal singularities (see Theorem 8.2).
This paper is organized as follows: in the preliminary section, we give definitions of multiplier ideals, test ideals, and BCM test ideals. In §3, we quickly review the theory of ultraproducts in commutative algebra including non-standard and relative hulls. In §4, we prove some fundamental results on BCM algebras constructed via ultraproducts following [Reference Schoutens23]. In §5, we review the relationship between approximations and reductions modulo
![]() $p\gg 0$
and consider approximations of multiplier ideals. In §6, we show Theorem 1.1, the main theorem of this paper. In §7, using a generalized module closure, we show Theorem 1.2 as an application of Theorem 1.1. In §8, we show that
$p\gg 0$
and consider approximations of multiplier ideals. In §6, we show Theorem 1.1, the main theorem of this paper. In §7, using a generalized module closure, we show Theorem 1.2 as an application of Theorem 1.1. In §8, we show that
![]() $\mathcal {B}$
-regularity is equivalent to log-terminal singularities. Finally in §9, we discuss a question, a variant of [Reference Dietz and Rebecca7, Quest. 2.7], to handle BCM algebras that cannot be constructed via ultraproducts, and consider the equivalence of BCM-rationality and being rational singularities.
$\mathcal {B}$
-regularity is equivalent to log-terminal singularities. Finally in §9, we discuss a question, a variant of [Reference Dietz and Rebecca7, Quest. 2.7], to handle BCM algebras that cannot be constructed via ultraproducts, and consider the equivalence of BCM-rationality and being rational singularities.
2 Preliminaries
Throughout this paper, all rings will be commutative with unity.
2.1 Multiplier ideals
Here, we briefly review the definition of multiplier ideals and refer the reader to [Reference Lazarsfeld16], [Reference Sato and Takagi21] for more details. Throughout this subsection, we assume that X is a normal integral scheme essentially of finite type over a field of characteristic zero or
![]() $X=\operatorname {Spec} \widehat {R}$
, where
$X=\operatorname {Spec} \widehat {R}$
, where
![]() $(R,\mathfrak {m})$
is a normal local domain essentially of finite type over a field of characteristic zero and
$(R,\mathfrak {m})$
is a normal local domain essentially of finite type over a field of characteristic zero and
![]() $\widehat {R}$
is its
$\widehat {R}$
is its
![]() $\mathfrak {m}$
-adic completion.
$\mathfrak {m}$
-adic completion.
Definition 2.1. A proper birational morphism
![]() $f:Y\to X$
between integral schemes is said to be a resolution of singularities of X if Y is regular. When
$f:Y\to X$
between integral schemes is said to be a resolution of singularities of X if Y is regular. When
![]() $\Delta $
is a
$\Delta $
is a
![]() $\mathbb {Q}$
-Weil divisor on X and
$\mathbb {Q}$
-Weil divisor on X and
![]() $\mathfrak {a} \subseteq \mathcal {O}_X$
is a nonzero coherent ideal sheaf, a resolution
$\mathfrak {a} \subseteq \mathcal {O}_X$
is a nonzero coherent ideal sheaf, a resolution
![]() $f:Y \to X$
is said to be a log resolution of
$f:Y \to X$
is said to be a log resolution of
![]() $(X,\Delta ,\mathfrak {a})$
if
$(X,\Delta ,\mathfrak {a})$
if
![]() $\mathfrak {a}\mathcal {O}_Y=\mathcal {O}_Y(-F)$
is invertible and if the union of the exceptional locus
$\mathfrak {a}\mathcal {O}_Y=\mathcal {O}_Y(-F)$
is invertible and if the union of the exceptional locus
![]() $\operatorname {Exc} (f)$
of f and the support F and the strict transform
$\operatorname {Exc} (f)$
of f and the support F and the strict transform
![]() $f_*^{-1}\Delta $
of
$f_*^{-1}\Delta $
of
![]() $\Delta $
is a simple normal crossing divisor.
$\Delta $
is a simple normal crossing divisor.
If
![]() $f:Y\to X$
is a proper birational morphism with Y a normal integral scheme and
$f:Y\to X$
is a proper birational morphism with Y a normal integral scheme and
![]() $\Delta $
is a
$\Delta $
is a
![]() $\mathbb {Q}$
-Weil divisor, then we can choose
$\mathbb {Q}$
-Weil divisor, then we can choose
![]() $K_Y$
such that
$K_Y$
such that
![]() $f^*(K_X+\Delta )-K_Y$
is a divisor supported on the exceptional locus of f. With this convention:
$f^*(K_X+\Delta )-K_Y$
is a divisor supported on the exceptional locus of f. With this convention:
Definition 2.2. Let
![]() $\Delta \geqslant 0$
be an effective
$\Delta \geqslant 0$
be an effective
![]() $\mathbb {Q}$
-Weil divisor on X such that
$\mathbb {Q}$
-Weil divisor on X such that
![]() $K_X+\Delta $
is
$K_X+\Delta $
is
![]() $\mathbb {Q}$
-Cartier, let
$\mathbb {Q}$
-Cartier, let
![]() $\mathfrak {a}\subseteq \mathcal {O}_X$
be a nonzero coherent ideal sheaf, and let
$\mathfrak {a}\subseteq \mathcal {O}_X$
be a nonzero coherent ideal sheaf, and let
![]() $t>0$
be a positive real number. Then the multiplier ideal sheaf
$t>0$
be a positive real number. Then the multiplier ideal sheaf
![]() $\mathcal {J}(X,\Delta ,\mathfrak {a}^t)$
associated with
$\mathcal {J}(X,\Delta ,\mathfrak {a}^t)$
associated with
![]() $(X,\Delta ,\mathfrak {a}^t)$
is defined by
$(X,\Delta ,\mathfrak {a}^t)$
is defined by
where
![]() $f:Y\to X$
is a log resolution of
$f:Y\to X$
is a log resolution of
![]() $(X,\Delta ,\mathfrak {a})$
. Note that this definition is independent of the choice of log resolution.
$(X,\Delta ,\mathfrak {a})$
. Note that this definition is independent of the choice of log resolution.
Definition 2.3. Let X be a normal integral scheme essentially of finite type over a field of characteristic zero. We say that X has rational singularities if X is Cohen–Macaulay at x and if for any projective birational morphism
![]() $f:Y\to \operatorname {Spec} \mathcal {O}_{X,x}$
with Y a normal integral scheme, the natural morphism
$f:Y\to \operatorname {Spec} \mathcal {O}_{X,x}$
with Y a normal integral scheme, the natural morphism
![]() $f_*\omega _Y\to \omega _{X,x}$
is an isomorphism.
$f_*\omega _Y\to \omega _{X,x}$
is an isomorphism.
2.2 Tight closure and test ideals
In this subsection, we quickly review the basic notion of tight closure and test ideals. We refer the reader to [Reference Blickle, Schwede, Takagi and Zhang4], [Reference Hara and Yoshida11], [Reference Hochster and Huneke13], [Reference Takagi29].
Definition 2.4. Let R be a normal domain of characteristic
![]() $p>0$
, let
$p>0$
, let
![]() $\Delta \geqslant 0$
be an effective
$\Delta \geqslant 0$
be an effective
![]() $\mathbb {Q}$
-Weil divisor, let
$\mathbb {Q}$
-Weil divisor, let
![]() $\mathfrak {a}\subseteq R$
be a nonzero ideal, and let
$\mathfrak {a}\subseteq R$
be a nonzero ideal, and let
![]() $t>0$
be a real number. Let
$t>0$
be a real number. Let
![]() $E=\bigoplus E(R/\mathfrak {m})$
be the direct sum, taken over all maximal ideals
$E=\bigoplus E(R/\mathfrak {m})$
be the direct sum, taken over all maximal ideals
![]() $\mathfrak {m}$
of R, of the injective hulls
$\mathfrak {m}$
of R, of the injective hulls
![]() $E_R(R/\mathfrak {m})$
of the residue fields
$E_R(R/\mathfrak {m})$
of the residue fields
![]() $R/\mathfrak {m}$
.
$R/\mathfrak {m}$
.
-
(1) Let I be an ideal of R. The
 $(\Delta ,\mathfrak {a}^t)$
-tight closure
$(\Delta ,\mathfrak {a}^t)$
-tight closure
 $I^{*\Delta ,\mathfrak {a}^t}$
of I is defined as follows:
$I^{*\Delta ,\mathfrak {a}^t}$
of I is defined as follows:
 $x\in I^{*\Delta ,\mathfrak {a}^t}$
if and only if there exists a nonzero element
$x\in I^{*\Delta ,\mathfrak {a}^t}$
if and only if there exists a nonzero element
 $c\in R^{\circ }$
such that for all large
$c\in R^{\circ }$
such that for all large $$ \begin{align*} c\mathfrak{a}^{\lceil t(q-1)\rceil}x^q\subseteq I^{[q]}R(\lceil (q-1)\Delta\rceil) \end{align*} $$
$$ \begin{align*} c\mathfrak{a}^{\lceil t(q-1)\rceil}x^q\subseteq I^{[q]}R(\lceil (q-1)\Delta\rceil) \end{align*} $$
 $q=p^e$
, where
$q=p^e$
, where
 $I^{[q]}=\{f^q|f\in I\}$
and
$I^{[q]}=\{f^q|f\in I\}$
and
 $R^{\circ }=R\setminus \{0\}$
.
$R^{\circ }=R\setminus \{0\}$
.
-
(2) If M is an R-module, then the
 $(\Delta , \mathfrak {a}^t)$
-tight closure
$(\Delta , \mathfrak {a}^t)$
-tight closure
 $0_M^{*\Delta ,\mathfrak {a}^t}$
is defined as follows:
$0_M^{*\Delta ,\mathfrak {a}^t}$
is defined as follows:
 $z\in 0_M^{*\Delta , \mathfrak {a}^t}$
if and only if there exists a nonzero element
$z\in 0_M^{*\Delta , \mathfrak {a}^t}$
if and only if there exists a nonzero element
 $c\in R^{\circ }$
such that for all large
$c\in R^{\circ }$
such that for all large $$ \begin{align*} (c\mathfrak{a}^{\lceil t(q-1)\rceil})^{1/q}\otimes z=0 \quad \text{in} \quad R(\lceil (q-1)\Delta\rceil)^{1/q}\otimes_R M \end{align*} $$
$$ \begin{align*} (c\mathfrak{a}^{\lceil t(q-1)\rceil})^{1/q}\otimes z=0 \quad \text{in} \quad R(\lceil (q-1)\Delta\rceil)^{1/q}\otimes_R M \end{align*} $$
 $q=p^e$
.
$q=p^e$
.
-
(3) The (big) test ideal
 $\tau (R,\Delta ,\mathfrak {a}^t)$
associated with
$\tau (R,\Delta ,\mathfrak {a}^t)$
associated with
 $(R,\Delta ,\mathfrak {a}^t)$
is defined by
$(R,\Delta ,\mathfrak {a}^t)$
is defined by  $$ \begin{align*} \tau (R,\Delta,\mathfrak{a}^t)=\operatorname{Ann}_R(0_E^{*\Delta,\mathfrak{a}^t}). \end{align*} $$
$$ \begin{align*} \tau (R,\Delta,\mathfrak{a}^t)=\operatorname{Ann}_R(0_E^{*\Delta,\mathfrak{a}^t}). \end{align*} $$
When
 $\mathfrak {a}=R$
, then we simply denote the ideal
$\mathfrak {a}=R$
, then we simply denote the ideal
 $\tau (R,\Delta )$
. We call the triple
$\tau (R,\Delta )$
. We call the triple
 $(R,\Delta ,\mathfrak {a}^t)$
is strongly F-regular if
$(R,\Delta ,\mathfrak {a}^t)$
is strongly F-regular if
 $\tau (R,\Delta ,\mathfrak {a}^t)=R$
.
$\tau (R,\Delta ,\mathfrak {a}^t)=R$
.
Definition 2.5 [Reference Fedder and Watanabe8].
Let R be an F-finite Noetherian local domain of characteristic
![]() $p>0$
of dimension d. We say that R is F-rational if any ideal
$p>0$
of dimension d. We say that R is F-rational if any ideal
![]() $I=(x_1,\dots ,x_d)$
generated by a system of parameters satisfies
$I=(x_1,\dots ,x_d)$
generated by a system of parameters satisfies
![]() $I=I^*$
.
$I=I^*$
.
2.3 Big Cohen–Macaulay algebras
In this subsection, we will briefly review the theory of BCM algebras. Throughout this subsection, we assume that local rings
![]() $(R,\mathfrak {m})$
are Noetherian.
$(R,\mathfrak {m})$
are Noetherian.
Definition 2.6. Let
![]() $(R,\mathfrak {m})$
be a local ring, and let
$(R,\mathfrak {m})$
be a local ring, and let
![]() $\mathbf {x} = x_1,\dots , x_n$
be a system of parameters. R-algebra B is said to be BCM with respect to
$\mathbf {x} = x_1,\dots , x_n$
be a system of parameters. R-algebra B is said to be BCM with respect to
![]() $\mathbf {x}$
if
$\mathbf {x}$
if
![]() $\mathbf {x}$
is a regular sequence on B. B is called a (balanced) BCM algebra if it is BCM with respect to
$\mathbf {x}$
is a regular sequence on B. B is called a (balanced) BCM algebra if it is BCM with respect to
![]() $\mathbf {x}$
for every system of parameters
$\mathbf {x}$
for every system of parameters
![]() $\mathbf {x}$
.
$\mathbf {x}$
.
Remark 2.7 [Reference Bruns and Herzog5, Cor. 8.5.3].
If B is BCM with respect to
![]() $\mathbf {x}$
, then the
$\mathbf {x}$
, then the
![]() $\mathfrak {m}$
-adic completion
$\mathfrak {m}$
-adic completion
![]() $\widehat {B}$
is (balanced) BCM.
$\widehat {B}$
is (balanced) BCM.
About the existence of BCM algebras of residue characteristic
![]() $p>0$
, the following are proved in [Reference Bhatt3], [Reference Hochster and Huneke14].
$p>0$
, the following are proved in [Reference Bhatt3], [Reference Hochster and Huneke14].
Theorem 2.8. If
![]() $(R,\mathfrak {m})$
is an excellent local domain of residue characteristic
$(R,\mathfrak {m})$
is an excellent local domain of residue characteristic
![]() $p>0$
, then the p-adic completion of absolute integral closure
$p>0$
, then the p-adic completion of absolute integral closure
![]() $R^+$
is a (balanced) BCM R-algebra.
$R^+$
is a (balanced) BCM R-algebra.
Using BCM algebras, we can define a class of singularities.
Definition 2.9. If R is an excellent local ring of dimension d, and let B be a BCM R-algebra. We say that R is BCM-rational with respect to B (or simply
![]() $\text {BCM}_B$
-rational) if R is Cohen–Macaulay and if
$\text {BCM}_B$
-rational) if R is Cohen–Macaulay and if
![]() $H_{\mathfrak {m}}^d(R)\to H_{\mathfrak {m}}^d(B)$
is injective. We say that R is BCM-rational if R is
$H_{\mathfrak {m}}^d(R)\to H_{\mathfrak {m}}^d(B)$
is injective. We say that R is BCM-rational if R is
![]() $\text {BCM}_B$
-rational for any BCM algebra B.
$\text {BCM}_B$
-rational for any BCM algebra B.
We explain BCM test ideals introduced in [Reference Ma and Schwede19].
Setting 2.10. Let
![]() $(R,\mathfrak {m})$
be a normal local domain of dimension d.
$(R,\mathfrak {m})$
be a normal local domain of dimension d.
-
(i)
 $\Delta \geqslant 0$
is a
$\Delta \geqslant 0$
is a
 $\mathbb {Q}$
-Weil divisor on
$\mathbb {Q}$
-Weil divisor on
 $\operatorname {Spec} R$
such that
$\operatorname {Spec} R$
such that
 $K_R+\Delta $
is
$K_R+\Delta $
is
 $\mathbb {Q}$
-Cartier.
$\mathbb {Q}$
-Cartier. -
(ii) Fixing
 $\Delta $
, we also fix an embedding
$\Delta $
, we also fix an embedding
 $R\subseteq \omega _R \subseteq \operatorname {Frac} R$
, where
$R\subseteq \omega _R \subseteq \operatorname {Frac} R$
, where
 $\omega _R$
is the canonical module.
$\omega _R$
is the canonical module. -
(iii) Since
 $K_R + \Delta $
is effective and
$K_R + \Delta $
is effective and
 $\mathbb {Q}$
-Cartier, there exist an integer
$\mathbb {Q}$
-Cartier, there exist an integer
 $n>0$
and
$n>0$
and
 $f\in R$
such that
$f\in R$
such that
 $n(K_R+\Delta )=\operatorname {div} (f)$
.
$n(K_R+\Delta )=\operatorname {div} (f)$
.
Definition 2.11. With notation as in Setting 2.10, if B is a BCM
![]() $R[f^{1/n}]$
-algebra, then we define
$R[f^{1/n}]$
-algebra, then we define
![]() $0_{H_{\mathfrak {m}}^d(\omega _R)}^{B,K_R+\Delta }$
to be
$0_{H_{\mathfrak {m}}^d(\omega _R)}^{B,K_R+\Delta }$
to be
![]() $\operatorname {Ker} \psi $
, where
$\operatorname {Ker} \psi $
, where
![]() $\psi $
is the homomorphism determined by the below commutative diagram:
$\psi $
is the homomorphism determined by the below commutative diagram:

If R is
![]() $\mathfrak {m}$
-adically complete, then we define
$\mathfrak {m}$
-adically complete, then we define
We call
![]() $\tau _B(R,\Delta )$
the BCM test ideal of
$\tau _B(R,\Delta )$
the BCM test ideal of
![]() $(R,\Delta )$
with respect to B. We say that
$(R,\Delta )$
with respect to B. We say that
![]() $(R,\Delta )$
is BCM regular with respect to B (or simply
$(R,\Delta )$
is BCM regular with respect to B (or simply
![]() $\text {BCM}_{B}$
regular) if
$\text {BCM}_{B}$
regular) if
![]() $\tau _B(R,\Delta )=R$
.
$\tau _B(R,\Delta )=R$
.
Proposition 2.12 [Reference Ma and Schwede19].
Let
![]() $(R,\mathfrak {m})$
be a complete normal local domain of characteristic
$(R,\mathfrak {m})$
be a complete normal local domain of characteristic
![]() $p>0$
, let
$p>0$
, let
![]() $\Delta \geqslant 0$
be an effective
$\Delta \geqslant 0$
be an effective
![]() $\mathbb {Q}$
-Weil divisor on
$\mathbb {Q}$
-Weil divisor on
![]() $\operatorname {Spec} R,$
and let B be a BCM
$\operatorname {Spec} R,$
and let B be a BCM
![]() $R^+$
-algebra. Fix an effective canonical divisor
$R^+$
-algebra. Fix an effective canonical divisor
![]() $K_R\geqslant 0$
. Suppose that
$K_R\geqslant 0$
. Suppose that
![]() $K_R+\Delta $
is
$K_R+\Delta $
is
![]() $\mathbb {Q}$
-Cartier. Then
$\mathbb {Q}$
-Cartier. Then
3 Ultraproducts
3.1 Basic notions
In this subsection, we quickly review basic notions from the theory of ultraproduct. The reader is referred to [Reference Schoutens22], [Reference Schoutens26] for details. We fix an infinite set W. We use
![]() $\mathcal {P}(W)$
to denote the power set of W.
$\mathcal {P}(W)$
to denote the power set of W.
Definition 3.1. A nonempty subset
![]() $\mathcal {F} \subseteq \mathcal {P}(W)$
is called a filter if the following two conditions hold.
$\mathcal {F} \subseteq \mathcal {P}(W)$
is called a filter if the following two conditions hold.
-
(i) If
 $A, B \in \mathcal {F}$
, then
$A, B \in \mathcal {F}$
, then
 $A \cap B\in \mathcal {F}$
.
$A \cap B\in \mathcal {F}$
. -
(ii) If
 $A \in \mathcal {F}$
and
$A \in \mathcal {F}$
and
 $A \subseteq B \subseteq W$
, then
$A \subseteq B \subseteq W$
, then
 $B \in \mathcal {F}$
.
$B \in \mathcal {F}$
.
Definition 3.2. Let
![]() $\mathcal {F}$
be a filter on W.
$\mathcal {F}$
be a filter on W.
-
(1)
 $\mathcal {F}$
is called an ultrafilter if for all
$\mathcal {F}$
is called an ultrafilter if for all
 $A \in \mathcal {P}(W)$
, we have
$A \in \mathcal {P}(W)$
, we have
 $A \in \mathcal {F}$
or
$A \in \mathcal {F}$
or
 $A^c \in \mathcal {F}$
, where
$A^c \in \mathcal {F}$
, where
 $A^c$
is the complement of A.
$A^c$
is the complement of A. -
(2)
 $\mathcal {F}$
is called principal if there exists a finite subset
$\mathcal {F}$
is called principal if there exists a finite subset
 $A\subseteq W$
such that
$A\subseteq W$
such that
 $A \in \mathcal {F}$
.
$A \in \mathcal {F}$
.
Remark 3.3. By Zorn’s lemma, non-principal ultrafilters always exist.
Remark 3.4. Ultrafilters are an equivalent notion to two-valued finitely additive measures. If we have an ultrafilter
![]() $\mathcal {F}$
on W, then
$\mathcal {F}$
on W, then
 $$ \begin{align*} m(A):= \left\{\!\!\! \begin{array}{ll} 1 & (A\in \mathcal{F}) \\ 0 & (A \notin \mathcal{F}) \end{array} \right. \end{align*} $$
$$ \begin{align*} m(A):= \left\{\!\!\! \begin{array}{ll} 1 & (A\in \mathcal{F}) \\ 0 & (A \notin \mathcal{F}) \end{array} \right. \end{align*} $$
is a two-valued finitely additive measure. Conversely, if
![]() $m:\mathcal {P}(W)\to \{0,1\}$
is a nonzero finitely additive measure, then
$m:\mathcal {P}(W)\to \{0,1\}$
is a nonzero finitely additive measure, then
![]() $\mathcal {F}:=\{A\subseteq W|m(A)=1\}$
is an ultrafilter. Here,
$\mathcal {F}:=\{A\subseteq W|m(A)=1\}$
is an ultrafilter. Here,
![]() $\mathcal {F}$
is principal if and only if there exists an element
$\mathcal {F}$
is principal if and only if there exists an element
![]() $w_0$
of W such that
$w_0$
of W such that
![]() $m(\{w_0\})=1$
. Hence,
$m(\{w_0\})=1$
. Hence,
![]() $\mathcal {F}$
is not principal if and only if
$\mathcal {F}$
is not principal if and only if
![]() $m(A)=0$
for any finite subset A of W.
$m(A)=0$
for any finite subset A of W.
Definition 3.5. Let
![]() $A_w$
be a family of sets indexed by W and
$A_w$
be a family of sets indexed by W and
![]() $\mathcal {F}$
be an ultrafilter on W. Suppose that
$\mathcal {F}$
be an ultrafilter on W. Suppose that
![]() $a_w\in A_w$
for all
$a_w\in A_w$
for all
![]() $w\in W$
and
$w\in W$
and
![]() $\varphi $
is a predicate. We say
$\varphi $
is a predicate. We say
![]() $\varphi (a_w)$
holds for almost all w if
$\varphi (a_w)$
holds for almost all w if
![]() $\{w\in W|\varphi (a_w) \text { holds}\}\in \mathcal {F}$
.
$\{w\in W|\varphi (a_w) \text { holds}\}\in \mathcal {F}$
.
Remark 3.6. This is an analog of “almost everywhere” or “almost surely” in analysis. The difference is that m is not countably but finitely additive. We can consider elements in
![]() $\mathcal {F}$
as “large” sets and elements in the complement
$\mathcal {F}$
as “large” sets and elements in the complement
![]() $\mathcal {F}^c$
as “small” sets. If
$\mathcal {F}^c$
as “small” sets. If
![]() $\mathcal {F}$
is not principal, all finite subsets of W are “small.”
$\mathcal {F}$
is not principal, all finite subsets of W are “small.”
Definition 3.7. Let
![]() $A_w$
be a family of sets indexed by W and
$A_w$
be a family of sets indexed by W and
![]() $\mathcal {F}$
be a non-principal ultrafilter on W. The ultraproduct of
$\mathcal {F}$
be a non-principal ultrafilter on W. The ultraproduct of
![]() $A_w$
is defined by
$A_w$
is defined by
where
![]() $(a_w)\sim (b_w)$
if and only if
$(a_w)\sim (b_w)$
if and only if
![]() $\{w\in W|a_w=b_w\}\in \mathcal {F}$
. We denote the equivalence class of
$\{w\in W|a_w=b_w\}\in \mathcal {F}$
. We denote the equivalence class of
![]() $(a_w)$
by
$(a_w)$
by
![]() $\operatorname *{\mathrm {ulim}}_w a_w$
.
$\operatorname *{\mathrm {ulim}}_w a_w$
.
Remark 3.8 [Reference Lyu17, Sec. 3].
If
![]() $A_w$
are local rings, then the ultraproduct is equivalent to the localization of
$A_w$
are local rings, then the ultraproduct is equivalent to the localization of
![]() $\prod A_w$
at a maximal ideal.
$\prod A_w$
at a maximal ideal.
Example 3.9. We use
![]() $^*\mathbb {N}$
and
$^*\mathbb {N}$
and
![]() $^*\mathbb {R}$
to denote the ultraproduct of
$^*\mathbb {R}$
to denote the ultraproduct of
![]() $|W|$
copies of
$|W|$
copies of
![]() $\mathbb {N}$
and
$\mathbb {N}$
and
![]() $\mathbb {R,}$
respectively.
$\mathbb {R,}$
respectively.
![]() $^*\mathbb {N}$
is a semiring and
$^*\mathbb {N}$
is a semiring and
![]() $^*\mathbb {R}$
is a field (see Definition-Proposition 3.10 and Theorem 3.20).
$^*\mathbb {R}$
is a field (see Definition-Proposition 3.10 and Theorem 3.20).
![]() $^*\mathbb {N}$
is a non-standard model of Peano arithmetic.
$^*\mathbb {N}$
is a non-standard model of Peano arithmetic.
![]() $^*\mathbb {R}$
is a system of hyperreal numbers used in non-standard analysis.
$^*\mathbb {R}$
is a system of hyperreal numbers used in non-standard analysis.
Definition-Proposition 3.10. Let
![]() $A_{1w},\dots , A_{nw}$
,
$A_{1w},\dots , A_{nw}$
,
![]() $B_w$
be families of sets indexed by W and
$B_w$
be families of sets indexed by W and
![]() $\mathcal {F}$
be a non-principal ultrafilter. Suppose that
$\mathcal {F}$
be a non-principal ultrafilter. Suppose that
![]() $f_w:A_{1w}\times \dots \times A_{nw}\to B_w$
is a family of maps. Then we define the ultraproduct
$f_w:A_{1w}\times \dots \times A_{nw}\to B_w$
is a family of maps. Then we define the ultraproduct
![]() $f_\infty = \operatorname *{\mathrm {ulim}}_w f_w : A_{1\infty }\times \dots \times A_{n\infty }\to B_\infty $
of
$f_\infty = \operatorname *{\mathrm {ulim}}_w f_w : A_{1\infty }\times \dots \times A_{n\infty }\to B_\infty $
of
![]() $f_w$
by
$f_w$
by
This is well-defined.
Corollary 3.11. Let
![]() $A_w$
be a family of rings. Suppose that
$A_w$
be a family of rings. Suppose that
![]() $B_w$
is an
$B_w$
is an
![]() $A_w$
-algebra and
$A_w$
-algebra and
![]() $M_w$
is an
$M_w$
is an
![]() $A_w$
-module for almost all w. Then the following hold:
$A_w$
-module for almost all w. Then the following hold:
-
(1)
 $A_\infty $
is a ring.
$A_\infty $
is a ring. -
(2)
 $B_\infty $
is an
$B_\infty $
is an
 $A_\infty $
-algebra.
$A_\infty $
-algebra. -
(3)
 $M_\infty $
is an
$M_\infty $
is an
 $A_\infty $
-module.
$A_\infty $
-module.
Proof. Let
![]() $0:=\operatorname *{\mathrm {ulim}}_w 0$
,
$0:=\operatorname *{\mathrm {ulim}}_w 0$
,
![]() $1:=\operatorname *{\mathrm {ulim}}_w 1$
in
$1:=\operatorname *{\mathrm {ulim}}_w 1$
in
![]() $A_\infty $
,
$A_\infty $
,
![]() $B_\infty $
and
$B_\infty $
and
![]() $0:=\operatorname *{\mathrm {ulim}}_w 0$
in
$0:=\operatorname *{\mathrm {ulim}}_w 0$
in
![]() $M_\infty $
. By the above Definition–Proposition,
$M_\infty $
. By the above Definition–Proposition,
![]() $A_\infty $
,
$A_\infty $
,
![]() $B_\infty $
have natural additions, subtractions, and multiplications and we have a natural ring homomorphism
$B_\infty $
have natural additions, subtractions, and multiplications and we have a natural ring homomorphism
![]() $A_\infty \to B_\infty $
. Similarly,
$A_\infty \to B_\infty $
. Similarly,
![]() $M_\infty $
has a natural addition and a scalar multiplication between elements of
$M_\infty $
has a natural addition and a scalar multiplication between elements of
![]() $M_\infty $
and
$M_\infty $
and
![]() $A_\infty $
.
$A_\infty $
.
Proposition 3.12. Suppose that, for almost all w, we have an exact sequence
of abelian groups. Then
is an exact sequence of abelian groups. In particular,
![]() $\operatorname *{\mathrm {ulim}}_w:\prod _w\operatorname {Ab}\to \operatorname {Ab}$
is an exact functor.
$\operatorname *{\mathrm {ulim}}_w:\prod _w\operatorname {Ab}\to \operatorname {Ab}$
is an exact functor.
Proof. Let
![]() $f_w:L_w\to M_w$
and
$f_w:L_w\to M_w$
and
![]() $g_w:M_w\to N_w$
be the morphisms in the given exact sequence. Here, we only prove the injectivity of
$g_w:M_w\to N_w$
be the morphisms in the given exact sequence. Here, we only prove the injectivity of
![]() $\operatorname *{\mathrm {ulim}}_w f_w$
and the surjectivity of
$\operatorname *{\mathrm {ulim}}_w f_w$
and the surjectivity of
![]() $\operatorname *{\mathrm {ulim}}_w g_w$
. Suppose that
$\operatorname *{\mathrm {ulim}}_w g_w$
. Suppose that
![]() $\operatorname *{\mathrm {ulim}}_w f_w(a_w)=0$
for
$\operatorname *{\mathrm {ulim}}_w f_w(a_w)=0$
for
![]() $\operatorname *{\mathrm {ulim}}_w a_w \in \operatorname *{\mathrm {ulim}}_w L_w$
. Then
$\operatorname *{\mathrm {ulim}}_w a_w \in \operatorname *{\mathrm {ulim}}_w L_w$
. Then
![]() $f_w(a_w)=0$
for almost all w. Since
$f_w(a_w)=0$
for almost all w. Since
![]() $f_w$
is injective for almost all w, we have
$f_w$
is injective for almost all w, we have
![]() $a_w=0$
for almost all w. Therefore,
$a_w=0$
for almost all w. Therefore,
![]() $\operatorname *{\mathrm {ulim}}_w a_w=0$
in
$\operatorname *{\mathrm {ulim}}_w a_w=0$
in
![]() $\operatorname *{\mathrm {ulim}}_w L_w$
. Hence,
$\operatorname *{\mathrm {ulim}}_w L_w$
. Hence,
![]() $\operatorname *{\mathrm {ulim}}_w f_w$
is injective. Next, let
$\operatorname *{\mathrm {ulim}}_w f_w$
is injective. Next, let
![]() $\operatorname *{\mathrm {ulim}}_w c_w$
be any element in
$\operatorname *{\mathrm {ulim}}_w c_w$
be any element in
![]() $\operatorname *{\mathrm {ulim}}_w N_w$
. Since
$\operatorname *{\mathrm {ulim}}_w N_w$
. Since
![]() $g_w$
is surjective for almost all w, there exists
$g_w$
is surjective for almost all w, there exists
![]() $b_w\in M_w$
such that
$b_w\in M_w$
such that
![]() $g_w(b_w)=c_w$
for almost all w. Let
$g_w(b_w)=c_w$
for almost all w. Let
![]() $b=\operatorname *{\mathrm {ulim}}_w b_w$
. Then we have
$b=\operatorname *{\mathrm {ulim}}_w b_w$
. Then we have
![]() $(\operatorname *{\mathrm {ulim}}_w g_w)(b)=\operatorname *{\mathrm {ulim}}_w g_w(b_w)=\operatorname *{\mathrm {ulim}}_w c_w$
. Hence,
$(\operatorname *{\mathrm {ulim}}_w g_w)(b)=\operatorname *{\mathrm {ulim}}_w g_w(b_w)=\operatorname *{\mathrm {ulim}}_w c_w$
. Hence,
![]() $\operatorname *{\mathrm {ulim}}_w g_w$
is surjective. The rest of the proof is similar.
$\operatorname *{\mathrm {ulim}}_w g_w$
is surjective. The rest of the proof is similar.
Łoś’s theorem is a fundamental theorem in the theory of ultraproducts. We will prepare some notions needed to state the theorem.
Definition 3.13. The language
![]() $\mathcal {L}$
of rings is the set defined by
$\mathcal {L}$
of rings is the set defined by
Definition 3.14.
Terms of
![]() $\mathcal {L}$
are defined as follows:
$\mathcal {L}$
are defined as follows:
-
(i)
 $0$
,
$0$
,
 $1$
are terms.
$1$
are terms. -
(ii) Variables are terms.
-
(iii) If s, t are terms, then
 ${-(s)}, (s)+(t), (s)\cdot (t)$
are terms.
${-(s)}, (s)+(t), (s)\cdot (t)$
are terms. -
(iv) A string of symbols is a term only if it can be shown to be a term by finitely many applications of the above three rules.
We omit parentheses and “
![]() $\cdot $
” if there is no ambiguity.
$\cdot $
” if there is no ambiguity.
Example 3.15.
![]() $1+1$
,
$1+1$
,
![]() $x_1(x_2+1)$
,
$x_1(x_2+1)$
,
![]() $-(-x)$
are terms.
$-(-x)$
are terms.
Definition 3.16.
Formulas of
![]() $\mathcal {L}$
are defined as follows:
$\mathcal {L}$
are defined as follows:
-
(i) If
 $s $
, t are terms, then
$s $
, t are terms, then
 $(s=t)$
is a formula.
$(s=t)$
is a formula. -
(ii) If
 $\varphi , \psi $
are formulas, then
$\varphi , \psi $
are formulas, then
 $(\varphi \land \psi ), (\varphi \lor \psi ), (\varphi \to \psi ),(\lnot \varphi )$
are formulas.
$(\varphi \land \psi ), (\varphi \lor \psi ), (\varphi \to \psi ),(\lnot \varphi )$
are formulas. -
(iii) If
 $\varphi $
is a formula and x is a variable, then
$\varphi $
is a formula and x is a variable, then
 $\forall x \varphi , \exists x \varphi $
are formulas.
$\forall x \varphi , \exists x \varphi $
are formulas. -
(iv) A string of symbols is a formula only if it can be shown to be a formula by finitely many applications of the above three rules.
We omit parentheses if there is no ambiguity and use
![]() $\neq $
,
$\neq $
,
![]() $\nexists $
in the usual way.
$\nexists $
in the usual way.
Remark 3.17.
![]() $\varphi \land \psi $
means “
$\varphi \land \psi $
means “
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
,”
$\psi $
,”
![]() $\varphi \lor \psi $
means “
$\varphi \lor \psi $
means “
![]() $\varphi $
or
$\varphi $
or
![]() $\psi $
,”
$\psi $
,”
![]() $\varphi \to \psi $
means “
$\varphi \to \psi $
means “
![]() $\varphi $
implies
$\varphi $
implies
![]() $\psi $
,” and
$\psi $
,” and
![]() $\lnot \varphi $
means “
$\lnot \varphi $
means “
![]() $\varphi $
does not hold.”
$\varphi $
does not hold.”
Example 3.18. 0=1,
![]() $x=0 \land y\neq 1$
,
$x=0 \land y\neq 1$
,
![]() $\forall x \forall y (xy=yx)$
are formulas.
$\forall x \forall y (xy=yx)$
are formulas.
Remark 3.19. Variables in a formula
![]() $\varphi $
which is not bounded by
$\varphi $
which is not bounded by
![]() $\forall $
or
$\forall $
or
![]() $\exists $
are called free variables of
$\exists $
are called free variables of
![]() $\varphi $
. If
$\varphi $
. If
![]() $x_1,\dots ,x_n$
are free variables of
$x_1,\dots ,x_n$
are free variables of
![]() $\varphi $
, we denote
$\varphi $
, we denote
![]() $\varphi (x_1,\dots ,x_n)$
and we can substitute elements of a ring for
$\varphi (x_1,\dots ,x_n)$
and we can substitute elements of a ring for
![]() $x_1,\dots ,x_n$
.
$x_1,\dots ,x_n$
.
Theorem 3.20 (Łoś’s theorem in the case of rings).
Suppose that
![]() $\varphi (x_1,\dots ,x_n$
) is a formula of
$\varphi (x_1,\dots ,x_n$
) is a formula of
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $A_w$
is a family of rings indexed by a set W endowed with a non-principal ultrafilter. Let
$A_w$
is a family of rings indexed by a set W endowed with a non-principal ultrafilter. Let
![]() $a_{iw}\in A_w$
. Then
$a_{iw}\in A_w$
. Then
![]() $\varphi (\operatorname *{\mathrm {ulim}}_w a_{1w}, \dots , \operatorname *{\mathrm {ulim}}_w a_{nw})$
holds in
$\varphi (\operatorname *{\mathrm {ulim}}_w a_{1w}, \dots , \operatorname *{\mathrm {ulim}}_w a_{nw})$
holds in
![]() $A_\infty $
if and only if
$A_\infty $
if and only if
![]() $\varphi (a_{1w},\dots ,a_{nw})$
holds in
$\varphi (a_{1w},\dots ,a_{nw})$
holds in
![]() $A_w$
for almost all w.
$A_w$
for almost all w.
Remark 3.21. Even if
![]() $A_w$
are not rings, replacing
$A_w$
are not rings, replacing
![]() $\mathcal {L}$
properly, we can get the same theorem as above. We use one in the case of modules.
$\mathcal {L}$
properly, we can get the same theorem as above. We use one in the case of modules.
Example 3.22. Let A be a ring. If a property of rings is written by some formula, we can apply Łoś’s theorem.
-
(1) A is a field if and only if
 $\forall x (x=0 \lor \exists y(xy=1))$
holds.
$\forall x (x=0 \lor \exists y(xy=1))$
holds. -
(2) A is a domain if and only if
 $\forall x \forall y(xy=0\to (x=0\lor y=0))$
holds.
$\forall x \forall y(xy=0\to (x=0\lor y=0))$
holds. -
(3) A is a local ring if and only if
holds. $$ \begin{align*} \forall x \forall y (\nexists z (xz=1)\land \nexists w(yw=1)\to \nexists u((x+y)u=1)) \end{align*} $$
$$ \begin{align*} \forall x \forall y (\nexists z (xz=1)\land \nexists w(yw=1)\to \nexists u((x+y)u=1)) \end{align*} $$
-
(4) The condition that A is an algebraically closed field is written by countably many formulas, that is, the formula in (1) and for all
 $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,  $$ \begin{align*}\forall a_0 \dots a_{n-1} \exists x (x^n+a_{n-1}x^{n-1}+\dots +a_0=0).\end{align*} $$
$$ \begin{align*}\forall a_0 \dots a_{n-1} \exists x (x^n+a_{n-1}x^{n-1}+\dots +a_0=0).\end{align*} $$
-
(5) The condition that A is Noetherian cannot be written by formulas. Indeed, if
 $W=\mathbb {N}$
with some non-principal ultrafilter and
$W=\mathbb {N}$
with some non-principal ultrafilter and
 , then
, then
 $\operatorname *{\mathrm {ulim}}_n x^n\neq 0$
is in
$\operatorname *{\mathrm {ulim}}_n x^n\neq 0$
is in
 $\cap _n \mathfrak {m}_\infty ^n$
, where
$\cap _n \mathfrak {m}_\infty ^n$
, where
 $\mathfrak {m}_\infty $
is the maximal ideal of
$\mathfrak {m}_\infty $
is the maximal ideal of
 $A_\infty $
. Hence,
$A_\infty $
. Hence,
 $A_\infty $
is not Noetherian.
$A_\infty $
is not Noetherian.
Proposition 3.23 ([Reference Schoutens22, 2.8.2]; see Example 3.22).
If almost all
![]() $K_w$
are algebraically closed field, then
$K_w$
are algebraically closed field, then
![]() $K_\infty $
is an algebraically closed field.
$K_\infty $
is an algebraically closed field.
Theorem 3.24 (Lefschetz principle [Reference Schoutens22, Th. 2.4]).
Let W be the set of prime numbers endowed with some non-principal ultrafilter. Then
Proof. Let
![]() $C=\operatorname *{\mathrm {ulim}}_p\overline {\mathbb {F}_p}$
. By the above theorem, C is an algebraically closed field. For any prime number q, we have
$C=\operatorname *{\mathrm {ulim}}_p\overline {\mathbb {F}_p}$
. By the above theorem, C is an algebraically closed field. For any prime number q, we have
![]() $q\neq 0$
in
$q\neq 0$
in
![]() $\overline {\mathbb {F}_p}$
for almost all p. Hence,
$\overline {\mathbb {F}_p}$
for almost all p. Hence,
![]() $q\neq 0$
in C, that is, C is of characteristic zero. We can check that C has the same cardinality as
$q\neq 0$
in C, that is, C is of characteristic zero. We can check that C has the same cardinality as
![]() $\mathbb {C}$
. If two algebraically closed uncountable field of characteristic zero have the equal cardinality, then they are isomorphic. Hence,
$\mathbb {C}$
. If two algebraically closed uncountable field of characteristic zero have the equal cardinality, then they are isomorphic. Hence,
![]() $C\cong \mathbb {C}$
. (Note that this isomorphism is not canonical.)
$C\cong \mathbb {C}$
. (Note that this isomorphism is not canonical.)
3.2 Non-standard hulls
In this subsection, we will introduce the notion of non-standard hulls along [Reference Schoutens22], [Reference Schoutens26]. Throughout this subsection, let
![]() $\mathcal {P}$
be the set of prime numbers and we fix a non-principal ultrafilter on
$\mathcal {P}$
be the set of prime numbers and we fix a non-principal ultrafilter on
![]() $\mathcal {P}$
and an isomorphism
$\mathcal {P}$
and an isomorphism
![]() $\operatorname *{\mathrm {ulim}}_p \overline {\mathbb {F}_p}\cong \mathbb {C}$
.
$\operatorname *{\mathrm {ulim}}_p \overline {\mathbb {F}_p}\cong \mathbb {C}$
.
Let
![]() $\mathbb {C}[X_1,\dots ,X_n]_\infty :=\operatorname *{\mathrm {ulim}}_p\overline {\mathbb {F}_p}[X_1,\dots ,X_n]$
. Then we have the following proposition.
$\mathbb {C}[X_1,\dots ,X_n]_\infty :=\operatorname *{\mathrm {ulim}}_p\overline {\mathbb {F}_p}[X_1,\dots ,X_n]$
. Then we have the following proposition.
Proposition 3.25 [Reference Schoutens22, Th. 2.6].
We have a natural map
![]() $\mathbb {C}[X_1,\dots ,X_n]\to \mathbb {C}[X_1,\dots ,X_n]_\infty $
, which is faithfully flat.
$\mathbb {C}[X_1,\dots ,X_n]\to \mathbb {C}[X_1,\dots ,X_n]_\infty $
, which is faithfully flat.
Definition 3.26. The ring
![]() $\mathbb {C}[X_1,\dots ,X_n]_\infty $
is said to be the non-standard hull of
$\mathbb {C}[X_1,\dots ,X_n]_\infty $
is said to be the non-standard hull of
![]() $\mathbb {C}[X_1,\dots ,X_n]$
.
$\mathbb {C}[X_1,\dots ,X_n]$
.
Remark 3.27. If
![]() $n\geqslant 1$
, then
$n\geqslant 1$
, then
![]() $\mathbb {C}[X_1,\dots ,X_n]_\infty $
is not Noetherian. Let
$\mathbb {C}[X_1,\dots ,X_n]_\infty $
is not Noetherian. Let
![]() $y=\operatorname *{\mathrm {ulim}}_p X_1^p$
. Then, for any integer
$y=\operatorname *{\mathrm {ulim}}_p X_1^p$
. Then, for any integer
![]() $l\geqslant 1$
,
$l\geqslant 1$
,
![]() $X_1^p\in (X_1,\dots ,X_n)^l$
for almost all p. Hence,
$X_1^p\in (X_1,\dots ,X_n)^l$
for almost all p. Hence,
![]() $y\in (X_1,\dots ,X_n)^l$
for any l by Łoś’s theorem. Therefore,
$y\in (X_1,\dots ,X_n)^l$
for any l by Łoś’s theorem. Therefore,
![]() $\cap _l (X_1,\dots ,X_n)^l\neq 0$
. By Krull’s intersection theorem,
$\cap _l (X_1,\dots ,X_n)^l\neq 0$
. By Krull’s intersection theorem,
![]() $\mathbb {C}[X_1,\dots ,X_n]_\infty $
is not Noetherian.
$\mathbb {C}[X_1,\dots ,X_n]_\infty $
is not Noetherian.
Definition 3.28. Suppose that R is a finitely generated
![]() $\mathbb {C}$
-algebra. Let
$\mathbb {C}$
-algebra. Let
be a presentation of R. The non-standard hull
![]() $R_\infty $
of R is defined by
$R_\infty $
of R is defined by
Remark 3.29. The non-standard hull is independent of a representation of R. If
![]() $R\cong \mathbb {C}[X_1,\dots ,X_n]/I\cong \mathbb {C}[Y_1,\dots ,Y_m]/J$
, then
$R\cong \mathbb {C}[X_1,\dots ,X_n]/I\cong \mathbb {C}[Y_1,\dots ,Y_m]/J$
, then
![]() $\overline {\mathbb {F}_p}[X_1,\dots ,X_n]/I_p \cong \overline {\mathbb {F}_p}[Y_1,\dots ,Y_m]/J_p$
for almost all p (see Definitions 3.33 and 3.35).
$\overline {\mathbb {F}_p}[X_1,\dots ,X_n]/I_p \cong \overline {\mathbb {F}_p}[Y_1,\dots ,Y_m]/J_p$
for almost all p (see Definitions 3.33 and 3.35).
Remark 3.30. The natural map
![]() $R\to R_\infty $
is faithfully flat since this is a base change of the homomorphism
$R\to R_\infty $
is faithfully flat since this is a base change of the homomorphism
![]() $\mathbb {C}[X_1,\dots ,X_n]\to \mathbb {C}[X_1,\dots ,X_n]_\infty $
. By faithfully flatness, we have
$\mathbb {C}[X_1,\dots ,X_n]\to \mathbb {C}[X_1,\dots ,X_n]_\infty $
. By faithfully flatness, we have
![]() $IR_\infty \cap R=R$
for any ideal
$IR_\infty \cap R=R$
for any ideal
![]() $I\subseteq R$
.
$I\subseteq R$
.
Definition 3.31. Let
![]() $a\in \mathbb {C}$
. Since
$a\in \mathbb {C}$
. Since
![]() $\operatorname *{\mathrm {ulim}}_p \overline {\mathbb {F}_p}\cong \mathbb {C}$
, we have a family
$\operatorname *{\mathrm {ulim}}_p \overline {\mathbb {F}_p}\cong \mathbb {C}$
, we have a family
![]() $(a_p)_p$
of elements of
$(a_p)_p$
of elements of
![]() $\overline {\mathbb {F}_p}$
such that
$\overline {\mathbb {F}_p}$
such that
![]() $\operatorname *{\mathrm {ulim}} a_p=a$
. Then we call
$\operatorname *{\mathrm {ulim}} a_p=a$
. Then we call
![]() $(a_p)_p$
an approximation of a.
$(a_p)_p$
an approximation of a.
Proposition 3.32. Let
![]() $I=(f_1,\dots ,f_s)$
be an ideal of
$I=(f_1,\dots ,f_s)$
be an ideal of
![]() $\mathbb {C}[X_1,\dots , X_n]$
and
$\mathbb {C}[X_1,\dots , X_n]$
and
![]() $f_i=\sum a_{i\nu }X^\nu $
. Let
$f_i=\sum a_{i\nu }X^\nu $
. Let
![]() $I_p=(f_{1p},\dots ,f_{sp})\overline {\mathbb {F}_p}[X_1,\dots ,X_n]$
, where
$I_p=(f_{1p},\dots ,f_{sp})\overline {\mathbb {F}_p}[X_1,\dots ,X_n]$
, where
![]() $f_{ip}=\sum a_{i\nu p}X^\nu $
and each
$f_{ip}=\sum a_{i\nu p}X^\nu $
and each
![]() $(a_{i\nu p})_p$
is an approximation of
$(a_{i\nu p})_p$
is an approximation of
![]() $a_{i\nu }$
. Then we have
$a_{i\nu }$
. Then we have
and
Definition 3.33. Let R be a finitely generated
![]() $\mathbb {C}$
-algebra.
$\mathbb {C}$
-algebra.
-
(1) In the setting of Proposition 3.32, a family
 $R_p$
is said to be an approximation of R if
$R_p$
is said to be an approximation of R if
 $R_p$
is an
$R_p$
is an
 $\overline {\mathbb {F}_p}$
-algebra and
$\overline {\mathbb {F}_p}$
-algebra and
 $R_p \cong \overline {\mathbb {F}_p}[X_1,\dots ,X_n]/I_p$
for almost all p. Then we have
$R_p \cong \overline {\mathbb {F}_p}[X_1,\dots ,X_n]/I_p$
for almost all p. Then we have
 $R_\infty \cong \operatorname *{\mathrm {ulim}}_p R_p$
.
$R_\infty \cong \operatorname *{\mathrm {ulim}}_p R_p$
. -
(2) For an element
 $f\in R$
, a family
$f\in R$
, a family
 $f_p$
is said to be an approximation of f if
$f_p$
is said to be an approximation of f if
 $f_p\in R_p$
for almost all p and
$f_p\in R_p$
for almost all p and
 $f=\operatorname *{\mathrm {ulim}}_p f_p$
in
$f=\operatorname *{\mathrm {ulim}}_p f_p$
in
 $R_\infty $
. For
$R_\infty $
. For
 $f\in R_\infty $
, we define an approximation of f in the same way.
$f\in R_\infty $
, we define an approximation of f in the same way. -
(3) For an ideal
 $I=(f_1,\dots ,f_s) \subseteq R$
, a family
$I=(f_1,\dots ,f_s) \subseteq R$
, a family
 $I_p$
is said to be an approximation of I if
$I_p$
is said to be an approximation of I if
 $I_p$
is an ideal of
$I_p$
is an ideal of
 $R_p$
and
$R_p$
and
 $I_p=(f_{1p},\dots ,f_{sp})$
for almost all p. For finitely generated ideal
$I_p=(f_{1p},\dots ,f_{sp})$
for almost all p. For finitely generated ideal
 $I\subseteq R_\infty $
, we define an approximation of I in the same way.
$I\subseteq R_\infty $
, we define an approximation of I in the same way.
Remark 3.34. This is an abuse of notation since approximations should be denoted by
![]() $(R_p)_p$
,
$(R_p)_p$
,
![]() $(f_p)_p$
,
$(f_p)_p$
,
![]() $(I_p)_p$
, and so forth.
$(I_p)_p$
, and so forth.
Definition 3.35. Let
![]() $\varphi :R\to S$
be a
$\varphi :R\to S$
be a
![]() $\mathbb {C}$
-algebra homomorphism between finitely generated
$\mathbb {C}$
-algebra homomorphism between finitely generated
![]() $\mathbb {C}$
-algebras. Suppose that
$\mathbb {C}$
-algebras. Suppose that
![]() $R\cong \mathbb {C}[X_1,\dots ,X_n]/I$
and
$R\cong \mathbb {C}[X_1,\dots ,X_n]/I$
and
![]() $S\cong \mathbb {C}[Y_1,\dots ,Y_m]/J$
. Let
$S\cong \mathbb {C}[Y_1,\dots ,Y_m]/J$
. Let
![]() $f_i\in \mathbb {C}[Y_1,\dots ,Y_m]$
be a lifting of the image of
$f_i\in \mathbb {C}[Y_1,\dots ,Y_m]$
be a lifting of the image of
![]() $X_i\ \mod I$
under
$X_i\ \mod I$
under
![]() $\varphi $
. Then we define an approximation
$\varphi $
. Then we define an approximation
![]() $\varphi _p:R_p\to S_p$
of
$\varphi _p:R_p\to S_p$
of
![]() $\varphi $
as the morphism induced by
$\varphi $
as the morphism induced by
![]() $X_i\longmapsto f_{ip}$
. Let
$X_i\longmapsto f_{ip}$
. Let
![]() $\varphi _\infty :=\operatorname *{\mathrm {ulim}}_p\varphi _p$
, then the following diagram commutes.
$\varphi _\infty :=\operatorname *{\mathrm {ulim}}_p\varphi _p$
, then the following diagram commutes.

Proposition 3.36 [Reference Schoutens22, Cor. 4.2], [Reference Schoutens26, Th. 4.3.4].
Let R be a finitely generated
![]() $\mathbb {C}$
-algebra. An ideal
$\mathbb {C}$
-algebra. An ideal
![]() $I\subseteq R$
is prime if and only if
$I\subseteq R$
is prime if and only if
![]() $I_p$
is prime for almost all p if and only if
$I_p$
is prime for almost all p if and only if
![]() $IR_\infty $
is prime.
$IR_\infty $
is prime.
Definition 3.37. Let R be a local ring essentially of finite type over
![]() $\mathbb {C}$
. Suppose that
$\mathbb {C}$
. Suppose that
![]() $R\cong S_{\mathfrak {p}}$
, where S is a finitely generated
$R\cong S_{\mathfrak {p}}$
, where S is a finitely generated
![]() $\mathbb {C}$
-algebra and
$\mathbb {C}$
-algebra and
![]() $\mathfrak {p}$
is a prime ideal of S. Then we define the non-standard hull
$\mathfrak {p}$
is a prime ideal of S. Then we define the non-standard hull
![]() $R_\infty $
of R by
$R_\infty $
of R by
Remark 3.38. Since
![]() $S\to S_\infty $
is faithfully flat,
$S\to S_\infty $
is faithfully flat,
![]() $R\to R_\infty $
is faithfully flat.
$R\to R_\infty $
is faithfully flat.
Definition 3.39. Let S be a finitely generated
![]() $\mathbb {C}$
-algebra, let
$\mathbb {C}$
-algebra, let
![]() $\mathfrak {p}$
be a prime ideal of S, and let
$\mathfrak {p}$
be a prime ideal of S, and let
![]() $R\cong S_{\mathfrak {p}}$
.
$R\cong S_{\mathfrak {p}}$
.
-
(1) A family
 $R_p$
is said to be an approximation of R if
$R_p$
is said to be an approximation of R if
 $R_p$
is an
$R_p$
is an
 $\overline {\mathbb {F}_p}$
-algebra and
$\overline {\mathbb {F}_p}$
-algebra and
 $R_p \cong (S_p)_{\mathfrak {p}_p}$
for almost all p. Then we have
$R_p \cong (S_p)_{\mathfrak {p}_p}$
for almost all p. Then we have
 $R_\infty \cong \operatorname *{\mathrm {ulim}}_p R_p$
.
$R_\infty \cong \operatorname *{\mathrm {ulim}}_p R_p$
. -
(2) For an element
 $f\in R$
, a family
$f\in R$
, a family
 $f_p$
is said to be an approximation of f if
$f_p$
is said to be an approximation of f if
 $f_p\in R_p$
for almost all p and
$f_p\in R_p$
for almost all p and
 $f=\operatorname *{\mathrm {ulim}}_p f_p$
in
$f=\operatorname *{\mathrm {ulim}}_p f_p$
in
 $R_\infty $
. For
$R_\infty $
. For
 $f\in R_\infty $
, we define an approximation of f in the same way.
$f\in R_\infty $
, we define an approximation of f in the same way. -
(3) For an ideal
 $I=(f_1,\dots ,f_s) \subseteq R$
, a family
$I=(f_1,\dots ,f_s) \subseteq R$
, a family
 $I_p$
is said to be an approximation of I if
$I_p$
is said to be an approximation of I if
 $I_p$
is an ideal of
$I_p$
is an ideal of
 $R_p$
and
$R_p$
and
 $I_p=(f_{1p},\dots ,f_{sp})$
for almost all p. For finitely generated ideal
$I_p=(f_{1p},\dots ,f_{sp})$
for almost all p. For finitely generated ideal
 $I\subseteq R_\infty $
, we define an approximation of I in the same way.
$I\subseteq R_\infty $
, we define an approximation of I in the same way.
Definition 3.40. Let
![]() $S_1,S_2$
be finitely generated
$S_1,S_2$
be finitely generated
![]() $\mathbb {C}$
-algebras, and let
$\mathbb {C}$
-algebras, and let
![]() $\mathfrak {p}_1,\mathfrak {p}_2$
be prime ideals of
$\mathfrak {p}_1,\mathfrak {p}_2$
be prime ideals of
![]() $S_1,S_2,$
respectively. Suppose that
$S_1,S_2,$
respectively. Suppose that
![]() $R_i\cong (S_i)_{\mathfrak {p}_i}$
and
$R_i\cong (S_i)_{\mathfrak {p}_i}$
and
![]() $\varphi :R_1\to R_2$
is a local
$\varphi :R_1\to R_2$
is a local
![]() $\mathbb {C}$
-algebra homomorphism. Let
$\mathbb {C}$
-algebra homomorphism. Let
![]() $S_1\cong \mathbb {C}[X_1,\dots ,X_n]/I$
and
$S_1\cong \mathbb {C}[X_1,\dots ,X_n]/I$
and
![]() $f_j/g_j$
be the image of
$f_j/g_j$
be the image of
![]() $X_j$
under
$X_j$
under
![]() $\varphi $
, where
$\varphi $
, where
![]() $f_j\in S_2$
,
$f_j\in S_2$
,
![]() $g_j\in S_2\setminus \mathfrak {p}_2$
. Then we say that a homomorphism
$g_j\in S_2\setminus \mathfrak {p}_2$
. Then we say that a homomorphism
![]() $R_{1p}\to R_{2p}$
induced by
$R_{1p}\to R_{2p}$
induced by
![]() $X_j\longmapsto f_{jp}/g_{jp}$
is an approximation of
$X_j\longmapsto f_{jp}/g_{jp}$
is an approximation of
![]() $\varphi $
. Let
$\varphi $
. Let
![]() $\varphi _\infty :=\operatorname *{\mathrm {ulim}}_p \varphi _p$
. Then the following commutative diagram commutes:
$\varphi _\infty :=\operatorname *{\mathrm {ulim}}_p \varphi _p$
. Then the following commutative diagram commutes:

Definition 3.41. Let R be a finitely generated
![]() $\mathbb {C}$
-algebra or a local ring essentially of finite type over
$\mathbb {C}$
-algebra or a local ring essentially of finite type over
![]() $\mathbb {C}$
, and let M be a finitely generated R-module. Write M as the cokernel of a matrix A, that is, given by an exact sequence
$\mathbb {C}$
, and let M be a finitely generated R-module. Write M as the cokernel of a matrix A, that is, given by an exact sequence
where
![]() $m,n$
are positive integers. Let
$m,n$
are positive integers. Let
![]() $A_p$
be an approximation of A defined by entrywise approximations. Then the cokernel
$A_p$
be an approximation of A defined by entrywise approximations. Then the cokernel
![]() $M_p$
of the matrix
$M_p$
of the matrix
![]() $A_p$
is called an approximation of M and the ultraproduct
$A_p$
is called an approximation of M and the ultraproduct
![]() $M_\infty :=\operatorname *{\mathrm {ulim}}_p M_p$
is called the non-standard hull of M.
$M_\infty :=\operatorname *{\mathrm {ulim}}_p M_p$
is called the non-standard hull of M.
![]() $M_\infty $
is a finitely generated
$M_\infty $
is a finitely generated
![]() $R_\infty $
-module and independent of the choice of matrix A.
$R_\infty $
-module and independent of the choice of matrix A.
Remark 3.42. Tensoring the above exact sequence with
![]() $R_\infty $
, we have an exact sequence
$R_\infty $
, we have an exact sequence
Taking the ultraproduct of exact sequences
we have an exact sequence
Therefore,
![]() $M_\infty \cong M\otimes _R R_\infty $
. Note that if
$M_\infty \cong M\otimes _R R_\infty $
. Note that if
![]() $m,n$
are not integers but infinite cardinals, then the naive definition of an approximation of A does not work and the ultraproduct of
$m,n$
are not integers but infinite cardinals, then the naive definition of an approximation of A does not work and the ultraproduct of
![]() $R_p^{\oplus n}$
is not necessarily equal to
$R_p^{\oplus n}$
is not necessarily equal to
![]() $R_\infty ^{\oplus n}$
.
$R_\infty ^{\oplus n}$
.
Here, we state basic properties about non-standard hulls and approximations.
Proposition 3.43 [Reference Schoutens22, 2.9.5, 2.9.7, Ths. 4.5 and 4.6], [Reference Schoutens26, §4.3]; cf. [Reference Aschenbrenner and Schoutens2, 5.1].
Let R be a local ring essentially of finite type over
![]() $\mathbb {C}$
, then the following hold:
$\mathbb {C}$
, then the following hold:
-
(1) R has dimension d if and only if
 $R_p$
has dimension d for almost all p.
$R_p$
has dimension d for almost all p. -
(2)
 $\mathbf {x}=x_1,\dots ,x_i$
is an R-regular sequence if and only if
$\mathbf {x}=x_1,\dots ,x_i$
is an R-regular sequence if and only if
 $\mathbf {x}_p=x_{1p},\dots , x_{ip}$
is an
$\mathbf {x}_p=x_{1p},\dots , x_{ip}$
is an
 $R_p$
-regular sequence for almost all p if and only if
$R_p$
-regular sequence for almost all p if and only if
 $\mathbf {x}$
is an
$\mathbf {x}$
is an
 $R_\infty $
-regular sequence.
$R_\infty $
-regular sequence. -
(3)
 $\mathbf {x}=x_1,\dots ,x_d$
is a system of parameters of R if and only if
$\mathbf {x}=x_1,\dots ,x_d$
is a system of parameters of R if and only if
 $\mathbf {x}_p$
is a system of parameters of
$\mathbf {x}_p$
is a system of parameters of
 $R_p$
for almost all p.
$R_p$
for almost all p. -
(4) R is regular if and only if
 $R_p$
is regular for almost all p.
$R_p$
is regular for almost all p. -
(5) R is Gorenstein if and only if
 $R_p$
is Gorenstein for almost all p.
$R_p$
is Gorenstein for almost all p. -
(6) R is Cohen–Macaulay if and only if
 $R_p$
is Cohen–Macaulay for almost all p.
$R_p$
is Cohen–Macaulay for almost all p.
Proposition 3.44 [Reference Yamaguchi31, Prop. 3.9].
Let R be a local ring essentially of finite type over
![]() $\mathbb {C}$
. The following conditions are equivalent to each other.
$\mathbb {C}$
. The following conditions are equivalent to each other.
-
(1) R is normal.
-
(2)
 $R_p$
is normal for almost all p.
$R_p$
is normal for almost all p. -
(3)
 $R_\infty $
is normal.
$R_\infty $
is normal.
Definition 3.45. Let R be a normal local domain essentially of finite type over
![]() $\mathbb {C}$
, and let
$\mathbb {C}$
, and let
![]() $\Delta =\sum _i a_i\Delta _i$
be a
$\Delta =\sum _i a_i\Delta _i$
be a
![]() $\mathbb {Q}$
-Weil divisor. Assume that
$\mathbb {Q}$
-Weil divisor. Assume that
![]() $\Delta _i$
are prime divisors and
$\Delta _i$
are prime divisors and
![]() $\mathfrak {p}_i$
is a prime ideal associated with
$\mathfrak {p}_i$
is a prime ideal associated with
![]() $\Delta _i$
for each i. Suppose that
$\Delta _i$
for each i. Suppose that
![]() $\mathfrak {p}_{ip}$
is an approximation of
$\mathfrak {p}_{ip}$
is an approximation of
![]() $\mathfrak {p}_{i}$
and
$\mathfrak {p}_{i}$
and
![]() $\Delta _{ip}$
is a divisor associated with
$\Delta _{ip}$
is a divisor associated with
![]() $\mathfrak {p}_{ip}$
. We say
$\mathfrak {p}_{ip}$
. We say
![]() $\Delta _p:=\sum _i a_i\Delta _{ip}$
is an approximation of
$\Delta _p:=\sum _i a_i\Delta _{ip}$
is an approximation of
![]() $\Delta $
.
$\Delta $
.
Remark 3.46. If
![]() $\Delta $
is an effective integral divisor, then this definition is compatible with Definition 3.33 by [Reference Schoutens22, Th. 4.4]. Hence, if
$\Delta $
is an effective integral divisor, then this definition is compatible with Definition 3.33 by [Reference Schoutens22, Th. 4.4]. Hence, if
![]() $\Delta $
is
$\Delta $
is
![]() $\mathbb {Q}$
-Cartier, then
$\mathbb {Q}$
-Cartier, then
![]() $\Delta _p$
is
$\Delta _p$
is
![]() $\mathbb {Q}$
-Cartier for almost all p.
$\mathbb {Q}$
-Cartier for almost all p.
Lastly, we review some singularities introduced by Schoutens via ultraproducts.
Definition 3.47 [Reference Schoutens22, Def. 5.2], [Reference Schoutens25, Def. 3.1].
Suppose that R is a finitely generated
![]() $\mathbb {C}$
-algebra or a local domain essentially of finite type over
$\mathbb {C}$
-algebra or a local domain essentially of finite type over
![]() $\mathbb {C}$
. Let
$\mathbb {C}$
. Let
![]() $I\subseteq R$
be an ideal. The generic tight closure
$I\subseteq R$
be an ideal. The generic tight closure
![]() $I^{*\operatorname {gen}}$
of I is defined by
$I^{*\operatorname {gen}}$
of I is defined by
Remark 3.48. The generic tight closure
![]() $I^{*\operatorname {gen}}$
of I does not depend on the choice of approximation of I since any two approximations are almost equal.
$I^{*\operatorname {gen}}$
of I does not depend on the choice of approximation of I since any two approximations are almost equal.
Definition 3.49 [Reference Schoutens25, Def. 4.1 and Rem. 4.7], [Reference Schoutens23, Def. 4.3].
Suppose that R is a finitely generated
![]() $\mathbb {C}$
-algebra or a local ring essentially of finite type over
$\mathbb {C}$
-algebra or a local ring essentially of finite type over
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
-
(1) R is said to be weakly generically F-regular if
 $I^{*\operatorname {gen}}=I$
for any ideal
$I^{*\operatorname {gen}}=I$
for any ideal
 $I\subseteq R$
.
$I\subseteq R$
. -
(2) R is said to be generically F-regular if
 $R_{\mathfrak {p}}$
is weakly generically F-regular for any prime ideal
$R_{\mathfrak {p}}$
is weakly generically F-regular for any prime ideal
 $\mathfrak {p}\in \operatorname {Spec} R$
.
$\mathfrak {p}\in \operatorname {Spec} R$
. -
(3) Let R be a local ring essentially of finite type over
 $\mathbb {C}$
. R is said to be generically F-rational if
$\mathbb {C}$
. R is said to be generically F-rational if
 $I^{*\operatorname {gen}}=I$
for some ideal I generated by a system of parameters.
$I^{*\operatorname {gen}}=I$
for some ideal I generated by a system of parameters.
Proposition 3.50 [Reference Schoutens25, Th. 4.3].
If R is generically F-rational, then
![]() $I^{*\operatorname {gen}}=I$
for any ideal I generated by part of a system of parameters.
$I^{*\operatorname {gen}}=I$
for any ideal I generated by part of a system of parameters.
Proposition 3.51 [Reference Schoutens25, Th. 6.2], [Reference Schoutens23, Prop. 4.5 and Th. 4.12].
If R is generically F-rational if and only if
![]() $R_p$
is F-rational for almost all p if and only if R has rational singularities.
$R_p$
is F-rational for almost all p if and only if R has rational singularities.
Definition 3.52 [Reference Schoutens24, 3.2].
Let R be a local ring essentially of finite type over
![]() $\mathbb {C}$
and
$\mathbb {C}$
and
![]() $R_p$
be an approximation. Let
$R_p$
be an approximation. Let
![]() $\varepsilon :=\operatorname *{\mathrm {ulim}}_p e_p \in {^*\mathbb {N}}$
. Then an ultra-Frobenius
$\varepsilon :=\operatorname *{\mathrm {ulim}}_p e_p \in {^*\mathbb {N}}$
. Then an ultra-Frobenius
![]() $F^\varepsilon :R\to R_\infty $
associated with
$F^\varepsilon :R\to R_\infty $
associated with
![]() $\varepsilon $
is defined by
$\varepsilon $
is defined by
![]() $x\longmapsto \operatorname *{\mathrm {ulim}}_p (F_p^{e_p}(x_p))$
, where
$x\longmapsto \operatorname *{\mathrm {ulim}}_p (F_p^{e_p}(x_p))$
, where
![]() $F_p$
is a Frobenius morphism in characteristic p.
$F_p$
is a Frobenius morphism in characteristic p.
Definition 3.53 [Reference Schoutens24, Def. 3.3].
Let R be a local domain essentially of finite type over
![]() $\mathbb {C}$
. R is said to be ultra-F-regular if, for each
$\mathbb {C}$
. R is said to be ultra-F-regular if, for each
![]() $c\in R^{\circ }$
, there exists
$c\in R^{\circ }$
, there exists
![]() $\varepsilon \in {^*\mathbb {N}}$
such that
$\varepsilon \in {^*\mathbb {N}}$
such that
is pure.
Proposition 3.54 [Reference Schoutens24, Th. A].
Let R be a
![]() $\mathbb {Q}$
-Gorenstein normal local domain essentially of finite type over
$\mathbb {Q}$
-Gorenstein normal local domain essentially of finite type over
![]() $\mathbb {C}$
. Then R is ultra-F-regular if and only if R has log-terminal singularities.
$\mathbb {C}$
. Then R is ultra-F-regular if and only if R has log-terminal singularities.
3.3 Relative hulls
In this subsection, we introduce the concept of relative hulls and approximations of schemes, cohomologies, and so forth. We refer the reader to [Reference Schoutens22], [Reference Schoutens24], [Reference Schoutens25].
Definition 3.55 (Cf. [Reference Schoutens25]).
Let R be a local ring essentially of finite type over
![]() $\mathbb {C}$
. Suppose that X is a finite tuple of indeterminates and
$\mathbb {C}$
. Suppose that X is a finite tuple of indeterminates and
![]() $f\in R[X]$
is a polynomial such that
$f\in R[X]$
is a polynomial such that
![]() $f=\sum _{\nu } a_\nu X^\nu $
, where
$f=\sum _{\nu } a_\nu X^\nu $
, where
![]() $\nu $
is a multi-index. If
$\nu $
is a multi-index. If
![]() $a_{\nu p}$
is an approximation of
$a_{\nu p}$
is an approximation of
![]() $a_{\nu }$
for each
$a_{\nu }$
for each
![]() $\nu $
, then the sequence of polynomials
$\nu $
, then the sequence of polynomials
![]() $f_p:=\sum _\nu a_{\nu p} X^\nu $
is said to be an R-approximation of f. If
$f_p:=\sum _\nu a_{\nu p} X^\nu $
is said to be an R-approximation of f. If
![]() $I:=(f_1,\dots ,f_s)$
is an ideal in
$I:=(f_1,\dots ,f_s)$
is an ideal in
![]() $R[X]$
, then we call
$R[X]$
, then we call
![]() $I_{p}:=(f_{1p},\dots ,f_{sp})R_p[X]$
an R-approximation of I, and if
$I_{p}:=(f_{1p},\dots ,f_{sp})R_p[X]$
an R-approximation of I, and if
![]() $S=R[X]/I$
, then we call
$S=R[X]/I$
, then we call
![]() $S_p:=R_p[X]/I_p$
an R-approximation of S.
$S_p:=R_p[X]/I_p$
an R-approximation of S.
Remark 3.56. Any two R-approximations of a polynomial f are almost equal. Similarly, any two R-approximations of an ideal I are almost equal.
Definition 3.57 (Cf. [Reference Schoutens25]).
Let S be a finitely generated R-algebra, and let
![]() $S_p$
be an R-approximation of S, then we call
$S_p$
be an R-approximation of S, then we call
![]() $S_\infty =\operatorname *{\mathrm {ulim}} _p S_p$
the (relative) R-hull of S.
$S_\infty =\operatorname *{\mathrm {ulim}} _p S_p$
the (relative) R-hull of S.
Definition 3.58 (Cf. [Reference Schoutens24]).
If X is an affine scheme
![]() $\operatorname {Spec} S$
of finite type over
$\operatorname {Spec} S$
of finite type over
![]() $\operatorname {Spec} R$
, then we call
$\operatorname {Spec} R$
, then we call
![]() $X_p:=\operatorname {Spec} S_p$
is an R-approximation of X.
$X_p:=\operatorname {Spec} S_p$
is an R-approximation of X.
Definition 3.59 (Cf. [Reference Schoutens24]).
Suppose that
![]() $f:Y\to X$
is a morphism of affine schemes of finite type over
$f:Y\to X$
is a morphism of affine schemes of finite type over
![]() $\operatorname {Spec} R$
. If
$\operatorname {Spec} R$
. If
![]() $X=\operatorname {Spec} S, Y=\operatorname {Spec} T$
and
$X=\operatorname {Spec} S, Y=\operatorname {Spec} T$
and
![]() $\varphi :S\to T$
is the morphism corresponding to f, then we call
$\varphi :S\to T$
is the morphism corresponding to f, then we call
![]() $f_p:Y_p\to X_p$
is an R-approximation of f, where
$f_p:Y_p\to X_p$
is an R-approximation of f, where
![]() $f_p$
is a morphism of
$f_p$
is a morphism of
![]() $R_p$
-schemes induced by an R-approximation
$R_p$
-schemes induced by an R-approximation
![]() $\varphi _p:S_p\to T_p$
.
$\varphi _p:S_p\to T_p$
.
Definition 3.60 (Cf. [Reference Schoutens24]).
Let S be a finitely generated R-algebra, and let M be a finitely generated S-module. Write M as the cokernel of a matrix A, that is, given by an exact sequence
where
![]() $m,n$
are positive integers. Let
$m,n$
are positive integers. Let
![]() $A_p$
be an R-approximation of A defined by entrywise R-approximations. Then the cokernel
$A_p$
be an R-approximation of A defined by entrywise R-approximations. Then the cokernel
![]() $M_p$
of the matrix
$M_p$
of the matrix
![]() $A_p$
is called an R-approximation of M and the ultraproduct
$A_p$
is called an R-approximation of M and the ultraproduct
![]() $M_\infty :=\operatorname *{\mathrm {ulim}}_p M_p$
is called the R-hull of M.
$M_\infty :=\operatorname *{\mathrm {ulim}}_p M_p$
is called the R-hull of M.
![]() $M_\infty $
is independent of the choice of the matrix A and
$M_\infty $
is independent of the choice of the matrix A and
![]() $M_\infty \cong M\otimes _S S_\infty $
.
$M_\infty \cong M\otimes _S S_\infty $
.
Remark 3.61. If M is not finitely generated, then we cannot define an R-approximation of M in this way. It is crucial that any two R-approximations of A is equal for almost all p.
Definition 3.62 [Reference Schoutens24].
Let X be a scheme of finite type over
![]() $\operatorname {Spec} R$
. Let
$\operatorname {Spec} R$
. Let
![]() $\mathfrak {U}=\{U_i\}$
is a finite affine open covering of X and
$\mathfrak {U}=\{U_i\}$
is a finite affine open covering of X and
![]() $U_{ip}$
be an R-approximation of
$U_{ip}$
be an R-approximation of
![]() $U_i$
. Gluing
$U_i$
. Gluing
![]() $\{U_{ip}\}$
together, we obtain a scheme
$\{U_{ip}\}$
together, we obtain a scheme
![]() $X_p$
of finite type over
$X_p$
of finite type over
![]() $\operatorname {Spec} R_p$
. We call
$\operatorname {Spec} R_p$
. We call
![]() $X_p$
an R-approximation of X.
$X_p$
an R-approximation of X.
Remark 3.63. Suppose that
![]() $\{U_{ijk}\}_k$
is a finite affine open covering of
$\{U_{ijk}\}_k$
is a finite affine open covering of
![]() $U_i\cap U_j$
and
$U_i\cap U_j$
and
![]() $\varphi _{ijk}:\mathcal {O}_{U_i}|_{U_k}\cong \mathcal {O}_{U_j}|_{U_k}$
are isomorphisms. Then R-approximations
$\varphi _{ijk}:\mathcal {O}_{U_i}|_{U_k}\cong \mathcal {O}_{U_j}|_{U_k}$
are isomorphisms. Then R-approximations
![]() $\varphi _p:\mathcal {O}_{U_{ip}}|_{U_{kp}}\to \mathcal {O}_{U_{jp}}|_{U_{kp}}$
are isomorphisms for almost all p (note that indices
$\varphi _p:\mathcal {O}_{U_{ip}}|_{U_{kp}}\to \mathcal {O}_{U_{jp}}|_{U_{kp}}$
are isomorphisms for almost all p (note that indices
![]() $ijk$
are finitely many). Hence, we can glue these together. For any other choice of finite affine open covering
$ijk$
are finitely many). Hence, we can glue these together. For any other choice of finite affine open covering
![]() $\mathfrak {U}'$
of X, the resulting R-approximation
$\mathfrak {U}'$
of X, the resulting R-approximation
![]() $X^{\prime }_p$
is isomorphic to
$X^{\prime }_p$
is isomorphic to
![]() $X_p$
for almost all p.
$X_p$
for almost all p.
Definition 3.64 (Cf. [Reference Schoutens24]).
Suppose that
![]() $f:Y\to X$
is a morphism between schemes of finite type over
$f:Y\to X$
is a morphism between schemes of finite type over
![]() $\operatorname {Spec} R$
. Let
$\operatorname {Spec} R$
. Let
![]() $\mathfrak {U}$
,
$\mathfrak {U}$
,
![]() $\mathfrak {V}$
be finite affine open coverings of X and Y, respectively, such that for any
$\mathfrak {V}$
be finite affine open coverings of X and Y, respectively, such that for any
![]() $V\in \mathfrak {V}$
, there exists some
$V\in \mathfrak {V}$
, there exists some
![]() $U\in \mathfrak {U}$
such that
$U\in \mathfrak {U}$
such that
![]() $f(V)\subseteq U$
. Let
$f(V)\subseteq U$
. Let
![]() $\mathfrak {U}_p$
,
$\mathfrak {U}_p$
,
![]() $\mathfrak {V}_p$
be R-approximations of
$\mathfrak {V}_p$
be R-approximations of
![]() $\mathfrak {U}$
,
$\mathfrak {U}$
,
![]() $\mathfrak {V}$
and
$\mathfrak {V}$
and
![]() $(f|_V)_p$
an R-approximation of
$(f|_V)_p$
an R-approximation of
![]() $f|_V$
. We define an R-approximation
$f|_V$
. We define an R-approximation
![]() $f_p$
of f by the morphism determined by
$f_p$
of f by the morphism determined by
![]() $(f|V)_p$
.
$(f|V)_p$
.
Remark 3.65. In the same way as the above Remark 3.63,
![]() $(f|_V)_p$
and
$(f|_V)_p$
and
![]() $(f|_{V'})_p$
agree on
$(f|_{V'})_p$
agree on
![]() $V\cap V'$
for any two opens
$V\cap V'$
for any two opens
![]() $V,V'\in \mathfrak {V}$
for almost all p.
$V,V'\in \mathfrak {V}$
for almost all p.
Definition 3.66 (Cf. [Reference Schoutens24]).
Let X be a scheme of finite type over
![]() $\operatorname {Spec} R$
, and let
$\operatorname {Spec} R$
, and let
![]() $\mathcal {F}$
be a coherent
$\mathcal {F}$
be a coherent
![]() $\mathcal {O}_X$
-module. Let
$\mathcal {O}_X$
-module. Let
![]() $\mathfrak {U}$
be a finite affine open covering of X. For any
$\mathfrak {U}$
be a finite affine open covering of X. For any
![]() $U\in \mathfrak {U}$
, we have an R-approximation
$U\in \mathfrak {U}$
, we have an R-approximation
![]() $M_{Up}$
of
$M_{Up}$
of
![]() $M_{U}$
such that
$M_{U}$
such that
![]() $M_{U}$
is a finitely generated
$M_{U}$
is a finitely generated
![]() $\mathcal {O}_U$
-module and
$\mathcal {O}_U$
-module and
![]() $\widetilde {M_U}\cong \mathcal {F}|_U$
. We define an R-approximation
$\widetilde {M_U}\cong \mathcal {F}|_U$
. We define an R-approximation
![]() $\mathcal {F}_p$
of
$\mathcal {F}_p$
of
![]() $\mathcal {F}$
by the coherent
$\mathcal {F}$
by the coherent
![]() $\mathcal {O}_{X_p}$
-module determined by
$\mathcal {O}_{X_p}$
-module determined by
![]() $\widetilde {M_{Up}}$
.
$\widetilde {M_{Up}}$
.
Definition 3.67 (Cf. [Reference Schoutens24]).
Let X be a separated scheme of finite type over
![]() $\operatorname {Spec} R$
, and let
$\operatorname {Spec} R$
, and let
![]() $\mathcal {F}$
be a coherent
$\mathcal {F}$
be a coherent
![]() $\mathcal {O}_X$
-module. Then the ultra-cohomology of
$\mathcal {O}_X$
-module. Then the ultra-cohomology of
![]() $\mathcal {F}$
is defined by
$\mathcal {F}$
is defined by
Remark 3.68. In the above setting, let
![]() $\mathfrak {U}=\{U_i\}_{i=1,\dots ,n}$
be a finite affine open covering of X, let
$\mathfrak {U}=\{U_i\}_{i=1,\dots ,n}$
be a finite affine open covering of X, let
 $$ \begin{align*} C^j(\mathfrak{U}, \mathcal{F}):=\prod_{i_0<\dots<i_j}\mathcal{F}(U_{i_0\dots i_j}), \end{align*} $$
$$ \begin{align*} C^j(\mathfrak{U}, \mathcal{F}):=\prod_{i_0<\dots<i_j}\mathcal{F}(U_{i_0\dots i_j}), \end{align*} $$
where
![]() $U_{i_0\dots i_j}:=U_{i_0}\cap \dots \cap U_{i_j}$
, and let
$U_{i_0\dots i_j}:=U_{i_0}\cap \dots \cap U_{i_j}$
, and let
 $$ \begin{align*} (C^j(\mathfrak{U},\mathcal{F}))_p:=\prod_{i_0\dots i_j}(\mathcal{F}(U_{i_0\dots i_j}))_p, \end{align*} $$
$$ \begin{align*} (C^j(\mathfrak{U},\mathcal{F}))_p:=\prod_{i_0\dots i_j}(\mathcal{F}(U_{i_0\dots i_j}))_p, \end{align*} $$
where
![]() $\mathcal {F}(U_{i_0\dots i_j})_p$
is an R-approximation considered as
$\mathcal {F}(U_{i_0\dots i_j})_p$
is an R-approximation considered as
![]() $\mathcal {O}(U_{i_0\dots i_j})$
-module. Then
$\mathcal {O}(U_{i_0\dots i_j})$
-module. Then
coincides with the jth term of the Čech complex of
![]() $X_p$
,
$X_p$
,
![]() $\mathfrak {U}_p,$
and
$\mathfrak {U}_p,$
and
![]() $\mathcal {F}_p$
. We have a commutative diagram
$\mathcal {F}_p$
. We have a commutative diagram

Since
![]() $\operatorname *{\mathrm {ulim}}_p (\text{-})$
is an exact functor, we have
$\operatorname *{\mathrm {ulim}}_p (\text{-})$
is an exact functor, we have
If X is separated, then
![]() $X_p$
is separated for almost all p. This can be checked by taking a finite affine open covering and observing that if the diagonal morphism
$X_p$
is separated for almost all p. This can be checked by taking a finite affine open covering and observing that if the diagonal morphism
![]() $\Delta _{X/\operatorname {Spec} R}$
is a closed immersion, then
$\Delta _{X/\operatorname {Spec} R}$
is a closed immersion, then
![]() $\Delta _{X_p/\operatorname {Spec} R_p}$
is also a closed immersion for almost all p. Hence, we have the map
$\Delta _{X_p/\operatorname {Spec} R_p}$
is also a closed immersion for almost all p. Hence, we have the map
Note that we do not know whether this map is injective or not.
Proposition 3.69. Let R be a local ring essentially of finite type over
![]() $\mathbb {C}$
of dimension d,
$\mathbb {C}$
of dimension d,
![]() $\mathbf {x}=x_1,\dots ,x_d$
a system of parameters and M a finitely generated R-module. Then we have a natural homomorphism
$\mathbf {x}=x_1,\dots ,x_d$
a system of parameters and M a finitely generated R-module. Then we have a natural homomorphism
![]() $H_{\mathfrak {m}}^d(M)\to \operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}_p}^d(M_p)$
.
$H_{\mathfrak {m}}^d(M)\to \operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}_p}^d(M_p)$
.
Proof. Since
![]() $M_{x_1\cdots \hat {x_i}\cdots x_d}$
is a finitely generated
$M_{x_1\cdots \hat {x_i}\cdots x_d}$
is a finitely generated
![]() $R_{x_1\cdots \hat {x_i}\cdots x_d}$
-module and
$R_{x_1\cdots \hat {x_i}\cdots x_d}$
-module and
![]() $M_{x_1\cdots x_d}$
is a finitely generated
$M_{x_1\cdots x_d}$
is a finitely generated
![]() $R_{x_1\cdots x_d}$
-module, we have an R-approximation
$R_{x_1\cdots x_d}$
-module, we have an R-approximation
![]() $(M_{x_1\cdots \hat {x_1}\cdots x_d})_p\cong (M_p)_{x_{1p}\cdots \hat {x_{ip}}\cdots x_{dp}}$
and
$(M_{x_1\cdots \hat {x_1}\cdots x_d})_p\cong (M_p)_{x_{1p}\cdots \hat {x_{ip}}\cdots x_{dp}}$
and
![]() $(M_{x_1\cdots x_d})_p\cong (M_p)_{x_{1p}\cdots x_{dp}}$
for almost all p. We have a commutative diagram
$(M_{x_1\cdots x_d})_p\cong (M_p)_{x_{1p}\cdots x_{dp}}$
for almost all p. We have a commutative diagram

Taking the cokernel of rows, we have the desired map.
Remark 3.70. We do not know whether
![]() $H_{\mathfrak {m}}^d(M)\to \operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}_p}^d(M_p)$
is injective or not.
$H_{\mathfrak {m}}^d(M)\to \operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}_p}^d(M_p)$
is injective or not.
Proposition 3.71. Let R be a local ring essentially of finite type over
![]() $\mathbb {C}$
of dimension d,
$\mathbb {C}$
of dimension d,
![]() $\mathbf {x}=x_,\dots ,x_d$
be a system of parameters and
$\mathbf {x}=x_,\dots ,x_d$
be a system of parameters and
![]() $M_p$
be an
$M_p$
be an
![]() $R_p$
-module for almost all p. Then we have a natural homomorphism
$R_p$
-module for almost all p. Then we have a natural homomorphism
![]() $H_{\mathfrak {m}}^d(\operatorname *{\mathrm {ulim}}_p M_p)\to \operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}}^d(M_p)$
.
$H_{\mathfrak {m}}^d(\operatorname *{\mathrm {ulim}}_p M_p)\to \operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}}^d(M_p)$
.
Proof. We have a commutative diagram

Taking the cokernel of rows, we have the desired map.
4 Big Cohen–Macaulay algebras constructed via ultraproducts
In [Reference Schoutens23], Schoutens constructed the canonical BCM algebra in characteristic zero. Following the idea of [Reference Schoutens23], we will deal with BCM algebras constructed via ultraproducts in slightly general settings. In this section, suppose that
![]() $(R,\mathfrak {m})$
is a local domain essentially of finite type over
$(R,\mathfrak {m})$
is a local domain essentially of finite type over
![]() $\mathbb {C}$
and
$\mathbb {C}$
and
![]() $R_p$
is an approximation of R.
$R_p$
is an approximation of R.
Definition 4.1 [Reference Schoutens23, §2].
Suppose that R is a local domain essentially of finite type over
![]() $\mathbb {C}$
. Then we define the canonical BCM algebra
$\mathbb {C}$
. Then we define the canonical BCM algebra
![]() $\mathcal {B}(R)$
of R by
$\mathcal {B}(R)$
of R by
Setting 4.2. Let R be a local domain essentially of finite type over
![]() $\mathbb {C}$
of dimension d, and let
$\mathbb {C}$
of dimension d, and let
![]() $B_p$
be a BCM
$B_p$
be a BCM
![]() ${R_p}^+$
-algebra for almost all p. We use B to denote
${R_p}^+$
-algebra for almost all p. We use B to denote
![]() $\operatorname *{\mathrm {ulim}}_p B_p$
.
$\operatorname *{\mathrm {ulim}}_p B_p$
.
Proposition 4.4.
![]() $\mathcal {B}(R)$
is a domain over
$\mathcal {B}(R)$
is a domain over
![]() $R^+$
-algebra.
$R^+$
-algebra.
Proof. By Łoś’s theorem,
![]() $\mathcal {B}(R)$
is a domain over
$\mathcal {B}(R)$
is a domain over
![]() $R_\infty =\operatorname *{\mathrm {ulim}}_p R_p$
. Hence,
$R_\infty =\operatorname *{\mathrm {ulim}}_p R_p$
. Hence,
![]() $\mathcal {B}(R)$
is an R-algebra. Let
$\mathcal {B}(R)$
is an R-algebra. Let
![]() $f=\sum a_{n} x^n\in \mathcal {B}(R)[x]$
be a monic polynomial in one variable over
$f=\sum a_{n} x^n\in \mathcal {B}(R)[x]$
be a monic polynomial in one variable over
![]() $\mathcal {B}(R)$
and let
$\mathcal {B}(R)$
and let
![]() $f_p=\sum a_{np}x^n$
be an approximation of f. Since
$f_p=\sum a_{np}x^n$
be an approximation of f. Since
![]() $f_p$
is a monic polynomial for almost all p and
$f_p$
is a monic polynomial for almost all p and
![]() $R_p^+$
is absolutely integrally closed,
$R_p^+$
is absolutely integrally closed,
![]() $f_p$
has a root
$f_p$
has a root
![]() $c_p$
in
$c_p$
in
![]() $R_p^+$
for almost all p. Hence,
$R_p^+$
for almost all p. Hence,
![]() $c:=\operatorname *{\mathrm {ulim}}_p c_p\in \mathcal {B}(R)$
is a root of f by Łoś’s theorem. Hence,
$c:=\operatorname *{\mathrm {ulim}}_p c_p\in \mathcal {B}(R)$
is a root of f by Łoś’s theorem. Hence,
![]() $\mathcal {B}(R)$
is absolutely integrally closed. In particular,
$\mathcal {B}(R)$
is absolutely integrally closed. In particular,
![]() $\mathcal {B}(R)$
contains an absolute integral closure
$\mathcal {B}(R)$
contains an absolute integral closure
![]() $R^+$
of R.
$R^+$
of R.
Corollary 4.5. In Setting 4.2, B is an
![]() $R^+$
-algebra.
$R^+$
-algebra.
Proof. Since
![]() $B_p$
is an
$B_p$
is an
![]() $R_p^+$
-algebra for almost all p, B is an
$R_p^+$
-algebra for almost all p, B is an
![]() $R^+$
-algebra by the above proposition.
$R^+$
-algebra by the above proposition.
Proposition 4.6. In Setting 4.2, B is a BCM R-algebra.
Proof. Assume that B is not a BCM R-algebra. Since
![]() $B_p\neq \mathfrak {m}_p B_p$
for almost all p, we have
$B_p\neq \mathfrak {m}_p B_p$
for almost all p, we have
![]() $B\neq \mathfrak {m} B$
. Hence, there exists part of system of parameters
$B\neq \mathfrak {m} B$
. Hence, there exists part of system of parameters
![]() $x_1,\dots ,x_i$
of R such that
$x_1,\dots ,x_i$
of R such that
![]() $(x_1,\dots ,x_{i-1})B\subsetneq (x_1,\dots ,x_{i-1})B:_B x_i$
. Then there exists
$(x_1,\dots ,x_{i-1})B\subsetneq (x_1,\dots ,x_{i-1})B:_B x_i$
. Then there exists
![]() $y\in B$
such that
$y\in B$
such that
![]() $x_i y\in (x_1,\dots ,x_{i-1})B$
and
$x_i y\in (x_1,\dots ,x_{i-1})B$
and
![]() $y\notin (x_1,\dots ,x_{i-1})B$
. Taking approximations, we have
$y\notin (x_1,\dots ,x_{i-1})B$
. Taking approximations, we have
![]() $x_{ip}y_p\in (x_{1p},\dots ,x_{(i-1)p})B_p$
and
$x_{ip}y_p\in (x_{1p},\dots ,x_{(i-1)p})B_p$
and
![]() $y_p\notin (x_{1p}\dots ,x_{(i-1)p})B_p$
for almost all p. Since
$y_p\notin (x_{1p}\dots ,x_{(i-1)p})B_p$
for almost all p. Since
![]() $x_{1p},\dots ,x_{ip}$
is part of a system of parameters of
$x_{1p},\dots ,x_{ip}$
is part of a system of parameters of
![]() $R_p$
and
$R_p$
and
![]() $B_p$
is a BCM
$B_p$
is a BCM
![]() $R_p$
-algebra for almost all p,
$R_p$
-algebra for almost all p,
![]() $x_{1p},\dots ,x_{ip}$
is a regular sequence for almost all p. This is a contradiction. Therefore, B is a BCM R-algebra.
$x_{1p},\dots ,x_{ip}$
is a regular sequence for almost all p. This is a contradiction. Therefore, B is a BCM R-algebra.
Lemma 4.7. In Setting 4.2, the natural homomorphism
![]() $H_{\mathfrak {m}}^d(B)\to \operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}_p}^d(B_p)$
is injective.
$H_{\mathfrak {m}}^d(B)\to \operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}_p}^d(B_p)$
is injective.
Proof. Let
![]() $x=x_1\cdots x_d$
be the product of a system of parameters and
$x=x_1\cdots x_d$
be the product of a system of parameters and
![]() $\lbrack \frac {z}{x^t}\rbrack $
be an element of
$\lbrack \frac {z}{x^t}\rbrack $
be an element of
![]() $H_{\mathfrak {m}}^d(B)$
such that the image in
$H_{\mathfrak {m}}^d(B)$
such that the image in
![]() $\operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}_p}^d(B_p)$
is zero. Then there exists
$\operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}_p}^d(B_p)$
is zero. Then there exists
![]() $s_p\in \mathbb {N}$
such that
$s_p\in \mathbb {N}$
such that
![]() $x^{s_p}z\in (x_{1p}^{s_p+t},\dots ,x_{dp}^{s_p+t})B_p$
for almost all p. Since
$x^{s_p}z\in (x_{1p}^{s_p+t},\dots ,x_{dp}^{s_p+t})B_p$
for almost all p. Since
![]() $B_p$
is a BCM
$B_p$
is a BCM
![]() $R_p$
-algebra for almost all p,
$R_p$
-algebra for almost all p,
![]() $z\in (x_{1p}^t,\dots ,x_{dp}^t)B_p$
for almost all p. Hence,
$z\in (x_{1p}^t,\dots ,x_{dp}^t)B_p$
for almost all p. Hence,
![]() $z\in (x_1^t,\dots ,x_d^t)B$
and
$z\in (x_1^t,\dots ,x_d^t)B$
and
![]() $\lbrack \frac {z}{x^t} \rbrack =0$
in
$\lbrack \frac {z}{x^t} \rbrack =0$
in
![]() $H_{\mathfrak {m}}^d(B)$
.
$H_{\mathfrak {m}}^d(B)$
.
We generalize [Reference Schoutens23, Th. 4.2] to the cases other than the canonical BCM algebra.
Proposition 4.8 (Cf. [Reference Schoutens23, Th. 4.2], [Reference Ma and Schwede19, Prop. 3.7]).
In Setting 4.2, R is
![]() $\text {BCM}_B$
-rational if and only if R has rational singularities. In particular, R has rational singularities if R is BCM-rational.
$\text {BCM}_B$
-rational if and only if R has rational singularities. In particular, R has rational singularities if R is BCM-rational.
Proof. Let
![]() $x:=x_1\cdots x_d$
is the product of a system of parameters. Suppose that R has rational singularities. By [Reference Schoutens23, Prop. 4.11] and [Reference Hara9],
$x:=x_1\cdots x_d$
is the product of a system of parameters. Suppose that R has rational singularities. By [Reference Schoutens23, Prop. 4.11] and [Reference Hara9],
![]() $R_p$
is F-rational for almost all p. Let
$R_p$
is F-rational for almost all p. Let
![]() $\eta :=\lbrack \frac {z}{x^t} \rbrack $
be an element of
$\eta :=\lbrack \frac {z}{x^t} \rbrack $
be an element of
![]() $H_{\mathfrak {m}}^d(R)$
such that
$H_{\mathfrak {m}}^d(R)$
such that
![]() $\eta =0$
in
$\eta =0$
in
![]() $H_{\mathfrak {m}}^d(B)$
. Then we have a commutative diagram
$H_{\mathfrak {m}}^d(B)$
. Then we have a commutative diagram

By [Reference Ma and Schwede19, Prop. 3.5],
![]() $H_{\mathfrak {m}_p}^d(R_p)\to H_{\mathfrak {m}_p}^d(B_p)$
is injective for almost all p. Hence,
$H_{\mathfrak {m}_p}^d(R_p)\to H_{\mathfrak {m}_p}^d(B_p)$
is injective for almost all p. Hence,
![]() $\operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}_p}^d(R_p)\to \operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}_p}^d(B_p)$
is injective. Therefore,
$\operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}_p}^d(R_p)\to \operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}_p}^d(B_p)$
is injective. Therefore,
![]() $\lbrack \frac {z_p}{x_p^t}\rbrack =0$
in
$\lbrack \frac {z_p}{x_p^t}\rbrack =0$
in
![]() $H_{\mathfrak {m}_p}^d(R_p)$
for almost all p. Since
$H_{\mathfrak {m}_p}^d(R_p)$
for almost all p. Since
![]() $R_p$
is Cohen–Macaulay for almost all p, we have
$R_p$
is Cohen–Macaulay for almost all p, we have
![]() $z_p\in (x_{1p}^t,\dots ,x_{dp}^t)$
for almost all p. Hence,
$z_p\in (x_{1p}^t,\dots ,x_{dp}^t)$
for almost all p. Hence,
![]() $z\in (x_1^t,\dots ,x_d^t)$
by Łoś’s theorem. Therefore,
$z\in (x_1^t,\dots ,x_d^t)$
by Łoś’s theorem. Therefore,
![]() $H_{\mathfrak {m}}^d(R)\to H_{\mathfrak {m}}^d(B)$
is injective. Conversely, suppose that R is
$H_{\mathfrak {m}}^d(R)\to H_{\mathfrak {m}}^d(B)$
is injective. Conversely, suppose that R is
![]() $\text {BCM}_B$
-rational. Let
$\text {BCM}_B$
-rational. Let
![]() $I=(x_1,\dots ,x_d)$
be an ideal generated by the system of parameters. Let
$I=(x_1,\dots ,x_d)$
be an ideal generated by the system of parameters. Let
![]() $z\in I^{*\operatorname {gen}}$
. Since
$z\in I^{*\operatorname {gen}}$
. Since
![]() $I_p^*\subseteq I_pB_p\cap R_p$
by [Reference Smith27, Th. 5.1] for almost all p, we have
$I_p^*\subseteq I_pB_p\cap R_p$
by [Reference Smith27, Th. 5.1] for almost all p, we have
![]() $\lbrack \frac {z_p}{x_p}\rbrack =0$
in
$\lbrack \frac {z_p}{x_p}\rbrack =0$
in
![]() $H_{\mathfrak {m}_p}^d(B_p)$
for almost all p. Since
$H_{\mathfrak {m}_p}^d(B_p)$
for almost all p. Since
![]() $H_{\mathfrak {m}}^d(B)\to \operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}_p}^d(B_p)$
and
$H_{\mathfrak {m}}^d(B)\to \operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}_p}^d(B_p)$
and
![]() $H_{\mathfrak {m}}^d(R)\to H_{\mathfrak {m}}^d(B)$
are injective, we have
$H_{\mathfrak {m}}^d(R)\to H_{\mathfrak {m}}^d(B)$
are injective, we have
![]() $\lbrack \frac {z}{x}\rbrack =0$
in
$\lbrack \frac {z}{x}\rbrack =0$
in
![]() $H_{\mathfrak {m}}^d(R)$
. Since R is Cohen–Macaulay,
$H_{\mathfrak {m}}^d(R)$
. Since R is Cohen–Macaulay,
![]() $z\in I$
. Therefore, R is generically F-rational. By Proposition 3.51 (see [Reference Schoutens25, Th. 6.2]), R has rational singularities.
$z\in I$
. Therefore, R is generically F-rational. By Proposition 3.51 (see [Reference Schoutens25, Th. 6.2]), R has rational singularities.
5 Approximations of multiplier ideals
In this section, we will explain the relationship between approximations and reductions modulo
![]() $p\gg 0$
. Note that an isomorphism
$p\gg 0$
. Note that an isomorphism
![]() $\operatorname *{\mathrm {ulim}}_p \overline {\mathbb {F}_p}\cong \mathbb {C}$
is fixed.
$\operatorname *{\mathrm {ulim}}_p \overline {\mathbb {F}_p}\cong \mathbb {C}$
is fixed.
Definition 5.1. Let R be a finitely generated
![]() $\mathbb {C}$
-algebra. A pair
$\mathbb {C}$
-algebra. A pair
![]() $(A,R_A)$
is called a model of R if the following two conditions hold:
$(A,R_A)$
is called a model of R if the following two conditions hold:
-
(i)
 $A \subseteq \mathbb {C}$
is a finitely generated
$A \subseteq \mathbb {C}$
is a finitely generated
 $\mathbb {Z}$
-subalgebra.
$\mathbb {Z}$
-subalgebra. -
(ii)
 $R_A$
is a finitely generated A-algebra such that
$R_A$
is a finitely generated A-algebra such that
 $R_A\otimes _A\mathbb {C}\cong R$
.
$R_A\otimes _A\mathbb {C}\cong R$
.
Proposition 5.2 [Reference Schoutens23, Lem. 4.10].
Let A be a finitely generated
![]() $\mathbb {Z}$
-subalgebra of
$\mathbb {Z}$
-subalgebra of
![]() $\mathbb {C}$
. There exists a family
$\mathbb {C}$
. There exists a family
![]() $(\gamma _p)_p$
which satisfies the following two conditions:
$(\gamma _p)_p$
which satisfies the following two conditions:
-
(i)
 $\gamma _p:A\to \overline {\mathbb {F}_p}$
is a ring homomorphism for almost all p.
$\gamma _p:A\to \overline {\mathbb {F}_p}$
is a ring homomorphism for almost all p. -
(ii) For any
 $x\in A$
,
$x\in A$
,
 $x=\operatorname *{\mathrm {ulim}}_p\gamma _p(x)$
.
$x=\operatorname *{\mathrm {ulim}}_p\gamma _p(x)$
.
Proposition 5.3 (Cf. [Reference Schoutens23, Cor. 4.10]).
Let R be a finitely generated
![]() $\mathbb {C}$
-algebra, and let
$\mathbb {C}$
-algebra, and let
![]() $\mathbf {a}=a_1,\dots , a_l$
be finitely many elements of R. Let
$\mathbf {a}=a_1,\dots , a_l$
be finitely many elements of R. Let
![]() $R_p$
be an approximation of R. Then there exists a model
$R_p$
be an approximation of R. Then there exists a model
![]() $(A,R_A)$
which satisfies the following conditions:
$(A,R_A)$
which satisfies the following conditions:
-
(i) There exists a family
 $(\gamma _p)$
as in Proposition 5.2.
$(\gamma _p)$
as in Proposition 5.2. -
(ii)
 $\mathbf {a}\subseteq R_A$
.
$\mathbf {a}\subseteq R_A$
. -
(iii)
 $R_A\otimes _A \overline {\mathbb {F}_p}\cong R_p$
for almost all p.
$R_A\otimes _A \overline {\mathbb {F}_p}\cong R_p$
for almost all p. -
(iv) For any
 $x\in R_A$
, the ultraproduct of the image of x under
$x\in R_A$
, the ultraproduct of the image of x under
 $\operatorname {id}_{R_A}\otimes _A \gamma _p$
is x.
$\operatorname {id}_{R_A}\otimes _A \gamma _p$
is x.
Proof. Let
![]() $X=X_1,\dots ,X_n$
and
$X=X_1,\dots ,X_n$
and
![]() $R\cong \mathbb {C}[X]/I$
for some ideal
$R\cong \mathbb {C}[X]/I$
for some ideal
![]() $I\subseteq \mathbb {C}[X]$
. Take any model
$I\subseteq \mathbb {C}[X]$
. Take any model
![]() $(A,R_A)$
which contains
$(A,R_A)$
which contains
![]() $\mathbf {a}$
. Enlarging this model, we may assume that there exits an ideal
$\mathbf {a}$
. Enlarging this model, we may assume that there exits an ideal
![]() $I_A\subseteq A[X]$
such that
$I_A\subseteq A[X]$
such that
![]() $R_A\cong A[X]/I_A$
and
$R_A\cong A[X]/I_A$
and
![]() $I_A\otimes _A \mathbb {C}=I$
in
$I_A\otimes _A \mathbb {C}=I$
in
![]() $\mathbb {C}[X]$
. Take
$\mathbb {C}[X]$
. Take
![]() $(\gamma _p)$
as in Proposition 5.2. Let
$(\gamma _p)$
as in Proposition 5.2. Let
![]() $I=(f_1,\dots , f_m)$
. For
$I=(f_1,\dots , f_m)$
. For
![]() $f=\sum _\nu c_\nu X^\nu \in A[X]\subseteq \mathbb {C}[X]$
, by the definition of approximations,
$f=\sum _\nu c_\nu X^\nu \in A[X]\subseteq \mathbb {C}[X]$
, by the definition of approximations,
![]() $f_p:=\sum _\nu \gamma _p(c_\nu )X^\nu \in \overline {\mathbb {F}_p}[X]$
is an approximation of f. Hence, by the definition of approximations of finitely generated
$f_p:=\sum _\nu \gamma _p(c_\nu )X^\nu \in \overline {\mathbb {F}_p}[X]$
is an approximation of f. Hence, by the definition of approximations of finitely generated
![]() $\mathbb {C}$
-algebras,
$\mathbb {C}$
-algebras,
![]() $R_A\otimes _A\overline {\mathbb {F}_p}\cong \overline {\mathbb {F}_p}[X]/(f_{1p},\dots ,f_{mp})\overline {\mathbb {F}_p}[X]$
is an approximation of R. Since two approximations are isomorphic for almost all p,
$R_A\otimes _A\overline {\mathbb {F}_p}\cong \overline {\mathbb {F}_p}[X]/(f_{1p},\dots ,f_{mp})\overline {\mathbb {F}_p}[X]$
is an approximation of R. Since two approximations are isomorphic for almost all p,
![]() $R_A\otimes _A\overline {\mathbb {F}_p}\cong R_p$
for almost all p. The condition (iv) is clear by the above argument.
$R_A\otimes _A\overline {\mathbb {F}_p}\cong R_p$
for almost all p. The condition (iv) is clear by the above argument.
Remark 5.4. Let
![]() $\mathfrak {p} =(x_1,\dots ,x_n) \subseteq R$
be a prime ideal. Enlarging the model
$\mathfrak {p} =(x_1,\dots ,x_n) \subseteq R$
be a prime ideal. Enlarging the model
![]() $(A,R_A)$
, we may assume that
$(A,R_A)$
, we may assume that
![]() $x_1,\dots ,x_n\in R_A$
. Let
$x_1,\dots ,x_n\in R_A$
. Let
![]() $\mu _p$
be the kernel of
$\mu _p$
be the kernel of
![]() $\gamma _p:A\to \overline {\mathbb {F}_p}$
. Then this is a maximal ideal of A and
$\gamma _p:A\to \overline {\mathbb {F}_p}$
. Then this is a maximal ideal of A and
![]() $A/\mu _p$
is a finite field.
$A/\mu _p$
is a finite field.
![]() $\mathfrak {p}_{\mu _p}=(x_1,\dots ,x_n) R_A/\mu _p R_A $
is prime for almost all p since this is a reduction to
$\mathfrak {p}_{\mu _p}=(x_1,\dots ,x_n) R_A/\mu _p R_A $
is prime for almost all p since this is a reduction to
![]() $p\gg 0$
. On the other hand,
$p\gg 0$
. On the other hand,
![]() $\mathfrak {p}_p:=(x_1,\dots ,x_n)R_A\otimes _A\overline {\mathbb {F}_p}\subseteq R_p$
is an approximation of
$\mathfrak {p}_p:=(x_1,\dots ,x_n)R_A\otimes _A\overline {\mathbb {F}_p}\subseteq R_p$
is an approximation of
![]() $\mathfrak {p}$
. Hence,
$\mathfrak {p}$
. Hence,
![]() $\mathfrak {p}_p$
is prime for almost all p. Here,
$\mathfrak {p}_p$
is prime for almost all p. Here,
![]() $(R_p)_{\mathfrak {p}_p}$
is an approximation of
$(R_p)_{\mathfrak {p}_p}$
is an approximation of
![]() $R_{\mathfrak {p}}$
. Thus we have a flat local homomorphism
$R_{\mathfrak {p}}$
. Thus we have a flat local homomorphism
![]() $(R_A/\mu _p R_A)_{\mathfrak {p}_{\mu _p}}\to R_p$
with
$(R_A/\mu _p R_A)_{\mathfrak {p}_{\mu _p}}\to R_p$
with
![]() $\mathfrak {p}_{\mu _p}R_p=\mathfrak {p}_p$
. Moreover, if
$\mathfrak {p}_{\mu _p}R_p=\mathfrak {p}_p$
. Moreover, if
![]() $\mathfrak {p}$
is maximal, then
$\mathfrak {p}$
is maximal, then
![]() $\mathfrak {p}_{\mu _p},\mathfrak {p}_p$
are maximal for almost all p. Then, the map
$\mathfrak {p}_{\mu _p},\mathfrak {p}_p$
are maximal for almost all p. Then, the map
![]() $R_A/\mathfrak {p}_{\mu _p}\to R_p/\mathfrak {p}_p\cong \overline {\mathbb {F}_p}$
is a separable field extension since
$R_A/\mathfrak {p}_{\mu _p}\to R_p/\mathfrak {p}_p\cong \overline {\mathbb {F}_p}$
is a separable field extension since
![]() $R_A/\mathfrak {p}_{\mu _p}$
is a finite field.
$R_A/\mathfrak {p}_{\mu _p}$
is a finite field.
The next result is a generalization of [Reference Yamaguchi31, Th. 4.6] from ideal pairs to triples.
Proposition 5.5. Let R be a normal local domain essentially of finite type over
![]() $\mathbb {C}$
, let
$\mathbb {C}$
, let
![]() $\Delta \geqslant 0$
be an effective
$\Delta \geqslant 0$
be an effective
![]() $\mathbb {Q}$
-Weil divisor such that
$\mathbb {Q}$
-Weil divisor such that
![]() $K_R+\Delta $
is
$K_R+\Delta $
is
![]() $\mathbb {Q}$
-Cartier, let
$\mathbb {Q}$
-Cartier, let
![]() $\mathfrak {a}$
be a nonzero ideal, and let
$\mathfrak {a}$
be a nonzero ideal, and let
![]() $t>0$
be a real number. Suppose that
$t>0$
be a real number. Suppose that
![]() $R_p$
,
$R_p$
,
![]() $\Delta _p$
,
$\Delta _p$
,
![]() $\mathfrak {a}_p$
are approximations. Then
$\mathfrak {a}_p$
are approximations. Then
![]() $\tau (R_p,\Delta _p,\mathfrak {a}_p^t)$
is an approximation of
$\tau (R_p,\Delta _p,\mathfrak {a}_p^t)$
is an approximation of
![]() $\mathcal {J}(\operatorname {Spec} R,\Delta ,\mathfrak {a}^t)$
.
$\mathcal {J}(\operatorname {Spec} R,\Delta ,\mathfrak {a}^t)$
.
Proof. Let
![]() $R=S_{\mathfrak {p}}$
, where S is a normal domain of finite type over
$R=S_{\mathfrak {p}}$
, where S is a normal domain of finite type over
![]() $\mathbb {C}$
and
$\mathbb {C}$
and
![]() $\mathfrak {p}$
is a prime ideal. Let
$\mathfrak {p}$
is a prime ideal. Let
![]() $\mathfrak {m}$
be a maximal ideal contains
$\mathfrak {m}$
be a maximal ideal contains
![]() $\mathfrak {p}$
. Then there exists a model
$\mathfrak {p}$
. Then there exists a model
![]() $(A,S_A)$
of S such that the properties in Proposition 5.3 hold and
$(A,S_A)$
of S such that the properties in Proposition 5.3 hold and
![]() $S_A$
containing a system of generators of
$S_A$
containing a system of generators of
![]() $\mathcal {J}(\operatorname {Spec} R,\Delta ,\mathfrak {a}^t)$
and
$\mathcal {J}(\operatorname {Spec} R,\Delta ,\mathfrak {a}^t)$
and
![]() $\Delta _A$
,
$\Delta _A$
,
![]() $\mathfrak {a}_A$
can be defined properly. Let
$\mathfrak {a}_A$
can be defined properly. Let
![]() $\mu _p$
be maximal ideals of
$\mu _p$
be maximal ideals of
![]() $S_A$
as in Remark 5.4, and let
$S_A$
as in Remark 5.4, and let
![]() $\mathfrak {m}_{\mu _p}, \mathfrak {p}_{\mu _p}$
be reductions to
$\mathfrak {m}_{\mu _p}, \mathfrak {p}_{\mu _p}$
be reductions to
![]() $p\gg 0$
. Since, for almost all p,
$p\gg 0$
. Since, for almost all p,
![]() $(S_A/\mu _p)_{\mathfrak {m}_{\mu _p}}\to (S_{\mathfrak {m}})_p$
is a flat local homomorphism such that
$(S_A/\mu _p)_{\mathfrak {m}_{\mu _p}}\to (S_{\mathfrak {m}})_p$
is a flat local homomorphism such that
![]() $S_A/\mathfrak {m}_{\mu _p}\to (S/\mathfrak {m})_p\cong \overline {\mathbb {F}_p}$
is a separable field extension, we have
$S_A/\mathfrak {m}_{\mu _p}\to (S/\mathfrak {m})_p\cong \overline {\mathbb {F}_p}$
is a separable field extension, we have
by a generalization of [Reference Srinivas and Takagi28, Lem. 1.5]. Since the localization commutes with test ideals [Reference Hara and Takagi10, Prop. 3.1], we have
for almost all p. Since the reduction of multiplier ideals modulo
![]() $p\gg 0$
is the test ideal [Reference Takagi29, Th. 3.2],
$p\gg 0$
is the test ideal [Reference Takagi29, Th. 3.2],
![]() $\tau ((S_A/\mu _p)_{\mathfrak {p}_{\mu _p}}, \Delta _{(S_A/\mu _p)_{\mathfrak {p}_{\mu _p}}},\mathfrak {a}^t_{(S_A/\mu _p)_{\mathfrak {p}_{\mu _p}}})$
is a reduction of
$\tau ((S_A/\mu _p)_{\mathfrak {p}_{\mu _p}}, \Delta _{(S_A/\mu _p)_{\mathfrak {p}_{\mu _p}}},\mathfrak {a}^t_{(S_A/\mu _p)_{\mathfrak {p}_{\mu _p}}})$
is a reduction of
to characteristic
![]() $p\gg 0$
. Hence,
$p\gg 0$
. Hence,
![]() $\tau (R_p,\Delta _p,\mathfrak {a}^t_p)$
is an approximation of
$\tau (R_p,\Delta _p,\mathfrak {a}^t_p)$
is an approximation of
![]() $\mathcal {J}(\operatorname {Spec} R,\Delta ,\mathfrak {a}^t)$
.
$\mathcal {J}(\operatorname {Spec} R,\Delta ,\mathfrak {a}^t)$
.
6 BCM test ideal with respect to a big Cohen–Macaulay algebra constructed via ultraproducts
Throughout this section, we assume that
![]() $(R,\mathfrak {m})$
is a normal local domain essentially of finite type over
$(R,\mathfrak {m})$
is a normal local domain essentially of finite type over
![]() $\mathbb {C}$
. Fix a canonical divisor
$\mathbb {C}$
. Fix a canonical divisor
![]() $K_R$
such that
$K_R$
such that
![]() $R\subseteq \omega _R:=R(K_R)\subseteq \operatorname {Frac}(R)$
. Let
$R\subseteq \omega _R:=R(K_R)\subseteq \operatorname {Frac}(R)$
. Let
![]() $\Delta \geqslant 0$
be an effective
$\Delta \geqslant 0$
be an effective
![]() $\mathbb {Q}$
-Weil divisor such that
$\mathbb {Q}$
-Weil divisor such that
![]() $K_R+\Delta $
is
$K_R+\Delta $
is
![]() $\mathbb {Q}$
-Cartier. Suppose that
$\mathbb {Q}$
-Cartier. Suppose that
![]() $\operatorname {div} f=n(K_R+\Delta )$
for
$\operatorname {div} f=n(K_R+\Delta )$
for
![]() $f\in R^{\circ }$
,
$f\in R^{\circ }$
,
![]() $n\in \mathbb {N}$
. Let
$n\in \mathbb {N}$
. Let
![]() $B_p$
be a BCM
$B_p$
be a BCM
![]() $R_p^+$
-algebra for almost all p and
$R_p^+$
-algebra for almost all p and
![]() $B:=\operatorname *{\mathrm {ulim}}_p B_p$
. We use
$B:=\operatorname *{\mathrm {ulim}}_p B_p$
. We use
![]() $\widehat {R}$
to denote the completion of R with respect to
$\widehat {R}$
to denote the completion of R with respect to
![]() $\mathfrak {m}$
and
$\mathfrak {m}$
and
![]() $\widehat {\Delta }$
to denote the flat pullback of
$\widehat {\Delta }$
to denote the flat pullback of
![]() $\Delta $
by
$\Delta $
by
![]() $\operatorname {Spec} \widehat {R}\to \operatorname {Spec} R$
.
$\operatorname {Spec} \widehat {R}\to \operatorname {Spec} R$
.
Proposition 6.1. In the setting as above, we have
Proof. Consider the following commutative diagram:

By Proposition 2.12, we have
for almost all p. Let
![]() $x_1,\dots ,x_d$
be a system of parameters, and let
$x_1,\dots ,x_d$
be a system of parameters, and let
![]() $x=x_1\cdots x_d$
be the product of them. Take
$x=x_1\cdots x_d$
be the product of them. Take
![]() $a\in \mathcal {J}(R,\Delta )=\operatorname *{\mathrm {ulim}}_p \tau (R_p,\Delta _p)\cap R$
and
$a\in \mathcal {J}(R,\Delta )=\operatorname *{\mathrm {ulim}}_p \tau (R_p,\Delta _p)\cap R$
and
![]() $\lbrack \frac {z}{x^t}\rbrack \in 0_{H_{\mathfrak {m}}^d(\omega _{R})}^{B,K_R+\Delta }$
. Let J be a divisorial ideal which is isomorphic to
$\lbrack \frac {z}{x^t}\rbrack \in 0_{H_{\mathfrak {m}}^d(\omega _{R})}^{B,K_R+\Delta }$
. Let J be a divisorial ideal which is isomorphic to
![]() $\omega _R$
and
$\omega _R$
and
![]() $g\in R^\circ $
an element such that
$g\in R^\circ $
an element such that
![]() $\omega _R \xrightarrow {\cdot g} J$
is an isomorphism. As in Proof of [Reference Takagi29, Th. 2.8], we have
$\omega _R \xrightarrow {\cdot g} J$
is an isomorphism. As in Proof of [Reference Takagi29, Th. 2.8], we have
![]() $g_p z_p x_p^t\in ((x_{1p}^{2t},\dots ,x_{dp}^{2t})J_p)^{*\Delta _p}$
for almost all p. Hence,
$g_p z_p x_p^t\in ((x_{1p}^{2t},\dots ,x_{dp}^{2t})J_p)^{*\Delta _p}$
for almost all p. Hence,
![]() $a_p g_p z_p x_p^t\in (x_{1p}^{2t},\dots ,x_{dp}^{2t})J_p$
for almost all p. Therefore,
$a_p g_p z_p x_p^t\in (x_{1p}^{2t},\dots ,x_{dp}^{2t})J_p$
for almost all p. Therefore,
![]() $agzx^t\in (x_1^{2t},\dots ,x_d^{2t})J$
and
$agzx^t\in (x_1^{2t},\dots ,x_d^{2t})J$
and
![]() $\lbrack \frac {az}{x^t} \rbrack =0$
in
$\lbrack \frac {az}{x^t} \rbrack =0$
in
![]() $H_{\mathfrak {m}}^d(\omega _R)$
. Hence, we have
$H_{\mathfrak {m}}^d(\omega _R)$
. Hence, we have
![]() $a\in \operatorname {Ann}_R 0_{H_{\mathfrak {m}}^d(\omega _{R})}^{B,K_R+\Delta }$
. In conclusion, we have
$a\in \operatorname {Ann}_R 0_{H_{\mathfrak {m}}^d(\omega _{R})}^{B,K_R+\Delta }$
. In conclusion, we have
![]() $\mathcal {J} (R,\Delta )\widehat {R}\subseteq \tau _{\widehat {B}}(\widehat {R},\widehat {\Delta })$
.
$\mathcal {J} (R,\Delta )\widehat {R}\subseteq \tau _{\widehat {B}}(\widehat {R},\widehat {\Delta })$
.
Lemma 6.2 [Reference Takagi29, Th. 2.13].
Let
![]() $(R,\mathfrak {m})$
be an F-finite normal local domain of characteristic
$(R,\mathfrak {m})$
be an F-finite normal local domain of characteristic
![]() $p>0$
and
$p>0$
and
![]() $\Delta \geqslant 0$
be an effective
$\Delta \geqslant 0$
be an effective
![]() $\mathbb {Q}$
-Weil divisor on
$\mathbb {Q}$
-Weil divisor on
![]() $X:=\operatorname {Spec} R$
such that
$X:=\operatorname {Spec} R$
such that
![]() $K_X+\Delta $
is
$K_X+\Delta $
is
![]() $\mathbb {Q}$
-Cartier. Let
$\mathbb {Q}$
-Cartier. Let
![]() $f:Y\to X$
be a proper birational morphism with X normal. Suppose that
$f:Y\to X$
be a proper birational morphism with X normal. Suppose that
![]() $Z:=f^{-1}(\mathfrak {m})$
and
$Z:=f^{-1}(\mathfrak {m})$
and
![]() $\delta :H_{\mathfrak {m}}^d(R(K_X))\to H_Z^d(Y,\mathcal {O}_Y(\lfloor f^{*}(K_X+\Delta )\rfloor )$
is the Matlis dual of the natural inclusion map
$\delta :H_{\mathfrak {m}}^d(R(K_X))\to H_Z^d(Y,\mathcal {O}_Y(\lfloor f^{*}(K_X+\Delta )\rfloor )$
is the Matlis dual of the natural inclusion map
![]() $H^0(Y,\mathcal {O}_Y(\lceil K_Y-f^*(K_X+\Delta ) \rceil ))\hookrightarrow R$
. Then
$H^0(Y,\mathcal {O}_Y(\lceil K_Y-f^*(K_X+\Delta ) \rceil ))\hookrightarrow R$
. Then
![]() $\operatorname {Ker} \delta \subseteq 0_E^{*\Delta }$
, where E is the injective hull of the residue field
$\operatorname {Ker} \delta \subseteq 0_E^{*\Delta }$
, where E is the injective hull of the residue field
![]() $R/\mathfrak {m}$
of R.
$R/\mathfrak {m}$
of R.
Proof. By [Reference Takagi29, Th. 2.13], we have
![]() $\tau (R,\Delta )\subseteq H^0(Y,\mathcal {O}_Y(\lceil K_Y-f^*(K_X+\Delta ) \rceil ))$
. Hence,
$\tau (R,\Delta )\subseteq H^0(Y,\mathcal {O}_Y(\lceil K_Y-f^*(K_X+\Delta ) \rceil ))$
. Hence,
 $$ \begin{align*} \operatorname{Ker} \delta&=\operatorname{Ann}_E H^0(Y,\mathcal{O}_Y(\lceil K_Y-f^*(K_X+\Delta) \rceil))\\ &\subseteq \operatorname{Ann}_E \tau(R,\Delta) \\ &=\operatorname{Ann}_E \tau(R,\Delta)\widehat{R} \\ &=\operatorname{Ann}_E \tau(\widehat{R},\widehat{\Delta}) \\ &=\operatorname{Ann}_E \operatorname{Ann}_{\widehat{R}} 0_E^{*\Delta} \\ &= 0_E^{*\Delta}.\\[-36pt] \end{align*} $$
$$ \begin{align*} \operatorname{Ker} \delta&=\operatorname{Ann}_E H^0(Y,\mathcal{O}_Y(\lceil K_Y-f^*(K_X+\Delta) \rceil))\\ &\subseteq \operatorname{Ann}_E \tau(R,\Delta) \\ &=\operatorname{Ann}_E \tau(R,\Delta)\widehat{R} \\ &=\operatorname{Ann}_E \tau(\widehat{R},\widehat{\Delta}) \\ &=\operatorname{Ann}_E \operatorname{Ann}_{\widehat{R}} 0_E^{*\Delta} \\ &= 0_E^{*\Delta}.\\[-36pt] \end{align*} $$
Remark 6.3. Moreover, we have
![]() $\operatorname {Ker} \delta =0_E^{*\Delta }$
if f is a reduction of a log resolution in characteristic zero modulo
$\operatorname {Ker} \delta =0_E^{*\Delta }$
if f is a reduction of a log resolution in characteristic zero modulo
![]() $p\gg 0$
by [Reference Takagi29, Th. 3.2].
$p\gg 0$
by [Reference Takagi29, Th. 3.2].
Theorem 6.4. Let R be a normal local domain essentially of finite type over
![]() $\mathbb {C}$
. Fix an effective canonical divisor
$\mathbb {C}$
. Fix an effective canonical divisor
![]() $K_R\geqslant 0$
on
$K_R\geqslant 0$
on
![]() $\operatorname {Spec} R$
. Let
$\operatorname {Spec} R$
. Let
![]() $\Delta \geqslant 0$
be an effective
$\Delta \geqslant 0$
be an effective
![]() $\mathbb {Q}$
-Weil divisor on
$\mathbb {Q}$
-Weil divisor on
![]() $\operatorname {Spec} R$
such that
$\operatorname {Spec} R$
such that
![]() $K_R+\Delta $
is
$K_R+\Delta $
is
![]() $\mathbb {Q}$
-Cartier and
$\mathbb {Q}$
-Cartier and
![]() $B_p$
is a BCM
$B_p$
is a BCM
![]() $R_p^+$
-algebra for almost all p. Suppose that
$R_p^+$
-algebra for almost all p. Suppose that
![]() $n(K_R+\Delta )=\operatorname {div} (f)$
for
$n(K_R+\Delta )=\operatorname {div} (f)$
for
![]() $f\in R^\circ , n\in \mathbb {N}$
. Then we have
$f\in R^\circ , n\in \mathbb {N}$
. Then we have
Proof. Thanks to Proposition 6.1, it suffices to prove
![]() $\tau _{\widehat {B}}(\widehat {R},\widehat {\Delta })\subseteq \mathcal {J}(\widehat {R},\widehat {\Delta })$
. Let
$\tau _{\widehat {B}}(\widehat {R},\widehat {\Delta })\subseteq \mathcal {J}(\widehat {R},\widehat {\Delta })$
. Let
![]() $\mu :Y\to X:=\operatorname {Spec} R$
be a log resolution of
$\mu :Y\to X:=\operatorname {Spec} R$
be a log resolution of
![]() $(X,\Delta )$
, and let
$(X,\Delta )$
, and let
![]() $Z:=\mu ^{-1}(\mathfrak {m})$
. Considering approximations, we have a corresponding morphisms
$Z:=\mu ^{-1}(\mathfrak {m})$
. Considering approximations, we have a corresponding morphisms
![]() $\mu _p:Y_p\to X_p:=\operatorname {Spec} R_p$
,
$\mu _p:Y_p\to X_p:=\operatorname {Spec} R_p$
,
![]() $Z_p=\mu _p^{-1}(\mathfrak {m}_p)$
for almost all p. Then we have a commutative diagram
$Z_p=\mu _p^{-1}(\mathfrak {m}_p)$
for almost all p. Then we have a commutative diagram

where
![]() $\mathcal {L}:=\mathcal {O}_Y(\lfloor \mu ^*(K_X+\Delta ) \rfloor )$
and the middle row is exact. Similarly, we have the following commutative diagram for almost all p:
$\mathcal {L}:=\mathcal {O}_Y(\lfloor \mu ^*(K_X+\Delta ) \rfloor )$
and the middle row is exact. Similarly, we have the following commutative diagram for almost all p:

where the middle row is exact. Assume that
![]() $\eta \in \operatorname {Ker} \delta $
. Then
$\eta \in \operatorname {Ker} \delta $
. Then
![]() $u^{d-1}(\gamma (\eta ))\in \operatorname {Im} \rho _\infty ^{d-1}$
. Therefore,
$u^{d-1}(\gamma (\eta ))\in \operatorname {Im} \rho _\infty ^{d-1}$
. Therefore,
![]() $\gamma _p(\eta _p) \in \operatorname {Im}\rho _p^{d-1}$
for almost all p. Hence,
$\gamma _p(\eta _p) \in \operatorname {Im}\rho _p^{d-1}$
for almost all p. Hence,
![]() $\eta _p\in \operatorname {Ker} \delta _p$
for almost all p. By Lemma 6.2,
$\eta _p\in \operatorname {Ker} \delta _p$
for almost all p. By Lemma 6.2,
![]() $\eta _p\in 0_{H_{\mathfrak {m}_p}^d(\omega _{R_p})}^{*\Delta _p}$
for almost all p. Hence, by Propositon 2.12, we have
$\eta _p\in 0_{H_{\mathfrak {m}_p}^d(\omega _{R_p})}^{*\Delta _p}$
for almost all p. Hence, by Propositon 2.12, we have
![]() $\eta _p\in 0_{H_{m_p}^d(\omega _{R_p})}^{B_p,K_{R_p}+\Delta _p}$
for almost all p. We have a commutative diagram
$\eta _p\in 0_{H_{m_p}^d(\omega _{R_p})}^{B_p,K_{R_p}+\Delta _p}$
for almost all p. We have a commutative diagram

where
![]() $\psi $
,
$\psi $
,
![]() $\psi _p$
are the morphisms as in Definition 2.11. Since
$\psi _p$
are the morphisms as in Definition 2.11. Since
![]() $\psi _\infty (\operatorname *{\mathrm {ulim}}_p \eta _p)=0$
and
$\psi _\infty (\operatorname *{\mathrm {ulim}}_p \eta _p)=0$
and
![]() $H_{\mathfrak {m}}^d(B) \to \operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}_p}^d(B_p)$
is injective by Lemma 4.7, we have
$H_{\mathfrak {m}}^d(B) \to \operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}_p}^d(B_p)$
is injective by Lemma 4.7, we have
![]() $\psi (\eta )=0$
in
$\psi (\eta )=0$
in
![]() $H_{\mathfrak {m}}^d(B)$
. Hence,
$H_{\mathfrak {m}}^d(B)$
. Hence,
![]() $\eta \in 0_{H_{\mathfrak {m}}^d(\omega _R)}^{B,K_R+\Delta }$
. Therefore, we have
$\eta \in 0_{H_{\mathfrak {m}}^d(\omega _R)}^{B,K_R+\Delta }$
. Therefore, we have
 $$ \begin{align*} \tau_{\widehat{B}}(\widehat{R},\widehat{\Delta})&\subseteq \operatorname{Ann}_{\widehat{R}}(\operatorname{Ker} \delta)\\ &= \operatorname{Ann}_{\widehat{R}}\operatorname{Ann}_{H_{\mathfrak{m}}^d(\omega_R)}\mathcal{J}(R,\Delta)\\ &= \mathcal{J}(\widehat{R},\widehat{\Delta}).\\[-36pt] \end{align*} $$
$$ \begin{align*} \tau_{\widehat{B}}(\widehat{R},\widehat{\Delta})&\subseteq \operatorname{Ann}_{\widehat{R}}(\operatorname{Ker} \delta)\\ &= \operatorname{Ann}_{\widehat{R}}\operatorname{Ann}_{H_{\mathfrak{m}}^d(\omega_R)}\mathcal{J}(R,\Delta)\\ &= \mathcal{J}(\widehat{R},\widehat{\Delta}).\\[-36pt] \end{align*} $$
Remark 6.5. We can generalize the notion of ultra-test ideals in [Reference Yamaguchi31, Def. 5.5] to the pair
![]() $(R,\Delta )$
. Using Lemma 6.2 instead of [Reference Hara and Yoshida11, Th. 6.9], we can show that generalized ultra-test ideals are equal to multiplier ideals.
$(R,\Delta )$
. Using Lemma 6.2 instead of [Reference Hara and Yoshida11, Th. 6.9], we can show that generalized ultra-test ideals are equal to multiplier ideals.
7 Generalized module closures and applications
We introduce the notion of generalized module closures inspired by [Reference Pérez and Rebecca20]. Using the generalized module closures, we will generalize [Reference Yamaguchi31, Cor. 5.30]. We also use [Reference Ma and Schwede19, §6.1] as reference in the following arguments.
Setting 7.1. Suppose that R is a normal local domain essentially of finite type over
![]() $\mathbb {C}$
of dimension d,
$\mathbb {C}$
of dimension d,
![]() $K_R\geqslant 0$
is a fixed effective canonical divisor and
$K_R\geqslant 0$
is a fixed effective canonical divisor and
![]() $\Delta \geqslant 0$
is an effective
$\Delta \geqslant 0$
is an effective
![]() $\mathbb {Q}$
-Weil divisor such that
$\mathbb {Q}$
-Weil divisor such that
![]() $K_R+\Delta $
is
$K_R+\Delta $
is
![]() $\mathbb {Q}$
-Cartier. Moreover, we assume that
$\mathbb {Q}$
-Cartier. Moreover, we assume that
![]() $B_p$
is a BCM
$B_p$
is a BCM
![]() $R_p^+$
-algebra for almost all p,
$R_p^+$
-algebra for almost all p,
![]() $B:=\operatorname *{\mathrm {ulim}}_p B_p$
and
$B:=\operatorname *{\mathrm {ulim}}_p B_p$
and
![]() $r(K_R+\Delta )=\operatorname {div} f$
for
$r(K_R+\Delta )=\operatorname {div} f$
for
![]() $f\in R$
,
$f\in R$
,
![]() $r\in \mathbb {N}$
. Let
$r\in \mathbb {N}$
. Let
![]() $R'\subseteq R^+$
be an integrally closed finite extension of R such that
$R'\subseteq R^+$
be an integrally closed finite extension of R such that
![]() $f^{1/r}\in R'$
and
$f^{1/r}\in R'$
and
![]() $\pi ^*\Delta $
is Weil divisor, where
$\pi ^*\Delta $
is Weil divisor, where
![]() $\pi :\operatorname {Spec} R'\to \operatorname {Spec} R$
.
$\pi :\operatorname {Spec} R'\to \operatorname {Spec} R$
.
Definition 7.2. Assume Setting 7.1 and let
![]() $g\in R^\circ $
and
$g\in R^\circ $
and
![]() $t>0$
be a positive rational number. We use
$t>0$
be a positive rational number. We use
![]() $\widehat {B_\Delta }$
to denote
$\widehat {B_\Delta }$
to denote
For any
![]() $\widehat {R}$
-modules
$\widehat {R}$
-modules
![]() $N\subseteq M$
, we define
$N\subseteq M$
, we define
![]() $N_M^{\operatorname {cl}_{\widehat {B_\Delta },g^t}}$
as follows:
$N_M^{\operatorname {cl}_{\widehat {B_\Delta },g^t}}$
as follows:
![]() $x\in N_M^{\operatorname {cl}_{\widehat {B_\Delta },g^t}}$
if and only if
$x\in N_M^{\operatorname {cl}_{\widehat {B_\Delta },g^t}}$
if and only if
![]() $g^t\otimes x\in \operatorname {Im}(\widehat {B_\Delta }\otimes _{\widehat {R}}N\to \widehat {B_\Delta }\otimes _{\widehat {R}}M)$
. We use
$g^t\otimes x\in \operatorname {Im}(\widehat {B_\Delta }\otimes _{\widehat {R}}N\to \widehat {B_\Delta }\otimes _{\widehat {R}}M)$
. We use
![]() $\tau _{\operatorname {cl}_{\widehat {B_\Delta },g^t}}(\widehat {R})$
to denote
$\tau _{\operatorname {cl}_{\widehat {B_\Delta },g^t}}(\widehat {R})$
to denote
 $$ \begin{align*} \bigcap_{N\subseteq M}(N:_{\widehat{R}}N_M^{\operatorname{cl}_{\widehat{B_\Delta}},g^t}), \end{align*} $$
$$ \begin{align*} \bigcap_{N\subseteq M}(N:_{\widehat{R}}N_M^{\operatorname{cl}_{\widehat{B_\Delta}},g^t}), \end{align*} $$
where M runs through all
![]() $\widehat {R}$
-modules and N runs through all
$\widehat {R}$
-modules and N runs through all
![]() $\widehat {R}$
-submodules of M.
$\widehat {R}$
-submodules of M.
Proposition 7.3. In Setting 7.1, if
![]() $g\in R^\circ $
and
$g\in R^\circ $
and
![]() $t>0$
is a positive rational number, then we have
$t>0$
is a positive rational number, then we have
 $$ \begin{align*} \tau_{\operatorname{cl}_{\widehat{B_\Delta},g^t}}(\widehat{R})=\bigcap_{M}\operatorname{Ann}_{\widehat{R}}0_M^{\operatorname{cl}_{\widehat{B_\Delta},g^t}}=\operatorname{Ann}_{\widehat{R}}0_E^{\operatorname{cl}_{\widehat{B_\Delta},g^t}}, \end{align*} $$
$$ \begin{align*} \tau_{\operatorname{cl}_{\widehat{B_\Delta},g^t}}(\widehat{R})=\bigcap_{M}\operatorname{Ann}_{\widehat{R}}0_M^{\operatorname{cl}_{\widehat{B_\Delta},g^t}}=\operatorname{Ann}_{\widehat{R}}0_E^{\operatorname{cl}_{\widehat{B_\Delta},g^t}}, \end{align*} $$
where M runs through all
![]() $\widehat {R}$
-modules and E is the injective hull of the residue field of R.
$\widehat {R}$
-modules and E is the injective hull of the residue field of R.
Proof. We can prove this by arguments similar to [Reference Pérez and Rebecca20, Lem. 3.3 and Prop. 3.9].
Proposition 7.4. In Setting 7.1, if
![]() $g\in R^\circ $
and
$g\in R^\circ $
and
![]() $t>0$
is a positive rational number, then we have
$t>0$
is a positive rational number, then we have
Proof. Since the reflexive hull
![]() $(R'(\pi ^*\Delta )\otimes _R \omega _R)^{**}$
is equal to
$(R'(\pi ^*\Delta )\otimes _R \omega _R)^{**}$
is equal to
![]() $R'(\operatorname {div} (f^{\frac {1}{r}}))$
, we have
$R'(\operatorname {div} (f^{\frac {1}{r}}))$
, we have
![]() $H_{\mathfrak {m}}^d(R'(\pi ^*\Delta )\otimes _R \omega _R)\cong H_{\mathfrak {m}}^d(R'(\operatorname {div} (f^{\frac {1}{r}})))$
. Hence, we have
$H_{\mathfrak {m}}^d(R'(\pi ^*\Delta )\otimes _R \omega _R)\cong H_{\mathfrak {m}}^d(R'(\operatorname {div} (f^{\frac {1}{r}})))$
. Hence, we have
 $$ \begin{align*} \widehat{B_\Delta}\otimes_{\widehat{R}} E &\cong B\otimes_{R'}H_{\mathfrak{m}}^d(R'(\pi^*\Delta)\otimes_R\omega_R) \\ &\cong B\otimes_{R'}H_{\mathfrak{m}}^d(R'(\operatorname{div} (f^{\frac{1}{r}}))). \end{align*} $$
$$ \begin{align*} \widehat{B_\Delta}\otimes_{\widehat{R}} E &\cong B\otimes_{R'}H_{\mathfrak{m}}^d(R'(\pi^*\Delta)\otimes_R\omega_R) \\ &\cong B\otimes_{R'}H_{\mathfrak{m}}^d(R'(\operatorname{div} (f^{\frac{1}{r}}))). \end{align*} $$
Then there exists a commutative diagram

where
![]() $\psi $
is the second map of
$\psi $
is the second map of
The result follows by the above commutative diagram.
Definition 7.5. Let
![]() $R\hookrightarrow S$
be an injective local homomorphism of normal local domains essentially of finite type over
$R\hookrightarrow S$
be an injective local homomorphism of normal local domains essentially of finite type over
![]() $\mathbb {C}$
. Fix
$\mathbb {C}$
. Fix
![]() $K_R, K_S\geqslant 0$
effective canonical divisors on
$K_R, K_S\geqslant 0$
effective canonical divisors on
![]() $\operatorname {Spec} R$
and on
$\operatorname {Spec} R$
and on
![]() $\operatorname {Spec} S$
, respectively. Let
$\operatorname {Spec} S$
, respectively. Let
![]() $\Delta _R,\Delta _S\geqslant 0$
be effective
$\Delta _R,\Delta _S\geqslant 0$
be effective
![]() $\mathbb {Q}$
-Weil divisors on
$\mathbb {Q}$
-Weil divisors on
![]() $\operatorname {Spec} R$
and on
$\operatorname {Spec} R$
and on
![]() $\operatorname {Spec} S$
, respectively, such that
$\operatorname {Spec} S$
, respectively, such that
![]() $K_R+\Delta _R$
,
$K_R+\Delta _R$
,
![]() $K_S+\Delta _S$
are
$K_S+\Delta _S$
are
![]() $\mathbb {Q}$
-Cartier. Let
$\mathbb {Q}$
-Cartier. Let
![]() $\mathfrak {a}\subseteq R$
be a nonzero ideal and
$\mathfrak {a}\subseteq R$
be a nonzero ideal and
![]() $t>0$
be a positive rational number. Suppose that
$t>0$
be a positive rational number. Suppose that
![]() $\widehat {B_{\Delta _R}}$
and
$\widehat {B_{\Delta _R}}$
and
![]() $\widehat {B_{\Delta _S}}$
are defined as in Definition 7.2. Then, for an
$\widehat {B_{\Delta _S}}$
are defined as in Definition 7.2. Then, for an
![]() $\widehat {R}$
-module M and an
$\widehat {R}$
-module M and an
![]() $\widehat {S}$
-module N, we define
$\widehat {S}$
-module N, we define
![]() $0_{M}^{\operatorname {cl}_{\widehat {B_{\Delta _R}},\mathfrak {a}^t}}$
,
$0_{M}^{\operatorname {cl}_{\widehat {B_{\Delta _R}},\mathfrak {a}^t}}$
,
![]() $0_{N}^{\operatorname {cl}_{\widehat {B_{\Delta _S}}\mathfrak {a}^t}}$
by
$0_{N}^{\operatorname {cl}_{\widehat {B_{\Delta _S}}\mathfrak {a}^t}}$
by
 $$ \begin{align*} 0_{M}^{\operatorname{cl}_{\widehat{B_{\Delta_R}},\mathfrak{a}^t}}:=\bigcap_{n\in\mathbb{N}}\bigcap_{g\in\mathfrak{a}^{\lceil nt \rceil}}0_{M}^{\operatorname{cl}_{\widehat{B_{\Delta_R}},g^{\frac{1}{n}}}},\\ 0_{N}^{\operatorname{cl}_{\widehat{B_{\Delta_S}}\mathfrak{a}^t}}:=\bigcap_{n\in\mathbb{N}}\bigcap_{g\in\mathfrak{a}^{\lceil nt \rceil}}0_{N}^{\operatorname{cl}_{\widehat{B_{\Delta_S}}g^{\frac{1}{n}}}}. \end{align*} $$
$$ \begin{align*} 0_{M}^{\operatorname{cl}_{\widehat{B_{\Delta_R}},\mathfrak{a}^t}}:=\bigcap_{n\in\mathbb{N}}\bigcap_{g\in\mathfrak{a}^{\lceil nt \rceil}}0_{M}^{\operatorname{cl}_{\widehat{B_{\Delta_R}},g^{\frac{1}{n}}}},\\ 0_{N}^{\operatorname{cl}_{\widehat{B_{\Delta_S}}\mathfrak{a}^t}}:=\bigcap_{n\in\mathbb{N}}\bigcap_{g\in\mathfrak{a}^{\lceil nt \rceil}}0_{N}^{\operatorname{cl}_{\widehat{B_{\Delta_S}}g^{\frac{1}{n}}}}. \end{align*} $$
We use
![]() $\tau _{\operatorname {cl}_{\widehat {B_{\Delta _R}},\mathfrak {a}^t}}(\widehat {R})$
,
$\tau _{\operatorname {cl}_{\widehat {B_{\Delta _R}},\mathfrak {a}^t}}(\widehat {R})$
,
![]() $\tau _{\operatorname {cl}_{\widehat {B_{\Delta _S}},\mathfrak {a}^t}}(\widehat {S})$
to denote
$\tau _{\operatorname {cl}_{\widehat {B_{\Delta _S}},\mathfrak {a}^t}}(\widehat {S})$
to denote
 $$ \begin{align*} \bigcap_M \operatorname{Ann}_{\widehat{R}}0_M^{\operatorname{cl}_{\widehat{B_{\Delta_R}},\mathfrak{a}^t}}, \\ \bigcap_N \operatorname{Ann}_{\widehat{S}}0_N^{\operatorname{cl}_{\widehat{B_{\Delta_S}},\mathfrak{a}^t}}, \end{align*} $$
$$ \begin{align*} \bigcap_M \operatorname{Ann}_{\widehat{R}}0_M^{\operatorname{cl}_{\widehat{B_{\Delta_R}},\mathfrak{a}^t}}, \\ \bigcap_N \operatorname{Ann}_{\widehat{S}}0_N^{\operatorname{cl}_{\widehat{B_{\Delta_S}},\mathfrak{a}^t}}, \end{align*} $$
where M runs through all
![]() $\widehat {R}$
-modules and N runs through all
$\widehat {R}$
-modules and N runs through all
![]() $\widehat {S}$
-modules.
$\widehat {S}$
-modules.
Proposition 7.6. In the setting of Definition 7.5, we have
 $$ \begin{align*} \operatorname{Ann}_{\widehat{R}}0_{E_R}^{\operatorname{cl}_{\widehat{B_{\Delta_R}},\mathfrak{a}^t}}=\bigcap_M \operatorname{Ann}_{\widehat{R}}0_M^{\operatorname{cl}_{\widehat{B_{\Delta_R}},\mathfrak{a}^t}}, \\ \operatorname{Ann}_{\widehat{S}}0_{E_S}^{\operatorname{cl}_{\widehat{B_{\Delta_S}},\mathfrak{a}^t}}=\bigcap_N \operatorname{Ann}_{\widehat{S}}0_N^{\operatorname{cl}_{\widehat{B_{\Delta_S}},\mathfrak{a}^t}}, \end{align*} $$
$$ \begin{align*} \operatorname{Ann}_{\widehat{R}}0_{E_R}^{\operatorname{cl}_{\widehat{B_{\Delta_R}},\mathfrak{a}^t}}=\bigcap_M \operatorname{Ann}_{\widehat{R}}0_M^{\operatorname{cl}_{\widehat{B_{\Delta_R}},\mathfrak{a}^t}}, \\ \operatorname{Ann}_{\widehat{S}}0_{E_S}^{\operatorname{cl}_{\widehat{B_{\Delta_S}},\mathfrak{a}^t}}=\bigcap_N \operatorname{Ann}_{\widehat{S}}0_N^{\operatorname{cl}_{\widehat{B_{\Delta_S}},\mathfrak{a}^t}}, \end{align*} $$
where
![]() $M,N$
run through all
$M,N$
run through all
![]() $\widehat {R}$
-modules and
$\widehat {R}$
-modules and
![]() $\widehat {S}$
-modules, respectively, and
$\widehat {S}$
-modules, respectively, and
![]() $E_R$
,
$E_R$
,
![]() $E_S$
are the injective hulls of the residue fields of R and S, respectively.
$E_S$
are the injective hulls of the residue fields of R and S, respectively.
Proof. We can show this by arguments similar to Proposition 7.3.
Proposition 7.7. In the setting of Definition 7.5, we have
Proof. Let E be the injective hull of the residue field of R. Then
 $$ \begin{align*} 0_E^{\operatorname{cl}_{\widehat{B_{\Delta_R}},\mathfrak{a}^t}} &= \bigcap_{n\in \mathbb{N}}\bigcap_{g\in\mathfrak{a}^{\lceil nt \rceil}} 0_E^{\operatorname{cl}_{\widehat{B_{\Delta_R}}, g^{\frac{1}{n}}}} \\ &= \bigcap_{n\in\mathbb{N}}\bigcap_{g\in\mathfrak{a}^{\lceil nt \rceil}}\operatorname{Ann}_E \mathcal{J}(\widehat{R},\widehat{\Delta},g^{\frac{1}{n}}) \\ &= \operatorname{Ann}_E \sum_{n\in \mathbb{N}}\sum_{g\in\mathfrak{a}^{\lceil nt \rceil}}\mathcal{J} (\widehat{R},\widehat{\Delta},g^{\frac{1}{n}}) \\ &= \operatorname{Ann}_E \mathcal{J}(\widehat{R},\widehat{\Delta},(\mathfrak{a} \widehat{R})^t), \end{align*} $$
$$ \begin{align*} 0_E^{\operatorname{cl}_{\widehat{B_{\Delta_R}},\mathfrak{a}^t}} &= \bigcap_{n\in \mathbb{N}}\bigcap_{g\in\mathfrak{a}^{\lceil nt \rceil}} 0_E^{\operatorname{cl}_{\widehat{B_{\Delta_R}}, g^{\frac{1}{n}}}} \\ &= \bigcap_{n\in\mathbb{N}}\bigcap_{g\in\mathfrak{a}^{\lceil nt \rceil}}\operatorname{Ann}_E \mathcal{J}(\widehat{R},\widehat{\Delta},g^{\frac{1}{n}}) \\ &= \operatorname{Ann}_E \sum_{n\in \mathbb{N}}\sum_{g\in\mathfrak{a}^{\lceil nt \rceil}}\mathcal{J} (\widehat{R},\widehat{\Delta},g^{\frac{1}{n}}) \\ &= \operatorname{Ann}_E \mathcal{J}(\widehat{R},\widehat{\Delta},(\mathfrak{a} \widehat{R})^t), \end{align*} $$
where the second equality follows from Theorem 6.4. Hence, we have
The next lemma is a generalization of [Reference Takagi30, Th. 3.2].
Lemma 7.8. Let R be a normal local domain essentially of finite type over
![]() $\mathbb {C}$
, and let
$\mathbb {C}$
, and let
![]() $\Delta \geqslant 0$
be an effective
$\Delta \geqslant 0$
be an effective
![]() $\mathbb {Q}$
-Weil divisor such that
$\mathbb {Q}$
-Weil divisor such that
![]() $K_R+\Delta $
is
$K_R+\Delta $
is
![]() $\mathbb {Q}$
-Cartier. Let
$\mathbb {Q}$
-Cartier. Let
![]() $\mathfrak {a}_1,\dots ,\mathfrak {a}_n\subseteq R$
be nonzero ideals, and let
$\mathfrak {a}_1,\dots ,\mathfrak {a}_n\subseteq R$
be nonzero ideals, and let
![]() $t>0$
be a positive rational number. Then we have
$t>0$
be a positive rational number. Then we have
 $$ \begin{align*} \mathcal{J}(R,\Delta,(\mathfrak{a}_1+\dots+\mathfrak{a}_n)^t)=\sum_{\lambda_1+\dots+\lambda_n=t}\mathcal{J}(R,\Delta,\mathfrak{a}_1^{\lambda_1}\cdots \mathfrak{a}_n^{\lambda_n}). \end{align*} $$
$$ \begin{align*} \mathcal{J}(R,\Delta,(\mathfrak{a}_1+\dots+\mathfrak{a}_n)^t)=\sum_{\lambda_1+\dots+\lambda_n=t}\mathcal{J}(R,\Delta,\mathfrak{a}_1^{\lambda_1}\cdots \mathfrak{a}_n^{\lambda_n}). \end{align*} $$
Lemma 7.9. In the setting of Definition 7.5, we have
 $$ \begin{align*} \sum_{n\in\mathbb{N}}\sum_{g\in\mathfrak{a}^{\lceil nt \rceil}}\mathcal{J}(S,\Delta_S,g^{\frac{1}{n}})=\mathcal{J}(S,\Delta_S,(\mathfrak{a} S)^t). \end{align*} $$
$$ \begin{align*} \sum_{n\in\mathbb{N}}\sum_{g\in\mathfrak{a}^{\lceil nt \rceil}}\mathcal{J}(S,\Delta_S,g^{\frac{1}{n}})=\mathcal{J}(S,\Delta_S,(\mathfrak{a} S)^t). \end{align*} $$
Proof.
![]() $\sum _{n\in \mathbb {N}}\sum _{g\in \mathfrak {a}^{\lceil nt \rceil }}\mathcal {J}(S,\Delta _S,g^{1/n})\subseteq \mathcal {J}(S,\Delta _S,(\mathfrak {a} S)^t)$
is clear. If
$\sum _{n\in \mathbb {N}}\sum _{g\in \mathfrak {a}^{\lceil nt \rceil }}\mathcal {J}(S,\Delta _S,g^{1/n})\subseteq \mathcal {J}(S,\Delta _S,(\mathfrak {a} S)^t)$
is clear. If
![]() $t=q/p$
,
$t=q/p$
,
![]() $p,q>0$
and
$p,q>0$
and
![]() $\mathfrak {a}=(g_1,\dots ,g_l)$
, then
$\mathfrak {a}=(g_1,\dots ,g_l)$
, then
 $$ \begin{align*} \sum_{n\in\mathbb{N}}\sum_{g\in\mathfrak{a}^{\lceil nt \rceil}}\mathcal{J}(S,\Delta_S,g^{\frac{1}{n}}) & \supseteq \sum_{n\in \mathbb{N}}\sum_{i_1+\dots+i_l=nq}\mathcal{J}(S,\Delta_S,(g_1^{i_1}\cdots g_l^{i_l})^{\frac{1}{np}}) \\ &=\mathcal{J}(S,\Delta_S,(\mathfrak{a} S)^t), \end{align*} $$
$$ \begin{align*} \sum_{n\in\mathbb{N}}\sum_{g\in\mathfrak{a}^{\lceil nt \rceil}}\mathcal{J}(S,\Delta_S,g^{\frac{1}{n}}) & \supseteq \sum_{n\in \mathbb{N}}\sum_{i_1+\dots+i_l=nq}\mathcal{J}(S,\Delta_S,(g_1^{i_1}\cdots g_l^{i_l})^{\frac{1}{np}}) \\ &=\mathcal{J}(S,\Delta_S,(\mathfrak{a} S)^t), \end{align*} $$
by the above lemma.
Theorem 7.10. Let
![]() $R\hookrightarrow S$
be a pure local homomorphism of normal local domains essentially of finite type over
$R\hookrightarrow S$
be a pure local homomorphism of normal local domains essentially of finite type over
![]() $\mathbb {C}$
. Fix effective canonical divisors
$\mathbb {C}$
. Fix effective canonical divisors
![]() $K_R$
and
$K_R$
and
![]() $K_S$
on
$K_S$
on
![]() $\operatorname {Spec} R$
and
$\operatorname {Spec} R$
and
![]() $\operatorname {Spec} S$
, respectively. Let
$\operatorname {Spec} S$
, respectively. Let
![]() $\Delta _R, \Delta _S \geqslant 0$
be effective
$\Delta _R, \Delta _S \geqslant 0$
be effective
![]() $\mathbb {Q}$
-Weil divisors on
$\mathbb {Q}$
-Weil divisors on
![]() $\operatorname {Spec} R$
,
$\operatorname {Spec} R$
,
![]() $\operatorname {Spec} S$
such that
$\operatorname {Spec} S$
such that
![]() $K_R+\Delta _R$
,
$K_R+\Delta _R$
,
![]() $K_S+\Delta _S$
are
$K_S+\Delta _S$
are
![]() $\mathbb {Q}$
-Cartier. Take normal domains
$\mathbb {Q}$
-Cartier. Take normal domains
![]() $R',S'$
and morphisms
$R',S'$
and morphisms
![]() $\pi _R,\pi _S$
as in Setting 7.1. Moreover, let
$\pi _R,\pi _S$
as in Setting 7.1. Moreover, let
![]() $\mathfrak {a}\subseteq R$
be a nonzero ideal, and let
$\mathfrak {a}\subseteq R$
be a nonzero ideal, and let
![]() $t>0$
be a positive rational number. If
$t>0$
be a positive rational number. If
![]() $R'(\pi _R^*\Delta _R)\subseteq S'(\pi _S^*\Delta _S)$
, then we have
$R'(\pi _R^*\Delta _R)\subseteq S'(\pi _S^*\Delta _S)$
, then we have
Proof. Since
![]() $R\hookrightarrow S$
is pure,
$R\hookrightarrow S$
is pure,
![]() $\widehat {R} \hookrightarrow \widehat {S}$
is pure (see [Reference Chakraborty, Gurjar and Miyanishi6, Cor. 3.2.1]). Since
$\widehat {R} \hookrightarrow \widehat {S}$
is pure (see [Reference Chakraborty, Gurjar and Miyanishi6, Cor. 3.2.1]). Since
![]() $R\to \widehat {R}$
,
$R\to \widehat {R}$
,
![]() $S\to \widehat {S}$
are pure, it is enough to show
$S\to \widehat {S}$
are pure, it is enough to show
Let
![]() $\mathcal {B}(R)$
,
$\mathcal {B}(R)$
,
![]() $\mathcal {B}(S)$
be the canonical BCM algebras. Let
$\mathcal {B}(S)$
be the canonical BCM algebras. Let
![]() $\widehat {\mathcal {B}_{\Delta _R}}:=\widehat {\mathcal {B}(R)_{\Delta _R}}$
and
$\widehat {\mathcal {B}_{\Delta _R}}:=\widehat {\mathcal {B}(R)_{\Delta _R}}$
and
![]() $\widehat {\mathcal {B}_{\Delta _S}}:=\widehat {\mathcal {B}(S)_{\Delta _S}}$
. Take an
$\widehat {\mathcal {B}_{\Delta _S}}:=\widehat {\mathcal {B}(S)_{\Delta _S}}$
. Take an
![]() $\widehat {R}$
-module M. Then we have a commutative diagram
$\widehat {R}$
-module M. Then we have a commutative diagram

Tensoring the commutative diagram with M, we have

Hence, we have
 $$ \begin{align*} 0_{M}^{\operatorname{cl}_{\widehat{\mathcal{B}_{\Delta_R}},\mathfrak{a}^t}}\subseteq 0_{\widehat{S}\otimes_{\widehat{R}}M}^{\operatorname{cl}_{\widehat{\mathcal{B}_{\Delta_S}},\mathfrak{a}^t}}. \end{align*} $$
$$ \begin{align*} 0_{M}^{\operatorname{cl}_{\widehat{\mathcal{B}_{\Delta_R}},\mathfrak{a}^t}}\subseteq 0_{\widehat{S}\otimes_{\widehat{R}}M}^{\operatorname{cl}_{\widehat{\mathcal{B}_{\Delta_S}},\mathfrak{a}^t}}. \end{align*} $$
Then we have
 $$ \begin{align*} \mathcal{J}(\widehat{R},\widehat{\Delta_R},\mathfrak{a}^t)&=\bigcap_{M} \operatorname{Ann}_{\widehat{R}}0_M^{\operatorname{cl}_{\widehat{\mathcal{B}_{\Delta_R}},\mathfrak{a}^t}} \\ &\supseteq \bigcap_{M}\operatorname{Ann}_{\widehat{R}}0_{M\otimes S}^{\operatorname{cl}_{\widehat{\mathcal{B}_{\Delta_S}},\mathfrak{a}^t}} \\ &\supseteq \bigcap_N \operatorname{Ann}_{\widehat{R}}0_N^{\operatorname{cl}_{\widehat{\mathcal{B}_{\Delta_S}},\mathfrak{a}^t}}\\ &= \bigcap_N (\operatorname{Ann}_{\widehat{S}}0_N^{\operatorname{cl}_{\widehat{\mathcal{B}_{\Delta_S}},\mathfrak{a}^t}}\cap \widehat{R}) \\ &= (\operatorname{Ann}_{\widehat{S}}0_{E_S}^{\operatorname{cl}_{\widehat{\mathcal{B}_{\Delta_S}},\mathfrak{a}^t}})\cap \widehat{R} \\ &= (\operatorname{Ann}_{\widehat{S}}\bigcap_{n\in\mathbb{N}}\bigcap_{g\in\mathfrak{a}^{\lceil nt \rceil}} 0_{E_S}^{\operatorname{cl}_{\widehat{\mathcal{B}_{\Delta_S}},g^{\frac{1}{n}}}})\cap \widehat{R} \\ &= (\operatorname{Ann}_{\widehat{S}}\operatorname{Ann}_{E_S}\sum_{n\in\mathbb{N}}\sum_{g\in \mathfrak{a}^{\lceil nt \rceil}}\mathcal{J}(\widehat{S},\widehat{\Delta_S},g^{\frac{1}{n}}))\cap \widehat{R} \\ &= \mathcal{J}(\widehat{S},\widehat{\Delta_S},(\mathfrak{a} \widehat{S})^t))\cap \widehat{R}, \end{align*} $$
$$ \begin{align*} \mathcal{J}(\widehat{R},\widehat{\Delta_R},\mathfrak{a}^t)&=\bigcap_{M} \operatorname{Ann}_{\widehat{R}}0_M^{\operatorname{cl}_{\widehat{\mathcal{B}_{\Delta_R}},\mathfrak{a}^t}} \\ &\supseteq \bigcap_{M}\operatorname{Ann}_{\widehat{R}}0_{M\otimes S}^{\operatorname{cl}_{\widehat{\mathcal{B}_{\Delta_S}},\mathfrak{a}^t}} \\ &\supseteq \bigcap_N \operatorname{Ann}_{\widehat{R}}0_N^{\operatorname{cl}_{\widehat{\mathcal{B}_{\Delta_S}},\mathfrak{a}^t}}\\ &= \bigcap_N (\operatorname{Ann}_{\widehat{S}}0_N^{\operatorname{cl}_{\widehat{\mathcal{B}_{\Delta_S}},\mathfrak{a}^t}}\cap \widehat{R}) \\ &= (\operatorname{Ann}_{\widehat{S}}0_{E_S}^{\operatorname{cl}_{\widehat{\mathcal{B}_{\Delta_S}},\mathfrak{a}^t}})\cap \widehat{R} \\ &= (\operatorname{Ann}_{\widehat{S}}\bigcap_{n\in\mathbb{N}}\bigcap_{g\in\mathfrak{a}^{\lceil nt \rceil}} 0_{E_S}^{\operatorname{cl}_{\widehat{\mathcal{B}_{\Delta_S}},g^{\frac{1}{n}}}})\cap \widehat{R} \\ &= (\operatorname{Ann}_{\widehat{S}}\operatorname{Ann}_{E_S}\sum_{n\in\mathbb{N}}\sum_{g\in \mathfrak{a}^{\lceil nt \rceil}}\mathcal{J}(\widehat{S},\widehat{\Delta_S},g^{\frac{1}{n}}))\cap \widehat{R} \\ &= \mathcal{J}(\widehat{S},\widehat{\Delta_S},(\mathfrak{a} \widehat{S})^t))\cap \widehat{R}, \end{align*} $$
where M runs through all
![]() $\widehat {R}$
-modules, N runs through all
$\widehat {R}$
-modules, N runs through all
![]() $\widehat {S}$
-modules, and
$\widehat {S}$
-modules, and
![]() $E_S$
is the injective hull of the residue field of S.
$E_S$
is the injective hull of the residue field of S.
As a corollary, we have a generalization of [Reference Yamaguchi31, Cor. 5.30] to the case that
![]() $\mathfrak {a}$
is not necessarily a principal ideal.
$\mathfrak {a}$
is not necessarily a principal ideal.
Corollary 7.11. Let
![]() $R\hookrightarrow S$
be a pure local homomorphism of normal local domains essentially of finite type over
$R\hookrightarrow S$
be a pure local homomorphism of normal local domains essentially of finite type over
![]() $\mathbb {C}$
. Suppose that R is
$\mathbb {C}$
. Suppose that R is
![]() $\mathbb {Q}$
-Gorenstein. Fix effective canonical divisors
$\mathbb {Q}$
-Gorenstein. Fix effective canonical divisors
![]() $K_R$
and
$K_R$
and
![]() $K_S$
on
$K_S$
on
![]() $\operatorname {Spec} R$
and
$\operatorname {Spec} R$
and
![]() $\operatorname {Spec} S$
, respectively. Let
$\operatorname {Spec} S$
, respectively. Let
![]() $\Delta _S$
be an effective
$\Delta _S$
be an effective
![]() $\mathbb {Q}$
-Weil divisor on
$\mathbb {Q}$
-Weil divisor on
![]() $\operatorname {Spec} S$
such that
$\operatorname {Spec} S$
such that
![]() $K_S+\Delta _S$
is
$K_S+\Delta _S$
is
![]() $\mathbb {Q}$
-Cartier. Let
$\mathbb {Q}$
-Cartier. Let
![]() $\mathfrak {a}\subseteq R$
be a nonzero ideal and
$\mathfrak {a}\subseteq R$
be a nonzero ideal and
![]() $t>0$
a positive rational number. Then we have
$t>0$
a positive rational number. Then we have
Proof. Let
![]() $R'$
be the integral closure of
$R'$
be the integral closure of
![]() $R[f^{1/r}]$
in
$R[f^{1/r}]$
in
![]() $R^+$
. Then the result follows from Theorem 7.10.
$R^+$
. Then the result follows from Theorem 7.10.
8
 $\mathcal {B}$
-regularity
$\mathcal {B}$
-regularity
As another application of the main theorem, we will give a partial answer to [Reference Schoutens24, Rem. 3.10]. For this, we will review the definition of
![]() $\mathcal {B}$
-regularity.
$\mathcal {B}$
-regularity.
Definition 8.1 [Reference Schoutens23, Def. 4.3].
Let R be a normal
![]() $\mathbb {Q}$
-Gorenstein local domain essentially of finite type over
$\mathbb {Q}$
-Gorenstein local domain essentially of finite type over
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
-
(1) R is said to be weakly
 $\mathcal {B}$
-regular if
$\mathcal {B}$
-regular if
 $R\to \mathcal {B}(R)$
is cyclically pure.
$R\to \mathcal {B}(R)$
is cyclically pure. -
(2) R is said to be
 $\mathcal {B}$
-regular if every localization of R at a prime ideal is weakly
$\mathcal {B}$
-regular if every localization of R at a prime ideal is weakly
 $\mathcal {B}$
-regular.
$\mathcal {B}$
-regular.
Theorem 8.2. Let R be a normal
![]() $\mathbb {Q}$
-Gorenstein local domain. Then the following are equivalent:
$\mathbb {Q}$
-Gorenstein local domain. Then the following are equivalent:
-
(1) R has log-terminal singularities.
-
(2) R is ultra-F-regular.
-
(3) R is weakly generically F-regular.
-
(4) R is generically F-regular.
-
(5) R is weakly
 $\mathcal {B}$
-regular.
$\mathcal {B}$
-regular. -
(6) R is
 $\mathcal {B}$
-regular.
$\mathcal {B}$
-regular. -
(7)
 $\widehat {R}$
is
$\widehat {R}$
is
 $\text {BCM}_{\widehat {\mathcal {B}(R)}}$
-regular.
$\text {BCM}_{\widehat {\mathcal {B}(R)}}$
-regular.
Proof. The equivalence of (1) and (2) follows from Proposition 3.54 and the equivalence of (1) and (7) follows from Theorem 6.4. Since, if R has log-terminal singularities, then every localization of R at a prime ideal is log-terminal, it is enough to show the equivalence of (1), (3), and (5). (1) is equivalent to (3) by [Reference Yamaguchi31, Th. 5.24 and Proof of Th. 5.25]. Lastly, we will show the equivalence of (5) and (7). Let E be the injective hull of the residue field of R. By Proposition 7.4, we have
![]() $0_E^{\operatorname {cl}_{\mathcal {B}(R)\otimes _R\widehat {R}}}=0_E^{\mathcal {B}(R),K_R}$
. Hence,
$0_E^{\operatorname {cl}_{\mathcal {B}(R)\otimes _R\widehat {R}}}=0_E^{\mathcal {B}(R),K_R}$
. Hence,
![]() $E\to \mathcal {B}(R)\otimes _R E$
is injective if and only if
$E\to \mathcal {B}(R)\otimes _R E$
is injective if and only if
![]() $\widehat {R}$
is
$\widehat {R}$
is
![]() $\text {BCM}_{\widehat {\mathcal {B}(R)}}$
-regular.
$\text {BCM}_{\widehat {\mathcal {B}(R)}}$
-regular.
![]() $R\to \mathcal {B}(R)$
is pure if and only if
$R\to \mathcal {B}(R)$
is pure if and only if
![]() $E\to \mathcal {B}(R)\otimes _R E$
is injective by [Reference Hochster and Huneke15, Lem. 2.1(e)].
$E\to \mathcal {B}(R)\otimes _R E$
is injective by [Reference Hochster and Huneke15, Lem. 2.1(e)].
![]() $R\to \mathcal {B}(R)$
is pure if and only if
$R\to \mathcal {B}(R)$
is pure if and only if
![]() $R\to \mathcal {B}(R)$
is cyclically pure by [Reference Hochster12, Th. 1.7]. Therefore, (5) is equivalent to (7).
$R\to \mathcal {B}(R)$
is cyclically pure by [Reference Hochster12, Th. 1.7]. Therefore, (5) is equivalent to (7).
Remark 8.3. For the equivalence of (5) and (7) (see [Reference Ma and Schwede19, Prop. 6.14]).
9 Further questions and remarks
In this section, we will consider whether R is BCM-rational if R has rational singularities. The next question is a variant of [Reference Dietz and Rebecca7, Quest. 2.7].
Question 1. Let R be a local domain essentially of finite type over
![]() $\mathbb {C}$
, and let B be a BCM R-algebra. If S is finitely generated R-algebra such that the following diagram commutes:
$\mathbb {C}$
, and let B be a BCM R-algebra. If S is finitely generated R-algebra such that the following diagram commutes:

then does there exist a BCM
![]() $R_p$
-algebra for almost all p which fits into the following commutative diagram:
$R_p$
-algebra for almost all p which fits into the following commutative diagram:

where
![]() $S_p$
is an R-approximation of S?
$S_p$
is an R-approximation of S?
Proposition 9.1 (Cf. [Reference Ma and Schwede19, Conj. 3.9]).
Let R be a normal local domain essentially of finite type over
![]() $\mathbb {C}$
of dimension d. Suppose that R has rational singularities. If Question 1 has an affirmative answer, then R is BCM-rational.
$\mathbb {C}$
of dimension d. Suppose that R has rational singularities. If Question 1 has an affirmative answer, then R is BCM-rational.
Proof. Let B be a BCM
![]() $R^+$
-algebra. Suppose that
$R^+$
-algebra. Suppose that
![]() $\eta \in \operatorname {Ker} (H_m^d(R)\to H_{\mathfrak {m}}^d(B))$
. Then there exists a finitely generated R-subalgebra of B such that the image of
$\eta \in \operatorname {Ker} (H_m^d(R)\to H_{\mathfrak {m}}^d(B))$
. Then there exists a finitely generated R-subalgebra of B such that the image of
![]() $\eta $
in
$\eta $
in
![]() $H_m^d(S)$
is zero. If Question 1 has an affirmative answer, we can take
$H_m^d(S)$
is zero. If Question 1 has an affirmative answer, we can take
![]() $S_p$
and
$S_p$
and
![]() $B_p$
as in Question 1. Then we have a commutative diagram
$B_p$
as in Question 1. Then we have a commutative diagram

By the proof of Proposition 4.8,
![]() $\operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}_p}^d(R_p)\to \operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}_p}^d(S_p)$
is injective. Therefore, the image of
$\operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}_p}^d(R_p)\to \operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}_p}^d(S_p)$
is injective. Therefore, the image of
![]() $\eta $
in
$\eta $
in
![]() $\operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}_p}^d(R_p)$
is zero. Suppose that
$\operatorname *{\mathrm {ulim}}_p H_{\mathfrak {m}_p}^d(R_p)$
is zero. Suppose that
![]() $\eta =\lbrack \frac {y}{x^t}\rbrack $
, where
$\eta =\lbrack \frac {y}{x^t}\rbrack $
, where
![]() $y\in R$
,
$y\in R$
,
![]() $t\in \mathbb {N}$
and x is the product of a system of parameters
$t\in \mathbb {N}$
and x is the product of a system of parameters
![]() $x_1,\dots ,x_d$
of R. Since
$x_1,\dots ,x_d$
of R. Since
![]() $R_p$
is Cohen–Macaulay for almost all p,
$R_p$
is Cohen–Macaulay for almost all p,
![]() $y_p\in (x_{1p}^t,\dots , x_{dp}^t)$
for almost all p. Hence,
$y_p\in (x_{1p}^t,\dots , x_{dp}^t)$
for almost all p. Hence,
![]() $y\in (x_1^t,\dots ,x_d^t)$
and
$y\in (x_1^t,\dots ,x_d^t)$
and
![]() $\eta =0$
in
$\eta =0$
in
![]() $H_{\mathfrak {m}}^d(R)$
. Thus,
$H_{\mathfrak {m}}^d(R)$
. Thus,
![]() $H_{\mathfrak {m}}^d(R)\to H_{\mathfrak {m}}^d(B)$
is injective.
$H_{\mathfrak {m}}^d(R)\to H_{\mathfrak {m}}^d(B)$
is injective.
The next result follows from a similar argument.
Proposition 9.2. Let R be a normal local domain essentially of finite type over
![]() $\mathbb {C}$
of dimension d. Fix an effective canonical divisor
$\mathbb {C}$
of dimension d. Fix an effective canonical divisor
![]() $K_R$
on
$K_R$
on
![]() $\operatorname {Spec} R$
. Let
$\operatorname {Spec} R$
. Let
![]() $\Delta \geqslant 0$
be an effective
$\Delta \geqslant 0$
be an effective
![]() $\mathbb {Q}$
-Weil divisor on
$\mathbb {Q}$
-Weil divisor on
![]() $\operatorname {Spec} R$
such that
$\operatorname {Spec} R$
such that
![]() $K_R+\Delta $
is
$K_R+\Delta $
is
![]() $\mathbb {Q}$
-Cartier. Suppose that C is a BCM
$\mathbb {Q}$
-Cartier. Suppose that C is a BCM
![]() $R^+$
-algebra. If Question 1 has an affirmative answer, then we have
$R^+$
-algebra. If Question 1 has an affirmative answer, then we have
Definition 9.3 (Cf. [Reference Ma and Schwede19, Def. 6.9]).
Let R be a normal local domain essentially of finite type over
![]() $\mathbb {C}$
. Fix an effective canonical divisor
$\mathbb {C}$
. Fix an effective canonical divisor
![]() $K_R$
on
$K_R$
on
![]() $\operatorname {Spec} R$
. Let
$\operatorname {Spec} R$
. Let
![]() $\Delta \geqslant 0$
be a
$\Delta \geqslant 0$
be a
![]() $\mathbb {Q}$
-Weil divisor on
$\mathbb {Q}$
-Weil divisor on
![]() $\operatorname {Spec} R$
such that
$\operatorname {Spec} R$
such that
![]() $K_R+\Delta $
is
$K_R+\Delta $
is
![]() $\mathbb {Q}$
-Cartier. Suppose that
$\mathbb {Q}$
-Cartier. Suppose that
![]() $n(K_R+\Delta )=\operatorname {div}(f)$
for
$n(K_R+\Delta )=\operatorname {div}(f)$
for
![]() $f\in R^\circ $
,
$f\in R^\circ $
,
![]() $n\in \mathbb {N}$
. We define
$n\in \mathbb {N}$
. We define
 $$ \begin{align*} 0_{H_{\mathfrak{m}}^d(R)}^{\mathscr{B},K_R+\Delta}:=\{\eta\in H_{\mathfrak{m}}^d(R)| \quad &\exists C \text{ BCM } R^+ \text{-algebra}\\ &{\text{such that }f^{\frac{1}{n}}\eta =0 \text{ in } H_{\mathfrak{m}}^d(C)\}.} \end{align*} $$
$$ \begin{align*} 0_{H_{\mathfrak{m}}^d(R)}^{\mathscr{B},K_R+\Delta}:=\{\eta\in H_{\mathfrak{m}}^d(R)| \quad &\exists C \text{ BCM } R^+ \text{-algebra}\\ &{\text{such that }f^{\frac{1}{n}}\eta =0 \text{ in } H_{\mathfrak{m}}^d(C)\}.} \end{align*} $$
We define the BCM test ideal
![]() $\tau _{\mathscr {B}}(R,\Delta )$
of
$\tau _{\mathscr {B}}(R,\Delta )$
of
![]() $(\widehat {R},\widehat {\Delta })$
by
$(\widehat {R},\widehat {\Delta })$
by
Corollary 9.4 (Cf. [Reference Ma and Schwede19, Th. 6.21]).
In the setting of the above proposition, if Question 1 has an affirmative answer, then we have
Acknowledgments
The author wishes to express his gratitude to his supervisor Professor Shunsuke Takagi for his valuable advice and suggestions. The author would also like to thank Hans Schoutens for helpful comments on this paper. The author would also like to thank the referee who provided useful comments and suggestions.