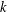 $k$TH YAU NUMBER OF ISOLATED HYPERSURFACE SINGULARITIES AND AN INEQUALITY CONJECTURE
$k$TH YAU NUMBER OF ISOLATED HYPERSURFACE SINGULARITIES AND AN INEQUALITY CONJECTURE
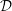 ${\mathcal{D}}$-modules related to the
${\mathcal{D}}$-modules related to the 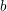 $b$-function and Hamiltonian flow
$b$-function and Hamiltonian flow
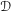 ${\mathcal{D}}$-MODULES
${\mathcal{D}}$-MODULES