Research Article
The mean value theorem and analytic functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 289-295
-
- Article
-
- You have access
- Export citation
Finite automorphism groups of laminated near-rings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 297-306
-
- Article
-
- You have access
- Export citation
Cauchy problems for second order hyperbolic differential equations with constant coefficients
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 307-311
-
- Article
-
- You have access
- Export citation
An algebraic filtration of H*(MO;ℤ2)
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 313-317
-
- Article
-
- You have access
- Export citation
Some bifurcation problems in cholesteric liquid crystal theory
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 319-332
-
- Article
-
- You have access
- Export citation
A stochastic proof of an extension of a theorem of Rado
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 333-336
-
- Article
-
- You have access
- Export citation
On Brown–McCoy radical classes in categories
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 337-341
-
- Article
-
- You have access
- Export citation
Isomorphisms between radical weighted convolution algebras
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 343-351
-
- Article
-
- You have access
- Export citation
On compact action in JB-algebras
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 353-360
-
- Article
-
- You have access
- Export citation
Upper faithful d.g. near-rings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 361-370
-
- Article
-
- You have access
- Export citation
Semigroups under a sandwich operation
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 371-382
-
- Article
-
- You have access
- Export citation
Metric and algebraic perturbations of function algebras
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 383-391
-
- Article
-
- You have access
- Export citation
Obituary
Geoffrey Timms, O.B.E., Ph.D., F.R.S.E.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 393-394
-
- Article
-
- You have access
- Export citation
Book Reviews
J. W. S. Cassels and a Committee appointed by the London Mathematical Society (eds.) The collected papers of J. E. Littlewood, 2 volumes (Oxford University Press, 1982), xxxviii + 1675 pp. £120 the set.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 395-396
-
- Article
-
- You have access
- Export citation
L. K. Hua Introduction to number theory (translated by P. Shiu) (Springer-Verlag, Berlin-Heidelberg-New York, 1982), xviii + 572 pp. DM 96.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 396
-
- Article
-
- You have access
- Export citation
T. A. Whitelaw, An Introduction to Linear Algrbra, (Blackie, 1983), ix + 241 pp., £7·95 (paper covers).
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 396-397
-
- Article
-
- You have access
- Export citation
R. D. Richtmyer, Principles of advanced mathematical physics, Volume II (Springer-Verlag, 1981), xii + 322 pp., DM72.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 397-398
-
- Article
-
- You have access
- Export citation
L. W. Beineke and R. J. Wilson (eds.), Selected topics in graph theory (Academic Press, 1979), pp. 451, £34·40.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 398
-
- Article
-
- You have access
- Export citation
P. Billingsley, Probability and measure (Wiley, 1979), pp. 532, £28·95.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 398-399
-
- Article
-
- You have access
- Export citation
C.-H. Sah, Hilbert's third problem: scissors congruence (Pitman, 1979), pp. 240, £9·95.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 399-400
-
- Article
-
- You have access
- Export citation



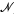
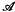
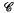 of φ at
of φ at