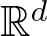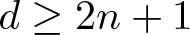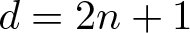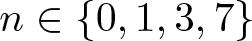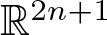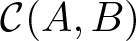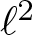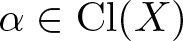Research Article
Unit sphere fibrations in Euclidean space
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2024, pp. 287-298
-
- Article
- Export citation
The Schwarzian norm estimates for Janowski convex functions
- Part of:
-
- Published online by Cambridge University Press:
- 12 February 2024, pp. 299-315
-
- Article
- Export citation
A boundary maximum principle for stationary pairs of varifolds with fixed contact angle
- Part of:
-
- Published online by Cambridge University Press:
- 08 March 2024, pp. 316-335
-
- Article
- Export citation
Structure of generalized Yamabe solitons and its applications
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2024, pp. 336-348
-
- Article
- Export citation
Normalized solutions to the quasilinear Schrödinger equations with combined nonlinearities
- Part of:
-
- Published online by Cambridge University Press:
- 12 April 2024, pp. 349-387
-
- Article
- Export citation
Canonical decompositions and algorithmic recognition of spatial graphs
- Part of:
-
- Published online by Cambridge University Press:
- 14 March 2024, pp. 388-430
-
- Article
- Export citation
L2 to Lp bounds for spectral projectors on the Euclidean two-dimensional torus
- Part of:
-
- Published online by Cambridge University Press:
- 15 March 2024, pp. 431-459
-
- Article
- Export citation
On the fractional powers of a Schrödinger operator with a Hardy-type potential
- Part of:
-
- Published online by Cambridge University Press:
- 12 April 2024, pp. 460-507
-
- Article
- Export citation
Proof of some conjectural congruences involving Apéry and Apéry-like numbers
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2024, pp. 508-527
-
- Article
- Export citation
Discriminant and integral basis of number fields defined by exponential Taylor polynomials
- Part of:
-
- Published online by Cambridge University Press:
- 08 April 2024, pp. 528-541
-
- Article
- Export citation
Unbounded Sturm attractors for quasilinear parabolic equations
- Part of:
-
- Published online by Cambridge University Press:
- 08 March 2024, pp. 542-565
-
- Article
- Export citation
On the structure of some one-generator braces
- Part of:
-
- Published online by Cambridge University Press:
- 20 March 2024, pp. 566-576
-
- Article
- Export citation
On the moduli of hypersurfaces in toric orbifolds
- Part of:
-
- Published online by Cambridge University Press:
- 14 March 2024, pp. 577-616
-
- Article
- Export citation
Minimal monoids generating varieties with complex subvariety lattices
- Part of:
-
- Published online by Cambridge University Press:
- 22 March 2024, pp. 617-642
-
- Article
- Export citation
A remark on a conjecture on the symmetric Gaussian problem
- Part of:
-
- Published online by Cambridge University Press:
- 15 April 2024, pp. 643-661
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PEM series 2 volume 67 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 16 May 2024, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
PEM series 2 volume 67 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 16 May 2024, pp. b1-b2
-
- Article
-
- You have access
- Export citation