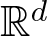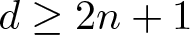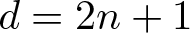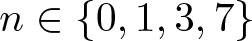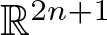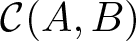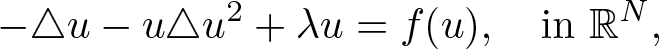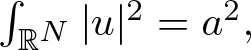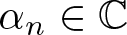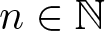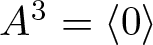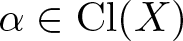Most read
This page lists the top ten most read articles for this journal based on the number of full text views and downloads recorded on Cambridge Core over the last 90 days. This list is updated on a daily basis.
Unit sphere fibrations in Euclidean space
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2024, pp. 287-298
-
- Article
- Export citation
The Schwarzian norm estimates for Janowski convex functions
- Part of:
-
- Published online by Cambridge University Press:
- 12 February 2024, pp. 299-315
-
- Article
- Export citation
A boundary maximum principle for stationary pairs of varifolds with fixed contact angle
- Part of:
-
- Published online by Cambridge University Press:
- 08 March 2024, pp. 316-335
-
- Article
- Export citation
Structure of generalized Yamabe solitons and its applications
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2024, pp. 336-348
-
- Article
- Export citation
Normalized solutions to the quasilinear Schrödinger equations with combined nonlinearities
- Part of:
-
- Published online by Cambridge University Press:
- 12 April 2024, pp. 349-387
-
- Article
- Export citation
Canonical decompositions and algorithmic recognition of spatial graphs
- Part of:
-
- Published online by Cambridge University Press:
- 14 March 2024, pp. 388-430
-
- Article
- Export citation
L2 to Lp bounds for spectral projectors on the Euclidean two-dimensional torus
- Part of:
-
- Published online by Cambridge University Press:
- 15 March 2024, pp. 431-459
-
- Article
-
- You have access
- HTML
- Export citation
On the fractional powers of a Schrödinger operator with a Hardy-type potential
- Part of:
-
- Published online by Cambridge University Press:
- 12 April 2024, pp. 460-507
-
- Article
-
- You have access
- HTML
- Export citation
Proof of some conjectural congruences involving Apéry and Apéry-like numbers
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2024, pp. 508-527
-
- Article
- Export citation
Discriminant and integral basis of number fields defined by exponential Taylor polynomials
- Part of:
-
- Published online by Cambridge University Press:
- 08 April 2024, pp. 528-541
-
- Article
- Export citation
Unbounded Sturm attractors for quasilinear parabolic equations
- Part of:
-
- Published online by Cambridge University Press:
- 08 March 2024, pp. 542-565
-
- Article
- Export citation
On the structure of some one-generator braces
- Part of:
-
- Published online by Cambridge University Press:
- 20 March 2024, pp. 566-576
-
- Article
- Export citation
On the moduli of hypersurfaces in toric orbifolds
- Part of:
-
- Published online by Cambridge University Press:
- 14 March 2024, pp. 577-616
-
- Article
- Export citation
Minimal monoids generating varieties with complex subvariety lattices
- Part of:
-
- Published online by Cambridge University Press:
- 22 March 2024, pp. 617-642
-
- Article
- Export citation
A remark on a conjecture on the symmetric Gaussian problem
- Part of:
-
- Published online by Cambridge University Press:
- 15 April 2024, pp. 643-661
-
- Article
- Export citation
PEM series 2 volume 67 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 16 May 2024, pp. f1-f2
-
- Article
-
- You have access
- Export citation
PEM series 2 volume 67 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 16 May 2024, pp. b1-b2
-
- Article
-
- You have access
- Export citation