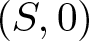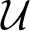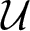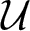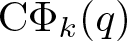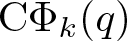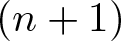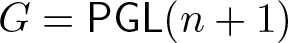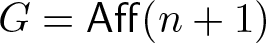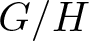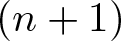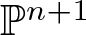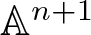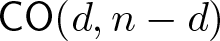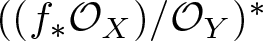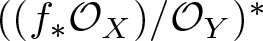FirstView articles
Research Article
Solid bases and functorial constructions for (p-)Banach spaces of analytic functions
- Part of:
-
- Published online by Cambridge University Press:
- 09 September 2024, pp. 1-32
-
- Article
- Export citation
Equisingularity in pencils of curves on germs of reduced complex surfaces
- Part of:
-
- Published online by Cambridge University Press:
- 04 June 2024, pp. 1-23
-
- Article
- Export citation
A classification of automorphic Lie algebras on complex tori
- Part of:
-
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Coactions and skew products for topological quivers
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2024, pp. 1-26
-
- Article
- Export citation
Characterization of continuous homomorphisms on entire slice monogenic functions
- Part of:
-
- Published online by Cambridge University Press:
- 17 May 2024, pp. 1-29
-
- Article
- Export citation
On the smoothness of slowly varying functions
- Part of:
-
- Published online by Cambridge University Press:
- 16 May 2024, pp. 1-16
-
- Article
- Export citation
A variational principle of amenable random metric mean dimensions
- Part of:
-
- Published online by Cambridge University Press:
- 16 May 2024, pp. 1-24
-
- Article
- Export citation
On the convexity of the quaternionic essential numerical range
- Part of:
-
- Published online by Cambridge University Press:
- 15 May 2024, pp. 1-14
-
- Article
- Export citation
Powers of commutators in linear algebraic groups
- Part of:
-
- Published online by Cambridge University Press:
- 14 May 2024, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Growth of hypercyclic functions: a continuous path between
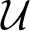 $\mathcal{U}$-frequent hypercyclicity and hypercyclicity
$\mathcal{U}$-frequent hypercyclicity and hypercyclicity
- Part of:
-
- Published online by Cambridge University Press:
- 08 May 2024, pp. 1-36
-
- Article
- Export citation
Some congruences for 12-coloured generalized Frobenius partitions
- Part of:
-
- Published online by Cambridge University Press:
- 02 May 2024, pp. 1-16
-
- Article
- Export citation
Inhomogeneous Poisson processes in the disk and interpolation
- Part of:
-
- Published online by Cambridge University Press:
- 30 April 2024, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weak amenability for dual Banach algebras
- Part of:
-
- Published online by Cambridge University Press:
- 29 April 2024, pp. 1-9
-
- Article
- Export citation
Projectively and affinely invariant PDEs on hypersurfaces
- Part of:
-
- Published online by Cambridge University Press:
- 25 April 2024, pp. 1-26
-
- Article
- Export citation
Annihilators and decompositions of singularity categories
- Part of:
-
- Published online by Cambridge University Press:
- 23 April 2024, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Propagation of anisotropic Gabor wave front sets
- Part of:
- Partial differential equations
- Miscellaneous topics - Partial differential equations
- Integral, integro-differential, and pseudodifferential operators
- Partial differential equations on manifolds; differential operators
- Distributions, generalized functions, distribution spaces
- General quantum mechanics and problems of quantization
- Groups and semigroups of linear operators, their generalizations and applications
-
- Published online by Cambridge University Press:
- 22 April 2024, pp. 1-25
-
- Article
- Export citation
Pushforward of structure sheaf and virtual global generation
- Part of:
-
- Published online by Cambridge University Press:
- 18 April 2024, pp. 1-11
-
- Article
- Export citation